Y x nađite period funkcije. Periodičnost funkcija y = sin x, y = cos x - Hipermarket znanja
Argument x, tada se naziva periodičnim ako postoji broj T takav da je za bilo koji x F(x + T) = F(x). Taj se broj T naziva periodom funkcije.
Može postojati nekoliko razdoblja. Na primjer, funkcija F = const uzima istu vrijednost za bilo koju vrijednost argumenta, pa se stoga svaki broj može smatrati njezinom periodom.
Obično vas zanima najmanji period funkcije različit od nule. Radi sažetosti, jednostavno se naziva razdoblje.
Klasičan primjer periodičkih funkcija je trigonometrijski: sinus, kosinus i tangens. Njihov period je isti i jednak 2π, odnosno sin(x) = sin(x + 2π) = sin(x + 4π) i tako dalje. No, naravno, trigonometrijske funkcije nisu jedine periodične.
Za jednostavne, osnovne funkcije, jedini način da se utvrdi jesu li periodične ili neperiodične je proračun. Ali za složene funkcije već postoji nekoliko jednostavnih pravila.
Ako je F(x) s periodom T, a za nju je definirana derivacija, tada je ta derivacija f(x) = F′(x) također periodična funkcija s periodom T. Uostalom, vrijednost derivacije u točki x je jednak tangensu tangentnog kuta grafa njegove antiderivacije u ovoj točki na x-os, a budući da se antiderivacija periodički ponavlja, derivacija se također mora ponavljati. Na primjer, derivacija funkcije sin(x) jednaka je cos(x) i periodična je. Uzimanje derivata cos(x) daje vam –sin(x). Frekvencija ostaje nepromijenjena.
Međutim, suprotno nije uvijek točno. Dakle, funkcija f(x) = const je periodična, ali njezina antiderivacija F(x) = const*x + C nije.
Ako je F(x) periodična funkcija s periodom T, tada je G(x) = a*F(kx + b), gdje su a, b i k konstante, a k nije jednako nuli - također periodična funkcija , a period mu je T/k. Na primjer, sin(2x) je periodična funkcija, a njezin period je π. To se može vizualno prikazati na sljedeći način: množenjem x s nekim brojem, čini se da komprimirate graf funkcije vodoravno točno toliko puta
Ako su F1(x) i F2(x) periodičke funkcije, a njihove su periode jednake T1 odnosno T2, tada zbroj tih funkcija također može biti periodičan. Međutim, njegovo razdoblje neće biti jednostavan zbroj razdoblja T1 i T2. Ako je rezultat dijeljenja T1/T2 racionalan broj, tada je zbroj funkcija periodičan, a njegov period jednak najmanjem zajedničkom višekratniku (LCM) perioda T1 i T2. Na primjer, ako je period prve funkcije 12, a period druge 15, tada će period njihovog zbroja biti jednak LCM (12, 15) = 60.
Vizualno se to može prikazati na sljedeći način: funkcije dolaze s različitim "širinama koraka", ali ako je omjer njihovih širina racionalan, tada će se prije ili kasnije (točnije, upravo kroz LCM koraka) ponovno izjednačiti, i njihov će zbroj započeti novo razdoblje.
Međutim, ako je omjer perioda iracionalan, tada ukupna funkcija uopće neće biti periodična. Na primjer, neka je F1(x) = x mod 2 (ostatak kada se x podijeli s 2), i F2(x) = sin(x). T1 će ovdje biti jednak 2, a T2 će biti jednak 2π. Omjer perioda jednak je π – iracionalnom broju. Dakle, funkcija sin(x) + x mod 2 nije periodična.
Video lekcija "Periodičnost funkcija y = sin x, y = cos x" otkriva pojam periodičnosti funkcije, razmatra opis primjera rješavanja problema u kojima se koristi pojam periodičnosti funkcije. Ova video lekcija je vizualna pomoć za objašnjavanje teme učenicima. Također, ovaj priručnik može postati samostalan dio nastave, oslobađajući nastavnika za individualni rad s učenicima.
Vidljivost u predstavljanju ove teme je vrlo važna. Da bi se prikazalo ponašanje funkcije, njezino crtanje, mora se vizualizirati. Nije uvijek moguće napraviti konstrukcije pomoću ploče i krede tako da budu razumljive svim učenicima. U video tutorialu je moguće dijelove crteža istaknuti bojom prilikom konstruiranja te napraviti transformacije pomoću animacije. Tako konstrukcije postaju razumljivije većini učenika. Također, značajke video lekcija doprinose boljem pamćenju gradiva.
Demonstracija počinje uvođenjem teme lekcije, kao i podsjećanjem učenika na gradivo naučeno u prethodnim lekcijama. Posebno je sažet popis svojstava koja su identificirana u funkcijama y = sin x, kao i y = cos x. Među svojstvima funkcija koje se razmatraju, domena definicije, raspon vrijednosti, paritet (neparnost), druge značajke su zabilježene - ograničenost, monotonost, kontinuitet, točke najmanje (najveće) vrijednosti. Obavještavamo učenike da se u ovoj lekciji proučava još jedno svojstvo funkcije - periodičnost.
Prikazana je definicija periodičke funkcije y=f(x), gdje je xϵX, u kojoj je uvjet f(x-T)= f(x)= f(x+T) za neki T≠0. Inače se broj T naziva periodom funkcije.
Za razmatrane funkcije sinusa i kosinusa ispunjavanje uvjeta provjerava se pomoću formula redukcije. Očito je da oblik identiteta sin(x-2π)=sinx=sin(x+2π) odgovara obliku izraza koji definira uvjet periodičnosti funkcije. Ista jednakost može se primijetiti za kosinus cos (x-2π)= cos x= cos (x+2π). To znači da su te trigonometrijske funkcije periodične.
Dalje je navedeno kako svojstvo periodičnosti pomaže u izgradnji grafova periodičnih funkcija. Razmatra se funkcija y = sin x. Na ekranu se konstruira koordinatna ravnina na kojoj su apscise od -6π do 8π označene s korakom π. Dio sinusnog grafikona iscrtan je na ravnini, predstavljen jednim valom na segmentu. Slika pokazuje kako se graf funkcije formira preko cijele definicijske domene pomicanjem konstruiranog fragmenta, što rezultira dugom sinusoidom.
Graf funkcije y = cos x konstruiran je pomoću svojstva njezine periodičnosti. Da biste to učinili, na slici je konstruirana koordinatna ravnina na kojoj je prikazan fragment grafikona. Napominje se da je takav fragment obično konstruiran na segmentu [-π/2;3π/2]. Slično kao kod grafa sinusne funkcije, konstrukcija kosinusnog grafa se izvodi pomakom fragmenta. Kao rezultat konstrukcije nastaje duga sinusoida.
Izrada grafikona periodične funkcije ima značajke koje se mogu koristiti. Stoga su dani u općenitom obliku. Napominje se da se za konstruiranje grafa takve funkcije prvo konstruira grana grafa na određenom intervalu duljine T. Zatim je potrebno konstruiranu granu pomaknuti desno i lijevo za T, 2T, 3T, itd. Ujedno se ističe još jedna značajka perioda - za svaki cijeli broj k≠0, broj kT je ujedno i period funkcije. Međutim, T se naziva glavni period, jer je najmanji od svih. Za trigonometrijske funkcije sinus i kosinus osnovni period je 2π. Međutim, periode su također 4π, 6π, itd.
Zatim se predlaže razmatranje pronalaženja glavnog perioda funkcije y = cos 5x. Rješenje počinje s pretpostavkom da je T period funkcije. To znači da mora biti ispunjen uvjet f(x-T)= f(x)= f(x+T). U ovom identitetu, f(x)= cos 5x, i f(x+T)=cos 5(x+T)= cos (5x+5T). U ovom slučaju, cos (5x+5T)= cos 5x, dakle 5T=2πn. Sada možete pronaći T=2π/5. Problem je riješen.
U drugom zadatku treba pronaći glavnu periodu funkcije y=sin(2x/7). Pretpostavlja se da je glavni period funkcije T za danu funkciju f(x)= sin(2x/7), a nakon perioda f(x+T)=sin(2x/7)(x+T) = sin(2x/7 +(2/7)T). nakon redukcije dobivamo (2/7)T=2πn. Međutim, treba pronaći glavni period, pa uzimamo najmanju vrijednost (2/7)T=2π, iz koje nalazimo T=7π. Problem je riješen.
Na kraju demonstracije rezultati primjera sumirani su u obliku pravila za određivanje osnovnog perioda funkcije. Primijećeno je da su za funkcije y=sinkx i y=coskx glavni periodi 2π/k.
Video lekcija "Periodičnost funkcija y = sin x, y = cos x" može se koristiti u tradicionalnoj lekciji matematike kako bi se povećala učinkovitost lekcije. Također se preporučuje da ovaj materijal koristi nastavnik koji pruža učenje na daljinu kako bi se povećala jasnoća objašnjenja. Video se može preporučiti učeniku s poteškoćama kako bi produbio svoje razumijevanje teme.
DEKODIRANJE TEKSTA:
“Periodičnost funkcija y = cos x, y = sin x.”
Za konstruiranje grafova funkcija y = sin x i y = cos x korištena su svojstva funkcija:
1 područje definicije,
2 vrijednosno područje,
3 par ili nepar,
4 monotonija,
5 ograničenje,
6 kontinuitet,
7 najveća i najniža vrijednost.
Danas ćemo proučavati još jedno svojstvo: periodičnost funkcije.
DEFINICIJA. Funkcija y = f (x), gdje je x ϵ X (grčki je jednak ef od x, gdje x pripada skupu x), naziva se periodičkom ako postoji broj T različit od nule takav da za bilo koji x iz za skup X vrijedi dvostruka jednakost: f (x - T)= f (x) = f (x + T)(eff iz x minus te jednako je ef iz x i jednako ef iz x plus te). Broj T koji zadovoljava ovu dvostruku jednakost naziva se periodom funkcije
A budući da su sinus i kosinus definirani na cijelom brojevnom pravcu i za bilo koji x zadovoljene su jednakosti sin(x - 2π)= sin x= sin(x+ 2π) (sinus od x minus dva pi jednako je sinusu od x i jednako na sinus od x plus dva pi ) I
cos (x- 2π)= cos x = cos (x+ 2π) (kosinus od x minus dva pi jednak je kosinusu od x i jednak kosinusu od x plus dva pi), tada su sinus i kosinus periodične funkcije s period od 2π.
Periodičnost vam omogućuje brzu izgradnju grafikona funkcije. Doista, da bi se konstruirao graf funkcije y = sin x, dovoljno je nacrtati jedan val (najčešće na segmentu (od nula do dva pi), a zatim pomicanjem izgrađenog dijela grafa duž x -osi udesno i ulijevo za 2π, zatim za 4π i tako dalje da dobijete sinusni val.
(pokaži pomak udesno i ulijevo za 2π, 4π)
Slično za graf funkcije
y = cos x, ali jedan val najčešće gradimo na segmentu [; ] (od minus pi preko dva do tri pi kroz dva).
Rezimirajmo gore navedeno i izvucimo zaključak: da biste konstruirali graf periodične funkcije s periodom T, prvo trebate konstruirati granu (ili val, ili dio) grafa na bilo kojem intervalu duljine T (najčešće ovo je interval sa krajevima u točkama 0 i T ili - i (minus te za dva i te za dva), a zatim pomaknite ovu granu duž x(x) osi desno i lijevo za T, 2T, 3T, itd.
Očito, ako je funkcija periodična s periodom T, tada je za svaki cijeli broj k0 (ka nije jednak nuli) broj oblika kT (ka te) također period te funkcije. Obično pokušavaju izdvojiti najmanji pozitivni period, koji se naziva glavni period.
Kao period funkcija y = cos x, y = sin x, moglo bi se uzeti - 4π, 4π, - 6π, 6π, itd. (minus četiri pi, četiri pi, minus šest pi, šest pi, i tako dalje) . Ali broj 2π je glavni period obje funkcije.
Pogledajmo primjere.
PRIMJER 1. Odredite glavnu periodu funkcije y = cos5x (y je jednak kosinusu od pet x).
Riješenje. Neka je T glavni period funkcije y = cos5x. Stavimo
f (x) = cos5x, zatim f (x + T) = cos5(x + T) = cos (5x + 5T) (eff od x plus te je jednako kosinusu pet pomnoženom sa zbrojem x i te je jednak kosinusu zbroja pet x i pet te).
cos (5x + 5T) = cos5x. Stoga je 5T = 2πn (pet te jednako je dva pi en), ali prema uvjetu treba pronaći glavnu periodu, što znači 5T = 2π. Dobivamo T=
(period ove funkcije je dva pi podijeljeno s pet).
Odgovor: T=.
PRIMJER 2. Odredite glavnu periodu funkcije y = sin (y je jednak sinusu kvocijenta dva x sedam).
Riješenje. Neka je T glavni period funkcije y = sin. Stavimo
f (x) = sin, zatim f (x + T) = sin (x + T) = sin (x + T) (ef od x plus te jednako je sinusu umnoška dviju sedmina i zbroja x a te je jednako sinusu zbroja dviju sedmina x i dviju sedmina te).
Da bi broj T bio period funkcije, mora biti zadovoljen identitet
sin (x + T) = sin. Otuda je T= 2πn (dvije sedmine te jednake su dva pi en), ali prema uvjetu treba pronaći glavnu periodu, što znači T= 2π. Dobijamo T=7
(period ove funkcije je sedam pi).
Odgovor: T=7.
Rezimirajući rezultate dobivene u primjerima, možemo zaključiti: glavni period funkcija y = sin kx ili y = cos kx (y je jednak sinusu ka x ili y je jednak kosinusu ka x) jednak je (dva pi podijeljeno s ka).
Cilj: sažeti i sistematizirati znanja učenika o temi „Periodičnost funkcija“; razvijati vještine primjene svojstava periodičke funkcije, pronalaženja najmanjeg pozitivnog perioda funkcije, konstruiranja grafova periodičke funkcije; promicati interes za proučavanje matematike; njegovati zapažanje i točnost.
Oprema: računalo, multimedijski projektor, kartice sa zadacima, slajdovi, satovi, tablice s ukrasima, elementi narodnih zanata
“Matematika je ono što ljudi koriste kako bi kontrolirali prirodu i sebe.”
A.N. Kolmogorov
Tijekom nastave
I. Organizacijska faza.
Provjera spremnosti učenika za nastavni sat. Izvijestite o temi i ciljevima lekcije.
II. Provjera domaće zadaće.
Provjeravamo domaće zadaće pomoću uzoraka i razgovaramo o najtežim točkama.
III. Generalizacija i sistematizacija znanja.
1. Usmeni frontalni rad.
Teorijska pitanja.
1) Formirajte definiciju perioda funkcije
2) Navedite najmanji pozitivni period funkcija y=sin(x), y=cos(x)
3). Koji je najmanji pozitivni period funkcija y=tg(x), y=ctg(x)
4) Kružnicom dokažite ispravnost relacija:
y=sin(x) = sin(x+360º)
y=cos(x) = cos(x+360º)
y=tg(x) = tg(x+180º)
y=ctg(x) = ctg(x+180º)
tg(x+π n)=tgx, n € Z
ctg(x+π n)=ctgx, n € Z
sin(x+2π n)=sinx, n € Z
cos(x+2π n)=cosx, n € Z
5) Kako nacrtati periodičku funkciju?
Usmene vježbe.
1) Dokažite sljedeće relacije
a) sin(740º) = sin(20º)
b) cos(54º ) = cos(-1026º)
c) sin(-1000º) = sin(80º)
2. Dokažite da je kut od 540º jedna od perioda funkcije y= cos(2x)
3. Dokažite da je kut od 360º jedna od perioda funkcije y=tg(x)
4. Transformirajte ove izraze tako da kutovi uključeni u njih ne prelaze 90º u apsolutnoj vrijednosti.
a) tg375º
b)ctg530º
c) sin1268º
d)cos(-7363º)
5. Gdje ste naišli na riječi PERIOD, PERIODIČNOST?
Odgovori učenika: Razdoblje u glazbi je struktura u kojoj je prikazana više ili manje cjelovita glazbena misao. Geološko razdoblje je dio ere i podijeljeno je na epohe s periodom od 35 do 90 milijuna godina.
Vrijeme poluraspada radioaktivne tvari. Periodni razlomak. Periodika je tiskana publikacija koja izlazi u točno određenim rokovima. Mendeljejevljev periodni sustav.
6. Na slikama su prikazani dijelovi grafova periodičkih funkcija. Odredite period funkcije. Odredite period funkcije.
Odgovor: T=2; T=2; T=4; T=8.
7. Gdje ste se u životu susreli s konstrukcijom elemenata koji se ponavljaju?
Odgovor učenika: Elementi ornamenata, narodna umjetnost.
IV. Kolektivno rješavanje problema.
(Rješavanje problema na slajdovima.)
Razmotrimo jedan od načina proučavanja funkcije za periodičnost.
Ova metoda izbjegava poteškoće povezane s dokazivanjem da je određeni period najmanji, a također eliminira potrebu za doticanjem pitanja o aritmetičkim operacijama na periodičkim funkcijama i periodičnosti složene funkcije. Obrazloženje se temelji samo na definiciji periodične funkcije i na sljedećoj činjenici: ako je T period funkcije, onda je nT(n?0) njezin period.
Zadatak 1. Naći najmanji pozitivni period funkcije f(x)=1+3(x+q>5)
Rješenje: Pretpostavimo da je T-period ove funkcije. Tada je f(x+T)=f(x) za sve x € D(f), tj.
1+3(x+T+0,25)=1+3(x+0,25)
(x+T+0,25)=(x+0,25)
Stavimo x=-0,25 što dobivamo
(T)=0 T=n, n € Z
Dobili smo da su sve periode dotične funkcije (ako postoje) među cijelim brojevima. Odaberimo najmanji pozitivan broj među tim brojevima. ovo je 1. Provjerimo hoće li to stvarno biti period 1.
f(x+1) =3(x+1+0,25)+1
Budući da je (T+1)=(T) za bilo koji T, tada je f(x+1)=3((x+0,25)+1)+1=3(x+0,25)+1=f(x ), tj. 1 – razdoblje f. Budući da je 1 najmanji od svih pozitivnih cijelih brojeva, tada je T=1.
Zadatak 2. Pokažite da je funkcija f(x)=cos 2 (x) periodična i pronađite njenu glavnu periodu.
Zadatak 3. Odredite glavni period funkcije
f(x)=sin(1,5x)+5cos(0,75x)
Pretpostavimo T-period funkcije, tada za bilo koji x relacija vrijedi
sin1,5(x+T)+5cos0,75(x+T)=sin(1,5x)+5cos(0,75x)
Ako je x=0, tada
sin(1,5T)+5cos(0,75T)=sin0+5cos0
sin(1,5T)+5cos(0,75T)=5
Ako je x=-T, onda
sin0+5cos0=sin(-1,5T)+5cos0,75(-T)
5= – sin(1,5T)+5cos(0,75T)
| sin(1,5T)+5cos(0,75T)=5 – sin(1,5T)+5cos(0,75T)=5 |
Zbrajajući to, dobivamo:
10cos(0,75T)=10
2π n, n € Z
Izaberimo najmanji pozitivan broj od svih “sumnjivih” brojeva za period i provjerimo je li to period za f. Ovaj broj
f(x+)=sin(1,5x+4π )+5cos(0,75x+2π )= sin(1,5x)+5cos(0,75x)=f(x)
To znači da je to glavni period funkcije f.
Zadatak 4. Provjerimo je li funkcija f(x)=sin(x) periodična
Neka je T period funkcije f. Tada za bilo koji x
sin|x+T|=grijeh|x|
Ako je x=0, tada je sin|T|=sin0, sin|T|=0 T=π n, n € Z.
Pretpostavimo. Da je za neki n broj π n period
funkcija koja se razmatra π n>0. Tada je sin|π n+x|=sin|x|
To implicira da n mora biti i paran i neparan broj, ali to je nemoguće. Dakle, ova funkcija nije periodična.
Zadatak 5. Provjerite je li funkcija periodična
f(x)= 
Neka je tada T period od f
, dakle sinT=0, T=π n, n € Z. Pretpostavimo da je za neki n broj π n doista period ove funkcije. Tada će broj 2π n biti period
Budući da su brojnici jednaki, jednaki su im i nazivnici
To znači da funkcija f nije periodična.
Rad u skupinama.
Zadaci za grupu 1.
Zadaci za grupu 2.
Provjerite je li funkcija f periodična i pronađite njen osnovni period (ako postoji).
f(x)=cos(2x)+2sin(2x)
Zadaci za grupu 3.
Na kraju rada grupe prezentiraju svoja rješenja.
VI. Sažimanje lekcije.
Odraz.
Nastavnik daje učenicima kartice s crtežima i traži da obojaju dio prvog crteža u skladu s mjerom u kojoj misle da su ovladali metodama proučavanja funkcije za periodičnost, a dio drugog crteža - u skladu sa svojim doprinos radu na satu.
VII. Domaća zadaća
1). Provjeriti je li funkcija f periodična i pronaći njen osnovni period (ako postoji)
b). f(x)=x 2 -2x+4
c). f(x)=2tg(3x+5)
2). Funkcija y=f(x) ima period T=2 i f(x)=x 2 +2x za x € [-2; 0]. Pronađite vrijednost izraza -2f(-3)-4f(3,5)
Književnost/
U srpnju 2020. NASA pokreće ekspediciju na Mars. Letjelica će na Mars dostaviti elektronički medij s imenima svih prijavljenih sudionika ekspedicije.
Prijave sudionika su otvorene. Nabavite svoju kartu za Mars koristeći ovaj link.
Ako je ovaj post riješio vaš problem ili vam se samo svidio, podijelite link do njega sa svojim prijateljima na društvenim mrežama.
Jednu od ovih opcija koda potrebno je kopirati i zalijepiti u kôd vaše web stranice, po mogućnosti između oznaka i ili odmah nakon oznake. Prema prvoj opciji, MathJax se brže učitava i manje usporava stranicu. Ali druga opcija automatski prati i učitava najnovije verzije MathJaxa. Ako umetnete prvi kod, trebat će ga povremeno ažurirati. Ako umetnete drugi kod, stranice će se učitavati sporije, ali nećete morati stalno pratiti ažuriranja MathJaxa.
Najlakši način povezivanja MathJaxa je u Bloggeru ili WordPressu: na kontrolnoj ploči web-mjesta dodajte widget dizajniran za umetanje JavaScript koda treće strane, kopirajte prvu ili drugu verziju koda za preuzimanje prikazanog gore u njega i postavite widget bliže na početak predloška (usput, to uopće nije potrebno, jer se MathJax skripta učitava asinkrono). To je sve. Sada naučite sintaksu označavanja MathML-a, LaTeX-a i ASCIIMathML-a i spremni ste za umetanje matematičkih formula u web stranice svoje web stranice.
Još jedan doček Nove godine... mraz i snježne pahulje na prozorskom staklu... Sve me to ponukalo da ponovno pišem o... fraktalima i onome što Wolfram Alpha zna o njima. Postoji zanimljiv članak na tu temu, koji sadrži primjere dvodimenzionalnih fraktalnih struktura. Ovdje ćemo pogledati složenije primjere trodimenzionalnih fraktala.
Fraktal se može vizualno prikazati (opisati) kao geometrijski lik ili tijelo (što znači da su oboje skup, u ovom slučaju skup točaka), čiji detalji imaju isti oblik kao i sam originalni lik. To jest, ovo je samoslična struktura, proučavajući pojedinosti koje kada se povećaju, vidjet ćemo isti oblik kao i bez povećanja. Dok ćemo u slučaju običnog geometrijskog lika (ne fraktala) pri povećanju vidjeti detalje koji su jednostavnijeg oblika od samog izvornog lika. Na primjer, pri dovoljno velikom povećanju, dio elipse izgleda kao isječak ravne linije. To se ne događa s fraktalima: s bilo kakvim njihovim povećanjem, ponovno ćemo vidjeti isti složeni oblik, koji će se ponavljati uvijek iznova sa svakim povećanjem.
Benoit Mandelbrot, utemeljitelj znanosti o fraktalima, napisao je u svom članku Fraktali i umjetnost u ime znanosti: "Fraktali su geometrijski oblici koji su jednako složeni u svojim detaljima kao iu svom ukupnom obliku. To jest, ako je dio fraktala će se povećati do veličine cjeline, izgledat će kao cjelina, bilo točno, bilo možda s malom deformacijom."
Trigonometrijske funkcije su periodične, odnosno ponavljaju se nakon određenog razdoblja. Kao rezultat toga, dovoljno je proučavati funkciju na tom intervalu i proširiti otkrivena svojstva na sva ostala razdoblja.
upute1. Ako vam je dan primitivni izraz u kojem postoji samo jedna trigonometrijska funkcija (sin, cos, tg, ctg, sec, cosec), a kut unutar funkcije nije pomnožen nikakvim brojem, a sama nije podignuta do bilo kojeg stupnja - koristite definiciju. Za izraze koji sadrže sin, cos, sec, cosec, hrabro postavite period na 2P, a ako jednadžba sadrži tg, ctg, onda P. Recimo, za funkciju y=2 sinx+5, period će biti jednak 2P .
2. Ako se kut x ispod predznaka trigonometrijske funkcije pomnoži s nekim brojem, tada, da biste pronašli period te funkcije, podijelite tipični period s tim brojem. Recimo da vam je dana funkcija y = sin 5x. Tipični period za sinus je 2P; podijelite li ga s 5, dobit ćete 2P/5 - ovo je željeni period ovog izraza.
3. Da biste pronašli period trigonometrijske funkcije podignute na potenciju, procijenite paritet potencije. Za ravnomjeran stupanj smanjite tipično razdoblje za pola. Recimo, ako vam je dana funkcija y = 3 cos^2x, tada će se tipični period 2P smanjiti 2 puta, tako da će period biti jednak P. Imajte na umu da su funkcije tg, ctg periodične na P na svaki stupanj.
4. Ako vam je dana jednadžba koja sadrži umnožak ili kvocijent dviju trigonometrijskih funkcija, prvo pronađite period za sve njih zasebno. Nakon toga pronađite najmanji broj koji bi sadržavao cijeli broj obje točke. Recimo da je dana funkcija y=tgx*cos5x. Za tangentu period je P, za kosinus 5x period je 2P/5. Najmanji broj u koji se mogu smjestiti oba ova razdoblja je 2P, stoga je željeno razdoblje 2P.
5. Ako vam je teško učiniti kako je predloženo ili sumnjate u rezultat, pokušajte to učiniti kako je definirano. Uzmite T kao period funkcije; on je veći od nule. Zamijenite izraz (x + T) umjesto x u jednadžbu i riješite dobivenu jednakost kao da je T parametar ili broj. Kao rezultat toga, otkrit ćete vrijednost trigonometrijske funkcije i moći pronaći najmanji period. Recimo, kao rezultat olakšice dobivate sin identiteta (T/2) = 0. Minimalna vrijednost T pri kojoj se izvodi je 2P, to će biti rezultat zadatka.
Periodična funkcija je funkcija koja ponavlja svoje vrijednosti nakon nekog razdoblja različitog od nule. Period funkcije je broj koji, kada se doda argumentu funkcije, ne mijenja vrijednost funkcije.
Trebat će vam
- Poznavanje elementarne matematike i osnova ponavljanja.
1. Označimo period funkcije f(x) brojem K. Naš zadatak je otkriti tu vrijednost K. Da bismo to učinili, zamislimo da funkcija f(x), koristeći definiciju periodične funkcije, izjednačujemo f(x+K)=f(x).
2. Rješavamo dobivenu jednadžbu s nepoznatom K, kao da je x konstanta. Ovisno o vrijednosti K, bit će nekoliko opcija.
3. Ako je K>0 – to je period vaše funkcije Ako je K=0 – funkcija f(x) nije periodična Ako rješenje jednadžbe f(x+K)=f(x) vrijedi ne postoji za bilo koji K koji nije jednak nuli, tada se takva funkcija naziva aperiodična i također nema period.
Video na temu
Bilješka!
Sve trigonometrijske funkcije su periodične, a sve polinomske funkcije sa stupnjem većim od 2 su aperiodične.
Koristan savjet
Period funkcije koja se sastoji od 2 periodičke funkcije je najmanji univerzalni višekratnik perioda tih funkcija.
Trigonometrijske jednadžbe su jednadžbe koje sadrže trigonometrijske funkcije nepoznatog argumenta (na primjer: 5sinx-3cosx =7). Da biste naučili kako ih riješiti, morate znati neke načine kako to učiniti.
1. Rješavanje takvih jednadžbi sastoji se od 2 faze.Prva je reforma jednadžbe da poprimi svoj najjednostavniji oblik. Najjednostavnije trigonometrijske jednadžbe su: Sinx=a; Cosx=a, itd.
2. Drugo je dobiveno rješenje najjednostavnije trigonometrijske jednadžbe. Postoje osnovni načini rješavanja jednadžbi ovog tipa: Rješavanje algebarskim putem. Ova metoda je poznata iz škole, iz tečaja algebre. Inače se naziva metoda zamjene i supstitucije varijable. Koristeći redukcijske formule, transformiramo, napravimo zamjenu i zatim pronađemo korijene.
3. Rastavljanje jednadžbe na faktore. Prvo pomaknemo sve članove ulijevo i faktoriziramo ih.
4. Svođenje jednadžbe na homogenu. Jednadžbe se nazivaju homogene jednadžbe ako su svi članovi istog stupnja, a sinus i kosinus istog kuta.Da biste je riješili, potrebno je: prvo sve njezine članove prenijeti s desne strane na lijevu stranu; maknuti sve univerzalne faktore iz zagrada; izjednačiti faktore i zagrade s nulom; izjednačene zagrade daju homogenu jednadžbu nižeg stupnja, koju treba podijeliti s cos (ili sin) do najvišeg stupnja; riješiti dobivenu algebarsku jednadžbu u vezi s tan.
5. Sljedeća metoda je prelazak na polukut. Recimo, riješite jednadžbu: 3 sin x – 5 cos x = 7. Prijeđimo na polukut: 6 sin (x / 2) · cos (x / 2) – 5 cos? (x / 2) + 5 sin ? (x / 2) = 7 sin ? (x / 2) + 7 cos ? (x/ 2) , nakon čega sve članove svedemo u jedan dio (najbolje desnu stranu) i riješimo jednadžbu.
6. Unos pomoćnog kuta. Kada zamijenimo cjelobrojnu vrijednost cos(a) ili sin(a). Znak "a" je pomoćni kut.
7. Metoda pretvorbe umnoška u zbroj. Ovdje morate primijeniti odgovarajuće formule. Recimo zadano: 2 sin x · sin 3x = cos 4x. Riješite to transformiranjem lijeve strane u zbroj, to jest: cos 4x – cos 8x = cos 4x ,cos 8x = 0 ,8x = p / 2 + pk , x = p / 16 + pk / 8.
8. Konačna metoda naziva se višenamjenska supstitucija. Transformiramo izraz i napravimo promjenu, recimo Cos(x/2)=u, a zatim riješimo jednadžbu s parametrom u. Pri kupnji totala vrijednost preračunavamo u suprotnost.
Video na temu
Ako promatramo točke na kružnici, tada su točke x, x + 2π, x + 4π itd. međusobno se podudaraju. Dakle, trigonometrijske funkcije na ravnoj liniji periodički ponavljaju svoju vrijednost. Ako je period funkcije poznat, moguće je konstruirati funkciju na tom periodu i ponoviti je na ostalima.
1. Period je broj T takav da je f(x) = f(x+T). Da biste pronašli razdoblje, riješite odgovarajuću jednadžbu, zamijenivši x i x+T kao argument. U ovom slučaju za funkcije koriste već dobro poznata razdoblja. Za funkcije sinus i kosinus period je 2π, a za funkcije tangens i kotangens je π.
2. Neka je dana funkcija f(x) = sin^2(10x). Razmotrimo izraz sin^2(10x) = sin^2(10(x+T)). Koristite formulu za smanjenje stupnja: sin^2(x) = (1 – cos 2x)/2. Zatim dobijete 1 – cos 20x = 1 – cos 20(x+T) ili cos 20x = cos (20x+20T). Znajući da je period kosinusa 2π, 20T = 2π. To znači T = π/10. T je minimalni ispravni period, a funkcija će se ponoviti nakon 2T, i nakon 3T, te u drugom smjeru duž osi: -T, -2T itd.
Koristan savjet
Koristite formule za smanjenje stupnja funkcije. Ako već znate razdoblja nekih funkcija, pokušajte postojeću funkciju svesti na poznate.
Ispitivanje parnosti i neparnosti funkcije pomaže u izgradnji grafikona funkcije i razumijevanju prirode njezina ponašanja. Za ovo istraživanje trebate usporediti ovu funkciju napisanu za argument "x" i za argument "-x".
1. Zapišite funkciju koju želite proučavati u obliku y=y(x).
2. Zamijenite argument funkcije s “-x”. Zamijenite ovaj argument u funkcionalni izraz.
3. Pojednostavite izraz.
4. Dakle, imate istu funkciju napisanu za argumente “x” i “-x”. Pogledajte ova dva unosa. Ako je y(-x)=y(x), onda je to parna funkcija. Ako je y(-x)=-y(x), onda je to neparna funkcija. Ako je nemoguće recimo za funkciju da je y (-x)=y(x) ili y(-x)=-y(x), tada je to po svojstvu parnosti funkcija univerzalnog oblika. Odnosno, nije ni paran ni neparan.
5. Zapišite svoje nalaze. Sada ih možete koristiti u konstruiranju grafa funkcije ili u budućem analitičkom proučavanju svojstava funkcije.
6. O parnosti i neparnosti funkcije može se govoriti i u slučaju kada je graf funkcije već zadan. Recimo da je graf poslužio kao rezultat fizičkog eksperimenta. Ako je graf funkcije simetričan u odnosu na os ordinata, tada je y(x) parna funkcija. Ako je graf funkcije simetričan u odnosu na os apscise, tada x(y) je parna funkcija. x(y) je funkcija inverzna funkciji y(x). Ako je graf funkcije simetričan oko ishodišta (0,0), tada je y(x) neparna funkcija. Inverzna funkcija x(y) također će biti neparna.
7. Važno je zapamtiti da ideja parnosti i neparnosti funkcije ima izravnu vezu s domenom definiranja funkcije. Ako, recimo, parna ili neparna funkcija ne postoji u x=5, onda ne postoji ni u x=-5, što se ne može reći za funkciju univerzalnog oblika. Pri utvrđivanju parnog i neparnog pariteta obratite pozornost na domenu funkcije.
8. Pronalaženje funkcije za parnost i neparnost korelira s pronalaženjem skupa vrijednosti funkcije. Da biste pronašli skup vrijednosti parne funkcije, dovoljno je pogledati polovicu funkcije, desno ili lijevo od nule. Ako pri x>0 parna funkcija y(x) uzima vrijednosti od A do B, tada će uzeti iste vrijednosti i pri x0 neparna funkcija y(x) preuzima raspon vrijednosti od A na B, zatim na x sin^2 ? + cos^2 ? = 1. Treći i četvrti identitet dobivaju se dijeljenjem s b^2 i a^2: a^2/b^2 + 1 = c^2/b^2 => tg^2 ? + 1 = 1/cos^2 ?;1 + b^2/a^2 = c^2/a^2 => 1 + 1/tg^2 ? = 1/sin^ ? ili 1 + ctg^2 ? = 1/sin^2 ?.Peti i šesti glavni identitet dokazuju se određivanjem zbroja šiljastih kutova pravokutnog trokuta, koji je jednak 90° ili?/2.Teži trigonometrijski identiteti: formule za zbrajanje argumenata, dvostruki i trostruki kut, smanjenje stupnja, reformiranje zbroja ili umnoška funkcija, kao i formule za trigonometrijsku zamjenu, odnosno izraze osnovnih trigonometrijskih funkcija u terminima tan polukuta: sin ?= (2*tg ?/2)/ (1 + tan^2 ?/2);cos ? = (1 – tg^2 ?/2)/(1 = tg^2 ?/2);tg ? = (2*tg ?/2)/(1 – tg^2 ?/2).
Potreba da se pronađe minimalna vrijednost matematičke funkcije je od stvarnog interesa u rješavanju primijenjenih problema, recimo, u ekonomiji. Minimiziranje gubitaka od velike je važnosti za poslovne aktivnosti.
1. Da bi se našla minimalna vrijednost funkcije, potrebno je odrediti pri kojoj će vrijednosti argumenta x0 biti zadovoljena nejednakost y(x0)? y(x), gdje je x? x0. Kao i obično, ovaj problem se rješava na određenom intervalu ili u svakom rasponu vrijednosti funkcije, ako nije naveden. Jedan aspekt rješenja je pronalaženje fiksnih točaka.
2. Stacionarna točka je vrijednost argumenta pri kojoj derivacija funkcije postaje nula. Prema Fermatovom teoremu, ako diferencijabilna funkcija u nekoj točki poprimi ekstremnu vrijednost (u ovom slučaju, lokalni minimum), tada je ta točka stacionarna.
3. Funkcija često poprima svoju minimalnu vrijednost upravo u ovoj točki, ali se ne može uvijek odrediti. Štoviše, nije uvijek moguće s preciznošću reći čemu je jednak minimum funkcije ili ima li beskonačno malu vrijednost. Zatim, kao i obično, pronađu granicu kojoj teži dok se smanjuje.
4. Da bi se odredila minimalna vrijednost funkcije, potrebno je izvršiti slijed radnji koji se sastoji od četiri faze: pronalaženje domene definiranja funkcije, dobivanje fiksnih točaka, pregled vrijednosti funkcije na tim točaka i na krajevima intervala pronalaženje minimuma.
5. Ispada da je neka funkcija y(x) dana na intervalu s granicama u točkama A i B. Nađite domenu njezine definicije i utvrdite je li interval njezin podskup.
6. Izračunajte derivaciju funkcije. Izjednačite dobiveni izraz s nulom i pronađite korijene jednadžbe. Provjerite nalaze li se te stacionarne točke unutar razmaka. Ako nisu, onda se ne uzimaju u obzir u daljnjoj fazi.
7. Ispitajte jaz za vrstu granica: otvorene, zatvorene, složene ili nemjerljive. Ovo određuje kako ćete tražiti minimalnu vrijednost. Recimo da je segment [A, B] zatvoreni interval. Uključite ih u funkciju i izračunajte vrijednosti. Učinite isto sa stacionarnom točkom. Odaberite najniži ukupni iznos.
8. S otvorenim i nemjerljivim intervalima situacija je nešto teža. Ovdje ćete morati tražiti jednostrana ograničenja koja ne daju uvijek jednoznačan rezultat. Recimo, za interval s jednom zatvorenom i jednom probušenom granicom [A, B), treba pronaći funkciju na x = A i jednostrani limit y na x? B-0.
Umjetna gravitacija više nije znanstvena fantastika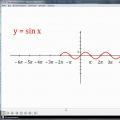
Periodičnost funkcija y = sin x, y = cos x - Hipermarket znanja
Izvještaji DNR i LPR: Snažne bitke kod Gorlovke, granatiranje Donjecka iz artiljerije, sukobi duž cijele linije fronta