Разложение чисел на простые множители, способы и примеры разложения. Получить каноническое разложение числа на простые сомножители

Лекция 14 Случайные процессы Каноническое разложение случайных процессов. Спектральное разложение стационарного случайного процесса. СлуЛекция 14
Случайные процессы
Каноническое разложение случайных процессов.
Спектральное разложение стационарного случайного
процесса. Случайные процессы с независимыми
сечениями. Марковские процессы и цепи Маркова.
Нормальные случайные процессы. Периодически
нестационарные случайные процессы
(Ахметов С.К.)

Каноническое разложение случайных процессов

Любой СП X(t) м.б. представлен в
виде его разложения, т.е. в виде суммы
элементарных процессов:
Vk – случайные величины
φk(t) – неслучайные функции (синусоиды, экспоненты, степенные
функции и т.д)
Частный случай такого разложения-Каноническое
разложение
СП X(t), имеющее вид
mx(t) = M – математическое ожидание СП X(t)
V1, V2…Vk – некоррелированные и центрированные СВ
D1, D2 …Dk- дисперсии СВ V1, V2…Vk
φk(t) – неслучайные функции аргумента t
Случайные величины V1, V2…Vk называются коэффициентами канонического
разложения,
а неслучайные функции φ1(t), φ2(t) φk(t) - координатными функциями
канонического разложения

Основные характеристики СП, заданного каноническим разложением

M – математическое ожидание СП X(t)
Kx(t,t’) – корреляционная функция СП X(t)
Выражение
- каноническое разложение корреляционной
функции
Если t=t’, то в соответствие с первым
свойством корреляционной функции
Выражение
Dk(t) –
дисперсия
каноническое разложение дисперсии СП X(t)

Спектральное разложение стационарного СП

Стационарный СП м.б. представлен каноническим разложением
Vk и Uk – некоррелированные и центрированные СВ с дисперсиями
D = D = Dk
ω – неслучайная величина (частота)
В этом случае каноническое разложение корреляционной функции
определяется выражением
Представленное
каноническое
разложение
СП
X(t)
называется
спектральным разложением СП и
выражается в виде
Θk - фаза гармонического колебания элементарного стационарного СП,
являющаяся СВ равномерно распределенной в интервале (0, 2π);
Zk – СВ, представляющая собой амплитуду гармонического колебания
элементарного стационарного СП

Спектральное разложение стационарного СП (2)

Случайные величины Θk и Zk зависимы и для них справедливо:
Vk = Zk cos Θk
Uk = Zk sin Θk
Стационарный СП м.б. представлен в виде суммы гармонических
колебаний со случайными амплитудами Zk и случайными фазами Θk на
различных неслучайных частотах ωk
Корреляционная функция стационарного СП X(t) является четной
функцией своего аргумента, т.е. kx(τ) = kx(-τ). Поэтому ее на интервале (-Т,
Т) можно разложить в ряд Фурье по четным (косинусам) гармоникам:
Дисперсия стационарного СП X(t) равна
сумме
дисперсий
всех
гармоник
его
спектрального разложения
Зависимость Dk = f(wk) называется дискретным спектром дисперсий или
дискретным спектром стационарного СП.

Спектральное разложение стационарного СП (3)

При ∆ω
→ 0 произойдет переход к непрерывному спектру
Sx(ω) - спектральная плотность
Таким образом, корреляционная функция и спектральная плотность
связаны косинус – преобразованием Фурье. Следовательно, спектральная
плотность стационарного СП м.б. выражена через корреляционную
функцию формулой

Случайные процессы с независимыми сечениями

В гидрологии считается, что ряд соответствует модели случайной
величины, если отсутствует значимая корреляция между членами этого ряда
при любом сдвиге τ.
Случайный процесс с независимыми сечениями – это СП, для которого
при значениях t и t’
mx(t) = mx
Dx (t) = Dx
Kx(t,t’) = kx(τ) = {Dx при τ = 0 и 0 при τ ≠ 0}
Такой процесс является стационарным и обладает эргодическим
свойством
Для таких процессов характеристики одномерного закона распределения
можно оценить как по любому сечению, так и по любой (достаточно
продолжительной) реализации
У таких процессов отсутствует корреляция между членами внутри любой
реализации
Принимая такую модель, допускается, что ряд гидрологических величин
представляет собой одну реализацию СП
Случайный процесс с независимыми сечениями иногда называют
«белым шумом» по аналогии с белым светом

Марковские процессы и цепи Маркова

Случайный процесс
называется марковским, если для любого
момента времени t вероятность каждого из состояний системы в будущем
(при t > t0) зависит только от ее состояния в настоящем (при t = t0) и не
зависит от ее состояния в прошлом (при t < t0)
Марковской цепью или простой марковской цепью называется
марковский процесс с дискретным состоянием и дискретным временем
Марковский СП полностью описывается двумерным законом
распределения. Если Марковский процесс является стационарным и
эргодическим, то его характеристики можно оценить по одной
реализации.
Цепь, в которой условные вероятности состояний в будущем зависят
от ее состояния на нескольких предыдущих шагах, называется сложной
цепью Маркова.

Нормальные (Гауссовские) случайные процессы

Нормальным (гауссовским) случайным процессом X(t) называется
СП, у которого во всех сечениях СВ X(ti) имеет нормальное
распределение
Периодически нестационарные СП
При изучении годовых, месячных, суточных и т.д. процессов, обычно,
наблюдаются внутригодовые и т.д. колебания. В этом случае, в качестве
математической модели можно использовать модель периодически
нестационарного случайного процесса (ПНСП)
Случайный процесс называют периодически нестационарным, если
его вероятностные характеристики инварианты относительно сдвигов на
положительное число Т. Например, при шаге дискретности один месяц
инвариантность должна сохраняться при сдвигах 12, 24, 36 и т.д.

Данная статья дает ответы на вопрос о разложении числа на простыне множители. Рассмотрим общее представление о разложении с примерами. Разберем каноническую форму разложения и его алгоритм. Будут рассмотрены все альтернативные способы при помощи использования признаков делимости и таблицы умножения.

Yandex.RTB R-A-339285-1

Что значит разложить число на простые множители?

Разберем понятие простые множители. Известно, что каждый простой множитель – это простое число. В произведении вида 2 · 7 · 7 · 23 имеем, что у нас 4 простых множителя в виде 2 , 7 , 7 , 23 .

Разложение на множители предполагает его представление в виде произведений простых. Если нужно произвести разложение числа 30 , тогда получим 2 , 3 , 5 . Запись примет вид 30 = 2 · 3 · 5 . Не исключено, что множители могут повторяться. Такое число как 144 имеет 144 = 2 · 2 · 2 · 2 · 3 · 3 .

Не все числа предрасположены к разложению. Числа, которые больше 1 и являются целыми можно разложить на множители. Простые числа при разложении делятся только на 1 и на самого себя, поэтому невозможно представить эти числа в виде произведения.

При z , относящемуся к целым числам, представляется в виде произведения а и b , где z делится на а и на b . Составные числа раскладывают на простые множители при помощи основной теоремы арифметики. Если число больше 1 , то его разложение на множители p 1 , p 2 , … , p n принимает вид a = p 1 , p 2 , … , p n . Разложение предполагается в единственном варианте.

Каноническое разложение числа на простые множители

При разложении множители могут повторяться. Их запись выполняется компактно при помощи степени. Если при разложении числа а имеем множитель p 1 , который встречается s 1 раз и так далее p n – s n раз. Таким образом разложение примет вид a=p 1 s 1 · a = p 1 s 1 · p 2 s 2 · … · p n s n . Эта запись имеет название канонического разложения числа на простые множители.

При разложении числа 609840 получим, что 609 840 = 2 · 2 · 2 · 2 · 3 · 3 · 5 · 7 · 11 · 11 ,его канонический вид будет 609 840 = 2 4 · 3 2 · 5 · 7 · 11 2 . При помощи канонического разложения можно найти все делители числа и их количество.

Чтобы правильно разложить на множители необходимо иметь представление о простых и составных числах. Смысл заключается в том, чтобы получить последовательное количество делителей вида p 1 , p 2 , … , p n чисел a , a 1 , a 2 , … , a n - 1 , это дает возможность получить a = p 1 · a 1 , где a 1 = a: p 1 , a = p 1 · a 1 = p 1 · p 2 · a 2 , где a 2 = a 1: p 2 , … , a = p 1 · p 2 · … · p n · a n , где a n = a n - 1: p n . При получении a n = 1 , то равенство a = p 1 · p 2 · … · p n получим искомое разложение числа а на простые множители. Заметим, что p 1 ≤ p 2 ≤ p 3 ≤ … ≤ p n .

Для нахождения наименьших общих делителей необходимо использовать таблицу простых чисел. Это выполняется на примере нахождения наименьшего простого делителя числа z . При взятии простых чисел 2 , 3 , 5 , 11 и так далее, причем на них делим число z . Так как z не является простым числом, следует учитывать, что наименьшим простым делителем не будет больше z . Видно, что не существуют делителей z , тогда понятно, что z является простым числом.

Пример 1

Рассмотрим на примере числа 87 . При его делении на 2 имеем, что 87: 2 = 43 с остатком равным 1 . Отсюда следует, что 2 делителем не может являться, деление должно производиться нацело. При делении на 3 получим, что 87: 3 = 29 . Отсюда вывод – 3 является наименьшим простым делителем числа 87 .

При разложении на простые множители необходимо пользоваться таблицей простых чисел, где a . При разложении 95 следует использовать около 10 простых чисел, а при 846653 около 1000 .

Рассмотрим алгоритм разложения на простые множители:

• нахождение наименьшего множителя при делителе p 1 числа a по формуле a 1 = a: p 1 , когда a 1 = 1 , тогда а является простым числом и включено в разложение на множители, когда не равняется 1 , тогда a = p 1 · a 1 и следуем к пункту, находящемуся ниже;
• нахождение простого делителя p 2 числа a 1 при помощи последовательного перебора простых чисел, используя a 2 = a 1: p 2 , когда a 2 = 1 , тогда разложение примет вид a = p 1 · p 2 , когда a 2 = 1 , тогда a = p 1 · p 2 · a 2 , причем производим переход к следующему шагу;
• перебор простых чисел и нахождение простого делителя p 3 числа a 2 по формуле a 3 = a 2: p 3 , когда a 3 = 1 , тогда получим, что a = p 1 · p 2 · p 3 , когда не равняется 1 , тогда a = p 1 · p 2 · p 3 · a 3 и производим переход к следующему шагу;
• производится нахождение простого делителя p n числа a n - 1 при помощи перебора простых чисел с p n - 1 , а также a n = a n - 1: p n , где a n = 1 , шаг является завершающим, в итоге получаем, что a = p 1 · p 2 · … · p n .

Результат алгоритма записывается в виде таблицы с разложенными множителями с вертикальной чертой последовательно в столбик. Рассмотрим рисунок, приведенный ниже.

Полученный алгоритм можно применять при помощи разложения чисел на простые множители.

Во время разложения на простые множители следует придерживаться основного алгоритма.

Пример 2

Произвести разложение числа 78 на простые множители.

Решение

Для того, чтобы найти наименьший простой делитель, необходимо перебрать все простые числа, имеющиеся в 78 . То есть 78: 2 = 39 . Деление без остатка, значит это первый простой делитель, который обозначим как p 1 . Получаем, что a 1 = a: p 1 = 78: 2 = 39 . Пришли к равенству вида a = p 1 · a 1 , где 78 = 2 · 39 . Тогда a 1 = 39 , то есть следует перейти к следующему шагу.

Остановимся на нахождении простого делителя p 2 числа a 1 = 39 . Следует перебрать простые числа, то есть 39: 2 = 19 (ост. 1). Так как деление с остатком, что 2 не является делителем. При выборе числа 3 получаем, что 39: 3 = 13 . Значит, что p 2 = 3 является наименьшим простым делителем 39 по a 2 = a 1: p 2 = 39: 3 = 13 . Получим равенство вида a = p 1 · p 2 · a 2 в виде 78 = 2 · 3 · 13 . Имеем, что a 2 = 13 не равно 1 , тогда следует переходит дальше.

Наименьший простой делитель числа a 2 = 13 ищется при помощи перебора чисел, начиная с 3 . Получим, что 13: 3 = 4 (ост. 1). Отсюда видно, что 13 не делится на 5 , 7 , 11 , потому как 13: 5 = 2 (ост. 3), 13: 7 = 1 (ост. 6) и 13: 11 = 1 (ост. 2). Видно, что 13 является простым числом. По формуле выглядит так: a 3 = a 2: p 3 = 13: 13 = 1 . Получили, что a 3 = 1 , что означает завершение алгоритма. Теперь множители записываются в виде 78 = 2 · 3 · 13 (a = p 1 · p 2 · p 3) .

Ответ: 78 = 2 · 3 · 13 .

Пример 3

Разложить число 83 006 на простые множители.

Решение

Первый шаг предусматривает разложение на простые множители p 1 = 2 и a 1 = a: p 1 = 83 006: 2 = 41 503 , где 83 006 = 2 · 41 503 .

Второй шаг предполагает, что 2 , 3 и 5 не простые делители для числа a 1 = 41 503 , а 7 простой делитель, потому как 41 503: 7 = 5 929 . Получаем, что p 2 = 7 , a 2 = a 1: p 2 = 41 503: 7 = 5 929 . Очевидно, что 83 006 = 2 · 7 · 5 929 .

Нахождение наименьшего простого делителя p 4 к числу a 3 = 847 равняется 7 . Видно, что a 4 = a 3: p 4 = 847: 7 = 121 , поэтому 83 006 = 2 · 7 · 7 · 7 · 121 .

Для нахождения простого делителя числа a 4 = 121 используем число 11 , то есть p 5 = 11 . Тогда получим выражение вида a 5 = a 4: p 5 = 121: 11 = 11 , и 83 006 = 2 · 7 · 7 · 7 · 11 · 11 .

Для числа a 5 = 11 число p 6 = 11 является наименьшим простым делителем. Отсюда a 6 = a 5: p 6 = 11: 11 = 1 . Тогда a 6 = 1 . Это указывает на завершение алгоритма. Множители запишутся в виде 83 006 = 2 · 7 · 7 · 7 · 11 · 11 .

Каноническая запись ответа примет вид 83 006 = 2 · 7 3 · 11 2 .

Ответ: 83 006 = 2 · 7 · 7 · 7 · 11 · 11 = 2 · 7 3 · 11 2 .

Пример 4

Произвести разложение числа 897 924 289 на множители.

Решение

Для нахождения первого простого множителя произвести перебор простых чисел, начиная с 2 . Конец перебора приходится на число 937 . Тогда p 1 = 937 , a 1 = a: p 1 = 897 924 289: 937 = 958 297 и 897 924 289 = 937 · 958 297 .

Второй шаг алгоритма заключается в переборе меньших простых чисел. То есть начинаем с числа 937 . Число 967 можно считать простым, потому как оно является простым делителем числа a 1 = 958 297 . Отсюда получаем, что p 2 = 967 , то a 2 = a 1: p 1 = 958 297: 967 = 991 и 897 924 289 = 937 · 967 · 991 .

Третий шаг говорит о том, что 991 является простым числом, так как не имеет ни одного простого делителя, который не превосходит 991 . Примерное значение подкоренного выражения имеет вид 991 < 40 2 . Иначе запишем как 991 < 40 2 . Отсюда видно, что p 3 = 991 и a 3 = a 2: p 3 = 991: 991 = 1 . Получим, что разложение числа 897 924 289 на простые множители получается как 897 924 289 = 937 · 967 · 991 .

Ответ: 897 924 289 = 937 · 967 · 991 .

Использование признаков делимости для разложения на простые множители

Чтобы разложить число на простые множители, нужно придерживаться алгоритма. Когда имеются небольшие числа, то допускается использование таблицы умножения и признаков делимости. Это рассмотрим на примерах.

Пример 5

Если необходимо произвести разложение на множители 10 , то по таблице видно: 2 · 5 = 10 . Получившиеся числа 2 и 5 являются простыми, поэтому они являются простыми множителями для числа 10 .

Пример 6

Если необходимо произвести разложение числа 48 , то по таблице видно: 48 = 6 · 8 . Но 6 и 8 – это не простые множители, так как их можно еще разложить как 6 = 2 · 3 и 8 = 2 · 4 . Тогда полное разложение отсюда получается как 48 = 6 · 8 = 2 · 3 · 2 · 4 . Каноническая запись примет вид 48 = 2 4 · 3 .

Пример 7

При разложении числа 3400 можно пользоваться признаками делимости. В данном случае актуальны признаки делимости на 10 и на 100 . Отсюда получаем, что 3 400 = 34 · 100 , где 100 можно разделить на 10 , то есть записать в виде 100 = 10 · 10 , а значит, что 3 400 = 34 · 10 · 10 . Основываясь на признаке делимости получаем, что 3 400 = 34 · 10 · 10 = 2 · 17 · 2 · 5 · 2 · 5 . Все множители простые. Каноническое разложение принимает вид 3 400 = 2 3 · 5 2 · 17 .

Когда мы находим простые множители, необходимо использовать признаки делимости и таблицу умножения. Если представить число 75 в виде произведения множителей, то необходимо учитывать правило делимости на 5 . Получим, что 75 = 5 · 15 , причем 15 = 3 · 5 . То есть искомое разложение пример вид произведения 75 = 5 · 3 · 5 .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Случайная величина Vназываетсяцентрированной , если ее математическое ожидание равно 0. Элементарным центрированным случайным процессом называется произведение центрированной случайной величиныVна неслучайную функцию φ(t):X(t)=Vφ(t). Элементарный центрированный случайный процесс имеет следующие характеристики:

Выражение вида
, где φ k ( t ), k =1;2;…-неслучайные функции; , k =1;2;…-некоррелированные центрированные случайные величины, называется каноническим разложением случайного процесса X ( t ), при этом случайные величины называются коэффициентами канонического разложения; а неслучайные функции φ k ( t ) - координатными функциями канонического разложения.

Рассмотрим характеристики случайного процесса

Так как по условию
то

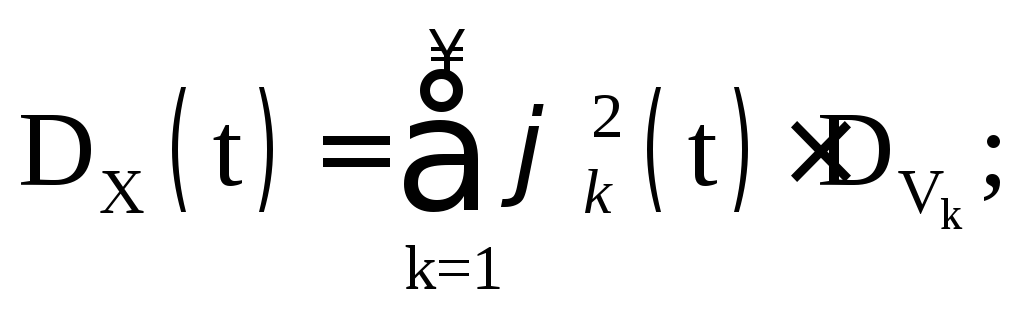
Очевидно, что один и тот же случайный процесс имеет различные виды канонического разложения в зависимости от выбора координатных функций. Более того, даже при состоявшемся выборе координатных функций существует произвол в распределении случайных величин V к. На практике по итогам экспериментов получают оценки для математического ожидания и корреляционной функции:
. После разложения
в двойной ряд Фурье по координатным функциям φ к (t):

получают значения дисперсий
случайных величинV k .

4.2. Понятие обобщенной функции. Дельта-функция Дирака. Интегральное каноническое представление случайных процессов.

Обобщенной функцией называется предел последовательности однопараметрического семейства непрерывных функций.

Дельта-функция Дирака
- это обобщенная функция, являющаяся результатом предельного перехода при
в семействе функций

Среди свойств -функции отметим следующее:

2.

3. Если f(t)- непрерывная функция, то

Случайный процесс Х( t ), корреляционная функция которого имеет вид называется нестационарным «белым шумом». Если W ( t 1 )= W - const , то Х( t )-стационарный «белый шум».

Как следует из определения, никакие два, даже сколь угодные близкие, сечения «белого шума» не коррелированны. Выражение W(t) называетсяинтенсивностью «белого шума».

Интегральным каноническим представлением случайного процесса Х( t ) называется выражение вида
где
- случайная центрированная функция;
- неслучайная функция непрерывных аргументов

Корреляционная функция такого случайного процесса имеет вид:

Можно показать, что существует неслучайная функция G(λ) такая, что

где G(λ 1) - плотность дисперсии; δ(х) - дельта-функция Дирака. Получаем

Следовательно, дисперсия случайного процесса Х(t):

.

4.3. Линейные и нелинейные преобразования случайных процессов

Рассматривается следующая задача: на вход системы (устройства, преобразователя) Sподается «входной сигнал», имеющий характер случайного процесса Х(t). Система преобразовывает его в «выходной сигнал»Y(t):

.

Формально преобразование случайного процесса Х(t) вY(t) может быть описано с помощью так называемого оператора системы А t:

Y(t)=A t (Х(t)).

Индекс tпоказывает, что данный оператор осуществляет преобразование по времени. Возможны следующие постановки задачи о преобразовании случайного процесса.

Известны законы распределения или общие характеристики случайного процесса Х(t) на входе в системуS, задан оператор А t системыS, требуется определить закон распределения или общие характеристики случайного процессаY(t) на выходе системыS.

Известны законы распределения (общие характеристики) случайного процесса Х(t) и требования к случайному процессуY(t); надо определить вид оператора А t системыS, наилучшим образом удовлетворяющего заданным требованиям кY(t).

Известны законы распределения (общие характеристики) случайного процесса Y(t) и задан оператор А t системыS; требуется определить законы распределения или общие характеристики случайного процесса Х(t).

Принята следующая классификация операторов А t системыS:

Операторы системы

Линейные LНелинейныеN

Линейные однородные L 0 Линейные неоднородныеL н

Рассмотрим воздействие линейной неоднородной системы

L н (...)=L 0 (…)+φ(t)

на случайный процесс Х(t), имеющий следующее каноническое разложение:

.

Получаем:

введем обозначения

тогда каноническое разложение Y(t) приобретает вид:

.

Математическое ожидание случайного процессаY(t):

корреляционная функция случайного процесса Y(t):

следовательно,

С другой стороны

Дисперсия случайного процесса Y(t):

В заключении этого пункта отметим, что операторы дифференцирования и интегрирования случайных процессов являются линейными однородными.

2. Рассматривается квадратичное преобразование:

Y(t)=(X(t)) 2 ,

V k -центрированные случайные величины, имеющие симметричное относительно нуля распределение; любые четыре из них независимы в совокупности. Тогда

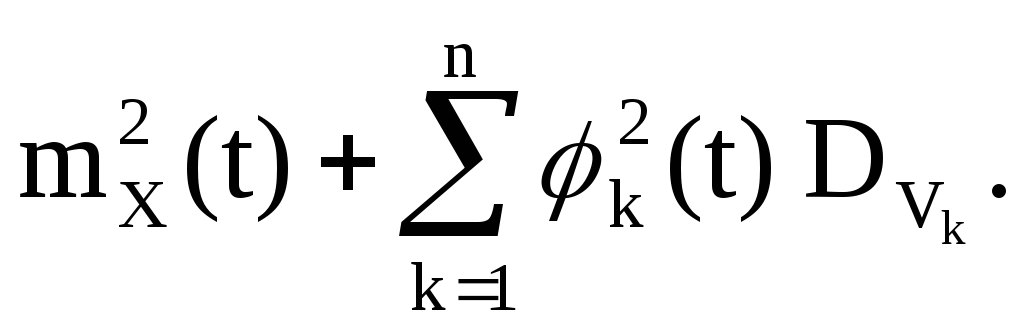
Введем неслучайные функции

и случайные величины

тогда случайный процесс Y(t) приобретает вид

Получено каноническое разложение случайного процесса Y(t). Корреляционная функцияY(t):

Формулировка. Дано натуральное число n (n > 1) . Получить его каноническое разложение на простые сомножители, то есть представить в виде произведения простых сомножителей. При этом в разложении допустимо указывать множитель 1. Например, 264 = 2 * 2 * 2 * 3 * 11 (программе допустимо выдать ответ 264 = 1 * 2 * 2 * 2 * 3 * 11).

Решение. Данная задача имеет достаточно красивое решение.

Из основной теоремы арифметики известно, что для любого натурального числа больше 1 существует его каноническое разложение на простые сомножители, причем это разложение единственно с точностью до порядка следования множителей. То есть, например, 12 = 2 * 2 * 2 и 12 = 3 * 2 * 2 – это одинаковые разложения.

Рассмотрим каноническую форму любого числа на конкретном примере. Например, 264 = 2 * 2 * 2 * 3 * 11. Каким образом можно выявить эту структуру? Чтобы ответить на этот вопрос, вспомним изложенные в любом школьном курсе алгебры правила деления одночленов, представив, что числа в каноническом разложении являются переменными. Как известно, если разделить выражение на переменную в некоторой степени, содержащуюся в этом выражении в той же степени, оно вычеркивается в ее записи.

То есть, если мы разделим 264 на 2, то в его каноническом разложении уйдет одна двойка. Затем мы можем проверить, делится ли снова получившееся частное на 2. Ответ будет положительным, но третий раз деление даст остаток. Тогда нужно брать для рассмотрения следующее натуральное число 3 – на него частное разделится один раз. В итоге, проходя числовую прямую в положительном направлении, мы дойдем до числа 11, и после деления на 11 n станет равно 1, что будет говорить о необходимости закончить процедуру.

Почему при таком «вычеркивании» найденных сомножителей мы не получим делимостей на составные числа? На самом деле, здесь все просто – любое составное число является произведением простых сомножителей, меньших его. В итоге получается, что мы вычеркнем из n все сомножители любого составного числа, пока дойдем до него самого в цепочке делений. Например, при таком переборе n никогда не разделится на 4, так как «по пути» к этому числу мы вычеркнем из n все сомножители-двойки.

Алгоритм на естественном языке:

1) Ввод n ;

2) Присвоение переменной p числа 2;

3) Вывод числа n , знака равенства и единицы для оформления разложения;

4) Запуск цикла с предусловием n < > 1 . В цикле:

1. Если m mod p = 0 , то вывести на экран знак умножения и переменную p, затем разделить n на p , иначе увеличить значение i на 1;

1. program PrimeFactors;
2. n, p: word;
3. begin
4. p:= 2;
5. readln(n);
6. write(n, ‘ = 1’);
7. while n <> 1 do begin
8. if (n mod p) = 0 then begin
9. write(‘ * ‘, p);
10. n:= n div p
11. else begin
12. inc(p)