Знайти похідну та побудувати графік онлайн. Схема побудови графіка функції дослідження функцій на екстремум за допомогою похідних вищого порядку обчислення коренів рівнянь методами хорд та дотичних
Одна з можливих схем дослідження функції та побудови се графіка розкладається на наступні етапи розв'язання задачі: 1. Область визначення функції (О.О.Ф.). 2. Крапки розриву функції, їх характер. Вертикальні асимптоти. 3. парність, непарність, періодичність функції. 4. Точки перетину графіка з осями координат. 5. Поведінка функції на нескінченності. Горизонтальні та похилі асимптоти. 6. Інтервали монотонності функції, точки максимуму та мінімуму. 7. Напрями опуклості кривої. Точки перегину. 8. Графік функції. Приклад 1. Побудувати графік функції у = 1. (Вереіора або локон Марії Аньєї). - вся числова вісь. 2. Точок розриву немає; вертикальних асимптотів немає. 3. Функція парна: , отже графік її симетричний щодо осі Оу\ неперіодична. З парності функції випливає, що досить побудувати її графік на напівпрямий х ^ О, а потім дзеркально відобразити його в осі Оу. 4. При х = 0 маємо Ух, так що графік функції лежить у верхній напівплощині у > 0. похилих асимптот немає. Так що функція зростає при і зменшується, коли. Точка х = 0 – критична. При переході х через точку х = 0 похідна у"(х) змінює знак з мінусу на плюс. Отже, точка х = 0 - точка максимуму, y(Q) = I. Результат цей досить очевидний: /(х) = T^ IV* Друга похідна перетворюється на нуль у точках х = .Досліджуємо точку х = 4- (далі міркування симетрії). графіка функції Результати дослідження зведемо в таблицю: Точка перегину max Точка перегину У таблиці стрілка У» вказує на зростання функції, стрілка \ на її спадання.Графік функції зображений на рис.33. ).- вся числова вісь, виключаючи точку 2. Точка розриву функції.Маємо так що пряма х = 0 - вертикальна асимптота.3. Ох у точці (-1,0), похилих і горизонтальних асимптот немає, звідки критична точка. Друга похідна функції у точці, так що х = - точка мінімуму. Друга похідна звертається у вулик у точці та змінює свій знак при переході через цю точку. Отже, точка – точка перегину кривої. Для) маємо е. опуклість кривої спрямована вниз; для I маємо. опуклість кривої спрямована нагору. Результати дослідження зводимо в таблицю: Не існує Немає Точка перегину Немає. Вертикальна асимптота тора похідна перетворюється на нуль при х = е,/2. і при переході х через цю точку у" змінює знак Отже, - абсцис точки перегину кривої. Результати дослідження зводимо в таблицю: Точка перегину. Графік функції зображено на рис. 37. Приклад 4. Побудувати графік функції вся числова вісь, виключаючи точку Точка точка розриву 2-го роду функції, тому що Km - то пряма вертикальна асимптота графіка функції - Функція загального положення, неперіодична - Вважаючи у = 0, маємо, звідки так що графік функції перетинає вісь Ох в точці Отже, графік функції має похилу асимптоту отримуємо - критична точка. Друга похідна функції у" = Д > 0 всюди в області визначення, зокрема, у точці - точка мінімуму функції. 7. Оскільки, то всюди в області визначення функції опуклість її графіка спрямована вниз. Результати дослідження зводимо в таблицю: Немає Немає Немає. х = 0 - вертикальна асимптота Графік функції зображено на рис. Приклад 5. Побудувати графік функції вся числова вісь. 2. Безперервна всюди. Вертикальних асимптотів немає. 3. Загального стану, неперіодична. 4. Функція перетворюється на нуль при 5. Таким чином, графік функції має похилу асимптоту Похідна перетворюється на нуль у точці і не існує при. При переході через точку) похідна не змінює знак, отже у точці х = 0 екстремуму немає. При переході точки х через точку похідна) змінює знак з «+» на Значить у функція має максимум. При переході х через точку х = 3 (х > I) похідна у "(х) змінює знак тобто в точці х = 3 функція має мінімум. 7. Знаходимо другу похідну Схема побудови графіка функції Дослідження функцій на екстремум за допомогою похідних вищого порядка Обчислення коренів рівнянь методами хорд і дотичних перегину з вертикальною дотичною.У точці х = 3 перегину графіка немає.Усюди в напівплощині х > 0 опуклість кривої спрямована вгору.Результати дослідження зводимо в таблицю: Не існує Не існує Не існує Не існує Точка перегину (0.0) з вертикальної дотичної Графік функції представлений на рис. 39. §7. Дослідження функцій на екстремум за допомогою похідних вищого порядку Для пошуку точок максимуму та мінімуму функцій може бути використана формула Тейлора. Теорема It. Нехай функція /(х) у певній околиці точки xq має похідну п-го порядку, безперервну в точці хо- Нехай 0. Тоді якщо число п - непарне, то функція f(x) у точці х0 не має екстремуму; коли ж п - парне, то точці х0 функція f(x) має максимум, якщо /(п)(х0)< 0, и минимум, если /. В силу определения точек максимума и минимума вопрос о том, имеет ли функция f(x) в точке х0 экстремум, сводится к тому, существует ли такое <5 > 0, що в інтервалі, різницю - / (х0) зберігає знак. За формулою Тейлора як за умовою, то з (1) отримуємо 1умову / (п * (г) безперервна вточкего і Ф Тому в силу стійкості нака безперервної функції існує таке, що в інтервалі () не змінюється і збігається зі знаком / (п) ( хо) Розглянемо можливі випадки: 1) п - парне число і / Тоді I тому в силу (2) . Відповідно до визначення це означає, що точка го є точка мінімуму функції / (г). 2) п - парне в. Тоді будемо мати i разом з цим і тому точка го буде в цьому: проходить точкою максимуму функції / (г). 3) п - непарне число, / - Тоді при х > х0 знак > збігатиметься зі знаком / (п) (го), а при г го буде протилежним. Тому 1ри скільки завгодно малому 0 знак різниці / (г) - / (го) не буде одним і тим же 1ля всіх х е (го - 6, го + £). Отже, у цьому випадку функція /(г) у точці го жстремуму не має. приклад. Розглянемо функції Л. Легко бачити, що точка х = 0 є критичною точкою обох функцій. Для функції у = х4 перша з відмінних від нуля похідних у точці х = 0 є похідна 4-го порядку: Отже, тут п = 4 - парне в. Отже, у точці х = 0 функція у = х4 має мінімум. Для функції у = х) перша з відмінних від нуля в точці х = 0 похідних є похідною 3-го порядку. Тож у разі п = 3 - непарне, й у точці х = 0 функція у = х3 екстремуму немає. Зауваження. За допомогою формули Тейлора можна довести наступну теорему, що виражає достатні умови точки перегину. "еорема 12. Нехай функція /(г) в деякій околиці точки г0 має производп-го порядку, безперервну в точці xq. Нехай, але /(п)(*о) Ф 0- Тоді, якщо п - непарне число, то точка Мо(х0, f(xо)) є точка перегину графіка функції у = f(x) Найпростіший приклад доставляє функція § 8. Обчислення коренів рівнянь методами хорд і дотичних Завдання полягає в знаходженні дійсного кореня рівняння. 1) функція f(x) безперервна на відрізку [а, 6]; "(x), що зберігають на цьому відрізку постійний знак. З умов 1) та 2) в силу теореми Больцано-Коші (с. 220) випливає, що функція /(ж) звертається в нуль принаймні в одній точці £ € ( а, Ь), т. е. рівняння (1) має принаймні один дійсний корінь £ в інтервалі (а, 6). знак, то f(x) монотонна на [а, Ь] і тому в інтервалі (а, Ь) рівняння (1) має тільки один дійсний корінь Розглянемо метод обчислення наближеного значення цього єдиного дійсного кореня £ € (а, 6) рівняння ( I) з будь-яким ступенем точності. Можливі чотири випадки (рис. 40): 1) Мал. 40 Візьмемо для визначеності випадок, коли f\x) > 0, f"(x) > 0 на відрізку [а, 6) (рис.41). З'єднаємо точки А(а, /(а)) і В(Ь, f(b)) хордою А В. Це відрізок прямий, що проходить через точки А і В, рівняння якої Точка aj, в якій хорда АВ перетинає вісь Ох, розташована між аі(і є кращим наближенням до ніж а. Вважаючи (2) у = 0, знайдемо З рис. 41 неважко помітити, що точка а буде завжди розташована з того боку від якої знаки f(x) і f"(x) протилежні. Проведемо тепер дотичну до кривої у = / (х) в точці B(b, f(b)), тобто в тому кінці дуги ^АВ, в якому f(x) і /"(я) мають один і той же знак. Це істотна умова: без його дотримання точка перетину дотичної з віссю Ох може зовсім не давати наближення до шуканого кореня.Точка Ь\, в якій дотична перетинає вісь Ох, розташована між £ і b з тієї ж сторони, що і 6, і є кращим наближенням до Ь. Вважаючи в (3) у = 0, знайдемо Ь: Схема побудови графіка функції Дослідження функцій на екстремум за допомогою похідних вищого порядку Обчислення коренів рівнянь методами хорд і дотичних Таким чином, маємо Нехай абсолютна похибка наближення З кореня £ задана заздалегідь. За абсолютну похибку наближених значень aj і 6 кореня £ можна взяти величину | 6i - ai |. Якщо ця похибка більша за допустиму, то, приймаючи відрізок за вихідний, знайдемо наступні наближення кореня де. Продовжуючи цей процес, отримаємо дві послідовності наближених значень Послідовності (ап) та (bn) монотонні та обмежені і, отже, мають межі. Нехай Можна показати, що якщо виконані вище сформульовані умови 1 єдиному кореню рівняння / Приклад. Знайти корінь (рівняння г2 - 1 = 0 на відрізку . Таким чином, виконані всі умови, що забезпечують існування єдиного кореня (рівняння х2 - 1 = 0 на відрізку . і метод повинен спрацювати. 8 у нашому випадку а = 0, b = 2). п = I з (4) і (5) знаходимо При п = 2 отримуємо що дає наближення до точного значення кореня (з абсолютною похибкою Вправи Побудуйте графіки функцій: Знайдіть найбільше та найменше значення функцій на заданих відрізках: Досліджуйте поведінку функцій в околицях заданих точок за допомогою похідних вищих порядків: Відповіді
На жаль, не всі студенти та школярі знають і люблять алгебру, але готувати домашні завдання, вирішувати контрольні та складати іспити доводиться кожному. Особливо важко багатьом даються завдання на побудову графіків функцій: якщо десь щось не зрозумів, не довчив, упустив — помилки є неминучими. Але ж кому хочеться отримувати погані оцінки?
Не бажаєте поповнити когорту хвостистів та двієчників? Для цього у вас є 2 шляхи: засісти за підручники та заповнити прогалини знань або скористатися віртуальним помічником — сервісом автоматичної побудови графіків функцій за заданими умовами. З рішенням чи без. Сьогодні ми познайомимо вас із кількома з них.
Найкраще, що є в Desmos.com, це інтерфейс, що гнучко настроюється, інтерактивність, можливість розносити результати по таблицях і безкоштовно зберігати свої роботи в базі ресурсу без обмежень за часом. А недолік — у тому, що сервіс не повністю перекладено російською мовою.
Grafikus.ru
Grafikus.ru - ще один цікавий російськомовний калькулятор для побудови графіків. Причому він будує їх у двовимірному, а й у тривимірному просторі.
Ось неповний перелік завдань, з якими цей сервіс успішно справляється:
- Креслення 2D-графіків простих функцій: прямих, парабол, гіпербол, тригонометричних, логарифмічних і т.д.
- Креслення 2D-графіків параметричних функцій: кіл, спіралей, фігур Ліссажу та інших.
- Креслення 2D-графіків у полярних координатах.
- Побудова 3D поверхонь простих функцій.
- Побудова 3D поверхонь параметричних функцій.
Готовий результат відкривається у окремому вікні. Користувачеві доступні опції скачування, друку та копіювання посилання на нього. Для останнього доведеться авторизуватись на сервісі через кнопки соцмереж.

Координатна площина Grafikus.ru підтримує зміну меж осей, підписів до них, кроку сітки, а також – ширини та висоти самої площини та розміру шрифту.
Найсильніша сторона Grafikus.ru – можливість побудови 3D-графіків. В іншому він працює не гірше і не краще, ніж ресурси-аналоги.
Onlinecharts.ru
Онлайн помічник Onlinecharts.ru будує не графіки, а діаграми практично всіх існуючих видів. В тому числі:
- Лінійні.
- Стовпчасті.
- Кругові.
- З областями.
- Радіальні.
- XY графіки.
- Пухирцеві.
- Крапкові.
- Полярні бульки.
- піраміди.
- Спідометри.
- Стовпчасто-лінійні.

Користуватись ресурсом дуже просто. Зовнішній вигляд діаграми (колір фону, сітки, ліній, покажчиків, форма кутів, шрифти, прозорість, спецефекти тощо) повністю визначається користувачем. Дані для створення можна ввести як вручну, так і імпортувати з таблиці CSV-файлу, що зберігається на комп'ютері. Готовий результат доступний для скачування на ПК у вигляді картинки, PDF-, CSV- або SVG-файлів, а також для збереження онлайн на фотохостингу ImageShack.Us або особистому кабінеті Onlinecharts.ru. Перший варіант можуть використовувати всі, другий лише зареєстровані.
Стоїть завдання: провести повне дослідження функції та побудувати її графік.
Кожен студент пройшов через такі завдання.
Подальший виклад передбачає хороше знання. Рекомендуємо звертатися до цього розділу у разі виникнення питань.
Алгоритм дослідження функції складається з наступних кроків.
- по-перше, знаходимо похідну;
- по-друге, знаходимо критичні точки;
- по-третє, розбиваємо область визначення критичними точками на інтервали;
- по-четверте, визначаємо знак похідної кожному з проміжків. Знак «плюс» буде відповідати проміжку зростання, знак «мінус» - проміжку спадання.
- по-перше, знаходимо другу похідну;
- по-друге, знаходимо нулі чисельника та знаменника другої похідної;
- по-третє, розбиваємо область визначення одержаними точками на інтервали;
- по-четверте, визначаємо знак другої похідної кожному з проміжків. Знак «плюс» буде відповідати проміжку увігнутості, знак «мінус» - проміжку опуклості.
Знаходження області визначення функції.
Це дуже важливий крок дослідження функції, тому що всі подальші дії будуть проводитись на ділянці визначення.
У нашому прикладі потрібно знайти нулі знаменника і виключити їх із дійсних чисел.

(В інших прикладах можуть бути коріння, логарифми тощо. Нагадаємо, що в цих випадках область визначення шукається наступним чином:
для кореня парного ступеня, наприклад, - область визначення перебуває з нерівності;
для логарифму - область визначення перебуває з нерівності).
Дослідження поведінки функції межі області визначення, перебування вертикальних асимптот.
На межах області визначення функція має вертикальні асимптотиякщо в цих граничних точках нескінченні.
У прикладі граничними точками області визначення є .
Досліджуємо поведінку функції при наближенні до цих точок ліворуч та праворуч, для чого знайдемо односторонні межі: 
Оскільки односторонні межі нескінченні, то прямі є вертикальними асимптотами графіка.
Дослідження функції на парність чи непарність.
Функція є парноїякщо . Четність функції свідчить про симетрію графіка щодо осі ординат.
Функція є непарною, якщо ![]() . Непарність функції вказує на симетрію графіка щодо початку координат.
. Непарність функції вказує на симетрію графіка щодо початку координат.
Якщо жодна з рівностей не виконується, то маємо функція загального виду.
У прикладі виконується рівність , отже, наша функція парна. Враховуватимемо це при побудові графіка - він буде симетричний щодо осі oy.
Знаходження проміжків зростання та зменшення функції, точок екстремуму.
Проміжки зростання та зменшення є рішеннями нерівностей і відповідно.
Точки, в яких похідна звертається до нуля, називають стаціонарними.
Критичними точками функціїназивають внутрішні точки області визначення, у яких похідна функції дорівнює нулю чи немає.
ЗАУВАЖЕННЯ(Чи включати критичні точки в проміжки зростання та спадання).
Ми будемо включати критичні точки у проміжки зростання та спадання, якщо вони належать області визначення функції.
Таким чином, щоб визначити проміжки зростання та зменшення функції
Поїхали!
Знаходимо похідну в області визначення (у разі виникнення складнощів, дивіться розділ ). 
Знаходимо критичні точки для цього:
Наносимо ці точки на числову вісь і визначаємо знак похідної всередині кожного отриманого проміжку. Як варіант, можна взяти будь-яку точку з проміжку та обчислити значення похідної у цій точці. Якщо значення позитивне, то ставимо плюсик над цим проміжком і переходимо до наступного, якщо негативне, ставимо мінус і т.д. Наприклад,  Отже, над першим зліва інтервалом ставимо плюс.
Отже, над першим зліва інтервалом ставимо плюс.
Робимо висновок:
Схематично плюсами/мінусами відзначені проміжки де похідна позитивна/негативна. Зростаючі / спадні стрілочки показують напрям зростання / спадання.
Крапками екстремуму функціїє точки, в яких функція визначена та проходячи через які похідна змінює знак.
У прикладі точкою екстремуму є точка х=0 . Значення функції у цій точці дорівнює ![]() . Так як похідна змінює знак з плюсу на мінус при проходженні через точку х = 0 то (0; 0) є точкою локального максимуму. (Якби похідна змінювала знак із мінуса на плюс, то ми мали б точку локального мінімуму).
. Так як похідна змінює знак з плюсу на мінус при проходженні через точку х = 0 то (0; 0) є точкою локального максимуму. (Якби похідна змінювала знак із мінуса на плюс, то ми мали б точку локального мінімуму).
Знаходження проміжків опуклості та увігнутості функції та точок перегину.
Проміжки увігнутості та опуклості функції знаходяться при розв'язках нерівностей та відповідно.
Іноді увігнутість називають опуклістю вниз, а опуклість – опуклістю вгору.
Тут також справедливі зауваження, подібні до зауважень з пункту про проміжки зростання і спадання.
Таким чином, щоб визначити проміжки увігнутості та опуклості функції:
Поїхали!
Знаходимо другу похідну області визначення. 
У прикладі нулів чисельника немає, нулі знаменника .
Наносимо ці точки на числову вісь і визначаємо знак другої похідної всередині кожного отриманого проміжку. 
Робимо висновок:
Крапка називається точкою перегинуякщо в даній точці існує дотична до графіка функції і друга похідна функції змінює знак при проходженні через.
Іншими словами, точками перегину можуть бути точки, проходячи через які друга похідна змінює знак, у самих точках або дорівнює нулю, або немає, але ці точки входять у область визначення функції.
У прикладі точок перегину немає, оскільки друга похідна змінює знак проходячи через точки , що вони входять у область визначення функції.
Знаходження горизонтальних та похилих асимптот.
Горизонтальні чи похилі асимптоти слід шукати лише тоді, коли функція визначена на нескінченності.
Похилі асимптотишукаються у вигляді прямих , де і ![]() .
.
Якщо k=0 і b не дорівнює нескінченності, то похила асимптота стане горизонтальною.
Хто такі взагалі ці асимптоти?
Це лінії, до яких наближається графік функції на нескінченності. Таким чином вони дуже допомагають при побудові графіка функції.
Якщо горизонтальних або похилих асимптот немає, але функція визначена на плюс нескінченності та (або) мінус нескінченності, то слід обчислити межу функції на плюс нескінченності та (або) мінус нескінченності, щоб мати уявлення про поведінку графіка функції.
Для нашого прикладу 
- Горизонтальна асимптота.
На цьому дослідження функції завершується, переходимо до побудови графіка.
Обчислюємо значення функції у проміжних точках.
Для більш точної побудови графіка рекомендуємо знайти кілька значень функції в проміжних точках (тобто в будь-яких точках області визначення функції).
Для нашого прикладу знайдемо значення функції в точках х=-2, х=-1, х=-3/4, х=-1/4. У силу парності функції, ці значення збігатимуться зі значеннями в точках х=2, х=1, х=3/4, х=1/4. 
Побудова графіка.
Спочатку будуємо асимптоти, наносимо точки локальних максимумів та мінімумів функції, точки перегину та проміжні точки. Для зручності побудови графіка можна нанести і схематичне позначення проміжків зростання, спадання, опуклості та увігнутості, не дарма ж ми проводили дослідження функції =). 
Залишилося провести лінії графіка через зазначені точки, наближаючи до асимптотів і слідуючи стрілочкам. 
Цим шедевром образотворчого мистецтва завдання повного дослідження функції та побудови графіка закінчено.
p align="justify"> Графіки деяких елементарних функцій можна будувати з використанням графіків основних елементарних функцій.
Якщо завдання необхідно провести повне дослідження функції f (x) = x 2 4 x 2 - 1 з побудовою його графіка, тоді розглянемо цей принцип докладно.
Для вирішення завдання даного типу слід використовувати властивості та графіки основних елементарних функцій. Алгоритм дослідження включає кроки:
Знаходження області визначення
Оскільки дослідження проводяться на області визначення функції, необхідно розпочинати з цього кроку.
Приклад 1
Заданий приклад передбачає знаходження нулів знаменника у тому, щоб виключити їх із ОДЗ.
4 x 2 - 1 = 0 x = ± 1 2 ⇒ x ∈ - ∞; - 1 2 ∪ - 1 2; 1 2 ∪ 1 2; + ∞
В результаті можна отримати коріння, логарифми, і таке інше. Тоді ОДЗ можна шукати для кореня парного ступеня типу g (x) 4 за нерівністю g (x) ≥ 0 для логарифму log a g (x) за нерівністю g (x) > 0 .
Дослідження меж ОДЗ та знаходження вертикальних асимптот
На межах функції є вертикальні асимптоти, коли односторонні межі таких точках нескінченні.
Приклад 2
Наприклад розглянемо прикордонні точки, рівні x = ± 1 2 .
Тоді необхідно проводити дослідження функції для знаходження односторонньої межі. Тоді отримуємо, що: lim x → - 1 2 - 0 f (x) = lim x → - 1 2 - 0 x 2 4 x 2 - 1 = = lim x → - 1 2 - 0 x 2 (2 x - 1 ) (2 x + 1) = 1 4 (-2) · - 0 = + ∞ lim x → - 1 2 + 0 f (x) = lim x → - 1 2 + 0 x 2 4 x - 1 = = lim x → - 1 2 + 0 x 2 (2 x - 1) (2 x + 1) = 1 4 (- 2) · (+ 0) = - ∞ lim x → 1 2 - 0 f (x) = lim x → 1 2 - 0 x 2 4 x 2 - 1 = = lim x → 1 2 - 0 x 2 (2 x - 1) (2 x + 1) = 1 4 (- 0) · 2 = - ∞ lim x → 1 2 - 0 f(x) = lim x → 1 2 - 0 x 2 4 x 2 - 1 = = lim x → 1 2 - 0 x 2 (2 x - 1) (2 x + 1) = 1 4 ( + 0) · 2 = + ∞
Звідси видно, що односторонні межі є нескінченними, отже, прямі x = ± 1 2 - вертикальні асимптоти графіка.
Дослідження функції та на парність чи непарність
Коли виконується умова y(-x) = y(x), функція вважається парною. Це свідчить, що графік розташовується симетрично щодо Про у. Коли виконується умова y(-x) = -y(x), функція вважається непарною. Отже, симетрія йде щодо початку координат. При невиконанні хоча б однієї нерівності отримуємо функцію загального виду.
Виконання рівності y(-x) = y(x) говорить про те, що функція парна. При побудові необхідно врахувати, що буде симетричність щодо У.
Для вирішеннянерівності застосовуються проміжки зростання та спадання з умовами f "(x) ≥ 0 і f "(x) ≤ 0 відповідно.
Визначення 1
Стаціонарні точки- Це такі точки, які звертають похідну в нуль.
Критичні точки- це внутрішні точки з області визначення, де похідна функції дорівнює нулю чи немає.
При вирішенні необхідно враховувати такі зауваження:
- при наявних проміжках зростання та спадання нерівності виду f "(x) > 0 критичні точки до рішення не включаються;
- точки, в яких функція визначена без кінцевої похідної, необхідно включати в проміжки зростання та спадання (наприклад, y = x 3 , де точка х = 0 робить функцію певною, похідна має значення нескінченності у цій точці, y " = 1 3 · x 2 3 , y "(0) = 10 = ∞, х = 0 включається в проміжок зростання);
- щоб уникнути розбіжностей, рекомендовано користуватися математичною літературою, яка рекомендована міністерством освіти.
Включення критичних точок у проміжки зростання і спадання у разі, якщо вони задовольняють області визначення функції.
Визначення 2
Для визначення проміжків зростання та зменшення функції необхідно знайти:
- похідну;
- критичні точки;
- розбити область визначення за допомогою критичних точок на інтервали;
- визначити знак похідної кожному з проміжків, де + є зростанням, а - є спаданням.
Приклад 3
Знайти похідну в області визначення f "(x) = x 2 "(4 x 2 - 1) - x 2 4 x 2 - 1 "(4 x 2 - 1) 2 = - 2 x (4 x 2 - 1) 2 .
Рішення
Для вирішення потрібно:
- знайти стаціонарні точки, даний приклад має в своєму розпорядженні х = 0;
- знайти нулі знаменника, приклад набуває значення нуль при x = ± 1 2 .
Виставляємо крапки на числовій осі для визначення похідної на кожному проміжку. Для цього достатньо взяти будь-яку точку з проміжку та зробити обчислення. При позитивному результаті графіку зображаємо + , що означає зростання функції, а - означає її спадання.
Наприклад, f "(- 1) = - 2 · (- 1) 4 - 1 2 - 1 2 = 2 9 > 0 , отже, перший інтервал зліва має знак +. Розглянемо на числовий прямий.
Відповідь:
- відбувається зростання функції на проміжку - ∞; - 1 2 і (- 1 2; 0];
- відбувається убування на проміжку [0; 1 2) та 1 2 ; + ∞.
На схемі з допомогою + і - зображується позитивність і негативність функції, а стрілочки – спадання і зростання.
Точки екстремуму функції – точки, де функція визначена і якими похідна змінює знак.
Приклад 4
Якщо розглянути приклад, де х = 0 тоді значення функції в ній дорівнює f (0) = 0 2 4 · 0 2 - 1 = 0 . При зміні знака похідної з + на - і проходження через точку х = 0 тоді точка з координатами (0 ; 0) вважається точкою максимуму. При зміні знака з – на + отримуємо точку мінімуму.
Випуклість і увігнутість визначається при розв'язанні нерівностей виду f "" (x) ≥ 0 і f "" (x) ≤ 0 . Рідше використовують назву опуклість вниз замість увігнутості, а опуклість вгору замість опуклості.
Визначення 3
Для визначення проміжків увігнутості та опуклостінеобхідно:
- знайти другу похідну;
- знайти нулі функції другої похідної;
- розбити область визначення точками, що з'явилися, на інтервали;
- визначити знак проміжку.
Приклад 5
Знайти другу похідну в галузі визначення.
Рішення
f " " (x) = - 2 x (4 x 2 - 1) 2 " = = (- 2 x) " (4 x 2 - 1) 2 - - 2 x 4 x 2 - 1 2 " (4 x 2 - 1) 4 = 24 x 2 + 2 (4 x 2 - 1) 3
Знаходимо нулі чисельника та знаменника, де на прикладі нашого прикладу маємо, що нулі знаменника x = ± 1 2
Тепер необхідно нанести крапки на числову вісь та визначити знак другої похідної з кожного проміжку. Отримаємо, що

Відповідь:
- функція є опуклою з проміжку - 1 2; 1 2;
- функція є увігнутою з проміжків - ∞; - 1 2 і 1 2; + ∞.
Визначення 4
Точка перегину- Це точка виду x 0; f(x0) . Коли в ній є дотична до графіка функції, то її проходження через x 0 функція змінює знак на протилежний.
Інакше висловлюючись, це така точка, якою проходить друга похідна і змінює знак, а самих точках дорівнює нулю чи немає. Усі точки вважаються областю визначення функції.
У прикладі було видно, що точки перегину відсутні, оскільки друга похідна змінює знак під час проходження через точки x = ± 12. Вони, своєю чергою, до області визначення не входять.
Знаходження горизонтальних та похилих асимптот
При визначенні функції на нескінченності потрібно шукати горизонтальні та похилі асимптоти.
Визначення 5
Похилі асимптотизображуються за допомогою прямих, заданих рівнянням y = k x + b , де k = lim x → f (x) x і b = lim x → f (x) - k x .
При k = 0 і b, не рівному нескінченності, отримуємо, що похила асимптота стає горизонтальною.
Інакше висловлюючись, асимптотами вважають лінії, яких наближається графік функції на нескінченності. Це сприяє швидкій побудові графіка функції.
Якщо асимптоти відсутні, але функція визначається на обох нескінченностях, необхідно порахувати межу функції на цих нескінченностях, щоб зрозуміти, як поводитиметься графік функції.
Приклад 6
На прикладі розглянемо, що
k = lim x → ∞ f (x) x = lim x → ∞ x 2 4 x 2 - 1 x = 0 b = lim x → ∞ (f (x) - k x) = lim x → ∞ x 2 4 x 2 - 1 = 1 4 ⇒ y = 1 4
є горизонтальною асимптотою. Після дослідження функції можна приступати до її побудови.
Обчислення значення функції у проміжних точках
Щоб побудова графіка була найточнішою, рекомендовано знаходити кілька значень функції у проміжних точках.
Приклад 7
З розглянутого нами прикладу необхідно визначити значення функції в точках х = - 2, х = - 1, х = - 3 4, х = - 1 4 . Так як функція парна, отримаємо, що значення збігатимуться зі значеннями в цих точках, тобто отримаємо х = 2, х = 1, х = 34, х = 14.
Запишемо і вирішимо:
F (- 2) = f (2) = 2 2 4 · 2 2 - 1 = 4 15 ≈ 0 , 27 f (- 1) - f (1) = 1 2 4 · 1 2 - 1 = 1 3 ≈ 0 , 33 f - 3 4 = f 3 4 = 3 4 2 4 3 4 2 - 1 = 9 20 = 0 , 45 f - 1 4 = f 1 4 = 1 4 2 4 · 1 4 2 - 1 = - 1 12 ≈ - 0 , 08
Для визначення максимумів та мінімумів функції, точок перегину, проміжних точок необхідно будувати асимптоти. Для зручного позначення фіксуються проміжки зростання, спадання, опуклість, увігнутість. Розглянемо малюнку, зображеному нижче.

Необхідно через зазначені точки проводити лінії графіка, що дозволить наблизити до асимптотів, слідуючи стрілочкам.

У цьому закінчується повне дослідження функції. Трапляються випадки побудови деяких елементарних функцій, для яких застосовують геометричні перетворення.
Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl+Enter
 Сфера, куля, сегмент та сектор
Сфера, куля, сегмент та сектор Спеціальність «Сестринська справа» (бакалаврат)
Спеціальність «Сестринська справа» (бакалаврат)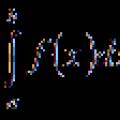 Найпростіші властивості інтегралів
Найпростіші властивості інтегралів