2. Рівняння прямої - види рівняння прямої: проходить через точку, загальне, канонічне, параметричне і т.д.
Визначення.У декартовій прямокутній системі координат вектор з компонентами (А, В) перпендикулярний до прямої, заданої рівнянням Ах + Ву + С = 0.
приклад. Знайти рівняння прямої, що проходить через точку А(1, 2) перпендикулярно до вектора (3, -1).
Рішення. Складемо при А = 3 і В = -1 рівняння прямої: 3х - у + С = 0. Для знаходження коефіцієнта С підставимо в отриманий вираз координати заданої точки А. Отримуємо: 3 - 2 + C = 0, отже С = -1. Разом: шукане рівняння: 3х - у - 1 = 0.
Рівняння пряме, що проходить через дві точки
Нехай у просторі задані дві точки M 1 (x 1 , y 1 , z 1) і M 2 (x 2 , y 2 , z 2), тоді рівняння прямої, що проходить через ці точки:

Якщо якийсь із знаменників дорівнює нулю, слід прирівняти нулю відповідний чисельник. На площині записане вище рівняння прямої спрощується

якщо х 1 ≠ х 2 і х = х 1 якщо х 1 = х 2 .
Дроб = k називається кутовим коефіцієнтомпрямий.
приклад. Знайти рівняння прямої, що проходить через точки А(1, 2) та В(3, 4).
Рішення.Застосовуючи записану вище формулу, отримуємо:

Рівняння прямої за точкою та кутовим коефіцієнтом
Якщо загальне рівняння прямої Ах + Ву + С = 0 привести до вигляду:

та позначити  , то отримане рівняння називається рівнянням прямої з кутовим коефіцієнтомk.
, то отримане рівняння називається рівнянням прямої з кутовим коефіцієнтомk.
Рівняння прямої по точці та напрямному вектору
За аналогією з пунктом, що розглядає рівняння прямої через вектор нормалі, можна ввести завдання прямої через точку і напрямний вектор прямої.
Визначення.Кожен ненульовий вектор (α 1 , α 2), компоненти якого задовольняють умові А α 1 + В α 2 = 0 називається напрямним вектором прямої
Ах + Ву + З = 0.
приклад. Знайти рівняння прямої з напрямним вектором (1, -1) і проходить через точку А(1, 2).
Рішення.Рівняння шуканої прямої будемо шукати у вигляді: Ax + By + C = 0. Відповідно до визначення, коефіцієнти повинні задовольняти умови:
1 * A + (-1) * B = 0, тобто. А = В.
Тоді рівняння прямої має вигляд: Ax + Ay + C = 0, або x + y + C / A = 0. при х = 1, у = 2 отримуємо С/A = -3, тобто. шукане рівняння:
Рівняння прямої у відрізках
Якщо в загальному рівнянні прямий Ах + Ву + С = 0 С 0, то, розділивши на -С, отримаємо:  або
або

Геометричний сенс коефіцієнтів у тому, що коефіцієнт а є координатою точки перетину прямої з віссю Ох, а b - Координацією точки перетину прямий з віссю Оу.
приклад.Задано загальне рівняння прямої х – у + 1 = 0. Знайти рівняння цієї прямої у відрізках.
С = 1, а = -1, b = 1.
Нормальне рівняння прямої
Якщо обидві частини рівняння Ах + Ву + С = 0 розділити на число  , Яке називається нормуючим множником, то отримаємо
, Яке називається нормуючим множником, то отримаємо
xcosφ + ysinφ - p = 0 -
нормальне рівняння прямої. Знак ± нормуючого множника треба вибирати так, щоб μ*С< 0. р – длина перпендикуляра, опущенного из начала координат на прямую, а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.
приклад. Дано загальне рівняння прямої 12х - 5у - 65 = 0. Потрібно написати різні типи рівнянь цієї прямої.
рівняння цієї прямої у відрізках: 
рівняння цієї прямої з кутовим коефіцієнтом: (ділимо на 5)

нормальне рівняння прямої:
 ; cos φ = 12/13; sin φ= -5/13; p = 5.
; cos φ = 12/13; sin φ= -5/13; p = 5.
C слід зазначити, що не кожну пряму можна уявити рівнянням у відрізках, наприклад, прямі, паралельні осям або проходять через початок координат.
приклад. Пряма відсікає на координатних осях рівні позитивні відрізки. Скласти рівняння прямої, якщо площа трикутника, утвореного цими відрізками, дорівнює 8 см 2 .
Рішення.Рівняння прямої має вигляд: , ab/2 = 8; a = 4; -4. a = -4 не підходить за умовою завдання. Разом: або х + у - 4 = 0.
приклад. Скласти рівняння прямої, що проходить через точку А(-2, -3) та початок координат.
Рішення.
Рівняння прямої має вигляд:  де х 1 = у 1 = 0; x 2 = -2; y 2 = -3.
де х 1 = у 1 = 0; x 2 = -2; y 2 = -3.
Розглянемо, як скласти рівняння прямої, що проходить через дві точки на прикладах.
приклад 1.
Скласти рівняння прямої, що проходить через точки A(-3; 9) та B(2;-1).
1 спосіб - складемо рівняння прямої з кутовим коефіцієнтом.
Рівняння прямої з кутовим коефіцієнтом має вигляд. Підставивши координати точок A і B у рівняння прямої (x= -3 та y=9 — у першому випадку, x=2 та y= -1 — у другому), отримуємо систему рівнянь, з якої знаходимо значення k і b:
Склавши почленно 1-е та 2-е рівняння, отримаємо: -10 = 5k, звідки k = -2. Підставивши до другого рівняння k= -2, знайдемо b: -1=2·(-2)+b, b=3.
Таким чином, y=-2x+3 - шукане рівняння.
2 спосіб - складемо загальне рівняння прямої.
Загальне рівняння прямої має вигляд. Підставивши координати точок A та B у рівняння, отримуємо систему:
Оскільки кількість невідомих більша за кількість рівнянь, система не можна розв'язати. Але можна всі змінні висловити через одну. Наприклад, через b.
Помноживши перше рівняння системи на -1 і склавши почленно з другим:
отримаємо: 5a-10b = 0. Звідси a = 2b.
Підставимо отриманий вираз у друге рівняння: 2 · 2b -b + c = 0; 3b+c=0; c=-3b.
Підставляємо a = 2b, c = -3b рівняння ax + by + c = 0:
2bx+by-3b=0. Залишилося розділити обидві частини на b:
Загальне рівняння прямої легко приводиться до рівняння прямої з кутовим коефіцієнтом:
3 спосіб - складемо рівняння прямої, що проходить через 2 точки.
Рівняння прямої, що проходить через дві точки, має:
![]()
Підставимо в це рівняння координати точок A(-3; 9) та B(2;-1)
(тобто x 1 = -3, y 1 = 9, x 2 = 2, y 2 = -1):
![]()
і спростимо:
звідки 2x+y-3=0.
У шкільному курсі найчастіше використовується рівняння прямої з кутовим коефіцієнтом. Але найпростіший спосіб - вивести і використовувати формулу рівняння прямої, що проходить через дві точки.
Зауваження.
Якщо під час встановлення координат заданих точок один із знаменників рівняння
![]()
виявиться рівним нулю, то шукане рівняння виходить прирівнюємо до нуля відповідного чисельника.
приклад 2.
Скласти рівняння прямої, що проходить через дві точки C(5;-2) та D(7;-2).
Підставляємо в рівняння прямої, що проходить через 2 точки координати точок C і D.
Ця стаття є частиною теми рівняння прямої на площині. Тут ми розберемо з усіх боків: почнемо з доказу теореми, яка задає вигляд загального рівняння прямої, далі розглянемо неповне загальне рівняння прямої, наведемо приклади неповних рівнянь прямої з графічними ілюстраціями, на закінчення зупинимося на переході від загального рівняння прямої до інших видів і наведемо докладні рішення характерних завдань на складання загального рівняння прямої.
Навігація на сторінці.
Загальне рівняння прямої – основні відомості.
Розберемо цей алгоритм під час вирішення прикладу.
приклад.
Напишіть параметричні рівняння прямої, яка задана загальним рівнянням прямої ![]() .
.
Рішення.
Спочатку наведемо вихідне загальне рівняння прямої до канонічного рівняння прямої:
Тепер приймаємо ліву та праву частини отриманого рівняння рівними параметру. Маємо 
Відповідь:

Із загального рівняння прямого виду отримати рівняння прямої з кутовим коефіцієнтом можливо лише тоді, коли . Що потрібно зробити для переходу? По-перше, в лівій загального рівняння прямий залишити тільки доданок, інші доданки потрібно перенести у праву частину з протилежним знаком: ![]() . По-друге, розділити обидві частини отриманої рівності на число B, яке відмінно від нуля,
. По-друге, розділити обидві частини отриманої рівності на число B, яке відмінно від нуля, ![]() . І все.
. І все.
приклад.
Пряму в прямокутній системі координат Oxy задає загальне рівняння прямої. Отримайте рівняння цієї прямої з кутовим коефіцієнтом.
Рішення.
Проведемо необхідні дії: .
Відповідь:
Коли пряма задана повним загальним рівнянням прямої, легко отримати рівняння прямої у відрізках виду . Для цього переносимо число С у праву частину рівності з протилежним знаком, ділимо обидві частини отриманої рівності на -С, і в ув'язненні переносимо в знаменники коефіцієнти при змінних x і y: 
Розглянемо рівняння прямої проходить через точку та нормальний вектор. Нехай у системі координат задана точка та ненульовий вектор (рис. 1).
Визначення
Як бачимо, існує єдина пряма , що проходить через точку перпендикулярно до напрямку вектора (у цьому випадку називають нормальним векторомпрямий).

Мал. 1
Доведемо, що лінійне рівняння
це рівняння прямої , тобто координати кожної точки прямої задовольняють рівняння (1), але координати точки, що не лежить на рівняння (1) не задовольняють.
Для доказу звернемо увагу, що скалярний добуток векторів і = в координатній формі збігається з лівою частиною рівняння (1).
Далі використовуємо очевидну властивість прямої: вектори і перпендикулярні тоді, і тільки тоді, коли точка лежить на . А за умови перпендикулярності обох векторів їх скалярний твір (2) перетворюється на всіх точок , що лежать на , і тільки для них. Отже, (1) – рівняння прямої .
Визначення
Рівняння (1) називається рівнянням прямої, що проходить через цю точкуіз нормальним вектором = .
Перетворимо рівняння (1)
Позначивши = , отримаємо
Отже, прямий лінії відповідає лінійне рівняння виду (3). Навпаки, за цим рівнянням виду (3), де хоча б один із коефіцієнтів і не дорівнює нулю, можна побудувати пряму.
Справді, хай пара чисел задовольняє рівняння (3), тобто
Віднімаючи останнє від (3), отримаємо співвідношення , яке визначає пряму за вектором та точкою .
Дослідження загального рівняння прямої
Корисно знати особливості розміщення прямий окремих випадках, коли одне чи два з чисел рівні нулю.
1. Загальне рівняння виглядає так: . Йому задовольняє точка, отже, пряма проходить через початок координат. Його можна записати: = x (див. рис. 2).

Мал. 2
Вважаємо, що:
Якщо покласти , тоді виходить ще одна точка (див. рис. 2).
2. , тоді рівняння має такий вигляд , де = –. Нормальний вектор лежить на осі, пряма. Таким чином, пряма перпендикулярна в точці або паралельна осі (див. рис. 3). Зокрема, якщо і тоді, і рівняння - це рівняння осі ординат.

Мал. 3
3. Аналогічно, при рівнянні записується , де . Вектор належить осі. Пряма у точці (рис. 4).

Якщо ж, тоді рівняння осі.
Дослідження можна сформулювати у такій формі: пряма паралельна до тієї координатної осі, зміна якої в загальному рівнянні прямої відсутня.
Наприклад:
Побудуємо пряму за загальним рівнянням за умови, що нерівні нулю. Для цього достатньо знайти дві точки, що лежать на цій прямій. Такі точки іноді зручніше знаходити на координатних осях.
Припустимо, тоді = -.
При , Тоді = -.
Позначимо - = , - = . Знайдені точки та . Відкладемо на осях і через них проведемо пряму (див. рис. 5).

Мал. 5
Від загального можна перейти до рівняння, до якого входитимуть числа та :
І тоді виходить:
Або, згідно з позначенням, отримаємо рівняння,
Яке називається рівнянням прямої у відрізках. Числа та з точністю до знака дорівнюють відрізкам, які відсікаються прямою на координатних осях.
Рівняння прямої з кутовим коефіцієнтом
Щоб дізнатися, що таке рівняння прямої з кутовим коефіцієнтом, розглянемо рівняння (1):
Позначивши – = , отримаємо
рівняння прямої, яка проходить через точку у заданому напрямку. Геометричне зміст коефіцієнта зрозуміло з рис. 6.
У = = , де – найменший кут, який потрібно повернути позитивний напрямок осі навколо загальної точки до поєднання її з прямої . Очевидно, якщо кут – гострий, тоді title="Rendered by QuickLaTeX.com" height="17" width="97" style="vertical-align: -4px;">; если же – тупой угол, тогда .!}
Розкриємо дужки в (5) і спростимо його:
де. Співвідношення (6) – рівняння прямий з кутовим коефіцієнтом. При , - Відрізок, який відсікає пряму на осі (див. рис. 6).
Зверніть увагу!
Для переходу від загального рівняння до рівняння прямої з кутовим коефіцієнтом необхідно спочатку вирішити щодо .

Мал. 6
= - x + - =
де зазначено = -, = -. Якщо ж , тоді дослідження загального рівняння вже відомо, що така пряма перпендикулярна осі .
Розглянемо канонічний рівняння прямий за допомогою прикладу.
Нехай у системі координат задана точка та ненульовий вектор (рис. 7).

Мал. 7
Необхідно скласти рівняння прямої, що проходить через точку паралельно вектору, який називається напрямним вектором. Довільна точка належить цій прямій і тоді, коли . Оскільки вектор – заданий, а вектор , тоді за умовою паралельності, координати цих векторів пропорційні, тобто:
Визначення
Співвідношення (7) називається рівнянням прямої, яка проходить через задану точку в заданому напрямку або канонічного рівняння прямої.
Зауважимо, що до рівняння виду (7) можна перейти, наприклад, від рівняння пучка прямих (4)
або від рівняння прямої через точку та нормальний вектор (1):
Вище передбачалося, що напрямний вектор – ненульовий, але може статися, що з його координат, наприклад, . Тоді вираз (7) формально запишеться:
який взагалі немає сенсу. Однак, приймають та отримують рівняння прямої перпендикулярної осі . Справді, з рівняння видно, що пряма визначена точкою та напрямним вектором перпендикулярним осі . Якщо у цьому рівнянні звільнитися від знаменника, тоді отримаємо:
Або - рівняння прямої, перпендикулярної осі. Аналогічно було б отримано для вектора.
Параметричне рівняння прямої
Щоб зрозуміти, що таке параметричне рівняння прямої, необхідно повернутись до рівняння (7) і прирівняти кожен дріб (7) до параметра . Так як хоча б один із знаменників у (7) не дорівнює нулю, а відповідний чисельник може набувати довільних значень, тоді область зміни параметра – вся числова вісь.
Визначення
Рівняння (8) називається параметричним рівнянням прямої.
Приклади завдань на пряму лінію
Звичайно ж, складно щось вирішити виключно за визначеннями, адже потрібно вирішити самостійно хоча б кілька прикладів або завдань, які допоможуть закріпити пройдений матеріал. Тому давайте розберемо основні завдання на пряму лінію, оскільки схожі завдання часто трапляються на іспитах та заліках.
Канонічне та параметричне рівняння
Приклад 1
На прямій лінії заданої рівнянням знайти точку , які знаходяться від точки цієї прямої на відстані 10 одиниць.
Рішення:
Нехай шуканаточка пряма, тоді для відстані запишемо . За умови . Оскільки точка належить прямий , яка має нормальний вектор , тоді рівняння прямий можна записати: = = і далі виходить:
Тоді відстань. За умови , або . З параметричного рівняння:
Приклад 2
Завдання
Крапка рухається рівномірно зі швидкістю за напрямом вектора від початкової точки. Знайти координати точки через від початку руху.
Рішення
Спочатку потрібно знайти одиничний вектор. Його координати - це напрямні косинуси:
Тоді вектор швидкості:
X = x =.
Канонічне рівняння прямої тепер запишеться:
= = , = - Параметричне рівняння. Після цього потрібно скористатися параметричним рівнянням прямої при .
Рішення:
Рівняння прямої, яка проходить через точку, знаходимо за формулою пучка прямих , де кутовий коефіцієнтдля прямої і = для прямої.
Враховуючи малюнок, де видно, що між прямими і – два кути: один гострий, а другий – тупий. Згідно з формулою (9) - це той кут між прямими і , на який потрібно повернути пряму проти годинникової стрілки щодо їх точки перетину до поєднання її з прямою.

Отже, формулу згадали, з кутами розібралися і тепер можна повернутись до нашого прикладу. Отже, враховуючи формулу (9) знаходимо спочатку рівняння катета .

Так як поворот прямої на кут проти годинникової стрілки щодо точки призводить до суміщення з прямою тоді в формулі (9) а . З рівняння:
За формулою пучка рівняння прямої запишеться:
Аналогічно знаходимо , а ,
Рівняння прямої:
Рівняння прямої - види рівняння прямої: проходить через точку, загальне, канонічне, параметричне і т.д.оновлено: 22 листопада, 2019 автором: Статті.Ру
Властивості прямої в евклідовій геометрії.
Через будь-яку точку можна провести безліч прямих.
Через будь-які дві точки, що не збігаються, можна провести єдину пряму.
Дві несхожі прямі на площині або перетинаються в єдиній точці, або є
паралельними (випливає з попереднього).
У тривимірному просторі існують три варіанти взаємного розташування двох прямих:
- прямі перетинаються;
- прямі паралельні;
- прямі схрещуються.
Пряма лінія— крива алгебри першого порядку: в декартовій системі координат пряма лінія
задається на площині рівнянням першого ступеня (лінійне рівняння).
Загальне рівняння прямої.
Визначення. Будь-яка пряма на площині може бути задана рівнянням першого порядку
Ах + Ву + С = 0,
причому постійні А, Вне дорівнюють нулю одночасно. Це рівняння першого порядку називають загальним
рівнянням прямої.Залежно від значень постійних А, Ві Зможливі такі окремі випадки:
. C = 0, А ≠0, В ≠ 0- Пряма проходить через початок координат
. А = 0, В ≠0, С ≠0 ( By + C = 0)- Пряма паралельна осі Ох
. В = 0, А ≠ 0, С ≠ 0 (Ax + C = 0)- Пряма паралельна осі Оу
. В = С = 0, А ≠0- Пряма збігається з віссю Оу
. А = С = 0, В ≠0- Пряма збігається з віссю Ох
Рівняння прямої може бути представлене в різному вигляді залежно від будь-яких заданих
початкових умов.
Рівняння прямої за точкою та вектором нормалі.
Визначення. У декартовій системі прямокутної координат вектор з компонентами (А, В)
перпендикулярний до прямої, заданої рівнянням
Ах + Ву + З = 0.
приклад. Знайти рівняння прямої, що проходить через точку А(1, 2)перпендикулярно вектору (3, -1).
Рішення. Складемо при А = 3 і В = -1 рівняння прямої: 3х - у + С = 0. Для знаходження коефіцієнта С
підставимо в отриманий вираз координати заданої точки А. Отримуємо: 3 - 2 + C = 0, отже
З = -1. Разом: шукане рівняння: 3х - у - 1 = 0.
Рівняння пряме, що проходить через дві точки.
Нехай у просторі задані дві точки M 1 (x 1 , y 1 , z 1)і M2 (x 2, y 2 , z 2),тоді рівняння прямої,
проходить через ці точки:
Якщо один із знаменників дорівнює нулю, слід прирівняти нулю відповідний чисельник. на
площині записане вище рівняння прямої спрощується:

якщо х 1 ≠ х 2і х = х 1, якщо х 1 = х 2 .
Дріб = kназивається кутовим коефіцієнтом прямий.
приклад. Знайти рівняння прямої, що проходить через точки А(1, 2) та В(3, 4).
Рішення. Застосовуючи записану вище формулу, отримуємо:

Рівняння прямої за точкою та кутовим коефіцієнтом.
Якщо загальне рівняння прямої Ах + Ву + С = 0привести до вигляду:

та позначити  , то отримане рівняння називається
, то отримане рівняння називається
рівнянням прямої з кутовим коефіцієнтом k.
Рівняння прямої по точці та напрямному вектору.
За аналогією з пунктом, що розглядає рівняння прямої через вектор нормалі, можна ввести завдання
прямий через точку та напрямний вектор прямий.
Визначення. Кожен ненульовий вектор (α 1 , α 2), компоненти якого задовольняють умові
Аα 1 + Вα 2 = 0називається напрямний вектор прямий.
Ах + Ву + З = 0.
приклад. Знайти рівняння прямої з напрямним вектором (1, -1) і проходить через точку А(1, 2).
Рішення. Рівняння шуканої прямої шукатимемо у вигляді: Ax+By+C=0.Відповідно до визначення,
коефіцієнти повинні задовольняти умови:
1 * A + (-1) * B = 0, тобто. А = В.
Тоді рівняння прямої має вигляд: Ax + Ay + C = 0,або x + y + C/A = 0.
при х = 1, у = 2отримуємо С/A = -3, тобто. шукане рівняння:
х + у - 3 = 0
Рівняння прямої у відрізках.
Якщо в загальному рівнянні прямий Ах + Ву + С = 0 С 0, то, розділивши на -С, отримаємо:
 або , де
або , де

Геометричний зміст коефіцієнтів у тому, що коефіцієнт а є координатою точки перетину
прямий з віссю Ох,а b- координатою точки перетину прямої з віссю Оу.
приклад. Задано загальне рівняння прямої х – у + 1 = 0.Знайти рівняння цієї прямої у відрізках.
С = 1, а = -1, b = 1.
Нормальне рівняння прямої.
Якщо обидві частини рівняння Ах + Ву + С = 0розділити на число  , Яке називається
, Яке називається
нормуючим множником, то отримаємо
xcosφ + ysinφ - p = 0 -нормальне рівняння прямої.
Знак ± нормуючого множника треба вибирати так, щоб μ * С< 0.
р- Довжина перпендикуляра, опущеного з початку координат на пряму,
а φ - Кут, утворений цим перпендикуляром з позитивним напрямом осі Ох.
приклад. Дано загальне рівняння прямої 12х - 5у - 65 = 0. Потрібно написати різні типи рівнянь
цієї прямої.
Рівняння цієї прямої у відрізках:

Рівняння цієї прямої з кутовим коефіцієнтом: (ділимо на 5)

Рівняння прямої:

cos φ = 12/13; sin φ= -5/13; p = 5.
Слід зазначити, що не кожну пряму можна уявити рівнянням у відрізках, наприклад, прямі,
паралельні осям або проходять через початок координат.
Кут між прямими на площині.
Визначення. Якщо задані дві прямі y = k 1 x + b 1 , y = k 2 x + b 2, то гострий кут між цими прямими
визначатиметься як

Дві прямі паралельні, якщо k 1 = k 2. Дві прямі перпендикулярні,
якщо k 1 = -1/ k 2 .
Теорема.
Прямі Ах + Ву + С = 0і А 1 х + В 1 у + С 1 = 0паралельні, коли пропорційні коефіцієнти
А 1 = λА, 1 = λВ. Якщо ще й З 1 = λС, То прямі збігаються. Координати точки перетину двох прямих
перебувають як розв'язання системи рівнянь цих прямих.
Рівняння прямої, що проходить через дану точку перпендикулярно даної прямої.
Визначення. Пряма, що проходить через точку М 1 (х 1, у 1)і перпендикулярна до прямої у = kx + b
є рівнянням:

Відстань від точки до прямої.
Теорема. Якщо задана точка М(х 0 у 0),та відстань до прямої Ах + Ву + С = 0визначається як:

Доведення. Нехай крапка М 1 (х 1, у 1)- основа перпендикуляра, опущеного з точки Мна задану
пряму. Тоді відстань між точками Мі М 1:
![]() (1)
(1)
Координати x 1і у 1можуть бути знайдені як розв'язання системи рівнянь:

Друге рівняння системи - це рівняння прямої, що проходить через задану точку М0 перпендикулярно
заданої прямої. Якщо перетворити перше рівняння системи на вигляд:
A(x - x 0) + B(y - y 0) + Ax 0 + By 0 + C = 0,
то, вирішуючи, отримаємо:

Підставляючи ці вирази рівняння (1), знаходимо:

Теорему доведено.
 Микола Мартинов, який убив на дуелі М
Микола Мартинов, який убив на дуелі М Проекції вектора переміщення Модуль переміщення тіла за час
Проекції вектора переміщення Модуль переміщення тіла за час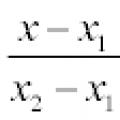 Рівняння прямої - види рівняння прямої: проходить через точку, загальне, канонічне, параметричне і т.п.
Рівняння прямої - види рівняння прямої: проходить через точку, загальне, канонічне, параметричне і т.п.