Bàn sin 60 độ. Hình sin, côsin, tiếp tuyến và phương diện - mọi thứ bạn cần biết tại OGE và SỬ DỤNG

Lượng giác, như một môn khoa học, có nguồn gốc từ phương Đông cổ đại. Các tỷ lệ lượng giác đầu tiên được phát triển bởi các nhà thiên văn học để tạo ra một lịch chính xác và định hướng bởi các vì sao. Các phép tính này liên quan đến lượng giác mặt cầu, trong quá trình học ở trường, các em học tỉ số các cạnh và góc của một tam giác phẳng.

Lượng giác là một nhánh của toán học liên quan đến các tính chất của các hàm lượng giác và mối quan hệ giữa các cạnh và góc của tam giác.

Trong thời kỳ hoàng kim của văn hóa và khoa học vào thiên niên kỷ 1 sau Công nguyên, kiến ​​thức đã lan truyền từ Phương Đông cổ đại đến Hy Lạp. Nhưng những khám phá chính về lượng giác là công lao của những người đàn ông của Caliphate Ả Rập. Đặc biệt, nhà khoa học người Thổ Nhĩ Kỳ al-Marazvi đã giới thiệu các hàm như tiếp tuyến và cotang, biên soạn các bảng giá trị đầu tiên cho sin, tiếp tuyến và cotang. Các nhà khoa học Ấn Độ đưa ra khái niệm sin và cosin. Rất nhiều sự chú ý được dành cho lượng giác trong các tác phẩm của những nhân vật vĩ đại thời cổ đại như Euclid, Archimedes và Eratosthenes.

Các đại lượng cơ bản của lượng giác

Các hàm lượng giác cơ bản của một đối số là sin, cosin, tiếp tuyến và cotang. Mỗi người trong số họ có đồ thị riêng: sin, cosine, tiếp tuyến và cotang.

Các công thức tính giá trị của các đại lượng này dựa trên định lý Pitago. Học sinh được biết đến nhiều hơn trong công thức: “Quần Pythagore, bằng nhau về mọi hướng”, vì bằng chứng được đưa ra trên ví dụ về tam giác vuông cân.

Sin, côsin và các phụ thuộc khác thiết lập mối quan hệ giữa các góc nhọn và các cạnh của bất kỳ tam giác vuông nào. Chúng tôi đưa ra công thức tính các đại lượng này cho góc A và theo dõi mối quan hệ của các hàm lượng giác:

Như bạn thấy, tg và ctg là các hàm nghịch đảo. Nếu chúng ta biểu diễn chân a là tích của sin A và cạnh huyền c, và chân b là cos A * c, thì chúng ta nhận được các công thức sau cho tiếp tuyến và cotang:

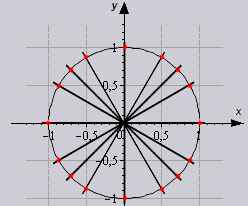
vòng tròn lượng giác

Về mặt đồ thị, tỷ lệ của các đại lượng đã đề cập có thể được biểu diễn như sau:

Trong trường hợp này, hình tròn đại diện cho tất cả các giá trị có thể có của góc α - từ 0 ° đến 360 °. Như hình bên có thể thấy, mỗi hàm nhận giá trị âm hoặc dương tùy thuộc vào góc độ. Ví dụ, sin α sẽ có dấu “+” nếu α thuộc phần tư I và II của hình tròn, nghĩa là nó nằm trong khoảng từ 0 ° đến 180 °. Với α từ 180 ° đến 360 ° (phần tư III và IV), sin α chỉ có thể là một giá trị âm.

Chúng ta hãy thử xây dựng các bảng lượng giác cho các góc cụ thể và tìm hiểu ý nghĩa của các đại lượng.

Các giá trị của α bằng 30 °, 45 °, 60 °, 90 °, 180 °, v.v. được gọi là các trường hợp đặc biệt. Giá trị của các hàm lượng giác đối với chúng được tính toán và trình bày dưới dạng các bảng đặc biệt.

Những góc này không được chọn một cách tình cờ. Ký hiệu π trong bảng là cho radian. Rad là góc mà độ dài của cung tròn tương ứng với bán kính của nó. Giá trị này được đưa ra để thiết lập mối quan hệ phổ quát; khi tính bằng radian, chiều dài thực của bán kính tính bằng cm không quan trọng.

Các góc trong bảng cho các hàm lượng giác tương ứng với các giá trị rađian:

Vì vậy, không khó để đoán rằng 2π là một đường tròn đầy đủ hoặc 360 °.

Tính chất của các hàm lượng giác: sin và côsin

Để xem xét và so sánh các tính chất cơ bản của sin và côsin, tiếp tuyến và cotang, cần phải vẽ các hàm số của chúng. Điều này có thể được thực hiện dưới dạng một đường cong nằm trong một hệ tọa độ hai chiều.

Hãy xem xét một bảng so sánh các thuộc tính của sóng hình sin và sóng côsin:

hình sin	sóng cosine
y = sin x	y = cos x
ODZ [-1; một]	ODZ [-1; một]
sin x = 0, với x = πk, trong đó k ϵ Z	cos x = 0, với x = π / 2 + πk, trong đó k ϵ Z
sin x = 1, với x = π / 2 + 2πk, trong đó k ϵ Z	cos x = 1, với x = 2πk, trong đó k ϵ Z
sin x = - 1, tại x = 3π / 2 + 2πk, trong đó k ϵ Z	cos x = - 1, với x = π + 2πk, trong đó k ϵ Z
sin (-x) = - sin x, tức là hàm lẻ	cos (-x) = cos x, tức là hàm chẵn
	hàm số tuần hoàn, chu kỳ nhỏ nhất là 2π
sin x ›0, với x thuộc phần I và II hoặc từ 0 ° đến 180 ° (2πk, π + 2πk)	cos x ›0, với x thuộc phần tư I và IV hoặc từ 270 ° đến 90 ° (- π / 2 + 2πk, π / 2 + 2πk)
sin x ‹0, với x thuộc phần tư III và IV hoặc từ 180 ° đến 360 ° (π + 2πk, 2π + 2πk)	cos x ‹0, với x thuộc phần tư II và III hoặc từ 90 ° đến 270 ° (π / 2 + 2πk, 3π / 2 + 2πk)
tăng trên các khoảng [- π / 2 + 2πk, π / 2 + 2πk]	tăng trên khoảng [-π + 2πk, 2πk]
giảm trên các khoảng [π / 2 + 2πk, 3π / 2 + 2πk]	giảm trong khoảng thời gian
đạo hàm (sin x) '= cos x	đạo hàm (cos x) ’= - sin x

Việc xác định xem một hàm là chẵn hay không rất đơn giản. Chỉ cần hình dung một đường tròn lượng giác với các dấu hiệu của đại lượng lượng giác là đủ và nhẩm “gấp” đồ thị so với trục OX. Nếu các dấu giống nhau thì hàm là chẵn, ngược lại là hàm lẻ.

Sự ra đời của radian và liệt kê các thuộc tính chính của sóng hình sin và côsin cho phép chúng ta đưa ra mô hình sau:

Rất dễ dàng để xác minh tính đúng đắn của công thức. Ví dụ, đối với x = π / 2, sin bằng 1, cũng như cosin của x = 0. Việc kiểm tra có thể được thực hiện bằng cách xem bảng hoặc bằng cách truy tìm các đường cong hàm cho các giá trị đã cho.

Tính chất của tangentoid và cotangentoid

Đồ thị của hàm tiếp tuyến và hàm phương khác nhau đáng kể so với hình sin và sóng côsin. Các giá trị tg và ctg luôn nghịch biến với nhau.

1. Y = tgx.
2. Tiếp tuyến có xu hướng đến các giá trị của y tại x = π / 2 + πk, nhưng không bao giờ đạt tới chúng.
3. Chu kì dương nhỏ nhất của tangentoid là π.
4. Tg (- x) \ u003d - tg x, tức là, hàm là số lẻ.
5. Tg x = 0, cho x = πk.
6. Chức năng ngày càng tăng.
7. Tg x ›0, với x ϵ (πk, π / 2 + πk).
8. Tg x ‹0, với x ϵ (- π / 2 + πk, πk).
9. Đạo hàm (tg x) '= 1 / cos 2 ⁡x.

Hãy xem xét biểu diễn đồ họa của cotangentoid dưới đây trong văn bản.

Các đặc tính chính của cotangentoid:

1. Y = ctgx.
2. Không giống như các hàm sin và côsin, trong tiếp tuyến Y có thể nhận các giá trị của tập tất cả các số thực.
3. Cotangentoid có xu hướng đến các giá trị của y tại x = πk, nhưng không bao giờ đạt tới chúng.
4. Chu kỳ dương nhỏ nhất của cotangentoid là π.
5. Ctg (- x) \ u003d - ctg x, tức là, hàm là số lẻ.
6. Ctg x = 0, cho x = π / 2 + πk.
7. Chức năng đang giảm dần.
8. Ctg x ›0, với x ϵ (πk, π / 2 + πk).
9. Ctg x ‹0, với x ϵ (π / 2 + πk, πk).
10. Đạo hàm (ctg x) '= - 1 / sin 2 ⁡x Sửa

Dữ liệu tham chiếu cho tiếp tuyến (tg x) và cotang (ctg x). Định nghĩa hình học, tính chất, đồ thị, công thức. Bảng tiếp tuyến và cotang, đạo hàm, tích phân, khai triển chuỗi. Biểu thức thông qua các biến phức tạp. Kết nối với các hàm hypebol.

Định nghĩa hình học

| BD | - độ dài dây cung của đường tròn có tâm tại điểm A.
α là góc tính bằng radian.

Đường tiếp tuyến ( tgα) là một hàm lượng giác phụ thuộc vào góc α giữa cạnh huyền và chân của tam giác vuông, bằng tỉ số độ dài chân đối | BC | đến độ dài của chân liền kề | AB | .

Cotangent ( ctgα) là một hàm lượng giác phụ thuộc vào góc α giữa cạnh huyền và chân của tam giác vuông, bằng tỉ số độ dài của chân kề | AB | đến độ dài của chân đối diện | BC | .

Đường tiếp tuyến

Ở đâu N- trọn.

Trong văn học phương Tây, tiếp tuyến được biểu thị như sau:
.
;
;
.

Đồ thị của hàm số tiếp tuyến, y = tg x

Cotangent

Ở đâu N- trọn.

Trong văn học phương Tây, cotang được biểu thị như sau:
.
Ký hiệu sau cũng đã được thông qua:
;
;
.

Đồ thị của hàm cotang, y = ctg x

Tính chất của tiếp tuyến và cotang

Định kỳ

Các hàm y = tg x và y = ctg xđều tuần hoàn với chu kỳ π.

Ngang bằng

Các hàm tiếp tuyến và cotang là hàm lẻ.

Miền định nghĩa và giá trị, tăng dần, giảm dần

Các hàm tiếp tuyến và cotang liên tục trên miền xác định của chúng (xem phần chứng minh về tính liên tục). Các tính chất chính của tiếp tuyến và cotang được trình bày trong bảng ( N- số nguyên).

	y = tg x	y = ctg x
Phạm vi và tính liên tục
Phạm vi giá trị	-∞ < y < +∞	-∞ < y < +∞
Tăng dần		-
Giảm dần	-
Cực trị	-	-
Zeros, y = 0
Giao điểm với trục y, x = 0	y = 0	-

Công thức

Biểu thức về sin và côsin

; ;
; ;
;

Công thức về tiếp tuyến và phương của tổng và hiệu

Phần còn lại của các công thức rất dễ lấy, chẳng hạn

Sản phẩm của tiếp tuyến

Công thức tổng và hiệu của các tiếp tuyến

Bảng này hiển thị các giá trị của tiếp tuyến và cotang đối với một số giá trị của đối số.

Biểu thức dưới dạng số phức

Biểu thức dưới dạng hàm hyperbolic

;
;

Các dẫn xuất

; .

.
Đạo hàm bậc n đối với biến x của hàm số:
.
Suy ra công thức của tiếp tuyến>>>; cho cotangent>>>

Tích phân

Mở rộng thành chuỗi

Để có được khai triển tiếp tuyến theo lũy thừa của x, bạn cần thực hiện một số thuật ngữ của khai triển trong một chuỗi lũy thừa cho các hàm tội lỗi x và cos x và chia các đa thức này cho nhau ,. Điều này dẫn đến các công thức sau đây.

Tại .

tại .
ở đâu B n- Số Bernoulli. Chúng được xác định từ quan hệ lặp lại:
;
;
ở đâu .
Hoặc theo công thức Laplace:

Hàm nghịch đảo

Các hàm ngược đối với tiếp tuyến và cotang lần lượt là arctang và arccotang.

Arctangent, arctg

, ở đâu N- trọn.

Arc tiếp tuyến, arcctg

, ở đâu N- trọn.

Người giới thiệu:
TRONG. Bronstein, K.A. Semendyaev, Sổ tay Toán học cho Kỹ sư và Sinh viên của các Cơ sở Giáo dục Đại học, Lan, 2009.
G. Korn, Sổ tay Toán học dành cho Nhà nghiên cứu và Kỹ sư, 2012.

Vào thế kỷ thứ năm trước Công nguyên, nhà triết học Hy Lạp cổ đại Zeno xứ Elea đã sáng tạo ra các aporias nổi tiếng của mình, trong đó nổi tiếng nhất là aporia "Achilles và con rùa". Đây là âm thanh của nó:

Giả sử Achilles chạy nhanh hơn rùa gấp mười lần và chậm hơn nó một nghìn bước. Trong thời gian Achilles chạy quãng đường này, con rùa bò hàng trăm bước theo cùng một hướng. Khi Achilles đã chạy được một trăm bước, con rùa sẽ bò thêm 10 bước nữa, và cứ tiếp tục như vậy. Quá trình sẽ tiếp tục vô thời hạn, Achilles sẽ không bao giờ đuổi kịp con rùa.

Suy luận này đã trở thành một cú sốc hợp lý cho tất cả các thế hệ tiếp theo. Aristotle, Diogenes, Kant, Hegel, Gilbert ... Tất cả họ, bằng cách này hay cách khác, đều được coi là aporias của Zeno. Cú sốc quá mạnh đến nỗi " ... các cuộc thảo luận vẫn tiếp tục vào thời điểm hiện tại, cộng đồng khoa học vẫn chưa đi đến được quan điểm chung về bản chất của nghịch lý ... phân tích toán học, lý thuyết tập hợp, các phương pháp tiếp cận vật lý và triết học mới đã tham gia vào nghiên cứu vấn đề này. ; không ai trong số họ trở thành một giải pháp được chấp nhận rộng rãi cho vấn đề ..."[Wikipedia," Zeno's Aporias "]. Mọi người đều hiểu rằng họ đang bị lừa, nhưng không ai hiểu lừa dối là gì.

Từ quan điểm của toán học, Zeno trong aporia của mình đã chứng minh rõ ràng sự chuyển đổi từ giá trị sang. Sự chuyển đổi này ngụ ý áp dụng thay vì các hằng số. Theo như tôi hiểu, công cụ toán học để áp dụng các đơn vị đo lường thay đổi hoặc chưa được phát triển, hoặc nó chưa được áp dụng cho aporia của Zeno. Việc áp dụng logic thông thường của chúng ta sẽ dẫn chúng ta vào một cái bẫy. Chúng ta, theo quán tính của suy nghĩ, áp dụng các đơn vị thời gian không đổi cho nghịch đảo. Từ quan điểm vật lý, có vẻ như thời gian đang chậm lại đến mức hoàn toàn dừng lại vào thời điểm Achilles đuổi kịp con rùa. Nếu thời gian ngừng trôi, Achilles không thể vượt qua con rùa được nữa.

Nếu chúng ta xoay chuyển logic mà chúng ta quen thuộc, mọi thứ sẽ rơi vào đúng vị trí. Achilles chạy với tốc độ không đổi. Mỗi đoạn tiếp theo của đường dẫn của nó ngắn hơn đoạn trước đó mười lần. Theo đó, thời gian dành cho việc vượt qua nó ít hơn mười lần so với lần trước. Nếu chúng ta áp dụng khái niệm "vô hạn" trong tình huống này, thì sẽ đúng khi nói "Achilles sẽ nhanh chóng vượt qua con rùa một cách vô hạn."

Làm thế nào để tránh cái bẫy hợp lý này? Giữ nguyên trong các đơn vị thời gian không đổi và không chuyển sang các giá trị tương hỗ. Trong ngôn ngữ của Zeno, nó trông như thế này:

Trong thời gian Achilles phải chạy một nghìn bước, con rùa đã bò cả trăm bước theo cùng một hướng. Trong khoảng thời gian tiếp theo, bằng khoảng thời gian đầu tiên, Achilles sẽ chạy thêm một nghìn bước nữa và rùa sẽ bò một trăm bước. Bây giờ Achilles đã đi trước rùa tám trăm bước.

Cách tiếp cận này mô tả thực tế một cách đầy đủ mà không có bất kỳ nghịch lý logic nào. Nhưng đây không phải là một giải pháp hoàn chỉnh cho vấn đề. Tuyên bố của Einstein về tính không thể vượt qua của tốc độ ánh sáng rất giống với aporia "Achilles và con rùa" của Zeno. Chúng tôi vẫn chưa nghiên cứu, suy nghĩ lại và giải quyết vấn đề này. Và giải pháp phải được tìm kiếm không phải ở số lượng lớn vô hạn, mà là đơn vị đo lường.

Một aporia thú vị khác của Zeno kể về một mũi tên bay:

Một mũi tên đang bay là bất động, vì tại mỗi thời điểm nó dừng lại, và vì nó dừng ở mọi thời điểm, nên nó luôn dừng lại.

Trong aporia này, nghịch lý logic được khắc phục rất đơn giản - đủ để làm rõ rằng tại mỗi thời điểm mũi tên đang bay nằm lại ở các điểm khác nhau trong không gian, mà trên thực tế, là chuyển động. Có một điểm khác cần được lưu ý ở đây. Từ một bức ảnh chụp một chiếc ô tô trên đường, không thể xác định được thực tế chuyển động của nó hay khoảng cách đến nó. Để xác định thực tế chuyển động của ô tô, cần có hai bức ảnh được chụp từ cùng một điểm tại các thời điểm khác nhau, nhưng chúng không thể được sử dụng để xác định khoảng cách. Để xác định khoảng cách tới ô tô, bạn cần hai bức ảnh được chụp từ các điểm khác nhau trong không gian cùng một lúc, nhưng bạn không thể xác định thực tế của chuyển động từ chúng (đương nhiên, bạn vẫn cần thêm dữ liệu để tính toán, lượng giác sẽ giúp bạn). Điều tôi muốn đặc biệt chỉ ra là hai điểm trong thời gian và hai điểm trong không gian là hai thứ khác nhau không nên nhầm lẫn vì chúng mang lại những cơ hội khám phá khác nhau.

Thứ tư, ngày 4 tháng bảy năm 2018

Sự khác biệt giữa tập hợp và tập hợp được mô tả rất rõ trong Wikipedia. Chúng ta nhìn.

Như bạn có thể thấy, "tập hợp không thể có hai phần tử giống nhau", nhưng nếu có các phần tử giống nhau trong tập hợp, một tập hợp như vậy được gọi là "tập hợp nhiều". Những sinh vật hợp lý sẽ không bao giờ hiểu được logic của sự phi lý như vậy. Đây là cấp độ của những con vẹt biết nói và những con khỉ được huấn luyện, trong đó tâm trí hoàn toàn không có từ "." Các nhà toán học đóng vai trò như những người huấn luyện bình thường, rao giảng những ý tưởng vô lý của họ cho chúng ta.

Ngày xửa ngày xưa, các kỹ sư xây dựng cây cầu đã đi thuyền dưới gầm cầu trong quá trình thử nghiệm cây cầu. Nếu cây cầu bị sập, người kỹ sư tầm thường đã chết dưới đống đổ nát do mình tạo ra. Nếu cây cầu có thể chịu được tải trọng, người kỹ sư tài năng đã xây dựng những cây cầu khác.

Dù các nhà toán học có giấu giếm đằng sau cụm từ "nhớ tôi đi, tôi đang ở trong nhà", hay đúng hơn là "toán học nghiên cứu các khái niệm trừu tượng", thì vẫn có một dây rốn gắn bó họ với thực tế. Dây rốn này là tiền. Chúng ta hãy áp dụng lý thuyết tập hợp toán học cho chính các nhà toán học.

Chúng tôi học toán rất tốt và bây giờ chúng tôi đang ngồi ở bàn tính tiền, trả lương. Ở đây, một nhà toán học đến với chúng tôi vì tiền của anh ta. Chúng tôi đếm toàn bộ số tiền cho anh ta và đặt nó trên bàn của chúng tôi thành các chồng khác nhau, trong đó chúng tôi đặt các tờ tiền có cùng mệnh giá. Sau đó, chúng tôi lấy một hóa đơn từ mỗi cọc và đưa cho nhà toán học "bộ lương toán học" của anh ta. Chúng tôi giải thích toán học rằng anh ta sẽ nhận được phần còn lại của các hóa đơn chỉ khi anh ta chứng minh rằng tập hợp không có các phần tử giống nhau không bằng tập hợp có các phần tử giống hệt nhau. Đây là nơi vui vẻ bắt đầu.

Trước hết, logic của các đại biểu sẽ hoạt động: "bạn có thể áp dụng nó cho người khác, nhưng không áp dụng cho tôi!" Hơn nữa, sẽ bắt đầu đảm bảo rằng có các số tiền khác nhau trên các tờ tiền có cùng mệnh giá, có nghĩa là chúng không thể được coi là các phần tử giống hệt nhau. Chà, chúng tôi tính tiền lương bằng tiền xu - không có con số nào trên đồng xu. Ở đây nhà toán học sẽ điên cuồng nhớ lại vật lý: các đồng xu khác nhau có lượng chất bẩn khác nhau, cấu trúc tinh thể và sự sắp xếp của các nguyên tử cho mỗi đồng xu là duy nhất ...

Và bây giờ tôi có một câu hỏi thú vị nhất: đâu là ranh giới ngoài ranh giới mà các phần tử của một tập hợp nhiều biến thành các phần tử của một tập hợp và ngược lại? Một dòng như vậy không tồn tại - mọi thứ được quyết định bởi các pháp sư, khoa học ở đây thậm chí còn không gần gũi.

Nhìn đây. Chúng tôi lựa chọn các sân bóng có cùng diện tích sân. Diện tích của các trường là như nhau, có nghĩa là chúng ta có một tập đa. Nhưng nếu chúng ta xem xét tên của các sân vận động giống nhau, chúng ta nhận được rất nhiều, bởi vì các tên khác nhau. Như bạn có thể thấy, cùng một tập hợp các phần tử vừa là một tập hợp vừa là một tập hợp đồng thời là một tập hợp nhiều phần tử. Như thế nào mới đúng? Và ở đây, nhà toán học-shaman-shuller lấy ra một con át chủ bài từ trong tay áo của mình và bắt đầu cho chúng ta biết về một tập hợp hoặc một tập hợp. Trong mọi trường hợp, anh ấy sẽ thuyết phục chúng tôi rằng anh ấy đúng.

Để hiểu cách các pháp sư hiện đại vận hành với lý thuyết tập hợp, gắn nó với thực tế, chỉ cần trả lời một câu hỏi: các phần tử của một tập hợp này khác với các phần tử của một tập hợp khác như thế nào? Tôi sẽ cho bạn thấy, không có bất kỳ "có thể hình dung như không phải là một tổng thể duy nhất" hoặc "không thể hình dung như một tổng thể duy nhất."

Chủ nhật, ngày 18 tháng ba năm 2018

Tổng các chữ số của một số là một điệu nhảy của các pháp sư với tambourine, không liên quan gì đến toán học. Đúng vậy, trong các bài học toán học, chúng ta được dạy để tìm tổng các chữ số của một số và sử dụng nó, nhưng họ là những pháp sư để dạy cho con cháu của họ kỹ năng và trí tuệ của họ, nếu không, các pháp sư sẽ chết.

Bạn có cần bằng chứng không? Mở Wikipedia và cố gắng tìm trang "Tổng các chữ số của một số". Cô ấy không tồn tại. Không có công thức nào trong toán học mà bạn có thể tìm thấy tổng các chữ số của bất kỳ số nào. Rốt cuộc, các con số là các ký hiệu đồ họa mà chúng ta viết các con số và trong ngôn ngữ toán học, nhiệm vụ có vẻ như thế này: "Tìm tổng các ký hiệu đồ họa đại diện cho một số bất kỳ." Các nhà toán học không thể giải quyết vấn đề này, nhưng các pháp sư có thể làm được điều đó về mặt yếu tố.

Hãy tìm hiểu xem chúng ta làm gì và làm như thế nào để tìm tổng các chữ số của một số đã cho. Và do đó, giả sử chúng ta có số 12345. Để tìm tổng các chữ số của số này cần phải làm gì? Hãy xem xét tất cả các bước theo thứ tự.

1. Viết số trên một tờ giấy. Chúng ta đã làm gì? Chúng tôi đã chuyển đổi số thành một biểu tượng đồ họa số. Đây không phải là một phép toán.

2. Chúng tôi cắt một hình ảnh đã nhận thành nhiều hình ảnh có chứa các số riêng biệt. Cắt một bức tranh không phải là một phép toán.

3. Chuyển đổi các ký tự đồ họa riêng lẻ thành số. Đây không phải là một phép toán.

4. Cộng các số kết quả. Bây giờ đó là toán học.

Tổng các chữ số của số 12345 là 15. Đây là "các khóa học cắt và may" từ các pháp sư được sử dụng bởi các nhà toán học. Nhưng đó không phải là tất cả.

Theo quan điểm của toán học, không quan trọng chúng ta viết số nào trong hệ thống số nào. Vì vậy, trong các hệ thống số khác nhau, tổng các chữ số của cùng một số sẽ khác nhau. Trong toán học, hệ thống số được biểu thị dưới dạng chỉ số con ở bên phải số. Với một số lớn 12345, tôi không muốn đánh lừa đầu của mình, hãy xem xét số 26 từ bài viết về. Hãy viết số này trong hệ thống số nhị phân, bát phân, thập phân và thập lục phân. Chúng tôi sẽ không xem xét từng bước dưới kính hiển vi, chúng tôi đã làm điều đó rồi. Hãy nhìn vào kết quả.

Như bạn thấy, trong các hệ thống số khác nhau, tổng các chữ số của cùng một số là khác nhau. Kết quả này không liên quan gì đến toán học. Nó giống như việc tìm diện tích của một hình chữ nhật theo mét và cm sẽ cho bạn những kết quả hoàn toàn khác.

Số 0 trong tất cả các hệ thống số trông giống nhau và không có tổng các chữ số. Đây là một lập luận khác ủng hộ thực tế rằng. Một câu hỏi cho các nhà toán học: làm thế nào nó được biểu thị trong toán học mà nó không phải là một số? Đối với các nhà toán học, không có gì ngoài các con số tồn tại? Đối với các pháp sư, tôi có thể cho phép điều này, nhưng đối với các nhà khoa học thì không. Thực tế không chỉ có những con số.

Kết quả thu được cần được coi là bằng chứng rằng các hệ thống số là đơn vị đo các số. Rốt cuộc, chúng ta không thể so sánh các con số với các đơn vị đo lường khác nhau. Nếu các hành động giống nhau với các đơn vị đo khác nhau của cùng một đại lượng dẫn đến kết quả khác nhau sau khi so sánh chúng, thì điều này không liên quan gì đến toán học.

Toán học thực sự là gì? Đây là khi kết quả của một hành động toán học không phụ thuộc vào giá trị của con số, đơn vị đo lường được sử dụng và người thực hiện hành động này.

Ký vào cửa Mở cửa và nói:

Oái oăm! Đây không phải là phòng vệ sinh của phụ nữ sao?
- Người phụ nữ trẻ tuổi! Đây là một phòng thí nghiệm để nghiên cứu sự thánh thiện vô hạn của các linh hồn khi lên trời! Nimbus trên đầu và mũi tên lên. Nhà vệ sinh khác gì?

Nữ ... Một vầng hào quang trên đỉnh và một mũi tên hướng xuống là nam.

Nếu bạn có một tác phẩm nghệ thuật thiết kế nhấp nháy trước mắt bạn vài lần trong ngày,

Sau đó, không có gì ngạc nhiên khi bạn đột nhiên tìm thấy một biểu tượng lạ trên ô tô của mình:

Cá nhân tôi đã cố gắng tự mình nhìn thấy âm bốn độ ở một người đang ngồi (một hình ảnh) (bố cục của một số hình ảnh: dấu trừ, số bốn, ký hiệu độ). Và tôi không coi cô gái này là một kẻ ngốc không biết vật lý. Cô ấy chỉ có một khuôn mẫu vòng cung trong nhận thức về hình ảnh đồ họa. Và các nhà toán học luôn dạy chúng ta điều này. Đây là một ví dụ.

1A không phải là "âm bốn độ" hoặc "một a". Đây là "pooping man" hay số "hai mươi sáu" trong hệ thống số thập lục phân. Những người liên tục làm việc trong hệ thống số này sẽ tự động coi số và chữ cái như một biểu tượng đồ họa.

Trong bài viết, chúng ta sẽ hiểu đầy đủ về nó trông như thế nào bảng giá trị lượng giác, sin, cosine, tiếp tuyến và cotang. Xét giá trị cơ bản của các hàm số lượng giác, theo góc 0,30,45,60,90, ..., 360 độ. Và chúng ta hãy xem cách sử dụng các bảng này trong việc tính giá trị của các hàm lượng giác.
Đầu tiên hãy xem xét bảng cosin, sin, tiếp tuyến và cotang từ một góc 0, 30, 45, 60, 90, .. độ. Định nghĩa của các đại lượng này giúp xác định giá trị của các hàm của góc 0 và 90 độ:

sin 0 0 \ u003d 0, cos 0 0 \ u003d 1. tg 00 \ u003d 0, cotang của 00 sẽ là không xác định
sin 90 0 = 1, cos 90 0 = 0, ctg90 0 = 0, tiếp tuyến của 90 0 sẽ không xác định

Nếu chúng ta lấy các tam giác vuông có góc từ 30 đến 90 độ. Chúng tôi nhận được:

sin 30 0 = 1/2, cos 30 0 = √3 / 2, tg 30 0 = √3 / 3, ctg 30 0 = √3
sin 45 0 = √2 / 2, cos 45 0 = √2 / 2, tg 45 0 = 1, ctg 45 0 = 1
sin 60 0 = √3 / 2, cos 60 0 = 1/2, tg 60 0 = √3, ctg 60 0 = √3 / 3

Chúng tôi đại diện cho tất cả các giá trị thu được trong biểu mẫu bảng lượng giác:

Bảng sin, cosin, tiếp tuyến và cotang!

Nếu chúng ta sử dụng công thức ép kiểu, bảng của chúng ta sẽ tăng lên, các giá trị cho góc lên đến 360 độ sẽ được thêm vào. Nó sẽ giống như:

Ngoài ra, dựa trên các tính chất của tuần hoàn, bảng có thể được tăng lên nếu chúng ta thay các góc bằng 0 0 +360 0 * z .... 330 0 +360 0 * z, trong đó z là một số nguyên. Trong bảng này, có thể tính giá trị của tất cả các góc tương ứng với các điểm trong một đường tròn duy nhất.

Chúng ta hãy xem rõ cách sử dụng bảng trong giải pháp.
Mọi thứ rất đơn giản. Vì giá trị chúng ta cần nằm ở giao điểm của các ô chúng ta cần. Ví dụ, chúng ta hãy lấy cos của một góc 60 độ, trong bảng nó sẽ như thế này:

Trong bảng cuối cùng của các giá trị chính của các hàm lượng giác, chúng ta thực hiện theo cách tương tự. Nhưng trong bảng này có thể tìm ra tiếp tuyến từ góc 1020 độ sẽ là bao nhiêu, nó = -√3 Hãy kiểm tra 1020 0 = 300 0 +360 0 * 2. Chúng ta cùng tìm bảng.

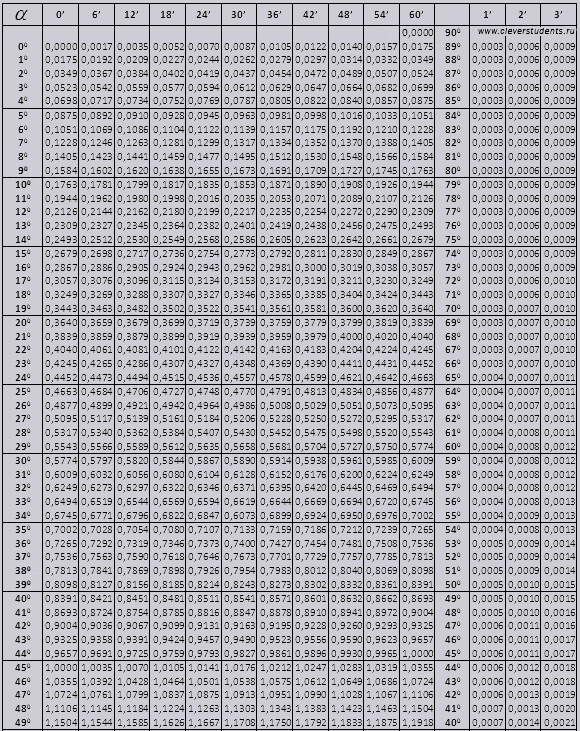
Bàn Bradis. Đối với sin, cosin, tiếp tuyến và cotang.

Các bảng của Bradys được chia thành nhiều phần, chúng bao gồm các bảng của cosin và sin, tiếp tuyến và cotang - được chia thành hai phần (tg của một góc đến 90 độ và ctg của các góc nhỏ).

Sin và côsin

góc tg từ 00 đến 760, góc ctg từ 140 đến 900.

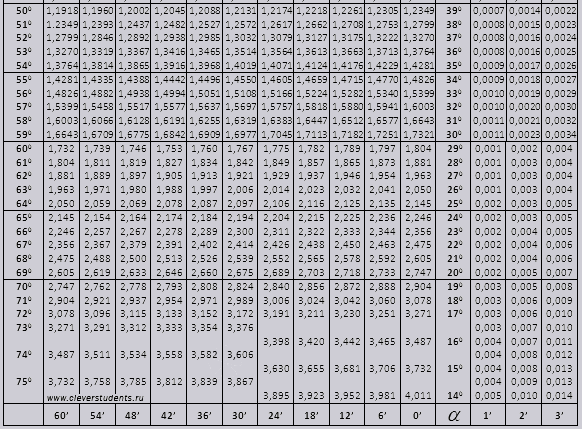
tg đến 900 và ctg góc nhỏ.

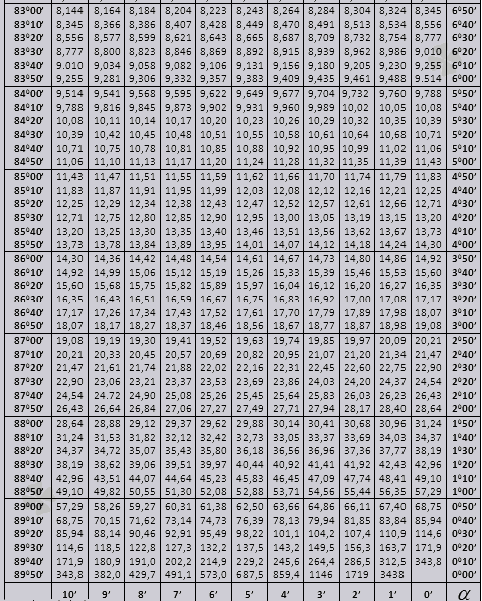
Hãy tìm cách sử dụng bảng Bradis trong việc giải quyết vấn đề.

Hãy tìm sin chỉ định (chỉ định ở cột từ mép trái) 42 phút (chỉ định ở dòng trên cùng). Bằng cách vượt qua, chúng tôi đang tìm kiếm một chỉ định, nó là = 0,3040.

Giá trị của phút được chỉ định với khoảng thời gian là sáu phút, điều gì sẽ xảy ra nếu giá trị chúng ta cần nằm trong khoảng thời gian này. Hãy dành 44 phút, và chỉ có 42 trong bảng. Chúng tôi lấy 42 làm cơ sở và sử dụng các cột bổ sung ở phía bên phải, thực hiện lần sửa thứ 2 và thêm vào 0,3040 + 0,0006, chúng tôi nhận được 0,3046.

Với sin 47 phút, chúng tôi lấy 48 phút làm cơ sở và trừ đi 1 hiệu chỉnh từ nó, tức là 0,3057 - 0,0003 = 0,3054

Khi tính cos, chúng ta làm tương tự như sin, chỉ khác là chúng ta lấy hàng dưới cùng của bảng làm cơ sở. Ví dụ cos 20 0 = 0,9397

Các giá trị tg của một góc tới 90 0 và cot của một góc nhỏ là đúng và không có hiệu chỉnh nào trong chúng. Ví dụ, tìm tg 78 0 37min = 4,967


và ctg 20 0 13 phút = 25,83

Vâng, ở đây chúng ta đã xem xét các bảng lượng giác chính. Chúng tôi hy vọng thông tin này cực kỳ hữu ích cho bạn. Các câu hỏi của bạn trên các bảng, nếu có, hãy ghi vào phần bình luận!

Ghi chú: Tường chắn bùn - tấm chắn bùn để bảo vệ tường. Theo liên kết Chắn bùn không khung không khung (http://www.spi-polymer.ru/otboyniki/) và tìm hiểu thêm.

1. Hàm lượng giác là các hàm cơ bản có đối số là góc. Các hàm lượng giác mô tả mối quan hệ giữa các cạnh và các góc nhọn trong một tam giác vuông. Các lĩnh vực ứng dụng của hàm số lượng giác vô cùng đa dạng. Vì vậy, ví dụ, bất kỳ quá trình tuần hoàn nào có thể được biểu diễn dưới dạng tổng của các hàm lượng giác (chuỗi Fourier). Các hàm này thường xuất hiện khi giải các phương trình vi phân và hàm số.

2. Hàm số lượng giác bao gồm 6 hàm số sau: xoang, cô sin, đường tiếp tuyến,cotangent, đương căt và cosecant. Đối với mỗi hàm số này, có một hàm lượng giác nghịch đảo.

3. Thật tiện lợi khi giới thiệu định nghĩa hình học của các hàm số lượng giác bằng cách sử dụng vòng tròn đơn vị. Hình dưới đây cho thấy một hình tròn có bán kính r = 1. Điểm M (x, y) được đánh dấu trên đường tròn. Góc giữa vectơ bán kính OM và chiều dương của trục Ox là α.

4. xoang góc α là tỉ số giữa hoành độ y của điểm M (x, y) với bán kính r:
sinα = y / r.
Vì r = 1 nên sin bằng hoành độ của điểm M (x, y).

5. cô sin góc α là tỷ số giữa hoành độ x của điểm M (x, y) với bán kính r:
cosα = x / r

6. đường tiếp tuyến góc α là tỉ số giữa hoành độ y của điểm M (x, y) với hoành độ x của nó:
tanα = y / x, x ≠ 0

7. Cotangent góc α là tỉ số giữa hoành độ x của điểm M (x, y) với hoành độ y:
cotα = x / y, y ≠ 0

8. đương căt góc α là tỷ số giữa bán kính r với hoành độ x của điểm M (x, y):
secα = r / x = 1 / x, x ≠ 0

9. Cosecant góc α là tỉ số giữa bán kính r với hoành độ y của điểm M (x, y):
cscα = r / y = 1 / y, y ≠ 0

10. Trong hình tròn đơn vị của hình chiếu x, y, các điểm M (x, y) và bán kính r tạo thành một tam giác vuông, trong đó x, y là chân và r là cạnh huyền. Do đó, các định nghĩa trên về hàm số lượng giác áp dụng cho tam giác vuông được xây dựng như sau:
xoang góc α là tỷ số của chân đối diện với cạnh huyền.
cô sin góc α là tỷ số của chân kề cạnh cạnh huyền.
đường tiếp tuyến góc α gọi là chân đối diện với cạnh kề.
Cotangent góc α gọi là chân kề đối diện.
đương căt góc α là tỷ số của cạnh huyền với chân kề.
Cosecant góc α là tỉ số giữa cạnh huyền và chân đối diện.

11. đồ thị hàm sin
y = sinx, miền: x∈R, miền: −1≤sinx≤1

12. Đồ thị của hàm cosin
y = cosx, miền: x∈R, khoảng: −1≤cosx≤1

13. đồ thị hàm số tiếp tuyến
y = tanx, miền: x∈R, x ≠ (2k + 1) π / 2, miền: −∞

14. Đồ thị của hàm cotang
y = cotx, miền: x∈R, x ≠ kπ, miền: −∞

15. Đồ thị của hàm secant
y = secx, miền: x∈R, x ≠ (2k + 1) π / 2, miền: secx∈ (−∞, −1] ∪∪)