Tìm ra loại điểm kỳ dị của hàm số. Chuỗi Laurent cô lập các điểm kỳ dị và phân loại của chúng

Để cho zq - điểm kỳ dị của hàm f (z), t.s. f (z) nhưng là phân tích tại thời điểm này (cụ thể, có thể không được xác định tại nó). Nếu tồn tại một vùng lân cận bị thủng như vậy của điểm zq (tức là tập O z - zq f (z) là bí danh, sau đó zo gọi là điểm kỳ dị bị cô lập chức năng f (z).Định nghĩa này cũng được giữ nguyên trong trường hợp zn = oo, nếu iốt là vùng lân cận bị thủng của một điểm zq = oo hiểu bộ z> Tôi - sự xuất hiện của một số vòng tròn có tâm tại điểm gốc. Nói cách khác, điểm kỳ dị zq được cho là bị cô lập nếu tồn tại một vùng lân cận của điểm này, trong đó có các điểm kỳ lạ khác với zq. Ở mọi nơi bên dưới, chúng tôi chỉ xem xét các điểm đơn lẻ của một ký tự có giá trị duy nhất (hàm f (z) giả định là duy nhất).

Tùy thuộc vào hành vi của chức năng f (z) tại z -> zq Có ba loại điểm kỳ dị. Điểm kỳ dị biệt lập hàm zq f (z) gọi là:

1) điểm kỳ dị có thể tháo rời nếu có một giới hạn hữu hạn

2) cây sào nếu có một giới hạn

3) điểm cốt yếu, nếu f (z) không có giới hạn hữu hạn hay vô hạn đối với z-> zq.

VÍ DỤ 26.1. Hãy để chúng tôi chứng minh rằng cả ba loại điểm kỳ dị đều được thực hiện. Xem xét f(z)= điểm zq = 0 bị cô lập

điểm kỳ dị của chức năng này. Sử dụng công thức (22.12), chúng tôi thu được khai triển

từ đó nó tồn tại lim fi (z)= 1. Do đó, zq = 0 là

là một điểm kỳ dị có thể tháo rời của hàm fi (z).

Hàm số f'j (z) =--- có một cực tại một điểm zo= 1 vì

2 r“X

Hãy xem xét ngay chức năng ) z (z)= e 1 ^ r và chỉ ra rằng zo = O là một điểm kỳ dị cần thiết của chức năng này. Khi phấn đấu z về 0 dọc theo trục thực, giới hạn bên trái và bên phải của hàm f (z) khác nhau: lim Với 1 / 1 = 0, lim với 1 / * = hệ điều hành. Điều này nghĩa là,

x-> 0-0 x-> 0 + 0

Gì f: i (z) không có giới hạn hữu hạn cũng không có giới hạn vô hạn cho 2 -> Ồ, tức là zq = 0 là một điểm kỳ dị về cơ bản của hàm này. (Lưu ý rằng vì điểm có xu hướng z-iy về 0 trên hàm trục ảo

không có giới hạn nào cả.)

Tất nhiên, cũng có những điểm kỳ dị không biệt lập. Ví dụ. chức năng có cực tại các điểm z n = -, P= ± 1, ± 2, ...

Do đó, Zq = 0 là điểm kỳ dị không biệt lập của hàm này: trong bất kỳ vùng lân cận (nhỏ tùy ý) nào của điểm này có các điểm kỳ dị khác g p.

Để cho zo-điểm kỳ dị cô lập cuối cùng của một hàm f (z). sau đó f (z) tương tự trong một số vùng lân cận bị thủng 0 Zo của điểm zo vùng lân cận này có thể được coi là một vành đai với bán kính bên trong r = 0. Theo Định lý 25.1, trong vùng lân cận đang xét, hàm f (z) có thể được mở rộng trong một chuỗi Laurent (25,2). Chúng tôi sẽ chỉ ra rằng hành vi của hàm cho 2 -> zq (tức là loại điểm kỳ dị zo) phụ thuộc vào hình thức của phần chính của sự phân hủy (25.2); tình huống này giải thích nguồn gốc của thuật ngữ “phần chính”.

LÝ THUYẾT 2G.2. Một zo điểm kỳ dị biệt lập của hàm f (z) có thể di chuyển được nếu và chỉ khi khai triển Lorap trong vùng lân cận bị thủng của điểm này có giá trị

những thứ kia. chỉ bao gồm một phần chính xác, và tất cả các hệ số của phần chính bằng dấu đầu dòng.

Bằng chứng. 1. Để zo là một điểm kỳ dị có thể tháo rời. Hãy để chúng tôi chứng minh rằng khai triển Laurent của hàm f (z) có dạng (26.1). Kể từ điểm kỳ dị zo có thể tháo rời, khi đó có một giới hạn hữu hạn lim f (z) = A. Do đó, f (z) giới hạn trong một số vùng lân cận bị thủng 0 z - zq của điểm zo, những thứ kia. ) (z) cho tất cả z từ khu phố này. Lấy bất kỳ R. U р /? |, Và sử dụng công thức (25.3) cho các hệ số của chuỗi Laurent:

Đối với các hệ số của phần chính của khai triển n =- 1, -2, ... Đối với các giá trị như vậy P chúng ta có p ~ n-e 0 lúc R-> 0. Vì giá trị R có thể được chọn nhỏ tùy ý, sau đó Mr ~ " có thể to nhỏ tùy ý. Kể từ khi | c t, | ^ Mr ~ n và cn không phụ thuộc vào p, thì cn = 0 cho và= - 1, -2, ..., đã được chứng minh.

2. Bây giờ chúng ta giả sử rằng khai triển Laurent có dạng (26.1). Loạt (26.1) là một loạt lũy thừa và. do đó, không chỉ hội tụ ở khu vực bị thủng, mà còn ở toàn bộ khu vực lân cận z-zq bao gồm cả dấu chấm zô; tổng của nó S (z) là phân tích cho z và S (z) = ) (z)ở 0 z - zo R. Do đó, tồn tại một giới hạn hữu hạn lim ) (z)\ u003d Pm 5 (r) \ u003d 5 (r) - Do đó, điểm kỳ dị zq

Z-> Zo Z- * Zo

dùng một lần. Định lý đã được chứng minh.

Bình luận. Nó dựa trên chứng minh của định lý rằng trong một lân cận thủng 0 z - zo của một điểm kỳ dị di động, hàm f (z) trùng với hàm S (r), là hàm giải tích trong toàn bộ vùng lân cận z - zô. Do đó, nếu chúng ta đặt / (th) = S (zq), sau đó, mà không thay đổi các giá trị của hàm f (z) tại bất kỳ điểm nào của vùng lân cận bị thủng, chúng tôi thực hiện phân tích hàm này trong r, tức là "Loại bỏ" đối tượng địa lý. Điều này giải thích thuật ngữ "điểm kỳ dị có thể tháo rời". Điều tự nhiên là coi những điểm đó là điểm thường xuyên chứ không phải là điểm kỳ dị của hàm f (z).

Ví dụ, hãy xem xét chức năng

Trong ví dụ 26.1, chỉ ra rằng Pm (n) = 1. tức là điểm kỳ lạ

zq = 0 có thể tháo rời. Đặt / i (0) = 1, do đó chúng tôi loại bỏ điểm kỳ dị và thu được một hàm có tính giải tích tại điểm zq = 0 (và trong toàn bộ mặt phẳng C).

Bây giờ chúng ta hãy mô tả đặc điểm của các cực trong điều kiện mở rộng Laurent.

Định lý 26.3. Điểm kỳ dị Zo cô lập của hàm f (z) là cực nếu và chỉ khi, khi phần chính của khai triển Laurent với tâm Zq chỉ có một số hữu hạn

từ hệ số 0 với n:

Bằng chứng. 1. Để zq - cực, tức là lim / ( z) = oo.

Hãy để chúng tôi chứng minh rằng khai triển Laurent của hàm f (z) có dạng (2G.2). Kể từ khi lim f (z)= oo. sau đó tồn tại một vùng lân cận bị thủng của điểm

ki zq. trong đó f (z) là phân tích và không có số 0. Sau đó, hàm g (z) = 1 /f (z) cũng sẽ được phân tích trong vùng lân cận bị thủng này và g (z)= 0. Do đó, Zo là dùng một lần * -? * 0

điểm kỳ dị của hàm g (z). Hãy xác định lại g (z) tại điểm zo, đặt g (zo)= 0. Sau đó g (z) trở thành phân tích trong toàn bộ vùng lân cận của điểm (không bị thủng) z 0, và z0 sẽ là số không cô lập của nó. Biểu thị bởi N tính đa dạng (thứ tự) của số không này. Như được trình bày trong §23, trong vùng lân cận của điểm hàm zq g (z) có thể biểu diễn trong biểu mẫu (xem (23.2))

và (z $) f 0 và y> (z) là phân tích trong một số vùng lân cận của điểm zo- Tại vì ip (z) liên tục tại điểm zo và g> (zo) F 0 "sau đó ip (z) không có số không trong một số vùng lân cận của điểm này. Do đó hàm 1 / -p (z) cũng sẽ được phân tích trong vùng lân cận này và do đó, mở rộng trong đó trong một chuỗi Taylor:

Mở ngoặc và thay đổi ký hiệu của các hệ số, chúng ta viết phần mở rộng cuối cùng dưới dạng

nơi c_jv = 1> o f 0. Do đó, phần chính của khai triển Laurent của f (r) chỉ chứa một số hạng hữu hạn; chúng ta đã đạt đến sự bình đẳng cần thiết (26,2).

2. Để vào một vùng lân cận bị thủng của một điểm thứ tự hàm số ) (z)được biểu diễn bằng khai triển Laurent (26.2) (ở dạng mở rộng hơn, xem (26.3)), phần chính của nó chỉ chứa một số lượng hữu hạn các số hạng, và Với- d " f 0. Chúng ta phải chứng minh rằng Zq - cực chức năng f (z). Nhân bình đẳng (26,3) với (G - G o) iV, chúng tôi nhận được hàm

Chuỗi trong (26.4) là một chuỗi lũy thừa hội tụ đến một hàm giải tích không chỉ trong vùng bị đánh thủng mà còn trong toàn bộ vùng lân cận của điểm Zq. Do đó, hàm h (z) trở thành phân tích trong vùng lân cận này nếu chúng ta mở rộng nó trong thứ bằng cách thiết lập h (zo)= s_dg f 0. Sau đó

Do đó, điểm o là một điểm cực, và Định lý 26.3 được chứng minh.

Tính đa dạng (thứ tự) của hàm số 0 g (z)= 1 // (r) được gọi là trật tự cực hàm / (r). Nếu một N- thứ tự của cực là th, sau đó g (z)= (r - Zo) N ip (z), và (đi) F 0, và như được chỉ ra trong phần đầu của chứng minh Định lý 26.3, khai triển của f (r) có dạng (26.3), trong đó c_ / v f 0. Ngược lại, nếu f (r) khai triển thành chuỗi (26.3) và e-z F 0, sau đó

t.s. N- bậc cực của hàm f (r). Bằng cách này, thứ tự của cực zq của hàm/ (G) bằng số hệ số khác không hàng đầu của phần chính của phần mở rộng Laurent trong vùng lân cận bị thủng của điểm zq(tức là bằng một số như vậy N, cái gì s_dg f 0 và sp= 0 lúc P > N).

Hãy để chúng tôi chứng minh khẳng định sau, điều này thuận tiện) cho các ứng dụng.

Hệ quả 26.4. Điểm zq là một cực của bậc N của tiểu thuyết/ (G) nếu và chỉ nếu/ (G) đại diện trong biểu mẫu

trong đó h (z) là một hàm giải tích trong vùng lân cận của một điểm thứ tự và h (zo) f 0.

Bằng chứng. Hàm số cp (z) = l / h (z) là giải tích trong một số vùng lân cận của điểm r. Điều kiện của Hệ quả 26.4 tương đương với điều kiện sau:

Đó là lý do tại sao zq - đa số không N chức năng g (z). và do đó cực kỳ đa dạng N chức năng / (2).

II ví dụ 26.5. Tìm các điểm kỳ dị biệt lập của một hàm và xác định loại của chúng.

D e u c tio n. Những điểm mà tại đó (z 2 + 1 ) (z+ H) 2 = 0. Nếu z 2 L- 1 = 0 thì 2 = ± r nếu (z 4- H) 2 = 0, thì z= -3. Do đó, hàm có ba điểm kỳ dị z= r, 22 = -r, Z3 = - 3. Cân nhắc z:

G - cực bậc nhất (chúng tôi đã sử dụng Hệ quả 26.4). Tương tự có thể chứng minh rằng 22 = -tôi cũng là một cực của bậc nhất. Trong 2h chúng ta có:

Chúng ta hãy chuyển sang việc xem xét các điểm kỳ dị về cơ bản.

Định lý 26.6. Điểm kỳ dị cô lập zq của một hàm f (z) về cơ bản là số ít nếu và chỉ khi phần chính của khai triển Laurent có tâm tại zq có vô số điểm khác với. không, hệ số với p.

Bằng chứng. Định lý 26.6 tiếp theo trực tiếp từ Định lý 26.2 và 26.3. Thật vậy, nếu điểm zq về cơ bản là số ít, khi đó phần chính của khai triển Laurent không được vắng mặt hoặc chứa một số lượng hữu hạn các số hạng (nếu không thì điểm Zq sẽ có thể tháo rời hoặc một cực). Do đó, số lượng các số hạng trong phần chính phải là vô hạn.

Ngược lại, nếu phần chính chứa vô số thành viên, thì Zq không thể là một điểm di động cũng không phải là một cực. Do đó, điểm này về cơ bản là số ít.

Theo định nghĩa, một điểm kỳ dị về cơ bản được đặc trưng bởi thực tế là hàm f (2) không có giới hạn hữu hạn hoặc vô hạn đối với z ->zq. Định lý sau đây đưa ra một ý tưởng đầy đủ hơn về hành vi bất thường của một hàm trong vùng lân cận của một điểm kỳ dị về cơ bản.

Định lý 26.7 (Định lý Sochocki). Nếu zq về cơ bản là số ít, thì điểm của hàm f (z), sau đó cho bất kỳ số phức nào L, bao gồm A = oo, có một dãy các điểm z n sao cho z n -> zo và lim f (zn) = NHƯNG.

n-> hệ điều hành

Bằng chứng. Trước hết hãy xem xét trường hợp A = oo. Trong phần đầu tiên của phần chứng minh Định lý 2G.2, chúng tôi đã thiết lập rằng nếu f (z)được giới hạn trong một số vùng lân cận bị thủng của điểm r0, sau đó tất cả các hệ số c, n = - 1, - 2, ... của phần chính bằng 0 (và do đó, điểm kỳ dị ở thứ có thể tháo rời). Vì theo giả thiết r0 về cơ bản là một điểm kỳ dị, nên hàm f (r) là không bị ràng buộc trong bất kỳ vùng lân cận bị thủng nào của điểm r0. Hãy để chúng tôi lấy một số vùng lân cận hẹp 0 Z sao cho f (zi)> 1 (nếu | / (r) | z - zo R / 2 có một điểm z-2 , trong đó | / (dd) | > 2, v.v.: trong khu phố bị thủng O 71. Rõ ràng là rn -e go và lim / (r «) = oo. Do đó, trong trường hợp A = oo, Định lý 26.7

chứng minh.

Hãy để bây giờ A f oo. Trước tiên, giả sử rằng có một vùng lân cận 0 bị thủng

= -yy---- sẽ được phân tích trong vùng lân cận bị thủng này và do đó,

/ (G) - NHƯNG

do đó, r là một điểm kỳ dị biệt lập của hàm Φ (r). Hãy biểu diễn. rằng r0 là một điểm kỳ dị về cơ bản của Φ (r). Hãy để nó sai. Khi đó tồn tại giới hạn lim Φ (r), hữu hạn hoặc vô hạn. Tại vì

/ (r) = A +, thì Hsh / (r) cũng tồn tại, điều này mâu thuẫn với điều kiện

F (g) ~ : - * z 0

quan điểm của định lý. Vì vậy, r0 là một điểm kỳ dị về cơ bản của hàm Φ (r). Theo những gì đã chứng minh ở trên, tồn tại một dãy các điểm r n sao cho r n o và lim Φ (r n) = oo. Từ đây

Chúng tôi đã chứng minh khẳng định bắt buộc theo giả định rằng f (r) F A trong một số vùng lân cận bị thủng của điểm r. Bây giờ chúng ta hãy giả định rằng điều này không đúng, tức là trong bất kỳ vùng lân cận bị thủng nhỏ tùy tiện nào của điểm có một điểm như vậy G ", rằng f (r ") = A. Khi đó với bất kỳ P trong vùng lân cận bị thủng 0 f (z u) = L. Do đó, khẳng định bắt buộc là đúng P-yuo

trong mọi trường hợp, và Định lý 26.7 được chứng minh.

Theo Định lý 26.7 của (Sokhotsky), trong bất kỳ vùng lân cận bị thủng (nhỏ tùy ý) nào của một điểm kỳ dị về cơ bản, hàm f (r) nhận các giá trị gần bằng bất kỳ số nào trong mặt phẳng phức C mở rộng.

Để nghiên cứu các điểm kỳ dị biệt lập, các khai triển Taylor nổi tiếng của các hàm cơ bản cơ bản thường hữu ích.

VÍ DỤ 2G.8. Xác định loại điểm kỳ dị zq = 0 cho hàm

Giải quyết và e. Chúng tôi mở rộng tử số và mẫu số trong một chuỗi Taylor theo lũy thừa của r. Thay vào (22.11) 3 z thay vì r và trừ đi 1, chúng ta nhận được

Sử dụng (22.12), chúng tôi thu được khai triển của mẫu số:

Chuỗi trong các mở rộng này hội tụ trong toàn bộ mặt phẳng phức hợp €. Chúng ta có

và / 2 (2) tương tự nhau trong vùng lân cận của điểm zo = 0 (và thậm chí trong toàn bộ mặt phẳng) và / 2 (20) F 0, sau đó h (z) cũng được phân tích ở một số vùng lân cận của điểm gF 0. Theo Hệ quả 26.4, điểm Zo = 0 là cực của thứ tự N = 4.

II ví dụ 26.9. Tìm điểm số ít của một hàm f (z)= sin j - và xác định loại của chúng.

P e trong e và e. Hàm có một điểm kỳ dị cuối cùng zq = 1. Tại các điểm khác từ C, hàm w =--- phân tích; do đó hàm sin w sẽ được phân tích.

Thay thế trong khai triển của sin (22.12) - thay vì r, chúng ta nhận được

Chúng ta đã thu được khai triển của hàm sin trong một chuỗi Laurent trong vùng lân cận bị thủng của điểm 20 = 1. Vì khai triển kết quả chứa vô số số hạng có lũy thừa âm (r - 1), nên zq = 1 là một điểm kỳ dị cần thiết (trong trường hợp này, phần mở rộng Laurent chỉ bao gồm phần chính và phần chính xác bị thiếu).

Lưu ý rằng trong trường hợp này, cũng có thể thiết lập bản chất của điểm kỳ dị trực tiếp từ định nghĩa mà không cần dùng đến mở rộng chuỗi. Thật vậy, có các chuỗi (r ") và (2") hội tụ với zo= 1, và như vậy f (z "n)= 1, / (2 ") = 0 (tự chỉ định các chuỗi như vậy). Vì vậy, f (z) không có giới hạn khi z -> 1 và do đó là điểm zq - 1 về cơ bản là số ít.

Hãy để chúng tôi giới thiệu khái niệm về khai triển Laurent của một hàm trong vùng lân cận của một điểm Zq = 00 và xem xét mối liên hệ giữa sự mở rộng và bản chất của điểm kỳ dị tại điểm này. Lưu ý rằng các định nghĩa của một điểm kỳ dị biệt lập và loại của nó (có thể tháo rời, cực hoặc về cơ bản là số ít) được chuyển sang trường hợp zq = oc không đổi. Nhưng Định lý 26.2. 26.3 và 26.6, liên quan đến bản chất của các mở rộng Laurent, cần được thay đổi. Vấn đề là các thành viên c n (z - 2o) tr. P= -1, -2, ..., phần chính, xác định "tính bất thường" của hàm gần điểm cuối Zq, vì 2 có xu hướng oo, chúng sẽ hoạt động “chính xác” (có xu hướng về 0). Ngược lại, các thành viên của bộ phận thông thường với P= 1,2, ... sẽ có xu hướng oo; chúng xác định bản chất của điểm kỳ dị trong Zq = oo. Do đó, phần chính của sự mở rộng trong khu vực lân cận của oo sẽ là các điều khoản có sức mạnh tích cực P, và sửa - với phủ định.

Hãy giới thiệu một biến mới w = 12. Hàm số tv = 1/2, được mở rộng để u (oo) = 0, 1-1 và ánh xạ vùng lân cận một cách phù hợp z> Rđiểm zq = 00 trong vùng lân cận của | w | wq = 0. Nếu hàm f (z) phân tích trong một vùng lân cận bị thủng R z Zq = oc, thì hàm G (w) = f (l / w) sẽ được phân tích trong vùng lân cận màu vàng 0 wo = 0. Vì đối với 2 -> oo sẽ có w-> 0, sau đó

Đó là lý do tại sao G (w) có ở điểm wq = 0 là điểm kỳ dị cùng loại với f (z) tại điểm Zq = 00. Hãy để chúng tôi khai triển hàm G (w) trong một chuỗi Laurent trong vùng lân cận bị thủng của điểm wo = 0:

Các tổng ở phía bên phải của (26.5) lần lượt thể hiện phần chính xác và phần chính của phần mở rộng. Hãy chuyển sang biến z, thay thế w = 1/ z:

biểu thị P\ u003d -A *, 6 * \ u003d 6_ "\ u003d với p và nhận thấy rằng G (l / z) = f (z), chúng tôi nhận được

Sự phân hủy (2G.G) được gọi là Khai triển Laurent của hàm f (z) trong vùng lân cận bị thủng của điểm zq= oo. Tổng đầu tiên trong (2G.6) được gọi là phần bên phải, và tổng thứ hai là phần chính sự phân hủy này. Vì các tổng này tương ứng với các phần chính xác và chính của khai triển (26.5), khai triển (26.6) thỏa mãn các tương tự của Định lý 26.2, 26.3 và 26.6. Do đó, định lý sau đây là một phép tương tự của Định lý 26.2.

Định lý 26.10. Điểm kỳ dị biệt lậpZq - hệ điều hành (chức năng/ (G) có thể tháo rời nếu và chỉ khi phần mở rộng Laurent trong vùng lân cận bị thủng của điểm này có dạng

t.s. chỉ bao gồm phần chính xác.

Chúng tôi đặt / (oo) = co. Hàm được xác định bởi chuỗi (26.7) hội tụ trong vùng lân cận z> Rđiểm 2o \ u003d oc, được gọi là phân tích tại điểm z o = oo. (Lưu ý rằng định nghĩa này tương đương với tính phân tích của hàm G (w) tại điểm wo = 0.)

Ví dụ 26.11. Khảo sát điểm kỳ dị zq = oo của hàm

Vì giới hạn là hữu hạn, nên zo = oo là một điểm kỳ dị di động của hàm f (r). Nếu chúng ta đặt / (oo) = lim J (z)= 0, sau đó f (z) sẽ trở thành

tic tại điểm Zo= hệ điều hành. Hãy để chúng tôi chỉ ra cách tìm khai triển tương ứng (26,7). Hãy chuyển sang biến w = 1 fz. Thay thế z= 1 /? E, chúng tôi nhận được

(đẳng thức cuối cùng hợp lệ trong vùng lân cận bị thủng của điểm ww = 0, nhưng chúng tôi sẽ mở rộng định nghĩa (7 (0) = 0). Hàm kết quả có các điểm kỳ dị w =± i, w =-1/3 và tại điểm Wq = 0 là giải tích. Mở rộng chức năng G (w) theo độ w(như đã được thực hiện trong Ví dụ 25.7) và thay thế vào chuỗi lũy thừa kết quả w = 1 / z người ta có thể có được sự mở rộng (26.7) của hàm f (z).

Định lý 26.3 cho trường hợp zo= oo sẽ được viết lại dưới dạng sau.

Định lý 26.12. Điểm kỳ dị biệt lập go = os hàm f (z) là một cực nếu và chỉ khi phần chính của khai triển Laurent (26.6) chỉ có một số hữu hạn các hệ số khác 0 Với":

Ở đây chuỗi là phần thông thường, và đa thức trong ngoặc đơn là phần chính của khai triển. Tính đa dạng của cực trong oc được định nghĩa là tính đa dạng của cực wq = 0 hàm G (z). Dễ dàng nhận thấy rằng số cực trùng với số N trong (26,8).

Q p | (i 2 + 1) (z + 3) 2

Một nhiệm vụ. Cho thấy rằng chức năng f (z) =-- -- có trong

điểm zo = thứ tự cực oo 3.

Định lý 26.6 về một điểm kỳ dị cần thiết được viết lại cho trường hợp zo= os gần như nguyên văn, và chúng tôi không đi sâu vào nó một cách chi tiết.

Mô hình được mô tả bởi hệ thống hai phương trình vi phân tự trị.

mặt phẳng pha. Chân dung giai đoạn. phương pháp isocline. isoclines chính. Trạng thái ổn định ổn định. Các hệ thống tuyến tính. Các loại điểm chính: nút, yên ngựa, tiêu điểm, trung tâm. Ví dụ: các phản ứng hóa học bậc một.

Kết quả thú vị nhất về mô hình định tính các đặc tính của hệ thống sinh học thu được trên mô hình của hai phương trình vi phân, cho phép nghiên cứu định tính bằng cách sử dụng phương pháp mặt phẳng pha. Xét một hệ hai phương trình vi phân thông thường tự trị có dạng tổng quát

(4.1)

P (x, y), Q (x, y)- các chức năng liên tục được xác định trong một số miền G Máy bay Euclide ( x, y- Tọa độ Descartes) và có trong khu vực này các đạo hàm liên tục có bậc không thấp hơn bậc đầu tiên.

Vùng đất G có thể là không giới hạn hoặc có giới hạn. Nếu các biến x, y có ý nghĩa sinh học cụ thể (nồng độ các chất, sự phong phú của các loài), thường là diện tích G là góc phần tư dương của nửa mặt phẳng bên phải:

0 £ x< ¥ ,0 £ y< ¥ .

Nồng độ của các chất hoặc sự phong phú của các loài cũng có thể bị giới hạn từ trên cao bởi thể tích của bình hoặc bởi khu vực của môi trường sống. Khi đó phạm vi của các biến có dạng:

0 £ x< x 0 , 0 £ y< y 0 .

Biến x, y thay đổi theo thời gian theo hệ phương trình (4.1), sao cho mỗi trạng thái của hệ tương ứng với một cặp giá trị của biến ( x, y).

Ngược lại, với mỗi cặp biến ( x, y) tương ứng với một trạng thái nhất định của hệ thống.

Hãy xem xét một mặt phẳng với các trục tọa độ, trên đó giá trị của các biến được vẽ x, y. Mọi điểm M mặt phẳng này tương ứng với một trạng thái nhất định của hệ thống. Một mặt phẳng như vậy được gọi là mặt phẳng pha và mô tả tổng thể của tất cả các trạng thái của hệ thống. Điểm M (x, y) được gọi là điểm mô tả hoặc điểm biểu diễn.

Hãy để ở thời điểm ban đầu t = t 0 đại diện cho tọa độ điểm M 0 (x(t 0), y(t 0)). Vào mỗi thời điểm tiếp theo trong thời gian tđiểm mô tả sẽ di chuyển theo những thay đổi trong giá trị của các biến x(t), y(t). Tập hợp các điểm M(x(t), y (t)) trên mặt phẳng pha, vị trí của nó tương ứng với các trạng thái của hệ thống trong quá trình thay đổi các biến số theo thời gian x (t), y (t) theo phương trình (4.1), được gọi là quỹ đạo pha.

Tập hợp các quỹ đạo pha cho các giá trị ban đầu khác nhau của các biến mang lại một "chân dung" dễ dàng nhìn thấy của hệ thống. Tòa nhà chân dung giai đoạn cho phép bạn rút ra kết luận về bản chất của những thay đổi trong các biến x, y mà không cần biết các nghiệm phân tích của hệ phương trình ban đầu(4.1).

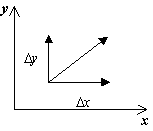
Để vẽ chân dung pha, cần phải xây dựng trường vectơ chỉ hướng cho các quỹ đạo của hệ thống tại mỗi điểm của mặt phẳng pha. Bằng cách chỉ định một gia sốD t> 0,chúng tôi nhận được số gia tương ứng D x và D y từ các biểu thức:

D x = P (x, y)D t,

D y = Q (x, y)D t

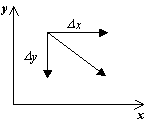
hướng vector dy / dxỞ điểm ( x, y) phụ thuộc vào dấu hiệu của các chức năng P (x, y), Q (x, y) và có thể được đưa ra bởi một bảng:

P (x, y)> 0, Q (x, y)> 0
P (x, y)<0,Q(x,y)<0
P (x, y)> 0, Q (x, y)<0
P (x, y)<0,Q(x,y)>0

.(4.2)

Lời giải cho phương trình này y = y(x, c), hoặc ngầm hiểu F(x, y)= c,ở đâu Với là hằng số của tích phân, cho họ các đường cong tích phân của phương trình (4.2) - quỹ đạo pha hệ thống (4.1) trên máy bay x, y.

Phương pháp Isocline

Để tạo chân dung theo pha, người ta sử dụng phương pháp isocline - các đường thẳng được vẽ trên mặt phẳng pha cắt các đường cong tích phân ở một góc cụ thể. Phương trình isocline dễ dàng nhận được từ (4.2). Chúng ta hãy đặt

ở đâu NHƯNG– một hằng số nhất định. Nghĩa NHƯNG biểu diễn tang của độ dốc của tiếp tuyến với quỹ đạo pha và có thể nhận các giá trị từ -¥ đến + ¥ . Thay thế thay vì dy / dx trong (4.2) số lượng NHƯNG chúng tôi nhận được phương trình isocline:

.(4.3)

Công thức (4.3) xác định tại mỗi điểm của mặt phẳng là tiếp tuyến duy nhất của đường cong tích phân tương ứng, ngoại trừ điểm tại đó P (x, y)= 0, Q (x, y) = 0 , trong đó hướng của tiếp tuyến trở thành không xác định, vì giá trị của đạo hàm trở nên không xác định:

.

Điểm này là giao điểm của tất cả các đường đẳng - điểm đặc biệt. Nó đồng thời làm biến mất các đạo hàm thời gian của các biến x và y.

Do đó, tại điểm kỳ dị, tốc độ thay đổi của các biến bằng không. Do đó, điểm kỳ dị của phương trình vi phân của quỹ đạo pha (4.2) tương ứng với trạng thái tĩnh của hệ thống(4.1), và tọa độ của nó là giá trị tĩnh của các biến x, y.

Đặc biệt quan tâm là isoclines chính:

dy / dx = 0, P(x, y)=0 – đường đẳng của các tiếp tuyến ngang và

dy / dx =¥ , Q(x, y)=0 – đường đẳng của các tiếp tuyến thẳng đứng.

Bằng cách xây dựng các đường đẳng chính và tìm điểm giao của chúng (x, y), tọa độ thỏa mãn các điều kiện:

Do đó, chúng ta sẽ tìm thấy giao điểm của tất cả các đường đẳng của mặt phẳng pha, tại đó hướng của tiếp tuyến với quỹ đạo pha là không xác định. Nó - điểm kỳ lạ, tương ứng trạng thái tĩnh của hệ thống(Hình 4.2).

Hệ thống (4.1) có càng nhiều trạng thái dừng càng có nhiều điểm giao nhau của các đường đẳng chính trên mặt phẳng pha.

Mỗi quỹ đạo pha tương ứng với một tập hợp các chuyển động của một hệ động lực đi qua các trạng thái giống nhau và chỉ khác nhau bởi quy chiếu đầu thời gian.

Nếu các điều kiện của định lý Cauchy được thỏa mãn thì qua mỗi điểm của không gian x, y, tđi qua một đường cong tích phân duy nhất. Điều này cũng đúng, nhờ sự tự chủ, đối với quỹ đạo pha: quỹ đạo pha duy nhất đi qua mỗi điểm của mặt phẳng pha.

Trạng thái ổn định ổn định

Để hệ ở trạng thái cân bằng.

Sau đó, điểm đại diện được đặt tại một trong những điểm kỳ lạ của hệ thống, theo định nghĩa:

.

Điểm kỳ dị có ổn định hay không được xác định bằng việc điểm đại diện có rời đi hay không với độ lệch nhỏ so với trạng thái tĩnh. Khi áp dụng cho một hệ hai phương trình, định nghĩa về tính ổn định trong ngôn ngữe, dnhư sau.

Trạng thái cân bằng là ổn định nếu đối với bất kỳ khu vực nào cho trước sai lệch so với trạng thái cân bằng (e )khu vực có thể được chỉ định d (e ), xung quanh trạng thái cân bằng và có đặc tính là không có quỹ đạo nào bắt đầu bên trong vùng d , sẽ không bao giờ đến được biên giới e . (Hình 4.4)

Đối với một lớp hệ thống lớn - hệ thống thô sơ – Bản chất của hành vi không thay đổi với một sự thay đổi nhỏ trong loại phương trình, thông tin về loại hành vi trong vùng lân cận của trạng thái tĩnh có thể thu được bằng cách nghiên cứu không phải bản gốc, nhưng đơn giản hóa. tuyến tính hóa hệ thống.

Các hệ thống tuyến tính.

Xét một hệ hai phương trình tuyến tính:

.(4.4)

Nơi đây A B C D- hằng số, x, y- Hệ tọa độ Descartes trên mặt phẳng pha.

Giải pháp chung sẽ được tìm kiếm dưới dạng:

.(4.5)

Thay thế các biểu thức này trong (4.4) và giảm bớt e l t:

(4.6)

Hệ phương trình đại số (4.6) với ẩn số A, B chỉ có nghiệm khác không nếu định thức của nó, bao gồm các hệ số của ẩn số, bằng 0:

.

Mở rộng định thức này, ta thu được phương trình đặc trưng của hệ:

.(4.7)

Nghiệm của phương trình này cho các giá trị của chỉ sốl 1,2 , theo đó các giá trị khác không có thể có cho Một và B nghiệm của phương trình (4.6). Những giá trị này là

.(4.8)

Nếu biểu thức căn là âm, thìl 1,2 số liên hợp phức tạp. Giả sử rằng cả hai nghiệm của phương trình (4.7) đều có phần thực khác không và không có nhiều nghiệm. Khi đó nghiệm tổng quát của hệ (4.4) có thể được biểu diễn dưới dạng tổ hợp tuyến tính của số mũ với số mũl 1 , l 2 :

(4.9)

Để phân tích bản chất của quỹ đạo có thể có của hệ thống trên mặt phẳng pha, chúng tôi sử dụng phép biến đổi tọa độ thuần nhất tuyến tính,điều này sẽ đưa hệ thống đến hình thức kinh điển:

,(4.10)

cho phép biểu diễn thuận tiện hơn trên mặt phẳng pha so với hệ thống ban đầu (4.4). Hãy giới thiệu các tọa độ mớiξ , η theo các công thức:

(4.1)

Từ khóa học đại số tuyến tính, người ta biết rằng nếu các phần thực không bằng 0l 1 , l 2 hệ thống ban đầu (4.4) với sự trợ giúp của các phép biến đổi (4.11) luôn có thể được chuyển đổi thành dạng chính tắc (4.10) và hành vi của nó trên mặt phẳng pha có thể được nghiên cứuξ , η . Hãy xem xét các trường hợp khác nhau có thể xuất hiện ở đây.

Rễ λ 1 , λ 2 - hợp lệ và cùng dấu

Trong trường hợp này, các hệ số biến đổi là thực, chúng ta chuyển từ mặt phẳng thựcx, yđến mặt phẳng thực ξ, η. Chia phương trình thứ hai (4.10) cho phương trình thứ nhất, ta thu được:

.(4.12)

Tích hợp phương trình này, chúng tôi thấy:

Ở đâu. (4,13)

Hãy để chúng tôi đồng ý để hiểu bởi λ 2 căn của phương trình đặc trưng với môđun lớn, điều này không vi phạm tính tổng quát của suy luận của chúng ta. Sau đó, vì trong trường hợp đang xét các gốc λ 1 , λ2 - hợp lệ và cùng dấu,một>1 , và chúng tôi đang xử lý các đường cong tích phân của loại parabol.

Tất cả các đường cong tích phân (ngoại trừ trục η , tương ứng với ) chạm vào điểm gốc của trục ξ, mà cũng là một đường cong tích phân của phương trình (4.11). Gốc tọa độ là một điểm kỳ dị.

Bây giờ chúng ta hãy tìm hiểu hướng chuyển động của điểm đại diện dọc theo các quỹ đạo pha. Nếu λ 1, λ 2 là âm, do đó, như có thể thấy trong các phương trình (4.10), | ξ |, | η | giảm dần theo thời gian. Điểm đại diện tiếp cận điểm gốc, nhưng không bao giờ đạt được nó. Nếu không, điều này sẽ mâu thuẫn với định lý Cauchy, trong đó nói rằng chỉ có một quỹ đạo pha đi qua mỗi điểm của mặt phẳng pha.

Một điểm kỳ dị như vậy mà các đường cong tích phân đi qua, giống như một họ các parabol đi qua điểm gốc, được gọi là một nút (Hình. 4.5)

Trạng thái cân bằng kiểu nút ở λ 1, λ 2 < 0 là ổn định theo Lyapunov, vì điểm đại diện di chuyển dọc theo tất cả các đường cong tích phân về phía gốc tọa độ. nó nút ổn định. Nếu λ 1, λ 2 > 0, sau đó | ξ |, | η | tăng dần theo thời gian và điểm đại diện dịch chuyển ra xa gốc tọa độ. Trong trường hợp này, điểm kỳ dị– nút thắt không ổn định .

Trên mặt phẳng pha x, y Đặc tính định tính chung của hoạt động của các đường cong tích phân sẽ vẫn còn, nhưng các tiếp tuyến của các đường cong tích phân sẽ không trùng với các trục tọa độ. Góc nghiêng của các tiếp tuyến này sẽ được xác định bằng tỷ số của các hệ số α , β , γ , δ trong phương trình (4.11).

Rễ λ 1 , λ 2 hợp lệ và có các dấu hiệu khác nhau.

Chuyển đổi từ tọa độ x, y đến tọa độ ξ, η lại có thật. Các phương trình cho các biến chính tắc một lần nữa có dạng (4.10), nhưng bây giờ các dấu hiệu λ 1, λ 2 khác nhau. Phương trình quỹ đạo pha có dạng:

Ở đâu, (4,14)

Tích hợp (4.14), chúng tôi thấy

(4.15)

nó phương trình xác định một họ các đường cong kiểu hypebol, trong đó cả hai trục tọa độ là những người không có triệu chứng (tại một=1 chúng ta sẽ có một họ các hypebol cân bằng). Các trục tọa độ cũng là các đường cong tích phân trong trường hợp này– đây sẽ là những đường cong tích phân duy nhất đi qua điểm gốc. Mỗitrong đó bao gồm quỹ đạo ba pha: của hai chuyển động hướng tới trạng thái cân bằng (hoặc đi khỏi trạng thái cân bằng) và từ trạng thái cân bằng. Tất cả các đường cong tích phân khác– là các hypebol không đi qua điểm gốc (Hình. 4.6) Điểm kỳ lạ này được gọi là "Yên xe ». Các đường mức gần núi yên xe hoạt động giống như quỹ đạo pha trong vùng lân cận của yên xe.

Chúng ta hãy xem xét bản chất của chuyển động của điểm đại diện dọc theo các quỹ đạo pha gần trạng thái cân bằng. Ví dụ,λ 1> 0, λ 2<0 . Khi đó điểm đại diện đặt trên trục ξ , sẽ di chuyển ra khỏi điểm gốc và được đặt trên trục η – sẽ tiếp cận vô thời hạn gốc tọa độ, mà không đạt được nó trong thời gian hữu hạn. Bất cứ nơi nào điểm đại diện ở thời điểm ban đầu (ngoại trừ điểm kỳ dị và các điểm trên đường tiệm cận η =0), cuối cùng nó sẽ di chuyển khỏi trạng thái cân bằng, ngay cả khi lúc đầu nó di chuyển dọc theo một trong những đường cong tích phân hướng tới một điểm kỳ dị.

Hiển nhiên là điểm kỳ dị kiểu yên ngựa luôn không ổn định . Chỉ trong những điều kiện ban đầu được lựa chọn đặc biệt trên đường tiệm cậnη =0 hệ thống sẽ tiến tới trạng thái cân bằng. Tuy nhiên, điều này không mâu thuẫn với khẳng định rằng hệ thống không ổn định. Nếu bạn đếm, rằng tất cả các trạng thái ban đầu của hệ thống trên mặt phẳng pha đều có xác suất như nhau, thì xác suất của trạng thái ban đầu tương ứng với chuyển động theo hướngđến điểm kỳ dị bằng không. Do đó, bất kỳ chuyển động thực nào cũng sẽ đưa hệ thống ra khỏi trạng thái cân bằng.Quay lại tọa độx, y,chúng ta có được bức tranh định tính giống nhau về bản chất của chuyển động của các quỹ đạo xung quanh gốc tọa độ.

Ranh giới giữa các trường hợp được xem xét của nút và yên là trường hợp khi nào một trong những chỉ số đặc trưng, ​​ví dụ λ 1 , biến mất, xảy ra khi yếu tố quyết định của hệ thống- biểu hiện adbc = 0(xem công thức 4.8 ). Trong trường hợp này, các hệ số của vế phải của phương trình (4.4) tỷ lệ với nhau:

và hệ thống có trạng thái cân bằng cho tất cả các điểm của đường thẳng:

Các đường cong tích phân còn lại là một họ các đường thẳng song song với hệ số góc , cùng với đó các điểm đại diện hoặc tiến đến trạng thái cân bằng hoặc di chuyển ra khỏi nó, tùy thuộc vào dấu của căn bậc hai của phương trình đặc trưng λ 2 = a + d.(Hình 4,7 ) Trong trường hợp này, tọa độ của trạng thái cân bằng phụ thuộc vào giá trị ban đầu của các biến.

Rễ λ 1 , λ 2 – tổ hợpliên hợp

Trong trường hợp này, thực tếx và y chúng tôi sẽ có các liên hợp phức tạp ξ , η (4.10) . Tuy nhiên, bằng cách đưa thêm một phép biến đổi trung gian nữa, trong trường hợp này cũng có thể giảm việc xem xét thành một phép biến đổi thuần nhất tuyến tính thực. Chúng ta hãy đặt:

(4.16)

ở đâu a, b, và u, v – giá trị thực. Có thể cho thấy rằng sự biến đổi từx, yđến u, v là, theo giả định của chúng tôi, thực, tuyến tính, đồng nhất với một định thức khác 0. Do các phương trình(4.10, 4.16) chúng ta có:

ở đâu

(4.17)

Chia phương trình thứ hai cho phương trình thứ nhất, chúng tôi nhận được:

cái nào dễ tích hợp hơn, nếu chúng ta chuyển sang hệ tọa độ cực (r, φ ) . Sau khi thay thế chúng tôi nhận được từ nơi:

.(4.18)

Do đó, trên mặt phẳng phau, vchúng tôi đang giải quyết một họ các đường xoắn ốc logarit, mỗi họ cótiệm cận tại gốc tọa độ.Điểm độc nhất là điểm tiệm cận của tất cả các đường cong tích phân có dạng xoắn ốc, lồng vào người bạnbạn bè, được gọi là tiêu điểm ( Hình.4.8 ) .

Chúng ta hãy xem xét bản chất của chuyển động của điểm biểu diễn dọc theo các quỹ đạo pha. Nhân bậc nhất của phương trình (4.17) vớiu, và thứ hai tới v và thêm, chúng tôi nhận được:

Ở đâu

Để cho một 1 < 0 (một 1 = Lạiλ ) . Sau đó, điểm đại diện liên tục tiếp cận điểm gốc mà không tiếp cận nó trong một thời gian hữu hạn. Điều này có nghĩa là quỹ đạo pha là xoắn ốc xoắn và tương ứng với các dao động tắt dần biến. Nó - tập trung ổn định .

Trong trường hợp tiêu điểm ổn định, như trường hợp nút ổn định, không chỉ điều kiện Lyapunov được thỏa mãn mà còn có yêu cầu nghiêm ngặt hơn. Cụ thể, đối với bất kỳ độ lệch ban đầu nào, hệ thống cuối cùng sẽ trở lại gần vị trí cân bằng như mong muốn. Sự ổn định như vậy, trong đó độ lệch ban đầu không những không tăng lên mà còn giảm dần, có xu hướng về 0, được gọi là ổn định tuyệt đối .

Nếu trong công thức (4.18) một 1 >0 , sau đó điểm đại diện di chuyển khỏi điểm gốc và chúng tôi đang xử lý tiêu điểm không ổn định . Khi di chuyển từ máy bayu, vđến mặt phẳng phax, yxoắn ốc cũng sẽ vẫn là xoắn ốc, nhưng sẽ bị biến dạng.

Bây giờ hãy xem xét trường hợp khimột 1 =0 . Quỹ đạo pha trên mặt phẳngu, vsẽ có những vòng kết nối cái nào trên máy bayx, yphù hợp với hình elip:

Do đó, tạimột 1=0 thông qua một điểm đặc biệtx = 0, y = 0 không có đường cong tích phân đi qua. Một điểm kỳ dị biệt lập như vậy, gần đó các đường cong tích phân là các đường cong khép kín, cụ thể là các hình elip nhúng vào nhau và bao quanh điểm kỳ dị, được gọi là tâm.

Do đó, có thể có sáu loại cân bằng, tùy thuộc vào bản chất của các gốc của phương trình đặc trưng (4.7). Chế độ xem quỹ đạo pha trên mặt phẳng x, y cho sáu trường hợp này được thể hiện trong Hình. 4.9.

Cơm. 4.9.Các dạng chân dung pha trong vùng lân cận của trạng thái đứng yên đối với hệ phương trình tuyến tính (4.4).

Năm loại trạng thái cân bằng là thô, bản chất của chúng không thay đổi với những thay đổi đủ nhỏ trong vế phải của phương trình (4.4). Trong trường hợp này, các thay đổi phải nhỏ không chỉ ở các vế bên phải mà còn ở các phái sinh bậc nhất của chúng. Trạng thái cân bằng thứ sáu - trung tâm - không thô. Với những thay đổi nhỏ trong các tham số của vế phải của phương trình, nó sẽ đi vào trọng tâm ổn định hoặc không ổn định.

Sơ đồ phân đôi

Hãy để chúng tôi giới thiệu ký hiệu:

. (4.11)

Khi đó, phương trình đặc trưng có thể được viết dưới dạng:

. (4.12)

Xét một mặt phẳng có tọa độ Descartes hình chữ nhật S , D và đánh dấu trên đó các khu vực tương ứng với một hoặc một loại trạng thái cân bằng khác, được xác định bởi bản chất của các gốc của phương trình đặc trưng

.(4.13)

Điều kiện cho sự ổn định của trạng thái cân bằng sẽ là sự hiện diện của một phần thực âm của yl 1 và l 2 . Điều kiện cần và đủ cho điều này là sự thỏa mãn các bất đẳng thứcS > 0, D > 0 . Trên sơ đồ (4.15), điều kiện này tương ứng với các điểm nằm trong phần tư đầu tiên của mặt phẳng tham số. Điểm kỳ dị sẽ là tiêu điểm nếul 1 và l 2 tổ hợp. Điều kiện này tương ứng với những điểm của mặt phẳng mà , những thứ kia. điểm giữa hai nhánh của một parabolS 2 = 4 D. Semiaxis điểm S = 0, D> 0, tương ứng với các trạng thái cân bằng của loại tâm. Tương tự như vậy,l 1 và l 2 - hợp lệ, nhưng các dấu hiệu khác nhau, tức là một điểm số ít sẽ là yên ngựa nếu D<0, vân vân. Kết quả là, chúng tôi nhận được một sơ đồ phân vùng của mặt phẳng tham số S, D, thành các vùng tương ứng với các dạng trạng thái cân bằng khác nhau.

Cơm. 4.10. Sơ đồ phân đôi

đối với hệ phương trình tuyến tính 4.4

Nếu các hệ số của hệ thống tuyến tính A B C D phụ thuộc vào một số tham số, sau đó khi tham số này được thay đổi, các giá trị cũng sẽ thay đổiS , D . Khi đi qua các ranh giới, bản chất của chân dung pha thay đổi về chất. Do đó, các ranh giới như vậy được gọi là ranh giới phân đôi - ở các phía đối diện của ranh giới, hệ thống có hai chân dung pha khác nhau về mặt cấu trúc liên kết và do đó, hai loại hành vi khác nhau.

Sơ đồ cho thấy những thay đổi như vậy có thể diễn ra như thế nào. Nếu loại trừ những trường hợp đặc biệt - gốc tọa độ - thì ta dễ dàng nhận thấy yên ngựa có thể đi vào một điểm nút, ổn định hoặc không ổn định khi qua trục y. Một nút ổn định có thể di chuyển đến yên ngựa hoặc tiêu điểm ổn định, v.v. Lưu ý rằng sự chuyển đổi tiêu điểm ổn định - tiêu điểm ổn định và nút không ổn định - không ổn định không phải là phân nhánh, vì cấu trúc liên kết của không gian pha không thay đổi trong trường hợp này. Chúng ta sẽ nói chi tiết hơn về cấu trúc liên kết của không gian pha và các phép chuyển phân đôi trong Bài giảng 6.

Dưới sự chuyển đổi phân đôi, bản chất của sự ổn định của điểm kỳ dị thay đổi. Ví dụ, một tiêu điểm ổn định qua trung tâm có thể chuyển thành một tiêu điểm không ổn định. Sự phân đôi này được gọi là Andronov-Hopf phân đôi bởi tên của các nhà khoa học đã nghiên cứu nó. Với sự phân đôi này trong hệ thống phi tuyến, một chu kỳ giới hạn được sinh ra và hệ thống trở nên tự dao động (xem bài 8).

Thí dụ. Hệ thống các phản ứng hóa học tuyến tính

Vật chất X từ ngoài vào với tốc độ không đổi, biến thành chất Y và với tốc độ tỉ lệ thuận với nồng độ của chất Y, được đưa ra khỏi quả cầu phản ứng. Tất cả các phản ứng đều có bậc nhất, ngoại trừ luồng vật chất từ ​​bên ngoài vào, có bậc bằng không. Sơ đồ phản ứng giống như sau:

(4.14)

và được mô tả bằng hệ phương trình:

(4.15)

Chúng tôi thu được nồng độ tĩnh bằng cách cân bằng các cạnh bên phải với 0:

.(4.16)

Xem xét chân dung pha của hệ thống. Chúng ta hãy chia phương trình thứ hai của hệ (4.16) cho phương trình thứ nhất. Chúng tôi nhận được:

.(4.17)

Phương trình (4.17) xác định hành vi của các biến trên mặt phẳng pha. Hãy để chúng tôi xây dựng một chân dung giai đoạn của hệ thống này. Đầu tiên, chúng ta vẽ các đường đẳng chính trên mặt phẳng pha. Phương trình đường đẳng của các tiếp tuyến thẳng đứng:

Phương trình đường đẳng của các tiếp tuyến nằm ngang:

Điểm kỳ dị (trạng thái đứng yên) nằm ở giao điểm của các đường đẳng chính.

Bây giờ chúng ta hãy xác định xem các trục tọa độ cắt các đường cong tích phân ở góc nào.

Nếu một x = 0, sau đó.

Do đó, tang của hệ số góc của tiếp tuyến với các đường cong tích phân y = y (x), vượt qua trục y x = 0, là âm trong nửa mặt phẳng trên (nhớ lại rằng các biến x, y có giá trị nồng độ, và do đó chúng tôi chỉ quan tâm đến góc phần tư phía trên bên phải của mặt phẳng pha). Trong trường hợp này, giá trị của góc nghiêng của tiếp tuyến tăng theo khoảng cách từ gốc tọa độ.

Xem xét trục y = 0. Tại giao điểm của trục này, các đường cong tích phân được mô tả bằng phương trình

Tại Tiếp tuyến của hệ số góc của các đường cong tích phân đi qua trục abscissa là dương và tăng từ 0 đến vô cùng khi tăng x.

Tại .

Sau đó, với sự gia tăng hơn nữa, tiếp tuyến của hệ số góc giảm giá trị tuyệt đối, vẫn âm và có xu hướng -1 tại x ® ¥ . Biết được hướng của các tiếp tuyến với các đường cong tích phân trên các đường đẳng chính và trên các trục tọa độ, ta dễ dàng dựng được bức tranh toàn cảnh về quỹ đạo pha.

Bản chất của sự ổn định của điểm kỳ dị sẽ được thiết lập bằng cách sử dụng phương pháp Lyapunov. Định thức đặc trưng của hệ thống có dạng:

.

Mở rộng định thức, ta thu được phương trình đặc trưng của hệ: , I E. các gốc của phương trình đặc trưng đều âm. Do đó, trạng thái tĩnh của hệ thống là một nút ổn định. Đồng thời, nồng độ của chất X có xu hướng chuyển sang trạng thái đứng yên luôn đơn điệu, nồng độ của chất Y có thể đi qua cực tiểu hoặc cực đại. Các chế độ dao động trong một hệ thống như vậy là không thể.

Chuỗi Taylor đóng vai trò như một công cụ hiệu quả để nghiên cứu các hàm giải tích trong hình tròn zol Để nghiên cứu các hàm giải tích trong một vùng hình khuyên, hóa ra có thể xây dựng các khai triển theo lũy thừa dương và âm (z - zq) của hình thức tổng quát hóa mở rộng Taylor. Chuỗi (1), được hiểu là tổng của hai chuỗi, được gọi là chuỗi Laurent. Rõ ràng rằng vùng hội tụ của chuỗi (1) là phần chung của các vùng hội tụ của mỗi chuỗi (2). Hãy tìm cô ấy. Khu vực hội tụ của chuỗi đầu tiên là một hình tròn có bán kính được xác định bởi công thức Cauchy-Hadamard Bên trong vòng tròn hội tụ, chuỗi (3) hội tụ theo một hàm giải tích và trong bất kỳ hình tròn nào có bán kính nhỏ hơn, nó hội tụ tuyệt đối và đồng nhất. Chuỗi thứ hai là chuỗi lũy thừa liên quan đến biến số. Chuỗi (5) hội tụ trong vòng tròn của nó hội tụ với hàm giải tích của biến phức m- * oo và trong bất kỳ vòng tròn nào có bán kính nhỏ hơn, nó hội tụ tuyệt đối và đồng nhất, nghĩa là miền hội tụ của chuỗi (4) là sự xuất hiện của đường tròn - Nếu thì miền hội tụ chung của chuỗi (3) và (4) - một vành tròn trong đó chuỗi (1) hội tụ sang một hàm phân tích. Hơn nữa, ở bất kỳ vòng nào, nó đều hội tụ tuyệt đối và đồng nhất. Ví dụ 1. Xác định vùng hội tụ của chuỗi rad Laurent Các điểm kỳ dị biệt lập và phân loại của chúng (z), có giá trị đơn và không chính trị trong một vòng tròn, có thể được biểu diễn trong vòng này dưới dạng tổng của một chuỗi hội tụ có hệ số Cn được xác định duy nhất và được tính bằng công thức trong đó 7p là một đường tròn bán kính m Hãy cho chúng ta cố định một điểm z tùy ý bên trong vòng R Chúng ta dựng các đường tròn có tâm tại điểm r có bán kính thỏa mãn các bất đẳng thức và xem xét một vành mới Theo định lý tích phân Cauchy cho miền liên thông nhân, chúng ta có Đối với tất cả các điểm £ dọc theo đường tròn 7d *, thỏa mãn quan hệ tổng của một chuỗi hội tụ đồng nhất 1 1. Do đó, phân số ^ có thể được biểu diễn dưới dạng vi- / "/ theo một cách hơi khác, đối với tất cả các điểm ξ trên vòng tròn ir> ta có quan hệ Do đó, phân số ^ có thể được biểu diễn dưới dạng tổng của một chuỗi hội tụ đều trong công thức (10) và (12) là các hàm giải tích trong một vòng tròn. Do đó, theo định lý Cauchy, giá trị của các tích phân tương ứng không thay đổi nếu các đường tròn 7 / r và 7r / được thay bằng bất kỳ đường tròn nào. Điều này cho phép chúng ta kết hợp các công thức (10) và (12). Thay các tích phân ở phía bên phải của công thức (8) bằng các biểu thức (9) và (11) của chúng, tương ứng, chúng ta thu được khai triển mong muốn. Vì z là một tùy ý điểm của vòng, theo đó chuỗi (14) hội tụ đến hàm f (z) ở mọi nơi trong vành này, và trong bất kỳ vành nào, chuỗi hội tụ đến hàm này một cách tuyệt đối và đồng nhất. Bây giờ chúng ta hãy chứng minh rằng phân rã của dạng (6) là duy nhất. Giả sử rằng một lần phân hủy nữa diễn ra Khi đó, ở mọi nơi bên trong vành R, chúng ta có Trên chu vi, chuỗi (15) hội tụ đồng nhất. Nhân cả hai vế của đẳng thức (với m là một số nguyên cố định và tích phân cả hai số hạng của chuỗi theo số hạng. Kết quả là chúng ta nhận được ở bên trái và ở bên phải - Csh. Như vậy, (4, \ u003d St. Vì m là một số tùy ý, nên chuỗi đẳng thức cuối cùng (6), các hệ số của chúng được tính bằng công thức (7), được gọi là chuỗi Laurent của hàm f (z) trong vành 7) đối với các hệ số của Chuỗi Laurent hiếm khi được sử dụng trong thực tế, vì theo quy luật, chúng yêu cầu các phép tính phức tạp. Thông thường, nếu có thể, các khai triển Taylor đã tạo sẵn của các hàm cơ bản được sử dụng. Dựa trên tính duy nhất của khai triển, bất kỳ phương pháp hợp pháp nào cũng dẫn đến giống nhau Ví dụ 2 Xét chuỗi Laurent khai triển các hàm của các miền khác nhau, giả sử Fuiscija / (z) có hai điểm kỳ dị: Do đó, có ba miền vành và, có tâm tại điểm r = 0. trong mỗi điểm mà hàm f (r) là giải tích: a) đường tròn là ngoại tiếp của đường tròn (Hình 27). Hãy để chúng tôi tìm các mở rộng Laurent của hàm / (z) trong mỗi vùng này. Chúng ta biểu diễn / (z) dưới dạng tổng của các phân số cơ bản a) Quan hệ Biến đổi đường tròn (16) như sau Sử dụng công thức tổng các số hạng của một cấp tiến hình học, chúng ta thu được b) Vành cho hàm -z vẫn hội tụ trong vành này, kể từ Chuỗi (19) cho hàm j ^ j cho | z | > 1 phân kỳ. Do đó, chúng tôi biến đổi hàm / (z) như sau: áp dụng công thức (19) một lần nữa, chúng tôi nhận được rằng chuỗi này hội tụ cho. Thay các khai triển (18) và (21) vào quan hệ (20), ta thu được c) Suy rộng của đường tròn đối với hàm -z với | z | > 2 phân kỳ và chuỗi (21) cho hàm Hãy biểu diễn hàm / (z) dưới dạng sau: /<*> Sử dụng công thức (18) và (19), chúng ta thu được OR 1 Ví dụ này cho thấy rằng đối với cùng một hàm f (z), nói chung, khai triển Laurent có dạng khác đối với các vành khác nhau. Ví dụ 3. Tìm phân tích của chuỗi 8 Laurent của hàm Chuỗi Laurent Các điểm kỳ dị biệt lập và phân loại của chúng trong vùng hình khuyên A Chúng ta sử dụng biểu diễn của hàm f (z) dưới dạng sau: và biến đổi số hạng thứ hai Sử dụng Công thức tính tổng các số hạng của một cấp tiến hình học, ta thu được Thay các biểu thức tìm được vào công thức (22), ta có Ví dụ 4. Khai triển hàm trong một chuỗi Laurent trong vùng lân cận của zq = 0. Đối với một phức bất kỳ , chúng ta có Giả sử Khai triển này hợp lệ với bất kỳ điểm nào z Ф 0. Trong trường hợp này, vùng hình khuyên là toàn bộ mặt phẳng phức với một điểm z được ném ra - 0. Vùng này có thể được xác định theo mối quan hệ sau: Hàm này là giải tích trong vùng Từ công thức (13) cho các hệ số của chuỗi Laurent, bằng cách lập luận tương tự như trong đoạn trước, người ta có thể thu được các bất đẳng thức Kouiw. nếu hàm f (z) bị giới hạn trên một đường tròn, trong đó M là hằng số), thì các điểm kỳ dị cô lập Một điểm zo được gọi là điểm kỳ dị cô lập của hàm f (z) nếu tồn tại một lân cận hình khuyên của điểm ( tập hợp này đôi khi còn được gọi là vùng lân cận xuyên của điểm 2o), trong đó hàm f (z) có giá trị đơn và giải tích. Tại thời điểm zo chính nó, hàm hoặc không được xác định hoặc không có giá trị đơn và phân tích. Ba loại điểm kỳ dị được phân biệt tùy thuộc vào hoạt động của hàm / (z) khi tiếp cận điểm zo. Một điểm kỳ dị biệt lập được gọi là: 1) có thể tháo rời nếu tồn tại một điểm hữu hạn 2) chiều sâu nếu 3) một điểm kỳ dị về cơ bản nếu hàm f (z) không có giới hạn đối với Định lý 16. Một điểm kỳ dị cô lập z0 của hàm f (z) là điểm kỳ dị di động được nếu và chỉ khi khai triển Laurent của hàm f (z) trong vùng lân cận của điểm zo không chứa phần chính, tức là có dạng Let zo - điểm kỳ dị di động. Khi đó, tồn tại một hàm hữu hạn, và do đó hàm f (z) bị giới hạn trong vùng lân cận thăm dò của điểm r. lũy thừa (z - 20) bằng 0: Ngược lại, cho phép Laurent khai triển hàm / (r) trong vùng lân cận của điểm zq chỉ chứa phần đúng, tức là nó có dạng (23) và do đó , là Taylor. Dễ dàng thấy rằng đối với z - * z0 thì hàm / (r) có giá trị giới hạn: Định lý 17. Một điểm kỳ dị cô lập zq của hàm f (z) có thể thay đổi được nếu và chỉ khi hàm J (z) là bị giới hạn trong một số vùng lân cận bị thủng của điểm zq, Zgmechai thì không. Gọi r0 là một điểm kỳ dị di động của f (r). Giả sử chúng ta nhận được rằng hàm f (r) là giải tích trong một số đường tròn có tâm tại điểm thứ. Điều này xác định tên của điểm - dùng một lần. Định lý 18. Một điểm kỳ dị cô lập zq của hàm f (z) là cực nếu và chỉ khi phần chính của khai triển Laurent của hàm f (z) trong vùng lân cận của điểm chứa một số hữu hạn (và dương) của các số hạng khác 0, tức là, có dạng 4 Gọi z0 là một cực. Từ đó tồn tại một vùng lân cận bị thủng của điểm z0 trong đó hàm f (z) là giải tích và khác không. Sau đó, một hàm giải tích được xác định trong vùng lân cận này, và Do đó, điểm zq là một điểm kỳ dị di động (không) của hàm hoặc trong đó h (z) là một hàm giải tích, h (z0) ∩ 0. là hàm giải tích trong một vùng lân cận của điểm zq, và do đó, chúng ta có được điều đó Bây giờ chúng ta hãy giả sử rằng hàm f (z) có dạng phân rã (24) trong một vùng lân cận bị thủng của điểm zo. Điều này có nghĩa là trong vùng lân cận này, hàm f (z) là giải tích cùng với hàm. Đối với hàm g (z), khai triển có giá trị từ đó rõ ràng zq là một điểm kỳ dị di động của hàm g (z) và tồn tại Khi đó hàm có xu hướng tại 0 - cực của hàm Có một điểm đơn giản hơn thực tế. Điểm Zq là một cực của hàm f (z) nếu và chỉ khi hàm g (z) = y có thể được mở rộng thành một hàm giải tích trong vùng lân cận của điểm zq bằng cách đặt g (z0) = 0. Thứ tự của cực của hàm f (z) được gọi là bậc không của hàm jfa. Định lý 16 và 18 ngụ ý khẳng định sau. Định lý 19. Một mỏng kỳ dị cô lập về cơ bản là kỳ dị nếu và chỉ khi phần chính của khai triển Laurent trong vùng lân cận bị thủng của điểm này chứa vô số số hạng khác không. Ví dụ 5. Điểm kỳ dị của hàm là zo = 0. Ta có Dòng Laurent Các điểm kỳ dị biệt lập và phân loại của chúng Do đó, zo = 0 là một điểm kỳ dị di động được. Khai triển của hàm / (z) trong chuỗi Laurent trong vùng lân cận của điểm 0 chỉ chứa phần đúng: Ví dụ 7. f (z) = Điểm kỳ dị của hàm f (z) là zq = 0. Xét hành vi của hàm này trên trục thực và trục ảo: trên trục thực tại x 0, trên trục ảo Do đó, không hữu hạn cũng không giới hạn vô hạn f (z) tại z - * 0 không tồn tại. Do đó điểm r0 = 0 là một điểm kỳ dị về cơ bản của hàm f (z). Chúng ta hãy tìm khai triển Laurent của hàm f (z) trong một vùng lân cận của điểm 0. Đối với bất kỳ C phức tạp nào, chúng tôi có Chúng tôi đặt. Khi đó, khai triển Laurent chứa vô số số hạng với lũy thừa âm của z.

điểm kỳ lạ

Trong toán học.

1) Điểm độc nhất của đường cong được cho bởi phương trình F ( x, y) = 0, - điểm M 0 ( x 0, y 0), trong đó cả hai đạo hàm riêng của hàm F ( x, y) biến mất:

Ngoài ra, nếu không phải tất cả các đạo hàm riêng cấp hai của hàm F ( x, y) tại điểm M 0 bằng 0 thì O. t được gọi là nhân đôi. Nếu, cùng với sự biến mất của các đạo hàm thứ nhất tại điểm M 0, tất cả các đạo hàm thứ hai biến mất, nhưng không phải tất cả các đạo hàm thứ ba đều bằng 0, thì O. t được gọi là bộ ba, v.v. Khi nghiên cứu cấu trúc của một đường cong gần đôi O. t., Dấu hiệu của biểu thức đóng một vai trò quan trọng.

Nếu Δ> 0 thì O. t được gọi là cô lập; ví dụ, đường cong y 2 - x 4 + 4x 2= 0 gốc tọa độ là O. t. (Xem cơm. một ). Nếu Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - a 4= 0 gốc tọa độ là nút O. t. (Xem cơm. 2 ). Nếu Δ = 0, thì đường cong O. t là cô lập hoặc được đặc trưng bởi thực tế là các nhánh khác nhau của đường cong có một tiếp tuyến chung tại điểm này, ví dụ: tiếp tuyến và tạo thành một điểm, giống như một đường cong y 2 - x 3= 0 (xem cơm. 3 , một); b) đỉnh của loại thứ 2 - các nhánh khác nhau của đường cong nằm trên cùng một phía của tiếp tuyến chung, giống như một đường cong (y - x 2)2 - x 5= 0 (xem cơm. 3 , b); c) điểm tự tiếp xúc (đối với đường cong y 2 - x 4= 0 gốc tọa độ là một hoành độ; (cm. cơm. 3 , Trong). Cùng với O. t. Được chỉ định có nhiều O. t. Khác với những cái tên đặc biệt; ví dụ, một điểm tiệm cận là đỉnh của một đường xoắn ốc với số vòng quay vô hạn (xem Hình. cơm. bốn ), điểm ngắt, điểm góc, v.v.

2) Điểm kỳ dị của phương trình vi phân là điểm mà tại đó cả tử số và mẫu số ở vế phải của phương trình vi phân biến mất đồng thời (Xem Phương trình vi phân)

trong đó P và Q là các hàm phân biệt liên tục. Giả sử O. t. Nằm tại gốc tọa độ và sử dụng công thức Taylor (Xem công thức Taylor), chúng ta có thể biểu diễn phương trình (1) dưới dạng

trong đó P 1 ( x, y) và Q 1 ( x, y) là số thập phân liên quan đến

Cụ thể, nếu λ 1 ≠ λ 2 và λ 1 λ 2> 0 hoặc λ 1 = λ 2, thì O. t. Là một nút; tất cả các đường cong tích phân đi qua các điểm của một vùng lân cận đủ nhỏ của nút đều nhập vào nó. Nếu λ 1 ≠ λ 2 và λ 1 λ 2 i β, α ≠ 0 và β ≠ 0 thì O. t là tiêu điểm; tất cả các đường cong tích phân đi qua các điểm trong vùng lân cận đủ nhỏ của tiêu điểm đều là đường xoắn ốc với vô số lần quay trong bất kỳ vùng lân cận nhỏ tùy ý nào của tiêu điểm. Cuối cùng, nếu λ 1,2 = ± tôiβ, β ≠ 0, thì đặc tính của O. t. không được xác định bởi các số hạng tuyến tính trong các khai triển của P ( x, y) và Q ( x, y), như trường hợp trong tất cả các trường hợp trên; ở đây O. t. có thể là một tiêu điểm hoặc trung tâm, hoặc nó có thể có một ký tự phức tạp hơn. Trong vùng lân cận của trung tâm, tất cả các đường cong tích phân đều được đóng lại và chứa tâm bên trong chúng. Vì vậy, ví dụ, điểm (0, 0) là một nút cho các phương trình tại" = 2u / x(λ 1 = 1, λ 2 = 2; xem cơm. 5 , a) và y" = u / x(λ 1 = λ 2 = 1; xem cơm. 5 , b), một yên cho phương trình y "= -y / x(λ 1 = -1, λ 2 = 1 ; cm. cơm. 6 ), trọng tâm của phương trình y "=(x + y) / (x - y) (λ 1 = 1 - tôi, λ 2 = 1 + tôi; cm. cơm. 7 ) và trung tâm của phương trình y "= -x / y(λ 1 = -tôi, λ 2 = tôi; cm. cơm. tám ).

Nếu x, y) và Q ( x, y) là giải tích, vùng lân cận của O. t. bậc cao hơn có thể được chia thành các vùng: D 1 - chứa đầy đường cong tích phân, cả hai đầu nhập vào O. t. (vùng elip), D 2 - chứa đầy đường cong tích phân, một đầu nhập vào O. t. (vùng parabol), và D 3 - vùng được giới hạn bởi hai đường cong tích phân có trong O. t., giữa chúng có các đường cong tích phân của loại hypebol (vùng hypebol) (xem. cơm. 9 ). Nếu không có đường cong tích phân nào đi vào điểm O. thì điểm O. được gọi là điểm thuộc loại ổn định. Vùng lân cận của O. t. Ổn định bao gồm các đường cong tích phân khép kín chứa O. t. Bên trong chúng, giữa chúng nằm giữa các đường xoắn ốc (xem Hình. cơm. mười ).

Nghiên cứu của O. t. Phương trình vi phân, tức là về bản chất, nghiên cứu hành vi của các họ đường cong tích phân trong một vùng lân cận của O. t. M. Lyapunov a, A. Poincaré và những người khác).

3) Điểm kỳ dị của một hàm giải tích có giá trị đơn là điểm mà tại đó tính phân tích của hàm bị vi phạm (xem Các hàm giải tích). Nếu có một vùng lân cận của O. t. một, không có O. t., thì điểm mộtđược gọi là cô lập O. t. nếu một là một O.T biệt lập và tồn tại một O.T hữu hạn được gọi là O.T có thể di chuyển được. Bằng cách thay đổi định nghĩa của hàm tại điểm a (hoặc định nghĩa lại tại thời điểm này, cụ thể là, thiết lập f(một)= b, nó có thể đạt được một sẽ trở thành một điểm bình thường của hàm đã sửa. Ví dụ: dấu chấm z= 0 là một O.T. di động cho hàm f 1 ( z) = f(z), nếu z≠ 0, và f 1 (0), = 1, chấm z= 0 là một điểm bình thường [ f 1 (z) là phân tích tại điểm z= 0]. Nếu một một- O. t. cô lập và a được gọi là cực hoặc điểm kỳ dị không tuần tự của hàm f(z), nếu chuỗi Laurent) hoạt động f(z) trong một vùng lân cận của O. t. cô lập không chứa quyền hạn âm z - a, nếu một- có thể tháo rời O. t., chứa một số lũy thừa âm hữu hạn z - a, nếu một- cực (trong trường hợp này là thứ tự của cực Rđược định nghĩa là lũy thừa cao nhất của a - một điểm kỳ dị về cơ bản. Ví dụ, đối với hàm

p = 2, 3,…)

dấu chấm z= 0 là cực của thứ tự R, cho chức năng

dấu chấm z= 0 là một điểm kỳ dị cần thiết.

Trên ranh giới của đường tròn hội tụ của một chuỗi lũy thừa phải có ít nhất một điểm O. t của hàm số được biểu diễn bên trong đường tròn này bởi chuỗi lũy thừa đã cho. Tất cả các điểm biên của miền tồn tại của một hàm giải tích đơn giá trị (ranh giới tự nhiên) là các điểm biên của hàm này. Như vậy, tất cả các điểm của đường tròn đơn vị | z| = 1 là đặc biệt đối với hàm

Đối với một hàm giải tích đa trị, khái niệm “O. t. " khó hơn. Ngoài O. t., Trong các trang riêng lẻ của bề mặt Riemann của một hàm (nghĩa là O. t. Của các phần tử giải tích có giá trị đơn), bất kỳ điểm nhánh nào cũng là O. t. Của hàm. Các điểm nhánh biệt lập của một bề mặt Riemann (tức là các điểm nhánh sao cho trong một số vùng lân cận của chúng không có chức năng O.t. nào khác trong bất kỳ lá nào) được phân loại như sau. Nếu a là một điểm nhánh cô lập của bậc hữu hạn và tồn tại một a hữu hạn thì nó được gọi là cực tới hạn. Nếu một một là một điểm nhánh cô lập có bậc vô hạn, và a được gọi là siêu nghiệm O. t. Tất cả các điểm nhánh cô lập khác được gọi là điểm kỳ dị tới hạn về cơ bản. Ví dụ: dấu chấm z= 0 là một điểm tới hạn bình thường của hàm f ( z) = nhật ký z và một điểm kỳ dị quan trọng thiết yếu của hàm f (z) = sin log z.

Bất kỳ O. t. Nào, ngoại trừ một O. t. Có thể tháo rời, đều là một trở ngại đối với việc tiếp tục phân tích, tức là tiếp tục phân tích dọc theo một đường cong đi qua O. t. Là không thể thay đổi được.

Bách khoa toàn thư Liên Xô vĩ đại. - M.: Bách khoa toàn thư Liên Xô. 1969-1978 .

Xem "Điểm đặc biệt" là gì trong các từ điển khác:

Điểm ở đây. Xem thêm điểm kỳ dị (phương trình vi phân). Đặc điểm hoặc điểm kỳ dị trong toán học là một điểm mà tại đó một đối tượng toán học (thường là một hàm) không được xác định hoặc có hành vi bất thường (ví dụ, một điểm mà tại đó ... ... Wikipedia

Một hàm phân tích là một điểm mà tại đó các điều kiện của phân tích bị vi phạm. Nếu một hàm giải tích f (z) được xác định trong một số vùng lân cận của điểm z0 ở mọi nơi… Bách khoa toàn thư vật lý

Một hàm giải tích là điểm mà tại đó tính phân tích của một hàm bị vi phạm ... Từ điển Bách khoa toàn thư lớn

điểm kỳ lạ- - [Ya.N. Luginsky, M.S. Fezi Zhilinskaya, Yu.S. Kabirov. English Russian Dictionary of Electrical Engineering and Power Industry, Moscow, 1999] Các chủ đề kỹ thuật điện, các khái niệm cơ bản EN điểm kỳ dị ... Sổ tay phiên dịch kỹ thuật

1) OT của một hàm giải tích f (z) là một trở ngại đối với sự tiếp tục giải tích của một phần tử của hàm f (z) của một biến phức z dọc theo một đường nào đó trên mặt phẳng của biến này. Cho hàm giải tích f (z) được xác định bởi một số ... ... Bách khoa toàn thư toán học

Một hàm phân tích, điểm mà tại đó tính phân tích của hàm bị vi phạm. * * * ĐIỂM SINGULAR ĐIỂM DUY NHẤT của một hàm giải tích, một điểm mà tại đó độ phân tích của hàm bị vi phạm ... từ điển bách khoa

điểm kỳ lạ- ypatingasis taškas statusas T s viêm automatika atitikmenys: engl. điểm số ít vok. singularer Punkt, m rus. điểm số ít, fpranc. hạt điểm, m; point singulier, m… ga cuối Automatikosų žodynas

điểm kỳ lạ- ypatingasis taškas statusas T s viêm fizika atitikmenys: engl. điểm số ít vok. singularer Punkt, m rus. điểm số ít, fpranc. point singulier, m… ga cuối Fizikosų žodynas

Các khái niệm và định nghĩa cơ bản:

Điểm không của hàm giải tích f (z) là điểm “a” mà f (a) = 0.

Điểm không bậc “n” của hàm f (z) là điểm “a” nếu trừ fn (a) ¹0.

Một điểm kỳ dị "a" được gọi là điểm kỳ dị biệt lập của hàm f (z) nếu tồn tại một vùng lân cận của điểm này tại đó không có điểm kỳ dị nào khác ngoài "a".

Các điểm số ít biệt lập có ba loại:.

1 điểm đặc biệt có thể tháo rời;

3 điểm kỳ dị cần thiết.

Loại của một điểm kỳ dị có thể được xác định dựa trên hoạt động của hàm đã cho tại điểm kỳ dị tìm thấy, cũng như từ dạng của chuỗi Laurent thu được cho hàm trong vùng lân cận của điểm kỳ dị tìm thấy.

Xác định loại của một điểm kỳ dị bằng hành vi của hàm trong đó.

1. Các điểm số ít có thể tháo rời.

Một điểm kỳ dị biệt lập a của hàm f (z) được gọi là có thể di chuyển được nếu tồn tại một giới hạn hữu hạn.

2. Ba Lan.

Một điểm kỳ dị biệt lập a của hàm f (z) được gọi là điểm cực nếu .

3. Những điểm kỳ dị đáng kể.

Một điểm kỳ dị cô lập a của hàm f (z) được gọi là điểm kỳ dị cốt yếu nếu không tồn tại hữu hạn hoặc vô hạn.

Mối quan hệ sau đây diễn ra giữa các số không và các cực của hàm.

Đối với một điểm a là cực n bậc n của hàm f (Z), thì cần và đủ để điểm này là điểm không bậc n của hàm.

Nếu n = 1 cực được gọi là đơn giản.

Sự định nghĩa: Một điểm số ít biệt lập của một ký tự có giá trị duy nhất được gọi là:

a) có thể tháo rời nếu không có phần chính của sự phân hủy;

b) một cực nếu phần chính chứa một số lượng hữu hạn các phần tử;

c) một điểm kỳ dị về cơ bản nếu phần chính chứa vô số số hạng.

a) Như vậy, trong vùng lân cận của một điểm kỳ dị di động, phép khai triển có dạng:

nó thể hiện hàm tại tất cả các điểm của đường tròn | z-a |

Tại tâm z = a, đẳng thức là sai, bởi vì hàm tại z = a có một gián đoạn và bên phải là liên tục. Nếu giá trị của hàm ở trung tâm bị thay đổi, lấy nó bằng giá trị của phía bên phải, thì khoảng trống sẽ bị loại bỏ - do đó có tên - có thể tháo rời.

b) Trong vùng lân cận của cực bậc m, khai triển chuỗi Laurent có dạng:

c) Trong khu phố của một cây cột đơn giản

Các khoản khấu trừ và công thức tính toán của chúng.

Phần dư của một hàm giải tích f (z) tại một điểm kỳ dị biệt lập z 0 là một số phức bằng giá trị của tích phân , được lấy theo chiều dương dọc theo đường tròn L có tâm tại điểm z 0, nằm trong vùng phân tích của hàm f (z) (tức là trong vành 0<|z-z0|

Phần dư của hàm f (z) tại một điểm kỳ dị biệt lập z 0 được ký hiệu bằng ký hiệu Res f (z 0) hoặc Res (f (z); z 0). Bằng cách này,

Resf (z0) = . (22.15.1)

Nếu chúng ta đặt n = -1 vào công thức (22.15.1), thì chúng ta nhận được:

C-1 =

hoặc Res f (z 0) = C -1,

những thứ kia. Phần dư của hàm f (z) đối với điểm kỳ dị z 0 bằng hệ số của số hạng đầu tiên với số mũ âm trong khai triển của hàm f (z) trong một chuỗi Laurent.

Tính toán các khoản giảm trừ.

Điểm kỳ dị thông thường hoặc có thể tháo rời. Rõ ràng, nếu z = z 0 là một điểm kỳ dị chính quy hoặc di động của hàm f (z), thì Res f (z 0) = 0 (không có phần chính trong phép phân rã Laurent trong những trường hợp này, vì vậy c-1 = 0).

Cây sào. Gọi điểm z 0 là một cực đơn giản của hàm f (z). Khi đó chuỗi Laurent cho hàm f (z) trong vùng lân cận của điểm z 0 có dạng:

Từ đây

Do đó, chuyển đẳng thức này đến giới hạn là z --z 0, chúng ta thu được

Res f (z0) =

Thực chất là điểm đặc biệt. Nếu điểm z 0 về cơ bản là một điểm kỳ dị của hàm f (z), thì để tính phần dư của hàm tại điểm này, người ta thường xác định trực tiếp hệ số c-1 trong khai triển của hàm trong một chuỗi Laurent.

Phân loại sự kiện. Tổng, tích của các sự kiện, thuộc tính của chúng, biểu diễn đồ họa.

Các sự kiện được chia thành:

1. Ngẫu nhiên

2. Đáng tin cậy

3. Không thể

Đáng tin cậy - đây là một sự kiện nhất thiết phải xảy ra trong những điều kiện này (đêm sau là sáng).

Ngẫu nhiên là một sự kiện có thể xảy ra hoặc không (vượt qua một kỳ thi).

Điều không thể xảy ra là một sự kiện sẽ không xảy ra trong các điều kiện đã cho (lấy bút chì xanh ra khỏi hộp chỉ có bút đỏ).