Στοιχεία μιας ακολουθίας σημείων που αυξάνονται μονοτονικά σε αξία. Το θεώρημα του Weierstrass για το όριο μιας μονότονης ακολουθίας
Οριακό θεώρημα Weierstrass μονοτονική ακολουθία
Οποιαδήποτε μονότονη οριοθετημένη ακολουθία (xn)Εχει τελικό όριο, ίσο με το ακριβές άνω όριο, sup(xn)για ένα μη μειούμενο και ακριβές κάτω όριο, inf(xn)για μια μη αυξανόμενη ακολουθία.
Οποιαδήποτε μονότονη απεριόριστη ακολουθία έχει ένα άπειρο όριο ίσο με συν άπειρο για μια μη φθίνουσα ακολουθία και μείον άπειρο για μια μη αύξουσα ακολουθία.
Απόδειξη
1) μη φθίνουσα οριοθετημένη ακολουθία.
(1.1)
.
Δεδομένου ότι η ακολουθία είναι περιορισμένη, έχει ένα σφιχτό άνω όριο
.
Αυτό σημαίνει ότι:
- για όλα n,
(1.2) ;
(1.3) .
.
Εδώ χρησιμοποιήσαμε και το (1.3). Σε συνδυασμό με το (1.2), βρίσκουμε:
στο .
Από τότε
,
ή
στο .
Το πρώτο μέρος του θεωρήματος έχει αποδειχθεί.
2)
Ας είναι τώρα η σειρά μη αυξανόμενη οριοθετημένη ακολουθία:
(2.1)
για όλα n.
Εφόσον η ακολουθία είναι περιορισμένη, έχει ένα σφιχτό κάτω όριο
.
Αυτό σημαίνει τα εξής:
- για όλα τα n ισχύουν οι ακόλουθες ανισότητες:
(2.2) ; - Για οποιονδηποτε θετικός αριθμός, υπάρχει ένας αριθμός, ανάλογα με το ε, για τον οποίο
(2.3) .
.
Εδώ χρησιμοποιήσαμε και το (2.3). Λαμβάνοντας υπόψη το (2.2), βρίσκουμε:
στο .
Από τότε
,
ή
στο .
Αυτό σημαίνει ότι ο αριθμός είναι το όριο της ακολουθίας.
Το δεύτερο μέρος του θεωρήματος είναι αποδεδειγμένο.
Τώρα εξετάστε τις απεριόριστες ακολουθίες.
3)
Ας είναι η σειρά απεριόριστη μη φθίνουσα ακολουθία.
Εφόσον η ακολουθία δεν είναι φθίνουσα, οι ακόλουθες ανισότητες ισχύουν για όλα τα n:
(3.1)
.
Δεδομένου ότι η ακολουθία είναι μη φθίνουσα και απεριόριστη, είναι απεριόριστη στη δεξιά πλευρά. Τότε για οποιονδήποτε αριθμό Μ υπάρχει ένας αριθμός, ανάλογα με το Μ, για τον οποίο
(3.2)
.
Εφόσον η ακολουθία δεν είναι φθίνουσα, τότε όταν έχουμε:
.
Εδώ χρησιμοποιήσαμε και το (3.2).
.
Αυτό σημαίνει ότι το όριο της ακολουθίας είναι συν το άπειρο:
.
Το τρίτο μέρος του θεωρήματος είναι αποδεδειγμένο.
4) Τέλος, εξετάστε την περίπτωση όταν απεριόριστη μη αυξανόμενη ακολουθία.
Παρόμοια με την προηγούμενη, αφού η ακολουθία είναι μη αυξανόμενη, λοιπόν
(4.1)
για όλα n.
Δεδομένου ότι η ακολουθία είναι μη αυξανόμενη και απεριόριστη, είναι απεριόριστη στην αριστερή πλευρά. Τότε για οποιονδήποτε αριθμό Μ υπάρχει ένας αριθμός, ανάλογα με το Μ, για τον οποίο
(4.2)
.
Εφόσον η ακολουθία δεν είναι αύξουσα, τότε όταν έχουμε:
.
Άρα, για οποιονδήποτε αριθμό M υπάρχει ένας φυσικός αριθμός που εξαρτάται από το M, έτσι ώστε για όλους τους αριθμούς να ισχύουν οι ακόλουθες ανισώσεις:
.
Αυτό σημαίνει ότι το όριο της ακολουθίας είναι ίσο με μείον το άπειρο:
.
Το θεώρημα είναι αποδεδειγμένο.
Παράδειγμα λύσης προβλήματος
Χρησιμοποιώντας το θεώρημα του Weierstrass, αποδείξτε σύγκλιση ακολουθίας:
,
,
. . . ,
,
. . .
Τότε βρείτε το όριο του.
Ας αναπαραστήσουμε την ακολουθία με τη μορφή επαναλαμβανόμενων τύπων:
,
.
Ας το αποδείξουμε δεδομένη σειράπεριορίζεται παραπάνω από την τιμή
(P1) .
Πραγματοποιούμε την απόδειξη χρησιμοποιώντας τη μέθοδο μαθηματική επαγωγή.
.
Αφήστε . Επειτα
.
Η ανισότητα (Α1) αποδεικνύεται.
Ας αποδείξουμε ότι η ακολουθία αυξάνεται μονότονα.
;
(P2) .
Αφού , τότε ο παρονομαστής του κλάσματος και ο πρώτος παράγοντας στον αριθμητή είναι θετικοί. Λόγω του περιορισμού των όρων της ακολουθίας από ανισότητα (Α1), ο δεύτερος παράγοντας είναι επίσης θετικός. Να γιατί
.
Δηλαδή, η ακολουθία είναι αυστηρά αυξανόμενη.
Δεδομένου ότι η ακολουθία αυξάνεται και οριοθετείται παραπάνω, είναι μια οριοθετημένη ακολουθία. Επομένως, σύμφωνα με το θεώρημα του Weierstrass, έχει ένα όριο.
Ας βρούμε αυτό το όριο. Ας το συμβολίσουμε με ένα:
.
Ας χρησιμοποιήσουμε το γεγονός ότι
.
Ας το εφαρμόσουμε στο (A2), χρησιμοποιώντας τις αριθμητικές ιδιότητες των ορίων συγκλίνουσας ακολουθίας:
.
Η συνθήκη ικανοποιείται από τη ρίζα.
Ορισμός 1. Η ακολουθία ονομάζεται μειώνεται
(μη αυξανόμενη
), εάν για όλους  η ανισότητα ισχύει
η ανισότητα ισχύει  .
.
Ορισμός 2. Συνέπεια  που ονομάζεται αυξανόμενη
(μη φθίνουσα
), εάν για όλους
που ονομάζεται αυξανόμενη
(μη φθίνουσα
), εάν για όλους  η ανισότητα ισχύει
η ανισότητα ισχύει  .
.
Ορισμός 3. Οι φθίνουσες, μη αυξανόμενες, αύξουσες και μη φθίνουσες ακολουθίες ονομάζονται μονότονος Ακολουθίες, ονομάζονται επίσης φθίνουσες και αυξανόμενες ακολουθίες αυστηρά μονότονη ακολουθίες.
Προφανώς, μια μη φθίνουσα ακολουθία οριοθετείται από κάτω και μια μη αυξανόμενη ακολουθία οριοθετείται από πάνω. Επομένως, οποιαδήποτε μονοτονική ακολουθία είναι προφανώς περιορισμένη στη μία πλευρά.
Παράδειγμα 1. Συνέπεια  αυξάνεται, δεν μειώνεται,
αυξάνεται, δεν μειώνεται,  μειώνεται
μειώνεται  δεν αυξάνεται
δεν αυξάνεται  – μη μονοτονική ακολουθία.
– μη μονοτονική ακολουθία.
Για τις μονοτονικές ακολουθίες, τα ακόλουθα διαδραματίζουν σημαντικό ρόλο:
Θεώρημα 1. Εάν μια μη φθίνουσα (μη αυξανόμενη) ακολουθία οριοθετείται πάνω (κάτω), τότε συγκλίνει.
Απόδειξη. Αφήστε τη σειρά  δεν μειώνεται και οριοθετείται από πάνω, δηλ.
δεν μειώνεται και οριοθετείται από πάνω, δηλ.  και πολλά
και πολλά  περιορισμένη από πάνω. Με το Θεώρημα 1 § 2 υπάρχει
περιορισμένη από πάνω. Με το Θεώρημα 1 § 2 υπάρχει  . Ας το αποδείξουμε
. Ας το αποδείξουμε  .
.
Ας πάρουμε  αυθαιρετώς. Επειδή η ΕΝΑ– ακριβές άνω φράγμα, υπάρχει αριθμός Ν
τέτοια που
αυθαιρετώς. Επειδή η ΕΝΑ– ακριβές άνω φράγμα, υπάρχει αριθμός Ν
τέτοια που  . Εφόσον η ακολουθία είναι μη φθίνουσα, τότε για όλους
. Εφόσον η ακολουθία είναι μη φθίνουσα, τότε για όλους  έχουμε, δηλ.
έχουμε, δηλ.  , Να γιατί
, Να γιατί  για όλα
για όλα  , και αυτό σημαίνει ότι
, και αυτό σημαίνει ότι  .
.
Για μια μη αυξανόμενη ακολουθία που οριοθετείται παρακάτω, η απόδειξη είναι παρόμοια με ( Οι μαθητές μπορούν να αποδείξουν αυτή τη δήλωση στο σπίτι μόνοι τους). Το θεώρημα είναι αποδεδειγμένο.
Σχόλιο. Το θεώρημα 1 μπορεί να διατυπωθεί διαφορετικά.
Θεώρημα 2. Για να συγκλίνει μια μονοτονική ακολουθία είναι απαραίτητο και αρκετό να είναι οριοθετημένη.
Η επάρκεια διαπιστώνεται στο Θεώρημα 1, η αναγκαιότητα - στο Θεώρημα 2 της § 5.
Η συνθήκη της μονοτονίας δεν είναι απαραίτητη για τη σύγκλιση μιας ακολουθίας, αφού μια συγκλίνουσα ακολουθία δεν είναι απαραίτητα μονότονη. Για παράδειγμα, η σειρά  δεν είναι μονότονο, αλλά συγκλίνει στο μηδέν.
δεν είναι μονότονο, αλλά συγκλίνει στο μηδέν.
Συνέπεια. Αν η ακολουθία  αυξάνεται (μειώνεται) και περιορίζεται από πάνω (από κάτω), τότε
αυξάνεται (μειώνεται) και περιορίζεται από πάνω (από κάτω), τότε  (
( ).
).
Πράγματι, από το Θεώρημα 1  (
( ).
).
Ορισμός 4. Αν  στο
στο  , τότε καλείται η ακολουθία σύστημα συστολής ένθετων τμημάτων
.
, τότε καλείται η ακολουθία σύστημα συστολής ένθετων τμημάτων
.
Θεώρημα 3 (αρχή των ένθετων τμημάτων). Κάθε συσταλτικό σύστημα ένθετων τμημάτων έχει, και επιπλέον, ένα μοναδικό σημείο Με, που ανήκει σε όλα τα τμήματα αυτού του συστήματος.
Απόδειξη. Ας αποδείξουμε ότι το θέμα Μευπάρχει. Επειδή η  , Οτι
, Οτι  και επομένως η σειρά
και επομένως η σειρά  δεν μειώνεται, αλλά η σειρά
δεν μειώνεται, αλλά η σειρά  δεν αυξάνεται. Εν
δεν αυξάνεται. Εν  Και
Και  περιορισμένη γιατί. Στη συνέχεια, από το Θεώρημα 1, υπάρχουν
περιορισμένη γιατί. Στη συνέχεια, από το Θεώρημα 1, υπάρχουν  Και
Και  , αλλά από τότε
, αλλά από τότε  , Οτι
, Οτι  =
= . Βρέθηκε σημείο Μεανήκει σε όλα τα τμήματα του συστήματος, αφού από τη συνέπεια του Θεωρήματος 1
. Βρέθηκε σημείο Μεανήκει σε όλα τα τμήματα του συστήματος, αφού από τη συνέπεια του Θεωρήματος 1  ,
, , δηλ.
, δηλ.  για όλες τις αξίες n.
για όλες τις αξίες n.
Ας δείξουμε τώρα ότι η ουσία Με- ο μοναδικός. Ας υποθέσουμε ότι υπάρχουν δύο τέτοια σημεία: ΜεΚαι ρεκαι ας για σιγουριά  . Στη συνέχεια το τμήμα
. Στη συνέχεια το τμήμα  ανήκει σε όλα τα τμήματα
ανήκει σε όλα τα τμήματα  , δηλ.
, δηλ.  για όλα n, κάτι που είναι αδύνατο, αφού
για όλα n, κάτι που είναι αδύνατο, αφού  και, επομένως, ξεκινώντας από έναν ορισμένο αριθμό,
και, επομένως, ξεκινώντας από έναν ορισμένο αριθμό,  . Το θεώρημα είναι αποδεδειγμένο.
. Το θεώρημα είναι αποδεδειγμένο.
Σημειώστε ότι το ουσιαστικό εδώ είναι ότι λαμβάνονται υπόψη κλειστά διαστήματα, δηλ. τμήματα. Εάν λάβουμε υπόψη ένα σύστημα διαστημάτων συστολής, τότε η αρχή είναι, γενικά μιλώντας, εσφαλμένη. Για παράδειγμα, διαστήματα  , προφανώς συμβόλαιο σε ένα σημείο
, προφανώς συμβόλαιο σε ένα σημείο  , ωστόσο σημείο
, ωστόσο σημείο  δεν ανήκει σε κανένα διάστημα αυτού του συστήματος.
δεν ανήκει σε κανένα διάστημα αυτού του συστήματος.
Ας εξετάσουμε τώρα παραδείγματα συγκλίνουσες μονοτονικές ακολουθίες.
1) Αριθμός μι.
Ας εξετάσουμε τώρα τη σειρά  . Πώς συμπεριφέρεται; Βάση
. Πώς συμπεριφέρεται; Βάση
βαθμούς  , Να γιατί
, Να γιατί  ? Στην άλλη πλευρά,
? Στην άλλη πλευρά,  , ΕΝΑ
, ΕΝΑ  , Να γιατί
, Να γιατί  ? Ή δεν υπάρχει όριο;
? Ή δεν υπάρχει όριο;
Για να απαντήσετε σε αυτές τις ερωτήσεις, εξετάστε τη βοηθητική ακολουθία  . Ας αποδείξουμε ότι μειώνεται και οριοθετείται παρακάτω. Ταυτόχρονα θα χρειαστούμε
. Ας αποδείξουμε ότι μειώνεται και οριοθετείται παρακάτω. Ταυτόχρονα θα χρειαστούμε
Λήμμα. Αν  , τότε για όλες τις φυσικές αξίες nέχουμε
, τότε για όλες τις φυσικές αξίες nέχουμε

(ανισότητα Bernoulli).
Απόδειξη. Ας χρησιμοποιήσουμε τη μέθοδο της μαθηματικής επαγωγής.
Αν  , Οτι
, Οτι  , δηλ. η ανισότητα είναι αλήθεια.
, δηλ. η ανισότητα είναι αλήθεια.
Ας υποθέσουμε ότι ισχύει για  και να αποδείξει την εγκυρότητά του για
και να αποδείξει την εγκυρότητά του για  +1.
+1.
σωστά  . Ας πολλαπλασιάσουμε αυτή την ανισότητα επί
. Ας πολλαπλασιάσουμε αυτή την ανισότητα επί  :
:
Ετσι, . Αυτό σημαίνει, σύμφωνα με την αρχή της μαθηματικής επαγωγής, η ανισότητα του Bernoulli ισχύει για όλες τις φυσικές τιμές n. Το λήμμα είναι αποδεδειγμένο.
Ας δείξουμε ότι η ακολουθία  μειώνεται. Εχουμε
μειώνεται. Εχουμε
 Η ανισότητα του Μπερνούλι
Η ανισότητα του Μπερνούλι  , και αυτό σημαίνει ότι η ακολουθία
, και αυτό σημαίνει ότι η ακολουθία  μειώνεται.
μειώνεται.
Το όριο από κάτω προκύπτει από την ανισότητα  Η ανισότητα του Μπερνούλι
Η ανισότητα του Μπερνούλι  για όλες τις φυσικές αξίες n.
για όλες τις φυσικές αξίες n.
Με το Θεώρημα 1 υπάρχει  , που συμβολίζεται με το γράμμα μι. Να γιατί
, που συμβολίζεται με το γράμμα μι. Να γιατί  .
.
Αριθμός μιπαράλογο και υπερβατικό, μι= 2,718281828… . Είναι, ως γνωστόν, η βάση των φυσικών λογαρίθμων.
Σημειώσεις. 1) Η ανισότητα του Bernoulli μπορεί να χρησιμοποιηθεί για να το αποδείξει αυτό  στο
στο  . Πράγματι, αν
. Πράγματι, αν  , Οτι
, Οτι  . Στη συνέχεια, σύμφωνα με την ανισότητα του Bernoulli, με
. Στη συνέχεια, σύμφωνα με την ανισότητα του Bernoulli, με  . Ως εκ τούτου, στο
. Ως εκ τούτου, στο  έχουμε
έχουμε  , αυτό είναι
, αυτό είναι  στο
στο  .
.
2) Στο παράδειγμα που συζητήθηκε παραπάνω, η βάση του πτυχίου  τείνει στο 1, και ο εκθέτης n- Προς την
τείνει στο 1, και ο εκθέτης n- Προς την  , δηλαδή υπάρχει αβεβαιότητα της μορφής
, δηλαδή υπάρχει αβεβαιότητα της μορφής  . Η αβεβαιότητα αυτού του είδους, όπως δείξαμε, αποκαλύπτεται από το αξιοσημείωτο όριο
. Η αβεβαιότητα αυτού του είδους, όπως δείξαμε, αποκαλύπτεται από το αξιοσημείωτο όριο  .
.
2)
 (*)
(*)
Ας αποδείξουμε ότι αυτή η ακολουθία συγκλίνει. Για να γίνει αυτό, δείχνουμε ότι οριοθετείται από κάτω και δεν αυξάνεται. Σε αυτή την περίπτωση, χρησιμοποιούμε την ανισότητα  για όλα
για όλα  , που είναι συνέπεια της ανισότητας
, που είναι συνέπεια της ανισότητας  .
.
Εχουμε  βλέπε η ανισότητα είναι μεγαλύτερη!
βλέπε η ανισότητα είναι μεγαλύτερη!  , δηλ. η ακολουθία οριοθετείται παρακάτω από τον αριθμό
, δηλ. η ακολουθία οριοθετείται παρακάτω από τον αριθμό  .
.
Περαιτέρω,  από τότε
από τότε 
 , δηλ. η σειρά δεν αυξάνεται.
, δηλ. η σειρά δεν αυξάνεται.
Με το Θεώρημα 1 υπάρχει  , που συμβολίζουμε Χ. Περνώντας στην ισότητα (*) στο όριο στο
, που συμβολίζουμε Χ. Περνώντας στην ισότητα (*) στο όριο στο  , παίρνουμε
, παίρνουμε
 , δηλ.
, δηλ.  , που
, που  (παίρνουμε το σύμβολο συν, αφού όλοι οι όροι της ακολουθίας είναι θετικοί).
(παίρνουμε το σύμβολο συν, αφού όλοι οι όροι της ακολουθίας είναι θετικοί).
Η ακολουθία (*) χρησιμοποιείται στον υπολογισμό  κατά προσέγγιση. Πίσω
κατά προσέγγιση. Πίσω  πάρτε οποιοδήποτε θετικό αριθμό. Για παράδειγμα, ας βρούμε
πάρτε οποιοδήποτε θετικό αριθμό. Για παράδειγμα, ας βρούμε  . Αφήνω
. Αφήνω  . Επειτα
. Επειτα  ,. Ετσι,
,. Ετσι,  .
.
3)
 .
.
Εχουμε  . Επειδή η
. Επειδή η  στο
στο  , υπάρχει ένας αριθμός Ν, έτσι ώστε για όλους
, υπάρχει ένας αριθμός Ν, έτσι ώστε για όλους  η ανισότητα ισχύει
η ανισότητα ισχύει  . Η σειρά λοιπόν
. Η σειρά λοιπόν  , ξεκινώντας από κάποιο αριθμό Ν, μειώνεται και οριοθετείται παρακάτω, αφού
, ξεκινώντας από κάποιο αριθμό Ν, μειώνεται και οριοθετείται παρακάτω, αφού  για όλες τις αξίες n. Αυτό σημαίνει ότι από το Θεώρημα 1 υπάρχει
για όλες τις αξίες n. Αυτό σημαίνει ότι από το Θεώρημα 1 υπάρχει  . Επειδή η
. Επειδή η  , έχουμε
, έχουμε  .
.
Ετσι,  .
.
4)
 , στα δεξιά - n
ρίζες.
, στα δεξιά - n
ρίζες.
Χρησιμοποιώντας τη μέθοδο της μαθηματικής επαγωγής θα δείξουμε ότι  για όλες τις αξίες n. Εχουμε
για όλες τις αξίες n. Εχουμε  . Αφήνω
. Αφήνω  . Στη συνέχεια, από εδώ λαμβάνουμε μια δήλωση που βασίζεται στην αρχή της μαθηματικής επαγωγής. Χρησιμοποιώντας αυτό το γεγονός, βρίσκουμε, δηλ. ακολουθία
. Στη συνέχεια, από εδώ λαμβάνουμε μια δήλωση που βασίζεται στην αρχή της μαθηματικής επαγωγής. Χρησιμοποιώντας αυτό το γεγονός, βρίσκουμε, δηλ. ακολουθία  αυξάνεται και οριοθετείται από πάνω. Επομένως υπάρχει γιατί
αυξάνεται και οριοθετείται από πάνω. Επομένως υπάρχει γιατί  .
.
Ετσι,  .
.
Η μονοτονία της ακολουθίας
Μονοτονική ακολουθία- μια ακολουθία που ικανοποιεί ένα από παρακάτω συνθήκες:
Από τις μονοτονικές ακολουθίες ξεχωρίζουν οι εξής: αυστηρά μονότονηακολουθίες που ικανοποιούν μία από τις ακόλουθες συνθήκες:
Μερικές φορές χρησιμοποιείται μια παραλλαγή ορολογίας στην οποία ο όρος "αυξανόμενη ακολουθία" θεωρείται συνώνυμος για τον όρο "μη φθίνουσα ακολουθία" και ο όρος "φθίνουσα ακολουθία" θεωρείται ως συνώνυμος για τον όρο "μη αυξανόμενη ακολουθία". ". Σε μια τέτοια περίπτωση, η αύξουσα και φθίνουσα ακολουθία από τον παραπάνω ορισμό ονομάζονται «αυστηρά αυξανόμενη» και «αυστηρά φθίνουσα», αντίστοιχα.
Μερικές γενικεύσεις
Μπορεί να αποδειχθεί ότι οι παραπάνω προϋποθέσεις δεν πληρούνται για όλους τους αριθμούς, αλλά μόνο για αριθμούς από ένα συγκεκριμένο εύρος
(εδώ επιτρέπεται η αντιστροφή του δεξιού περιγράμματος Ν+ στο άπειρο). Στην περίπτωση αυτή καλείται η ακολουθία μονοτονικό στο διάστημα Εγώ και η ίδια η γκάμα Εγώπου ονομάζεται ένα διάστημα μονοτονίαςακολουθίες.
Παραδείγματα
δείτε επίσης
Ίδρυμα Wikimedia. 2010.
Δείτε τι είναι η "Μονοτονικότητα μιας ακολουθίας" σε άλλα λεξικά:
Ένας κλάδος των μαθηματικών που μελετά τις ιδιότητες διαφόρων συναρτήσεων. Η θεωρία των συναρτήσεων εμπίπτει σε δύο τομείς: τη θεωρία των συναρτήσεων μιας πραγματικής μεταβλητής και τη θεωρία των συναρτήσεων μιας μιγαδικής μεταβλητής, η διαφορά μεταξύ των οποίων είναι τόσο μεγάλη που... ... Εγκυκλοπαίδεια Collier
Η δοκιμή ψευδοτυχαίων ακολουθιών είναι ένα σύνολο μεθόδων για τον προσδιορισμό του βαθμού εγγύτητας μιας δεδομένης ψευδοτυχαίας ακολουθίας με μια τυχαία. Τέτοιο μέτρο είναι συνήθως η παρουσία ομοιόμορφης κατανομής, μεγάλης... ... Wikipedia
Αυτός ο όρος έχει άλλες έννοιες, βλέπε Μέτρο. Το μέτρο ενός συνόλου είναι μια μη αρνητική ποσότητα, που ερμηνεύεται διαισθητικά ως το μέγεθος (όγκος) του συνόλου. Στην πραγματικότητα, αυτό είναι ένα μέτρο αριθμητική συνάρτηση, βάζοντας το καθένα σε αντιστοιχία... ... Wikipedia
Διάσημος συγγραφέας. Γένος. στο Orel το 1871. ο πατέρας του ήταν τοπογράφος γης. Σπούδασε στο γυμνάσιο Oryol και στα πανεπιστήμια της Αγίας Πετρούπολης και της Μόσχας, σύμφωνα με Νομική σχολή. Ο μαθητής είχε μεγάλη ανάγκη. Τότε ήταν που έγραψε την πρώτη του ιστορία «για... ... Μεγάλη βιογραφική εγκυκλοπαίδεια
Αριθμητικές μέθοδοι επίλυσης μεθόδων που αντικαθιστούν τη λύση ενός προβλήματος οριακής τιμής με μια λύση διακριτό πρόβλημα(βλ. Πρόβλημα γραμμικής οριακής τιμής· αριθμητικές μέθοδοι επίλυσης και Μη γραμμική εξίσωση· αριθμητικές μέθοδοι επίλυσης). Σε πολλές περιπτώσεις, ειδικά όταν εξετάζουμε... ... Μαθηματική Εγκυκλοπαίδεια
Το χειρόγραφο Voynich γράφτηκε χρησιμοποιώντας άγνωστο σύστημαγράμματα Voynich Manuscript (eng. Voyni ... Wikipedia
Γραμμένο με άγνωστο σύστημα γραφής Το χειρόγραφο Voynich είναι ένα μυστηριώδες βιβλίο που γράφτηκε πριν από περίπου 500 χρόνια από έναν άγνωστο συγγραφέα, σε μια άγνωστη γλώσσα, χρησιμοποιώντας ένα άγνωστο αλφάβητο. Χειρόγραφο Voynich... ...Βικιπαίδεια
Sigismondo d'India (ιταλικά: Sigismondo d India, περίπου 1582, Παλέρμο; έως 19 Απριλίου 1629, Μόντενα) Ιταλός συνθέτης. Περιεχόμενα 1 Βιογραφία 2 Δημιουργικότητα ... Wikipedia
Εκσυγχρονισμός- (Εκσυγχρονισμός) Ο εκσυγχρονισμός είναι η διαδικασία αλλαγής κάτι σύμφωνα με τις απαιτήσεις της νεωτερικότητας, η μετάβαση σε πιο προηγμένες συνθήκες, μέσω της εισαγωγής διαφόρων νέων ενημερώσεων Η θεωρία του εκσυγχρονισμού, οι τύποι εκσυγχρονισμού, οι οργανικές... ... Εγκυκλοπαίδεια Επενδυτών
Ενα από τα κύρια μαθηματικές έννοιες, η έννοια του οποίου έχει υποβληθεί σε μια σειρά από γενικεύσεις με την ανάπτυξη των μαθηματικών. I. Ακόμη και στα «Στοιχεία» του Ευκλείδη (3ος αιώνας π.Χ.), οι ιδιότητες του V., που σήμερα αποκαλούνται, διατυπώθηκαν σαφώς για να τα διακρίνουν από... ... Μεγάλη Σοβιετική Εγκυκλοπαίδεια
Αν όλοι φυσικός αριθμός n ανατίθεται σε ορισμένους πραγματικός αριθμός x n , τότε λένε ότι δίνεται σειρά αριθμών
Χ 1 , Χ 2 , … x n , …
Αριθμός ΧΤο 1 ονομάζεται μέλος της ακολουθίας με τον αριθμό 1 ή πρώτος όρος της ακολουθίας, αριθμός Χ 2 - μέλος της ακολουθίας με τον αριθμό 2 ή το δεύτερο μέλος της ακολουθίας κ.λπ. Ο αριθμός x n ονομάζεται μέλος της ακολουθίας με αριθμό n.
Υπάρχουν δύο τρόποι για να καθορίσετε τις ακολουθίες αριθμών - με και με επαναλαμβανόμενη φόρμουλα.
Ακολουθία χρησιμοποιώντας τύποι για τον γενικό όρο μιας ακολουθίας– αυτή είναι μια διαδοχική εργασία
Χ 1 , Χ 2 , … x n , …
χρησιμοποιώντας έναν τύπο που εκφράζει την εξάρτηση του όρου x n από τον αριθμό του n.
Παράδειγμα 1. Αριθμητική ακολουθία
1, 4, 9, … n 2 , …
δίνεται χρησιμοποιώντας τον κοινό τύπο όρου
x n = n 2 , n = 1, 2, 3, …
Ο καθορισμός μιας ακολουθίας χρησιμοποιώντας έναν τύπο που εκφράζει ένα μέλος ακολουθίας x n μέσω των μελών ακολουθίας με προηγούμενους αριθμούς ονομάζεται προσδιορισμός μιας ακολουθίας χρησιμοποιώντας επαναλαμβανόμενη φόρμουλα.
Χ 1 , Χ 2 , … x n , …
που ονομάζεται με αυξανόμενη σειρά, περισσότεροπροηγούμενο μέλος.
Με άλλα λόγια, για όλους n
Χ n + 1 >Χ n
Παράδειγμα 3. Ακολουθία φυσικών αριθμών
1, 2, 3, … n, …
είναι αύξουσα ακολουθία.
Ορισμός 2. Αριθμητική ακολουθία
Χ 1 , Χ 2 , … x n , …
που ονομάζεται φθίνουσα ακολουθίααν κάθε μέλος αυτής της ακολουθίας πιο λιγοπροηγούμενο μέλος.
Με άλλα λόγια, για όλους n= 1, 2, 3, … η ανισότητα ικανοποιείται
Χ n + 1 < Χ n
Παράδειγμα 4. Ακολουθία

δίνεται από τον τύπο
είναι φθίνουσα ακολουθία.
Παράδειγμα 5. Αριθμητική ακολουθία
1, - 1, 1, - 1, …
δίνεται από τον τύπο
x n = (- 1) n , n = 1, 2, 3, …
δεν είναι ούτε αυξάνεται ούτε μειώνεταιαλληλουχία.
Ορισμός 3. Ονομάζονται αύξουσα και φθίνουσα ακολουθία αριθμών μονοτονικές ακολουθίες.
Οριοθετημένες και Απεριόριστες Ακολουθίες
Ορισμός 4. Αριθμητική ακολουθία
Χ 1 , Χ 2 , … x n , …
που ονομάζεται περιορισμένος από πάνω,αν υπάρχει αριθμός Μ τέτοιος ώστε κάθε μέλος αυτής της ακολουθίας πιο λιγοαριθμοί Μ.
Με άλλα λόγια, για όλους n= 1, 2, 3, … η ανισότητα ικανοποιείται
Ορισμός 5. Αριθμητική ακολουθία
Χ 1 , Χ 2 , … x n , …
που ονομάζεται οριοθετείται από κάτω,αν υπάρχει αριθμός m τέτοιος ώστε κάθε μέλος αυτής της ακολουθίας περισσότεροαριθμοί m.
Με άλλα λόγια, για όλους n= 1, 2, 3, … η ανισότητα ικανοποιείται
Ορισμός 6. Αριθμητική ακολουθία
Χ 1 , Χ 2 , … x n , …
ονομάζεται περιορισμένη αν περιορίζεται τόσο πάνω όσο και κάτω.
Με άλλα λόγια, υπάρχουν αριθμοί Μ και μ τέτοιοι ώστε για όλους n= 1, 2, 3, … η ανισότητα ικανοποιείται
Μ< x n < M
Ορισμός 7. Αριθμητικές ακολουθίες που δεν περιορίζονται, που ονομάζεται απεριόριστες ακολουθίες.
Παράδειγμα 6. Αριθμητική ακολουθία
1, 4, 9, … n 2 , …
δίνεται από τον τύπο
x n = n 2 , n = 1, 2, 3, … ,
οριοθετείται από κάτω, για παράδειγμα, ο αριθμός 0. Ωστόσο, αυτή η ακολουθία απεριόριστο από πάνω.
Παράδειγμα 7. Ακολουθία
δίνεται από τον τύπο
είναι περιορισμένη σειρά, γιατί για όλους n= 1, 2, 3, … η ανισότητα ικανοποιείται
Στον ιστότοπό μας μπορείτε επίσης να εξοικειωθείτε με το εκπαιδευτικό υλικό που αναπτύχθηκε από δασκάλους του εκπαιδευτικού κέντρου Resolventa για την προετοιμασία για τις εξετάσεις Unified State και τις Unified State Exam στα μαθηματικά.
Για μαθητές που θέλουν να προετοιμαστούν καλά και να περάσουν Ενιαία κρατική εξέταση στα μαθηματικά ή τη ρωσική γλώσσαεπί υψηλή βαθμολογία, Το εκπαιδευτικό κέντροΔιευθύνει η «Resolventa».
| προπαρασκευαστικά μαθήματα για μαθητές των τάξεων 10 και 11 |
Μερικές φορές τέτοιες ακολουθίες ονομάζονται αυστηρά αυξανόμενο και, και ο όρος "V. p." ισχύει για ακολουθίες που ικανοποιούν όλες τις συνθήκες.Τέτοιες ακολουθίες ονομάζονται. επίσης μη φθίνουσα. Κάθε μη φθίνουσα ακολουθία που οριοθετείται παραπάνω έχει ένα πεπερασμένο όριο και κάθε ακολουθία που δεν οριοθετείται παραπάνω έχει ένα άπειρο όριο ίσο με +άπειρο. L. D. Kudryavtsev.
Μαθηματική εγκυκλοπαίδεια. - Μ.: Σοβιετική Εγκυκλοπαίδεια. I. M. Vinogradov. 1977-1985.
Δείτε τι είναι το "INCURING SEQUENCE" σε άλλα λεξικά:
αυξανόμενη ακολουθία- - [L.G. Sumenko. Αγγλο-ρωσικό λεξικό για την τεχνολογία της πληροφορίας. M.: State Enterprise TsNIIS, 2003.] Θέματα ΤΕΧΝΟΛΟΓΙΑ της ΠΛΗΡΟΦΟΡΙΑΣγενικά EN αύξουσα ακολουθία... Οδηγός Τεχνικού Μεταφραστή
Το καθήκον της εύρεσης της μεγαλύτερης αυξανόμενης υποακολουθίας είναι να βρεθεί η μεγαλύτερη αυξανόμενη υποακολουθία σε μια δεδομένη ακολουθία στοιχείων. Περιεχόμενα 1 Δήλωση προβλήματος 2 Σχετικοί αλγόριθμοι ... Wikipedia
Μονοτονική συνάρτηση είναι μια συνάρτηση της οποίας η προσαύξηση δεν αλλάζει πρόσημο, δηλαδή είτε είναι πάντα μη αρνητική είτε πάντα μη θετική. Εάν επιπλέον η προσαύξηση δεν είναι μηδέν, τότε η συνάρτηση λέγεται ότι είναι αυστηρά μονότονη. Περιεχόμενα 1 Ορισμοί 2 ... ... Wikipedia
Ακολουθία Μια αριθμητική ακολουθία είναι μια ακολουθία στοιχείων στον χώρο αριθμών. Αριθμητικοί αριθμοί... Βικιπαίδεια
Αυτή είναι μια ακολουθία της οποίας τα στοιχεία δεν μειώνονται όσο αυξάνεται ο αριθμός ή, αντίθετα, δεν αυξάνονται. Τέτοιες αλληλουχίες συναντώνται συχνά στην έρευνα και έχουν μια σειρά από χαρακτηριστικά γνωρίσματακαι πρόσθετες ιδιότητες.... ... Wikipedia
Μονότονη ακολουθία είναι μια ακολουθία που ικανοποιεί μία από τις ακόλουθες προϋποθέσεις: για οποιονδήποτε αριθμό ισχύει η ανισότητα (μη φθίνουσα ακολουθία), για οποιονδήποτε αριθμό ισχύει η ανισότητα (μη αύξουσα... ... Wikipedia
Ένας κλάδος της θεωρίας αριθμών στον οποίο μελετώνται και χαρακτηρίζονται μετρικά (δηλαδή με βάση τη θεωρία μετρήσεων) σύνολα αριθμών που έχουν ορισμένες αριθμητικές ιδιότητες. ιδιότητες. Η Μ.τ.χ. σχετίζεται στενά με τη θεωρία πιθανοτήτων, η οποία μερικές φορές την καθιστά δυνατή... ... Μαθηματική Εγκυκλοπαίδεια
Δηλώνει ότι κάθε οριοθετημένη αύξουσα ακολουθία έχει ένα όριο και αυτό το όριο είναι ίσο με την ακριβή της πάνω άκρη. Παρά την απλότητα της απόδειξης, αυτό το θεώρημα αποδεικνύεται πολύ βολικό για την εύρεση των ορίων πολλών... ... Wikipedia
Ένα θεώρημα που δίνει μια εκτίμηση για την πυκνότητα του αθροίσματος δύο ακολουθιών. Έστω A=(0, a 1, a.2,..., a i, ...) μια αύξουσα ακολουθία ακεραίων και η πυκνότητα της ακολουθίας είναι Anaz. η ποσότητα είναι το αριθμητικό άθροισμα δύο... ... Μαθηματική Εγκυκλοπαίδεια
Ο χώρος συζευγμένος με τον χώρο των βασικών (αρκετά καλών) συναρτήσεων. Σημαντικός ρόλοςΕδώ παίζουν χώροι Frechet (τύπου FS) και έντονα συζευγμένοι χώροι (τύπου DFS). Ένας χώρος τύπου FS είναι το προβολικό όριο ενός συμπαγούς... ... Μαθηματική Εγκυκλοπαίδεια
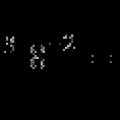 Τύποι δυνάμεων και ριζών
Τύποι δυνάμεων και ριζών Μονομερείς προτάσεις (8η τάξη) Επιλογή ρωσικής γλώσσας 2 Παλαιοί Ρώσοι αρχιτέκτονες
Μονομερείς προτάσεις (8η τάξη) Επιλογή ρωσικής γλώσσας 2 Παλαιοί Ρώσοι αρχιτέκτονες Πότε χρησιμοποιείται κόμμα;
Πότε χρησιμοποιείται κόμμα;