Πώς να βρείτε το κέντρο βάρους μιας φιγούρας με ακανόνιστο σχήμα. Οι θέσεις του κέντρου βάρους κάποιων μορφών

Ορθογώνιο παραλληλόγραμμο. Δεδομένου ότι το ορθογώνιο έχει δύο άξονες συμμετρίας, το κέντρο βάρους του βρίσκεται στην τομή των αξόνων συμμετρίας, δηλ. στο σημείο τομής των διαγωνίων του ορθογωνίου.

Τρίγωνο. Το κέντρο βάρους βρίσκεται στο σημείο τομής των διάμεσών του. Είναι γνωστό από τη γεωμετρία ότι οι διάμεσοι ενός τριγώνου τέμνονται σε ένα σημείο και διαιρούνται σε αναλογία 1:2 από τη βάση.

Ενας κύκλος. Δεδομένου ότι ο κύκλος έχει δύο άξονες συμμετρίας, το κέντρο βάρους του βρίσκεται στην τομή των αξόνων συμμετρίας.

Ημικύκλιο. Το ημικύκλιο έχει έναν άξονα συμμετρίας, τότε το κέντρο βάρους βρίσκεται σε αυτόν τον άξονα. Μια άλλη συντεταγμένη του κέντρου βάρους υπολογίζεται με τον τύπο: .

Πολλά δομικά στοιχεία κατασκευάζονται από τυπικά προϊόντα έλασης - γωνίες, δοκοί I, κανάλια και άλλα. Όλες οι διαστάσεις, καθώς και τα γεωμετρικά χαρακτηριστικά των προφίλ σε έλαση, είναι δεδομένα πίνακα που βρίσκονται στη βιβλιογραφία αναφοράς σε τυπικούς πίνακες συλλογής (GOST 8239-89, GOST 8240-89).

Παράδειγμα 1 Προσδιορίστε τη θέση του κέντρου βάρους του σχήματος που φαίνεται στο σχήμα.

Λύση:

Επιλέγουμε τους άξονες συντεταγμένων έτσι ώστε ο άξονας Ox να διέρχεται κατά μήκος της ακραίας κάτω συνολικής διάστασης και ο άξονας Oy - κατά μήκος της ακραίας αριστερής συνολικής διάστασης.

Διαχωρίζουμε ένα σύνθετο σχήμα στον ελάχιστο αριθμό απλών ψηφίων:

ορθογώνιο 20x10;

τρίγωνο 15x10;

κύκλος R=3 cm.

Υπολογίζουμε το εμβαδόν κάθε απλού σχήματος, τις συντεταγμένες του κέντρου βάρους. Τα αποτελέσματα των υπολογισμών καταχωρούνται στον πίνακα

Εικόνα Αρ.	Η περιοχή του σχήματος Α	Συντεταγμένες κέντρου βάρους

Απάντηση: C(14,5; 4,5)

Παράδειγμα 2 . Προσδιορίστε τις συντεταγμένες του κέντρου βάρους ενός σύνθετου τμήματος που αποτελείται από ένα φύλλο και κυλινδρικά προφίλ.

Λύση.

Επιλέγουμε τους άξονες συντεταγμένων, όπως φαίνεται στο σχήμα.

Σημειώνουμε τους αριθμούς με αριθμούς και γράφουμε τα απαραίτητα δεδομένα από τον πίνακα:

Εικόνα Αρ.	Η περιοχή του σχήματος Α	Συντεταγμένες κέντρου βάρους

Υπολογίζουμε τις συντεταγμένες του κέντρου βάρους του σχήματος χρησιμοποιώντας τους τύπους:

Απάντηση: C(0; 10)

Εργαστηριακή εργασία Νο 1 «Προσδιορισμός του κέντρου βάρους σύνθετων επίπεδων μορφών»

Στόχος: Προσδιορίστε το κέντρο βάρους ενός δεδομένου επίπεδου μιγαδικού σχήματος με πειραματικές και αναλυτικές μεθόδους και συγκρίνετε τα αποτελέσματά τους.

Εντολή εργασίας

Σχεδιάστε σε σημειωματάρια την επίπεδη φιγούρα σας σε μέγεθος, υποδεικνύοντας τους άξονες συντεταγμένων.

Προσδιορίστε αναλυτικά το κέντρο βάρους.

1. Σπάστε το σχήμα στον ελάχιστο αριθμό ψηφίων, τα κέντρα βάρους των οποίων ξέρουμε πώς να προσδιορίσουμε.

   Να αναφέρετε τον αριθμό των περιοχών και τις συντεταγμένες του κέντρου βάρους κάθε σχήματος.

   Να υπολογίσετε τις συντεταγμένες του κέντρου βάρους κάθε σχήματος.

   Υπολογίστε το εμβαδόν κάθε σχήματος.

   Υπολογίστε τις συντεταγμένες του κέντρου βάρους ολόκληρου του σχήματος χρησιμοποιώντας τους τύπους (βάλτε τη θέση του κέντρου βάρους στο σχέδιο του σχήματος):

Εγκατάσταση για πειραματικό προσδιορισμό των συντεταγμένων του κέντρου βάρους με ανάρτηση αποτελείται από ένα κατακόρυφο ράφι 1 (βλ. εικ.) στο οποίο είναι προσαρτημένη η βελόνα 2 . επίπεδη φιγούρα 3 Κατασκευασμένο από χαρτόνι, το οποίο είναι εύκολο να τρυπήσει μια τρύπα. τρύπες ΑΛΛΑ και ΣΤΟ τρυπημένα σε τυχαία σημεία (κατά προτίμηση στην πιο απομακρυσμένη απόσταση το ένα από το άλλο). Μια επίπεδη φιγούρα είναι κρεμασμένη σε μια βελόνα, πρώτα σε ένα σημείο ΑΛΛΑ , και μετά στο σημείο ΣΤΟ . Με τη βοήθεια ενός υδραυλικού 4 , στερεωμένη στην ίδια βελόνα, σχεδιάζεται μια κατακόρυφη γραμμή στο σχήμα με ένα μολύβι που αντιστοιχεί στη γραμμή του βάθους. Κέντρο βαρύτητας ΑΠΟ Η φιγούρα θα βρίσκεται στη διασταύρωση των κάθετων γραμμών που σχεδιάζονται όταν κρεμάτε τη φιγούρα σε σημεία ΑΛΛΑ και ΣΤΟ .

κέντρο βαρύτηταςΈνα άκαμπτο σώμα είναι ένα γεωμετρικό σημείο που συνδέεται άκαμπτα με αυτό το σώμα και είναι το κέντρο των δυνάμεων παράλληλης βαρύτητας που ασκούνται σε μεμονωμένα στοιχειώδη σωματίδια του σώματος (Εικόνα 1.6).

Διάνυσμα ακτίνας αυτού του σημείου

Εικόνα 1.6

Για ένα ομοιογενές σώμα, η θέση του κέντρου βάρους του σώματος δεν εξαρτάται από το υλικό, αλλά καθορίζεται από το γεωμετρικό σχήμα του σώματος.

Αν το ειδικό βάρος ενός ομοιογενούς σώματος γ , το βάρος του στοιχειώδους σωματιδίου του σώματος

Π k = γΔV κ (Π = γV ) αντικαταστήστε στον τύπο για τον προσδιορισμό r ντο , έχουμε

Από όπου, προβάλλοντας στους άξονες και περνώντας στο όριο, παίρνουμε τις συντεταγμένες του κέντρου βάρους ενός ομοιογενούς όγκου

Ομοίως, για τις συντεταγμένες του κέντρου βάρους μιας ομοιογενούς επιφάνειας με εμβαδόν μικρό (Εικόνα 1.7, α)

Εικόνα 1.7

Για τις συντεταγμένες του κέντρου βάρους μιας ομοιογενούς γραμμής μήκους μεγάλο (Εικόνα 1.7, β)

Μέθοδοι προσδιορισμού των συντεταγμένων του κέντρου βάρους

Με βάση τους γενικούς τύπους που ελήφθησαν νωρίτερα, είναι δυνατό να υποδειχθούν μέθοδοι για τον προσδιορισμό των συντεταγμένων των κέντρων βάρους των στερεών σωμάτων:

1 Αναλυτικός(με ενσωμάτωση).

2 Μέθοδος συμμετρίας. Αν το σώμα έχει επίπεδο, άξονα ή κέντρο συμμετρίας, τότε το κέντρο βάρους του βρίσκεται αντίστοιχα στο επίπεδο συμμετρίας, στον άξονα συμμετρίας ή στο κέντρο συμμετρίας.

3 Πειραματικός(μέθοδος ανάρτησης σώματος).

4 δυνατός. Το σώμα χωρίζεται σε έναν πεπερασμένο αριθμό μερών, για καθένα από τα οποία η θέση του κέντρου βάρους ντο και περιοχή μικρό γνωστός. Για παράδειγμα, η προβολή ενός σώματος σε ένα επίπεδο xOy (Εικόνα 1.8) μπορεί να αναπαρασταθεί ως δύο επίπεδες φιγούρες με εμβαδά μικρό 1 και μικρό 2 (S=S 1 + Σ 2 ). Τα κέντρα βάρους αυτών των μορφών βρίσκονται στα σημεία ντο 1 (Χ 1 , y 1 ) και ντο 2 (Χ 2 , y 2 ) . Τότε οι συντεταγμένες του κέντρου βάρους του σώματος είναι

Εικόνα 1.8

5Πρόσθεση(μέθοδος αρνητικών περιοχών ή όγκων). Μια ειδική περίπτωση της μεθόδου κατάτμησης. Ισχύει για σώματα με εγκοπές εάν είναι γνωστά τα κέντρα βάρους του σώματος χωρίς την αποκοπή και την αποκοπή. Για παράδειγμα, πρέπει να βρείτε τις συντεταγμένες του κέντρου βάρους ενός επίπεδου σχήματος (Εικόνα 1.9):

Εικόνα 1.9

Κέντρα βάρους των απλούστερων μορφών

Εικόνα 1.10

1 τρίγωνο

Το κέντρο βάρους της περιοχής του τριγώνου συμπίπτει με το σημείο τομής των μέσων του (Εικόνα 1.10, α).

DM=MB , CM= (1/3)ΕΙΜΑΙ .

2 Τόξο κύκλου

Το τόξο έχει άξονα συμμετρίας (Εικόνα 1.10, β). Το κέντρο βάρους βρίσκεται σε αυτόν τον άξονα, δηλ. y ντο = 0 .

δλ – στοιχείο τόξου, δλ = Rdφ , R είναι η ακτίνα του κύκλου, x = Rcosφ , L= 2aR ,

Συνεπώς:

Χ ντο = R(sina/α) .

3 Κυκλικός τομέας

Τομέας ακτίνας R με κεντρική γωνία 2 α έχει άξονα συμμετρίας Βόδι , στο οποίο βρίσκεται το κέντρο βάρους (Εικόνα 1.10, γ).

Χωρίζουμε τον τομέα σε στοιχειώδεις τομείς, που μπορούν να θεωρηθούν τρίγωνα. Τα κέντρα βάρους των στοιχειωδών τομέων βρίσκονται στο τόξο ενός κύκλου ακτίνας (2/3) R .

Το κέντρο βάρους του τομέα συμπίπτει με το κέντρο βάρους του τόξου ΑΒ :

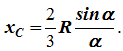
14. Μέθοδοι προσδιορισμού της κίνησης ενός σημείου.

Με τη μέθοδο του διανύσματος για τον καθορισμό της κίνησης, η θέση ενός σημείου προσδιορίζεται από το διάνυσμα ακτίνας που λαμβάνεται από ένα σταθερό σημείο στο επιλεγμένο σύστημα αναφοράς.

Με τη μέθοδο συντεταγμένων για τον προσδιορισμό της κίνησης, οι συντεταγμένες ενός σημείου καθορίζονται σε συνάρτηση με το χρόνο:

Αυτές είναι οι παραμετρικές εξισώσεις της τροχιάς ενός κινούμενου σημείου, στο οποίο ο χρόνος παίζει το ρόλο μιας παραμέτρου t . Για να γράψετε την εξίσωσή του σε ρητή μορφή, είναι απαραίτητο να εξαιρεθείτε από αυτά t .

Με τη φυσική μέθοδο προσδιορισμού της κίνησης, η τροχιά του σημείου, η αρχή στην τροχιά με την ένδειξη της θετικής κατεύθυνσης αναφοράς, ο νόμος μεταβολής της συντεταγμένης του τόξου τίθενται: s=s(t) . Αυτή η μέθοδος είναι βολική στη χρήση εάν η τροχιά του σημείου είναι γνωστή εκ των προτέρων.

15. 1.2 Ταχύτητα σημείου

Εξετάστε την κίνηση ενός σημείου σε μια μικρή χρονική περίοδο Δt :

μέση ταχύτητα ενός σημείου σε μια χρονική περίοδο Dt . Η ταχύτητα ενός σημείου σε μια δεδομένη στιγμή

Σημειακή ταχύτηταείναι ένα κινηματικό μέτρο της κίνησής του, ίσο με τη χρονική παράγωγο του διανύσματος ακτίνας αυτού του σημείου στο υπό εξέταση πλαίσιο αναφοράς. Το διάνυσμα της ταχύτητας κατευθύνεται εφαπτομενικά στην τροχιά του σημείου προς την κατεύθυνση της κίνησης.

Συγγραφέας: Ας πάρουμε ένα αυθαίρετο σχήμα σώματος. Είναι δυνατόν να το κρεμάσετε σε μια κλωστή έτσι ώστε μετά το κρέμασμα να διατηρεί τη θέση του (δηλαδή να μην αρχίζει να γυρίζει) όταν όποιοςαρχικός προσανατολισμός (εικ. 27.1);

Με άλλα λόγια, υπάρχει τέτοιο σημείο, σε σχέση με το οποίο το άθροισμα των ροπών των δυνάμεων της βαρύτητας που δρουν σε διαφορετικά μέρη του σώματος, θα ήταν ίσο με μηδέν στο όποιοςπροσανατολισμός του σώματος στο διάστημα;

Αναγνώστης: Ναι, ετσι νομιζω. Ένα τέτοιο σημείο λέγεται το κέντρο βάρους του σώματος.

Απόδειξη.Για απλότητα, θεωρήστε ένα σώμα με τη μορφή μιας επίπεδης πλάκας αυθαίρετου σχήματος αυθαίρετα προσανατολισμένου στο χώρο (Εικ. 27.2). Πάρτε το σύστημα συντεταγμένων Χ 0στομε την αρχή στο κέντρο μάζας - ένα σημείο ΑΠΟ, έπειτα x Γ = 0, στο Γ = 0.

Αντιπροσωπεύουμε αυτό το σώμα ως μια συλλογή μεγάλου αριθμού σημειακών μαζών m i, η θέση καθενός από τα οποία δίνεται από το διάνυσμα ακτίνας .

Εξ ορισμού του κέντρου μάζας και της συντεταγμένης x Γ = .

Αφού στο σύστημα συντεταγμένων μας x Γ= 0, τότε . Ας πολλαπλασιάσουμε αυτήν την εξίσωση επί σολκαι παρε

Όπως φαίνεται από το σχ. 27.2, | x i| είναι ο ώμος της δύναμης. Κι αν x i> 0, τότε η στιγμή της δύναμης Μ ι> 0, και αν x j < 0, то Mj < 0, поэтому с учетом знака можно утверждать, что для любого x iστιγμή της δύναμης θα είναι M i = m i gx i .Τότε η ισότητα (1) είναι ισοδύναμη με , όπου Μ ιείναι η στιγμή της βαρύτητας. Και αυτό σημαίνει ότι με έναν αυθαίρετο προσανατολισμό του σώματος, το άθροισμα των ροπών των δυνάμεων βαρύτητας που ασκούνται στο σώμα θα είναι ίσο με μηδέν σε σχέση με το κέντρο μάζας του.

Προκειμένου το σώμα που εξετάζουμε να βρίσκεται σε ισορροπία, είναι απαραίτητο να το εφαρμόσουμε σε ένα σημείο ΑΠΟδύναμη Τ = mgδείχνοντας κάθετα προς τα πάνω. Η στιγμή αυτής της δύναμης για το σημείο ΑΠΟισούται με μηδέν.

Δεδομένου ότι ο συλλογισμός μας δεν εξαρτιόταν σε καμία περίπτωση από το πώς ακριβώς είναι προσανατολισμένο το σώμα στο διάστημα, αποδείξαμε ότι το κέντρο βάρους συμπίπτει με το κέντρο μάζας, το οποίο ήταν αυτό που έπρεπε να αποδειχθεί.

Πρόβλημα 27.1.Βρείτε το κέντρο βάρους μιας αβαρούς ράβδου μήκους μεγάλο, στα άκρα του οποίου στερεώνονται δύο σημειακές μάζες t 1 και t 2 .

t 1 t 2 μεγάλο	Λύση. Δεν θα ψάξουμε για το κέντρο βάρους, αλλά για το κέντρο μάζας (αφού είναι ένα και το αυτό). Ας εισαγάγουμε τον άξονα Χ(Εικ. 27.3). Ρύζι. 27.3
x C =?

Απάντηση: μακριά από τη μάζα t 1 .

ΝΑ ΣΤΑΜΑΤΗΣΕΙ! Αποφασίστε μόνοι σας: B1-B3.

Δήλωση 1 . Εάν ένα ομοιογενές επίπεδο σώμα έχει άξονα συμμετρίας, το κέντρο βάρους βρίσκεται σε αυτόν τον άξονα.

Πράγματι, για οποιαδήποτε σημειακή μάζα m i, που βρίσκεται στα δεξιά του άξονα συμμετρίας, υπάρχει η ίδια σημειακή μάζα που βρίσκεται συμμετρικά ως προς την πρώτη (Εικ. 27.4). Στην περίπτωση αυτή, το άθροισμα των ροπών των δυνάμεων .

Δεδομένου ότι ολόκληρο το σώμα μπορεί να αναπαρασταθεί ως χωρισμένο σε παρόμοια ζεύγη σημείων, η συνολική ροπή βαρύτητας σε σχέση με οποιοδήποτε σημείο που βρίσκεται στον άξονα συμμετρίας είναι μηδέν, πράγμα που σημαίνει ότι το κέντρο βάρους του σώματος βρίσκεται επίσης σε αυτόν τον άξονα. Αυτό οδηγεί σε ένα σημαντικό συμπέρασμα: εάν το σώμα έχει πολλούς άξονες συμμετρίας, τότε το κέντρο βάρους βρίσκεται στη διασταύρωση αυτών των αξόνων(Εικ. 27.5).

Ρύζι. 27.5

Δήλωση 2. Αν δύο σώματα με μάζες t 1 και t 2 συνδέονται σε ένα, τότε το κέντρο βάρους ενός τέτοιου σώματος θα βρίσκεται σε μια ευθεία γραμμή που συνδέει τα κέντρα βάρους του πρώτου και του δεύτερου σώματος (Εικ. 27.6).

Ρύζι. 27.6 Ρύζι. 27.7

Απόδειξη.Ας τακτοποιήσουμε το σύνθετο σώμα έτσι ώστε το τμήμα που συνδέει τα κέντρα βάρους των σωμάτων να είναι κατακόρυφο. Τότε το άθροισμα των ροπών βαρύτητας του πρώτου σώματος ως προς το σημείο ΑΠΟΤο 1 ισούται με μηδέν και το άθροισμα των ροπών βαρύτητας του δεύτερου σώματος γύρω από το σημείο ΑΠΟ 2 είναι μηδέν (Εικ. 27.7).

σημειώσε ότι ώμοςβαρύτητα οποιασδήποτε σημειακής μάζας t iτο ίδιο σε σχέση με οποιοδήποτε σημείο του τμήματος ΑΠΟ 1 ΑΠΟ 2, και επομένως η ροπή βαρύτητας σε σχέση με οποιοδήποτε σημείο που βρίσκεται στο τμήμα ΑΠΟ 1 ΑΠΟ 2 είναι τα ίδια. Επομένως, η βαρύτητα ολόκληρου του σώματος είναι μηδέν σε σχέση με οποιοδήποτε σημείο του τμήματος ΑΠΟ 1 ΑΠΟ 2. Έτσι, το κέντρο βάρους του σύνθετου σώματος βρίσκεται στο τμήμα ΑΠΟ 1 ΑΠΟ 2 .

Η δήλωση 2 συνεπάγεται ένα σημαντικό πρακτικό συμπέρασμα, το οποίο διατυπώνεται σαφώς με τη μορφή οδηγιών.

εντολή,

πώς να βρείτε το κέντρο βάρους ενός άκαμπτου σώματος εάν μπορεί να σπάσει

σε μέρη, οι θέσεις των κέντρων βάρους καθενός από τα οποία είναι γνωστές

1. Αντικαταστήστε κάθε εξάρτημα με μια μάζα που βρίσκεται στο κέντρο βάρους αυτού του τμήματος.

2. Βρείτε κέντρο βαρύτητας(και αυτό είναι το ίδιο με το κέντρο βάρους) του προκύπτοντος συστήματος σημειακών μαζών, επιλέγοντας ένα βολικό σύστημα συντεταγμένων Χ 0στο, σύμφωνα με τους τύπους:

Πράγματι, ας τοποθετήσουμε το σύνθετο σώμα με τέτοιο τρόπο ώστε το τμήμα ΑΠΟ 1 ΑΠΟΤο 2 ήταν οριζόντιο, και θα το κρεμάσουμε σε κλωστές στα σημεία ΑΠΟ 1 και ΑΠΟ 2 (Εικ. 27.8, ένα). Είναι σαφές ότι το σώμα θα βρίσκεται σε ισορροπία. Και αυτή η ισορροπία δεν θα διαταραχθεί αν αντικαταστήσουμε κάθε σώμα με σημειακές μάζες t 1 και t 2 (Εικ. 27.8, σι).

Ρύζι. 27.8

ΝΑ ΣΤΑΜΑΤΗΣΕΙ! Αποφασίστε μόνοι σας: C3.

Πρόβλημα 27.2.Οι μπάλες μάζας τοποθετούνται σε δύο κορυφές ενός ισόπλευρου τριγώνου tκαθε. Η τρίτη κορυφή περιέχει μια μπάλα μάζας 2 t(Εικ. 27.9, ένα). Τριγωνική πλευρά ένα. Προσδιορίστε το κέντρο βάρους αυτού του συστήματος.

t 2t ένα	Ρύζι. 27.9
x Γ = ? στο Γ = ?

Λύση. Εισάγουμε το σύστημα συντεταγμένων Χ 0στο(Εικ. 27.9, σι). Επειτα

,

.

Απάντηση: x Γ = ένα/2; ; το κέντρο βάρους βρίσκεται στο μισό ύψος ΕΝΑ Δ.

Η ικανότητα να παραμένετε σε ισορροπία χωρίς να κάνετε προσπάθεια είναι πολύ σημαντική για αποτελεσματικό διαλογισμό, γιόγκα, τσιγκόνγκ, αλλά και για χορό της κοιλιάς. Αυτή είναι η πρώτη απαίτηση που αντιμετωπίζουν οι αρχάριοι σε τέτοιου είδους δραστηριότητες και ένας από τους λόγους για τους οποίους είναι δύσκολο να κάνουν τα πρώτα βήματα χωρίς εκπαιδευτή. Μια ερώτηση που υποδηλώνει ότι ένα άτομο δεν γνωρίζει το κέντρο βάρους του μπορεί να φαίνεται κάπως διαφορετική. Στο τσιγκόνγκ, για παράδειγμα, ένα άτομο θα ρωτήσει πώς να είναι χαλαρό και εξακολουθεί να εκτελεί κινήσεις ενώ στέκεται, ένας αρχάριος χορευτής ανατολίτιδος δεν θα καταλάβει πώς να διαχωρίζει και να συντονίζει τις κινήσεις του κάτω και του άνω μέρους του σώματος, και στις δύο περιπτώσεις οι άνθρωποι θα καταπονηθούν και συχνά θα χάσουν την ισορροπία τους. Οι κινήσεις τους θα είναι αβέβαιες, αδέξιες.

Ως εκ τούτου, είναι σημαντικό να κατανοήσετε πώς να βρείτε το κέντρο βάρους σας μόνοι σας, απαιτεί τόσο διανοητική εργασία όσο και δεξιότητα, αλλά με την πάροδο του χρόνου η ικανότητα μεταβαίνει σε ένα ενστικτώδες επίπεδο.

Τι πρέπει να γίνει για να μην καταπονηθούν οι μύες και ταυτόχρονα να μην χρησιμοποιηθούν εξωτερικά στηρίγματα. Η απάντηση είναι προφανής, πρέπει να μετακινήσετε το στήριγμα προς τα μέσα. Πιο συγκεκριμένα, βασιστείτε σε έναν υπό όρους εσωτερικό άξονα. Πού πάει αυτός ο άξονας; Η έννοια του κέντρου βάρους είναι υπό όρους, αλλά παρόλα αυτά χρησιμοποιείται στη φυσική. Εκεί συνηθίζεται να ορίζεται ως το σημείο εφαρμογής των δυνάμεων βαρύτητας που προκύπτουν. Η προκύπτουσα δύναμη βαρύτητας είναι το σύνολο όλων των δυνάμεων βαρύτητας, λαμβάνοντας υπόψη την κατεύθυνση της δράσης τους.

Είναι δύσκολο μέχρι τώρα; Προμηθευτείτε την υπομονή.

Δηλαδή, αναζητούμε ένα σημείο στο σώμα μας που θα μας επιτρέψει να μην πέσουμε, χωρίς να πολεμήσουμε συνειδητά τη βαρύτητα. Αυτό σημαίνει ότι η βαρύτητα της γης πρέπει να κατευθύνεται έτσι ώστε να συγκλίνει με τις υπόλοιπες δυνάμεις που δρουν κάπου στο κέντρο του σώματός μας.

Μια τέτοια κατεύθυνση δυνάμεων δημιουργεί έναν υπό όρους άξονα στο κέντρο του σώματός μας, μια κατακόρυφη επιφάνεια, αυτή είναι η κατακόρυφος του κέντρου βάρους. Εκείνο το μέρος του σώματος στο οποίο ακουμπάμε στο έδαφος είναι το αποτύπωμά μας (ακουμπάμε στο έδαφος με τα πόδια μας). αυτό είναι το σημείο του κέντρου βάρους μέσα στο αποτύπωμα. Αν η κάθετη μετατοπιστεί από αυτό το μέρος, θα χάσουμε την ισορροπία μας και θα πέσουμε. Όσο μεγαλύτερη είναι η ίδια η περιοχή στήριξης, τόσο πιο εύκολο είναι για εμάς να μείνουμε κοντά στο κέντρο της και επομένως όλοι ενστικτωδώς θα κάνουμε ένα μακρύ βήμα ενώ στεκόμαστε σε μια ασταθή επιφάνεια. Δηλαδή, η περιοχή στήριξης δεν είναι μόνο τα ίδια τα πόδια, αλλά και ο χώρος μεταξύ τους.

Είναι επίσης σημαντικό να γνωρίζετε ότι το πλάτος της περιοχής της περιοχής στήριξης επηρεάζει περισσότερο από το μήκος. Στην περίπτωση του ανθρώπου, αυτό σημαίνει ότι είναι πιο πιθανό να πέσουμε στο πλάι παρά προς τα πίσω, και ακόμη περισσότερο προς τα εμπρός. Επομένως, όταν τρέχουμε, είναι πιο δύσκολο για εμάς να διατηρήσουμε την ισορροπία, το ίδιο μπορούμε να πούμε και για τα τακούνια. Αλλά στα φαρδιά, σταθερά παπούτσια, αντίθετα, είναι πιο εύκολο να αντισταθείς, ακόμα πιο εύκολο από το εντελώς ξυπόλητο. Ωστόσο, οι δραστηριότητες που αναφέρθηκαν στην αρχή απαιτούν πολύ μαλακά, ελαφριά παπούτσια ή καθόλου. Επομένως, δεν μπορούμε να βοηθήσουμε τους εαυτούς μας με τα παπούτσια.

Έτσι, είναι πολύ σημαντικό να βρείτε το κεντρικό σημείο της κάθετης γραμμής στο πόδι σας. Συνήθως δεν βρίσκεται στο κέντρο του ποδιού, όπως υποθέτουν κάποιοι αυτόματα, αλλά πιο κοντά στη φτέρνα, κάπου στα μισά του δρόμου από το κέντρο του ποδιού, στη φτέρνα.
Αλλά δεν είναι μόνο αυτό.

Εκτός από την κάθετη γραμμή του κέντρου βάρους, υπάρχει και μια οριζόντια, καθώς και μια ξεχωριστή για τα άκρα.
Η οριζόντια γραμμή για γυναίκες και άνδρες τρέχει λίγο διαφορετικά.

Μπροστά, στις γυναίκες, περνά χαμηλότερα, και στους άνδρες, πιο ψηλά. Στους άνδρες τρέχει κάπου 4-5 δάχτυλα κάτω από τον αφαλό και στις γυναίκες 10 περίπου. Πίσω από τη γυναικεία γραμμή τρέχει σχεδόν ένα koopchik και η αρσενική γραμμή είναι περίπου πέντε δάχτυλα ψηλότερα από αυτήν. Επιπλέον, για σταθερότητα την ώρα του διαλογισμού, είναι σημαντικό να προσέχετε την καθαρή γραμμή του κέντρου βάρους του γόνατος. Βρίσκεται λίγο πάνω από το οστό (κάτω πόδι), αλλά δύο ή τρία δάχτυλα κάτω από τον χόνδρο.

Κατά τη διάρκεια του διαλογισμού, καθώς και κατά τον χορό της κοιλιάς, δεν είναι πολύ καλό να απλώνετε τα πόδια πλατιά, το μέγιστο πλάτος αντιστοιχεί συνήθως στο πλάτος των ώμων.

Επομένως, πρέπει να βοηθήσετε λίγο τον εαυτό σας με τα γόνατά σας, προσπαθώντας να χτίσετε τον κάθετο άξονα όσο πιο ευθεία γίνεται. Σταθείτε μπροστά στον καθρέφτη, βρείτε όλα τα σημεία που περιγράφονται στον εαυτό σας. Τοποθετήστε τα πόδια σας στο πλάτος των ώμων. Χαλαρώστε τους μύες στα πόδια και το σώμα σας. Στη συνέχεια, ισιώστε την πλάτη σας χωρίς να καταπονήσετε το σώμα σας, χαλαρώστε τα πόδια σας με μια ελαφριά κάμψη στα γόνατά σας. Φανταστείτε τρεις κάθετες γραμμές, κάθε μία να τρέχει σε ένα αντίστοιχο σημείο στο πίσω μέρος του κορμού, μπροστά του και γύρω από τα γόνατα. Προσπαθήστε να τακτοποιήσετε τα σημεία έτσι ώστε ο μπροστινός άξονας του κορμού να βρίσκεται περίπου στα μισά του δρόμου μεταξύ του άξονα της πλάτης και του γονάτου. Σε αυτή την περίπτωση, τα γόνατα δεν πρέπει να είναι λυγισμένα ώστε να ξεπερνούν το δάχτυλο του ποδιού, θα πρέπει μόνο να είναι ελαφρώς λυγισμένα και καλά χαλαρά. Κατά προτίμηση πάνω από το κέντρο βάρους μέσα στην περιοχή στήριξης που βρήκαμε στο πόδι. Ταυτόχρονα, τα χέρια μπορούν να τοποθετηθούν ελεύθερα στους θεούς ή να βάλουν τις παλάμες στους γοφούς.

Πώς θα ξέρετε ότι έχετε βρει το κέντρο βάρους σας;

Θα νιώσετε μια ελαφριά ταλάντευση, αλλά ταυτόχρονα θα ξέρετε σίγουρα ότι δεν θα πέσετε.

Διάλεξη 4. Κέντρο βάρους.

Αυτή η διάλεξη καλύπτει τις ακόλουθες ερωτήσεις

1. Κέντρο βάρους άκαμπτου σώματος.

2. Συντεταγμένες των κέντρων βάρους ανομοιογενών σωμάτων.

3. Συντεταγμένες των κέντρων βάρους ομοιογενών σωμάτων.

4. Μέθοδοι προσδιορισμού των συντεταγμένων των κέντρων βάρους.

5. Κέντρα βάρους κάποιων ομοιογενών σωμάτων.

Η μελέτη αυτών των θεμάτων είναι απαραίτητη στο μέλλον για τη μελέτη της δυναμικής της κίνησης των σωμάτων, λαμβάνοντας υπόψη την τριβή ολίσθησης και την τριβή κύλισης, τη δυναμική του κέντρου μάζας ενός μηχανικού συστήματος, τις κινητικές ροπές, για την επίλυση προβλημάτων στον κλάδο "ΔΥΝΑΜΗ ΤΩΝ ΥΛΙΚΩΝ".

Φέρνοντας παράλληλες δυνάμεις.

Αφού εξετάσαμε την αναγωγή στο κέντρο ενός επίπεδου συστήματος και ενός αυθαίρετου χωρικού συστήματος δυνάμεων, επανερχόμαστε και πάλι στην εξέταση μιας ειδικής περίπτωσης ενός συστήματος παράλληλων δυνάμεων.

Φέρνοντας δύο παράλληλες δυνάμεις.

Κατά την εξέταση ενός τέτοιου συστήματος δυνάμεων, είναι δυνατές οι ακόλουθες τρεις περιπτώσεις αναγωγής.

1. Σύστημα δύο συγγραμμικών δυνάμεων. Θεωρήστε ένα σύστημα δύο παράλληλων και κατευθυνόμενων δυνάμεων στην ίδια κατεύθυνση Πκαι Q, εφαρμόζεται σε σημεία ΑΛΛΑκαι ΣΤΟ. Θα υποθέσουμε ότι οι δυνάμεις είναι κάθετες σε αυτό το τμήμα (Εικ. 1, ένα).

ΑΠΟ, που ανήκει στο τμήμα ΑΒκαι πληρούν την προϋπόθεση:

ΜΕΤΑ ΧΡΙΣΤΟΝ/ΝΔ = Q/Π.(1)

Κύριο διάνυσμα συστήματος RC = Π + Q modulo ισούται με το άθροισμα αυτών των δυνάμεων: RC = Π + Q.

ΑΠΟλαμβάνοντας υπόψη το (1) ισούται με μηδέν:Μντο = Π ∙ ΜΕΤΑ ΧΡΙΣΤΟΝ- Q∙ ΝΔ = 0.

Έτσι, ως αποτέλεσμα του καστ, πήραμε: RC ≠ 0, Μντο= 0. Αυτό σημαίνει ότι το κύριο διάνυσμα είναι ισοδύναμο με το προκύπτον που διέρχεται από το κέντρο αναγωγής, δηλαδή:

Το προκύπτον των συγγραμμικών δυνάμεων είναι ίσο σε απόλυτη τιμή με το άθροισμά τους και η γραμμή δράσης του διαιρεί το τμήμα που συνδέει τα σημεία εφαρμογής τους, αντιστρόφως ανάλογη με τις μονάδες αυτών των δυνάμεων εσωτερικά.

Σημειώστε ότι η θέση του σημείου ΑΠΟδεν θα αλλάξει αν οι δυνάμεις Rκαι Qστρίψτε μια γωνίαα . Τελεία ΑΠΟ, που έχει αυτή την ιδιότητα ονομάζεται κέντρο παράλληλων δυνάμεων.

2. Σύστημα δύο αντισυγγραμμικόκαι όχι ίσο σε μέτρο δυνάμεων. Μακάρι οι δυνάμεις Πκαι Q, εφαρμόζεται σε σημεία ΑΛΛΑκαι ΣΤΟ, παράλληλη, κατευθυνόμενη σε αντίθετες κατευθύνσεις και άνιση συντελεστή (Εικ. 1, σι).

Ας επιλέξουμε το σημείο ως κέντρο αναφοράς ΑΠΟ, που εξακολουθεί να ικανοποιεί τη σχέση (1) και βρίσκεται στην ίδια ευθεία, αλλά έξω από το τμήμα ΑΒ.

Ο κύριος φορέας αυτού του συστήματος RC = Π + QΤο modulo θα είναι τώρα ίσο με τη διαφορά μεταξύ των μονάδων των διανυσμάτων: RC = Q - Π.

Κύρια στιγμή για το κέντρο ΑΠΟείναι ακόμα μηδέν:Μντο = Π ∙ ΜΕΤΑ ΧΡΙΣΤΟΝ- Q∙ ΝΔ= 0, άρα

Επακόλουθο αντισυγγραμμικόκαι δυνάμεις που δεν είναι ίσες σε απόλυτη τιμή είναι ίσες με τη διαφορά τους, κατευθύνονται προς μια μεγαλύτερη δύναμη και η γραμμή δράσης της διαιρεί το τμήμα που συνδέει τα σημεία εφαρμογής τους, αντιστρόφως ανάλογες με τις μονάδες αυτών των δυνάμεων εξωτερικά.

Εικ.1

3. Σύστημα δύο αντισυγγραμμικόκαι δυνάμεις ίσες σε συντελεστή. Ας πάρουμε την προηγούμενη περίπτωση αναγωγής ως αρχική. Ας φτιάξουμε το ρεύμα R, και δύναμη Qας προσπαθήσουμε modulo to force R.

Στη συνέχεια στο Q → R στον τύπο (1) η αναλογία ΜΕΤΑ ΧΡΙΣΤΟΝ/ΝΔ → 1. Αυτό σημαίνει ότι ΜΕΤΑ ΧΡΙΣΤΟΝ → ΝΔ, δηλαδή η απόσταση ΜΕΤΑ ΧΡΙΣΤΟΝ →∞ .

Σε αυτή την περίπτωση, η ενότητα του κύριου διανύσματος RC → 0, και η μονάδα της κύριας ροπής δεν εξαρτάται από τη θέση του κέντρου μείωσης και παραμένει ίση με την αρχική τιμή:

Μντο = Π ∙ ΜΕΤΑ ΧΡΙΣΤΟΝ- Q∙ ΝΔ = Π ∙ ( ΜΕΤΑ ΧΡΙΣΤΟΝ- ΝΔ) =Π ∙ ΑΛΛΑσι.

Έτσι, στο όριο, έχουμε αποκτήσει ένα σύστημα δυνάμεων για το οποίο RC = 0, Μντο≠ 0, και το κέντρο μείωσης αφαιρείται στο άπειρο, το οποίο δεν μπορεί να αντικατασταθεί από το προκύπτον. Σε αυτό το σύστημα, δεν είναι δύσκολο να ανακαλύψεις ένα ζεύγος δυνάμεων, έτσι ένα ζεύγος δυνάμεων δεν έχει αποτέλεσμα.

Κέντρο του συστήματος των παράλληλων δυνάμεων.

Σκεφτείτε το σύστημα nδυνάμεις Πι, εφαρμόζεται σε σημείαA i (x i , y i , z i) και παράλληλα με τον άξοναΟβ με το διάνυσμα μεγάλο(Εικ. 2).

Εάν εξαιρέσουμε εκ των προτέρων την περίπτωση ενός συστήματος ισοδύναμου με ένα ζεύγος δυνάμεων, δεν είναι δύσκολο να αποδείξουμε, με βάση την προηγούμενη παράγραφο, την ύπαρξη του προκύπτοντοςR.

Προσδιορίστε τις συντεταγμένες του κέντρουντο(Χ ντο, y ντο, z ντο) παράλληλες δυνάμεις, δηλαδή οι συντεταγμένες του σημείου εφαρμογής του προκύπτοντος αυτού του συστήματος.

Για το σκοπό αυτό χρησιμοποιούμε το θεώρημα Varignon, βάσει του οποίου:

Μ0 (R) = Σ Μ0(Πι).

Εικ.2

Η διανυσματική ροπή δύναμης μπορεί να αναπαρασταθεί ως διασταυρούμενο γινόμενο, επομένως:

Μ 0 (R) = rc× R = Σ Μ0i(Πι) = Σ ( r i× Πι ).

Δεδομένου ότι R = R v ∙ μεγάλο, ένα Πι = P vi ∙ μεγάλο και χρησιμοποιώντας τις ιδιότητες του προϊόντος του διανύσματος, παίρνουμε:

rc × R v ∙ μεγάλο = Σ ( r i × P vi ∙ μεγάλο),

rc ∙ R v × μεγάλο = Σ ( r i ∙ P vi × μεγάλο) = Σ ( r i ∙ P vi ) × μεγάλο,

ή:

[ r c R v - Σ ( r i P vi )] × μεγάλο= 0.

Η τελευταία έκφραση είναι έγκυρη μόνο αν η έκφραση σε αγκύλες είναι μηδέν. Επομένως, παράλειψη του δείκτηvκαι λαμβάνοντας υπόψη ότι το προκύπτονR = Σ Πι , από εδώ παίρνουμε:

rc = (Σ Πι r i )/(Σ Πι ).

Προβάλλοντας την τελευταία διανυσματική ισότητα στον άξονα συντεταγμένων, λαμβάνουμε το επιθυμητό έκφραση συντεταγμένων του κέντρου παράλληλων δυνάμεων:

x γ = (Σ Πι x i)/(Σ Πι );

yc = (Σ Πι y i )/(Σ Πι );(2)

z γ = (Σ Πι z i )/(Σ Πι ).

Κέντρο βάρους του σώματος

Συντεταγμένες των κέντρων βάρους ενός ομοιογενούς σώματος.

Σκεφτείτε ένα άκαμπτο σώμα που ζυγίζει Πκαι όγκος Vστο σύστημα συντεταγμένων Oxyz, όπου τα τσεκούρια Χκαι yσυνδέεται με την επιφάνεια της γης και τον άξονα zκατευθύνεται στο ζενίθ.

Αν σπάσουμε το σώμα σε στοιχειώδη μέρη με όγκο∆ V Εγώ , τότε η δύναμη της έλξης θα δράσει σε κάθε μέρος του∆ Πικατευθύνεται προς το κέντρο της γης. Ας υποθέσουμε ότι οι διαστάσεις του σώματος είναι πολύ μικρότερες από τις διαστάσεις της Γης, τότε το σύστημα δυνάμεων που εφαρμόζεται στα στοιχειώδη μέρη του σώματος μπορεί να θεωρηθεί όχι συγκλίνον, αλλά παράλληλο (Εικ. 3), και όλα τα συμπεράσματα του προηγούμενου κεφαλαίου ισχύουν για αυτό.

Εικ.3

Ορισμός . Το κέντρο βάρους ενός άκαμπτου σώματος είναι το κέντρο των παράλληλων δυνάμεων βάρους των στοιχειωδών μερών αυτού του σώματος.

Θυμηθείτε ότι ειδικό βάροςστοιχειώδες μέρος του σώματος ονομάζεται η αναλογία του βάρους του∆ Πιστον όγκο Δ V Εγώ : γ Εγώ = ∆ Πι/ ∆ V Εγώ . Για ένα ομοιογενές σώμα, αυτή η τιμή είναι σταθερή:γ Εγώ = γ = Π/ V.

Αντικατάσταση σε (2) ∆ Πι = γ Εγώ ∙∆ V Εγώ αντί Πι, λαμβάνοντας υπόψη την τελευταία παρατήρηση και μειώνοντας τον αριθμητή και τον παρονομαστή κατάσολ, παίρνουμε εκφράσεις για τις συντεταγμένες του κέντρου βάρους ενός ομοιογενούς σώματος:

x γ = (Σ ∆ Vi∙ x i)/(Σ ∆ Vi);

yc = (Σ ∆ Vi∙ y i )/(Σ ∆ Vi);(3)

z γ = (Σ ∆ Vi∙ z i )/(Σ ∆ Vi).

Πολλά θεωρήματα είναι χρήσιμα για τον προσδιορισμό του κέντρου βάρους.

1) Αν ένα ομογενές σώμα έχει επίπεδο συμμετρίας, τότε το κέντρο βάρους του βρίσκεται σε αυτό το επίπεδο.

Αν τα τσεκούρια Χκαι στοτοποθετείται σε αυτό το επίπεδο συμμετρίας, στη συνέχεια για κάθε σημείο με συντεταγμένες. και συντονίζουν σύμφωνα με το (3), θα ισούται με μηδέν, γιατί συνολικάόλα όροι με αντίθετα πρόσημα εξαλείφονται ανά ζεύγη. Άρα το κέντρο βάρους είναιστο επίπεδο συμμετρίας.

2) Αν ένα ομοιογενές σώμα έχει άξονα συμμετρίας, τότε το κέντρο βάρους του σώματος βρίσκεται σε αυτόν τον άξονα.

Πράγματι, στην περίπτωση αυτή, αν ο άξοναςzσχεδιάστε κατά μήκος του άξονα συμμετρίας, για κάθε σημείο με συντεταγμένεςμπορείτε να βρείτε ένα σημείο με συντεταγμένεςκαι συντεταγμένες και υπολογίζεται με τον τύπο (3) θα είναι ίσο με μηδέν.

Το τρίτο θεώρημα αποδεικνύεται παρόμοια.

3) Αν ένα ομοιογενές σώμα έχει κέντρο συμμετρίας, τότε το κέντρο βάρους του σώματος βρίσκεται σε αυτό το σημείο.

Και μερικές ακόμη παρατηρήσεις.

Πρώτα. Εάν το σώμα μπορεί να χωριστεί σε μέρη για τα οποία είναι γνωστά το βάρος και η θέση του κέντρου βάρους, τότε δεν χρειάζεται να ληφθεί υπόψη κάθε σημείο, αλλά στους τύπους (3)Πι – να προσδιορίζεται ως το βάρος του σχετικού εξαρτήματος καιως συντεταγμένες του κέντρου βάρους του.

Δεύτερος. Εάν το σώμα είναι ομοιογενές, τότε το βάρος ενός ξεχωριστού μέρους του, όπου είναι το ειδικό βάρος του υλικού από το οποίο είναι κατασκευασμένο το σώμα, και Vi - τον όγκο αυτού του μέρους του σώματος. Και οι τύποι (3) θα έχουν πιο βολική μορφή. Για παράδειγμα,

Και ομοίως, πού - τον όγκο ολόκληρου του σώματος.

Τρίτη σημείωση. Αφήστε το σώμα να μοιάζει με μια λεπτή πλάκα με εμβαδόν φάκαι πάχος tξαπλωμένος στο αεροπλάνο Oxy. Αντικατάσταση σε (3)∆ V Εγώ =t ∙ ∆F Εγώ , παίρνουμε τις συντεταγμένες του κέντρου βάρους μιας ομοιογενούς πλάκας:

x γ = (Σ ∆ F i∙ x i) / (Σ ∆ F i);

yc = (Σ ∆ F i∙ y i ) / (Σ ∆ F i).

z γ = (Σ ∆ F i∙ z Εγώ ) / (Σ ∆ F i).

όπου – συντεταγμένες του κέντρου βάρους μεμονωμένων πλακών.είναι η συνολική επιφάνεια του σώματος.

Τέταρτη σημείωση. Για σώμα σε μορφή λεπτής καμπυλόγραμμης ράβδου με μήκος μεγάλομε εμβαδόν διατομής έναστοιχειώδης όγκος∆ V Εγώ = ένα ∙∆ μεγάλο Εγώ , να γιατί συντεταγμένες του κέντρου βάρους μιας λεπτής καμπυλόγραμμης ράβδουθα είναι ίσα:

x γ = (Σ ∆ L i∙ x i)/(Σ ∆ L i);

yc = (Σ ∆ L i∙ y i )/(Σ ∆ L i);(4)

z γ = (Σ ∆ L i∙ z i )/(Σ ∆ L i).

όπου – συντεταγμένες του κέντρου βάρουςΕγώ-ο τμήμα? .

Σημειώστε ότι σύμφωνα με τον ορισμό, το κέντρο βάρους είναι ένα γεωμετρικό σημείο. μπορεί επίσης να βρίσκεται έξω από τα όρια ενός δεδομένου σώματος (για παράδειγμα, για ένα δαχτυλίδι).

Σημείωση.

Σε αυτή την ενότητα του μαθήματος, δεν κάνουμε διάκριση μεταξύ βαρύτητας, βαρύτητας και σωματικού βάρους. Στην πραγματικότητα, η βαρύτητα είναι η διαφορά μεταξύ της βαρύτητας της Γης και της φυγόκεντρης δύναμης που προκαλείται από την περιστροφή της.

Συντεταγμένες των κέντρων βάρους ανομοιογενών σωμάτων.

Συντεταγμένες κέντρου βάρους ανομοιογενές στερεό(Εικ. 4) στο επιλεγμένο σύστημα αναφοράς ορίζονται ως εξής:

Εικ.4

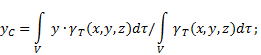
όπου - βάρος ανά μονάδα όγκου σώματος (ειδικό βάρος)

- ολόκληρο το σωματικό βάρος.

ανώμαλη επιφάνεια(Εικ. 5), τότε οι συντεταγμένες του κέντρου βάρους στο επιλεγμένο σύστημα αναφοράς καθορίζονται ως εξής:

Εικ.5

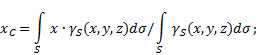
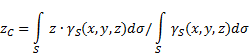
όπου - βάρος ανά μονάδα επιφάνειας σώματος

- ολόκληρο το σωματικό βάρος.

Αν το στερεό είναι ετερογενής γραμμή(Εικ. 6), τότε οι συντεταγμένες του κέντρου βάρους στο επιλεγμένο σύστημα αναφοράς καθορίζονται ως εξής:

Εικ.6

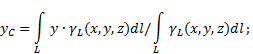
όπου - μονάδα βάρους σώματος μήκους,

Ολόκληρο το σωματικό βάρος.

Μέθοδοι προσδιορισμού των συντεταγμένων του κέντρου βάρους.

Με βάση τους γενικούς τύπους που ελήφθησαν παραπάνω, είναι δυνατό να υποδειχθούν συγκεκριμένες μέθοδοι τον προσδιορισμό των συντεταγμένων των κέντρων βάρους των σωμάτων.

1. Συμμετρία.Εάν ένα ομοιογενές σώμα έχει επίπεδο, άξονα ή κέντρο συμμετρίας (Εικ. 7), τότε το κέντρο βάρους του βρίσκεται αντίστοιχα στο επίπεδο συμμετρίας, στον άξονα συμμετρίας ή στο κέντρο συμμετρίας.

Εικ.7

2. Δυνατός.Το σώμα χωρίζεται σε έναν πεπερασμένο αριθμό μερών (Εικ. 8), για καθένα από τα οποία είναι γνωστά η θέση του κέντρου βάρους και η περιοχή.

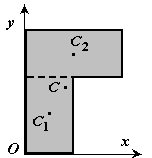
Εικ.8

S \u003d S 1 + S 2.

3.Μέθοδος αρνητικών περιοχών.Μια ειδική περίπτωση της μεθόδου κατάτμησης (Εικ. 9). Ισχύει για σώματα με εγκοπές εάν είναι γνωστά τα κέντρα βάρους του σώματος χωρίς την αποκοπή και την αποκοπή. Ένα σώμα με τη μορφή πλάκας με εγκοπή αντιπροσωπεύεται από έναν συνδυασμό συμπαγούς πλάκας (χωρίς εγκοπή) με μια περιοχή S1 και την περιοχή του κομμένου τμήματος S2.

Εικ.9

S \u003d S 1 - S 2.

4.μέθοδος ομαδοποίησης.Είναι μια καλή προσθήκη στις δύο τελευταίες μεθόδους. Αφού σπάσουμε το σχήμα στα συστατικά του στοιχεία, μπορεί να είναι βολικό να συνδυαστούν ξανά μερικά από αυτά, ώστε στη συνέχεια να απλοποιηθεί η λύση λαμβάνοντας υπόψη τη συμμετρία αυτής της ομάδας.

Κέντρα βάρους κάποιων ομοιογενών σωμάτων.

1) Κέντρο βάρους κυκλικού τόξου.Σκεφτείτε το τόξο ΑΒακτίνα κύκλουR με κεντρική γωνία. Λόγω της συμμετρίας, το κέντρο βάρους αυτού του τόξου βρίσκεται στον άξοναΒόδι(Εικ. 10).

Εικ.10

Ας βρούμε τη συντεταγμένησύμφωνα με τον τύπο . Για να το κάνετε αυτό, επιλέξτε στο τόξο ΑΒστοιχείο ΜΜ ’ μακρύς, η θέση του οποίου καθορίζεται από τη γωνία. Συντεταγμένη Χστοιχείο ΜΜ'θα είναι. Αντικατάσταση αυτών των τιμών Χκαιρε μεγάλο και έχοντας κατά νου ότι το ολοκλήρωμα πρέπει να επεκταθεί σε όλο το μήκος του τόξου, παίρνουμε:

όπου L το μήκος του τόξου ΑΒ ίσο με .

Από εδώ διαπιστώνουμε τελικά ότι το κέντρο βάρους του κυκλικού τόξου βρίσκεται στον άξονα συμμετρίας του σε απόσταση από το κέντροΩ ίσα

που είναι η γωνία μετρημένο σε ακτίνια.

2) Το κέντρο βάρους της περιοχής ενός τριγώνου. Σκεφτείτε ένα τρίγωνο που βρίσκεται στο επίπεδο Oxy, του οποίου οι συντεταγμένες κορυφής είναι γνωστές: A i (x i,y i ), (Εγώ= 1,2,3). Σπάζοντας το τρίγωνο σε στενές λωρίδες παράλληλες στο πλάι ΑΛΛΑ 1 ΑΛΛΑ 2 , καταλήγουμε στο συμπέρασμα ότι το κέντρο βάρους του τριγώνου πρέπει να ανήκει στη διάμεσο ΑΛΛΑ 3 Μ 3 (εικ.11) .

Εικ.11

Σπάζοντας το τρίγωνο σε λωρίδες παράλληλες προς την πλευρά ΑΛΛΑ 2 ΑΛΛΑ 3, μπορείτε να βεβαιωθείτε ότι πρέπει να βρίσκεται στη μέση ΑΛΛΑ 1 Μένας . Με αυτόν τον τρόπο, το κέντρο βάρους ενός τριγώνου βρίσκεται στο σημείο τομής των διαμέτρων του, το οποίο, όπως γνωρίζετε, χωρίζει το τρίτο μέρος από κάθε διάμεσο, μετρώντας από την αντίστοιχη πλευρά.

Ειδικότερα, για τον διάμεσο ΑΛΛΑ 1 Μ 1 παίρνουμε, δεδομένου ότι οι συντεταγμένες του σημείου Μ 1 - είναι ο αριθμητικός μέσος όρος των συντεταγμένων των κορυφών ΑΛΛΑ 2 και ΑΛΛΑ 3 :

x γ = Χ 1 + (2/3) ∙ (ΧΜ 1 - Χ 1 ) = Χ 1 + (2/3) ∙ [(Χ 2 + Χ 3 )/2 - Χ 1 ] = (Χ 1 + Χ 2 + Χ 3 )/3.

Έτσι, οι συντεταγμένες του κέντρου βάρους του τριγώνου είναι ο αριθμητικός μέσος όρος των συντεταγμένων των κορυφών του:

Χ ντο =(1/3) Σ x i ; y ντο =(1/3) Σ y i .

3) Το κέντρο βάρους της περιοχής του κυκλικού τομέα.Θεωρήστε έναν τομέα κύκλου ακτίνας Rμε κεντρική γωνία 2α , που βρίσκεται συμμετρικά ως προς τον άξονα Βόδι (Εικ. 12) .

Είναι προφανές ότι y ντο = 0, και η απόσταση από το κέντρο του κύκλου από τον οποίο κόβεται αυτός ο τομέας μέχρι το κέντρο βάρους του μπορεί να προσδιοριστεί από τον τύπο:

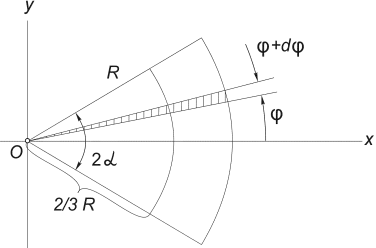
Εικ.12

Ο ευκολότερος τρόπος για να υπολογίσετε αυτό το ολοκλήρωμα είναι να διαιρέσετε τον τομέα ολοκλήρωσης σε στοιχειώδεις τομείς με γωνία ρεφ . Μέχρι απειροελάχιστα της πρώτης τάξης, ένας τέτοιος τομέας μπορεί να αντικατασταθεί από ένα τρίγωνο με βάση ίση με R × ρεφ και ύψος R. Η περιοχή ενός τέτοιου τριγώνου dF =(1/2)R 2 ∙ ρεφ , και το κέντρο βάρους του είναι 2/3 Rαπό πάνω, οπότε στο (5) βάζουμε Χ = (2/3)R∙ συν. Αντικατάσταση σε (5) φά= α R 2, παίρνουμε:

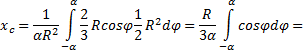
Χρησιμοποιώντας τον τελευταίο τύπο, υπολογίζουμε, συγκεκριμένα, την απόσταση από το κέντρο βάρους ημικύκλιο.

Αντικαθιστώντας στο (2) α = π /2, παίρνουμε: Χ ντο = (4 R)/(3 π) ≅ 0,4 R .

Παράδειγμα 1Ας προσδιορίσουμε το κέντρο βάρους του ομοιογενούς σώματος που φαίνεται στο Σχ. 13.

Εικ.13

Λύση.Το σώμα είναι ομοιογενές, αποτελούμενο από δύο μέρη που έχουν συμμετρικό σχήμα. Οι συντεταγμένες των κέντρων βάρους τους:

Οι τόμοι τους:

Επομένως, οι συντεταγμένες του κέντρου βάρους του σώματος

Παράδειγμα 2 Βρείτε το κέντρο βάρους μιας πλάκας λυγισμένης σε ορθή γωνία. Διαστάσεις - στο σχέδιο (Εικ. 14).

Εικ.14

Λύση. Συντεταγμένες κέντρα βάρους:

0.

Τετράγωνα:

Να γιατί:

Παράδειγμα 3 Σε τετράγωνο φύλλο cm κόψτε τετράγωνη τρύπα βλέπε (Εικ. 15). Βρείτε το κέντρο βάρους του φύλλου.Παράδειγμα 4 Βρείτε τη θέση του κέντρου βάρους της πλάκας που φαίνεται στο σχ. 16. Οι διαστάσεις δίνονται σε εκατοστά.

Εικ.16

Λύση. Χωρίζουμε το πιάτο σε σχήματα (Εικ. 17), κέντρατου οποίου η σοβαρότητα είναι γνωστή.

Οι περιοχές αυτών των σχημάτων και οι συντεταγμένες των κέντρων βάρους τους:

1) ένα ορθογώνιο με πλευρές 30 και 40 cm,μικρό 1 =30 ∙ 40=1200 εκ 2 ; x 1=15 cm; στο 1 \u003d 20 cm.

2) ορθογώνιο τρίγωνο με βάση 50 cm και ύψος 40 cm.μικρό 2 =0,5 ∙ 50 ∙ 40= 1000 εκ 2 ; Χ 2 \u003d 30 + 50 / 3 \u003d 46,7 cm; y 2 =40/3 =13,3 cm;

3) Ημικυκλική ακτίνα r = 20 cm;μικρό 3 =0,5 ∙π∙ 20 2 \u003d 628 cm 2 ; Χ 3 =4 R /3 π =8,5 cm; στο

Λύση. Θυμηθείτε ότι στη φυσική η πυκνότητα ενός σώματοςρ και το ειδικό του βάροςσολπου σχετίζονται με την αναλογία:γ = ρ σολ , όπουσολ - επιτάχυνση βαρύτητος. Για να βρείτε τη μάζα ενός τέτοιου ομοιογενούς σώματος, πρέπει να πολλαπλασιάσετε την πυκνότητα με τον όγκο του.

Εικ.19

Ο όρος «γραμμική» ή «γραμμική» πυκνότητα σημαίνει ότι για να προσδιοριστεί η μάζα της ράβδου ζευκτών, η γραμμική πυκνότητα πρέπει να πολλαπλασιαστεί με το μήκος αυτής της ράβδου.

Για να λύσετε το πρόβλημα, μπορείτε να χρησιμοποιήσετε τη μέθοδο κατάτμησης. Αντιπροσωπεύοντας ένα δεδομένο ζευκτό ως άθροισμα 6 μεμονωμένων ράβδων, παίρνουμε:

όπουL i μήκοςΕγώ -η ράβδος της φάρμας, καιx i , y i - συντεταγμένες του κέντρου βάρους του.

Η λύση σε αυτό το πρόβλημα μπορεί να απλοποιηθεί ομαδοποιώντας τις τελευταίες 5 ράβδους ζευκτών. Είναι εύκολο να δούμε ότι σχηματίζουν μια μορφή με κέντρο συμμετρίας που βρίσκεται στο μέσο της τέταρτης ράβδου, όπου βρίσκεται το κέντρο βάρους αυτής της ομάδας ράβδων.

Έτσι, ένα δεδομένο ζευκτό μπορεί να αναπαρασταθεί από έναν συνδυασμό μόνο δύο ομάδων ράβδων.

Η πρώτη ομάδα αποτελείται από την πρώτη ράβδο, για αυτόμεγάλο 1 = 4 m,Χ 1 = 0 m,y 1 = 2 μ. Η δεύτερη ομάδα ράβδων αποτελείται από πέντε ράβδους, για τις οποίεςμεγάλο 2 = 20 m,Χ 2 = 3 m,y 2 = 2 m.

Οι συντεταγμένες του κέντρου βάρους του αγροκτήματος βρίσκονται με τον τύπο:

Χ ντο = (μεγάλο 1 ∙ Χ 1 + μεγάλο 2 ∙ Χ 2 )/(μεγάλο 1 + μεγάλο 2 ) = (4∙0 + 20∙3)/24 = 5/2 m;

y ντο = (μεγάλο 1 ∙ y 1 + μεγάλο 2 ∙ y 2 )/(μεγάλο 1 + μεγάλο 2 ) = (4∙2 + 20∙2)/24 = 2 m.

Σημειώστε ότι το κέντρο ΑΠΟ βρίσκεται στη γραμμή σύνδεσης ΑΠΟ 1 και ΑΠΟ 2 και διαιρεί το τμήμα ΑΠΟ 1 ΑΠΟ 2 σχετικά με: ΑΠΟ 1 ΑΠΟ/SS 2 = (Χ ντο - Χ 1 )/(Χ 2 - Χ ντο ) = μεγάλο 2 / μεγάλο 1 = 2,5/0,5.

Ερωτήσεις για αυτοεξέταση

Ποιο είναι το κέντρο των παράλληλων δυνάμεων;

- Πώς καθορίζονται οι συντεταγμένες του κέντρου των παράλληλων δυνάμεων;

- Πώς προσδιορίζεται το κέντρο των παράλληλων δυνάμεων, το αποτέλεσμα των οποίων είναι μηδέν;

Ποια είναι η ιδιότητα του κέντρου των παράλληλων δυνάμεων;

- Ποιοι τύποι χρησιμοποιούνται για τον υπολογισμό των συντεταγμένων του κέντρου των παράλληλων δυνάμεων;

Ποιο είναι το κέντρο βάρους ενός σώματος;

- Γιατί οι δυνάμεις έλξης της Γης, που δρουν σε ένα σημείο του σώματος, μπορούν να ληφθούν ως σύστημα παράλληλων δυνάμεων;

- Να γράψετε τον τύπο για τον προσδιορισμό της θέσης του κέντρου βάρους ανομοιογενών και ομοιογενών σωμάτων, τον τύπο για τον προσδιορισμό της θέσης του κέντρου βάρους επίπεδων τμημάτων;

- Να γράψετε τον τύπο για τον προσδιορισμό της θέσης του κέντρου βάρους απλών γεωμετρικών σχημάτων: ορθογώνιο, τρίγωνο, τραπεζοειδές και μισό κύκλο;

Τι ονομάζεται στατική ροπή της περιοχής;

- Δώστε ένα παράδειγμα σώματος του οποίου το κέντρο βάρους βρίσκεται έξω από το σώμα.

- Πώς χρησιμοποιούνται οι ιδιότητες συμμετρίας για τον προσδιορισμό των κέντρων βάρους των σωμάτων;

- Ποια είναι η ουσία της μεθόδου των αρνητικών βαρών;

Πού βρίσκεται το κέντρο βάρους του κυκλικού τόξου;

Πώς μπορείτε να βρείτε γραφικά το κέντρο βάρους ενός τριγώνου;

- Γράψτε τον τύπο που καθορίζει το κέντρο βάρους του κυκλικού τομέα.

- Χρησιμοποιώντας τους τύπους που καθορίζουν τα κέντρα βάρους ενός τριγώνου και ενός κυκλικού τομέα, εξάγετε έναν παρόμοιο τύπο για ένα κυκλικό τμήμα.

- Ποιοι τύποι χρησιμοποιούνται για τον υπολογισμό των συντεταγμένων των κέντρων βάρους ομοιογενών σωμάτων, επίπεδων σχημάτων και ευθειών;

- Τι ονομάζεται στατική ροπή του εμβαδού ενός επίπεδου σχήματος ως προς τον άξονα, πώς υπολογίζεται και τι διάσταση έχει;

- Πώς να προσδιορίσετε τη θέση του κέντρου βάρους της περιοχής, εάν είναι γνωστή η θέση των κέντρων βάρους των επιμέρους τμημάτων της;

- Ποια βοηθητικά θεωρήματα χρησιμοποιούνται για τον προσδιορισμό της θέσης του κέντρου βάρους;