Βρείτε τον τύπο των ενικών σημείων της συνάρτησης. Η σειρά Laurent απομόνωσε μοναδικά σημεία και την ταξινόμησή τους

Αφήνω zq- μοναδικό σημείοσυναρτήσεις /(r), τ.σ. f(z)αλλά είναι αναλυτικό σε αυτό το σημείο (ιδίως, μπορεί να μην ορίζεται σε αυτό). Αν υπάρχει τέτοια τρυπημένη γειτονιά του σημείου zq (δηλαδή το σύνολο O z - Το zq f(z) είναι αιαλίτικο, λοιπόν zoπου ονομάζεται απομονωμένο ενικό σημείολειτουργίες f(z). Αυτός ο ορισμόςπαραμένει το ίδιο στην περίπτωση zn =ω, αν το ιώδιο τρυπιέται από την περιοχή του σημείου zq = oo κατανοώ σύνολο z>Εγώ - το εξωτερικό ενός κύκλου με το κέντρο του στην αρχή. Με άλλα λόγια, ένα ιδιαίτερο σημείο Το zq λέγεται ότι είναι απομονωμένο εάν υπάρχει μια γειτονιά αυτού του σημείου στην οποία το ist άλλων μοναδικών σημείων εκτός από zq. Σε όλα όσα ακολουθούν εξετάζουμε μόνο μοναδικά σημεία μοναδικού χαρακτήρα (τη συνάρτηση f(z)υποτίθεται ότι είναι σαφές).

Ανάλογα με τη συμπεριφορά της συνάρτησης f(z)στο z -> zqΥπάρχουν τρεις τύποι μοναδικών σημείων. Απομονωμένο ενικό σημείο συναρτήσεις zq f(z)που ονομάζεται:

1) αφαιρούμενο μοναδικό σημείο, εάν υπάρχει τελικό όριο

2) Πόλος, εάν υπάρχει όριο

3) ουσιαστικά ένα ιδιαίτερο σημείο,Αν f(z) δεν έχει ούτε πεπερασμένο ούτε άπειρο όριο στο z-> zq.

Παράδειγμα 26.1. Ας δείξουμε ότι πραγματοποιούνται και οι τρεις τύποι μοναδικών σημείων. Ας σκεφτούμε φά(z)= Σημείο zq = 0 απομονώνεται

ειδικό σημείο αυτής της λειτουργίας. Χρησιμοποιώντας τον τύπο (22.12), λαμβάνουμε την επέκταση

από το οποίο προκύπτει ότι υπάρχει lim fi(z)= 1. Επομένως zq = 0 είναι

είναι ένα αφαιρούμενο ενικό σημείο της συνάρτησης fi(z).

Λειτουργία f‘j(z) =---έχει ένα κοντάρι σε ένα σημείο zo= 1 γιατί

2 r" Χ

Ας εξετάσουμε τώρα τη συνάρτηση )з(z)= e 1 ^ r και δείξτε ότι ζω =Το O είναι ένα ουσιαστικά μοναδικό σημείο αυτής της συνάρτησης. Όταν προσπαθείς zστο μηδέν κατά μήκος του πραγματικού άξονα τα αριστερά και δεξιά όρια της συνάρτησης /z (z)διαφορετικά: λιμ Με 1 / 1 = 0, λιμ s 1 /* = os. Αυτό υπονοεί,

x->0-0 x->0+O

Τι f:i(z)δεν έχει ούτε πεπερασμένο ούτε άπειρο όριο στο 2 -> Α, δηλαδή. zq = O είναι ένα ουσιαστικά ενικό σημείο αυτής της συνάρτησης. (Σημειώστε ότι όπως τείνει το θέμα z - iyστο μηδέν κατά μήκος της συνάρτησης του φανταστικού άξονα

δεν έχει κανένα όριο.)

Υπάρχουν, φυσικά, μη μεμονωμένα μοναδικά σημεία. Για παράδειγμα. η συνάρτηση έχει πόλους σε σημεία z n = -, Π= ±1, ±2,...

Ως εκ τούτου, Zq = 0 είναι ένα μη απομονωμένο ενικό σημείο αυτής της συνάρτησης: σε οποιαδήποτε (ανεξάρτητα από το πόσο μικρή) γειτονιά αυτού του σημείου υπάρχουν άλλα μοναδικά σημεία ζ σελ.

Αφήνω ζω-πεπερασμένο απομονωμένο ενικό σημείο μιας συνάρτησης f(z).Επειτα f(z)είναι παρόμοια σε κάποια τρυπημένη γειτονιά του σημείου 0 Zo zoαυτή η γειτονιά μπορεί να θεωρηθεί ως ένας δακτύλιος με εσωτερική ακτίνα r = 0. Με το Θεώρημα 25.1, στην υπό εξέταση γειτονιά η συνάρτηση f(z)μπορεί να επεκταθεί σε σειρά Laurent (25.2). Θα δείξουμε ότι η συμπεριφορά της συνάρτησης στο 2 -> zq (δηλαδή ο τύπος του ενικού σημείου zo)εξαρτάται από τον τύπο του κύριου τμήματος της επέκτασης (25.2). Αυτή η περίσταση εξηγεί την προέλευση του όρου " κύριο μέρος”.

Θεώρημα 2G.2. Ένα απομονωμένο ενικό σημείο zo μιας συνάρτησης f(z) μπορεί να αφαιρεθεί εάν και μόνο εάν η επέκταση Lorapov σε μια διάτρητη γειτονιά αυτού του σημείου έχει oid

εκείνοι. αποτελείται μόνο από το σωστό μέρος, και όλοι οι συντελεστές του κύριου μέρους είναι ίσοι με τη σφαίρα.

Απόδειξη. 1. Αφήστε zo- αφαιρούμενο μοναδικό σημείο. Ας αποδείξουμε ότι η επέκταση Laurent της συνάρτησης f(z)έχει τη μορφή (26.1). Από το ειδικό σημείο zoαφαιρείται, τότε υπάρχει ένα πεπερασμένο όριο lim f(z) = Α.Ως εκ τούτου, f(z)οριοθετείται σε κάποια τρυπημένη γειτονιά του σημείου 0 z - zq zo,εκείνοι. )(z) για όλους zαπό αυτήν την περιοχή. Ας πάρουμε κανένα R. U р /?| και χρησιμοποιήστε τύπους (25.3) για τους συντελεστές της σειράς Laurent:

Για τους συντελεστές του κύριου μέρους της διαστολής n =- 1,-2,... Για τέτοιες τιμές Πέχουμε ρ~ σελ-e 0 σε R-> 0. Δεδομένου ότι η τιμή Rμπορεί να επιλεγεί αυθαίρετα μικρό, τότε κ.~"μπορεί να είναι όσο μικρό επιθυμείτε. Αφού |s t,| ^ Mr~pκαι c„δεν εξαρτώνται από το p, τότε c„ = 0 στο Και= - 1, -2,..., που ήταν αυτό που έπρεπε να αποδειχθεί.

2. Ας υποθέσουμε τώρα ότι η επέκταση Laurent έχει τη μορφή (26.1). Σειρά (26.1) είναι σειρά ισχύοςΚαι. επομένως, συγκλίνει όχι μόνο στην τρυπημένη περιοχή, αλλά και σε ολόκληρη τη γύρω περιοχή z-zq συμπεριλαμβανομένου του σημείου zo?το ποσό του S(z)είναι αναλυτική στο z και S(z) = )(z)στο 0 z - zo R.Επομένως, υπάρχει ένα πεπερασμένο όριο )(z)= Pt 5(g) = 5(th) - Επομένως, το ενικό σημείο zq

Ζ->Ζω Ζ-*Ζω

μεταθέσιμος. Το θεώρημα έχει αποδειχθεί.

Σχόλιο. Από την απόδειξη του θεωρήματος προκύπτει ότι σε διάτρητη γειτονιά 0 z - zo αφαιρούμενου ενικού σημείου η συνάρτηση f(z)συμπίπτει με τη συνάρτηση 5(r), η οποία είναι αναλυτική σε ολόκληρη τη γειτονιά z - zo. Επομένως, αν θέσουμε /(th) = S(zq), στη συνέχεια, χωρίς αλλαγή των τιμών της συνάρτησης f(z)σε οποιοδήποτε σημείο της τρυπημένης γειτονιάς, θα κάνουμε αυτή τη συνάρτηση αναλυτική στο Go, δηλ. Ας «καταργήσουμε» το χαρακτηριστικό. Αυτό εξηγεί τον όρο "αφαιρούμενο χαρακτηριστικό". Είναι φυσικό να θεωρούμε τέτοια σημεία κανονικά και όχι μεμονωμένα σημεία της συνάρτησης f(z).

Σκεφτείτε, για παράδειγμα, τη συνάρτηση

Στο παράδειγμα 26.1 φάνηκε ότι Pm Nr) = 1. δηλ. μοναδικό σημείο

zq = 0 αφαιρούμενο. Θέτοντας /i(0) = 1, εξαλείφουμε την ιδιομορφία και λαμβάνουμε μια συνάρτηση που είναι αναλυτική στο σημείο zq = 0 (και σε όλο το επίπεδο C).

Ας χαρακτηρίσουμε τώρα τους πόλους ως προς τις επεκτάσεις Laurent.

Θεώρημα 26.3. Ένα απομονωμένο ενικό σημείο Zo μιας συνάρτησης f(z) είναι πόλος αν και μόνο αν, όταν το κύριο μέρος της επέκτασης Laurent με κέντρο το Zq έχει μόνο έναν πεπερασμένο αριθμό διακριτών

από μηδενικούς συντελεστές με n:

Απόδειξη. 1. Αφήστε zq - πόλος, δηλ. lim/( z) = οο.

Ας αποδείξουμε ότι η επέκταση Laurent της συνάρτησης f(z)έχει τη μορφή (2G.2). Αφού λιμ f(z)= οο. τότε υπάρχει μια τρυπημένη γειτονιά του σημείου

κι zq. εν f(z)είναι αναλυτικό και δεν έχει μηδενικά. Στη συνέχεια η συνάρτηση g(z) = 1 /f(z)θα είναι επίσης αναλυτικό σε αυτήν την τρυπημένη γειτονιά, και λιμ g(z)= 0. Επομένως, Ζωείναι αφαιρούμενο *-? *0

ενικό σημείο της συνάρτησης g(z).Ας ορίσουμε g(z)στο σημείο zo, βάζοντας g(zo)= 0. Τότε g(z)θα γίνει αναλυτικό σε όλη τη γειτονιά του (όχι τρυπημένου) σημείου z 0,και z 0θα είναι το απομονωμένο μηδέν του. Ας υποδηλώσουμε με Νπολλαπλότητα (τάξη) αυτού του μηδενός. Όπως φάνηκε στην §23, στη γειτονιά του σημείου συνάρτηση zq g(z)μπορεί να αναπαρασταθεί με τη μορφή (βλ. (23.2))

και (z$) f 0 και y>(z)είναι αναλυτική σε κάποια γειτονιά του σημείου ζω-Επειδή ip(z)συνεχής σε ένα σημείο zoΚαι g>(zo) Ф 0" τότε ip(z)δεν έχει μηδενικά σε κάποια γειτονιά αυτού του σημείου. Επομένως η συνάρτηση 1 /-p(z)θα είναι επίσης αναλυτικό σε αυτή τη γειτονιά και, ως εκ τούτου, επεκτείνεται σε αυτήν σε μια σειρά Taylor:

Ανοίγοντας τις αγκύλες και αλλάζοντας τους χαρακτηρισμούς των συντελεστών, γράφουμε την τελευταία επέκταση στη φόρμα

όπου c_jv = 1>ο f 0. Έτσι, το κύριο μέρος της επέκτασης Laurent της συνάρτησης /(r) περιέχει μόνο τελικός αριθμόςμέλη? φτάσαμε στην επιθυμητή ισότητα (26.2).

2. Αφήστε τη διάτρητη γειτονιά των σημείων ουλειτουργία )(z)αντιπροσωπεύεται από την επέκταση Laurent (26.2) (για μια πιο λεπτομερή μορφή, βλέπε (26.3)), το κύριο μέρος της οποίας περιέχει μόνο έναν πεπερασμένο αριθμό όρων, και Με-ρε" φά 0. Είναι απαραίτητο να αποδειχθεί ότι Zq - πόλος λειτουργίας f(z).Πολλαπλασιάζοντας την ισότητα (26,3) επί (ΣΟΛ - σολ o) iV , παίρνουμε τη συνάρτηση

Η σειρά στο (26.4) είναι μια σειρά ισχύος που συγκλίνει σε μια αναλυτική συνάρτηση όχι μόνο στο διάτρητο σημείο, αλλά και σε ολόκληρη τη γειτονιά του σημείου Zq. Επομένως η συνάρτηση h(z)θα γίνει αναλυτικό σε αυτή τη γειτονιά αν το ορίσουμε περαιτέρω στο go βάζοντας h(zo)= s_dg φά 0. Τότε

Έτσι, το σημείο ου είναι πόλος και το θεώρημα 26.3 αποδεικνύεται.

Πολλαπλότητα (τάξη) μηδενικής συνάρτησης g(z)= 1//(g) ονομάζεται σειρά πόλωνου συνάρτηση /(r). Αν Ν-η σειρά του πόλου του ου, λοιπόν g(z)= (g - Zo) N ip(z),και φύγε) φά 0, και, όπως φαίνεται στο πρώτο μέρος της απόδειξης του Θεωρήματος 26.3, η επέκταση της συνάρτησης /(r) έχει τη μορφή (26.3), όπου c_/v φά 0. Αντίστροφα, αν το /(r) επεκταθεί στη σειρά (26.3) και e-i F 0, λοιπόν

τ.σ. Ν-σειρά του πόλου της συνάρτησης /(r). Ετσι, σειρά πόλων της συνάρτησης zq/(ΣΟΛ) ίσος με τον αριθμό του υψηλότερου μη μηδενικού συντελεστή του κύριου τμήματος της επέκτασης Laurent στη διάτρητη γειτονιά του σημείου zq(δηλαδή ίσο με αυτόν τον αριθμό Ν,τι s_dg φά 0 και Sp= 0 σε Π > Ν).

Ας αποδείξουμε την ακόλουθη δήλωση, η οποία είναι βολική για εφαρμογές.

Συμπέρασμα 26.4. Το σημείο zq είναι πόλος τάξης Ν της μυθοπλασίας/(ΣΟΛ) τότε και μόνο όταν/(ΣΟΛ) αντιπροσωπεύσιμο στη μορφή

όπου h(z) - αναλυτική συνάρτησηκοντά σε ένα σημείοου και h(zo) f 0.

Απόδειξη. Λειτουργία cp(z) = l/h(z)είναι αναλυτική σε κάποια γειτονιά του σημείου η. Η συνθήκη του συμπερασμάτων 26.4 είναι ισοδύναμη με την ακόλουθη:

Να γιατί zq - μηδενική πολλαπλότητα Νλειτουργίες g(z).και επομένως ο πόλος της πολλαπλότητας Νσυναρτήσεις /(2).

II Παράδειγμα 26.5. Βρείτε μεμονωμένα ενικά σημεία μιας συνάρτησης και προσδιορίστε το είδος τους.

Λύση: Τα σημεία στα οποία (ζ 2 + 1 )(ζ+ Ζ) 2 = 0. Αν z 2 ΜΕΓΑΛΟ- 1 = 0, μετά 2 = ±gΑν (ζ 4- 3) 2 = 0, τότε z= -3. Επομένως η συνάρτηση έχει τρία μοναδικά σημεία z= g, 22 = -g, Ζ3 = - 3. Σκεφτείτε z:

G -πόλο πρώτης τάξης (χρησιμοποιήσαμε Συμπέρασμα 26.4). Μπορεί να αποδειχθεί με παρόμοιο τρόπο ότι 22 = -Εγώεπίσης πόλο πρώτης τάξης. Για 2z έχουμε:

Ας προχωρήσουμε εξετάζοντας ουσιαστικά μοναδικά σημεία.

Θεώρημα 26.6. Ένα απομονωμένο ενικό σημείο zq μιας συνάρτησης f(z) είναι ουσιαστικά ενικό αν και μόνο αν το κύριο μέρος της επέκτασης Laurent με κέντρο zq έχει άπειρα πολλά διαφορετικά από αυτά. μηδέν, συντελεστές από p.

Απόδειξη. Το Θεώρημα 26.6 προκύπτει απευθείας από τα Θεωρήματα 26.2 και 26.3. Πράγματι, αν το σημείο Το zq είναι ουσιαστικά ειδικό, τότε το κύριο μέρος της επέκτασης Laurent δεν μπορεί να απουσιάζει ή να περιέχει έναν πεπερασμένο αριθμό όρων (διαφορετικά το σημείο Το Zq θα είναι είτε αφαιρούμενο είτε κοντάρι). Επομένως, ο αριθμός των όρων στο κύριο μέρος πρέπει να είναι άπειρος.

Αντίστροφα, αν το κύριο μέρος περιέχει άπειρους όρους, τότε Το Zq δεν μπορεί να είναι ούτε αφαιρούμενο σημείο ούτε πόλος. Επομένως, αυτό το σημείο είναι ουσιαστικά ιδιαίτερο.

Σύμφωνα με τον ορισμό, ένα ουσιαστικά ενικό σημείο χαρακτηρίζεται από το γεγονός ότι η συνάρτηση /(2) δεν έχει ούτε πεπερασμένο ούτε άπειρο όριο για z ->zq. Περισσότερο πλήρη θέαΤο παρακάτω θεώρημα δείχνει πόσο ακανόνιστη είναι η συμπεριφορά μιας συνάρτησης σε μια γειτονιά ενός ουσιαστικά μοναδικού σημείου.

Θεώρημα 26.7 (θεώρημα Sokhotsky). Αν το zq είναι ουσιώδες για πρόσωπα, το σημείο της συνάρτησης f(z), τότε για κανέναν μιγαδικός αριθμός ΜΕΓΑΛΟ, συμπεριλαμβανομένου Α =ω, υπάρχει μια ακολουθία σημείων z n τέτοια ώστε z n -> zo καιλιμ f(zn) = ΕΝΑ.

ρ->ος

Απόδειξη. Ας εξετάσουμε πρώτα την υπόθεση Α = oo. Στο πρώτο μέρος της απόδειξης του Θεωρήματος 2G.2 διαπιστώσαμε ότι αν f(z)οριοθετείται σε κάποια διάτρητη γειτονιά του σημείου r, τότε όλοι οι συντελεστές c", n = - 1,- 2,... του κύριου μέρους είναι ίσα με μηδέν (και, επομένως, η ιδιομορφία στο go είναι αφαιρέσιμη). Εφόσον από την συνθήκη th είναι ένα ουσιαστικό ενικό σημείο, τότε σε οποιαδήποτε διάτρητη γειτονιά του σημείου ου η συνάρτηση f(r) είναι απεριόριστη. Ας πάρουμε κάποια ισχυρή γειτονιά 0 Z τέτοια ώστε f(zi) > 1 (αν |/(r)| z - zo I/2 υπάρχει ένα σημείο z-2 , στην οποία |/(εε)| > 2 κ.λπ.: στη τρυπημένη γειτονιά Ο 71. Είναι προφανές ότι r„ -e go και lim /(r“) = oo. Έτσι, στην περίπτωση A = oo, Θεώρημα 26.7

αποδεδειγμένος.

Αφήστε το τώρα A f oo. Ας υποθέσουμε πρώτα ότι υπάρχει μια τρυπημένη γειτονιά 0

= -εε---- θα είναι αναλυτική σε αυτή την τρυπημένη γειτονιά και, κατά συνέπεια,

/(G) - ΕΝΑ

Συνεπώς, το go είναι ένα απομονωμένο ενικό σημείο της συνάρτησης Φ(r). Θα σας δείξουμε. ότι το r είναι ουσιαστικά ενικό σημείο του Φ(r). Αυτό μπορεί να μην είναι αλήθεια. Τότε υπάρχει ένα όριο lim Ф(r), πεπερασμένο ή άπειρο. Για λίγο

/(r) = A + , τότε υπάρχει και Hsh /(r), που έρχεται σε αντίθεση με την συνθήκη

F(g) ~ :-*z 0

Βλέπω το θεώρημα. Έτσι, το r0 είναι ένα ουσιαστικά μοναδικό σημείο της συνάρτησης Φ(r). Σύμφωνα με όσα αποδείχθηκαν παραπάνω, υπάρχει μια ακολουθία σημείων r n τέτοια ώστε r n th και lim Ф(r n) = oo. Από εδώ

Έχουμε αποδείξει την απαιτούμενη δήλωση με την υπόθεση ότι /(r) Φ Ασε κάποια τρυπημένη γειτονιά του σημείου πά- Ας υποθέσουμε τώρα ότι αυτό είναι ψευδές, δηλ. σε οποιαδήποτε αυθαίρετα μικρή τρυπημένη γειτονιά του σημείου ου υπάρχει τέτοιο σημείο ΣΟΛ",ότι /(r") = L. Στη συνέχεια για οποιαδήποτε Πστη διάτρητη γειτονιά 0 f(z u) = А. Έτσι, η επιθυμητή πρόταση είναι αληθής Π-Γιούο

σε όλες τις περιπτώσεις, και το Θεώρημα 26.7 είναι αποδεδειγμένο.

Σύμφωνα με το Θεώρημα 26.7 (Sokhotsky), σε οποιαδήποτε (αυθαίρετα μικρή) τρυπημένη γειτονιά ενός ουσιαστικά μοναδικού σημείου, η συνάρτηση /(r) λαμβάνει τιμές αυθαίρετα κοντά σε οποιονδήποτε αριθμό από το εκτεταμένο μιγαδικό επίπεδο C.

Για τη μελέτη μεμονωμένων μοναδικών σημείων, οι ήδη γνωστές επεκτάσεις Taylor βασικών στοιχειωδών συναρτήσεων είναι συχνά χρήσιμες.

Παράδειγμα 2G.8. Προσδιορίστε τον τύπο του ενικού σημείου zq = 0 για τη συνάρτηση

Λύθηκε και ε. Ας επεκτείνουμε τον αριθμητή και τον παρονομαστή σε μια σειρά Taylor σε δυνάμεις του g. Αντικαθιστώντας στο (22.11) 3 zαντί για r και αφαιρώντας 1, παίρνουμε

Χρησιμοποιώντας το (22.12), λαμβάνουμε την επέκταση του παρονομαστή:

Οι σειρές σε αυτές τις επεκτάσεις συγκλίνουν σε ολόκληρο το μιγαδικό επίπεδο €. Εχουμε

και /2(2) είναι αναριτικά σε μια γειτονιά του σημείου ζω = 0 (και ακόμη και σε ολόκληρο το επίπεδο) και /2(20) φά 0, λοιπόν h(z)είναι επίσης αναλυτική σε κάποια γειτονιά του σημείου gF 0. Σύμφωνα με το συμπέρασμα 26.4, το σημείο Ζω =Το 0 είναι ο πόλος τάξης Ν=4.

II Παράδειγμα 26.9. Βρείτε μοναδικά σημεία μιας συνάρτησης f(z)= sin j - και προσδιορίστε το είδος τους.

R e in e i e. Η συνάρτηση έχει ένα μόνο πεπερασμένο ενικό σημείο zq = 1. Σε άλλα σημεία από το Γ η συνάρτηση w =--- αναλυτικός; εξ ου και η συνάρτηση αμαρτία wθα είναι αναλυτική.

Αντικαθιστώντας - αντί για r στη διαστολή του ημιτονοειδούς (22.12), παίρνουμε

Πήραμε αποσύνθεση λειτουργίες αμαρτία-στη σειρά Laurent σε μια διάτρητη γειτονιά του σημείου 2o = 1. Εφόσον η προκύπτουσα επέκταση περιέχει άπειρους όρους με αρνητικές δυνάμεις(ζ - 1), τότε zq = 1 είναι ένα ουσιαστικά ενικό σημείο (στο σε αυτήν την περίπτωσηη επέκταση Laurent αποτελείται μόνο από το κύριο μέρος, και σωστό μέροςαπών).

Σημειώστε ότι ήταν δυνατό να προσδιοριστεί η φύση της μοναδικότητας σε αυτήν την περίπτωση απευθείας από τον ορισμό, χωρίς να καταφύγουμε σε επέκταση σειρών. Πράγματι, υπάρχουν ακολουθίες (r",) και (2") που συγκλίνουν σε zo= 1, και έτσι ώστε f(z"n)= 1, /(2") = 0 (υποδείξτε μόνοι σας τέτοιες ακολουθίες). f(z)δεν έχει όριο στο z -> 1 και επομένως σημείο zq - 1 είναι ουσιαστικά ιδιαίτερο.

Ας εισαγάγουμε την έννοια της επέκτασης Laurent μιας συνάρτησης σε μια γειτονιά ενός σημείου Zq = 00 και εξετάστε τη σύνδεση μεταξύ της επέκτασης και της φύσης της μοναδικότητας σε αυτό το σημείο. Σημειώστε ότι οι ορισμοί ενός απομονωμένου μοναδικού σημείου και ο τύπος του (αφαιρούμενος, πόλος ή ουσιαστικά μοναδικός) μεταφέρονται στην περίπτωση zq = oc χωρίς αλλαγές. Αλλά Θεωρήματα 26.2. Τα 26.3 και 26.6, που σχετίζονται με τη φύση των επεκτάσεων Laurent, πρέπει να αλλάξουν. Το θέμα είναι ότι τα μέλη cn(z- 2o) σελ. Π= -1,-2,..., κύριο μέρος, που ορίζει την «ατυπία» της συνάρτησης κοντά στο τελικό σημείο Zq, καθώς το 2 τείνει στο oo, θα συμπεριφέρονται "σωστά" (τείνουν στο 0). Αντίθετα τα μέλη του ορθού μέρους με Π= 1,2,... θα τείνει σε oo; καθορίζουν τη φύση του χαρακτηριστικού σε Zq = oo. Επομένως, το κύριο μέρος της επέκτασης στην περιοχή του oo θα αποτελείται από όρους με θετικές δυνάμεις Π,και το σωστό - με αρνητικά.

Ας εισάγουμε μια νέα μεταβλητή w = 12. Λειτουργία τηλεόραση = 1/2, εκτεταμένο έτσι ώστε u(oo) = 0, ένα προς ένα και να χαρτογραφεί σύμφωνα με τη γειτονιά z > Rσημεία zq = 00 στην περιοχή |w| wq = 0. Αν η συνάρτηση f(z)αναλυτικά στην τρυπημένη γειτονιά R z Zq = oc, μετά η συνάρτηση G(w) = f(l/w)θα είναι αναλυτικό στη μεγάλη γειτονιά 0 wo = 0. Αφού στις 2 -> oo θα υπάρχει w-> 0, λοιπόν

Να γιατί G(w)έχει στο σημείο wq = 0 είναι ένα χαρακτηριστικό του ίδιου τύπου με f(z)στο σημείο Zq = 00. Ας επεκτείνουμε τη συνάρτηση G(w) σε μια σειρά Laurent σε μια διάτρητη γειτονιά του σημείου wo = 0:

Τα αθροίσματα στη δεξιά πλευρά του (26.5) αντιπροσωπεύουν το κανονικό και το κύριο μέρος της επέκτασης, αντίστοιχα. Ας προχωρήσουμε στη μεταβλητή z,αντικαθιστώντας w = 1/z:

Ορίζοντας Π= -A*, 6* = 6_„ = s pκαι παρατηρώντας ότι G(l/z) = f(z), παίρνουμε

Η αποσύνθεση (2G.G) ονομάζεται Laurent επέκταση της συνάρτησης f(z) σε διάτρητη γειτονιά του σημείου zq= οο. Το πρώτο άθροισμα στο (2G.6) ονομάζεται το δεξί μέρος, και το δεύτερο άθροισμα είναι κύριο μέρος αυτής της αποσύνθεσης. Εφόσον αυτά τα αθροίσματα αντιστοιχούν στα σωστά και κύρια μέρη της επέκτασης (26.5), τότε τα ανάλογα των Θεωρημάτων 26.2, 26.3 και 26.6 ισχύουν για την επέκταση (26.6). Έτσι, το παρακάτω θεώρημα θα είναι ανάλογο του Θεωρήματος 26.2.

Θεώρημα 26.10. Απομονωμένο ενικό σημείοZq - OS (λειτουργίες/(ΣΟΛ) αφαιρείται εάν και μόνο εάν η επέκταση Laurent σε μια διάτρητη γειτονιά αυτού του σημείου έχει τη μορφή

τ.σ. αποτελείται μόνο από το σωστό μέρος.

Ας βάλουμε /(οο) = συν.Συνάρτηση που ορίζεται από τη σειρά (26.7) που συγκλίνει στη γειτονιά z > Rσημείο 2o = oc, καλείται αναλυτική στο σημείο ζο = οο. (Σημειώστε ότι αυτός ο ορισμός είναι ισοδύναμος με την αναλυτικότητα της συνάρτησης G(w) στο σημείο ουα = 0.)

Παράδειγμα 26.11. Διερευνήστε το ενικό σημείο zq = oo της συνάρτησης

Αφού λοιπόν το όριο είναι πεπερασμένο ζω =Το oo είναι ένα αφαιρούμενο ενικό σημείο της συνάρτησης /(r). Αν βάλουμε /(οο) = λιμ J(z)= 0, λοιπόν f(z)θα γίνει αναλυτική

τικ στο σημείο Ζω= os. Ας υποδείξουμε πώς να βρείτε την αντίστοιχη επέκταση (26.7). Ας προχωρήσουμε στη μεταβλητή w = 1 fz.Αντικατάσταση z= 1 /?е, παίρνουμε

(η τελευταία ισότητα ισχύει σε μια διάτρητη γειτονιά του σημείου wо = 0, αλλά θα ορίσουμε περαιτέρω το (7(0) = 0). Η συνάρτηση που προκύπτει έχει μοναδικά σημεία w =±i, w =-1/3, και στο σημείο Το Wq = 0 είναι αναλυτικό. Λειτουργία ξεδίπλωσης G(w)κατά βαθμούς w(όπως έγινε στο παράδειγμα 25.7) και αντικαθιστώντας το προκύπτον σειρά ισχύος w = 1/z,μπορούμε να λάβουμε την επέκταση (26.7) της συνάρτησης f(z).

Θεώρημα 26.3 για την περίπτωση zo= oo θα ξαναγραφεί με την παρακάτω μορφή.

Θεώρημα 26.12. Απομονωμένο ενικό σημείοου = ος Η συνάρτηση f(z) είναι ένας πόλος εάν και μόνο εάν το κύριο μέρος της επέκτασης Laurent (26.6) έχει μόνο έναν πεπερασμένο αριθμό μη μηδενικών συντελεστώνΜε":

Εδώ η σειρά είναι το κανονικό μέρος και το πολυώνυμο σε αγκύλες είναι το κύριο μέρος της επέκτασης. Η πολλαπλότητα των πόλων στο oc ορίζεται ως η πολλαπλότητα των πόλων wq = 0 συναρτήσεις G(z).Είναι εύκολο να δούμε ότι η πολλαπλότητα του πόλου συμπίπτει με τον αριθμό Νσε (26,8).

Q p | (i 2 + 1)(z+3) 2

Εργο. Δείξτε ότι η συνάρτηση f(z) =-- -- έχει μέσα

σημείο ζω = oo πόλος τάξης 3.

Το θεώρημα 26.6 σε ένα ουσιαστικά μοναδικό σημείο μπορεί να ξαναγραφτεί για την περίπτωση zo= os σχεδόν αυτολεξεί, και δεν μένουμε αναλυτικά σε αυτό.

Μοντέλα που περιγράφονται από συστήματα δύο αυτόνομων διαφορικές εξισώσεις.

Επίπεδο φάσης. Πορτρέτο φάσης. Μέθοδος Isoclin. Κύριες ισοκλίνες. Βιωσιμότητα σταθερή κατάσταση. Γραμμικά συστήματα. Τύποι μοναδικών σημείων: κόμβος, σέλα, εστίαση, κέντρο. Παράδειγμα: χημικές αντιδράσειςπρώτη σειρά.

Τα πιο ενδιαφέροντα αποτελέσματα σχετικά με την ποιοτική μοντελοποίηση των ιδιοτήτων των βιολογικών συστημάτων προέκυψαν χρησιμοποιώντας μοντέλα δύο διαφορικών εξισώσεων που επιτρέπουν ποιοτική έρευναχρησιμοποιώντας τη μέθοδο επίπεδο φάσης. Θεωρήστε ένα σύστημα δύο αυτόνομων συνηθισμένων διαφορικών εξισώσεων γενική εικόνα

(4.1)

P(x,y), Q(x,y)- συνεχείς λειτουργίες, που ορίζεται σε κάποια περιοχή σολΕυκλείδειο επίπεδο ( x,y- Καρτεσιανές συντεταγμένες) και έχοντας σε αυτή την περιοχή συνεχείς παραγώγους τάξης όχι χαμηλότερες από την πρώτη.

Περιοχή σολμπορεί να είναι είτε απεριόριστο είτε περιορισμένο. Αν οι μεταβλητές x, yέχουν συγκεκριμένη βιολογική σημασία (συγκεντρώσεις ουσιών, αριθμός ειδών) τις περισσότερες φορές η περιοχή σολαντιπροσωπεύει το θετικό τεταρτημόριο του δεξιού ημιεπιπέδου:

0 £ Χ< ¥ ,0 £ y< ¥ .

Οι συγκεντρώσεις ουσιών ή ο αριθμός των ειδών μπορεί επίσης να περιοριστεί από πάνω από τον όγκο του σκάφους ή την περιοχή του οικοτόπου. Τότε το εύρος των μεταβλητών έχει τη μορφή:

0 £ Χ< x 0 , 0 £ y< y 0 .

Μεταβλητές x, yαλλαγή στο χρόνο σύμφωνα με το σύστημα των εξισώσεων (4.1), έτσι ώστε κάθε κατάσταση του συστήματος να αντιστοιχεί σε ένα ζεύγος μεταβλητών τιμών ( x, y).

Αντίθετα, κάθε ζεύγος μεταβλητών ( x, y) αντιστοιχεί ορισμένη κατάστασησυστήματα.

Θεωρήστε ένα επίπεδο με άξονες συντεταγμένων στο οποίο απεικονίζονται οι τιμές των μεταβλητών x,y. Κάθε σημείο Μαυτό το επίπεδο αντιστοιχεί σε μια ορισμένη κατάσταση του συστήματος. Αυτό το επίπεδο ονομάζεται επίπεδο φάσης και αντιπροσωπεύει το σύνολο όλων των καταστάσεων του συστήματος. Το σημείο M(x,y) ονομάζεται σημείο που αναπαριστά ή αναπαριστά.

Αφήνω μέσα στιγμή έναρξηςχρόνος t=t 0 συντεταγμένες του αντιπροσωπευτικού σημείου Μ 0 (Χ(t 0), y(t 0)). Σε κάθε επόμενη χρονική στιγμή tτο αντιπροσωπευτικό σημείο θα μετατοπιστεί σύμφωνα με τις αλλαγές στις τιμές των μεταβλητών Χ(t), y(t). Συλλογή πόντων Μ(Χ(t), y(t)) στο επίπεδο φάσης, η θέση του οποίου αντιστοιχεί στις καταστάσεις του συστήματος στη διαδικασία αλλαγής των μεταβλητών με την πάροδο του χρόνου x(t), y(t)σύμφωνα με τις εξισώσεις (4.1), καλείται τροχιά φάσης.

Το σύνολο των τροχιών φάσης για διαφορετικές αρχικές τιμές των μεταβλητών δίνει ένα εύκολα ορατό «πορτρέτο» του συστήματος. Κατασκευή πορτρέτο φάσηςσας επιτρέπει να βγάλετε συμπεράσματα σχετικά με τη φύση των αλλαγών στις μεταβλητές x, yχωρίς γνώση αναλυτικών λύσεων του αρχικού συστήματος εξισώσεων(4.1).

Για να απεικονιστεί ένα πορτρέτο φάσης, είναι απαραίτητο να κατασκευαστεί ένα διανυσματικό πεδίο κατευθύνσεων των τροχιών του συστήματος σε κάθε σημείο του επιπέδου φάσης. Ρύθμιση της αύξησηςρε t>0,παίρνουμε τις αντίστοιχες προσαυξήσεις ρε ΧΚαι ρε yαπό εκφράσεις:

ρε x=P(x,y)ρε t,

ρε y=Q(x,y)ρε t.

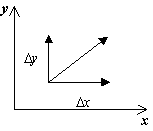
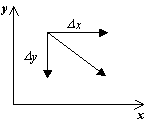
Διάνυσμα κατεύθυνση dy/dxστο σημείο ( x, y) εξαρτάται από το πρόσημο των συναρτήσεων P(x, y), Q(x, y)και μπορεί να δοθεί από έναν πίνακα:

P(x,y)>0,Q(x,y)>0
P(x,y)<0,Q(x,y)<0
P(x,y)>0,Q(x,y)<0
P(x,y)<0,Q(x,y)>0

.(4.2)

Λύση αυτής της εξίσωσης y = y(x,c), ή σιωπηρά φά(x,y)=c,Οπου Με– σταθερά ολοκλήρωσης, δίνει την οικογένεια των ολοκληρωτικών καμπυλών της εξίσωσης (4.2) - τροχιές φάσηςσύστημα (4.1) στο αεροπλάνο x, y.

Μέθοδος ισοκλίνης

Για να κατασκευάσουν ένα πορτρέτο φάσης χρησιμοποιούν ισοκλινή μέθοδος -σχεδιάζονται γραμμές στο επίπεδο φάσης που τέμνουν τις ακέραιες καμπύλες σε μια συγκεκριμένη γωνία. Η ισοκλινή εξίσωση μπορεί να ληφθεί εύκολα από το (4.2). Ας βάλουμε

Οπου ΕΝΑ– μια ορισμένη σταθερή τιμή. Εννοια ΕΝΑαντιπροσωπεύει την εφαπτομένη της γωνίας κλίσης της εφαπτομένης στην τροχιά φάσης και μπορεί να πάρει τιμές από -¥ σε + ¥ . Αντικατάσταση dy/dxστο (4.2) την ποσότητα ΕΝΑπαίρνουμε την ισοκλινή εξίσωση:

.(4.3)

Η εξίσωση (4.3) ορίζει σε κάθε σημείο του επιπέδου μια μοναδική εφαπτομένη στην αντίστοιχη ολοκληρωτική καμπύλη, με εξαίρεση το σημείο όπου P(x,y)= 0, Q (x,y) = 0 , στην οποία η κατεύθυνση της εφαπτομένης γίνεται αβέβαιη, αφού η τιμή της παραγώγου γίνεται αβέβαιη:

.

Αυτό το σημείο είναι το σημείο τομής όλων των ισοκλινών - ειδικό σημείο.Σε αυτό, οι χρονικές παράγωγοι των μεταβλητών εξαφανίζονται ταυτόχρονα ΧΚαι y.

Έτσι, σε ένα μοναδικό σημείο, οι ρυθμοί μεταβολής των μεταβλητών είναι μηδενικοί. Συνεπώς, το μοναδικό σημείο των διαφορικών εξισώσεων των τροχιών φάσης (4.2) αντιστοιχεί σε στατική κατάσταση του συστήματος(4.1), και οι συντεταγμένες του είναι οι σταθερές τιμές των μεταβλητών x, y.

Ιδιαίτερο ενδιαφέρον παρουσιάζουν κύριες ισοκλίνες:

dy/dx=0, P(x,y)=0 – ισοκλίνη οριζόντιων εφαπτομένων και

dy/dx=¥ , Ε(x,y)=0 – ισοκλίνη κάθετων εφαπτομένων.

Κατασκευάζοντας τις κύριες ισοκλίνες και βρίσκοντας το σημείο τομής τους (x,y), των οποίων οι συντεταγμένες πληρούν τις προϋποθέσεις:

θα βρούμε έτσι το σημείο τομής όλων των ισοκλινών του επιπέδου φάσης, στο οποίο η κατεύθυνση των εφαπτομένων στις τροχιές φάσης είναι αβέβαιη. Αυτό - μοναδικό σημείο, που αντιστοιχεί στατική κατάσταση του συστήματος(Εικ. 4.2).

Το σύστημα (4.1) έχει τόσες ακίνητες καταστάσεις όσα σημεία τομής των κύριων ισοκλινών στο επίπεδο φάσης.

Κάθε τροχιά φάσης αντιστοιχεί σε ένα σύνολο κινήσεων ενός δυναμικού συστήματος, που διέρχεται από τις ίδιες καταστάσεις και διαφέρει μεταξύ τους μόνο στην αρχή της μέτρησης του χρόνου.

Εάν ικανοποιούνται οι προϋποθέσεις του θεωρήματος του Cauchy, τότε μέσω κάθε σημείου του χώρου x, y, tυπάρχει μόνο μία ολοκληρωμένη καμπύλη. Το ίδιο ισχύει, λόγω αυτονομίας, για τις τροχιές φάσης: μια μονοφασική τροχιά διέρχεται από κάθε σημείο του επιπέδου φάσης.

Σταθερότητα σταθερής κατάστασης

Αφήστε το σύστημα να βρίσκεται σε κατάσταση ισορροπίας.

Τότε το αντιπροσωπευτικό σημείο βρίσκεται σε ένα από τα μοναδικά σημεία του συστήματος, στο οποίο, εξ ορισμού:

.

Το αν ένα μοναδικό σημείο είναι σταθερό ή όχι καθορίζεται από το εάν το σημείο που αναπαριστά φεύγει ή όχι με μια μικρή απόκλιση από τη στατική κατάσταση. Σε σχέση με ένα σύστημα δύο εξισώσεων, ο ορισμός της σταθερότητας στη γλώσσαμι, ρεως εξής.

Η κατάσταση ισορροπίας είναι σταθερή εάν για οποιοδήποτε δεδομένο εύρος αποκλίσεων από την κατάσταση ισορροπίας (μι )μπορείτε να καθορίσετε την περιοχή ρε (μι ), που περιβάλλει την κατάσταση ισορροπίας και έχει την ιδιότητα ότι δεν υπάρχει τροχιά που ξεκινά μέσα στην περιοχή ρε , δεν θα φτάσει ποτέ στα σύνορα μι . (Εικ. 4.4)

Για μια μεγάλη κατηγορία συστημάτων - πρόχειρα συστήματα – η φύση της συμπεριφοράς των οποίων δεν αλλάζει με μια μικρή αλλαγή στη μορφή των εξισώσεων, πληροφορίες σχετικά με τον τύπο συμπεριφοράς κοντά σε μια στατική κατάσταση μπορούν να ληφθούν εξετάζοντας όχι την αρχική, αλλά μια απλοποιημένη γραμμικοποιημένηΣύστημα.

Γραμμικά συστήματα.

Σκεφτείτε ένα σύστημα δύο γραμμικές εξισώσεις:

.(4.4)

Εδώ Α Β Γ Δ- σταθερές, x, y- Καρτεσιανές συντεταγμένες στο επίπεδο φάσης.

Θα αναζητήσουμε μια γενική λύση με τη μορφή:

.(4.5)

Ας αντικαταστήσουμε αυτές τις εκφράσεις στην (4.4) και ας μειώσουμε κατά μι μεγάλο t:

(4.6)

Αλγεβρικό σύστημα εξισώσεων (4.6) με αγνώστους Α, Βέχει μη μηδενική λύση μόνο αν η ορίζοντή της, που αποτελείται από συντελεστές για τους αγνώστους, είναι ίση με μηδέν:

.

Επεκτείνοντας αυτήν την ορίζουσα, λαμβάνουμε τη χαρακτηριστική εξίσωση του συστήματος:

.(4.7)

Η επίλυση αυτής της εξίσωσης δίνει τις τιμές των εκθετώνμεγάλο 1,2 , για τις οποίες είναι δυνατές μη μηδενικές τιμές ΕΝΑΚαι σιλύσεις της εξίσωσης (4.6). Αυτές οι έννοιες είναι

.(4.8)

Εάν η ριζική έκφραση είναι αρνητική, τότεμεγάλο 1,2 μιγαδικοί συζυγείς αριθμοί. Ας υποθέσουμε ότι και οι δύο ρίζες της εξίσωσης (4.7) έχουν μη μηδενικά πραγματικά μέρη και ότι δεν υπάρχουν πολλαπλές ρίζες. Τότε η γενική λύση του συστήματος (4.4) μπορεί να αναπαρασταθεί ως ένας γραμμικός συνδυασμός εκθετικών με εκθέτεςμεγάλο 1 , μεγάλο 2 :

(4.9)

Για να αναλύσουμε τη φύση των πιθανών τροχιών του συστήματος στο επίπεδο φάσης, χρησιμοποιούμε γραμμικός ομογενής μετασχηματισμός συντεταγμένων,που θα οδηγήσει το σύστημα σε κανονική μορφή:

,(4.10)

επιτρέποντας μια πιο βολική αναπαράσταση στο επίπεδο φάσης σε σύγκριση με το αρχικό σύστημα (4.4). Ας εισάγουμε νέες συντεταγμένεςξ , η σύμφωνα με τους τύπους:

(4.1)

Από την πορεία της γραμμικής άλγεβρας είναι γνωστό ότι στην περίπτωση της ανισότητας προς μηδέν τα πραγματικά μέρημεγάλο 1 , μεγάλο 2 το αρχικό σύστημα (4.4) μπορεί πάντα να μετασχηματιστεί χρησιμοποιώντας μετασχηματισμούς (4.11) στην κανονική μορφή (4.10) και η συμπεριφορά του στο επίπεδο φάσης μπορεί να μελετηθείξ , η . Ας εξετάσουμε τις διάφορες περιπτώσεις που μπορεί να παρουσιαστούν εδώ.

Ρίζες λ 1 , λ 2 – ισχύει και του ίδιου σημείου

Σε αυτή την περίπτωση οι συντελεστές μετασχηματισμού είναι πραγματικοί, μετακινούμαστε από το πραγματικό επίπεδοx,yστο πραγματικό επίπεδο ξ, η. Διαιρώντας τη δεύτερη των εξισώσεων (4.10) με την πρώτη, προκύπτει:

.(4.12)

Ενσωματώνοντας αυτή την εξίσωση, βρίσκουμε:

Όπου .(4.13)

Ας συμφωνήσουμε να καταλάβουμε από το λ 2 η ρίζα της χαρακτηριστικής εξίσωσης με μεγάλο συντελεστή, που δεν παραβιάζει τη γενικότητα του συλλογισμού μας. Τότε, αφού στην υπό εξέταση περίπτωση οι ρίζες λ 1 , λ 2 – ισχύει και του ίδιου σημείου,ένα>1 , και έχουμε να κάνουμε με ολοκληρωτικές καμπύλες παραβολικού τύπου.

Όλες οι ακέραιες καμπύλες (εκτός από τον άξονα η , που αντιστοιχεί σε ) άγγιγμα στην αρχή του άξονα ξ, που είναι και η ολοκληρωτική καμπύλη της εξίσωσης (4.11). Η προέλευση των συντεταγμένων είναι ένα ιδιαίτερο σημείο.

Ας μάθουμε τώρα την κατεύθυνση κίνησης του αντιπροσωπευτικού σημείου κατά μήκος των τροχιών φάσης. Αν λ 1 , λ 2 είναι αρνητικά, λοιπόν, όπως φαίνεται από τις εξισώσεις (4.10), |ξ|, |η| μειώνονται με την πάροδο του χρόνου. Το αντιπροσωπευτικό σημείο πλησιάζει την αρχή των συντεταγμένων, αλλά ποτέ, ωστόσο, δεν φτάνει σε αυτήν. Διαφορετικά, αυτό θα έρχονταν σε αντίθεση με το θεώρημα του Cauchy, το οποίο δηλώνει ότι μόνο μία τροχιά φάσης διέρχεται από κάθε σημείο του επιπέδου φάσης.

Ένα τόσο ιδιαίτερο σημείο από το οποίο περνούν οι ακέραιες καμπύλες, όπως μια οικογένεια παραβολών διέρχεται από την αρχή και ονομάζεται κόμβος (Εικ. 4.5)

Κατάσταση ισορροπίας τύπου κόμβου στο λ 1 , λ 2 < 0 είναι ο Lyapunov σταθερός, αφού το σημείο που αναπαριστά κινείται κατά μήκος όλων των ολοκληρωτικών καμπυλών προς την αρχή των συντεταγμένων. Αυτό σταθερός κόμπος. Αν λ 1 , λ 2 > 0, λοιπόν |ξ|, |η| αυξάνεται με την πάροδο του χρόνου και το αντιπροσωπευτικό σημείο απομακρύνεται από την αρχή των συντεταγμένων. Σε αυτή την περίπτωση, το ειδικό σημείο– ασταθής κόμβος .

Στο επίπεδο φάσης x, y Η γενική ποιοτική φύση της συμπεριφοράς των ολοκληρωτικών καμπυλών θα διατηρηθεί, αλλά οι εφαπτομένες στις ολοκληρωτικές καμπύλες δεν θα συμπίπτουν με τους άξονες συντεταγμένων. Η γωνία κλίσης αυτών των εφαπτομένων θα καθοριστεί από τον λόγο των συντελεστών α , β , γ , δ στις εξισώσεις (4.11).

Ρίζες λ 1 , λ 2 – είναι έγκυρα και διαφορετικών σημείων.

Μετατροπή απόσυντεταγμένες x,y στις συντεταγμένες ξ, η πάλι αληθινό. Οι εξισώσεις για τις κανονικές μεταβλητές έχουν πάλι τη μορφή (4.10), αλλά τώρα τα πρόσημα του λ 1 , λ 2 είναι διαφορετικά. Η εξίσωση των τροχιών φάσης έχει τη μορφή:

Όπου, (4.14)

Ενσωματώνοντας (4.14), βρίσκουμε

(4.15)

Αυτό η εξίσωση ορίζει μια οικογένεια καμπυλών υπερβολικού τύπου, όπου και οι δύο άξονες συντεταγμένων– ασύμπτωτες (στο ένα=1 θα είχαμε μια οικογένεια ισόπλευρων υπερβολών). Οι άξονες συντεταγμένων σε αυτή την περίπτωση είναι επίσης αναπόσπαστες καμπύλες– Αυτές θα είναι οι μόνες ολοκληρωμένες καμπύλες που θα περνούν από την αρχή. Καθεεκ των οποίων αποτελείται από τρεις τροχιές φάσεων: δύο κινήσεων σε κατάσταση ισορροπίας (ή από κατάσταση ισορροπίας) και από κατάσταση ισορροπίας. Όλες οι άλλες ακέραιες καμπύλες– είναι υπερβολές που δεν διέρχονται από την αρχή (Εικ. 4.6) Αυτό το ειδικό σημείο ονομάζεται "σαμάρι ». Οι γραμμές στάθμης κοντά σε μια σέλα βουνού συμπεριφέρονται παρόμοια με τις τροχιές φάσης κοντά σε μια σέλα.

Ας εξετάσουμε τη φύση της κίνησης του αντιπροσωπευτικού σημείου κατά μήκος των τροχιών φάσης κοντά στην κατάσταση ισορροπίας. Ας, για παράδειγμα,λ 1 >0 , λ 2<0 . Στη συνέχεια το αντιπροσωπευτικό σημείο τοποθετείται στον άξονα ξ , θα απομακρυνθεί από την αρχή και θα τοποθετηθεί στον άξονα η – θα προσεγγίζει επ' αόριστον την αρχή των συντεταγμένων, χωρίς να το φτάσω σε πεπερασμένο χρόνο. Όπου το αντιπροσωπευτικό σημείο βρίσκεται στην αρχική στιγμή (με εξαίρεση το ενικό σημείο και τα σημεία στην ασύμπτωτη η =0), τελικά θα απομακρυνθεί από την κατάσταση ισορροπίας, ακόμα κι αν αρχικά κινηθεί κατά μήκος μιας από τις ακέραιες καμπύλες προς το μοναδικό σημείο.

Είναι προφανές ότι ένα μοναδικό σημείο όπως η σέλα είναι πάντα ασταθές . Μόνο κάτω από ειδικά επιλεγμένες αρχικές συνθήκες στην ασύμπτωτηη =0 το σύστημα θα πλησιάσει σε κατάσταση ισορροπίας. Ωστόσο, αυτό δεν έρχεται σε αντίθεση με τη δήλωση σχετικά με την αστάθεια του συστήματος. Αν μετρήσουμε, ότι όλες οι αρχικές καταστάσεις του συστήματος στο επίπεδο φάσης είναι εξίσου πιθανές, τότε η πιθανότητα μιας τέτοιας αρχικής κατάστασης που αντιστοιχεί στην κίνηση προς την κατεύθυνσηΠρος την ενικό σημείο είναι ίσο με μηδέν. Επομένως, οποιαδήποτε πραγματική κίνηση θα απομακρύνει το σύστημα από την κατάσταση ισορροπίας.Επιστρέφοντας στις συντεταγμένεςx,y,θα πάρουμε την ίδια ποιοτική εικόνα για τη φύση της κίνησης των τροχιών γύρω από την αρχή των συντεταγμένων.

Το όριο μεταξύ των εξεταζόμενων περιπτώσεων ενός κόμβου και μιας σέλας είναι η περίπτωσηΟταν ένας από τους χαρακτηριστικούς δείκτες, για παράδειγμα λ 1 , εξαφανίζεται, το οποίο συμβαίνει όταν ο καθοριστικός παράγοντας του συστήματος- έκφραση ad-bc=0(βλ. τύπο 4.8 ). Στην περίπτωση αυτή, οι συντελεστές των δεξιών πλευρών των εξισώσεων (4.4) είναι ανάλογοι μεταξύ τους:

και το σύστημα έχει ως κατάσταση ισορροπίας όλα τα σημεία της ευθείας:

Οι υπόλοιπες ολοκληρωτικές καμπύλες είναι μια οικογένεια παράλληλων ευθειών με γωνιακό συντελεστή , κατά μήκος των οποίων τα αντιπροσωπευτικά σημεία είτε πλησιάζουν την κατάσταση ισορροπίας είτε απομακρύνονται από αυτήν, ανάλογα με το πρόσημο της δεύτερης ρίζας της χαρακτηριστικής εξίσωσης λ 2 = α+δ.(Εικ.4. 7 ) Σε αυτή την περίπτωση, οι συντεταγμένες της κατάστασης ισορροπίας εξαρτώνται από την αρχική τιμή των μεταβλητών.

Ρίζες λ 1 , λ 2 – συγκρότημακλίνω

Στην προκειμένη περίπτωση, στην πραγματικότηταΧΚαι yεμείς θα έχουν πολύπλοκα συζυγή ξ , η (4.10) . Ωστόσο, με την εισαγωγή ενός άλλου ενδιάμεσου μετασχηματισμού, είναι επίσης δυνατό σε αυτήν την περίπτωση να μειωθεί η θεώρηση σε έναν πραγματικό γραμμικό ομογενή μετασχηματισμό. Ας βάλουμε:

(4.16)

Οπου α, β,Και u,v – πραγματικές αξίες. Μπορεί να αποδειχθεί ότι ο μετασχηματισμός απόx,yΠρος την u,v είναι, σύμφωνα με τις υποθέσεις μας, πραγματικό, γραμμικό, ομοιογενές με μια ορίζουσα διαφορετική από το μηδέν. Δυνάμει των εξισώσεων(4.10, 4.16) έχουμε:

που

(4.17)

Διαιρώντας τη δεύτερη από τις εξισώσεις με την πρώτη, παίρνουμε:

που είναι πιο εύκολο να ενσωματωθεί, αν πάμε στο πολικό σύστημα συντεταγμένων (r, φ ) . Μετά την αντικατάστασηπαίρνουμε από πού:

.(4.18)

Έτσι, στο επίπεδο φάσηςu, vέχουμε να κάνουμε με μια οικογένεια λογαριθμικών σπειρών, καθεμία από τις οποίες έχειασυμπτωτικό σημείο στην αρχή.Ένα μοναδικό σημείο, το οποίο είναι το ασυμπτωτικό σημείο όλων των ολοκληρωτικών καμπυλών που έχουν τη μορφή σπειρών, φωλιασμένο στο καθέναφίλε, λέγεται Συγκεντρώνω ( Εικ.4.8 ) .

Ας εξετάσουμε τη φύση της κίνησης του αντιπροσωπευτικού σημείου κατά μήκος τροχιών φάσης. Πολλαπλασιάζοντας την πρώτη από τις εξισώσεις (4.17) μεu, και το δεύτερο επάνω vκαι προσθέτοντας, παίρνουμε:

Οπου

Αφήνω ένα 1 < 0 (ένα 1 = Σχετικά μελ ) . Στη συνέχεια, το σημείο αναπαράστασης προσεγγίζει συνεχώς την αρχή των συντεταγμένων χωρίς να φτάσει σε αυτήν σε έναν πεπερασμένο χρόνο. Αυτό σημαίνει ότι οι τροχιές φάσης είναι περιστρεφόμενες σπείρες και αντιστοιχούν σε αποσβεσμένες ταλαντώσειςμεταβλητές. Αυτό - σταθερή εστίαση .

Στην περίπτωση μιας σταθερής εστίασης, όπως και στην περίπτωση ενός σταθερού κόμβου, δεν ικανοποιείται μόνο η συνθήκη Lyapunov, αλλά και μια πιο αυστηρή απαίτηση. Δηλαδή, για οποιεσδήποτε αρχικές αποκλίσεις, το σύστημα, με την πάροδο του χρόνου, θα επιστρέψει όσο πιο κοντά είναι επιθυμητό στη θέση ισορροπίας. Μια τέτοια σταθερότητα, στην οποία οι αρχικές αποκλίσεις όχι μόνο δεν αυξάνονται, αλλά αποσυντίθενται, τείνοντας στο μηδέν, ονομάζεται απόλυτη σταθερότητα .

Αν στον τύπο (4.18) ένα 1 >0 , τότε το αντιπροσωπευτικό σημείο απομακρύνεται από την προέλευση, και έχουμε να κάνουμε με ασταθής εστίαση . Κατά τη μετακίνηση από αεροπλάνοu,vστο επίπεδο φάσηςΧ, yοι σπείρες θα παραμείνουν επίσης σπείρες, αλλά θα παραμορφωθούν.

Ας εξετάσουμε τώρα την περίπτωση ότανένα 1 =0 . Τροχιές φάσης στο αεροπλάνοu, vθα υπάρχουν κύκλοι που στο αεροπλάνοx,yαντιστοιχούν σε ελλείψεις:

Έτσι, ότανΑ'1=0 μέσω ειδικού σημείουx= 0, y= 0 δεν διέρχεται ολοκληρωτική καμπύλη. Ένα τέτοιο απομονωμένο ενιαίο σημείο, κοντά στο οποίο οι ολοκληρωτικές καμπύλες είναι κλειστές καμπύλες, ειδικότερα, ελλείψεις ενσωματωμένες μεταξύ τους και περικλείουν το μοναδικό σημείο, ονομάζεται κέντρο.

Έτσι, είναι δυνατοί έξι τύποι καταστάσεων ισορροπίας, ανάλογα με τη φύση των ριζών της χαρακτηριστικής εξίσωσης (4.7). Άποψη των τροχιών φάσης σε ένα επίπεδο x, yγια αυτές τις έξι περιπτώσεις φαίνεται στο Σχ. 4.9.

Ρύζι. 4.9.Τύποι πορτραίτων φάσης κοντά σε ακίνητη κατάσταση για σύστημα γραμμικών εξισώσεων (4.4).

Οι πέντε τύποι καταστάσεων ισορροπίας είναι πρόχειρες· ο χαρακτήρας τους δεν αλλάζει με αρκετά μικρές αλλαγές στη δεξιά πλευρά των εξισώσεων (4.4). Σε αυτήν την περίπτωση, οι αλλαγές όχι μόνο στις δεξιές πλευρές, αλλά και στα παράγωγα πρώτης τάξης τους θα πρέπει να είναι μικρές. Η έκτη κατάσταση ισορροπίας – το κέντρο – δεν είναι τραχιά. Με μικρές αλλαγές στις παραμέτρους της δεξιάς πλευράς των εξισώσεων, γίνεται σταθερή ή ασταθής εστίαση.

Διάγραμμα διακλάδωσης

Ας εισάγουμε τον ακόλουθο συμβολισμό:

. (4.11)

Τότε η χαρακτηριστική εξίσωση θα γραφτεί ως:

. (4.12)

Θεωρήστε ένα επίπεδο με ορθογώνιες καρτεσιανές συντεταγμένες μικρό , ρε και σημειώστε πάνω του τις περιοχές που αντιστοιχούν σε έναν ή τον άλλο τύπο κατάστασης ισορροπίας, η οποία καθορίζεται από τη φύση των ριζών της χαρακτηριστικής εξίσωσης

.(4.13)

Προϋπόθεση για τη σταθερότητα της κατάστασης ισορροπίας θα είναι η παρουσία αρνητικού πραγματικού μέρους του yμεγάλο 1 και μεγάλο 2 . Απαραίτητη και επαρκής προϋπόθεση για αυτό είναι η εκπλήρωση των ανισοτήτωνμικρό > 0, ρε > 0 . Στο διάγραμμα (4.15), αυτή η συνθήκη αντιστοιχεί σε σημεία που βρίσκονται στο πρώτο τέταρτο του επιπέδου παραμέτρων. Ένα μοναδικό σημείο θα είναι μια εστίαση ανμεγάλο 1 και μεγάλο 2 συγκρότημα. Αυτή η συνθήκη αντιστοιχεί σε εκείνα τα σημεία του επιπέδου για τα οποία , εκείνοι. σημεία ανάμεσα σε δύο κλάδους μιας παραβολήςμικρό 2 = 4 ρε. Σημεία άξονα μικρό = 0, ρε>0, αντιστοιχούν σε καταστάσεις ισορροπίας του τύπου κέντρου. Επίσης,μεγάλο 1 και μεγάλο 2 - ισχύουν, αλλά διαφορετικών σημείων, δηλ. ένα μοναδικό σημείο θα είναι μια σέλα αν ρε<0, και τα λοιπά. Ως αποτέλεσμα, παίρνουμε ένα διάγραμμα του διαμερίσματος του επιπέδου παραμέτρων μικρό, ρε, σε περιοχές που αντιστοιχούν σε διαφορετικούς τύπους καταστάσεων ισορροπίας.

Ρύζι. 4.10.Διάγραμμα διακλάδωσης

για σύστημα γραμμικών εξισώσεων 4.4

Αν οι συντελεστές του γραμμικού συστήματος Α Β Γ Δεξαρτώνται από μια συγκεκριμένη παράμετρο, τότε όταν αλλάξει αυτή η παράμετρος, θα αλλάξουν και οι τιμέςμικρό , ρε . Κατά τη διέλευση των ορίων, ο χαρακτήρας του πορτραίτου φάσης αλλάζει ποιοτικά. Επομένως, τέτοια όρια ονομάζονται όρια διακλάδωσης - στις απέναντι πλευρές του ορίου, το σύστημα έχει δύο τοπολογικά διαφορετικά πορτρέτα φάσης και, κατά συνέπεια, δύο διαφορετικούς τύπους συμπεριφοράς.

Το διάγραμμα δείχνει πώς μπορούν να συμβούν τέτοιες αλλαγές. Εάν εξαιρέσουμε ειδικές περιπτώσεις - την προέλευση των συντεταγμένων - τότε είναι εύκολο να δούμε ότι η σέλα μπορεί να μετατραπεί σε κόμβο, σταθερό ή ασταθές κατά τη διέλευση του άξονα τεταγμένων. Ένας σταθερός κόμπος μπορεί να μπει είτε σε μια σέλα είτε σε μια σταθερή εστίαση κ.λπ. Σημειώστε ότι οι μεταβάσεις σταθερός κόμβος - σταθερή εστίαση και ασταθής κόμβος - ασταθής εστίαση δεν είναι διακλαδώσεις, αφού η τοπολογία του χώρου φάσης δεν αλλάζει. Θα μιλήσουμε περισσότερα για την τοπολογία του χώρου φάσης και τις μεταβάσεις διακλάδωσης στη Διάλεξη 6.

Κατά τη διάρκεια των διακλαδώσεων μεταβάσεων, η φύση της σταθερότητας ενός μοναδικού σημείου αλλάζει. Για παράδειγμα, μια σταθερή εστίαση μέσω του κέντρου μπορεί να μετατραπεί σε ασταθή εστίαση. Αυτή η διχοτόμηση ονομάζεται Διχοτόμηση Andronov-Hopfμε τα ονόματα των επιστημόνων που το μελέτησαν. Κατά τη διάρκεια αυτής της διακλάδωσης σε μη γραμμικά συστήματα, γεννιέται ένας οριακός κύκλος και το σύστημα γίνεται αυτοταλαντούμενο (βλ. Διάλεξη 8).

Παράδειγμα. Σύστημα γραμμικής χημικής αντίδρασης

Ουσία Χρέει από έξω με σταθερή ταχύτητα, μετατρέπεται σε ουσία Υ και με ταχύτητα ανάλογη της συγκέντρωσης της ουσίας Υ, αφαιρείται από τη σφαίρα της αντίδρασης. Όλες οι αντιδράσεις είναι πρώτης τάξης, με εξαίρεση την εισροή ουσίας από το εξωτερικό, η οποία είναι μηδενικής τάξης. Το σχήμα αντίδρασης μοιάζει με:

(4.14)

και περιγράφεται από το σύστημα εξισώσεων:

(4.15)

Λαμβάνουμε σταθερές συγκεντρώσεις εξισώνοντας τις δεξιές πλευρές με μηδέν:

.(4.16)

Ας εξετάσουμε το πορτρέτο φάσης του συστήματος. Ας διαιρέσουμε τη δεύτερη εξίσωση του συστήματος (4.16) με την πρώτη. Παίρνουμε:

.(4.17)

Η εξίσωση (4.17) καθορίζει τη συμπεριφορά των μεταβλητών στο επίπεδο φάσης. Ας κατασκευάσουμε ένα πορτρέτο φάσης αυτού του συστήματος. Αρχικά, ας σχεδιάσουμε τις κύριες ισοκλίνες στο επίπεδο φάσης. Εξίσωση ισοκλινής κάθετης εφαπτομένης:

Εξίσωση ισοκλινής οριζόντιων εφαπτομένων:

Το ενικό σημείο (στάσιμη κατάσταση) βρίσκεται στη διασταύρωση των κύριων ισοκλινών.

Τώρα ας προσδιορίσουμε σε ποια γωνία τέμνονται οι άξονες συντεταγμένων με τις ακέραιες καμπύλες.

Αν x= 0, τότε.

Έτσι, η εφαπτομένη της εφαπτομένης στις ακέραιες καμπύλες y=y(x),τέμνοντας τον άξονα τεταγμένων x=0, είναι αρνητικό στο πάνω μισό επίπεδο (θυμηθείτε ότι οι μεταβλητές x, yέχουν τιμές συγκέντρωσης και επομένως μας ενδιαφέρει μόνο το πάνω δεξιό τεταρτημόριο του επιπέδου φάσης). Σε αυτή την περίπτωση, η εφαπτομένη της γωνίας της εφαπτομένης αυξάνεται με την απόσταση από την αρχή.

Εξετάστε τον άξονα y= 0. Στο σημείο που αυτός ο άξονας τέμνει τις ολοκληρωτικές καμπύλες, αυτές περιγράφονται από την εξίσωση

Στο η εφαπτομένη της κλίσης των ολοκληρωτικών καμπυλών που διασχίζουν τον άξονα της τετμημένης είναι θετική και αυξάνεται από το μηδέν στο άπειρο με την αύξηση Χ.

Στο .

Στη συνέχεια, με περαιτέρω αύξηση, η εφαπτομένη της γωνίας κλίσης μειώνεται σε απόλυτη τιμή, παραμένοντας αρνητική και τείνει στο -1 στο Χ ® ¥ . Γνωρίζοντας την κατεύθυνση των εφαπτομένων στις ολοκληρωτικές καμπύλες στις κύριες ισοκλίνες και στους άξονες συντεταγμένων, είναι εύκολο να κατασκευαστεί ολόκληρη η εικόνα των τροχιών φάσης.

Ας καθορίσουμε τη φύση της σταθερότητας του μοναδικού σημείου χρησιμοποιώντας τη μέθοδο Lyapunov. Η χαρακτηριστική ορίζουσα του συστήματος έχει τη μορφή:

.

Διευρύνοντας την ορίζουσα, παίρνουμε τη χαρακτηριστική εξίσωση του συστήματος: , δηλ. Οι ρίζες της χαρακτηριστικής εξίσωσης είναι και οι δύο αρνητικές. Κατά συνέπεια, η στατική κατάσταση του συστήματος είναι ένας σταθερός κόμβος. Σε αυτή την περίπτωση, η συγκέντρωση της ουσίας Χτείνει σε ακίνητη κατάσταση πάντα μονότονα, η συγκέντρωση της ουσίας Υ μπορεί να περάσει από min ή max. Οι ταλαντωτικοί τρόποι είναι αδύνατοι σε ένα τέτοιο σύστημα.

Οι σειρές Taylor χρησιμεύουν ως αποτελεσματικό εργαλείο για τη μελέτη συναρτήσεων που είναι αναλυτικές σε κύκλο zol Για να μελετηθούν συναρτήσεις που είναι αναλυτικές σε έναν τομέα δακτυλίου, αποδεικνύεται ότι είναι δυνατό να κατασκευαστούν επεκτάσεις σε θετικές και αρνητικές δυνάμεις (z - zq) της μορφής που γενικεύουν τις επεκτάσεις Taylor. Η σειρά (1), που νοείται ως το άθροισμα δύο σειρών, ονομάζεται σειρά Laurent. Είναι σαφές ότι η περιοχή σύγκλισης της σειράς (1) είναι το κοινό μέρος των περιοχών σύγκλισης κάθε σειράς (2). Ας τη βρούμε. Η περιοχή σύγκλισης της πρώτης σειράς είναι ένας κύκλος του οποίου η ακτίνα καθορίζεται από τον τύπο Cauchy-Hadamard. Μέσα στον κύκλο σύγκλισης, η σειρά (3) συγκλίνει σε μια αναλυτική συνάρτηση και σε οποιονδήποτε κύκλο μικρότερης ακτίνας, συγκλίνει απόλυτα και ομοιόμορφα. Η δεύτερη σειρά είναι μια σειρά ισχύος ως προς μια μεταβλητή.Η σειρά (5) συγκλίνει εντός του κύκλου σύγκλισής της προς την αναλυτική συνάρτηση μιας σύνθετης μεταβλητής m-*oo, και σε οποιονδήποτε κύκλο μικρότερης ακτίνας συγκλίνει απόλυτα και ομοιόμορφα, η οποία σημαίνει ότι η περιοχή σύγκλισης της σειράς (4) είναι το εξωτερικό του κύκλου - Εάν τότε υπάρχει μια κοινή περιοχή σύγκλισης των σειρών (3) και (4) - ένας κυκλικός δακτύλιος στην οποία η σειρά (1) συγκλίνει σε μια αναλυτική συνάρτηση. Επιπλέον, σε οποιοδήποτε δακτύλιο, συγκλίνει απόλυτα και ομοιόμορφα. Παράδειγμα 1. Προσδιορίστε την περιοχή σύγκλισης της σειράς Rad Laurent Απομονωμένα μοναδικά σημεία και την ταξινόμησή τους M Η περιοχή σύγκλισης της πρώτης σειράς είναι το εξωτερικό του κύκλου και η περιοχή σύγκλισης της δεύτερης σειράς είναι το εσωτερικό του κύκλου. αυτή η σειρά συγκλίνει σε κύκλους Θεώρημα 15. Οποιαδήποτε συνάρτηση f (z), μονοσήμαντη και μη πολιτική σε έναν κυκλικό δακτύλιο μπορεί να αναπαρασταθεί σε αυτόν τον δακτύλιο ως το άθροισμα μιας συγκλίνουσας σειράς, οι συντελεστές Cn της οποίας προσδιορίζονται μοναδικά και υπολογίζονται σύμφωνα με τους τύπους όπου το 7p είναι ένας κύκλος ακτίνας m. Ας καθορίσουμε ένα αυθαίρετο σημείο z μέσα στον δακτύλιο R. Ας κατασκευάσουμε κύκλους με κέντρα στο σημείο r, οι ακτίνες των οποίων ικανοποιούν τις ανισώσεις και θεωρούμε έναν νέο δακτύλιο Χρησιμοποιώντας το ολοκληρωτικό θεώρημα του Cauchy για ένα πολλαπλασιαζόμενο πεδίο ορισμού, έχουμε Μετασχηματίζουμε ξεχωριστά καθένα από τα ολοκληρώματα στο άθροισμα (8). Για όλα τα σημεία £ κατά μήκος του κύκλου 7d* ικανοποιείται η σχέση αθροίσματος της ομοιόμορφα συγκλίνουσας σειράς 1 1. Επομένως, το κλάσμα ^ μπορεί να αναπαρασταθεί σε vi- / "/ Πολλαπλασιάζοντας και τα δύο μέρη με μια συνεχή συνάρτηση (O και πραγματοποιώντας ολοκλήρωση όρου προς όρο κατά μήκος του κύκλου, προκύπτει ότι πραγματοποιούμε τον μετασχηματισμό του δεύτερου ολοκληρώματος κάπως διαφορετικά. Για όλα τα σημεία £ στον κύκλο ir> ισχύει η σχέση. Επομένως, το κλάσμα ^ μπορεί να αναπαρασταθεί ως το άθροισμα του Πολλαπλασιάζοντας και τις δύο πλευρές με μια συνεχή συνάρτηση) και ολοκληρώνοντας κατά μήκος του κύκλου 7/, προκύπτει ότι τα ολοκληρώματα στους τύπους (10) και (12) είναι αναλυτικές συναρτήσεις σε έναν κυκλικό δακτύλιο. Επομένως, δυνάμει του θεωρήματος του Cauchy, οι τιμές των αντίστοιχων ολοκληρωμάτων δεν θα αλλάξουν εάν αντικαταστήσουμε τους κύκλους 7/r και 7r/ με οποιονδήποτε κύκλο. Αυτό μας επιτρέπει να συνδυάσουμε τους τύπους (10) και (12) Αντικαθιστώντας τα ολοκληρώματα στη δεξιά πλευρά του τύπου (8) με τις εκφράσεις τους (9) και (11), αντίστοιχα, λαμβάνουμε την απαιτούμενη επέκταση. Επειδή το z είναι αυθαίρετο σημείο του δακτυλίου, προκύπτει ότι η σειρά (14) συγκλίνει στη συνάρτηση f(z) παντού σε αυτόν τον δακτύλιο, και σε οποιοδήποτε δακτύλιο η σειρά συγκλίνει σε αυτή τη συνάρτηση απολύτως και ομοιόμορφα. Ας αποδείξουμε τώρα ότι η αποσύνθεση της μορφής (6) είναι μοναδική. Ας υποθέσουμε ότι υπάρχει μια ακόμη επέκταση.Τότε παντού μέσα στον δακτύλιο R θα έχουμε Στον κύκλο, οι σειρές (15) συγκλίνουν ομοιόμορφα. Ας πολλαπλασιάσουμε και τις δύο πλευρές της ισότητας (όπου m είναι ένας σταθερός ακέραιος αριθμός και ενσωματώνουμε και τις δύο σειρές όρο προς όρο. Ως αποτέλεσμα, λαμβάνουμε στην αριστερή πλευρά και στη δεξιά - Sch. Έτσι, (4, = St. Αφού Το m είναι ένας αυθαίρετος αριθμός, η τελευταία ισότητα αποδεικνύει τη μοναδικότητα της επέκτασης. Η σειρά (6), οι συντελεστές της οποίας υπολογίζονται με τον τύπο (7), ονομάζεται σειρά Laurent της συνάρτησης f(z) στον δακτύλιο. σύνολο όρων αυτής της σειράς με μη αρνητικές δυνάμεις ονομάζεται το κανονικό μέρος της σειράς Laurent και με αρνητικές - το κύριο μέρος της. Οι τύποι (7) για τους συντελεστές της σειράς Laurent χρησιμοποιούνται σπάνια στην πράξη, επειδή, όπως Κατά κανόνα, απαιτούν δυσκίνητους υπολογισμούς. Συνήθως, αν είναι δυνατόν, χρησιμοποιούνται έτοιμες επεκτάσεις Taylor στοιχειωδών συναρτήσεων. Με βάση τη μοναδικότητα της επέκτασης, οποιαδήποτε νομική τεχνική οδηγεί στο ίδιο αποτέλεσμα. Παράδειγμα 2 Εξετάστε τις επεκτάσεις συναρτήσεων της σειράς Laurent σε διάφορους τομείς, υποθέτοντας ότι η f(r) έχει δύο μοναδικά σημεία: Συνεπώς, υπάρχουν τρία δακτυλιοειδή πεδία με κέντρο στο σημείο r = 0. Σε καθένα από αυτά η συνάρτηση f(r) είναι αναλυτική: α) κυκλικός δακτύλιος εξωτερικά του κύκλος (Εικ. 27). Ας βρούμε τις επεκτάσεις Laurent της συνάρτησης /(z) σε καθεμία από αυτές τις περιοχές. Ας αναπαραστήσουμε το /(z) ως άθροισμα στοιχειωδών κλασμάτων α) Κύκλος Μετασχηματίζουμε τη σχέση (16) ως εξής. Χρησιμοποιώντας τον τύπο για το άθροισμα των όρων μιας γεωμετρικής προόδου, παίρνουμε. Αντικαθιστούμε τις διαστολές που βρέθηκαν στον τύπο (17) : Αυτή η επέκταση είναι η σειρά Taylor της συνάρτησης /(z). β) Ο δακτύλιος για τη συνάρτηση -r παραμένει σύγκλινος σε αυτόν τον δακτύλιο, αφού η Σειρά (19) για τη συνάρτηση j^j για |z| > 1 αποκλίνει. Επομένως, μετασχηματίζουμε τη συνάρτηση /(z) ως εξής: και πάλι εφαρμόζοντας τον τύπο (19), λαμβάνουμε ότι Αυτή η σειρά συγκλίνει για. Αντικαθιστώντας τις διαστολές (18) και (21) στη σχέση (20), λαμβάνουμε γ) Το εξωτερικό του κύκλου για τη συνάρτηση -z για |z| > 2 αποκλίνει και η σειρά (21) για τη συνάρτηση- Ας αναπαραστήσουμε τη συνάρτηση /(z) στην ακόλουθη μορφή: /<*> Χρησιμοποιώντας τους τύπους (18) και (19), λαμβάνουμε OR 1 Αυτό το παράδειγμα δείχνει ότι για την ίδια συνάρτηση f(z) η επέκταση Laurent, γενικά μιλώντας, έχει διαφορετική μορφή για διαφορετικούς δακτυλίους. Παράδειγμα 3. Βρείτε την επέκταση της 8ης σειράς Laurent μιας συνάρτησης σειράς Laurent Απομονωμένα ενικά σημεία και η ταξινόμησή τους σε έναν τομέα δακτυλίου A Χρησιμοποιούμε την αναπαράσταση της συνάρτησης f(z) στην ακόλουθη μορφή: και μετασχηματίζουμε τον δεύτερο όρο Χρησιμοποιώντας το τύπος για το άθροισμα των όρων μιας γεωμετρικής προόδου, λαμβάνουμε Αντικαθιστώντας τις εκφράσεις που βρέθηκαν στον τύπο (22), έχουμε το Παράδειγμα 4. Αναπτύξτε τη συνάρτηση της σειράς Laurent στην περιοχή zq = 0. Για οποιοδήποτε μιγαδικό έχουμε Έστω αυτό η επέκταση ισχύει για οποιοδήποτε σημείο z Ф 0. Σε αυτήν την περίπτωση, η περιοχή δακτυλίου αντιπροσωπεύει ολόκληρο το μιγαδικό επίπεδο με ένα απορριφθέν σημείο z - 0. Αυτή η περιοχή μπορεί να οριστεί από την ακόλουθη σχέση: Αυτή η συνάρτηση είναι αναλυτική στην περιοχή Από τύπους ( 13) για τους συντελεστές της σειράς Laurent, χρησιμοποιώντας τον ίδιο συλλογισμό όπως στην προηγούμενη παράγραφο, μπορούμε να λάβουμε τις ανισότητες Kouiw. αν η συνάρτηση f(z) οριοθετείται σε κύκλο, όπου το M είναι σταθερά), τότε Απομονωμένα ενικά σημεία Το σημείο zo ονομάζεται απομονωμένο ενικό σημείο της συνάρτησης f(z) αν υπάρχει γειτονιά δακτυλίου του σημείου ( αυτό το σύνολο ονομάζεται μερικές φορές διάτρητη γειτονιά του σημείου 2o), για το οποίο η συνάρτηση f(z) είναι μοναδική και αναλυτική. Στο ίδιο το σημείο zo, η συνάρτηση είναι είτε απροσδιόριστη είτε όχι μονοσήμαντη και αναλυτική. Ανάλογα με τη συμπεριφορά της συνάρτησης /(r) κατά την προσέγγιση του σημείου zo, διακρίνονται τρεις τύποι μοναδικών σημείων. Ένα απομονωμένο ενικό σημείο ονομάζεται: 1) αφαιρούμενο αν υπάρχει πεπερασμένο 2) pmusach εάν 3) ουσιαστικά ενικό σημείο εάν η συνάρτηση f(z) δεν έχει όριο στο Ο τύπος ενός απομονωμένου ενικού σημείου σχετίζεται στενά με το φύση της επέκτασης Laurent της συνάρτησης από το τρυπημένο κέντρο του . Θεώρημα 16. Ένα απομονωμένο ενικό σημείο z0 μιας συνάρτησης f(z) είναι ένα αφαιρούμενο ενικό σημείο εάν και μόνο εάν η επέκταση Laurent της συνάρτησης f(z) σε μια γειτονιά του σημείου zo δεν περιέχει κύριο μέρος, δηλ. έχει τη μορφή Έστω zo αφαιρούμενο ενικό σημείο. Τότε υπάρχει ένα πεπερασμένο, επομένως, η συνάρτηση f(z) οριοθετείται σε μια προκολογική γειτονιά του σημείου z. Βάζουμε Βάσει των ανισοτήτων του Cauchy Εφόσον το p μπορεί να επιλεγεί να είναι αυθαίρετα μικρό, τότε όλοι οι συντελεστές σε αρνητικές δυνάμεις (z - 20) είναι ίσα με μηδέν: Αντίθετα, έστω ότι το Laurent η επέκταση της συνάρτησης /(r) σε μια γειτονιά του σημείου zq περιέχει μόνο το σωστό μέρος, δηλαδή έχει τη μορφή (23) και, επομένως, είναι Τέιλορ. Είναι εύκολο να δούμε ότι για z -* z0 η συνάρτηση /(z) έχει οριακή τιμή: Θεώρημα 17. Ένα απομονωμένο ενικό σημείο zq της συνάρτησης f(z) μπορεί να αφαιρεθεί εάν και μόνο εάν η συνάρτηση J(z) είναι οριοθετείται σε κάποια τρυπημένη γειτονιά του σημείου zq, Zgmechai όχι. Έστω r ένα αφαιρούμενο ενικό σημείο της συνάρτησης /(r). Υποθέτοντας ότι παίρνουμε ότι η συνάρτηση /(r) είναι αναλυτική σε κάποιον κύκλο με κέντρο στο σημείο r. Αυτό καθορίζει το όνομα του σημείου - αφαιρούμενο. Θεώρημα 18. Ένα απομονωμένο ενικό σημείο zq μιας συνάρτησης f(z) είναι πόλος εάν και μόνο αν το κύριο μέρος της επέκτασης Laurent της συνάρτησης f(z) σε μια γειτονιά του σημείου περιέχει έναν πεπερασμένο (και θετικό) αριθμό με μη μηδενικούς όρους, δηλ. έχει τη μορφή 4 Έστω z0 πόλος. Από τότε υπάρχει μια διάτρητη γειτονιά του σημείου z0 στην οποία η συνάρτηση f(z) είναι αναλυτική και μη μηδενική. Στη συνέχεια, σε αυτή τη γειτονιά ορίζεται μια αναλυτική συνάρτηση και Επομένως, το σημείο zq είναι ένα αφαιρούμενο ενικό σημείο (μηδέν) της συνάρτησης ή όπου h(z) είναι μια αναλυτική συνάρτηση, h(z0) Φ 0. Τότε h(zo) Φ Το 0 είναι επίσης αναλυτικό, τότε η συνάρτηση φ είναι αναλυτική σε μια γειτονιά του σημείου zq, και επομένως, από όπου προκύπτει ότι Ας υποθέσουμε τώρα ότι η συνάρτηση f(z) έχει μια επέκταση της μορφής (24) σε μια διάτρητη γειτονιά του το σημείο zо. Αυτό σημαίνει ότι σε αυτή τη γειτονιά η συνάρτηση f(z) είναι αναλυτική μαζί με τη συνάρτηση. Για τη συνάρτηση g(z) ισχύει η επέκταση, από την οποία φαίνεται ότι το zq είναι αφαιρούμενο ενικό σημείο της συνάρτησης g(z) και υπάρχει. Τότε η συνάρτηση στο 0 τείνει να είναι ο πόλος της συνάρτησης. είναι άλλο ένα απλό γεγονός. Το σημείο Zq είναι πόλος της συνάρτησης f(z) αν και μόνο αν η συνάρτηση g(z) = yj μπορεί να επεκταθεί σε μια αναλυτική συνάρτηση σε μια γειτονιά του σημείου zq θέτοντας g(z0) = 0. Η σειρά του πόλου της συνάρτησης f(z) ονομάζεται μηδενική τάξη της συνάρτησης jfa. Η ακόλουθη δήλωση προκύπτει από τα θεωρήματα 16 και 18. Θεώρημα 19. Ένα απομονωμένο ενικό σημείο είναι ουσιαστικά ενικό εάν και μόνο εάν το κύριο μέρος της επέκτασης Laurent σε μια διάτρητη γειτονιά αυτού του σημείου περιέχει άπειρους μη μηδενικούς όρους. Παράδειγμα 5. Το ενικό σημείο της συνάρτησης είναι zo = 0. Έχουμε μεμονωμένα μοναδικά σημεία της σειράς Laurent και την ταξινόμησή τους Επομένως, το zo = O είναι ένα αφαιρούμενο ενικό σημείο. Η επέκταση της συνάρτησης /(z) σε μια σειρά Laurent κοντά στο σημείο μηδέν περιέχει μόνο το σωστό μέρος: Παράδειγμα 7. /(z) = Το ενικό σημείο της συνάρτησης f(z) είναι zq = 0. Ας εξετάσουμε τη συμπεριφορά αυτής της συνάρτησης στον πραγματικό και στον φανταστικό άξονα: στον πραγματικό άξονα στο x 0, στον φανταστικό άξονα Κατά συνέπεια, υπάρχει δεν είναι ούτε πεπερασμένο ούτε άπειρο όριο για το f(z) στο z -* 0 δεν υπάρχει. Αυτό σημαίνει ότι το σημείο r = 0 είναι ένα ουσιαστικά ενικό σημείο της συνάρτησης f(z). Ας βρούμε την επέκταση Laurent της συνάρτησης f(z) κοντά στο σημείο μηδέν. Για οποιοδήποτε σύνθετο C έχουμε Set. Τότε η επέκταση Laurent περιέχει έναν άπειρο αριθμό όρων με αρνητικές δυνάμεις z.

Μοναδικό σημείο

στα μαθηματικά.

1) Ένα μοναδικό σημείο μιας καμπύλης που ορίζεται από την εξίσωση F ( x, y) = 0, - σημείο M 0 ( x 0, y 0), στην οποία και οι δύο επιμέρους παράγωγοι της συνάρτησης F ( x, y) πηγαίνετε στο μηδέν:

Αν όχι όλες οι δεύτερες μερικές παράγωγοι της συνάρτησης F ( x, y) στο σημείο Μ 0 ισούνται με μηδέν, τότε το Ο. τ. ονομάζεται διπλό. Εάν, μαζί με τις πρώτες παραγώγους που εξαφανίζονται στο σημείο Μ0, εξαφανίζονται όλες οι δεύτερες παράγωγοι, αλλά όχι όλες οι τρίτες παράγωγοι, τότε η εξίσωση ονομάζεται τριπλή κ.λπ. Κατά τη μελέτη της δομής μιας καμπύλης κοντά σε ένα διπλό O.t., το πρόσημο της έκφρασης παίζει σημαντικό ρόλο

Αν Δ > 0, τότε ο ανοιχτός χώρος ονομάζεται απομονωμένος. για παράδειγμα, στην καμπύλη y 2 - x 4 + 4x 2= 0 η αρχή των συντεταγμένων είναι ένα απομονωμένο Ο. t. (βλ. ρύζι. 1 ). Αν Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - a 4= 0 η αρχή των συντεταγμένων είναι το κομβικό O. t. (βλ. ρύζι. 2 ). Αν Δ = 0, τότε το γενικό σημείο της καμπύλης είτε είναι απομονωμένο είτε χαρακτηρίζεται από το γεγονός ότι διαφορετικοί κλάδοι της καμπύλης έχουν κοινή εφαπτομένη σε αυτό το σημείο, για παράδειγμα: α) σημείο αιχμής του 1ου είδους - διαφορετικοί κλάδοι της καμπύλης η καμπύλη βρίσκονται σε αντίθετες πλευρές της κοινής εφαπτομένης και σχηματίζουν ένα σημείο, σαν καμπύλη y 2 - x 3= 0 (βλ ρύζι. 3 ,ένα) β) σημείο αιχμής του 2ου είδους - διαφορετικοί κλάδοι της καμπύλης βρίσκονται στη μία πλευρά της κοινής εφαπτομένης, όπως μια καμπύλη (y - x 2)2 - x 5= 0 (βλ ρύζι. 3 , β); γ) σημείο αυτο-αφής (για καμπύλη y 2 - x 4= 0 η προέλευση είναι το σημείο επαφής του εαυτού. (εκ. ρύζι. 3 , V). Μαζί με τον υποδεικνυόμενο Ο. τ. υπάρχουν και πολλά άλλα Ο. τ. με ειδικές ονομασίες. για παράδειγμα, το ασυμπτωτικό σημείο είναι η κορυφή μιας σπείρας με άπειρο αριθμό στροφών (βλ. ρύζι. 4 ), σημείο τερματισμού, γωνιακό σημείο κ.λπ.

2) Ένα μοναδικό σημείο μιας διαφορικής εξίσωσης είναι το σημείο στο οποίο εξαφανίζονται ταυτόχρονα και ο αριθμητής και ο παρονομαστής της δεξιάς πλευράς της διαφορικής εξίσωσης (Βλ. Διαφορικές εξισώσεις)

όπου το P και το Q είναι συνεχώς διαφοροποιήσιμες συναρτήσεις. Υποθέτοντας ότι το O. t. βρίσκεται στην αρχή των συντεταγμένων και χρησιμοποιώντας τον τύπο Taylor (Βλ. τύπο Taylor), μπορούμε να αναπαραστήσουμε την εξίσωση (1) με τη μορφή

όπου P 1 ( x, y) και Q 1 ( x, y) - απειροελάχιστο σε σχέση με

Δηλαδή, αν λ 1 ≠ λ 2 και λ 1 λ 2 > 0 ή λ 1 = λ 2, τότε το Ο. τ. είναι κόμβος. όλες οι ολοκληρωτικές καμπύλες που διέρχονται από σημεία μιας αρκετά μικρής γειτονιάς ενός κόμβου εισέρχονται σε αυτό. Αν λ 1 ≠ λ 2 και λ 1 λ 2 i β, α ≠ 0 και β ≠ 0, τότε το γενικό σημείο είναι εστία. Όλες οι ολοκληρωτικές καμπύλες που διέρχονται από σημεία σε μια αρκετά μικρή γειτονιά της εστίασης αντιπροσωπεύουν σπείρες με άπειρο αριθμό στροφών σε οποιαδήποτε αυθαίρετα μικρή γειτονιά της εστίασης. Αν, τέλος, λ 1,2 = ± Εγώβ, β ≠ 0, τότε ο χαρακτήρας του O. t. δεν καθορίζεται μόνο με γραμμικούς όρους στις επεκτάσεις του P ( x, y) και Q ( x, y), όπως συνέβη σε όλες τις παραπάνω περιπτώσεις. εδώ το O. t. μπορεί να είναι εστία ή κέντρο ή μπορεί να έχει πιο σύνθετο χαρακτήρα. Στη γειτονιά του κέντρου, όλες οι ακέραιες καμπύλες είναι κλειστές και περιέχουν το κέντρο μέσα τους. Έτσι, για παράδειγμα, το σημείο (0, 0) είναι ένας κόμβος για τις εξισώσεις στο" = 2u/x(λ 1 = 1, λ 2 = 2, βλ ρύζι. 5 , α) και y" = u/x(λ 1 = λ 2 = 1, βλ ρύζι. 5 , β), σέλα για την εξίσωση y" = -y/x(λ 1 = -1, λ 2 = 1 ; εκ. ρύζι. 6 ), η εστίαση για την εξίσωση y" =(x + y) / (x - y) (λ 1 = 1 - Εγώ, λ 2 = 1 + Εγώ; εκ. ρύζι. 7 ) και το κέντρο για την εξίσωση y" = -x/y(λ 1 = -Εγώ, λ 2 = Εγώ; εκ. ρύζι. 8 ).

Αν x, y) και Q ( x, y) αναλυτική, μια γειτονιά ενός GP υψηλότερης τάξης μπορεί να χωριστεί σε περιοχές: D 1 - γεμάτη με ολοκληρωμένες καμπύλες, και τα δύο άκρα περιλαμβάνονται στο GP (ελλειπτικές περιοχές), D 2 - γεμάτη με ολοκληρωμένες καμπύλες, το ένα άκρο περιλαμβάνεται στο GP (παραβολικές περιοχές) και D 3 - περιοχές που οριοθετούνται από δύο ακέραιες καμπύλες που περιλαμβάνονται στη γενική θεωρία, μεταξύ των οποίων βρίσκονται ακέραιες καμπύλες υπερβολικού τύπου (υπερβολικές περιοχές) (βλ. ρύζι. 9 ). Εάν δεν υπάρχουν ολοκληρωμένες καμπύλες που περιλαμβάνονται σε ένα γενικό σημείο, τότε το γενικό σημείο ονομάζεται σημείο σταθερού τύπου. Μια γειτονιά ενός σταθερού ταλαντωτή αποτελείται από κλειστές ολοκληρωμένες καμπύλες που περιέχουν μια όσμωση μέσα της, μεταξύ των οποίων υπάρχουν σπείρες (βλ. ρύζι. 10 ).

Η μελέτη των διαφορικών εξισώσεων, δηλαδή ουσιαστικά η μελέτη της συμπεριφοράς των οικογενειών ολοκληρωτικών καμπυλών στη γειτονιά των διαφορικών εξισώσεων, αποτελεί έναν από τους κλάδους της ποιοτικής θεωρίας των διαφορικών εξισώσεων και παίζει σημαντικό ρόλο σε εφαρμογές, ιδίως σε ζητήματα σταθερότητας κίνησης (έργα των A. M. Lyapunov, A. Poincaré, κ.λπ.).

3) Ένα μοναδικό σημείο μιας αναλυτικής συνάρτησης μίας τιμής είναι το σημείο στο οποίο παραβιάζεται η αναλυτικότητα της συνάρτησης (βλ. Αναλυτικές συναρτήσεις). Αν υπάρχει γειτονιά Ο. τ. ένα, απαλλαγμένο από άλλα Ο. τ., στη συνέχεια σημείο ΕΝΑονομάζεται απομονωμένο Ο. τ. Αν ΕΝΑ- μια απομονωμένη γενική θεωρία και υπάρχει ένα πεπερασμένο α ονομάζεται αφαιρούμενη γενική θεωρία. Αλλάζοντας κατάλληλα τον ορισμό μιας συνάρτησης σε ένα σημείο α (ή επαναπροσδιορίζοντάς την σε αυτό το σημείο, εάν η συνάρτηση σε αυτό δεν έχει οριστεί καθόλου), δηλαδή, υποθέτοντας φά(ένα)= β, είναι δυνατό να επιτευχθεί αυτό έναθα γίνει ένα συνηθισμένο σημείο της διορθωμένης συνάρτησης. Για παράδειγμα, τελεία z= 0 είναι ένα αφαιρούμενο O. t. για τη συνάρτηση f 1 ( z) = φά(z), Αν z≠ 0, και φά 1 (0), = 1, τελεία z= 0 είναι ένα συνηθισμένο σημείο [ φά 1 (z) είναι αναλυτική στο σημείο z= 0]. Αν ΕΝΑ- ένα απομονωμένο Ο. τ. και ένα λέγεται πόλος ή ένα κατ' ουσία ενικό σημείο μιας συνάρτησης φά(z), εάν η σειρά Laurent) λειτουργεί φά(z) στην περιοχή απομονωμένου Ο. τ. δεν περιέχει αρνητικές δυνάμεις z - a, Αν ΕΝΑ- αφαιρούμενο Ο. τ., περιέχει πεπερασμένο αριθμό αρνητικών μοιρών z - a, Αν ΕΝΑ- κοντάρι (στην περίπτωση αυτή η σειρά του στύλου Rορίζεται ως ο υψηλότερος βαθμός α - ένα ουσιαστικά ειδικό σημείο. Για παράδειγμα, για τη συνάρτηση

p = 2, 3,…)

τελεία z= 0 είναι ο πόλος τάξης R, για λειτουργία

τελεία z= 0 είναι ένα ουσιαστικά μοναδικό σημείο.

Στο όριο του κύκλου σύγκλισης μιας σειράς ισχύος πρέπει να υπάρχει τουλάχιστον ένα DP της συνάρτησης που αντιπροσωπεύεται σε αυτόν τον κύκλο από τη δεδομένη σειρά ισχύος. Όλα τα οριακά σημεία του πεδίου ύπαρξης μιας μοναδικής αναλυτικής συνάρτησης (φυσικό όριο) είναι τα όρια αυτής της συνάρτησης. Έτσι, όλα τα σημεία του κύκλου μονάδας | z| = 1 είναι ειδικά για τη συνάρτηση

Για μια αναλυτική συνάρτηση πολλαπλών τιμών, η έννοια του «Ο. Τ." πιο δύσκολο. Εκτός από το O. t., σε μεμονωμένα φύλλα της επιφάνειας Riemann μιας συνάρτησης (δηλαδή το O. t. αναλυτικών στοιχείων μιας τιμής), κάθε σημείο διακλάδωσης είναι και το O. t. της συνάρτησης. Τα απομονωμένα σημεία διακλάδωσης μιας επιφάνειας Riemann (δηλαδή τέτοια σημεία διακλάδωσης που σε κάποια γειτονιά τους δεν υπάρχουν άλλες συναρτήσεις O. t. σε κανένα φύλλο) ταξινομούνται ως εξής. Αν το a είναι ένα απομονωμένο σημείο διακλάδωσης πεπερασμένης τάξης και υπάρχει ένα πεπερασμένο a, ονομάζεται κρίσιμος πόλος. Αν ΕΝΑ- ένα απομονωμένο σημείο διακλάδωσης άπειρης τάξης και το a ονομάζεται υπερβατικό O.t. Όλα τα άλλα απομονωμένα σημεία διακλάδωσης ονομάζονται κρίσιμα ουσιαστικά μοναδικά σημεία. Παραδείγματα: τελεία z= 0 είναι το συνηθισμένο κρίσιμο σημείο της συνάρτησης f ( z) = κούτσουρο zκαι το κρίσιμο ουσιαστικά ενικό σημείο της συνάρτησης φά (z) = αμαρτία ln z.

Κάθε γενική θεωρία, εκτός από μια αφαιρούμενη, αποτελεί εμπόδιο στην αναλυτική συνέχεια, δηλαδή, η αναλυτική συνέχεια κατά μήκος μιας καμπύλης που διέρχεται από ένα μη αναγώγιμο γενικό πρόβλημα είναι αδύνατη.

Μεγάλη Σοβιετική Εγκυκλοπαίδεια. - Μ.: Σοβιετική Εγκυκλοπαίδεια. 1969-1978 .

Δείτε τι είναι το "Singular point" σε άλλα λεξικά:

Σημεία εδώ. Δείτε επίσης ενικό σημείο (διαφορικές εξισώσεις). Ένα χαρακτηριστικό ή ιδιομορφία στα μαθηματικά είναι ένα σημείο στο οποίο ένα μαθηματικό αντικείμενο (συνήθως μια συνάρτηση) είναι απροσδιόριστο ή έχει ακανόνιστη συμπεριφορά (για παράδειγμα, ένα σημείο στο οποίο ... ... Wikipedia

Αναλυτική συνάρτηση είναι ένα σημείο στο οποίο παραβιάζονται οι συνθήκες της αναλυτικότητας. Αν η αναλυτική συνάρτηση f(z) δίνεται σε μια συγκεκριμένη γειτονιά του σημείου z0 παντού... Φυσική εγκυκλοπαίδεια

Αναλυτική συνάρτηση είναι το σημείο στο οποίο παραβιάζεται η αναλυτικότητα της συνάρτησης... Μεγάλο Εγκυκλοπαιδικό Λεξικό

μοναδικό σημείο- - [Ya.N.Luginsky, M.S.Fezi Zhilinskaya, Yu.S.Kabirov. Αγγλο-ρωσικό λεξικό ηλεκτρολογίας και μηχανικής ισχύος, Μόσχα, 1999] Θέματα ηλεκτρολογικής μηχανικής, βασικές έννοιες EN ενικό σημείο ... Οδηγός Τεχνικού Μεταφραστή

1) Μια αναλυτική συνάρτηση f(z) είναι ένα εμπόδιο στην αναλυτική συνέχεια ενός στοιχείου μιας συνάρτησης f(z) μιας σύνθετης μεταβλητής z κατά μήκος οποιασδήποτε διαδρομής στο επίπεδο αυτής της μεταβλητής. Έστω η αναλυτική συνάρτηση f(z) να οριστεί από κάποια... ... Μαθηματική Εγκυκλοπαίδεια

Αναλυτική συνάρτηση, το σημείο στο οποίο παραβιάζεται η αναλυτικότητα της συνάρτησης. * * * ΜΟΝΟ ΣΗΜΕΙΟ ΜΟΝΟ ΣΗΜΕΙΟ αναλυτικής συνάρτησης, το σημείο στο οποίο παραβιάζεται η αναλυτικότητα της συνάρτησης... εγκυκλοπαιδικό λεξικό

μοναδικό σημείο- ypatingasis taškas statusas T sritis automatika atitikmenys: αγγλ. ενικό σημείο vok. singulärer Punkt, m rus. ενικό σημείο, f pranc. σωματιδιακό σημείο σημείου, m; σημείο singulier, m … Automatikos terminų žodynas

μοναδικό σημείο- ypatingasis taškas statusas T sritis fizika atitikmenys: αγγλ. ενικό σημείο vok. singulärer Punkt, m rus. ενικό σημείο, f pranc. σημείο singulier, m … Fizikos terminų žodynas

Βασικές έννοιες και ορισμοί:

Το μηδέν της αναλυτικής συνάρτησης f(z) είναι το σημείο “a” για το οποίο f(a)=0.

Ένα μηδέν της τάξης "n" μιας συνάρτησης f(z) είναι ένα σημείο "a" εάν fn(a)10.

Ένα ενικό σημείο «a» ονομάζεται απομονωμένο ενικό σημείο μιας συνάρτησης f(z) εάν υπάρχει μια γειτονιά αυτού του σημείου στην οποία δεν υπάρχουν μοναδικά σημεία εκτός από το «a».

Υπάρχουν τρεις τύποι μεμονωμένων ενικών σημείων: .

1 αφαιρούμενα μοναδικά σημεία.

3 ουσιαστικά μοναδικά σημεία.

Ο τύπος του μοναδικού σημείου μπορεί να προσδιοριστεί με βάση τη συμπεριφορά μιας δεδομένης συνάρτησης στο ενιαίο σημείο που βρέθηκε, καθώς και από τη μορφή της σειράς Laurent που λαμβάνεται για τη συνάρτηση στη γειτονιά του ενικού σημείου που βρέθηκε.

Προσδιορισμός του τύπου ενός μοναδικού σημείου από τη συμπεριφορά της συνάρτησης σε αυτό.

1. Αφαιρούμενα μοναδικά σημεία.

Ένα απομονωμένο ενικό σημείο α μιας συνάρτησης f(z) ονομάζεται αφαιρούμενο αν υπάρχει πεπερασμένο όριο.

2.Πολωνοί.

Ένα απομονωμένο ενικό σημείο α μιας συνάρτησης f(z) ονομάζεται πόλος αν .

3. Ουσιαστικά μοναδικά σημεία.

Ένα απομονωμένο ενικό σημείο α μιας συνάρτησης f(z) ονομάζεται ουσιαστικά ενικό σημείο εάν δεν υπάρχει ούτε πεπερασμένο ούτε άπειρο.

Η παρακάτω σχέση υπάρχει μεταξύ των μηδενικών και των πόλων της συνάρτησης.

Για να είναι το σημείο α πόλος τάξης n της συνάρτησης f(Z), είναι απαραίτητο και αρκετό αυτό το σημείο να είναι μηδέν της τάξης n για τη συνάρτηση .

Αν n=1 ο πόλος λέγεται απλός.

Ορισμός:Ένα απομονωμένο μοναδικό σημείο αδιαμφισβήτητης φύσης ονομάζεται:

α) αφαιρείται εάν λείπει το κύριο μέρος της αποσύνθεσης·

β) έναν πόλο, εάν το κύριο μέρος περιέχει έναν πεπερασμένο αριθμό όρων.

γ) ένα ουσιαστικά ενικό σημείο αν το κύριο μέρος περιέχει άπειρο αριθμό όρων.

α) Έτσι, στη γειτονιά ενός αφαιρούμενου ενικού σημείου, η επέκταση έχει τη μορφή:

εκφράζει τη συνάρτηση σε όλα τα σημεία του κύκλου |z-a|

Στο κέντρο z=a η ισότητα δεν ισχύει, γιατί η συνάρτηση στο z=a έχει ασυνέχεια και η δεξιά πλευρά είναι συνεχής. Εάν η τιμή της συνάρτησης στο κέντρο αλλάξει, λαμβάνοντας την ίση με την τιμή της δεξιάς πλευράς, τότε το κενό θα εξαλειφθεί - εξ ου και το όνομα - αφαιρείται.

β) Στη γειτονιά ενός πόλου της τάξης m, η επέκταση της σειράς Laurent έχει τη μορφή:

γ) Σε γειτνίαση απλού στύλου

Εκπτώσεις και τύποι για τον υπολογισμό τους.

Το υπόλειμμα μιας αναλυτικής συνάρτησης f(z) σε ένα απομονωμένο ενικό σημείο z 0 είναι ένας μιγαδικός αριθμός ίσος με την τιμή του ολοκληρώματος , που λαμβάνεται στη θετική κατεύθυνση κατά μήκος του κύκλου L με κέντρο στο σημείο z 0 που βρίσκεται στο πεδίο της αναλυτικότητας της συνάρτησης f(z) (δηλαδή στον δακτύλιο 0<|z-z0|

Το υπόλειμμα της συνάρτησης f(z) σε ένα απομονωμένο ενικό σημείο z 0 συμβολίζεται με το σύμβολο Res f(z 0) ή Res (f(z), z 0). Ετσι,

Res f(z 0)= . (22.15.1)

Αν βάλουμε n=-1 στον τύπο (22.15.1), παίρνουμε:

C-1 =

ή Res f(z 0)= C-1,

εκείνοι. το υπόλειμμα της συνάρτησης f(z) ως προς το ενικό σημείο z 0 είναι ίσο με τον συντελεστή του πρώτου όρου με αρνητικό εκθέτη στην επέκταση της συνάρτησης f(z) στη σειρά Laurent.

Υπολογισμός εκπτώσεων.

Κανονικά ή αφαιρούμενα μοναδικά σημεία. Προφανώς, αν z=z 0 είναι κανονικό ή αφαιρούμενο ενικό σημείο της συνάρτησης f(z), τότε Res f(z 0)=0 (η επέκταση Laurent σε αυτές τις περιπτώσεις δεν έχει το κύριο μέρος, οπότε c-1=0) .

Πόλος. Έστω το σημείο z 0 απλός πόλος της συνάρτησης f(z). Τότε η σειρά Laurent για τη συνάρτηση f(z) στην περιοχή του σημείου z 0 έχει τη μορφή:

Από εδώ

Επομένως, περνώντας αυτή την ισότητα στο όριο z --z 0, λαμβάνουμε

Res f(z0)=

Ουσιαστικά ιδιαίτερο σημείο. Εάν το σημείο z 0 είναι ουσιαστικά μοναδικό σημείο της συνάρτησης f(z), τότε για να υπολογιστεί το υπόλοιπο της συνάρτησης σε αυτό το σημείο, συνήθως προσδιορίζεται άμεσα ο συντελεστής c-1 στην επέκταση της σειράς Laurent της συνάρτησης.

Ταξινόμηση γεγονότων. Άθροισμα, γινόμενο γεγονότων, ιδιότητές τους, γραφική παράσταση.

Οι εκδηλώσεις χωρίζονται σε:

1. Τυχαίο

2. Αξιόπιστο

3. Αδύνατον

Αξιόπιστο είναι ένα γεγονός που αναγκαστικά συμβαίνει υπό δεδομένες συνθήκες (η νύχτα ακολουθεί το πρωί).

Ένα τυχαίο συμβάν είναι ένα γεγονός που μπορεί να συμβεί ή να μην συμβεί (επιτυχία μιας εξέτασης).

Ένα αδύνατο γεγονός είναι ένα γεγονός που δεν θα συμβεί υπό δεδομένες συνθήκες (βγάζοντας ένα πράσινο μολύβι από ένα κουτί με μόνο κόκκινα).