What is called the order of a square matrix. Determinants of square matrices

A square matrix of the th order, in which there are ones on the main diagonal and all other elements are equal to zero, will be called the identity matrix and denoted by or simply. The name "unit matrix" is associated with the following property of the matrix: for any rectangular matrix

there are equalities

.

Obviously,

Let be a square matrix. Then the degree of the matrix is ​​determined in the usual way:

From the combination property of matrix multiplication it follows:

Here , are arbitrary non-negative integers.

Consider a polynomial (an entire rational function) with coefficients from the field:

Then by we mean the matrix

This is how a polynomial in a matrix is ​​defined.

Let the polynomial be equal to the product of the polynomials and :

.

A polynomial is obtained from and by term-by-term multiplication and reduction of similar terms. In this case, the rule of multiplication of powers is used: . Since all these actions are also valid when replacing a scalar quantity with a matrix, then

Hence, in particular,

that is, two polynomials from the same matrix always commute with each other.

Let us agree that the th supradiagonal (subdiagonal) in a rectangular matrix is ​​a series of elements that (respectively). Let us denote by a square matrix of the th order, in which the elements of the first supradiagonal are equal to one, and all other elements are equal to zero. Then

, etc.;

By virtue of these equalities, if:

The polynomial is relative, then

.

Similarly, if is a square matrix of the th order, in which all elements of the first subdiagonal are equal to one, and all the rest are equal to zero, then

.

We invite the reader to check following properties matrices and:

1° As a result of multiplying an arbitrary -matrix on the left by a matrix (matrix) of the th order, all rows of the matrix are crushed (lowered) one place up (down), the first (last) row of the matrix disappears, and the last (first) row of the product is filled with zeros. For example,

,

.

2° As a result of multiplying an arbitrary -matrix on the right by a matrix of the th order, all columns of the matrix are shifted to the right (left) by one place, while the last (first) column of the matrix disappears, and the first (last) column of the product is filled with zeros. For example,

.

.

2. We will call a square matrix special if . Otherwise, the square matrix is ​​called non-singular.

Let be a non-singular matrix (). Let's consider linear transformation with coefficient matrix

Considering equalities (23) as relative equations and noting that the determinant of the system of equations (23) by condition is different from zero, we can uniquely express using known formulas through:

. (24)

We have obtained the “inverse” transformation for (23). The coefficient matrix of this transformation

we will call the inverse matrix for the matrix . From (24) it is easy to see that

, (25)

where is the algebraic complement (adjunct) of the element in the determinant .

So, for example, if

And ,

.

Forming a composite transformation from this transformation (23) and the inverse (24) in one and the other order, in both cases we obtain identity transformation(with a unit coefficient matrix); That's why

. (26)

The validity of equalities (26) can also be verified by directly multiplying the matrices and . Indeed, by virtue of (25)

.

Likewise

.

It is easy to see that the matrix equations

they have no other solutions other than the solution. Indeed, multiplying both sides of the first equation on the left and the second on the right by and using the combinatory property of the product of matrices, as well as equality (26), in both cases we obtain:

In the same way it is proved that each of the matrix equations

where and are rectangular matrices of equal sizes, is a square matrix of the corresponding size, has one and only one solution:

And accordingly (29)

Matrices (29) are, as it were, the “left” and “right” quotients of the “division” of the matrix by the matrix . From (28) and (29) it follows, respectively (see page 22) and , i.e. . Comparing with (28), we have:

When a rectangular matrix is ​​multiplied from the left or right by a non-singular matrix, the rank of the original matrix does not change.

Let us also note that from (26) it follows, i.e.

For the product of two nonsingular matrices we have:

. (30)

3. All matrices of the th order form a ring with the identity element. Since in this ring the operation of multiplication by a number from the field is defined and there is a basis of linearly independent matrices through which all matrices of the th order are linearly expressed, then the ring of matrices of the th order is an algebra.

All square matrices of the th order form a commutative group with respect to the operation of addition. All nonsingular matrices of the th order form a (non-commutative) group with respect to the multiplication operation.

Square matrix is called upper triangular (lower triangular) if all matrix elements located under the main diagonal (above the main diagonal) are equal to zero:

, .

A diagonal matrix is ​​a special case of both an upper and lower triangular matrix.

Since the determinant of a triangular matrix is ​​equal to the product of its diagonal elements, a triangular (and, in particular, a diagonal) matrix is ​​non-singular only if all its diagonal elements are non-zero.

It is easy to check that the sum and product of two diagonal (upper triangular, lower triangular) matrices is a diagonal (upper triangular, lower triangular, respectively) matrix and that inverse matrix for a non-singular diagonal (upper triangular, lower triangular) matrix is ​​a matrix of the same type. That's why

1° All diagonal, all upper triangular, all lower triangular matrices th order form three commutative groups with respect to the operation of addition.

2° All nonsingular diagonal matrices form a commutative group under multiplication.

3° All nonsingular upper (lower) triangular matrices form a group (non-commutative) under multiplication

4. To conclude this section, let us point out two important operations over matrices - transpose the matrix and go to the conjugate matrix., then matrices.

If a square matrix coincides with its transpose () then such a matrix is ​​called symmetric. If a square matrix coincides with its conjugate (), then it is called Hermitian. In a symmetric matrix, elements symmetrically located relative to the main diagonal are equal, but in a Hermitian matrix they are complexly conjugate with each other. The diagonal elements of a Hermitian matrix are always real. Note that the product of two symmetric (Hermitian) matrices, generally speaking, is not a symmetric (Hermitian) matrix. By virtue of 3°, this occurs only in the case when the given two symmetric or Hermitian matrices commute with each other.

Encourages equality.

If a square matrix differs by a factor of -1 from its transpose (), then such a matrix is ​​called skew-symmetric. In a skew-symmetric matrix, any two elements located symmetrically relative to the main diagonal differ from each other by a factor of -1, and the diagonal elements are equal to zero. From 3° it follows that the product of two skew-symmetric matrices interchanged with each other is a symmetric matrix.

Matrices in mathematics are one of the most important objects having applied value. Often an excursion into the theory of matrices begins with the words: “A matrix is ​​a rectangular table...”. We will start this excursion from a slightly different direction.

Phone books of any size and with any amount of subscriber data are nothing more than matrices. Such matrices look approximately like this:

It is clear that we all use such matrices almost every day. These matrices come in a variety of numbers of rows (as different as a telephone company directory, which can have thousands, hundreds of thousands, or even millions of lines, and a new notebook you just started, which has fewer than ten lines) and columns (the directory officials some organization in which there may be columns such as position and office number and your same address book, where there may not be any data except the name, and thus there are only two columns in it - name and telephone number).

All sorts of matrices can be added and multiplied, as well as other operations can be performed on them, but there is no need to add and multiply telephone directories, there is no benefit from this, and besides, you can use your mind.

But many matrices can and should be added and multiplied and thus solve various pressing problems. Below are examples of such matrices.

Matrices in which the columns are the production of units of a particular type of product, and the rows are the years in which the production of this product is recorded:

You can add matrices of this type, which take into account the output of similar products by different enterprises, in order to obtain summary data for the industry.

Or matrices consisting, for example, of one column, in which the rows are the average cost of a particular type of product:

Matrices of two latest species can be multiplied, and the result is a row matrix containing the cost of all types of products by year.

Matrices, basic definitions

A rectangular table consisting of numbers arranged in m lines and n columns is called mn-matrix (or simply matrix ) and is written like this:

(1)

In matrix (1) the numbers are called its elements (as in the determinant, the first index means the number of the row, the second – the column at the intersection of which the element stands; i = 1, 2, ..., m; j = 1, 2, n).

The matrix is ​​called rectangular , If .

If m = n, then the matrix is ​​called square , and the number n is its in order .

Determinant of a square matrix A is a determinant whose elements are the elements of a matrix A. It is indicated by the symbol | A|.

The square matrix is ​​called not special (or non-degenerate , non-singular ), if its determinant is not zero, and special (or degenerate , singular ) if its determinant is zero.

The matrices are called equal , if they have the same number of rows and columns and all corresponding elements match.

The matrix is ​​called null , if all its elements are equal to zero. We will denote the zero matrix by the symbol 0 or .

For example,

Matrix-row (or lowercase ) is called 1 n-matrix, and matrix-column (or columnar ) – m 1-matrix.

Matrix A", which is obtained from the matrix A swapping rows and columns in it is called transposed relative to the matrix A. Thus, for matrix (1) the transposed matrix is

Matrix transition operation A" transposed with respect to the matrix A, is called matrix transposition A. For mn-matrix transposed is nm-matrix.

The matrix transposed with respect to the matrix is A, that is

(A")" = A .

Example 1. Find matrix A" , transposed with respect to the matrix

and find out whether the determinants of the original and transposed matrices are equal.

Main diagonal A square matrix is ​​an imaginary line connecting its elements, for which both indices are the same. These elements are called diagonal .

A square matrix in which all elements off the main diagonal are equal to zero is called diagonal . Not all diagonal elements of a diagonal matrix are necessarily nonzero. Some of them may be equal to zero.

A square matrix in which the elements on the main diagonal are equal to the same number, non-zero, and all others are equal to zero, is called scalar matrix .

Identity matrix is called a diagonal matrix in which all diagonal elements are equal to one. For example, the third-order identity matrix is ​​the matrix

Example 2. Given matrices:

Solution. Let us calculate the determinants of these matrices. Using the triangle rule, we find

Matrix determinant B let's calculate using the formula

We easily get that

Therefore, the matrices A and are non-singular (non-degenerate, non-singular), and the matrix B– special (degenerate, singular).

The determinant of the identity matrix of any order is obviously equal to one.

Solve the matrix problem yourself, and then look at the solution

Example 3. Given matrices

,

,

Determine which of them are non-singular (non-degenerate, non-singular).

Application of matrices in mathematical and economic modeling

Structured data about a particular object is simply and conveniently recorded in the form of matrices. Matrix models are created not only to store this structured data, but also to solve various problems with this data using linear algebra.

Thus, a well-known matrix model of the economy is the input-output model, introduced by the American economist of Russian origin Vasily Leontiev. This model is based on the assumption that the entire production sector of the economy is divided into n clean industries. Each industry produces only one type of product, and different industries produce various products. Due to this division of labor between industries, there are inter-industry connections, the meaning of which is that part of the production of each industry is transferred to other industries as a production resource.

Product volume i-th industry (measured by a specific unit of measurement), which was produced during the reporting period, is denoted by and is called full output i-th industry. Issues can be conveniently placed in n-component row of the matrix.

Number of units i-industry that needs to be spent j-industry for the production of a unit of its output is designated and called the direct cost coefficient.

Operations on matrices and their properties.

The concept of a determinant of the second and third orders.Properties of determinants and their calculation.

3. general description tasks.

4. Completing tasks.

5. Preparation of a report on laboratory work.

Glossary

Learn the definitions of the following terms:

Dimension A matrix is ​​a collection of two numbers, consisting of the number of its rows m and the number of columns n.

If m=n, then the matrix is ​​called square matrix of order n.

Operations on matrices: transposing a matrix, multiplying (dividing) a matrix by a number, adding and subtracting, multiplying a matrix by a matrix.

The transition from a matrix A to a matrix A m, the rows of which are the columns, and the columns are the rows of the matrix A, is called transposition matrices A.

Example: A = , A t = .

To multiply matrix by number, you need to multiply each element of the matrix by this number.

Example: 2A= 2· = .

Sum (difference) matrices A and B of the same dimension are called matrix C=A B, the elements of which are equal with ij = a ij b ij for all i And j.

Example: A = ; B = . A+B= = .

The work matrix A m n into matrix B n k is called matrix C m k , each element of which is c ij equal to the sum products of the elements of the i-th row of matrix A by the corresponding element of the j-th column of matrix B:

c ij = a i1 · b 1j + a i2 ·b 2j +…+ a in ·b nj .

To be able to multiply a matrix by a matrix, they must be agreed upon for multiplication, namely number of columns in the first matrix should be equal to number of lines in the second matrix.

Example: A= and B=.

А·В—impossible, because they are not consistent.

VA= . = = .

Properties of the matrix multiplication operation.

1. If matrix A has the dimension m n, and matrix B is the dimension n k, then the product A·B exists.

The product BA can exist only when m=k.

2. Matrix multiplication is not commutative, i.e. A·B is not always equal to BA·A even if both products are defined. However, if the relation А·В=В·А is satisfied, then the matrices A and B are called permutable.

Example. Calculate.

Minor element is the determinant of the order matrix, obtained by deleting the th row of the th column.

Algebraic complement element is called .

Laplace expansion theorem:

The determinant of a square matrix is ​​equal to the sum of the products of the elements of any row (column) by their algebraic complements.

Example. Calculate.

Solution. .

Properties of nth order determinants:

1) The value of the determinant will not change if the rows and columns are swapped.

2) If the determinant contains a row (column) of only zeros, then it is equal to zero.

3) When rearranging two rows (columns), the determinant changes sign.

4) A determinant that has two identical rows (columns) is equal to zero.

5) The common factor of the elements of any row (column) can be taken out of the determinant sign.

6) If each element of a certain row (column) is the sum of two terms, then the determinant is equal to the sum of two determinants, in each of which all rows (columns), except the one mentioned, are the same as in this determinant, and in the mentioned row ( Column) of the first determinant contains the first terms, the second - the second.

7) If two rows (columns) in the determinant are proportional, then it is equal to zero.

8) The determinant will not change if the corresponding elements of another row (column) are added to the elements of a certain row (column), multiplied by the same number.

9) The determinants of triangular and diagonal matrices are equal to the product of the elements of the main diagonal.

The method of accumulating zeros for calculating determinants is based on the properties of determinants.

Example. Calculate.

Solution. Subtract the double third from the first row, then use the expansion theorem in the first column.

~ .

Control questions(OK-1, OK-2, OK-11, PK-1) :

1. What is called a second-order determinant?

2. What basic properties determinants?

3. What is the minor of an element?

4. What is called the algebraic complement of an element of a determinant?

5. How to expand the third-order determinant into elements of a row (column)?

6. What is the sum of the products of the elements of any row (or column), the determinant of algebraic additions corresponding elements of another row (or column)?

7. What is the rule of triangles?

8. How are determinants of higher orders calculated using the order reduction method?

10. Which matrix is ​​called square? Null? What is a row matrix, column matrix?

11. Which matrices are called equal?

12. Give definitions of the operations of addition, multiplication of matrices, multiplication of a matrix by a number

13. What conditions must the sizes of matrices satisfy during addition and multiplication?

14. What are the properties of algebraic operations: commutativity, associativity, distributivity? Which of them are fulfilled for matrices during addition and multiplication, and which are not?

15. What is an inverse matrix? For what matrices is it defined?

16. Formulate a theorem on the existence and uniqueness of the inverse matrix.

17. Formulate a lemma on the transposition of a product of matrices.

General practical tasks(OK-1, OK-2, OK-11, PK-1) :

No. 1. Find the sum and difference of matrices A and B :

A)

b)

V)

No. 2. Follow these steps :

c) Z= -11A+7B-4C+D

If

No. 3. Follow these steps :

V)

No. 4. Using four methods of calculating the determinant of a square matrix, find the determinants of the following matrices :

No. 5. Find determinants of the nth order, based on the elements of the column (row) :

A) b)

No. 6. Find the determinant of a matrix using the properties of determinants:

A) b)

DEFINITION OF MATRIX. TYPES OF MATRICES

Matrix of size m× n called a set m·n numbers arranged in a rectangular table of m lines and n columns. This table is usually enclosed in parentheses. For example, the matrix might look like:

For brevity, a matrix can be denoted by one capital letter, For example, A or IN.

IN general view matrix size m× n write it like this

.

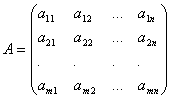The numbers that make up the matrix are called matrix elements. It is convenient to provide matrix elements with two indices a ij: The first indicates the row number and the second indicates the column number. For example, a 23– the element is in the 2nd row, 3rd column.

If a matrix has the same number of rows as the number of columns, then the matrix is ​​called square, and the number of its rows or columns is called in order matrices. In the above examples, the second matrix is ​​square - its order is 3, and the fourth matrix is ​​its order 1.

A matrix in which the number of rows is not equal to the number of columns is called rectangular. In the examples this is the first matrix and the third.

There are also matrices that have only one row or one column.

A matrix with only one row is called matrix - row(or string), and a matrix with only one column matrix - column.

A matrix whose elements are all zero is called null and is denoted by (0), or simply 0. For example,

.

Main diagonal of a square matrix we call the diagonal going from the upper left to the lower right corner.

A square matrix in which all elements below the main diagonal are equal to zero is called triangular matrix.

.

A square matrix in which all elements, except perhaps those on the main diagonal, are equal to zero, is called diagonal matrix. For example, or.

A diagonal matrix in which all diagonal elements are equal to one is called single matrix and is denoted by the letter E. For example, the 3rd order identity matrix has the form .

ACTIONS ON MATRICES

Matrix equality. Two matrices A And B are said to be equal if they have the same number of rows and columns and their corresponding elements are equal a ij = b ij. So if And , That A=B, If a 11 = b 11, a 12 = b 12, a 21 = b 21 And a 22 = b 22.

Transpose. Consider an arbitrary matrix A from m lines and n columns. It can be associated with the following matrix B from n lines and m columns, in which each row is a matrix column A with the same number (hence each column is a row of the matrix A with the same number). So if , That .

This matrix B called transposed matrix A, and the transition from A To B transposition.

Thus, transposition is a reversal of the roles of the rows and columns of a matrix. Matrix transposed to matrix A, usually denoted A T.

Communication between matrix A and its transpose can be written in the form .

For example. Find the matrix transposed of the given one.

Matrix addition. Let the matrices A And B consist of the same number of lines and the same number columns, i.e. have same sizes. Then in order to add matrices A And B needed for matrix elements A add matrix elements B standing in the same places. Thus, the sum of two matrices A And B called a matrix C, which is determined by the rule, for example,

Examples. Find the sum of matrices:

It is easy to verify that matrix addition obeys the following laws: commutative A+B=B+A and associative ( A+B)+C=A+(B+C).

Multiplying a matrix by a number. To multiply a matrix A per number k every element of the matrix is ​​needed A multiply by this number. Thus, the matrix product A per number k there is a new matrix, which is determined by the rule or .

For any numbers a And b and matrices A And B the following equalities hold:

Examples.

Matrix multiplication. This operation is carried out according to a peculiar law. First of all, we note that the sizes of the factor matrices must be consistent. You can multiply only those matrices in which the number of columns of the first matrix coincides with the number of rows of the second matrix (i.e., the length of the first row is equal to the height of the second column). The work matrices A not a matrix B called the new matrix C=AB, the elements of which are composed as follows:

Thus, for example, to obtain the product (i.e. in the matrix C) element located in the 1st row and 3rd column from 13, you need to take the 1st row in the 1st matrix, the 3rd column in the 2nd, and then multiply the row elements by the corresponding column elements and add the resulting products. And other elements of the product matrix are obtained using a similar product of the rows of the first matrix and the columns of the second matrix.

In general, if we multiply a matrix A = (a ij) size m× n to the matrix B = (b ij) size n× p, then we get the matrix C size m× p, whose elements are calculated as follows: element c ij is obtained as a result of the product of elements i th row of the matrix A to the corresponding elements j th matrix column B and their additions.

From this rule it follows that you can always multiply two square matrices of the same order, and as a result we obtain a square matrix of the same order. In particular, a square matrix can always be multiplied by itself, i.e. square it.

Another important case is the multiplication of a row matrix by a column matrix, and the width of the first must be equal to the height of the second, resulting in a first-order matrix (i.e. one element). Really,

.

Examples.

So these simple examples show that the matrices, generally speaking, do not commute with each other, i.e. A∙B ≠ B∙A . Therefore, when multiplying matrices, you need to carefully monitor the order of the factors.

It can be verified that matrix multiplication obeys associative and distributive laws, i.e. (AB)C=A(BC) And (A+B)C=AC+BC.

It is also easy to check that when multiplying a square matrix A to the identity matrix E of the same order we again obtain a matrix A, and AE=EA=A.

The following interesting fact can be noted. As you know, the product of 2 non-zero numbers is not equal to 0. For matrices this may not be the case, i.e. the product of 2 non-zero matrices may turn out to be equal to the zero matrix.

For example, If , That

.

THE CONCEPT OF DETERMINANTS

Let a second-order matrix be given - a square matrix consisting of two rows and two columns .

Second order determinant corresponding to a given matrix is ​​the number obtained as follows: a 11 a 22 – a 12 a 21.

The determinant is indicated by the symbol .

So, in order to find the second-order determinant, you need to subtract the product of the elements along the second diagonal from the product of the elements of the main diagonal.

Examples. Calculate second order determinants.

Similarly, we can consider a third-order matrix and its corresponding determinant.

Third order determinant, corresponding to a given square matrix of third order, is the number denoted and obtained as follows:

.

Thus, this formula gives the expansion of the third-order determinant in terms of the elements of the first row a 11, a 12, a 13 and reduces the calculation of the third-order determinant to the calculation of the second-order determinants.

Examples. Calculate the third order determinant.

Similarly, one can introduce the concepts of determinants of the fourth, fifth, etc. orders, lowering their order by expanding into the elements of the 1st row, with the “+” and “–” signs of the terms alternating.

So, unlike a matrix, which is a table of numbers, a determinant is a number that is assigned to the matrix in a certain way.

Points in space, product Rv gives another vector that determines the position of the point after rotation. If v is a row vector, the same transformation can be obtained using vR T, where R T - transposed to R matrix.

Encyclopedic YouTube

1 / 5

C# - Console - Olympiad - Square Spiral

Matrix: definition and basic concepts

Where to get strength and inspiration Recharging the 4 square matrix

Sum and difference of matrices, multiplication of a matrix by a number

Transposed matrix / Transposed matrix

Subtitles

Main diagonal

Elements a ii (i = 1, ..., n) form the main diagonal of a square matrix. These elements lie on an imaginary straight line from the left top corner to the lower right corner of the matrix. For example, the main diagonal of the 4x4 matrix in the figure contains the elements a 11 = 9, a 22 = 11, a 33 = 4, a 44 = 10.

The diagonal of a square matrix passing through the lower left and upper right corners is called side.

Special types

Name	Example with n = 3
Diagonal matrix	[ a 11 0 0 0 a 22 0 0 0 a 33 ] (\displaystyle (\begin(bmatrix)a_(11)&0&0\\0&a_(22)&0\\0&0&a_(33)\end(bmatrix)))
Lower triangular matrix	[ a 11 0 0 a 21 a 22 0 a 31 a 32 a 33 ] (\displaystyle (\begin(bmatrix)a_(11)&0&0\\a_(21)&a_(22)&0\\a_(31)&a_( 32)&a_(33)\end(bmatrix)))
Upper triangular matrix	[ a 11 a 12 a 13 0 a 22 a 23 0 0 a 33 ] (\displaystyle (\begin(bmatrix)a_(11)&a_(12)&a_(13)\\0&a_(22)&a_(23)\\ 0&0&a_(33)\end(bmatrix)))

Diagonal and triangular matrices

If all elements outside the main diagonal are zero, A called diagonal. If all elements above (below) the main diagonal are zero, A called the lower (upper) triangular matrix.

Identity matrix

Q(x) = x T Ax

accepts only positive values(respectively, negative values or both). If quadratic form takes only non-negative (respectively, only non-positive) values, a symmetric matrix is ​​called positively semidefinite (respectively, negative semidefinite). A matrix will be indeterminate if it is neither positive nor negative semidefinite.

A symmetric matrix is ​​positive definite if and only if all of its eigenvalues are positive. The table on the right shows two possible cases for 2x2 matrices.

If we use two different vectors, we obtain a bilinear form associated with A:

B A (x, y) = x T Ay.

Orthogonal matrix

Orthogonal matrix is a square matrix with real elements whose columns and rows are orthogonal unit vectors (i.e., orthonormal). You can also define an orthogonal matrix as a matrix whose inverse is equal to its transpose:

A T = A − 1 , (\displaystyle A^(\mathrm (T) )=A^(-1),)

where does it come from

A T A = A A T = E (\displaystyle A^(T)A=AA^(T)=E),

Orthogonal matrix A always reversible ( A −1 = A T), unitary ( A −1 = A*), and normal ( A*A = A.A.*). The determinant of any orthonormal matrix is ​​either +1 or −1. As a linear mapping, any orthonormal matrix with determinant +1 is a simple rotation, while any orthonormal matrix with determinant −1 is either a simple reflection or a composition of reflection and rotation.

Operations

Track

Determinant det( A) or | A| square matrix A is a number that determines some properties of the matrix. A matrix is ​​invertible if and only if its determinant is nonzero.