Tõenäosusteooria ja matemaatilise statistika alused. Tõenäosusteooria ja matemaatilise statistika põhimõisted
Tõenäosusteooria ja matemaatiline statistika
- Agekyan T.A. Veateooria alused astronoomidele ja füüsikutele (2. väljaanne). M.: Nauka, 1972 (djvu, 2,44 M)
- Agekyan T.A. Tõenäosusteooria astronoomidele ja füüsikutele. M.: Nauka, 1974 (djvu, 2,59 M)
- Anderson T. Aegridade statistiline analüüs. M.: Mir, 1976 (djvu, 14 M)
- Bakelman I.Ya. Werner A.L. Kantor B.E. Sissejuhatus diferentsiaalgeomeetriasse "üldiselt". M.: Nauka, 1973 (djvu, 5,71 M)
- Bernstein S.N. Tõenäosusteooria. M.-L.: GI, 1927 (djvu, 4,51 M)
- Billingsley P. Tõenäosusmõõtude konvergents. M.: Nauka, 1977 (djvu, 3,96 M)
- Kast J. Jenkins G. Aegridade analüüs: prognoos ja juhtimine. 1. number. M.: Mir, 1974 (djvu, 3,38 M)
- Kast J. Jenkins G. Aegridade analüüs: prognoos ja juhtimine. 2. number. M.: Mir, 1974 (djvu, 1,72 M)
- Borel E. Tõenäosus ja usaldusväärsus. M.: Nauka, 1969 (djvu, 1,19 M)
- Van der Waerden B.L. Matemaatika statistika. M.: IL, 1960 (djvu, 6,90 M)
- Vapnik V.N. Sõltuvuste taastamine empiiriliste andmete põhjal. M.: Nauka, 1979 (djvu, 6.18M)
- Ventzel E.S. Sissejuhatus operatsiooniuuringutesse. M.: Nõukogude raadio, 1964 (djvu, 8.43M)
- Ventzel E.S. Mänguteooria elemendid (2. väljaanne). Sari: Populaarsed loengud matemaatikast. 32. number M.: Nauka, 1961 (djvu, 648 K)
- Ventstel E.S. Tõenäosusteooria (4. väljaanne). M.: Nauka, 1969 (djvu, 8,05 M)
- Ventstel E.S., Ovcharov L.A. Tõenäosusteooria. Ülesanded ja harjutused. M.: Nauka, 1969 (djvu, 7,71 M)
- Vilenkin N.Ya., Potapov V.G. Praktiline tõenäosusteooria töövihik kombinatoorika ja matemaatilise statistika elementidega. M.: Haridus, 1979 (djvu, 1,12M)
- Gmurman V.E. Tõenäosusteooria ja matemaatilise statistika ülesannete lahendamise juhend (3. trükk). M.: Kõrgem. kool, 1979 (djvu, 4,24 M)
- Gmurman V.E. Tõenäosusteooria ja matemaatiline statistika (4. trükk). M.: Kõrgkool, 1972 (djvu, 3,75 M)
- Gnedenko B.V., Kolmogorov A.N. Sõltumatute juhuslike muutujate summade piirjaotused. M.-L.: GITTL, 1949 (djvu, 6,26 M)
- Gnedenko B.V., Khinchin A.Ya. Elementaarne sissejuhatus tõenäosusteooriasse (7. väljaanne). M.: Nauka, 1970 (djvu, 2,48 M)
- Tamm J.L. Tõenäosuslikud protsessid. M.: IL, 1956 (djvu, 8,48 M)
- David G. Tavastatistika. M.: Nauka, 1979 (djvu, 2,87 M)
- Ibragimov I.A., Linnik Yu.V. Sõltumatud ja statsionaarsed seotud suurused. M.: Nauka, 1965 (djvu, 6,05 M)
- Idier V., Dryard D., James F., Rus M., Sadoulet B. Statistilised meetodid eksperimentaalfüüsikas. M.: Atomizdat, 1976 (djvu, 5,95 M)
- Kamalov M.K. Ruutvormide jaotus normaalpopulatsiooni proovides. Taškent: UsSSRi Teaduste Akadeemia, 1958 (djvu, 6,29 M)
- Kassandra O.N., Lebedev V.V. Vaatlustulemuste töötlemine. M.: Nauka, 1970 (djvu, 867 K)
- Katz M. Tõenäosus ja sellega seotud küsimused füüsikas. M.: Mir, 1965 (djvu, 3,67 M)
- Katz M. Mitmed füüsika ja matemaatika tõenäosusprobleemid. M.: Nauka, 1967 (djvu, 1,50 M)
- Katz M. Statistiline sõltumatus tõenäosusteoorias, analüüsis ja arvuteoorias. M.: IL, 1963 (djvu, 964 K)
- Kendall M., Moran P. Geomeetrilised tõenäosused. M.: Nauka, 1972 (djvu, 1,40 M)
- Kendall M., Stewart A. 2. köide. Statistilised järeldused ja seosed. M.: Nauka, 1973 (djvu, 10 M)
- Kendall M., Stewart A. 3. köide. Mitmemõõtmeline statistiline analüüs ja aegread. M.: Nauka, 1976 (djvu, 7.96M)
- Kendall M., Stewart A. Vol. 1. Jaotuste teooria. M.: Nauka, 1965 (djvu, 6.02M)
- Kolmogorov A.N. Tõenäosusteooria põhimõisted (2. trükk) M.: Nauka, 1974 (djvu, 2,14M)
- Koltšin V.F., Sevastjanov B.A., Tšistjakov V.P. Juhuslikud paigutused. M.: Nauka, 1976 (djvu, 2,96 M)
- Kramer G. Statistika matemaatilised meetodid (2. trükk). M.: Mir, 1976 (djvu, 9.63M)
- Leman E. Statistiliste hüpoteeside testimine. M.: Teadus. 1979. aastal (djvu, 5.18M)
- Linnik Yu.V., Ostrovski I.V. Juhuslike suuruste ja vektorite dekompositsioonid. M.: Nauka, 1972 (djvu, 4,86M)
- Likholetov I.I., Matskevitš I.P. Juhend kõrgema matemaatika, tõenäosusteooria ja matemaatilise statistika probleemide lahendamiseks (2. trükk). Mn.: Vysh. kool, 1969 (djvu, 4,99 miljonit)
- Loev M. Tõenäosusteooria. M.: IL, 1962 (djvu, 7,38 M)
- Malakhov A.N. Juhuslike mitte-Gaussi protsesside ja nende teisenduste kumulantanalüüs. M.: Sov. raadio, 1978 (djvu, 6,72 M)
- Meshalkin L.D. Tõenäosusteooria ülesannete kogu. M.: MSU, 1963 (djvu, 1 004 K)
- Mitropolsky A.K. Hetketeooria. M.-L.: GIKSL, 1933 (djvu, 4,49 M)
- Mitropolsky A.K. Statistilise andmetöötluse tehnikad (2. väljaanne). M.: Nauka, 1971 (djvu, 8,35 M)
- Mosteller F., Rurke R., Thomas J. Tõenäosus. M.: Mir, 1969 (djvu, 4,82 M)
- Nalimov V.V. Matemaatilise statistika rakendamine aine analüüsimisel. M.: GIFML, 1960 (djvu, 4.11M)
- Neveu J. Tõenäosusteooria matemaatilised alused. M.: Mir, 1969 (djvu, 3,62 M)
- Preston K. Matemaatika. Uus välisteaduses nr.7. Gibbsi olekud loendatavatel komplektidel. M.: Mir, 1977 (djvu, 2,15 M)
- Saveljev L.Ya. Elementaarne tõenäosusteooria. 1. osa. Novosibirsk: NSU, 2005 (
Paljud tunnevad „tõenäosusteooria“ kontseptsiooni silmitsi seistes hirmu, arvates, et see on midagi tohutut, väga keerulist. Kuid tegelikult pole kõik nii traagiline. Täna vaatleme tõenäosusteooria põhikontseptsiooni ja õpime konkreetsete näidete abil probleeme lahendama.
Teadus
Mida uurib selline matemaatika haru nagu "tõenäosusteooria"? Ta märgib mustreid ja koguseid. Teadlased hakkasid selle teema vastu huvi tundma XVIII sajandil, kui nad hasartmänge uurisid. Tõenäosusteooria põhikontseptsioon on sündmus. See on mis tahes fakt, mis on kindlaks tehtud kogemuse või vaatluse kaudu. Aga mis on kogemus? Teine tõenäosusteooria põhikontseptsioon. See tähendab, et see asjaolude kogum ei loodud juhuslikult, vaid konkreetsel eesmärgil. Mis puutub vaatlusse, siis siin uurija ise ei osale eksperimendis, vaid on lihtsalt nende sündmuste tunnistaja, ta ei mõjuta toimuvat kuidagi.
Sündmused
Saime teada, et tõenäosusteooria põhikontseptsioon on sündmus, kuid me ei arvestanud klassifikatsiooniga. Kõik need on jagatud järgmistesse kategooriatesse:
- Usaldusväärne.
- Võimatu.
- Juhuslik.
Olenemata sellest, millised sündmused need on, mida vaadeldud või kogemuse käigus tekitati, kuuluvad need kõik sellele klassifikatsioonile. Kutsume teid iga tüübiga eraldi tutvuma.
Usaldusväärne üritus

See on asjaolu, mille puhul on võetud vajalikud meetmed. Olemuse paremaks mõistmiseks on parem tuua paar näidet. Selle seaduse alla kuuluvad füüsika, keemia, majandus ja kõrgem matemaatika. Tõenäosusteooria sisaldab sellist olulist mõistet nagu usaldusväärne sündmus. siin on mõned näidised:
- Töötame ja saame hüvitist töötasu näol.
- Eksamid sooritasime hästi, läbisime konkursi ja selle eest saame tasu õppeasutusse sisseastumise näol.
- Investeerisime raha panka ja vajadusel saame selle tagasi.
Sellised sündmused on usaldusväärsed. Kui oleme kõik vajalikud tingimused täitnud, saame kindlasti oodatud tulemuse.
Võimatud sündmused
Nüüd käsitleme tõenäosusteooria elemente. Teeme ettepaneku liikuda edasi järgmist tüüpi sündmuste, nimelt võimatu selgituse juurde. Esmalt sätestame kõige olulisema reegli – võimatu sündmuse tõenäosus on null.
Sellest sõnastusest ei saa probleemide lahendamisel kõrvale kalduda. Selguse huvides on siin näited sellistest sündmustest:
- Vesi külmus temperatuuril pluss kümme (see on võimatu).
- Elektripuudus ei mõjuta tootmist kuidagi (sama võimatu nagu eelmises näites).
Rohkem näiteid tuua ei tasu, kuna ülalkirjeldatu peegeldab väga selgelt selle kategooria olemust. Võimatut sündmust ei toimu katse ajal mitte mingil juhul.
Juhuslikud sündmused

Elementide uurimisel tuleks seda konkreetset tüüpi sündmusele pöörata erilist tähelepanu. Seda uurib teadus. Kogemuse tulemusena võib midagi juhtuda, aga ei pruugi. Lisaks saab testi läbi viia piiramatu arv kordi. Eredate näidete hulka kuuluvad:
- Mündi viskamine on kogemus või proovikivi, peade maandumine on sündmus.
- Palli pimesi kotist välja tõmbamine on proovikivi, punase palli saamine on sündmus ja nii edasi.
Selliseid näiteid võib olla piiramatu arv, kuid üldiselt peaks olemus olema selge. Sündmuste kohta saadud teadmiste kokkuvõtmiseks ja süstematiseerimiseks on toodud tabel. Tõenäosusteooria uurib ainult viimast tüüpi kõigist esitatud.
Nimi | määratlus | |
Usaldusväärne | Sündmused, mis toimuvad teatud tingimuste täitmisel 100% garantiiga. | Vastuvõtt õppeasutusse sisseastumiseksami hästi sooritamisel. |
Võimatu | Sündmused, mis ei juhtu mitte mingil juhul. | Plusskolmekümne soojakraadi juures sajab lund. |
Juhuslik | Sündmus, mis võib katse/testi ajal toimuda, kuid ei pruugi. | Tabamus või möödalaskmine korvpalli rõngasse viskamisel. |
Seadused
Tõenäosusteooria on teadus, mis uurib sündmuse toimumise võimalikkust. Nagu teistelgi, on sellel teatud reeglid. On olemas järgmised tõenäosusteooria seadused:
- Juhuslike muutujate jadade konvergents.
- Suurte arvude seadus.
Millegi keerulise võimaluse arvutamisel saate lihtsate sündmuste kogumit kasutada, et tulemus oleks lihtsam ja kiirem. Pange tähele, et tõenäosusteooria seadusi on teatud teoreemide abil lihtne tõestada. Soovitame teil esmalt tutvuda esimese seadusega.
Juhuslike muutujate jadade konvergents

Pange tähele, et konvergentsi on mitut tüüpi:
- Juhuslike muutujate jada koondub tõenäosusega.
- Peaaegu võimatu.
- Keskmine ruudu konvergents.
- Jaotuse konvergents.
Nii et kohe on väga raske olemust mõista. Siin on määratlused, mis aitavad teil seda teemat mõista. Alustame esimese vaatega. Jada nimetatakse koonduv tõenäosus, kui on täidetud järgmine tingimus: n kaldub lõpmatuseni, on arv, milleni jada kaldub, suurem kui null ja ühele lähedane.
Liigume edasi järgmise vaate juurde, peaaegu kindlasti. Jada väidetavalt läheneb peaaegu kindlasti juhuslikule suurusele, kus n kaldub lõpmatuseni ja P kaldub ühtsusele lähedasele väärtusele.
Järgmine tüüp on keskmine ruudu konvergents. SC konvergentsi kasutamisel taandatakse vektorjuhuslike protsesside uurimine nende koordinaatjuhuslike protsesside uurimisele.
Jääb alles viimane tüüp, vaatame seda lühidalt, et saaksime liikuda otse probleemide lahendamise juurde. Jaotuse lähenemisel on teine nimi - "nõrk" ja selgitame hiljem, miks. Nõrk konvergents on jaotusfunktsioonide konvergents piirava jaotusfunktsiooni järjepidevuse kõigis punktides.
Kindlasti peame kinni oma lubadusest: nõrk konvergents erineb kõigest eelnevast selle poolest, et tõenäosusruumis pole juhuslikku suurust defineeritud. See on võimalik, kuna tingimus moodustatakse ainult jaotusfunktsioone kasutades.
Suurte arvude seadus
Tõenäosusteooria teoreemid, näiteks:
- Tšebõševi ebavõrdsus.
- Tšebõševi teoreem.
- Tšebõševi üldistatud teoreem.
- Markovi teoreem.
Kui arvestada kõiki neid teoreeme, võib see küsimus venida mitukümmend lehte. Meie põhiülesanne on tõenäosusteooria rakendamine praktikas. Soovitame teil seda kohe teha. Kuid enne seda vaatame tõenäosusteooria aksioome, need on peamised abilised probleemide lahendamisel.
Aksioomid

Esimesega kohtusime juba siis, kui rääkisime võimatust sündmusest. Pidagem meeles: võimatu sündmuse tõenäosus on null. Tõime väga ilmeka ja meeldejääva näite: lund sadas maha kolmekümnekraadise õhutemperatuuri juures.
Teine on järgmine: usaldusväärne sündmus toimub tõenäosusega, mis on võrdne ühega. Nüüd näitame, kuidas seda matemaatilises keeles kirjutada: P(B)=1.
Kolmandaks: juhuslik sündmus võib juhtuda, kuid ei pruugi juhtuda, kuid võimalus on alati nullist üheni. Mida lähemal on väärtus ühele, seda suuremad on võimalused; kui väärtus läheneb nullile, on tõenäosus väga väike. Kirjutame selle matemaatilises keeles: 0<Р(С)<1.
Vaatleme viimast, neljandat aksioomi, mis kõlab nii: kahe sündmuse summa tõenäosus on võrdne nende tõenäosuste summaga. Kirjutame selle matemaatilises keeles: P(A+B)=P(A)+P(B).
Tõenäosusteooria aksioomid on kõige lihtsamad reeglid, mida pole raske meeles pidada. Proovime lahendada mõned probleemid juba omandatud teadmiste põhjal.
Loteriipilet

Kõigepealt vaatame kõige lihtsamat näidet – loterii. Kujutage ette, et ostsite hea õnne nimel ühe loteriipileti. Kui suur on tõenäosus, et võidate vähemalt kakskümmend rubla? Kokku osaleb ringluses tuhat piletit, millest ühel on auhinnaks viissada rubla, kümnel on sada rubla, viiekümnel on preemiaks kakskümmend ja sajal on viis. Tõenäosusprobleemid põhinevad õnne võimaluse leidmisel. Nüüd analüüsime koos ülaltoodud ülesande lahendust.
Kui kasutame viiesaja rubla suuruse võidu tähistamiseks tähte A, on A saamise tõenäosus 0,001. Kuidas me selle saime? Peate lihtsalt jagama "õnnelike" piletite arvu nende koguarvuga (antud juhul: 1/1000).
B on saja rubla võit, tõenäosus on 0,01. Nüüd tegutsesime samal põhimõttel nagu eelmises toimingus (10/1000)
C - võidud on kakskümmend rubla. Leiame tõenäosuse, see on 0,05.
Ülejäänud piletid meid ei huvita, kuna nende auhinnafond on tingimuses märgitust väiksem. Rakendame neljandat aksioomi: Tõenäosus võita vähemalt paarkümmend rubla on P(A)+P(B)+P(C). Täht P tähistab antud sündmuse toimumise tõenäosust, oleme need juba varasemates tegevustes leidnud. Jääb üle vaid vajalikud andmed kokku liita ja vastuseks saame 0,061. See number on vastus ülesande küsimusele.
Kaardipakk
Tõenäosusteooria probleemid võivad olla keerulisemad; võtame näiteks järgmise ülesande. Teie ees on kolmekümne kuuest kaardist koosnev pakk. Sinu ülesandeks on tõmmata kaks kaarti järjest ilma stäkki segamata, esimene ja teine kaart peavad olema ässad, mast ei oma tähtsust.
Esiteks leiame tõenäosuse, et esimene kaart on äss, selleks jagame neli kolmekümne kuuega. Nad panid selle kõrvale. Me võtame välja teise kaardi, see on äss, mille tõenäosus on kolm kolmkümmend viiendikku. Teise sündmuse tõenäosus sõltub sellest, millise kaardi me esimesena tõmbasime, mõtleme, kas see oli äss või mitte. Sellest järeldub, et sündmus B sõltub sündmusest A.
Järgmise sammuna tuleb leida samaaegse toimumise tõenäosus ehk korrutame A ja B. Nende korrutis leitakse järgmiselt: korrutame ühe sündmuse tõenäosuse teise sündmuse tingimusliku tõenäosusega, mille arvutame, eeldades, et esimene juhtus, st tõmbasime esimese kaardiga ässa.
Et kõik oleks selge, nimetagem sellist elementi sündmusteks. See arvutatakse eeldusel, et sündmus A on toimunud. See arvutatakse järgmiselt: P(B/A).
Jätkame oma ülesande lahendamist: P(A * B) = P(A) * P(B/A) või P(A * B) = P(B) * P(A/B). Tõenäosus on võrdne (4/36) * ((3/35)/(4/36). Arvutame ümardades lähima sajandikuni. Saime: 0,11 * (0,09/0,11) = 0,11 * 0, 82 = 0,09 Tõenäosus, et loosime kaks ässa järjest, on üheksa sajandikku.Väärtus on väga väike, sellest järeldub, et sündmuse toimumise tõenäosus on äärmiselt väike.
Unustatud number
Teeme ettepaneku analüüsida veel mitmeid tõenäosusteooriaga uuritavate ülesannete variante. Mõnede nende lahendamise näiteid olete selles artiklis juba näinud Proovime lahendada järgmise probleemi: poiss unustas oma sõbra telefoninumbri viimase numbri, kuid kuna kõne oli väga oluline, hakkas ta kõike ükshaaval valima. . Peame arvutama tõenäosuse, et ta ei helista rohkem kui kolm korda. Probleemi lahendus on kõige lihtsam, kui on teada tõenäosusteooria reeglid, seadused ja aksioomid.
Enne lahenduse otsimist proovige see ise lahendada. Teame, et viimane number võib olla nullist üheksani, see tähendab kokku kümme väärtust. Tõenäosus õige kätte saada on 1/10.
Järgmisena peame kaaluma sündmuse päritolu võimalusi, oletame, et poiss arvas õigesti ja kirjutas kohe õige, sellise sündmuse tõenäosus on 1/10. Teine võimalus: esimene kõne jääb vahele ja teine on sihtmärgil. Arvutame sellise sündmuse tõenäosuse: korrutame 9/10 1/9-ga ja tulemuseks saame ka 1/10. Kolmas variant: esimene ja teine kõne osutusid valel aadressil, alles kolmandaga jõudis poiss sinna, kuhu tahtis. Arvutame sellise sündmuse tõenäosuse: 9/10 korrutatuna 8/9 ja 1/8-ga, tulemuseks on 1/10. Meid ei huvita muud variandid vastavalt probleemi tingimustele, seega tuleb saadud tulemused lihtsalt kokku liita, lõpuks on meil 3/10. Vastus: tõenäosus, et poiss helistab mitte rohkem kui kolm korda, on 0,3.
Kaardid numbritega

Teie ees on üheksa kaarti, millest igaühele on kirjutatud number ühest üheksani, numbreid ei korrata. Need pandi karpi ja segati korralikult läbi. Peate arvutama selle tõenäosuse
- ilmub paarisarv;
- kahekohaline.
Enne lahenduse juurde asumist sätestame, et m on edukate juhtumite arv ja n on valikute koguarv. Leiame tõenäosuse, et arv on paaris. Pole keeruline arvutada, et paarisarvu on neli, see on meie m, kokku on üheksa võimalikku varianti, see tähendab, et m=9. Siis on tõenäosus 0,44 ehk 4/9.
Vaatleme teist juhtumit: valikute arv on üheksa ja edukaid tulemusi ei saa üldse olla, see tähendab, et m võrdub nulliga. Ka tõenäosus, et väljatõmmatud kaart sisaldab kahekohalist numbrit, on null.
SISSEJUHATUS
Paljud asjad on meile arusaamatud mitte sellepärast, et meie mõisted on nõrgad;
kuid kuna need asjad ei kuulu meie mõistete hulka.
Kozma Prutkov
Matemaatika õppimise põhieesmärk keskkoolis spetsialiseerunud õppeasutustes on anda õpilastele matemaatiliste teadmiste ja oskuste kogum, mis on vajalik teiste matemaatikat ühel või teisel määral kasutavate programmidistsipliinide õppimiseks, praktiliste arvutuste tegemiseks, kujundamiseks ja arendamiseks. loogilisest mõtlemisest.
Selles töös on kõik matemaatika sektsiooni "Tõenäosusteooria ja matemaatilise statistika alused" põhikontseptsioonid, mis on sätestatud programmis ja keskerihariduse riiklikus haridusstandardis (Vene Föderatsiooni haridusministeerium. M., 2002). ), tutvustatakse järjepidevalt, sõnastatakse peamised teoreemid, millest enamik ei ole tõestatud . Käsitletakse peamisi probleeme ja nende lahendamise meetodeid ning tehnoloogiaid nende meetodite rakendamiseks praktiliste probleemide lahendamisel. Ettekandele on lisatud üksikasjalikud kommentaarid ja arvukad näited.
Metoodilisi juhendeid saab kasutada õpitava materjaliga esmasel tutvumisel, loengutes märkmete tegemisel, praktilisteks tundideks valmistumisel, omandatud teadmiste, oskuste ja vilumuste kinnistamiseks. Lisaks on käsiraamat kasulik ka bakalaureuseõppe üliõpilastele võrdlusvahendina, mis võimaldab neil varem õpitut kiiresti meelde tuletada.
Töö lõpus on näited ja ülesanded, mida õpilased saavad sooritada enesekontrolli režiimis.
Juhend on mõeldud osa- ja täiskoormusega õppijatele.
PÕHIMÕISTED
Tõenäosusteooria uurib massiliste juhuslike sündmuste objektiivseid mustreid. See on matemaatilise statistika teoreetiline alus, mis tegeleb vaatlustulemuste kogumise, kirjeldamise ja töötlemise meetodite väljatöötamisega. Vaatluste (testide, katsete) kaudu, s.o. kogemus selle sõna laiemas tähenduses, tekib teadmine reaalse maailma nähtustest.
Oma praktilises tegevuses puutume sageli kokku nähtustega, mille tulemust ei ole võimalik ennustada, mille tulemus sõltub juhusest.
Juhuslikku nähtust saab iseloomustada selle esinemiste arvu ja katsete arvu suhtega, millest igaühes võib see kõigi katsete samadel tingimustel esineda või mitte esineda.
Tõenäosusteooria on matemaatika haru, milles uuritakse juhuslikke nähtusi (sündmusi) ja tuvastatakse mustreid, kui neid massiliselt korratakse.
Matemaatiline statistika on matemaatika haru, mis tegeleb statistiliste andmete kogumise, süstematiseerimise, töötlemise ja kasutamise meetodite uurimisega teaduspõhiste järelduste tegemiseks ja otsuste tegemiseks.
Sel juhul mõistetakse statistiliste andmete all arvude kogumit, mis esindavad meid huvitavate uuritavate objektide omaduste kvantitatiivseid omadusi. Statistilised andmed saadakse spetsiaalselt kavandatud katsete ja vaatluste tulemusena.
Statistilised andmed sõltuvad oma olemuselt paljudest juhuslikest teguritest, mistõttu on matemaatiline statistika tihedalt seotud tõenäosusteooriaga, mis on selle teoreetiline alus.
I. TÕENÄOSUS. TÕENÄOSUSTE LIIDEMIS- JA KORRUMISTEOREEMID
1.1. Kombinatoorika põhimõisted
Matemaatika harus, mida nimetatakse kombinatoorikaks, lahendatakse mõningaid probleeme, mis on seotud hulkade arvestamise ja nende hulkade elementide erinevate kombinatsioonide koostisega. Näiteks kui võtame 10 erinevat arvu 0, 1, 2, 3,: , 9 ja teeme neist kombinatsioonid, saame erinevad arvud, näiteks 143, 431, 5671, 1207, 43 jne.
Näeme, et mõned neist kombinatsioonidest erinevad ainult numbrite järjestuse poolest (näiteks 143 ja 431), teised - nendes sisalduvate numbrite poolest (näiteks 5671 ja 1207) ja teised erinevad ka numbrite arvu poolest. (näiteks 143 ja 43).
Seega vastavad saadud kombinatsioonid erinevatele tingimustele.
Sõltuvalt kompositsioonireeglitest saab eristada kolme tüüpi kombinatsioone: permutatsioonid, paigutused, kombinatsioonid.
Kõigepealt tutvume kontseptsiooniga faktoriaalne.
Nimetatakse kõigi naturaalarvude korrutis 1 kuni n (kaasa arvatud). n-faktoriaalne ja kirjutada.
Arvutage: a) ; b) ; V) .
Lahendus. A) .
b) Alates ![]() , siis saame selle sulgudest välja jätta
, siis saame selle sulgudest välja jätta
Siis saame
V) ![]() .
.
Ümberkorraldused.
Kombinatsiooni n elemendist, mis erinevad üksteisest ainult elementide järjestuse poolest, nimetatakse permutatsiooniks.
Permutatsioonid on tähistatud sümboliga P n , kus n on igas permutatsioonis sisalduvate elementide arv. ( R- prantsuskeelse sõna esimene täht permutatsioon- ümberkorraldamine).
Permutatsioonide arvu saab arvutada valemi abil
või kasutades faktoriaali:
Pidagem seda meeles 0!=1 ja 1!=1.
Näide 2. Mitmel viisil saab kuut erinevat raamatut ühele riiulile paigutada?
Lahendus. Vajalik arv viise võrdub 6 elemendi permutatsioonide arvuga, st.
Paigutused.
Postitused alates m elemendid sisse n igaühes nimetatakse selliseid ühendeid, mis erinevad üksteisest kas elementide endi (vähemalt ühe) või nende paigutuse järje poolest.
Paigutused on tähistatud sümboliga, kus m- kõigi saadaolevate elementide arv, n- elementide arv igas kombinatsioonis. ( A- prantsuskeelse sõna esimene täht kokkulepe, mis tähendab "paigutust, korda seadmist").
Samas arvatakse, et nm.
Paigutuste arvu saab arvutada valemi abil
![]() ,
,
need. kõigi võimalike paigutuste arv alates m elemendid poolt n võrdub tootega n järjestikused täisarvud, millest suurim on m.
Kirjutame selle valemi faktoriaalses vormis:
Näide 3. Mitu võimalust saab viie taotleja kohta koostada kolme vautšeri jagamiseks erineva profiiliga sanatooriumidele?
Lahendus. Vajalik valikute arv võrdub 3 elemendi 5 elemendi paigutuste arvuga, st.
![]() .
.
Kombinatsioonid.
Kombinatsioonid on kõik võimalikud kombinatsioonid m elemendid poolt n, mis erinevad üksteisest vähemalt ühe elemendi poolest (siin m Ja n- naturaalarvud ja n m).
Kombinatsioonide arv m elemendid poolt n on tähistatud ( KOOS- prantsuskeelse sõna esimene täht kombinatsioon- kombinatsioon).
Üldiselt arv m elemendid poolt n võrdne paigutuste arvuga alates m elemendid poolt n, jagatud permutatsioonide arvuga alates n elemendid:
Kasutades paigutuste ja permutatsioonide arvu faktoriaalvalemeid, saame:
![]()
Näide 4. 25-liikmelises meeskonnas peate eraldama neli teatud piirkonnas töötamiseks. Kui mitmel viisil saab seda teha?
Lahendus. Kuna valitud nelja inimese järjekord ei oma tähtsust, on selleks võimalusi.
Leiame esimese valemi abil
![]() .
.
Lisaks kasutatakse ülesannete lahendamisel järgmisi valemeid, mis väljendavad kombinatsioonide põhiomadusi:
(definitsiooni järgi eeldavad nad ja);
![]() .
.
1.2. Kombinatoorsete ülesannete lahendamine
Ülesanne 1. Teaduskonnas õpitakse 16 ainet. Esmaspäevaks peate oma ajakavasse panema 3 ainet. Kui mitmel viisil saab seda teha?
Lahendus. Kolme üksuse 16-st ajastamiseks on sama palju võimalusi kui saate korraldada 16 üksuse paigutust 3 kaupa.
Ülesanne 2. 15 objekti hulgast tuleb valida 10 objekti. Kui mitmel viisil saab seda teha?

Ülesanne 3. Võistlusest võttis osa neli võistkonda. Mitu võimalust on nende vahel istekohtade jaotamiseks?
![]() .
.
Ülesanne 4. Mitmel viisil saab moodustada kolmest sõdurist ja ühest ohvitserist koosneva patrulli, kui seal on 80 sõdurit ja 3 ohvitseri?
Lahendus. Patrullis saab valida sõduri
viisidel ja ohvitserid viisidel. Kuna iga ohvitser võib minna iga sõdurite meeskonnaga, on võimalusi ainult nii palju.
Ülesanne 5. Leia , kui on teada, et .
Alates , saame
![]() ,
,
![]() ,
,
![]()
Kombinatsiooni määratlusest järeldub, et . See. .
1.3. Juhusliku sündmuse mõiste. Sündmuste tüübid. Sündmuse tõenäosus
Nimetatakse mis tahes tegevus, nähtus, vaatlus, millel on mitu erinevat tulemust ja mis on teostatud teatud tingimustel test.
Selle tegevuse või vaatluse tulemust nimetatakse sündmus .
Kui sündmus antud tingimustel võib juhtuda või mitte juhtuda, siis seda nimetatakse juhuslik . Kui sündmus on kindel, siis seda nimetatakse usaldusväärne ja juhul, kui see ilmselgelt juhtuda ei saa, - võimatu.
Sündmused on nn Sobimatu , kui iga kord on võimalik ilmuda ainult üks neist.
Sündmused on nn liigend , kui teatud tingimustel ei välista ühe neist sündmustest teise esinemist sama katse ajal.
Sündmused on nn vastupidine , kui need katsetingimustes on ainsad tulemused kokkusobimatud.
Sündmused on tavaliselt tähistatud ladina tähestiku suurtähtedega: A, B, C, D, : .
Täielik sündmuste süsteem A 1 , A 2 , A 3 , : , A n on kokkusobimatute sündmuste kogum, millest vähemalt ühe esinemine on antud testi käigus kohustuslik.
Kui terviklik süsteem koosneb kahest kokkusobimatust sündmusest, nimetatakse selliseid sündmusi vastupidiseks ja tähistatakse A ja .
Näide. Karbis on 30 nummerdatud palli. Tehke kindlaks, millised järgmistest sündmustest on võimatud, usaldusväärsed või vastupidised:
võttis välja nummerdatud palli (A);
sai paarisarvuga palli (IN);
sai paaritu numbriga palli (KOOS);
sai palli ilma numbrita (D).
Millised neist moodustavad tervikliku rühma?
Lahendus . A- usaldusväärne üritus; D- võimatu sündmus;
Sisse ja KOOS- vastupidised sündmused.
Kogu sündmuste rühm koosneb A Ja D, V Ja KOOS.
Sündmuse tõenäosust peetakse juhusliku sündmuse toimumise objektiivse võimalikkuse mõõdupuuks.
1.4. Klassikaline tõenäosuse määratlus
Nimetatakse arvu, mis väljendab sündmuse toimumise objektiivse võimalikkuse mõõtu tõenäosus seda sündmust ja seda tähistab sümbol R(A).
Definitsioon. Sündmuse tõenäosus A on antud sündmuse toimumist soodustavate tulemuste m suhe A, numbrile n kõik tulemused (ebajärjekindlad, ainult võimalikud ja võrdselt võimalikud), st. .
Seetõttu on sündmuse tõenäosuse leidmiseks vaja, võttes arvesse testi erinevaid tulemusi, arvutada kõik võimalikud vastuolulised tulemused n, valige meid huvitavate tulemuste arv m ja arvutage suhe m To n.
Sellest määratlusest tulenevad järgmised omadused:
Iga testi tõenäosus on mittenegatiivne arv, mis ei ületa ühte.
Tõepoolest, nõutavate sündmuste arv m on vahemikus . Mõlema osa jagamine n, saame
2. Usaldusväärse sündmuse tõenäosus on võrdne ühega, sest .
3. Võimatu sündmuse tõenäosus on null, kuna .
Ülesanne 1. 1000 piletiga loteriis on 200 võitu. Üks pilet võetakse välja juhuslikult. Kui suur on tõenäosus, et see pilet võidab?
Lahendus. Erinevate tulemuste koguarv on n=1000. Võitmiseks soodsate tulemuste arv on m=200. Valemi järgi saame
![]() .
.
Ülesanne 2. 18 osast koosnevas partiis on 4 defektset. 5 osa valitakse juhuslikult. Leidke tõenäosus, et kaks neist viiest osast on defektsed.
Lahendus. Kõigi võrdselt võimalike sõltumatute tulemuste arv n võrdne kombinatsioonide arvuga 18 korda 5 s.o.
Loendame sündmust A soosiva arvu m. 5 juhuslikult võetud osa hulgas peaks olema 3 head ja 2 defektset. Kahe defektse osa valimise võimaluste arv neljast olemasolevast defektsest on võrdne kombinatsioonide arvuga 4 korda 2:
14 saadaoleva kvaliteetse osa hulgast kolme kvaliteetse osa valimise võimaluste arv on võrdne
![]() .
.
Mis tahes heade osade rühma saab kombineerida mis tahes defektsete osade rühmaga, seega on kombinatsioonide koguarv m ulatub
Sündmuse A nõutav tõenäosus on võrdne sellele sündmusele soodsate tulemuste m arvu ja kõigi võrdselt võimalike sõltumatute tulemuste arvu n suhtega:
![]() .
.
Lõpliku arvu sündmuste summa on sündmus, mis koosneb neist vähemalt ühe toimumisest.
Kahe sündmuse summat tähistatakse sümboliga A+B ja summa n sündmused sümboliga A 1 +A 2 + : +A n.
Tõenäosuste liitmise teoreem.
Kahe kokkusobimatu sündmuse summa tõenäosus on võrdne nende sündmuste tõenäosuste summaga.
Järeldus 1. Kui sündmused A 1, A 2, :,A n moodustavad tervikliku süsteemi, siis on nende sündmuste tõenäosuste summa võrdne ühega.
Järeldus 2. Vastandlike sündmuste tõenäosuste summa ja on võrdne ühega.
![]() .
.
Ülesanne 1. Loteriipileteid on 100. Teatavasti võidab 5 piletit 20 000 rubla, 10 piletit 15 000 rubla, 15 piletit 10 000 rubla, 25 piletit 2000 rubla. ja ülejäänu jaoks ei midagi. Leidke tõenäosus, et ostetud pilet saab vähemalt 10 000 rubla võidu.
Lahendus. Olgu A, B ja C sündmused, mis seisnevad selles, et ostetud pilet saab võidu vastavalt 20 000, 15 000 ja 10 000 rubla. kuna sündmused A, B ja C ei ühildu, siis
Ülesanne 2. Tehnikumi kirjavahetusosakond võtab linnadest vastu kontrolltöid matemaatikas A, B Ja KOOS. Linnalt testi saamise tõenäosus A võrdub 0,6, linnast IN- 0,1. Leia tõenäosus, et järgmine katse tuleb linnast KOOS.
Ema pesi raami ära
Pika suvepuhkuse lõpus on aeg naasta aeglaselt kõrgema matemaatika juurde ja avada pidulikult tühi Verdovi fail, et alustada uue jaotise loomist - . Tunnistan, et esimesed read pole lihtsad, kuid esimene samm on poolel teel, seega soovitan kõigil tutvuda hoolikalt sissejuhatava artikliga, pärast mida on teema valdamine 2 korda lihtsam! Ma ei liialda üldse. …Järgmise 1. septembri eel meenub mulle esimene klass ja aabits…. Tähed moodustavad silpe, silbid moodustavad sõnu, sõnad moodustavad lühikesi lauseid - Ema pesi raami. Pöörde- ja matemaatikastatistika valdamine on sama lihtne kui lugema õppimine! Kuid selleks peate teadma põhitermineid, mõisteid ja nimetusi ning mõningaid konkreetseid reegleid, mida selles õppetunnis käsitletakse.
Aga kõigepealt palun võtke vastu minu õnnitlused kooliaasta alguse puhul (jätkamine, lõpetamine, märkige sobiv) ja võtke vastu kingitus. Parim kingitus on raamat ja iseseisvaks tööks soovitan järgmist kirjandust:
1) Gmurman V.E. Tõenäosusteooria ja matemaatiline statistika
Legendaarne õpik, mis on läbinud üle kümne kordustrükki. Seda eristab arusaadavus ja materjali äärmiselt lihtne esitus ning esimesed peatükid on täiesti kättesaadavad, ma arvan, et juba 6.-7.klassi õpilastele.
2) Gmurman V.E. Juhend tõenäosusteooria ja matemaatilise statistika probleemide lahendamiseks
Sellesama Vladimir Efimovitši lahendusraamat koos üksikasjalike näidete ja probleemidega.
VAJALIKULT laadige mõlemad raamatud alla Internetist või hankige nende paberkandjal originaalid! Töötab ka 60ndate ja 70ndate versioon, mis on mannekeenide jaoks veelgi parem. Ehkki fraas "mannekeenide tõenäosusteooria" kõlab üsna naeruväärselt, kuna peaaegu kõik piirdub elementaarsete aritmeetiliste tehetega. Kohati jätavad nad siiski vahele derivaadid Ja integraalid, kuid seda ainult kohati.
Püüan saavutada sama esitusselguse, kuid pean hoiatama, et minu kursus on suunatud probleemi lahendamine ja teoreetilised arvutused on viidud miinimumini. Seega, kui vajate üksikasjalikku teooriat, teoreemide tõestusi (teoreemid-teoreemid!), siis vaadake õpikut. No kes tahab õppida probleeme lahendama tõenäosusteoorias ja matemaatilises statistikas võimalikult lühikese aja jooksul, järgne mulle!
Alustuseks piisab =)
Artikleid lugedes on soovitatav tutvuda (vähemalt põgusalt) vaadeldavate tüüpide lisaülesannetega. Lehel Valmislahendused kõrgema matemaatika jaoks Postitatakse vastavad pdf-id koos lahendusnäidetega. Samuti osutatakse märkimisväärset abi IDZ 18.1 Ryabushko(lihtsam) ja lahendas IDZ Tšudesenko kogu järgi(keerulisem).
1) Summa kaks sündmust ja sündmust nimetatakse, mis tähendab, et see juhtub või sündmus või sündmus või mõlemad sündmused korraga. Juhul, kui sündmused Sobimatu, viimane valik kaob, see tähendab, et see võib tekkida või sündmus või sündmus .
Reegel kehtib ka suurema hulga terminite, näiteks sündmuse kohta ![]() on see, mis juhtub vähemalt üks sündmustest
on see, mis juhtub vähemalt üks sündmustest ![]() , A kui sündmused ei sobi kokku – siis üks asi ja ainult üks asi sündmus sellest summast: või sündmus, või sündmus, või sündmus, või sündmus, või sündmus .
, A kui sündmused ei sobi kokku – siis üks asi ja ainult üks asi sündmus sellest summast: või sündmus, või sündmus, või sündmus, või sündmus, või sündmus .
Näiteid on palju:
Sündmused (täringu viskamisel 5 punkti ei ilmu) on see, mis välja tuleb või 1, või 2, või 3, või 4, või 6 punkti.
Sündmus (langeb mitte rohkem kaks punkti) on see, et kuvatakse 1 või 2punktid.
Sündmus ![]() (punkte on paarisarv) on see, mis ilmub või 2 või 4 või 6 punkti.
(punkte on paarisarv) on see, mis ilmub või 2 või 4 või 6 punkti.
Sündmus seisneb selles, et kaardipakist tõmmatakse punane kaart (süda). või tamburiin) ja sündmus ![]() – et "pilt" ekstraheeritakse (jack või daam või kuningas võiäss).
– et "pilt" ekstraheeritakse (jack või daam või kuningas võiäss).
Veidi huvitavam on lugu ühisüritustega:
Sündmus on see, et tekilt loositakse klubi või seitse või seitse klubi Vastavalt ülaltoodud määratlusele, vähemalt midagi- või mis tahes klubi või mis tahes seitse või nende "ristmik" - seitse klubi. Lihtne on arvutada, et see sündmus vastab 12 põhitulemusele (9 klubikaarti + 3 ülejäänud seitset).
Sündmus on see, et homme kell 12.00 tuleb VÄHEMALT ÜKS kokkuvõttev ühisüritus, nimelt:
– või on ainult vihm / ainult äike / ainult päike;
– või toimub ainult mõni sündmustepaar (vihm + äike / vihm + päike / äike + päike);
– või kõik kolm sündmust ilmuvad korraga.
See tähendab, et sündmus sisaldab 7 võimalikku tulemust.
Sündmuste algebra teine sammas:
2) Töö kaks sündmust ja nimetada sündmuseks, mis seisneb nende sündmuste ühises esinemises, teisisõnu tähendab korrutamine, et teatud asjaoludel Ja sündmus, Ja sündmus . Sarnane väide kehtib ka suurema hulga sündmuste kohta, näiteks annab teos mõista, et teatud tingimustel see juhtub Ja sündmus, Ja sündmus, Ja sündmus, …, Ja sündmus .
Mõelge testile, mille käigus visatakse kaks münti ja järgmised sündmused:
– 1. mündil ilmuvad pead;
– 1. münt maandab päid;
– 2. mündile ilmuvad pead;
– 2. münt maandab pead.
Seejärel:
Ja 2.) ilmuvad pead;
– sündmus on see, et mõlemal mündil (1 Ja 2.) see on pead;
– sündmus on see, et 1. münt maandub päid Ja 2. münt on sabad;
– sündmus on see, et 1. münt maandub päid Ja 2. mündil on kotkas.
Neid sündmusi on lihtne näha Sobimatu (sest see ei saa olla näiteks 2 pead ja 2 saba korraga) ja vorm täisgrupp (alates arvesse võetud Kõik kahe mündi viskamise võimalikud tagajärjed). Võtame need sündmused kokku: . Kuidas seda kirjet tõlgendada? Väga lihtne – korrutamine tähendab loogilist sidet JA ja lisaks – VÕI. Seega on summa arusaadavas inimkeeles hästi loetav: “tekkib kaks pead või kaks pead või 1. münt maandub päid Ja 2. saba peal või 1. münt maandub päid Ja 2. mündil on kotkas"
See oli näide, kui ühes testis kaasatud on mitu eset, antud juhul kaks münti. Teine levinud skeem praktilistes probleemides on uuesti testimine , kui näiteks sama täringut veeretatakse 3 korda järjest. Näitena kaaluge järgmisi sündmusi:
– 1. viskega saad 4 punkti;
– 2. viskega saad 5 punkti;
– 3. viskega saad 6 punkti.
Siis üritus ![]() on see, et 1. viskega saad 4 punkti Ja 2. viskega saad 5 punkti Ja 3. veeretamisel saad 6 punkti. Ilmselgelt tuleb kuubiku puhul kombinatsioone (tulemusi) oluliselt rohkem kui mündi viskamisel.
on see, et 1. viskega saad 4 punkti Ja 2. viskega saad 5 punkti Ja 3. veeretamisel saad 6 punkti. Ilmselgelt tuleb kuubiku puhul kombinatsioone (tulemusi) oluliselt rohkem kui mündi viskamisel.
...Ma saan aru, et võib-olla pole analüüsitavad näited väga huvitavad, aga need on asjad, millega probleemides sageli kokku puututakse ja millest pääsu pole. Lisaks mündile, kuubik ja kaardipakk, ootavad Sind mitmevärviliste kuulidega urnid, mitmed anonüümsed märklauda tulistavad ja väsimatu töömees, kes pidevalt mingeid detaile välja lihvib =)
Sündmuse tõenäosus
Sündmuse tõenäosus on tõenäosusteooria keskne mõiste. ...Tapjalik loogiline asi, aga kuskilt tuli alustada =) Selle definitsioonile on mitu lähenemist:
;
Tõenäosuse geomeetriline määratlus
;
Tõenäosuse statistiline määratlus
.
Selles artiklis keskendun tõenäosuse klassikalisele definitsioonile, mida kasutatakse õppeülesannetes kõige laiemalt.
Nimetused. Teatud sündmuse tõenäosust tähistab suur ladina täht ja sündmus ise on võetud sulgudes, toimides omamoodi argumendina. Näiteks:
Samuti kasutatakse väikest tähte laialdaselt tõenäosuse tähistamiseks. Eelkõige võite loobuda sündmuste ja nende tõenäosuste tülikatest määratlustest ![]() järgmise stiili kasuks::
järgmise stiili kasuks::
– tõenäosus, et mündiviske tulemuseks on pead;
– tõenäosus, et täringuvise annab 5 punkti;
– tõenäosus, et kaardipakist tõmmatakse klubi masti kaart.
See valik on praktiliste probleemide lahendamisel populaarne, kuna võimaldab oluliselt vähendada lahenduse salvestamist. Nagu esimesel juhul, on siingi mugav kasutada “rääkivaid” ala-/üleindekseid.
Kõik on juba ammu arvanud numbreid, mille ma just ülal kirjutasin, ja nüüd saame teada, kuidas need välja kukkusid:
Klassikaline tõenäosuse määratlus:
Teatud testis sündmuse toimumise tõenäosust nimetatakse suhteks, kus:
– kõigi koguarv võrdselt võimalik, elementaarne selle testi tulemused kogu ürituste grupp;
- kogus elementaarne tulemused, soodne sündmus.
Mündi viskamisel võivad välja kukkuda kas pead või sabad – need sündmused kujunevad täisgrupp, seega tulemuste koguarv; samal ajal igaüks neist elementaarne Ja võrdselt võimalik. Sündmust soosib tulemus (pead). Klassikalise tõenäosuse määratluse kohaselt: ![]() .
.
Samamoodi võivad täringu viskamise tulemusena ilmneda elementaarsed võrdselt võimalikud tulemused, mis moodustavad tervikliku rühma ja sündmust soosib üks tulemus (viie viskamine). Sellepärast: ![]() SEDA EI OLE AKTSEPTEERITUD TEHA (kuigi protsente oma peas hinnata pole keelatud).
SEDA EI OLE AKTSEPTEERITUD TEHA (kuigi protsente oma peas hinnata pole keelatud).
Tavapärane on kasutada ühiku murde, ja ilmselgelt võib tõenäosus piires varieeruda. Pealegi, kui , siis sündmus on võimatu, kui - usaldusväärne, ja kui , siis me räägime juhuslik sündmus.
! Kui saate mõne probleemi lahendamisel mõne muu tõenäosuse väärtuse, otsige viga!
Tõenäosuse määramise klassikalises lähenemisviisis saadakse äärmuslikud väärtused (null ja üks) täpselt sama arutluskäigu kaudu. Teatud urnist, milles on 10 punast palli, tõmmatakse juhuslikult 1 pall. Mõelge järgmistele sündmustele:
ühe katsega ei juhtu vähese tõenäosusega sündmust.
Seetõttu ei võida sa loteriis jackpotti, kui selle sündmuse tõenäosus on näiteks 0,00000001. Jah, jah, see oled sina – ainsa piletiga konkreetses tiraažis. Suurem arv pileteid ja suurem arv joonistusi teid aga palju ei aita. ...Kui ma sellest teistele räägin, kuulen peaaegu alati vastuseks: "aga keegi võidab." Olgu, teeme siis järgmise katse: palun ostke täna või homme suvalise loterii pilet (ärge viivitage!). Ja kui võidad... noh, vähemalt üle 10 kilorublase, siis pane kindlasti kirja – ma selgitan, miks see juhtus. Protsendi eest muidugi =) =)
Aga kurvastada pole vaja, sest on vastupidine põhimõte: kui mõne sündmuse tõenäosus on väga lähedane ühele, siis ühel katsel peaaegu kindel juhtub. Seetõttu pole enne langevarjuga hüppamist vaja karta, vastupidi, naerata! Mõlema langevarju ebaõnnestumiseks peavad ju tekkima täiesti mõeldamatud ja fantastilised asjaolud.
Kuigi see kõik on lüürika, sest olenevalt sündmuse sisust võib esimene põhimõte osutuda rõõmsaks, teine aga kurvaks; või isegi mõlemad paralleelsed.
Võib-olla sellest praegu klassis piisab Klassikalised tõenäosusprobleemid saame valemist maksimumi. Selle artikli viimases osas käsitleme ühte olulist teoreemi:
Täieliku rühma moodustavate sündmuste tõenäosuste summa on võrdne ühega. Jämedalt öeldes, kui sündmused moodustavad tervikliku rühma, siis 100% tõenäosusega juhtub üks neist. Lihtsamal juhul moodustavad tervikliku rühma vastupidised sündmused, näiteks:
– mündiviske tulemusena tekivad pead;
– mündiviske tulemuseks on pead.
Vastavalt teoreemile: ![]()
On täiesti selge, et need sündmused on võrdselt võimalikud ja nende tõenäosus on sama ![]() .
.
Tõenäosuste võrdsuse tõttu nimetatakse sageli võrdselt võimalikke sündmusi sama tõenäoline . Ja siin on keeleväänaja joobeastme määramiseks =)
Näide kuubikuga: sündmused on seega vastupidised ![]() .
.
Vaadeldav teoreem on mugav selle poolest, et võimaldab kiiresti leida vastupidise sündmuse tõenäosuse. Seega, kui viie veeremise tõenäosus on teada, on lihtne arvutada tõenäosus, et seda ei veereta:
![]()
See on palju lihtsam kui viie elementaarse tulemuse tõenäosuste kokkuvõtmine. Muide, elementaarsete tulemuste puhul kehtib ka see teoreem:
. Näiteks kui on tõenäosus, et laskur tabab sihtmärki, siis on tõenäosus, et ta tabab märki.
! Tõenäosusteoorias on tähtede kasutamine muudel eesmärkidel ebasoovitav.
Teadmiste päeva auks ma kodutöid ei anna =), kuid on väga oluline, et saaksite vastata järgmistele küsimustele:
- Mis tüüpi üritusi eksisteerib?
– Mis on sündmuse juhus ja võrdne võimalus?
– Kuidas te mõistate mõisteid sündmuste ühilduvus/ühildamatus?
– Mis on täielik sündmuste rühm, vastandlikud sündmused?
– Mida tähendab sündmuste liitmine ja korrutamine?
– Mis on tõenäosuse klassikalise definitsiooni olemus?
– Miks on tervikliku rühma moodustavate sündmuste tõenäosuste liitmise teoreem kasulik?
Ei, te ei pea midagi kokku toppima, need on lihtsalt tõenäosusteooria põhitõed - omamoodi aabits, mis mahub kiiresti teie pähe. Ja et see juhtuks võimalikult kiiresti, soovitan teil tundidega tutvuda
Tõenäosusteooria ja matemaatiline statistika
1. TEOREETILINE OSA
1 Juhuslike muutujate jadade ja tõenäosusjaotuste konvergents
Tõenäosusteoorias tuleb tegeleda juhuslike suuruste erinevat tüüpi konvergentsidega. Vaatleme järgmisi peamisi konvergentsi liike: tõenäosuse järgi, tõenäosusega üks, järgu p järgi, jaotuse järgi.
Olgu,... mingis tõenäosusruumis (, Ф, P) defineeritud juhuslikud muutujad.
Definitsioon 1. Juhuslike muutujate jada ... koondub tõenäosusega juhuslikuks muutujaks (tähistus:), kui mõni > 0
Definitsioon 2. Juhuslike muutujate jada ... koondub tõenäosusega üks (peaaegu kindlasti, peaaegu kõikjal) juhuslikule muutujale, kui
need. kui tulemuste hulk, mille puhul () ei ühti ()-ga, on null tõenäosusega.
Seda tüüpi konvergentsi tähistatakse järgmiselt: , või, või.
Definitsioon 3. Juhuslike muutujate jada ... nimetatakse keskmiseks-konvergendiks järku p, 0< p < , если
Definitsioon 4. Juhuslike muutujate jada... koondub jaotuses juhuslikuks muutujaks (tähistus:), kui mis tahes piiratud pideva funktsiooni korral
Konvergentsi juhuslike suuruste jaotuses defineeritakse ainult nende jaotusfunktsioonide konvergentsi kaudu. Seetõttu on seda tüüpi konvergentsist otstarbekas rääkida ka siis, kui juhuslikud suurused on määratud erinevates tõenäosusruumides.
1. teoreem.
a) (P-a.s.) jaoks on vajalik ja piisav, et mis tahes > 0 korral
) Jada () on põhitõenäosusega üks siis ja ainult siis, kui mis tahes > 0 korral.
Tõestus.
a) Olgu A = (: |- | ), A = A. Siis
Seetõttu on väide a) järgmise implikatsioonide ahela tulemus:
P(: )= 0 P() = 0 = 0 P(A) = 0, m 1 P(A) = 0, > 0 P() 0, n 0, > 0 P( ) 0,
n 0, > 0.) Tähistame = (: ), = . Siis (: (()) ei ole põhiline ) = ja samamoodi nagu punktis a) näidatakse, et (: (()) ei ole põhiline ) = 0 P( ) 0, n.
Teoreem on tõestatud
Teoreem 2. (Kauchy kriteerium peaaegu kindla konvergentsi jaoks)
Selleks, et juhuslike muutujate jada () koonduks tõenäosusega üks (mingile juhuslikule muutujale), on vajalik ja piisav, et see oleks tõenäosusega üks fundamentaalne.
Tõestus.
Kui, siis +
millest järeldub teoreemi tingimuste vajalikkus.
Nüüd olgu jada () põhiline tõenäosusega üks. Tähistame L = (: (()) mitte fundamentaalne). Siis on arvujada () kõigi jaoks põhiline ja Cauchy kriteeriumi järgi arvujadade jaoks on () olemas. Paneme
See määratletud funktsioon on juhuslik suurus ja.
Teoreem on tõestatud.
2 Iseloomulike funktsioonide meetod
Karakterfunktsioonide meetod on tõenäosusteooria analüütilise aparaadi üks peamisi tööriistu. Koos juhuslike muutujatega (reaalväärtuste võtmine) nõuab iseloomulike funktsioonide teooria kompleksväärtuslike juhuslike muutujate kasutamist.
Paljud juhuslike muutujatega seotud definitsioonid ja omadused on hõlpsasti ülekantavad keerukale juhtumile. Niisiis, matemaatiline ootus M ?kompleksväärtusega juhuslik suurus ?=?+?? loetakse kindlaks, kui matemaatilised ootused M on määratud ?neid ?. Sel juhul eeldame definitsiooni järgi M ?= M ? + ?M ?. Juhuslike elementide sõltumatuse definitsioonist järeldub, et kompleksväärtuslikud suurused ?1 =?1+??1 , ?2=?2+??2on sõltumatud siis ja ainult siis, kui juhuslike muutujate paarid on sõltumatud ( ?1 , ?1) ja ( ?2 , ?2), või, mis on sama, sõltumatu ?-algebra F ?1, ?1 ja F ?2, ?2.
Koos tühikuga L 2reaalsed juhuslikud muutujad lõpliku teise hetkega, saame arvesse võtta kompleksväärtuslike juhuslike muutujate Hilberti ruumi ?=?+?? koos M | ?|2?|2= ?2+?2ja skalaarkorrutis ( ?1 , ?2)= M ?1?2¯ , Kus ?2¯ - kompleksne konjugeeritud juhuslik suurus.
Algebralistes operatsioonides käsitletakse vektoreid Rn algebraliste veergudena,
Reavektoritena a* - (a1,a2,…,an). Kui Rn , siis nende skalaarkorrutist (a,b) mõistetakse suurusena. Selge see
Kui aRn ja R=||rij|| on maatriks järjestusega nхn
Definitsioon 1. Olgu F = F(x1,....,xn) - n-mõõtmeline jaotusfunktsioon punktis (, ()). Selle iseloomulikku funktsiooni nimetatakse funktsiooniks
2. definitsioon . Kui? = (?1,…,?n) on juhuslik vektor, mis on defineeritud tõenäosusruumis väärtustega in, siis selle iseloomulikku funktsiooni nimetatakse funktsiooniks
kus on F? = F?(х1,….,хn) - vektori jaotusfunktsioon?=(?1,…, ?n).
Kui jaotusfunktsiooni F(x) tihedus on f = f(x), siis
Sel juhul pole iseloomulik funktsioon midagi muud kui funktsiooni f(x) Fourier' teisendus.
(3) järeldub, et juhusliku vektori tunnusfunktsiooni ??(t) saab defineerida ka võrdsusega
Karakterfunktsioonide põhiomadused (n=1 korral).
Las olla? = ?(?) - juhuslik suurus, F? =F? (x) on selle jaotusfunktsioon ja iseloomulik funktsioon.
Tuleb märkida, et kui, siis.
Tõepoolest,
kus kasutasime ära asjaolu, et sõltumatute (piiratud) juhuslike muutujate korrutise matemaatiline ootus on võrdne nende matemaatiliste ootuste korrutisega.
Omadus (6) on võtmetähtsusega sõltumatute juhuslike suuruste summade piirteoreemide tõestamisel karakteristlike funktsioonide meetodil. Sellega seoses väljendatakse jaotusfunktsiooni üksikute terminite jaotusfunktsioonide kaudu palju keerulisemal viisil, nimelt kus * märk tähendab jaotuste keerdumist.
Iga jaotusfunktsiooni saab seostada juhusliku muutujaga, mille jaotusfunktsioon on see funktsioon. Seetõttu võime karakteristlike funktsioonide omaduste esitamisel piirduda juhuslike suuruste tunnusfunktsioonide arvestamisega.
1. teoreem. Las olla? - juhuslik suurus jaotusfunktsiooniga F=F(x) ja - sellele iseloomulik funktsioon.
Toimuvad järgmised omadused:
) on ühtlaselt pidev sisse;
) on reaalväärtuslik funktsioon siis ja ainult siis, kui F jaotus on sümmeetriline
)kui mõne n? 1 , siis on kõigi jaoks tuletised ja
)Kui on olemas ja on lõplik, siis
) Olgu kõigi n ? 1 ja
siis kõigile |t| Järgnev teoreem näitab, et karakteristlik funktsioon määrab üheselt jaotusfunktsiooni. Teoreem 2 (unikaalsus). Olgu F ja G kaks jaotusfunktsiooni, millel on sama tunnusfunktsioon, see tähendab kõigi jaoks Teoreem ütleb, et jaotusfunktsiooni F = F(x) saab selle iseloomulikust funktsioonist üheselt taastada. Järgmine teoreem annab funktsiooni F selge esituse. Teoreem 3 (üldistusvalem). Olgu F = F(x) jaotusfunktsioon ja sellele iseloomulik funktsioon. a) Mis tahes kahe punkti a, b (a< b), где функция F = F(х) непрерывна, ) Kui jaotusfunktsiooni F(x) tihedus on f(x), Teoreem 4. Selleks, et juhusliku vektori komponendid oleksid sõltumatud, on vajalik ja piisav, et selle tunnusfunktsioon oleks komponentide karakteristlike funktsioonide korrutis: Bochneri-Khinchini teoreem .
Olgu pidev funktsioon. Et see oleks iseloomulik, on vajalik ja piisav, et see oleks mittenegatiivne kindel, st iga reaalarvu t1, ... , tn ja mis tahes kompleksarvu korral Teoreem 5. Olgu juhusliku suuruse tunnusfunktsioon. a) Kui mõnele, siis on juhuslik suurus sammuga võre, st ) Kui kahe erineva punkti korral on irratsionaalarv, siis kas see on juhuslik suurus? on degenereerunud: kus a on mingi konstant. c) Kui, siis kas see on juhuslik suurus? degenereerunud. 1.3 Keskpiirteoreem sõltumatute identse jaotusega juhuslike suuruste jaoks Olgu () sõltumatute, identselt jaotatud juhuslike muutujate jada. Ootus M= a, dispersioon D= , S = ja Ф(х) on normaalseaduse jaotusfunktsioon parameetritega (0,1). Tutvustame teist juhuslike muutujate jada Teoreem. Kui 0<<, то при n P(< x) Ф(х) равномерно относительно х (). Sel juhul nimetatakse järjestust () asümptootiliselt normaalseks. Sellest, et M = 1 ja pidevuse teoreemidest järeldub, et koos nõrga konvergentsiga FM f() Mf() mis tahes pideva piiriga f korral on konvergents M f() Mf() iga pideva f korral. , nii et |f(x)|< c(1+|x|) при каком-нибудь. Tõestus. Ühtlane lähenemine on siin nõrga konvergentsi ja Ф(x) pidevuse tagajärg. Lisaks võime üldistust kaotamata eeldada, et a = 0, kuna vastasel juhul võiksime arvestada jadaga () ja jada () ei muutuks. Seetõttu piisab nõutava konvergentsi tõestamiseks, kui näidata, et (t) e, kui a = 0. Meil on (t) = , kus =(t). Kuna M on olemas, siis lagunemine on olemas ja kehtib Seetõttu n Teoreem on tõestatud. 1.4 Matemaatilise statistika põhiülesanded, nende lühikirjeldus Massilisi juhuslikke nähtusi reguleerivate mustrite loomine põhineb statistiliste andmete - vaatluste tulemuste - uurimisel. Matemaatilise statistika esimene ülesanne on näidata statistilise teabe kogumise ja rühmitamise viise. Matemaatilise statistika teiseks ülesandeks on välja töötada meetodid statistiliste andmete analüüsimiseks, olenevalt uuringu eesmärkidest. Mis tahes matemaatilise statistika ülesande lahendamisel on kaks teabeallikat. Esimene ja kõige kindlam (selgesõnaline) on vaatluste (katse) tulemus skalaarse või vektorjuhusliku muutuja mõne üldkogumi valimi kujul. Sel juhul saab valimi suurust n fikseerida või eksperimendi käigus suureneda (st saab kasutada nn järjestikuseid statistilise analüüsi protseduure). Teiseks allikaks on kogu a priori informatsioon uuritava objekti huvipakkuvate omaduste kohta, mis on praeguse hetkeni kogunenud. Formaalselt kajastub a priori info hulk esialgses statistilises mudelis, mis ülesande lahendamisel valitakse. Siiski pole vaja rääkida umbkaudsest määramisest sündmuse toimumise tõenäosuse tavapärases tähenduses katsete tulemuste põhjal. Mis tahes suuruse ligikaudse määramise all mõeldakse tavaliselt seda, et on võimalik näidata veapiirid, mille piires viga ei teki. Üksikute katsete tulemuste juhuslikkuse tõttu on sündmuse sagedus suvalise arvu katsete puhul juhuslik. Üksikkatsete tulemuste juhuslikkuse tõttu võib sagedus sündmuse tõenäosusest oluliselt erineda. Seega, kui defineerime sündmuse tundmatu tõenäosuse selle sündmuse sagedusena suure hulga katsete jooksul, ei saa me näidata veapiire ja tagada, et viga ei ületa neid piire. Seetõttu räägime matemaatilises statistikas tavaliselt mitte tundmatute suuruste ligikaudsetest väärtustest, vaid nende sobivatest väärtustest, hinnangutest. Tundmatute parameetrite hindamise probleem tekib juhtudel, kui üldkogumi jaotusfunktsioon on kuni parameetrini teada. Sel juhul on vaja leida statistika, mille valimi väärtust juhusliku valimi vaadeldava teostuse xn jaoks võiks pidada parameetri ligikaudseks väärtuseks. Statistikat, mille valimi väärtust mis tahes realisatsiooni xn jaoks võetakse tundmatu parameetri ligikaudse väärtusena, nimetatakse punkthinnanguks või lihtsalt hinnanguks ja see on punkthinnangu väärtus. Punkthinnang peab vastama väga spetsiifilistele nõuetele, et selle valimi väärtus vastaks parameetri tegelikule väärtusele. Võimalik on ka teine lähenemine vaadeldava probleemi lahendamisele: leida selline statistika ja kas tõenäosusega? kehtib järgmine ebavõrdsus: Sel juhul räägime intervallide hindamisest. Intervall nimetatakse usaldusvahemikuks koos usalduskoefitsiendiga?. Olles katsete tulemuste põhjal hinnanud üht või teist statistilist tunnust, tekib küsimus: kui järjepidev on eeldus (hüpotees), et tundmatul tunnusel on täpselt sama väärtus, mis saadi selle hindamise tulemusena katseandmetega? Nii tekib matemaatilise statistika teine oluline ülesannete klass - hüpoteeside kontrollimise probleemid. Teatud mõttes on statistilise hüpoteesi kontrollimise probleem parameetrite hindamise probleemi pöördvõrdeline. Parameetrit hinnates ei tea me midagi selle tegelikust väärtusest. Statistilise hüpoteesi testimisel eeldatakse millegipärast selle väärtust teada ja eksperimendi tulemuste põhjal on vaja seda eeldust kontrollida. Paljudes matemaatilise statistika probleemides vaadeldakse juhuslike muutujate jadasid, mis koonduvad ühes või teises mõttes mingi piirini (juhuslik muutuja või konstant), millal. Seega on matemaatilise statistika põhiülesanneteks hinnangute leidmise ja hinnatavatele tunnustele nende lähendamise täpsuse uurimise meetodite väljatöötamine ning hüpoteeside kontrollimise meetodite väljatöötamine. 5 Statistiliste hüpoteeside kontrollimine: põhimõisted Statistiliste hüpoteeside kontrollimise ratsionaalsete meetodite väljatöötamise ülesanne on üks matemaatilise statistika põhiülesandeid. Statistiline hüpotees (või lihtsalt hüpotees) on igasugune väide katses täheldatud juhuslike muutujate jaotuse tüübi või omaduste kohta. Olgu valim, mis on üldkogumi juhusliku valimi realisatsioon, mille jaotustihedus sõltub tundmatust parameetrist. Statistilisi hüpoteese parameetri tundmatu tegeliku väärtuse kohta nimetatakse parameetrilisteks hüpoteesideks. Veelgi enam, kui on skalaar, siis me räägime ühe parameetri hüpoteesidest ja kui see on vektor, siis me räägime mitme parameetri hüpoteesidest. Statistilist hüpoteesi nimetatakse lihtsaks, kui sellel on vorm kus on mingi määratud parameetri väärtus. Statistilist hüpoteesi nimetatakse keeruliseks, kui sellel on vorm kus on parameetrite väärtuste komplekt, mis koosneb rohkem kui ühest elemendist. Vormi kahe lihtsa statistilise hüpoteesi testimise korral kus on parameetri kaks antud (erinevat) väärtust, siis esimest hüpoteesi nimetatakse tavaliselt peamiseks ja teist alternatiivseks või konkureerivaks hüpoteesiks. Kriteerium ehk statistiline kriteerium hüpoteeside kontrollimisel on reegel, mille järgi valimiandmete põhjal otsustatakse kas esimese või teise hüpoteesi paikapidavus. Kriteerium määratakse kriitilise hulga abil, mis on juhusliku valimi valimiruumi alamhulk. Otsus tehakse järgmiselt: ) kui valim kuulub kriitilisse hulka, siis lükka põhihüpoteesi tagasi ja nõustu alternatiivse hüpoteesiga; ) kui valim ei kuulu kriitilisse hulka (s.t. kuulub valimiruumi hulga täiendisse), siis alternatiivne hüpotees lükatakse tagasi ja põhihüpotees aktsepteeritakse. Mis tahes kriteeriumi kasutamisel on võimalikud järgmist tüüpi vead: 1) nõustuma hüpoteesiga, kui see on tõene - esimest tüüpi viga; ) hüpoteesi aktsepteerimine, kui see on tõene, on II tüüpi viga. Esimest ja teist tüüpi vigade tegemise tõenäosust tähistatakse järgmiselt: kus on sündmuse tõenäosus eeldusel, et hüpotees on tõene. Näidatud tõenäosused arvutatakse juhusliku valimi jaotustiheduse funktsiooni abil: I tüüpi vea sooritamise tõenäosust nimetatakse ka kriteeriumi olulisuse tasemeks. Väärtust, mis võrdub põhihüpoteesi tagasilükkamise tõenäosusega, kui see on tõene, nimetatakse testi võimsuseks. 1.6 Sõltumatuse kriteerium Kahemõõtmelisest jaotusest on valim ((XY), ..., (XY)). L tundmatu jaotusfunktsiooniga, mille puhul on vaja testida hüpoteesi H: , kus on mõned ühemõõtmelised jaotusfunktsioonid. Metoodika põhjal saab koostada lihtsa sobivuse testi hüpoteesi H jaoks. Seda tehnikat kasutatakse diskreetsete mudelite jaoks, millel on piiratud arv tulemusi, seega nõustume, et juhuslik muutuja võtab teatud väärtustest lõpliku arvu s, mida tähistame tähtedega, ja teine komponent - k väärtused. Kui algsel mudelil on erinev struktuur, siis rühmitatakse juhuslike suuruste võimalikud väärtused eelnevalt eraldi esimeseks ja teiseks komponendiks. Sel juhul jagatakse hulk s intervallideks, seatud väärtus k intervalliks ja väärtuste komplekt ise N=sk ristkülikuteks. Tähistagem paari vaatluste arvuga (ristkülikusse kuuluvate valimielementide arvuga, kui andmed on rühmitatud), nii et. Vaatlustulemusi on mugav järjestada kahe märgi kontingentsitabeli kujul (tabel 1.1). Rakendustes tähendab see tavaliselt kahte kriteeriumi, mille järgi vaatlustulemusi klassifitseeritakse. Olgu P, i=1,…,s, j=1,…,k. Siis iseseisvuse hüpotees tähendab, et on olemas s+k konstandid sellised, et ja, s.t. Tabel 1.1 Summa . . .. . .. . . . . .. . .. . . . . . . . . . . . . . .Summa . . .n Seega taandub hüpotees H väitele, et sagedused (nende arv on N = sk) jaotatakse polünoomiseaduse järgi, mille tulemuste tõenäosus on kindlaksmääratud spetsiifiline struktuur (tulemite p tõenäosuse vektor määratakse väärtustega r = tundmatute parameetrite s + k-2. Selle hüpoteesi kontrollimiseks leiame maksimaalse tõenäosuse hinnangud tundmatute parameetrite jaoks, mis määravad vaadeldava skeemi. Kui nullhüpotees on tõene, siis on tõenäosusfunktsioonil L(p)=, kus kordaja c ei sõltu tundmatutest parameetritest. Siit, kasutades määramata kordajate Lagrange'i meetodit, saame, et nõutavad hinnangud on kujul Seetõttu statistika L() at, kuna piirjaotuse vabadusastmete arv võrdub N-1-r=sk-1-(s+k-2)=(s-1)(k-1). Seega saab piisavalt suure n korral kasutada järgmist hüpoteesi testimise reeglit: hüpotees H lükatakse tagasi siis ja ainult siis, kui tegelikest andmetest arvutatud t statistiline väärtus rahuldab ebavõrdsust. Sellel kriteeriumil on asümptootiliselt (at) antud olulisuse tase ja seda nimetatakse sõltumatuse kriteeriumiks. 2. PRAKTILINE OSA 1 Lahendused konvergentsi tüüpide probleemidele 1. Tõesta, et konvergents tähendab peaaegu kindlasti ka tõenäosuse lähenemist. Tooge näide, mis näitab, et vastupidine pole tõsi. Lahendus. Laske juhuslike muutujate jada peaaegu kindlasti läheneda juhuslikule suurusele x. Nii et kellelegi? > 0 Sellest ajast ja xn konvergentsist x-le järeldub peaaegu kindlasti, et xn koondub tõenäoliselt x-le, kuna sel juhul Kuid vastupidine väide ei vasta tõele. Olgu sõltumatute juhuslike muutujate jada, millel on sama jaotusfunktsioon F(x), mis võrdub nulliga punktis x? 0 ja võrdne x > 0 korral. Vaatleme jada See jada läheneb tõenäosusega nullile, kuna kipub nulli iga fikseeritud? Ja. Nullile lähenemist aga peaaegu kindlasti ei toimu. Tõesti kaldub ühtsusele, st tõenäosusega 1 mis tahes ja n korral on jadas realisatsioone, mis ületavad ?. Pange tähele, et teatud lisatingimuste olemasolul suurustele xn tähendab tõenäosuse konvergents peaaegu kindlasti lähenemist. Olgu xn monotoonne jada. Tõesta, et sel juhul tähendab xn-i tõenäosuse lähenemine x-le xn-i konvergentsi tõenäosusega 1. Lahendus. Olgu xn monotoonselt kahanev jada, st. Arutluskäigu lihtsustamiseks eeldame, et x º 0, xn ³ 0 kõigi n puhul. Laske xn koonduda tõenäosusega x-le, kuid konvergentsi peaaegu kindlasti ei toimu. Kas see on siis olemas? > 0, nii et kõigi n Kuid öeldu tähendab ka seda, et kõigi n mis on vastuolus xn konvergentsiga x tõenäosusega. Seega koondub monotoonse jada xn puhul, mis tõenäosusega koondub x-le, ka tõenäosusega 1 (peaaegu kindlasti). Jada xn koondub tõenäosusega x-le. Tõesta, et sellest jadast on võimalik eraldada jada, mis koondub x-le tõenäosusega 1 at. Lahendus. Laskma olla mõned positiivsete arvude jada ja lasta ja olla positiivsed arvud, nii et seeria. Koostame indeksite jada n1 Siis sari Kuna seeria läheneb, siis mis tahes? > 0, ülejäänud seeria kipub nulli. Siis aga kipub nulli ja Tõesta, et mis tahes positiivse järgu keskmine konvergents tähendab tõenäosuse lähenemist. Tooge näide, mis näitab, et vastupidine pole tõsi. Lahendus. Laske jada xn koonduda väärtusele x keskmiselt suurusjärgus p > 0, see tähendab Kasutame üldistatud Tšebõševi ebavõrdsust: meelevaldseks? > 0 ja p > 0 Seda suunates ja arvesse võttes saame selle see tähendab, et xn koondub tõenäosusega x-le. Tõenäosuse konvergents ei too aga kaasa konvergentsi keskmises järjekorras p > 0. Seda illustreerib järgmine näide. Vaatleme tõenäosusruumi áW, F, Rñ, kus F = B on Boreli s-algebra, R on Lebesgue'i mõõt. Määratleme juhuslike muutujate jada järgmiselt: Jada xn koondub tõenäosusega 0-le, kuna aga iga p > 0 korral see tähendab, et see ei lähe keskmiselt kokku. Olgu, mis kõigile n . Tõesta, et sel juhul koondub xn keskmises ruudus x-le. Lahendus. Pange tähele, et... Teeme hinnangu. Vaatleme juhuslikku muutujat. Las olla? - suvaline positiivne arv. Siis kell ja kell. Kui, siis ja. Seega,. Ja sellepärast? suvaliselt väike ja siis at, see tähendab keskmises ruudus. Tõesta, et kui xn koondub tõenäosusega x-le, siis tekib nõrk konvergents. Tooge näide, mis näitab, et vastupidine pole tõsi. Lahendus. Tõestame, et kui igas punktis x, mis on pidevuspunkt (see on nõrga konvergentsi vajalik ja piisav tingimus), on väärtuse xn jaotusfunktsioon ja - x väärtus. Olgu x funktsiooni F pidevuspunkt. Kui, siis vähemalt üks võrratustest või on tõene. Siis Samamoodi vähemalt ühe võrratuse või ja puhul Kui, siis nii väikeseks kui soovitakse? > 0 on olemas N nii, et kõigi n > N korral Teisest küljest, kui x on pidevuspunkt, kas on võimalik midagi sellist leida? > 0, mis suvaliselt väikeseks Niisiis, nii väikeseks kui soovite? ja on olemas N nii, et n puhul >N või mis on sama, See tähendab, et lähenemine ja toimub kõigis järjepidevuse punktides. Järelikult tuleneb tõenäosuse konvergentsist nõrk konvergents. Vastupidine väide üldiselt ei kehti. Selle kontrollimiseks võtame juhuslike muutujate jada, mis ei võrdu tõenäosusega 1 ja millel on sama jaotusfunktsioon F(x). Eeldame, et kõigi n suuruste ja on sõltumatud. Ilmselgelt toimub nõrk konvergents, kuna jada kõigil liikmetel on sama jaotusfunktsioon. Kaaluge: |Väärtuste sõltumatusest ja identsest jaotusest järeldub, et Valime kõigi mittedegenereerunud juhuslike muutujate jaotusfunktsioonide hulgast sellise F(x), mis on nullist erinev kõigi piisavalt väikeste ? korral. Siis ei kipu see n piiramatu kasvuga nulli ja tõenäosuse konvergentsi ei toimu. 7. Olgu nõrk konvergents, kus tõenäosusega 1 on konstant. Tõesta, et sel juhul koondub see tõenäosusega. Lahendus. Olgu tõenäosus 1 võrdne a. Siis tähendab nõrk konvergents mis tahes konvergentsi. Alates, siis kell ja kell. See tähendab kell ja kell. Sellest järeldub see kellegi jaoks? > 0 tõenäosus kipuvad nulli. See tähendab et kipub nulli, st läheneb tõenäosusele. 2.2 Keskküttekeskuse probleemide lahendamine Gammafunktsiooni Г(x) väärtus x= juures arvutatakse Monte Carlo meetodil. Leiame minimaalne vajalik arv teste, et tõenäosusega 0,95 võiksime eeldada, et arvutuste suhteline viga on alla ühe protsendi. Täpsuseni, mis meil on On teada, et Olles teinud muudatuse punktis (1), jõuame lõpliku intervalli integraalini: Meiega seega Nagu näha, saab seda esitada kujul, kus ja jaotub ühtlaselt edasi. Laske läbi viia statistilised testid. Siis on statistiline analoog kogus kus on ühtlase jaotusega sõltumatud juhuslikud muutujad. Kus CLT-st järeldub, et see on parameetritega asümptootiliselt normaalne. See tähendab, et minimaalne testide arv, mis tõenäosusega tagab arvutuse suhtelise vea, ei ole suurem kui võrdne. Vaadeldakse 2000 sõltumatust identselt jaotatud juhuslikust muutujast koosnevat jada, mille matemaatiline ootus on 4 ja dispersioon 1,8. Nende suuruste aritmeetiline keskmine on juhuslik suurus. Määrake tõenäosus, et juhuslik muutuja saab väärtuse vahemikus (3,94; 4,12). Olgu …,… sõltumatute juhuslike muutujate jada, millel on sama jaotus M=a=4 ja D==1,8. Seejärel on CLT rakendatav järjestusele (). Juhuslik väärtus Tõenäosus, et see võtab väärtuse vahemikus (): Kui n = 2000, saame 3,94 ja 4,12 3 Hüpoteeside kontrollimine sõltumatuse kriteeriumi abil Uuringu tulemusena selgus, et 782 heledasilmsel isal on ka heledasilmsed pojad ning 89 heledasilmsel isal on tumedasilmsed pojad. 50 tumedasilmsel isal on ka tumedasilmsed pojad ja 79 tumedasilmsel isal on heledasilmsed pojad. Kas isade silmavärvi ja nende poegade silmavärvi vahel on seos? Võtke usaldustasemeks 0,99. Tabel 2.1 LapsedIsadSum HelesilmsedTumedasilmsed Helesilmsed78279861Tumedasilmsed8950139Sum8711291000 H: Laste ja isade silmavärvi vahel pole mingit seost. H: Laste ja isade silmavärvi vahel on seos. s=k=2 =90,6052 1 vabadusastmega Arvutused tehti Mathematica 6-s. Kuna > , siis tuleks hüpotees H, mis käsitleb isade ja laste silmavärvi vahelise seose puudumist olulisuse tasemel, tagasi lükata ja nõustuda alternatiivse hüpoteesiga H. Märgitakse, et ravimi toime sõltub kasutusviisist. Kontrollige seda väidet tabelis esitatud andmete abil. 2.2 Võtke usaldustasemeks 0,95. Tabel 2.2 Tulemus Kasutusmeetod ABC Ebasoodne 111716 Soodne 202319 Lahendus. Selle probleemi lahendamiseks kasutame kahe tunnuse situatsioonitabelit. Tabel 2.3 Tulemus Taotlusmeetod Summa ABC Ebasoodne 11171644 Soodne 20231962 Summa 314035106 H: ravimite toime ei sõltu manustamisviisist H: ravimite toime sõltub kasutusviisist Statistika arvutatakse järgmise valemi abil s=2, k=3, =0,734626 2 vabadusastmega. Mathematica 6-s tehtud arvutused Jaotustabelitest leiame selle. Kuna< , то гипотезу H, про отсутствия зависимости действия лекарств от способа применения, при уровне значимости, следует принять. Järeldus Käesolevas artiklis esitatakse teoreetilised arvutused jaotisest „Sõltumatuskriteerium“, samuti „Tõenäosusteooria piirteoreemid“, kursusest „Tõenäosusteooria ja matemaatiline statistika“. Töö käigus testiti praktikas sõltumatuse kriteeriumi; Samuti kontrolliti antud sõltumatute juhuslike muutujate jadade puhul keskse piiri teoreemi täitumist. See töö aitas parandada minu teadmisi nende tõenäosusteooria osade kohta, töötada kirjanduslike allikatega ja omandada kindlalt sõltumatuse kriteeriumi kontrollimise tehnikat. tõenäosusliku statistilise hüpoteesi teoreem Linkide loend 1. Tõenäosusteooria ülesannete kogumine koos lahendustega. Uh. toetus / Toim. V.V. Semenets. - Harkov: KhTURE, 2000. - 320 lk. Gikhman I.I., Skorokhod A.V., Yadrenko M.I. Tõenäosusteooria ja matemaatiline statistika. - K.: Vištša kool, 1979. - 408 lk. Ivchenko G.I., Medvedev Yu.I., Matemaatiline statistika: õpik. toetus kolledžitele. - M.: Kõrgem. kool, 1984. - 248 lk., . Matemaatiline statistika: Õpik. ülikoolidele / V.B. Gorjainov, I.V. Pavlov, G.M. Tsvetkova ja teised; Ed. V.S. Zarubina, A.P. Krischenko. - M.: MSTU kirjastus im. N.E. Bauman, 2001. - 424 lk. Vajad abi teema uurimisel?
Meie spetsialistid nõustavad või pakuvad juhendamisteenust teid huvitavatel teemadel. Õpetamine
Esitage oma taotlus märkides teema kohe ära, et saada teada konsultatsiooni saamise võimalusest.
 Vene friikide ja kehamodifikaatorite kogu
Vene friikide ja kehamodifikaatorite kogu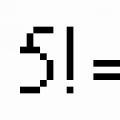 Tõenäosusteooria ja matemaatiline statistika
Tõenäosusteooria ja matemaatiline statistika Tõenäosusteooria ja matemaatilise statistika põhimõisted
Tõenäosusteooria ja matemaatilise statistika põhimõisted