Näited murdude ratsionaalsete funktsioonide integreerimisest. Ratsionaalfunktsioonide integreerimine Murdne – ratsionaalne funktsioon Kõige lihtsam

Eelnevalt käsitlesime integratsiooni üldisi meetodeid. Selles ja järgmistes lõikudes räägime konkreetsete funktsiooniklasside integreerimisest käsitletud tehnikate abil.

Lihtsamate ratsionaalsete funktsioonide integreerimine

Vaatleme vormi integraali \textstyle(\int R(x)\,dx), kus y=R(x) on ratsionaalne funktsioon. Igasuguseid asju ratsionaalne väljendus R(x) võib esitada kui \frac(P(x))(Q(x)), kus P(x) ja Q(x) on polünoomid. Kui see murd on vale, st kui lugeja aste on suurem või võrdne nimetaja astmega, siis saab seda esitada polünoomi ( terve osa) Ja õige murdosa. Seetõttu piisab õigete murdude integreerimisest.

Näitame, et selliste murdude integreerimine taandub integratsiooniks lihtmurrud, st vormi väljendid:

\mathsf(1))~\frac(A)(x-a);\quad \mathsf(2))~\frac(A)((x-a)^n);\quad \mathsf(3))~ \frac( Ax+B)(x^2+px+q);\quad \mathsf(4))~\frac(Ax+B)((x^2+px+q)^n).

Kus A,\,B,\,a,\,p,\,q - reaalarvud, ja ruutkolminoomil x^2+px+q pole pärisjuuri. Tüübi 1) ja 2) avaldisi nimetatakse 1. tüübi murdudeks ning 3. ja 4. tüüpi avaldisi nimetatakse 2. tüüpi murdudeks.

Esimest tüüpi murdude integraalid arvutatakse otse

\begin(joondatud)\mathsf(1))&~\int\frac(A)(x-a)\,dx= A\ln|x-a|+C;\\ \mathsf(2))&~ \int\frac (A)((x-a)^n)\,dx= A\int(x-a)^(-n)\,dx= A\,\frac((x-a)^(-n+1))(-n+ 1 )+C~(n=2,3,4,\ldots). \end (joondatud)

Vaatleme teist tüüpi murdude integraalide arvutamist: \mathsf(3))~ \int\frac(Ax+B)(x^2+px+q)\,dx\,.

Esiteks märgime seda

\int\frac(dt)(t^2+a^2)= \frac(1)(a)\operaatorinimi(arctg)\frac(t)(a)+C,\qquad \int\frac(t\ ,dt)(t^2+a^2)= \frac(1)(2)\ln(t^2+a^2)+C.

Integraali 3) arvutamise taandamiseks nendele kahele integraalile teisendame ruutkolminoomi x^2+px+q, eraldades sellest täisruudu:

x^2+px+q= (\left(x+\frac(p)(2)\right)\^2+ \left(q-\frac{p^2}{4}\right)\!. !}

Kuna eeldusel, et sellel trinoomil pole tegelikke juuri, siis q-\frac(p^2)(4)>0 ja saame panna q-\frac(p^2)(4)=a^2. Asendamine x+\frac(p)(2)=t,~ dx=dt teisendab integraali 3) näidatud kahe integraali lineaarseks kombinatsiooniks:

\begin(joonatud)\int\frac(Ax+B)(x^2+px+q)\,dx&= \int\frac(A\!\left(t-\frac(p)(2)\right )+B)(t^2+a^2)\,dt= A\int\frac(t\,dt)(t^2+a^2)+ \left(B-\frac(Ap)(2 )\right)\!\int\frac(dt)(t^2+a^2)=\\ &=\frac(A)(2)\ln(t^2+a^2)+ \frac( 1)(a)\!\left(B-\frac(Ap)(2)\right)\!\ \operaatorinimi(arctg)\frac(t)(a)+C. \end (joondatud)

Lõplikus vastuses tuleb ainult (t) asendada x+\frac(p)(2) ja (a) \sqrt(q-\frac(p^2)(4)). Kuna t^2+a^2=x^2+px+q, siis

\int\frac(Ax+B)(x^2+px+q)\,dx= \frac(A)(2)\ln(x^2+px+q)+ \frac(B-\dfrac( Ap)(2))(\sqrt(q-\dfrac(p^2)(4))) \operaatorinimi(arctg)\frac(x+\dfrac(p)(2))(\sqrt(q-\dfrac (p^2) (4)))+C.

Kaaluge juhtumit \mathsf(4))~ \int\frac(Ax+B)((x^2+px+q)^n)\,dx.

Sarnaselt eelmisele juhul määrame x+\frac(p)(2)=t. Saame:

\int\frac(Ax+B)((x^2+px+q)^n)\,dx= A\int\frac(t\,dt)((t^2+a^2)^n) + \left(B-\frac(Ap)(2)\right)\! \int\frac(dt)((t^2+a^2)^n)\,.

Esimene tähtaeg arvutatakse järgmiselt:

A\int\frac(t\,dt)((t^2+a^2)^n)= \frac(A)(2)\int(t^2+a^2)^(-n)\ ,d(t^2+a^2)= \frac(A)(2)\frac((t^2+a^2)^(-n+1))(-n+1)= \frac( A)(2(1-n)(t^2+a^2)^(n-1))\,.

Teine integraal arvutatakse kasutades korduv valem.

Näide 1. Arvutame \int\frac(3x+2)(x^2+2x+3)\,dx.

Lahendus. Meil on: x^2+2x+3=(x+1)^2+2. Paneme x+1=t. Siis dx=dt ja 3x+2=3(t-1)+2=3t-1 ning seetõttu

\begin(joondatud)\int\frac(3x+2)(x^2+2x+3)\,dx&= \int\frac(3t-1)(t^2+2)\,dt= \frac( 3)(2)\int\frac(2t\,dt)(t^2+2)- \int\frac(dt)(t^2+(\sqrt(2))^2)=\\ &= \frac(3)(2)\ln(t^2+2)- \frac(1)(\sqrt(2))\operaatorinimi(arctg)\frac(t)(\sqrt(2))+C= \\ &=\frac(3)(2)\ln(x^2+2x+3)- \frac(1)(\sqrt(2))\operaatorinimi(arctg)\frac(x+1)(\ sqrt(2))+C. \end (joondatud)

Näide 2. Arvutame \int\frac(x+2)((x^2+6x+10)^2)\,dx.

Lahendus. Meil on: x^2+6x+10=(x+3)^2+1. Tutvustame uut muutujat, määrates x+3=t. Siis dt=dx ja x+2=t-1 . Asendades muutuja integraalimärgi all, saame:

\begin(joonatud)\int\frac(x+2)((x^2+6x+10)^2)\,dx&= \int\frac(t-1)((t^2+1)^2 )\,dt= \frac(1)(2)\int\frac(2t\,dt)((t^2+1)^2)-\int\frac(dt)((t^2+1) ^2)=\\ &=-\frac(1)(2(t^2+1))- \int\frac(dt)((t^2+1)^2)\,. \end (joondatud))

Paneme I_2=\int\frac(dt)((t^2+1)^2). Meil on:

I_2=\frac(1)(2)I_1+\frac(1)(2)\frac(t)(t^2+1), Aga I_1=\int\frac(dt)(t^2+1)= \operaatorinimi(arctg)t Seega I_2= \frac(1)(2)\operaatorinimi(arctg)t+ \frac(t)(2(t^2+1)).

Lõpuks saame:

\begin(joonatud)\int\frac(x+2)((x^2+6x+10)^2)\,dx&=-\frac(1)(2(t^2+1))-\frac (1)(2)\operaatorinimi(arctg)t-\frac(t)(2(t^2+1))=\\ &=-\frac(1)(2(x^2+6x+10) )- \frac(1)(2)\operaatorinimi(arctg)(x+3)- \frac(x+3)(2(x^2+6x+10))+C=\\ &=\frac( -x-4)(2(x^2+6x+10))-\frac(1)(2)\operaatorinimi(arctg)(x+3)+C \end(joondatud)

Õigete murdude integreerimine

Mõelge õigele murdosale R(x)=\frac(P(x))(Q(x)), kus Q(x) on n-astme polünoom. Üldisust kaotamata võib eeldada, et Q(x) juhtiv koefitsient on võrdne 1-ga. Algebra kursusel on tõestatud, et sellist reaalkoefitsientidega polünoomi saab faktoriseerida reaalkoefitsientidega esimese ja teise astme teguriteks. :

Q(x)= (x-x_1)^(\alpha)\lpunktid (x-x_k)^(\beta) (x^2+p\,x+q)^(\gamma)\lpunktid (x^2) +r\,x+s)^(\delta).

kus x_1,\ldots,x_k on polünoomi Q(x) tegelikud juured ja ruudukujulised trinomaalid neil pole tõelisi juuri. Võib tõestada, et siis R(x) esitatakse lihtmurdude summana kujul 1) -4):

\begin (joondatud)R(x)=&\frac(P(x))(Q(x))= \frac(A_1)((x-x_1)^(\alpha))+ \frac(A_2)( (x-x_1)^(\alpha-1))+\ldots+ \frac(A_(\alpha))(x-x_1)\,+\\ &+\,\ldots+ \frac(B_1)((x- x_k)^(\beta))+ \frac(B_2)((x-x_k)^(\beta-1))+\ldots+ \frac(B_(\beta))(x-x_k)+ \frac(M_1x+ N_1)((x^2+p\,x+q)^(\gamma))\,+\\ &+\,\ldots+ \frac(M_(\gamma)+ N_(\gamma))(x^ 2+ p\,x+s)+ \frac(E_1x+F_1)((x^2+rx+s)^(\delta))+\ldots+ \frac(E_(\delta)x+F_(\delta ))(x^2+rx+s)\, \end(joondatud)

kus nimetajate eksponendid vähenevad järjestikku \alpha-lt 1-le, ..., \beta-lt 1-le, \gamma-lt 1-le, ..., \deltalt 1-le ja A_1,\ldots,F_(\delta)- ebakindlad koefitsiendid. Nende koefitsientide leidmiseks tuleb nimetajatest lahti saada ja kahe polünoomi võrdsuse saamisel kasutada määramatute kordajate meetodit.

Teine võimalus koefitsientide määramiseks A_1,\ldots, A_(\alpha), \ldots, F_(\delta) põhineb muutuja x väärtuste asendamisel. Asendades pärast nimetajate elimineerimist võrrandist (1) saadud võrrandisse x asemel suvalise arvu, jõuame lineaarvõrrand nõutavate koefitsientide suhtes. Asenduse teel vajalik kogus sellised muutuja osaväärtused saame koefitsientide leidmiseks võrrandisüsteemi. Kõige mugavam on muutuja privaatväärtusteks valida nimetaja juured (nii tegelikud kui ka komplekssed). Sel juhul kaovad peaaegu kõik võrdsuse (see tähendab kahe polünoomi võrdsust) paremal poolel olevad terminid, mis teeb ülejäänud koefitsientide leidmise lihtsaks. Kompleksväärtuste asendamisel pidage meeles, et kaks kompleksarvu on võrdsed siis ja ainult siis, kui nende reaal- ja mõtteline osa on vastavalt võrdsed. Seega igast võrdsusest, mis sisaldab kompleksarvud, saame kaks võrrandit.

Pärast määramata koefitsientide leidmist jääb üle arvutada saadud lihtsamate murdude integraalid. Kuna lihtsaimate murdude integreerimisel, nagu nägime, saadakse ainult ratsionaalfunktsioonid, arktangensid ja logaritmid, siis mis tahes ratsionaalfunktsiooni integraali väljendatakse ratsionaalfunktsiooni, arctangentide ja logaritmide kaudu.

Näide 3. Arvutame õige integraali ratsionaalne murd \int\frac(6x+1)(x^2+2x-3)\,dx.

Lahendus. Teguristame integrandi nimetaja:

x^2+2x-3=(x-1)(x+3).

Kirjutame välja integrandi ja esitame selle lihtmurdude summana:

\frac(6x+1)(x^2+2x-3)= \frac(A)(x-1)+\frac(B)(B+3)\,.

Vabastades end selles võrdsuses nimetajatest, saame:

6x+1=A\cpunkt (x+3)+B\cpunkt (x-1)\,.

Koefitsientide leidmiseks kasutame osaväärtuste asendusmeetodit. Koefitsiendi A leidmiseks paneme x=1. Siis võrrandist (2) saame 7=4A, kust A=7/4. Koefitsiendi B leidmiseks paneme x=-3. Siis võrdsusest (2) saame -17=-4B, kust B=17/4.

Niisiis, \frac(6x+1)(x^2+2x-3)= \frac(7)(4)\cdot\frac(1)(x-1)+ \frac(17)(4)\cdot\frac (1) (x+3). Tähendab,

\int\frac(6x+1)(x^2+2x-3)\,dx= \frac(7)(4)\int\frac(dx)(x-1)+ \frac(17)(4 )\int\frac(dx)(x+3)= \frac(7)(4)\ln|x-1|+ \frac(17)(4)\ln|x+3|+C.

Näide 4. Arvutame \int\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))\,dx.

Lahendus. Kirjutame välja integrandi ja esitame selle lihtmurdude summana. Nimetaja sisaldab tegurit x^2+2, millel pole pärisjuuri, see vastab murdosale 2. liigist: \frac(Ax+B)(x^2+2) kordaja (x-1)^2 vastab kahe esimest tüüpi murru summale: \frac(C)((x-1)^2)+ \frac(D)(x-1); lõpuks vastab tegur x+2 ühele 1. tüüpi \frac(E)(x+2) murdosale. Seega esitame integrandi funktsiooni nelja murdosa summana:

\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))= \frac(Ax+B)(x^2+2 )+ \frac(C)((x-1)^2)+ \frac(D)(x-1)+ \frac(E)(x+2)\,.

Vabastagem end selles võrdsuses nimetajatest. Saame:

\begin (joondatud) x^4+2x^2+8x+5&= (Ax+B)(x-1)^2(x+2)+ C(x^2+2)(x+2)\, +\\ &\phantom(=)+ D(x^2+2)(x-1)(x+2)+ E(x^2+2)(x-1)^2.\end(joondatud)

Integrandi nimetajal on kaks reaaljuurt: x=1 ja x=-2. Väärtuse x=1 asendamisel võrdsusega (4) saame 16=9C, millest leiame C=16/9. Asendades x=-2 saame 13=54E ja defineerime vastavalt E=13/54. Väärtuse x=i\,\sqrt(2) (polünoomi x^2+2 juur) asendamine võimaldab meil minna võrdusse

4-4+8\,i\,\sqrt(2)+5= (A\,i\,\sqrt(2)+B)\cdot (i\,\sqrt(2)-1)^2\ cdot (i\,\sqrt(2)+2).

See muundub järgmisele kujule:

(10A+2B)+(2A-5B)\sqrt(2)\,i= 5+8\sqrt(2)\,i, kust 10A+2B=5 ja (2A-5B)\sqrt(2)=8\sqrt(2).

Kahe muutujaga kahe võrrandisüsteemi lahendamine \begin(juhud)10A+2B=5,\\ 2A-5B=8,\end(juhtumid) leiame: A=\frac(41)(54),~ B=-\frac(35)(27).

Jääb kindlaks määrata koefitsiendi D väärtus. Selleks avame võrdsuses (4) olevad sulud, esitame sarnased terminid ja võrdleme seejärel x^4 koefitsiente. Saame:

A+D+E=1, see tähendab D=0.

Asendame koefitsientide leitud väärtused võrdsusega (3):

\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))= \frac(\drac(41)(54)\, x- \dfrac(35)(27))(x^2+2)+ \frac(16)(9)\frac(1)((x-1)^2)+ \frac(13)(54) \frac(1)(x+2)\,

ja seejärel jätkake integratsiooniga:

\begin(joondatud)\int\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))\,dx&= \frac( 41)(54)\int\frac(x\,dx)(x^2+2)- \frac(35)(27)\int\frac(dx)(x^2+2)+ \frac(16) )(9) \int\frac(dx)((x-1)^2)+ \frac(13)(54)\int\frac(dx)(x+2)=\\ &=\frac(41 )(108)\ln(x^2+2)- \frac(35)(27\sqrt(2))\operaatorinimi(arctg)\frac(x)(\sqrt(2))- \frac(16) (9(x-1))+ \frac(13)(54) \ln|x+2|+C.\end(joondatud)

Vale murdude integreerimine

Oletame, et peame funktsiooni integreerima y=\frac(f(x))(g(x)), kus f(x) ja g(x) on polünoomid ja polünoomi f(x) aste on suurem või võrdne polünoomi g(x) astmega. Sel juhul peate kõigepealt valima vale murdosa kogu osa \frac(f(x))(g(x)), st kujutage seda kujul

\frac(f(x))(g(x))=s(x)+ \frac(r(x))(g(x))\,

kus s(x) on polünoom, mille aste on võrdne polünoomide f(x) ja g(x) astmete vahega ja \frac(r(x))(g(x))- õige murd.

Siis on meil \int\frac(f(x))(g(x))\,dx= \int s(x)\,dx+ \int\frac(r(x))(g(x))\,dx\, ..

Näide 5. Arvutame valemurru integraali \int\frac(x^4-4x^3+x^2+16x-11)((x-1)(x+2)(x-3))\,dx.

Lahendus. Meil on:

\begin(joonatud)g(x)&=(x-1)(x+2)(x-3)= x^3-2x^2-5x+6,\\ f(x)&=x^4 -4x^3+x^2+16x-11. \end (joondatud)

Kogu osa eraldamiseks jagage f(x) g(x)-ga: \frac(f(x))(g(x))= x-2+\frac(2x^2+1)(x^3-2x^2-5x+6)\,.

Tähendab, \int\frac(x^4-4x^3+x^2+16x-11)((x-1)(x+2)(x-3))\,dx= \int(x-2)dx+ \int\frac(2x^2+1)((x-1)(x+2)(x-3))\,dx

Meil on: \int(x-2)dx=\frac(x^2)(2)-2x+C.

Integraali arvutamiseks \int\frac(2x^2+1)((x-1)(x+2)(x-3))\,dx Kasutatakse määramatute koefitsientide meetodit, nagu eespool. Pärast arvutusi, mille jätame lugeja hooleks, saame.

Ratsionaalmurrude integreerimine Murdmurrud - ratsionaalne funktsioon Lihtsamad ratsionaalmurrud Ratsionaalmurru lagundamine lihtmurdudeks Lihtmurdude integreerimine Üldreegel ratsionaalsete murdude integreerimine

n-astme polünoom. murdosa – ratsionaalne funktsioon murdosa – ratsionaalne funktsioon on funktsioon, mis võrdub kahe polünoomi suhtega: Ratsionaalmurdu nimetatakse õigeks, kui lugeja aste on väiksem kui nimetaja aste, st m< n , в противном случае дробь называется неправильной. многочлен степени m Всякую неправильную рациональную дробь можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(x) и правильной рациональной дроби:)()()(x. Q x. P xf n m)()()(x. Q x. R x. L x. Q x. P

Fractional – ratsionaalne funktsioon Vähenda vale murd To õiget sorti: 2 95 4 x xx 95 4 xx 2 x 3 x 34 2 xx 952 3 xx 2 2 x 23 42 xx 954 2 xx x 4 xx 84 2 93 x 3 63 x 15 2 95 4 x 2x3 x 3 x 2

Lihtsamad ratsionaalsed murrud Vormi õiged ratsionaalsed murrud: Neid nimetatakse tüüpide lihtsaimateks ratsionaalseteks murdudeks. kirves A); 2(Nkk ax A k)04(2 2 qp qpxx NMx); 2; 04(2 2 Nkkqp qpxx NMx k V V,

Ratsionaalmurru lagundamine lihtmurdudeks Teoreem: Iga õige ratsionaalne murd, mille nimetaja on faktoriseeritud: saab esitada unikaalsel viisil lihtmurdude summana: s k qxpxxxxxxx. Q)()()(22 2 11 2 21)()(x. Q x. P 1 xx A k k xx B)()(2 2 2 1 11 2 qxpx DCx 2 22 22 2 11)(qxpx Nx. M s ss qxpx Nx)

Ratsionaalmurru lagundamine lihtmurdudeks Selgitame teoreemi sõnastust järgmiste näidete abil: Ebakindlate koefitsientide A, B, C, D... leidmiseks kasutatakse kahte meetodit: koefitsientide võrdlemise meetodit ja meetodit. muutuja osaväärtustest. Vaatame esimest meetodit näite abil. 3 2) 3) (2 (4 xx x 2 x A 3 3 2 21) 3 () 3 (3 x B x B 1 2 x DCx 22 22 2 11) 1 (1 x x Nx. M)1 (3 22) 3 xx x 2 21 x A 22 2)1) (4 (987 xxx xx 4 x)

Ratsionaalmurru lagundamine lihtmurdudeks Esitage murd lihtmurdude summana: taandame lihtmurrud ühine nimetaja Võrdlustame saadud ja algsete murdude lugejad Võrdsustame samade astmete koefitsiendid x)52)(1(332 2 2 xxx xx 1 x A 52 2 xx CBx)52)(1()1)()52( 2 2 xxxx A 33252 35 32 0 1 2

Lihtsamate murdude integreerimine Leiame lihtsaimate ratsionaalsete murdude integraalid: Vaatame näite abil 3. tüüpi murdude integreerimist. dx ax A k dx qpxx NMx 2 ax axd A)(Cax. Aln)(axdax. A k C k ax. A k

Lihtmurrude integreerimine dx xx x 102 13 2 dx xx x 9) 12 (13 2 dx x x 9) 1 (13 2 dtdx tx tx 1 1 dt t t 9 1) 1 (3 2 dt t t 9 232 2tt 9 2 3 2 2 td 33 2 t arctgt C t arctgt 33 2 9 ln 2 32 C x arctgxx 3 1 3 2 102 ln.

Lihtmurdude integreerimine Integraal seda tüüpi asendust kasutades: taandatakse kahe integraali summaks: Esimene integraal arvutatakse diferentsiaalmärgi alla t sisestamisega. Teine integraal arvutatakse kordusvalemi abil: dx qpxx NMx k 2 V t p x 2 kk at dt N at dtt M 22122 1221222))(1(222 321 kkkk atk t k k aat dt

Lihtmurdude integreerimine a = 1; k = 3 323) 1 (t dt tartg t dt 1 21) 1) (12 (2222 322 1 21222 t t t dt) 1 (22 1 2 t t t t t t t t 2223) 1) (13 (2232 t 2 t c 3 g t ) (4)1(

Üldreegel ratsionaalsete murdude integreerimiseks Kui murd on vale, siis esitage see polünoomi ja õige murru summana. Olles arvutanud õige ratsionaalse murru nimetaja, esitage see määramata koefitsientidega lihtmurdude summana, leidke määramata koefitsiendid koefitsientide võrdlemise meetodil või muutuja osaväärtuste meetodil. Integreerige polünoom ja saadud lihtmurdude summa.

Näide Paneme murru õigele kujule. dx xxx 23 35 2 442 35 xxxxxx 23 2 2 x 345 2 xxx 442 34 xxx x 2 234 242 xxx 4425 23 xxx xxx 23 35 2 442 x 2 x 5 x 5 x 2 x 2 105 23 48 2 x x

Näide Faktoriseerime õige murru nimetaja Esitame murdosa lihtmurdude summana Leiame muutuja xxx xx osaväärtuste meetodil määramata koefitsiendid 23 2 2 48 2 2)1(48 xx xx 2) )1(1 x C x B x A 2 2)1 ()1(xx Cxx. Bxx. A 48)1()1(22 xx. Cxx. Bxx. A 5241 31 40 CBAx Cx Ax 3 12 4 C B A xxx xx 23 2 2 48 2)1 (3 1 124 xxx

Näide dx xx 2 2) 1 (3 1 124 52 2 2) 1 (3 1 12452 x dx dxxdxdxx C x xxxx x 1 3 1 ln 12 ln

Ratsionaalfunktsioon on murdosa vormist, mille lugejaks ja nimetajaks on polünoomid või polünoomide korrutised.

Näide 1. 2. samm.

.

Korrutame määramata koefitsiendid polünoomidega, mis ei ole selles üksikmurrus, kuid on teistes saadud murdudes:

Avame sulud ja võrdsustame algse integrandi lugeja saadud avaldisega:

Võrdsuse mõlemalt poolelt otsime termineid, millel on samad x astmed, ja koostame nendest võrrandisüsteemi:

.

Tühistame kõik x-id ja saame samaväärse võrrandisüsteemi:

.

Seega integrandi lõplik laiendamine summaks lihtmurrud:

.

Näide 2. 2. samm. Etapis 1 saime algse murdosa järgmise jaotuse lihtmurdude summaks koos ebakindlad koefitsiendid lugejates:

.

Nüüd hakkame otsima ebakindlaid koefitsiente. Selleks võrdsustame funktsiooniavaldises oleva algse murru lugeja avaldise lugejaga, mis saadakse pärast murdude summa taandamist ühiseks nimetajaks:

Nüüd peate looma ja lahendama võrrandisüsteemi. Selleks võrdsustame muutuja koefitsiendid vastava astmega funktsiooni algse avaldise lugejas ja sarnased koefitsiendid eelmises etapis saadud avaldises:

Lahendame saadud süsteemi:

Niisiis, siit

.

Näide 3. 2. samm. Etapis 1 saime algse murdosa järgmise jaotuse lihtsate murdude summaks, mille lugejate koefitsiendid on määramata:

Hakkame otsima ebakindlaid koefitsiente. Selleks võrdsustame funktsiooniavaldises oleva algse murru lugeja selle avaldise lugejaga, mis saadakse pärast murdude summa taandamist ühiseks nimetajaks:

Nagu eelmistes näidetes, koostame võrrandisüsteemi:

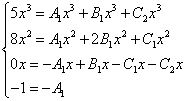
Vähendame x-e ja saame samaväärse võrrandisüsteemi:

Süsteemi lahendades saame järgmised väärtused ebakindlad koefitsiendid:

Saame integrandi lõpliku lagunemise lihtmurdude summaks:

.

Näide 4. 2. samm. Etapis 1 saime algse murdosa järgmise jaotuse lihtsate murdude summaks, mille lugejate koefitsiendid on määramata:

.

Juba varasematest näidetest teame, kuidas võrdsustada algmurru lugejat lugejas oleva avaldisega, mis saadakse pärast murdarvu lammutamist lihtmurdude summaks ja selle summa viimist ühise nimetajani. Seetõttu esitame lihtsalt kontrolli eesmärgil saadud võrrandisüsteemi:

Süsteemi lahendades saame ebakindlate koefitsientide järgmised väärtused:

Saame integrandi lõpliku lagunemise lihtmurdude summaks:

Näide 5. 2. samm. Etapis 1 saime algse murdosa järgmise jaotuse lihtsate murdude summaks, mille lugejate koefitsiendid on määramata:

.

Me taandame selle summa iseseisvalt ühiseks nimetajaks, võrdsustades selle avaldise lugeja algmurru lugejaga. Tulemus peaks olema järgmine süsteem võrrandid:

Süsteemi lahendades saame ebakindlate koefitsientide järgmised väärtused:

.

Saame integrandi lõpliku lagunemise lihtmurdude summaks:

.

Näide 6. 2. samm. Etapis 1 saime algse murdosa järgmise jaotuse lihtsate murdude summaks, mille lugejate koefitsiendid on määramata:

Teeme selle summaga samad toimingud nagu eelmistes näidetes. Tulemuseks peaks olema järgmine võrrandisüsteem:

Süsteemi lahendades saame ebakindlate koefitsientide järgmised väärtused:

.

Saame integrandi lõpliku lagunemise lihtmurdude summaks:

.

Näide 7. 2. samm. Etapis 1 saime algse murdosa järgmise jaotuse lihtsate murdude summaks, mille lugejate koefitsiendid on määramata:

.

Pärast teatud toiminguid saadud summaga tuleks saada järgmine võrrandisüsteem:

Süsteemi lahendades saame ebakindlate koefitsientide järgmised väärtused:

Saame integrandi lõpliku lagunemise lihtmurdude summaks:

.

Näide 8. 2. samm. Etapis 1 saime algse murdosa järgmise jaotuse lihtsate murdude summaks, mille lugejate koefitsiendid on määramata:

.

Teeme võrrandisüsteemi saamiseks mõned muudatused toimingutes, mis on juba automaatseks viidud. On kunstlik tehnika, mis mõnel juhul aitab vältida tarbetuid arvutusi. Viies murdude summa ühise nimetajani, saame ja võrdsustades selle avaldise lugeja algmurru lugejaga, saame.

“Matemaatik, nagu kunstnik või luuletaja, loob mustreid. Ja kui tema mustrid on stabiilsemad, siis ainult sellepärast, et need koosnevad ideedest... Matemaatiku mustrid, nii nagu kunstniku või poeedi mustrid, peavad olema ilusad; Ideed, nagu värvid või sõnad, peavad üksteisele vastama. Ilu on esimene nõue: maailmas pole kohta koledal matemaatikal».

G.H. Hardy

Esimeses peatükis märgiti, et primitiivid on üsna lihtsad funktsioonid, mida ei saa enam läbi väljendada elementaarsed funktsioonid. Sellega seoses omandavad tohutu praktilise tähtsuse need funktsiooniklassid, mille kohta saame täpselt öelda, et nende antiderivaadid on elementaarsed funktsioonid. See funktsioonide klass sisaldab ratsionaalsed funktsioonid, mis esindab kahe algebralise polünoomi suhet. Paljud probleemid viivad ratsionaalsete murdude integreerimiseni. Seetõttu on väga oluline, et oleks võimalik selliseid funktsioone integreerida.

2.1.1. Murdratsionaalfunktsioonid

Ratsionaalne murdosa(või murdosaline ratsionaalne funktsioon) on kahe algebralise polünoomi seos:

kus ja on polünoomid.

Tuletagem seda meelde polünoom (polünoom, kogu ratsionaalne funktsioon) naste nimetatakse vormi funktsiooniks

Kus - reaalarvud. Näiteks,

– esimese astme polünoom;

– neljanda astme polünoom jne.

Ratsionaalmurdu (2.1.1) nimetatakse õige, kui aste on kraadist madalam, s.o. n<m, muidu nimetatakse murdosa vale.

Iga vale murdosa saab esitada polünoomi (täisarvulise osa) ja õige murru (murruosa) summana. Vale murru tervik- ja murdosa eraldamist saab teha vastavalt polünoomide “nurgaga” jagamise reeglile.

Näide 2.1.1. Tuvastage järgmiste ebaõigete ratsionaalsete murdude terved ja murdosad:

A) , b) .

Lahendus . a) Kasutades “nurga” jagamisalgoritmi, saame

Seega saame

.

b) Siin kasutame ka “nurga” jagamise algoritmi:

Selle tulemusena saame

.

Teeme kokkuvõtte. Üldjuhul saab ratsionaalse murru määramatut integraali esitada polünoomi ja õige ratsionaalmurru integraalide summana. Polünoomide antiderivaatide leidmine pole keeruline. Seetõttu käsitleme edaspidi peamiselt õigeid ratsionaalseid murde.

2.1.2. Lihtsamad ratsionaalsed murrud ja nende integreerimine

Õigete ratsionaalsete murdude hulgas on neli tüüpi, mida liigitatakse järgmiselt lihtsaimad (elementaarsed) ratsionaalsed murrud:

3) ,

4) ,

kus on täisarv, , st. ruuttrinoom tal pole tõelisi juuri.

1. ja 2. tüübi lihtmurdude integreerimine ei tekita suuri raskusi:

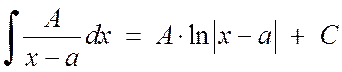, (2.1.3)

. (2.1.4)

Vaatleme nüüd 3. tüübi lihtmurdude integreerimist, kuid 4. tüübi murde me ei arvesta.

Alustame vormi integraalidega

.

See integraal arvutatakse tavaliselt nimetaja täiusliku ruudu eraldamise teel. Tulemuseks on järgmise vormi tabeliintegraal

või .

Näide 2.1.2. Leidke integraalid:

A) , b) .

Lahendus . a) Valige ruut kolmiku ruut:

Siit leiame

b) Eraldades täisruudu ruuttrinoomist, saame:

Seega

.

Integraali leidmiseks

võite eraldada nimetaja tuletise lugejas ja laiendada integraali kahe integraali summaks: esimene neist asendades taandub välimusele

,

ja teine ​​- eespool käsitletule.

Näide 2.1.3. Leidke integraalid:

.

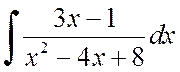Lahendus . Märka seda . Isoleerime nimetaja tuletise lugejas:

Esimene integraal arvutatakse asendamise abil :

Teises integraalis valime nimetajasse täiusliku ruudu

Lõpuks saame

2.1.3. Õige ratsionaalne murdosa laiendamine
lihtmurdude summaks

Mis tahes õige ratsionaalne murd saab unikaalsel viisil esitada lihtmurdude summana. Selleks tuleb nimetaja faktoriseerida. Kõrgemast algebrast on teada, et iga polünoom reaalkoefitsientidega

TEEMA: Ratsionaalsete murdude lõimimine.

Tähelepanu! Uurides üht integreerimise põhimeetodit: ratsionaalsete murdude integreerimist, tuleb rangete tõestuste tegemiseks arvestada kompleksvaldkonna polünoomidega. Seetõttu on vajalik eelnevalt õppima mõned kompleksarvude omadused ja tehted nendega.

Lihtratsionaalsete murdude integreerimine.

Kui P(z) Ja K(z) on kompleksvaldkonnas polünoomid, siis on need ratsionaalsed murrud. Seda nimetatakse õige, kui kraad P(z) vähem kraadi K(z) , Ja vale, kui kraad R mitte vähem kui kraad K.

Iga vale murdosa võib esitada järgmiselt: ,

P(z) = Q(z) S(z) + R(z),

a R(z) – polünoom, mille aste on astmest väiksem K(z).

Seega taandub ratsionaalsete murdude integreerimine polünoomide, st astmefunktsioonide ja õigete murdude integreerimisele, kuna see on õige murd.

Definitsioon 5. Lihtsamad (või elementaar-) murrud on järgmist tüüpi murded:

1) , 2) , 3) , 4) .

Uurime, kuidas nad integreeruvad.

3) (varem uuritud).

Teoreem 5. Iga õiget murdu saab esitada lihtmurdude summana (ilma tõestuseta).

Järeldus 1. Kui on õige ratsionaalne murd ja kui polünoomi juurte hulgas on ainult lihtreaaljuured, siis murdu lihtmurdude summaks on ainult 1. tüüpi lihtmurrud:

Näide 1.

Järeldus 2. Kui on õige ratsionaalne murd ja kui polünoomi juurte hulgas on ainult mitu reaaljuurt, siis murdu lagundamisel lihtmurdude summaks on ainult 1. ja 2. tüübi lihtmurrud. :

Näide 2.

Järeldus 3. Kui on õige ratsionaalne murd ja kui polünoomi juurte hulgas on ainult lihtsad komplekssed konjugaatjuured, siis murdu lagundamisel lihtmurdude summaks on ainult 3. tüüpi lihtmurrud:

Näide 3.

Järeldus 4. Kui on õige ratsionaalne murd ja kui polünoomi juurte hulgas on ainult mitu kompleksset konjugaatjuurt, siis murdu lagundamisel lihtmurdude summaks on ainult 3. ja 4. lihtmurrud. tüübid:

Tundmatute koefitsientide määramiseks antud laiendustes toimige järgmiselt. Tundmatuid koefitsiente sisaldava laienduse vasak ja parem pool korrutatakse kahe polünoomi võrdsusega. Sellest saadakse nõutavate koefitsientide võrrandid, kasutades:

1. võrdsus kehtib kõigi X väärtuste puhul (osalise väärtuse meetod). Sel juhul saadakse suvaline arv võrrandeid, millest mis tahes m võimaldab leida tundmatuid koefitsiente.

2. koefitsiendid langevad kokku X samade astmete korral (määramatute koefitsientide meetod). Sel juhul saadakse m - võrrandite süsteem m - tundmatutega, millest leitakse tundmatud koefitsiendid.

3. kombineeritud meetod.

Näide 5. Laienda murdosa kõige lihtsamatele.

Lahendus:

Leiame koefitsiendid A ja B.

1. meetod – eraväärtuse meetod:

2. meetod – määramata koefitsientide meetod:

Vastus:

Ratsionaalsete murdude integreerimine.

6. teoreem. Mis tahes ratsionaalse murru määramatu integraal mis tahes intervallil, mille nimetaja ei ole võrdne nulliga, on olemas ja seda väljendatakse elementaarfunktsioonide, nimelt ratsionaalsete murdude, logaritmide ja arctangentide kaudu.

Tõestus.

Kujutagem ette ratsionaalset murdosa kujul: . Sel juhul on viimane liige korralik murd ja teoreemi 5 kohaselt võib seda esitada lihtmurdude lineaarse kombinatsioonina. Seega taandatakse ratsionaalse murru integreerimine polünoomi integreerimiseks S(x) ja lihtmurrud, mille antiderivaadid, nagu on näidatud, on teoreemis näidatud kujul.

kommenteerida. Peamine raskus on sel juhul nimetaja lagunemine teguriteks, see tähendab kõigi selle juurte otsimine.

Näide 1. Leidke integraal