Generalizirane homogene diferencijalne jednadžbe prvog reda. Generalizirana homogena jednadžba Generalizirane homogene jednadžbe drugog reda
Diferencijalne jednadžbe u generaliziranim funkcijama
Neka postoji jednadžba. Ako je obična funkcija, tada je njezino rješenje antiderivativno, tj. Neka je sada generalizirana funkcija.
Definicija. Generalizirana funkcija naziva se antiderivativna generalizirana funkcija ako. Ako je singularna generalizirana funkcija, onda postoje slučajevi kada je njezin antiderivat regularna generalizirana funkcija. Na primjer, antiderivat je; antiderivacija je funkcija, a rješenje jednadžbe može se napisati kao: , gdje je.
Postoji linearna jednadžba th reda s konstantnim koeficijentima
gdje je generalizirana funkcija. Neka je diferencijalni polinom th reda.
Definicija. Generalizirano rješenje diferencijalne jednadžbe (8) je generalizirana funkcija za koju je ispunjena relacija:
Ako je kontinuirana funkcija, tada je jedino rješenje jednadžbe (8) klasično rješenje.
Definicija. Temeljno rješenje jednadžbe (8) je svaka generalizirana funkcija takva da.
Greenova funkcija temeljno je rješenje koje zadovoljava rubni, početni ili asimptotski uvjet.
Teorema. Rješenje jednadžbe (8) postoji i ima oblik:
osim ako nije definirana konvolucija.
Dokaz. Stvarno,. Prema svojstvu konvolucije slijedi: .
Lako je vidjeti da je temeljno rješenje ove jednadžbe, jer
Svojstva generaliziranih derivacija
Operacija diferenciranja je linearna i kontinuirana od do:
u ako u;

Svaka generalizirana funkcija je beskonačno diferencijabilna. Doista, ako, onda; zauzvrat itd.;
Rezultat diferencijacije ne ovisi o redoslijedu diferencijacije. Na primjer, ;
Ako je i, tada vrijedi Leibnizova formula za razlikovanje proizvoda. Na primjer, ;
Ako je generalizirana funkcija, tada;
Ako niz sastavljen od lokalno integrabilnih funkcija jednoliko konvergira na svakom kompaktnom skupu, tada se može diferencirati član po član bilo koji broj puta (kao generalizirana funkcija), a rezultirajući niz će konvergirati.
Primjer. Neka
Funkcija se naziva Heavisideova funkcija ili funkcija identiteta. Lokalno je integrabilna i stoga se može smatrati generaliziranom funkcijom. Možete pronaći njegovu izvedenicu. Po definiciji, tj. .
Generalizirane funkcije koje odgovaraju kvadratnim oblicima s kompleksnim koeficijentima
Do sada su se razmatrale samo kvadratne forme s realnim koeficijentima. U ovom odjeljku proučavamo prostor svih kvadratnih oblika s kompleksnim koeficijentima.
Zadatak je odrediti generaliziranu funkciju, gdje je kompleksan broj. Međutim, u općem slučaju, neće biti jednoznačna analitička funkcija od. Stoga se u prostoru svih kvadratnih formi izdvaja "gornja poluravnina" kvadratnih formi s pozitivno definiranim imaginarnim dijelom i određuje im se funkcija. Naime, ako kvadratni oblik pripada toj "poluravnini", tada se pretpostavlja gdje. Takva funkcija je analitička funkcija s jednom vrijednošću.
Sada možete mapirati funkciju u generičku funkciju:
gdje se integracija provodi po cijelom prostoru. Integral (13) konvergira u i analitička je funkcija u toj poluravnini. Analitički nastavljajući ovu funkciju, određuje se funkcional za ostale vrijednosti.
Za kvadratne oblike s pozitivno određenim imaginarnim dijelom pronalaze se singularne točke funkcija i izračunavaju rezidue tih funkcija u singularnim točkama.
Generalizirana funkcija analitički ne ovisi samo o koeficijentima kvadratne forme nego i o njima. Dakle, je analitička funkcija u gornjoj "poluravnini" svih kvadratnih oblika oblika gdje postoji pozitivno određen oblik. Dakle, jedinstveno je određena svojim vrijednostima na "imaginarnoj poluosi", tj. na skupu kvadratnih oblika oblika, gdje je pozitivno određena forma.
.
Diferencijalne jednadžbe.
§ 1. Osnovni pojmovi običnih diferencijalnih jednadžbi.
Definicija 1. Obična diferencijalna jednadžba n-ti red za funkciju g argument x naziva se relacija oblika
Gdje F je dana funkcija svojih argumenata. U nazivu ove klase matematičkih jednadžbi, izraz "diferencijal" naglašava da one uključuju derivacije  (funkcije nastale kao rezultat diferencijacije); pojam - "obični" govori da željena funkcija ovisi o samo jednom stvarnom argumentu.
(funkcije nastale kao rezultat diferencijacije); pojam - "obični" govori da željena funkcija ovisi o samo jednom stvarnom argumentu.
Obična diferencijalna jednadžba ne mora eksplicitno sadržavati argument x,
željenu funkciju  i bilo koji od njegovih derivata, ali najviši derivat
i bilo koji od njegovih derivata, ali najviši derivat  moraju biti uključeni u jednadžbu n-
narudžba. Na primjer
moraju biti uključeni u jednadžbu n-
narudžba. Na primjer
A)  je jednadžba prvog reda;
je jednadžba prvog reda;
b)  je jednadžba trećeg reda.
je jednadžba trećeg reda.
Pri pisanju običnih diferencijalnih jednadžbi često se koristi zapis derivacija kroz diferencijale:
V)  je jednadžba drugog reda;
je jednadžba drugog reda;
G)  je jednadžba prvog reda,
je jednadžba prvog reda,
tvoreći nakon dijeljenja po dx ekvivalentan oblik jednadžbe:  .
.
Funkcija  se zove rješenje obične diferencijalne jednadžbe ako, kada se zamijeni u nju, postane identitet.
se zove rješenje obične diferencijalne jednadžbe ako, kada se zamijeni u nju, postane identitet.
Na primjer, jednadžba 3. reda
Ima rješenje  .
.
Pronaći ovom ili drugom metodom, na primjer selekcijom, jednu funkciju koja zadovoljava jednadžbu ne znači njezino rješavanje. Riješiti običnu diferencijalnu jednadžbu znači pronaći svi funkcije koje tvore identitet kada se zamijene u jednadžbu. Za jednadžbu (1.1) obitelj takvih funkcija formirana je uz pomoć proizvoljnih konstanti i naziva se opće rješenje obične diferencijalne jednadžbe n reda, a broj konstanti se podudara s redom jednadžbe: g(x) : U ovom slučaju rješenje se naziva općim integralom jednadžbe (1.1).
Na primjer, opće rješenje diferencijalne jednadžbe  je sljedeći izraz: , a drugi član se također može napisati kao
je sljedeći izraz: , a drugi član se također može napisati kao  , budući da je proizvoljna konstanta
, budući da je proizvoljna konstanta  podijeljeno s 2 može se zamijeniti novom proizvoljnom konstantom
podijeljeno s 2 može se zamijeniti novom proizvoljnom konstantom  .
.
Zadavanjem nekih dopuštenih vrijednosti za sve proizvoljne konstante u općem rješenju ili u općem integralu dobivamo određenu funkciju koja više ne sadrži proizvoljne konstante. Ta se funkcija naziva posebnim rješenjem ili posebnim integralom jednadžbe (1.1). Za pronalaženje vrijednosti proizvoljnih konstanti, a time i određenog rješenja, koriste se različiti dodatni uvjeti jednadžbe (1.1). Na primjer, mogu se dati takozvani početni uvjeti za (1.2).
U desnim dijelovima početnih uvjeta (1.2) dane su numeričke vrijednosti funkcije i izvodnica, a ukupan broj početnih uvjeta jednak je broju proizvoljnih konstanti koje se određuju.
Problem nalaženja određenog rješenja jednadžbe (1.1) iz početnih uvjeta naziva se Cauchyjev problem.
§ 2. Obične diferencijalne jednadžbe 1. reda - osnovni pojmovi.
Obična diferencijalna jednadžba 1. reda ( n=1) ima oblik:  ili, ako se može razriješiti s obzirom na derivat:
ili, ako se može razriješiti s obzirom na derivat:  . Zajednička odluka g=
g(x,S) ili opći integral
. Zajednička odluka g=
g(x,S) ili opći integral  Jednadžbe 1. reda sadrže jednu proizvoljnu konstantu. Jedini početni uvjet za jednadžbu 1. reda
Jednadžbe 1. reda sadrže jednu proizvoljnu konstantu. Jedini početni uvjet za jednadžbu 1. reda  omogućuje određivanje vrijednosti konstante iz općeg rješenja ili iz općeg integrala. Tako će se naći određeno rješenje ili će se riješiti, što je također Cauchyjev problem. Pitanje postojanja i jedinstvenosti rješenja Cauchyjevog problema jedno je od središnjih u općoj teoriji običnih diferencijalnih jednadžbi. Posebno za jednadžbu prvog reda vrijedi teorem koji je ovdje prihvaćen bez dokaza.
omogućuje određivanje vrijednosti konstante iz općeg rješenja ili iz općeg integrala. Tako će se naći određeno rješenje ili će se riješiti, što je također Cauchyjev problem. Pitanje postojanja i jedinstvenosti rješenja Cauchyjevog problema jedno je od središnjih u općoj teoriji običnih diferencijalnih jednadžbi. Posebno za jednadžbu prvog reda vrijedi teorem koji je ovdje prihvaćen bez dokaza.
Teorem 2.1. Ako je u jednadžbi funkcija  i njegov djelomični izvod
i njegov djelomični izvod  kontinuirano u nekom području D avion XOY, au ovom području se daje bod
kontinuirano u nekom području D avion XOY, au ovom području se daje bod  , tada postoji i, štoviše, jedinstveno rješenje koje zadovoljava i jednadžbu i početni uvjet
, tada postoji i, štoviše, jedinstveno rješenje koje zadovoljava i jednadžbu i početni uvjet  .
.
Geometrijski opće rješenje jednadžbe 1. reda je familija krivulja u ravnini XOY, koji nemaju zajedničkih točaka i međusobno se razlikuju po jednom parametru - vrijednosti konstante C. Te se krivulje nazivaju integralne krivulje za danu jednadžbu. Integralne krivulje jednadžbe imaju očito geometrijsko svojstvo: u svakoj točki, tangens nagiba tangente na krivulju jednak je vrijednosti desne strane jednadžbe u toj točki:  . Drugim riječima, jednadžba je dana u ravnini XOY polje pravaca tangenti na integralne krivulje. Komentar: Treba napomenuti da za jednadžbu
. Drugim riječima, jednadžba je dana u ravnini XOY polje pravaca tangenti na integralne krivulje. Komentar: Treba napomenuti da za jednadžbu  dana je jednadžba i tzv.jednadžba u simetričnom obliku
dana je jednadžba i tzv.jednadžba u simetričnom obliku  .
.
§ 3. Diferencijalne jednadžbe prvog reda sa separabilnim varijablama.
Definicija. Diferencijalna jednadžba sa separabilnim varijablama je jednadžba oblika  (3.1)
(3.1)
ili jednadžba oblika (3.2)
Da bismo razdvojili varijable u jednadžbi (3.1), tj. reducirajte ovu jednadžbu na takozvanu jednadžbu s odvojenim varijablama, izvršite sljedeće radnje:
 ;
;
Sada trebamo riješiti jednadžbu g(g)= 0 . Ako ima pravo rješenje g= a, Da g= a također će biti rješenje jednadžbe (3.1).
Jednadžba (3.2) se svodi na odvojenu jednadžbu varijable dijeljenjem s umnoškom  :
:
 , što nam omogućuje da dobijemo opći integral jednadžbe (3.2):
, što nam omogućuje da dobijemo opći integral jednadžbe (3.2):  . (3.3)
. (3.3)
Integralne krivulje (3.3) dopunit ćemo rješenjima  ako postoje takva rješenja.
ako postoje takva rješenja.
Riješite jednadžbu: .
Razdvajanje varijabli:

 .
.
Integracijom, dobivamo 
Dalje od jednadžbi  I
I  pronaći x=1,
g=-1.
Ove odluke su privatne odluke.
pronaći x=1,
g=-1.
Ove odluke su privatne odluke.
§ 4. Homogene diferencijalne jednadžbe prvog reda.
Definicija 1. Jednadžba 1. reda naziva se homogenom ako je za njezinu desnu stranu za bilo koji  omjer
omjer  , koji se naziva uvjetom homogenosti za funkciju dviju varijabli nulte dimenzije.
, koji se naziva uvjetom homogenosti za funkciju dviju varijabli nulte dimenzije.
Primjer 1 Pokažite tu funkciju  - homogeno nulto mjerenje.
- homogeno nulto mjerenje.
Riješenje.
 ,
,
Q.E.D.
Teorema. Bilo koja funkcija  je homogena i, obrnuto, svaka homogena funkcija
je homogena i, obrnuto, svaka homogena funkcija  nulta dimenzija se svodi na formu
nulta dimenzija se svodi na formu  .
.
Dokaz.
Prva tvrdnja teorema je očita, jer  . Dokažimo drugu tvrdnju. Stavimo
. Dokažimo drugu tvrdnju. Stavimo  , zatim za homogenu funkciju
, zatim za homogenu funkciju  , što je trebalo dokazati.
, što je trebalo dokazati.
Definicija 2. Jednadžba (4.1)
u kojem M I N su homogene funkcije istog stupnja, tj. imati vlasništvo za sve  , naziva se homogenim.
, naziva se homogenim.
Očito se ova jednadžba uvijek može svesti na oblik  (4.2) , iako se to možda neće učiniti za njegovo rješavanje.
(4.2) , iako se to možda neće učiniti za njegovo rješavanje.
Homogena jednadžba se zamjenom željene funkcije svodi na jednadžbu sa separabilnim varijablama g prema formuli g=
zx,
Gdje z(x)
je nova željena funkcija. Nakon ove zamjene u jednadžbi (4.2), dobivamo:  ili
ili  ili
ili  .
.
Integriranjem dobivamo opći integral jednadžbe s obzirom na funkciju z(x)
 , koji nakon ponovljene zamjene
, koji nakon ponovljene zamjene  daje opći integral izvorne jednadžbe. Osim toga, ako
daje opći integral izvorne jednadžbe. Osim toga, ako  - korijeni jednadžbe
- korijeni jednadžbe  , zatim funkcije
, zatim funkcije  - rješenja homogene zadane jednadžbe. Ako
- rješenja homogene zadane jednadžbe. Ako  , tada jednadžba (4.2) poprima oblik
, tada jednadžba (4.2) poprima oblik
 i postaje jednadžba sa odvojivim varijablama. Njegova rješenja su poluizravna:
i postaje jednadžba sa odvojivim varijablama. Njegova rješenja su poluizravna:  .
.
Komentar. Ponekad je preporučljivo umjesto gornje zamjene koristiti zamjenu x= zy.
§ 5. Svođenje diferencijalnih jednadžbi na homogene.
Razmotrimo jednadžbu oblika  . (5.1)
. (5.1)
Ako  , onda je ova jednadžba supstitucijom , gdje je
, onda je ova jednadžba supstitucijom , gdje je  I
I  su nove varijable, i
su nove varijable, i  - neki konstantni brojevi određeni iz sustava
- neki konstantni brojevi određeni iz sustava 
Svedeno na homogenu jednadžbu 
Ako  , tada jednadžba (5.1) poprima oblik
, tada jednadžba (5.1) poprima oblik
 .
.
Pretpostavljajući z= sjekira+ po, dolazimo do jednadžbe koja ne sadrži nezavisnu varijablu.
Razmotrite primjere.
Primjer 1
Integriraj jednadžbu
i označite integralnu krivulju koja prolazi kroz točke: a) (2;2); b) (1;-1).
Riješenje.
Stavimo g= zx. Zatim dy= xdz+ zdx I
Skratimo za  i okupiti članove na dx I dz:
i okupiti članove na dx I dz:
Odvojimo varijable: 
 .
.
Integrirajući, dobivamo ;
ili  ,
,  .
.
Zamjena ovdje z na  , dobivamo opći integral zadane jednadžbe u obliku (5.2)
, dobivamo opći integral zadane jednadžbe u obliku (5.2)  ili
ili 
 .
.
Ova obitelj krugova  , čija središta leže na ravnoj liniji g =
x a koje su u ishodištu tangente na pravac g +
x = 0.
Ovo ravnog
= -
x
zauzvrat, određeno rješenje jednadžbe.
, čija središta leže na ravnoj liniji g =
x a koje su u ishodištu tangente na pravac g +
x = 0.
Ovo ravnog
= -
x
zauzvrat, određeno rješenje jednadžbe.
Sada Cauchyjev način zadatka:
A) uz pretpostavku općeg integrala x=2,
g=2,
pronaći C=2, pa je željeno rješenje  .
.
B) niti jedna kružnica (5.2) ne prolazi točkom (1;-1). Ali polucrta g = -
x,  prolazi kroz točku i daje željeno rješenje.
prolazi kroz točku i daje željeno rješenje.
Primjer 2 Riješite jednadžbu: .
Riješenje.
Jednadžba je poseban slučaj jednadžbe (5.1).
Determinanta  u ovom primjeru
u ovom primjeru  , pa moramo riješiti sljedeći sustav
, pa moramo riješiti sljedeći sustav 
Rješavanje, to dobivamo  . Izvođenje zamjene u zadanoj jednadžbi
. Izvođenje zamjene u zadanoj jednadžbi  , dobivamo homogenu jednadžbu. Integriranje sa zamjenom
, dobivamo homogenu jednadžbu. Integriranje sa zamjenom  , pronašli smo
, pronašli smo  .
.
Povratak na stare varijable x I g formule  , imamo .
, imamo .
§ 6. Generalizirana homogena jednadžba.
Jednadžba M(x,
g)
dx+
N(x,
g)
dy=0
naziva se generalizirano homogenim ako je moguće odabrati takav broj k da lijeva strana ove jednadžbe postane homogena funkcija nekog stupnja m relativno x,
g,
dx I dy pod uvjetom da x smatra se vrijednošću prvog mjerenja, g – k th mjerenje ,
dx I dy –
nula i (k-1)
th mjerenja. Na primjer, ovo bi bila jednadžba  . (6.1)
. (6.1)
Vrijedi pod pretpostavkom o mjerenjima
x,
g,
dx I dy pripadnici lijeve strane  I dy imat će dimenzije -2, 2 k I k-1. Njihovim izjednačavanjem dobivamo uvjet koji željeni broj mora zadovoljavati k: -2 = 2k=k-1. Ovaj uvjet je zadovoljen kada k= -1 (s takvim k svi članovi na lijevoj strani jednadžbe koja se razmatra imat će dimenziju -2). Prema tome, jednadžba (6.1) je generalizirano homogena.
I dy imat će dimenzije -2, 2 k I k-1. Njihovim izjednačavanjem dobivamo uvjet koji željeni broj mora zadovoljavati k: -2 = 2k=k-1. Ovaj uvjet je zadovoljen kada k= -1 (s takvim k svi članovi na lijevoj strani jednadžbe koja se razmatra imat će dimenziju -2). Prema tome, jednadžba (6.1) je generalizirano homogena.
Generalizirana homogena jednadžba se supstitucijom reducira na jednadžbu s razdvojivim varijablama  , Gdje z je nova nepoznata funkcija. Integrirajmo jednadžbu (6.1) naznačenom metodom. Jer k= -1, dakle
, Gdje z je nova nepoznata funkcija. Integrirajmo jednadžbu (6.1) naznačenom metodom. Jer k= -1, dakle  , nakon čega dobivamo jednadžbu .
, nakon čega dobivamo jednadžbu .
Integrirajući ga, nalazimo  , gdje
, gdje  . Ovo je opće rješenje jednadžbe (6.1).
. Ovo je opće rješenje jednadžbe (6.1).
§ 7. Linearne diferencijalne jednadžbe prvog reda.
Linearna jednadžba 1. reda je jednadžba koja je linearna u odnosu na željenu funkciju i njenu derivaciju. Izgleda kao:
 , (7.1)
, (7.1)
Gdje P(x)
I Q(x)
dane su kontinuirane funkcije od x.
Ako funkcija  ,
tada jednadžba (7.1) ima oblik:
,
tada jednadžba (7.1) ima oblik:  (7.2)
(7.2)
a naziva se linearna homogena jednadžba, inače  naziva se linearna nehomogena jednadžba.
naziva se linearna nehomogena jednadžba.
Linearna homogena diferencijalna jednadžba (7.2) je jednadžba sa separabilnim varijablama:

 (7.3)
(7.3)
Izraz (7.3) je opće rješenje jednadžbe (7.2). Naći opće rješenje jednadžbe (7.1) u kojoj je funkcija P(x) označava istu funkciju kao u jednadžbi (7.2), primjenjujemo metodu koja se zove metoda varijacije proizvoljne konstante i sastoji se u sljedećem: pokušat ćemo odabrati funkciju C=C(x) tako da bi opće rješenje linearne homogene jednadžbe (7.2) bilo rješenje nehomogene linearne jednadžbe (7.1). Tada za derivaciju funkcije (7.3) dobivamo:
 .
.
Zamjenom pronađene derivacije u jednadžbu (7.1) imat ćemo:
ili  .
.
Gdje  , gdje je proizvoljna konstanta. Kao rezultat toga, opće rješenje nehomogene linearne jednadžbe (7.1) bit će (7.4)
, gdje je proizvoljna konstanta. Kao rezultat toga, opće rješenje nehomogene linearne jednadžbe (7.1) bit će (7.4) 
Prvi član u ovoj formuli predstavlja opće rješenje (7.3) linearne homogene diferencijalne jednadžbe (7.2), a drugi član u formuli (7.4) je partikularno rješenje linearne nehomogene jednadžbe (7.1) dobiveno iz opće (7.4) ) sa  . Izdvojimo ovaj važan zaključak u obliku teorema.
. Izdvojimo ovaj važan zaključak u obliku teorema.
Teorema. Ako je poznato jedno posebno rješenje linearne nehomogene diferencijalne jednadžbe  , tada sva ostala rješenja imaju oblik
, tada sva ostala rješenja imaju oblik  , Gdje
, Gdje  je opće rješenje odgovarajuće linearne homogene diferencijalne jednadžbe.
je opće rješenje odgovarajuće linearne homogene diferencijalne jednadžbe.
Međutim, treba napomenuti da se za rješavanje linearne nehomogene diferencijalne jednadžbe 1. reda (7.1) češće koristi druga metoda, koja se ponekad naziva Bernoullijeva metoda. Rješenje jednadžbe (7.1) tražit ćemo u obliku  . Zatim
. Zatim  . Nađenu derivaciju zamijenimo u izvornu jednadžbu:
. Nađenu derivaciju zamijenimo u izvornu jednadžbu:  .
.
Spojimo, na primjer, drugi i treći član posljednjeg izraza i izbacimo funkciju u(x)
za zagrade:  (7.5)
(7.5)
Zahtijevamo da zagrada nestane:  .
.
Ovu jednadžbu rješavamo postavljanjem proizvoljne konstante C jednako nuli:  . S pronađenom funkcijom v(x)
natrag na jednadžbu (7.5):
. S pronađenom funkcijom v(x)
natrag na jednadžbu (7.5):  .
.
Rješavajući ga, dobivamo:  .
.
Stoga opće rješenje jednadžbe (7.1) ima oblik:
§ 8. Bernoullijeva jednadžba.
Definicija.
Diferencijalna jednadžba oblika  , Gdje
, Gdje  , naziva se Bernoullijeva jednadžba.
, naziva se Bernoullijeva jednadžba.
Pod pretpostavkom da  , obje strane Bernoullijeve jednadžbe podijelimo s
, obje strane Bernoullijeve jednadžbe podijelimo s  . Kao rezultat toga dobivamo:
. Kao rezultat toga dobivamo:  (8.1)
(8.1)
Predstavljamo novu funkciju  . Zatim
. Zatim  . Jednadžbu (8.1) množimo s
. Jednadžbu (8.1) množimo s  i u njoj prijeći na funkciju z(x)
:
i u njoj prijeći na funkciju z(x)
:  , tj. za funkciju z(x)
dobivena linearna nehomogena jednadžba 1. reda. Ova se jednadžba rješava metodama razmotrenim u prethodnom paragrafu. Zamijenimo u njegovo opće rješenje umjesto z(x)
izraz
, tj. za funkciju z(x)
dobivena linearna nehomogena jednadžba 1. reda. Ova se jednadžba rješava metodama razmotrenim u prethodnom paragrafu. Zamijenimo u njegovo opće rješenje umjesto z(x)
izraz  , dobivamo opći integral Bernoullijeve jednadžbe, koji se lako rješava u odnosu na g. Na
, dobivamo opći integral Bernoullijeve jednadžbe, koji se lako rješava u odnosu na g. Na  dodaje se otopina g(x)=0
. Bernoullijeva jednadžba također se može riješiti bez prijelaza na linearnu jednadžbu zamjenom
dodaje se otopina g(x)=0
. Bernoullijeva jednadžba također se može riješiti bez prijelaza na linearnu jednadžbu zamjenom  , i primjenom Bernoullijeve metode, o kojoj je detaljno raspravljano u § 7. Razmotrite primjenu ove metode za rješavanje Bernoullijeve jednadžbe na konkretnom primjeru.
, i primjenom Bernoullijeve metode, o kojoj je detaljno raspravljano u § 7. Razmotrite primjenu ove metode za rješavanje Bernoullijeve jednadžbe na konkretnom primjeru.
Primjer. Pronađite opće rješenje jednadžbe:  (8.2)
(8.2)
Riješenje.
Stoga opće rješenje ove jednadžbe ima oblik:  , g(x)=0.
, g(x)=0.
§ 9. Diferencijalne jednadžbe u totalnim diferencijalima.
Definicija. Ako je u jednadžbi M(x, g) dx+ N(x, g) dy=0 (9.1) lijeva strana je totalni diferencijal neke funkcije U(x, g) , tada se naziva jednadžba u totalnim diferencijalima. Ova se jednadžba može prepisati kao du(x, g)=0 , dakle, njegov opći integral je u(x, g)= c.
Na primjer, jednadžba xdy+
ydx=0
je jednadžba u totalnim diferencijalima, budući da se može prepisati u obliku d(xy)=0.
Opći integral bit će xy=
c je proizvoljna diferencijabilna funkcija. Diferenciramo (9.3) s obzirom na u
§ 10. Integrirajući faktor.
Ako jednadžba M(x, g) dx + N(x, g) dy = 0 nije jednadžba u ukupnim diferencijalima i postoji funkcija µ = µ(x, g) , tako da nakon množenja obje strane jednadžbe dobijemo jednadžbu
µ(Mdx + Ndy) = 0 u ukupnim razlikama, tj. µ(Mdx + Ndy)du, zatim funkcija µ(x, g) naziva se integrirajući faktor jednadžbe. U slučaju kada je jednadžba već jednadžba u ukupnim diferencijalima, pretpostavljamo µ = 1.
Ako se pronađe integrirajući faktor µ , tada se integracija ove jednadžbe svodi na množenje oba njezina dijela s µ i pronalaženje općeg integrala rezultirajuće jednadžbe u ukupnim diferencijalima.
Ako µ
je kontinuirano diferencijabilna funkcija od x I g, To  .
.
Iz toga slijedi da integrirajući faktor µ zadovoljava sljedeći PDE 1. reda:
 (10.1).
(10.1).
Ako se unaprijed zna da µ= µ(ω) , Gdje ω je dana funkcija iz x I g, tada se jednadžba (10.1) svodi na običnu (i, štoviše, linearnu) jednadžbu s nepoznatom funkcijom µ od nezavisne varijable ω :
 (10.2),
(10.2),
Gdje  , tj. razlomak je funkcija samo od ω
.
, tj. razlomak je funkcija samo od ω
.
Rješavanjem jednadžbe (10.2) nalazimo integrirajući faktor
 , S = 1.
, S = 1.
Konkretno, jednadžba M(x, g) dx + N(x, g) dy = 0 ima integrirajući faktor koji ovisi samo o x(ω = x) ili samo od g(ω = g) ako su ispunjeni sljedeći uvjeti:
 ,
, 
 ,
,  .
.
Klikom na gumb "Preuzmi arhivu" besplatno preuzimate potrebnu datoteku.
Prije preuzimanja ove datoteke sjetite se onih dobrih eseja, kontrolnih, seminarskih radova, diplomskih radova, članaka i drugih dokumenata koji nisu zatraženi na vašem računalu. Ovo je vaš rad, treba sudjelovati u razvoju društva i koristiti ljudima. Pronađite ove radove i pošaljite ih u bazu znanja.
Mi i svi studenti, diplomanti, mladi znanstvenici koji koriste bazu znanja u svom studiranju i radu bit ćemo vam jako zahvalni.
Za preuzimanje arhive s dokumentom unesite peteroznamenkasti broj u polje ispod i kliknite gumb "Preuzmi arhivu"
Slični dokumenti
Cauchyjevi problemi za diferencijalne jednadžbe. Graf rješenja diferencijalne jednadžbe prvog reda. Jednadžbe sa separabilnim varijablama i svođenje na homogene. Homogene i nehomogene linearne jednadžbe prvog reda. Bernoullijeva jednadžba.
predavanje, dodano 18.08.2012
Osnovni pojmovi teorije običnih diferencijalnih jednadžbi. Predznak jednadžbe u totalnim diferencijalima, konstrukcija općeg integrala. Najjednostavniji slučajevi nalaženja integrirajućeg faktora. Slučaj množitelja koji ovisi samo o X i samo o Y.
seminarski rad, dodan 24.12.2014
Osobitosti diferencijalnih jednadžbi kao odnosa između funkcija i njihovih izvodnica. Dokaz teorema postojanja i jedinstvenosti rješenja. Primjeri i algoritam za rješavanje jednadžbi u totalnim diferencijalima. Integrirajući faktor u primjerima.
seminarski rad, dodan 11.02.2014
Riccatijeve diferencijalne jednadžbe. Opće rješenje linearne jednadžbe. Pronalaženje svih mogućih rješenja Bernoullijeve diferencijalne jednadžbe. Rješenje jednadžbi sa separabilnim varijablama. Opća i posebna rješenja Clairautove diferencijalne jednadžbe.
seminarski rad, dodan 26.01.2015
Jednadžba sa separabilnim varijablama. Homogene i linearne diferencijalne jednadžbe. Geometrijska svojstva integralnih krivulja. Totalni diferencijal funkcije dviju varijabli. Određivanje integrala Bernoullijevim metodama i varijacije proizvoljne konstante.
sažetak, dodan 24.08.2015
Pojmovi i rješenja najjednostavnijih diferencijalnih jednadžbi i diferencijalnih jednadžbi proizvoljnog reda, uključujući one s konstantnim analitičkim koeficijentima. Sustavi linearnih jednadžbi. Asimptotsko ponašanje rješenja nekih linearnih sustava.
diplomski rad, dodan 10.6.2010
Opći integral jednadžbe, primjena Lagrangeove metode za rješavanje nehomogene linearne jednadžbe s nepoznatom funkcijom. Rješenje diferencijalne jednadžbe u parametarskom obliku. Eulerov uvjet, jednadžba prvog reda u ukupnim diferencijalima.
kontrolni rad, dodano 02.11.2011
def 1 kontrola tipa
nazvao homogena diferencijalna jednadžba prvog reda(ODA).
Th1 Neka su za funkciju zadovoljeni sljedeći uvjeti:
1) kontinuirano na
Tada ODE (1) ima zajednički integral, koji je za dan formulom:
gdje je neka antiderivacija funkcije S je proizvoljna konstanta.
Napomena 1 Ako je za neke uvjet zadovoljen, tada se u procesu rješavanja ODE (1) mogu izgubiti rješenja oblika, te takve slučajeve treba pažljivije tretirati i svaki od njih posebno provjeriti.
Tako iz teorema Th1 trebao bi opći algoritam za rješavanje ODE (1):
1) Napravite zamjenu:
2) Tako će se dobiti DE sa separabilnim varijablama koje treba integrirati;
3) Povratak na stare g varijable;
4) Provjerite vrijednosti za njihovu uključenost u rješenje original daljinski upravljač, pod kojim uvjetom
5) Zapišite odgovor.
Primjer 1 Riješite DE (4).
Riješenje: DE (4) je homogena diferencijalna jednadžba, budući da ima oblik (1). Izvršimo zamjenu (3), to će jednadžbu (4) dovesti u oblik:
Jednadžba (5) je opći integral DE (4).
Imajte na umu da bi se kod odvajanja varijabli i dijeljenja s mogla izgubiti rješenja, ali to nije rješenje za DE (4), što se lako provjerava izravnom zamjenom u jednakost (4), budući da ta vrijednost nije uključena u domenu definicije izvornog DE.
Odgovor:
Napomena 2 Ponekad se ODE mogu napisati u terminima diferencijala varijabli x I g. Preporuča se prijeći s ove DE notacije na izraz preko izvedenice i tek onda izvršiti zamjenu (3).
Svođenje diferencijalnih jednadžbi na homogene.
def 2 Funkcija se zove homogena funkcija stupnja k u području, za koje će biti ispunjena jednakost:
Evo najčešćih tipova DE koji se nakon raznih transformacija mogu svesti na oblik (1).
1) gdje je funkcija je homogen, nula stupnjeva, odnosno vrijedi sljedeća jednakost: DE (6) lako se može svesti na oblik (1) ako se stavi , koji se dalje integrira zamjenom (3).
2) (7), gdje su funkcije homogene istog stupnja k . DE obrasca (7) također se integrira pomoću promjene (3).
Primjer 2 Riješite DE (8).
Riješenje: Pokažimo da je DE (8) homogen. Dijelimo s onim što je moguće, budući da to nije rješenje diferencijalne jednadžbe (8).
Izvršimo zamjenu (3), to će jednadžbu (9) dovesti u oblik:
Jednadžba (10) je opći integral DE (8).
Imajte na umu da se prilikom odvajanja varijabli i dijeljenja s , rješenja koja odgovaraju vrijednostima i mogu biti izgubljena. Provjerimo ove izraze. Zamijenimo ih u DE (8):
Odgovor:
Zanimljivo je primijetiti da se prilikom rješavanja ovog primjera pojavljuje funkcija koja se zove "predznak" broja x(čitati " znak x“), definiran izrazom:
Napomena 3 Nije potrebno dovoditi DE (6) ili (7) u oblik (1), ako je očito da je DE homogen, tada je moguće odmah zamijeniti
3) DE oblika (11) integrira se kao ODE ako je , dok se supstitucija inicijalno izvodi:
(12), gdje je rješenje sustava: (13), a zatim upotrijebite zamjenu (3) za funkciju Nakon dobivanja općeg integrala vratite se na varijable x I na.
Ako je , tada, uz pretpostavku u jednadžbi (11), dobivamo DE sa separabilnim varijablama.
Primjer 3 Riješite Cauchyjev problem (14).
Riješenje: Pokažimo da je DE (14) sveden na homogeni DE i integriran prema gornjoj shemi:
Riješimo nehomogeni sustav linearnih algebarskih jednadžbi (15) Cramerovom metodom:
Mijenjamo varijable i integriramo dobivenu jednadžbu:
(16) – Opći integral DE (14). Kod dijeljenja varijabli, rješenja bi se mogla izgubiti kod dijeljenja s izrazom, koji se može eksplicitno dobiti nakon rješavanja kvadratne jednadžbe. Međutim, oni su uzeti u obzir u općem integralu (16) na
Nađimo rješenje Cauchyjevog problema: zamijenimo vrijednosti i u opći integral (16) i nađemo S.
Dakle, parcijalni integral će biti dan formulom:
Odgovor:
4) Moguće je neke DE dovesti do homogenih za novu, još nepoznatu funkciju, ako primijenimo zamjenu oblika:
Istovremeno, broj m odabire se pod uvjetom da rezultirajuća jednadžba, ako je moguće, postane homogena do neke mjere. Međutim, ako se to ne može učiniti, tada se razmatrani DE ne može na ovaj način svesti na homogeni.
Primjer 4 Riješite DU. (18)
Riješenje: Pokažimo da se DE (18) reducira na homogeni DE pomoću supstitucije (17), a zatim integrira pomoću zamjene (3):
Nađimo S:
Dakle, posebno rješenje DE (24) ima oblik
Pokazuje se kako prepoznati generaliziranu homogenu diferencijalnu jednadžbu. Razmatra se metoda za rješavanje generalizirane homogene diferencijalne jednadžbe prvog reda. Dan je primjer detaljnog rješenja takve jednadžbe.
SadržajDefinicija
Generalizirana homogena diferencijalna jednadžba prvog reda je jednadžba oblika:, gdje je ≠ 0 , α ≠ 1 , f - funkcija.
Kako odrediti je li diferencijalna jednadžba generalizirano homogena
Kako bismo odredili je li diferencijalna jednadžba generalizirano homogena, trebamo uvesti konstantu t i izvršiti zamjenu:
y → t α y, x → t x.
Ako uspijemo odabrati takvu vrijednost α pri kojoj će se konstanta t smanjivati, onda je to - generalizirana homogena diferencijalna jednadžba. Promjena derivacije y' pri takvoj zamjeni ima oblik:
.
Primjer
Odredite je li navedena jednadžba generalizirano homogena:
.
Izvršavamo promjenu y → t α y , x → t x , y′ → t α- 1 g':
;
.
Podijelite s t α+ 5
:
;
.
Jednadžba neće sadržavati t ako
4α - 6 = 0,
α = 3/2
.
Budući da je za α = 3/2
, t se smanjuje, tada ovo je generalizirana homogena jednadžba.
Metoda rješenja
Razmotrimo generaliziranu homogenu diferencijalnu jednadžbu prvog reda:
(1)
.
Pokažimo da se može svesti na homogenu jednadžbu supstitucijom:
t = xα.
Stvarno,
.
Odavde
;
.
(1)
:
;
.
Ovo je homogena jednadžba. Rješava se zamjenom:
y = z t,
gdje je z funkcija od t.
Prilikom rješavanja problema lakše je odmah primijeniti zamjenu:
y = z x α,
gdje je z funkcija od x.
Primjer rješavanja generalizirane homogene diferencijalne jednadžbe prvog reda
Riješite diferencijalnu jednadžbu
(P.1) .
Provjerimo je li navedena jednadžba generalizirano homogena. Za ovo u (P.1) napraviti zamjenu:
y → t α y , x → t x , y′ → t α- 1 g'.
.
Podijelite s t α :
.
t će se smanjiti ako stavimo α = - 1
. Dakle, ovo je generalizirana homogena jednadžba.
Vršimo zamjenu:
y = z x α = z x - 1
,
gdje je z funkcija od x.
.
Zamjenjujemo u izvornu jednadžbu (P.1):
(P.1) ;
;
.
Pomnožite s x i otvorite zagrade:
;
;
.
Podijelite varijable - pomnožite s dx i podijelite s x z 2
. Za z ≠ 0
imamo:
.
Integriramo pomoću tablice integrala:
;
;
;
.
Potencirati:
.
Zamijenimo konstantu e C → C i uklonimo predznak modula, budući da je izbor željenog predznaka određen izborom predznaka konstante C:
.
Vraćamo se na varijablu y. Zamijenite z = xy :
.
Podijeli s x:
(P.2) .
Kad podijelimo sa z 2
, pretpostavili smo da je z ≠ 0
. Sada razmotrite rješenje z = xy = 0
, ili y = 0
.
Budući da je za y = 0
, lijeva strana izraza (P.2) nije definiran, tada dobivenom općem integralu dodamo rješenje y = 0
.
;
.
Reference:
N.M. Gunther, R.O. Kuzmin, Zbirka zadataka iz više matematike, Lan, 2003.
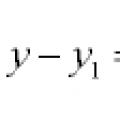 Jednadžbe pravaca i krivulja u ravnini
Jednadžbe pravaca i krivulja u ravnini Generalizirana homogena jednadžba Generalizirane homogene jednadžbe drugog reda
Generalizirana homogena jednadžba Generalizirane homogene jednadžbe drugog reda Zahvaljujući zarezu Zbog činjenice da u njihovim
Zahvaljujući zarezu Zbog činjenice da u njihovim