Waar zijn Euler-cirkels voor? Euler-cirkel

Euler-cirkels zijn een geometrisch diagram. Met zijn hulp kunt u de relaties tussen subsets (concepten) weergeven voor een visuele weergave.

De manier om concepten in de vorm van cirkels weer te geven, stelt je in staat verbeeldingskracht en logisch denken te ontwikkelen, niet alleen voor kinderen, maar ook voor volwassenen. Vanaf 4-5 jaar kunnen kinderen eenvoudige problemen oplossen met Euler-cirkels, eerst met uitleg van volwassenen en daarna zelfstandig. Door de methode voor het oplossen van problemen met behulp van Euler-cirkels onder de knie te krijgen, wordt het vermogen van het kind ontwikkeld om zijn kennis te analyseren, vergelijken, generaliseren en groeperen voor bredere toepassing.

Voorbeeld

Op de foto is een variatie van al het mogelijke speelgoed te zien. Een deel van het speelgoed zijn bouwsets; ze worden in een apart ovaal gemarkeerd. Dit maakt deel uit van een grote set "speelgoed" en tegelijkertijd een aparte set (een bouwset kan immers "Lego" zijn of primitieve bouwsets gemaakt van blokken voor kinderen). Een deel van de grote verscheidenheid aan „speelgoed” kan opwindspeelgoed zijn. Het zijn geen constructeurs, dus tekenen we er een apart ovaal voor. De gele ovale “opwindauto” verwijst zowel naar de set “speelgoed” als is onderdeel van de kleinere set “opwindspeelgoed”. Daarom wordt het in beide ovalen tegelijk afgebeeld.

Hier zijn enkele logische denktaken voor jonge kinderen:

Identificeer de cirkels die passen bij de beschrijving van het object. In dit geval is het raadzaam om aandacht te besteden aan die eigenschappen die het object permanent bezit en die het tijdelijk heeft. Een glazen glas met sap blijft bijvoorbeeld altijd glas, maar er zit niet altijd sap in. Of er is een soort brede definitie die verschillende concepten omvat; een dergelijke classificatie kan ook worden weergegeven met behulp van Euler-cirkels. Een cello is bijvoorbeeld een muziekinstrument, maar niet elk muziekinstrument is een cello.

Voor oudere kinderen kun je opties bieden voor rekenproblemen - van redelijk eenvoudig tot zeer complex. Bovendien zal het zelfstandig bedenken van deze taken voor kinderen ouders een zeer goede training voor de geest bieden.

1. Van de 27 vijfdeklassers studeren ze allemaal vreemde talen: Engels en Duits. 12 studeren Duits en 19 studeren Engels. Het is noodzakelijk om te bepalen hoeveel vijfdeklassers twee vreemde talen studeren; hoeveel mensen studeren geen Duits; hoeveel mensen studeren geen Engels; Hoeveel studeren alleen Duits en alleen Engels?

Tegelijkertijd duidt de eerste vraag van het probleem in het algemeen op de weg om dit probleem op te lossen, waarbij wordt aangegeven dat sommige leerlingen beide talen leren, in welk geval het gebruik van het diagram het voor kinderen ook gemakkelijker maakt om het probleem te begrijpen.

Trouwens, als je niet kunt beslissen welk beroep je moet kiezen, probeer dan een diagram te tekenen in de vorm van Euler-cirkels. Misschien helpt een tekening als deze u bij het maken van uw keuze:

De opties die zich op het kruispunt van alle drie de cirkels bevinden, zijn het beroep dat u niet alleen zal kunnen voeden, maar u ook zal plezieren.

En nog een teken...

Als je denkt dat je niets weet over zo'n concept als Euler-cirkels, dan vergis je je diep. Zelfs vanaf de basisschool zijn schematische afbeeldingen of cirkels bekend waarmee men de relaties tussen concepten en elementen van het systeem visueel kan begrijpen.

De methode, uitgevonden door Leonhard Euler, werd door de wetenschapper gebruikt om complexe wiskundige problemen op te lossen. Hij schilderde sets in cirkels en maakte dit diagram tot de basis van een dergelijk concept als symbolisch. De methode is ontworpen om de redenering gericht op het oplossen van een bepaald probleem zoveel mogelijk te vereenvoudigen. Daarom wordt de techniek zowel op de basisschool als in de academische omgeving actief gebruikt. Interessant genoeg werd een soortgelijke benadering eerder gebruikt door de Duitse filosoof Leibniz, en later overgenomen en in verschillende wijzigingen toegepast door beroemde geesten op het gebied van de wiskunde. Bijvoorbeeld rechthoekige diagrammen van het Tsjechische Bolzano, Schroeder, Venn, beroemd vanwege het maken van een populair diagram op basis van deze eenvoudige maar verrassend effectieve methode.

Cirkels vormen de basis van de zogenaamde ‘visuele internetmemes’, die gebaseerd zijn op de gelijkenis van kenmerken van individuele sets. Het is grappig, visueel en vooral begrijpelijk.

Cirkels van gedachten

Met cirkels kunt u de omstandigheden van een probleem duidelijk beschrijven en onmiddellijk de juiste beslissing nemen, of de richting van de beweging naar het juiste antwoord identificeren. Meestal worden Euler-cirkels gebruikt om logisch-wiskundige problemen op te lossen met betrekking tot verzamelingen, hun verenigingen of gedeeltelijke superposities. Het snijpunt van cirkels omvat objecten die de eigenschappen hebben van elk van de sets die in een cirkel zijn afgebeeld. Objecten die niet in de set zijn opgenomen, bevinden zich buiten een of andere cirkel. Als de concepten absoluut gelijkwaardig zijn, worden ze aangegeven met één cirkel, wat de vereniging is van twee sets met gelijke eigenschappen en volumes.

Logica van relaties

Met behulp van Euler-cirkels kun je een aantal alledaagse problemen oplossen en zelfs beslissen over de keuze voor een toekomstig beroep, je hoeft alleen maar je capaciteiten en verlangens te analyseren en hun maximale kruispunt te kiezen.

Nu wordt duidelijk dat de cirkels van Euler helemaal geen abstract wiskundig en filosofisch concept zijn uit de categorie van theoretische kennis, ze hebben een zeer toegepaste en praktische betekenis, waardoor je niet alleen met de eenvoudigste wiskundige problemen om kunt gaan, maar ook belangrijke problemen kunt oplossen. levensdilemma’s op een visuele en begrijpelijke manier voor iedereen.

Elk object of fenomeen heeft bepaalde eigenschappen (tekens).

Het blijkt dat het vormen van een concept over een object in de eerste plaats het vermogen betekent om het te onderscheiden van andere vergelijkbare objecten.

We kunnen zeggen dat een concept de mentale inhoud van een woord is.

Concept - het is een vorm van denken die objecten in hun meest algemene en essentiële kenmerken weergeeft.

Een concept is een vorm van denken, en niet een vorm van een woord, aangezien een woord slechts een label is waarmee we deze of gene gedachte markeren.

Woorden kunnen verschillend zijn, maar toch hetzelfde concept betekenen. In het Russisch - "potlood", in het Engels - "potlood", in het Duits - bleistift. Dezelfde gedachte heeft verschillende verbale uitdrukkingen in verschillende talen.

RELATIES TUSSEN BEGRIPPEN. EULER-CIRKELS.

Concepten die gemeenschappelijke kenmerken in hun inhoud hebben, worden genoemd VERGELIJKBAAR(“advocaat” en “plaatsvervanger”; “student” en “atleet”).

Anders worden de concepten overwogen ONVERGELIJKBAAR(“krokodil” en “notitieboekje”; “man” en “stoomboot”).

Als concepten naast gemeenschappelijke kenmerken ook gemeenschappelijke volume-elementen hebben, worden ze genoemd VERENIGBAAR.

Er zijn zes soorten relaties tussen vergelijkbare concepten. Het is handig om relaties tussen de reikwijdten van concepten aan te geven met behulp van Euler-cirkels (circulaire diagrammen waarbij elke cirkel de reikwijdte van een concept aangeeft).

SOORT RELATIE TUSSEN CONCEPTEN	AFBEELDING MET EULER-CIRKELS
GELIJKWAARDIGHEID (IDENTITEIT) De reikwijdte van de concepten vallen volledig samen. Die. Het zijn concepten die qua inhoud verschillen, maar waarin dezelfde volume-elementen worden bedacht.	1) A - Aristoteles B - grondlegger van de logica 2) A - vierkant B - gelijkzijdige rechthoek
ONDERSTEUNING (SUBORDINATIE) De reikwijdte van het ene concept valt volledig onder de reikwijdte van een ander, maar put deze niet uit.	1) A - persoon B - leerling 2) A - dier B - olifant
INTERSECTION (CROSSING) De volumes van twee concepten vallen gedeeltelijk samen. Dat wil zeggen dat concepten gemeenschappelijke elementen bevatten, maar ook elementen bevatten die slechts tot één van hen behoren.	1) A - advocaat B - plaatsvervanger 2) A - student B - atleet
COÖRDINATIE (COÖRDINATIE) Concepten die geen gemeenschappelijke elementen hebben, vallen volledig binnen de reikwijdte van het derde, bredere concept.	1) A - dier B - kat; C - hond; D - muis 2) A - edelmetaal B - goud; C-zilver; D - platina
TEGENOVERGESTELD (CONTRAPARITEIT) De concepten A en B vallen niet simpelweg binnen de reikwijdte van het derde concept, maar lijken zich aan de tegenovergestelde polen ervan te bevinden. Dat wil zeggen, concept A heeft in zijn inhoud zo'n kenmerk, dat in concept B wordt vervangen door het tegenovergestelde.	1) A - witte kat; B - rode kat (katten zijn zowel zwart als grijs) 2) A - hete thee; ijsthee (thee kan ook warm zijn) D.w.z. De concepten A en B omvatten niet de volledige reikwijdte van het concept waarin ze zijn opgenomen.
CONTRADITION (CONTRADITIONALITEIT) De relatie tussen concepten, waarvan er één de aanwezigheid van bepaalde kenmerken uitdrukt, en de andere - hun afwezigheid, dat wil zeggen, het ontkent eenvoudigweg deze kenmerken, zonder ze door andere te vervangen.	1) A - hoog huis B - laag huis 2) A - winnend ticket B - niet-winnend ticket D.w.z. de concepten A en niet-A omvatten de gehele reikwijdte van het concept waarin ze zijn opgenomen, aangezien er geen aanvullend concept tussen kan worden geplaatst.

Oefening : Bepaal het type relatie op basis van de reikwijdte van de onderstaande concepten. Teken ze met behulp van Euler-cirkels.

1) A - hete thee; B - ijsthee; C - thee met citroen

Hete thee (B) en ijsthee (C) staan in een tegenovergestelde relatie.

Thee met citroen (C) kan heet,

zo koud, maar het kan bijvoorbeeld ook warm zijn.

2)A- hout; IN- steen; MET- structuur; D- huis.

Is elk gebouw (C) een huis (D)? - Nee.

Is elk huis (D) een gebouw (C)? - Ja.

Iets van hout (A) is noodzakelijkerwijs een huis (D) of een gebouw (C) - Nee.

Maar je kunt een houten structuur vinden (bijvoorbeeld een hokje),

Je kunt ook een houten huis vinden.

Iets van steen (B) is niet noodzakelijkerwijs een huis (D) of gebouw (C).

Maar er kan ook een stenen gebouw of een stenen huis zijn.

3)A- Russische stad; IN- hoofdstad van Rusland;

MET- Moskou; D- stad aan de Wolga; E- Oeglitsj.

De hoofdstad van Rusland (B) en Moskou (C) zijn dezelfde stad.

Uglich (E) is een stad aan de Wolga (D).

Tegelijkertijd zijn Moskou, Oeglitsj, zoals elke stad aan de Wolga,

zijn Russische steden (A)

Ministerie van Onderwijs, Wetenschap en Jeugd van de Republiek van de Krim Kleine Academie van Wetenschappen "Iskatel"

Richting: wiskunde

G. Krasnoperekopsk– 2017

Werk voltooid:

Sjoemilina Maria Sergejevna,

leerling van klas 7-A van de gemeentelijke begroting algemene educatie instellingen "Secundair algemene educatie School nr. 5" gemeentelijke formatie stadsdeel Krasnoperekopsk

Wetenschappelijk adviseur:

Sheina Elena Nikolajevna, gemeentelijke begroting wiskundeleraar algemene educatie instellingen "Secundair algemene educatie school nr. 5 » gemeentelijke vorming stadsdeel Krasnoperekopsk

INLEIDING …………………………………………………………… 3

HOOFDSTUK 1. Een klein stukje geschiedenis................................................................. 5

HOOFDSTUK 2. Uit de verzamelingenleer…………………………………….7

2.1. Het concept van de set.……………………………………………..8

2.2. Operaties op sets.…………………………..9

HOOFDSTUK 3.Problemen oplossen met behulp van Euler-cirkels………………..10

CONCLUSIE.................................................................................22

LIJST VAN GEBRUIKTE BRONNEN…………….23

INVOERING

Niets helpt

vorming van een mentale cultuur,

als oplossing voor logische problemen. Wiskunde-

geen droge en saaie wetenschap, maar complete

ongebruikelijke en interessante ontdekkingen

Het oplossen van logische problemen is erg spannend. Er zijn mensen voor wie het oplossen van een logisch probleem een spannende, maar niet moeilijke taak is. Hun brein verlicht als een spotlight onmiddellijk alle ingenieuze constructies en ze komen ongewoon snel tot het juiste antwoord. Het is geweldig dat ze niet kunnen uitleggen hoe ze tot het besluit zijn gekomen.

Logische problemen vormen een grote klasse van niet-standaardproblemen. Dit omvat in de eerste plaats woordproblemen waarbij het nodig is om objecten te herkennen of ze in een bepaalde volgorde te ordenen volgens bestaande eigenschappen.

Er zijn veel technieken die worden gebruikt om tekstlogische problemen op te lossen. Heel vaak helpt de oplossing om een tekening te vinden. Door een afbeelding te gebruiken, wordt het oplossen van het probleem eenvoudig en duidelijk. Het weergeven van de omstandigheden van een probleem in de vorm van Euler-cirkels vereenvoudigt en vergemakkelijkt in de regel het pad naar de oplossing ervan.

Relevantie is dat de taken van praktische aard zijn, wat belangrijk is in het moderne leven. Problemen dwingen je om na te denken, om de oplossing van een probleem vanuit een andere hoek te benaderen, om uit een verscheidenheid aan oplossingen te kunnen kiezen, op de eenvoudigste, gemakkelijkste manier.

Doel van het werk:

Maak kennis met Euler-Venn-kringen;

Leer de methode voor het oplossen van problemen toe te passen met behulp van Euler-cirkels;

Maak taken met praktische inhoud.

Hoofdstuk 1. Een beetje geschiedenis

Leonhard Euler, de grootste wiskundigeXVIIIc., geboren in Zwitserland in 1707.In 1727 kwam hij op uitnodiging van de Sint-Petersburg Academie van Wetenschappen naar Rusland. In Sint-Petersburg bevond Euler zich in een kring van uitmuntende wetenschappers: wiskundigen, natuurkundigen, astronomen, en kreeg hij geweldige kansen om zijn werken te creëren en te publiceren. Hij werkte met passie en werd al snel, volgens de unanieme erkenning van zijn tijdgenoten, de eerste wiskundige ter wereld. De wetenschappelijke erfenis van Euler valt op door zijn omvang en veelzijdigheid. De lijst met zijn werken omvat meer dan 800 titels. De volledige verzamelde werken van de wetenschapper beslaan 72 delen. Tot zijn werken behoren de eerste leerboeken over differentiaal- en integraalrekening. Op het gebied van de getaltheorie zette Euler het werk van de Franse wiskundige P. Fermat voort.

Euler werkt veel op het gebied van wiskundige analyse. De wetenschapper was de eerste die een algemene doctrine van de logaritmische functie ontwikkelde. In de meetkunde legde Euler de basis voor een geheel nieuw onderzoeksgebied, dat later uitgroeide tot een onafhankelijke wetenschap: topologie.

De naam van Euler is gegeven aan een formule die het aantal hoekpunten (B), randen (P) en vlakken (G) van een convex veelvlak met elkaar verbindt: B -P + G = 2. Zelfs de belangrijkste resultaten van Eulers wetenschappelijke werk zijn moeilijk te voorspellen. lijst. Hier is de geometrie van krommen en oppervlakken, en de eerste presentatie van de variatierekening met talrijke nieuwe concrete resultaten. Hij schreef werken over hydraulica, scheepsbouw, artillerie, geometrische optica en zelfs muziektheorie. Voor het eerst geeft hij een analytische presentatie van de mechanica in plaats van de geometrische presentatie van Newton, en construeert hij de mechanica van een vast lichaam, en niet alleen van een materieel punt of een massieve plaat. Een van Eulers meest opmerkelijke prestaties heeft betrekking op astronomie en hemelmechanica. Hij construeerde een nauwkeurige theorie over de beweging van de maan, waarbij hij niet alleen rekening hield met de aantrekkingskracht van de aarde, maar ook van de zon. Dit is een voorbeeld van het oplossen van een heel moeilijk probleem.

De laatste 17 jaar van Eulers leven werden ontsierd door een bijna volledig verlies van gezichtsvermogen. Maar hij bleef net zo intens creëren als in zijn jeugd. Pas nu schreef hij niet meer zelf, maar dicteerde hij aan zijn studenten, die de meest omslachtige berekeningen voor hem uitvoerden.

Van 1761 tot 1768 schreef hij de beroemde 'Brieven aan een Duitse prinses', waarin Euler sprak over zijn methode, over het weergeven van sets in de vorm van cirkels. Dat is de reden waarom tekeningen in de vorm van cirkels meestal "Euleriaanse cirkels" worden genoemd. Euler merkte op dat de weergave van verzamelingen als cirkels “zeer geschikt is om onze redenering te vergemakkelijken.”

Na Euler werd dezelfde methode ontwikkeld door de Tsjechische wiskundige Bernard Bolzano (1781 – 1848). Alleen tekende hij, in tegenstelling tot Euler, geen cirkelvormige, maar rechthoekige diagrammen. De cirkelmethode van Euler werd ook gebruikt door de Duitse wiskundige Ernst Schroeder (1841 – 1902). Deze methode wordt veel gebruikt in zijn boek Algebra Logic. Maar grafische methoden bereikten hun grootste bloei in de werken van de Engelse logicus John Venn (1843 - 1923). Hij schetste deze methode het meest volledig in zijn boek ‘Symbolic Logic’, gepubliceerd in Londen in 1881. Ter ere van Venn worden de overeenkomstige tekeningen, in plaats van Euler-cirkels, soms Venn-diagrammen genoemd; in sommige boeken worden ze ook wel Euler-Venn-diagrammen (of cirkels) genoemd.

Hoofdstuk 2. Uit de verzamelingenleer

2.1. Het concept van de set.

Een van de belangrijkste concepten die in de wiskunde worden gebruikt, is het concept van verzameling. Er wordt geen definitie voor gegeven. Er kan worden uitgelegd dat een set een willekeurige verzameling objecten is, en dat de objecten zelf de elementen van een gegeven set zijn. We kunnen dus praten over een reeks leerlingen in een klas (elementen zijn leerlingen), een reeks dagen van de week (elementen zijn dagen van de week), een reeks natuurlijke delers van het getal 6 (elementen zijn getallen 1, 2, 3, 6), enz.

In algebra- en algebracursussen wordt bij het begin van de analyse meestal rekening gehouden met verzamelingen waarvan de elementen getallen zijn, en daarom worden ze getallensets genoemd.

In de regel worden sets aangegeven met hoofdletters van het Latijnse alfabet. Als de set bijvoorbeeldMbestaat uit cijfers 1; 2; 3, dan wordt het als volgt aangeduid:M= (1; 2; 3). Het feit dat het nummer 2 in deze set zit

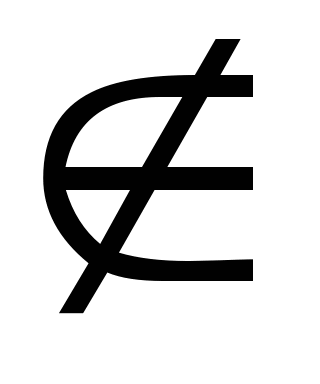(is een onderdeel van deze setM) wordt opgenomen met een speciaal pictogram als volgt: 2M; en het feit dat het getal 5 niet in deze set zit (is geen onderdeel van deze setM), zo geschreven: 5 M.

We kunnen ook een verzameling overwegen die geen enkel element bevat: de lege verzameling. Bijvoorbeeld: de verzameling priemfactoren van het getal 1 is een lege verzameling.

Voor sommige sets zijn er speciale notaties. De lege verzameling wordt dus aangegeven met het symbool , de verzameling van alle natuurlijke getallen – een letterN, de verzameling van alle gehele getallen – een letterZ, de verzameling van alle rationale getallen – de letterQ, en de verzameling van alle reële getallen is de letterR. Met behulp van Euler-Venn-cirkels kan dit als volgt worden weergegeven:

Figuur 1

Als elk element van de setAis een onderdeel van de setB, dan zeggen ze dat de setAis een deelverzameling van de verzamelingB.

Dit is als volgt geschreven:A B.

Fig. 2

2.2. Operaties op sets.

Je kunt bepaalde acties uitvoeren op sets: vind hun snijpunt, unie. Laten we deze bewerkingen definiëren en illustreren met behulp van cirkels.

Snijpunt van sets A En B noem hun gemeenschappelijk deel, dat wil zeggen de verzamelingCalle elementen die tot beide sets behorenA, en veelB

Het snijpunt van sets wordt aangegeven met het bord∩ en schrijf opA∩ B .

Afb.3

Unie van sets A En B noem een setjeC, bestaande uit alle elementen die tot ten minste één van deze sets behoren (AofB). De vereniging van sets wordt aangegeven door het teken
en schrijf op A
B

Hoofdstuk 3. Problemen oplossen met behulp van Euler-cirkels

Taak nr. 1.

Van de 52 schoolkinderen verzamelen er 23 badges, 35 verzamelen postzegels en 16 verzamelen zowel badges als postzegels.

De rest is niet geïnteresseerd in verzamelen. Hoeveel schoolkinderen zijn niet geïnteresseerd in verzamelen?

Oplossing.

De omstandigheden van dit probleem zijn niet zo gemakkelijk te begrijpen. Als je 23 en 35 optelt, krijg je ruim 52. Dit wordt verklaard doordat we sommige schoolkinderen hier dubbel hebben geteld, namelijk degenen die zowel insignes als postzegels verzamelen.

Om het probleem gemakkelijker op te lossen, laten we de gegevens ervan in het volgende diagram weergeven

Afb.5

In dit diagram vertegenwoordigt de grote cirkel alle betrokken schoolkinderen. CirkelZ toont schoolkinderen die badges verzamelen (23 in totaal), en de cirkelM - schoolkinderen verzamelen postzegels (35 in totaal). Op het snijpunt van cirkelsZ En M Het getal 16 is de moeite waard - dit zijn degenen die zowel insignes als postzegels verzamelen. Dit betekent dat 23 - 16 = 7 personen alleen badges verzamelen, 35 - 16 = 19 personen alleen postzegels verzamelen. In totaal worden postzegels en badges ingezameld door 19 + 7 + 16 = 42 personen. Dan blijven er 52 - 42 = 10 mensen over die niet van verzamelen houden. Dit nummer kan in het vrije veld van de cirkel worden ingevoerd. Antwoord: 10 personen.

Taak 2.

Er zitten 15 jongens in de klas. Hiervan spelen 10 mensen volleybal en 9 basketbal. Hoeveel jongens doen beide?

Oplossing.

Laten we de toestand weergeven met behulp van Euler-cirkels. Dit cijfer geeft ons enige redenering. Laten we deze redenering analyseren en het vereiste aantal invoeren in elk van de onderdelen die in het diagram zijn gevormd.

Laat x jongens allerlei sporten beoefenen. Dan spelen alleen (10e) jongens volleybal en alleen (9e) jongens basketbal. Laten we een vergelijking maken: 10's + x+ 9's = 15, waarvan x = 4

10's B

x 9'en

Afb.6

Antwoord: 4 personen.

Taak nr. 3.

Sommige jongens uit onze klas gaan graag naar de film. Het is bekend dat 15 kinderen de film "Scarecrow" hebben bekeken, 11 mensen hebben de film "Above the Sky" bekeken, waarvan 6 zowel "Scarecrow" als"Boven de hemel". Hoeveel mensen hebben alleen de film ‘Above the Sky’ gezien?

Oplossing:Laten we twee sets als volgt tekenen: We plaatsen 6 mensen die de films “Scarecrow” en “Above the Sky” hebben bekeken op het kruispunt van sets.

15 – 6 = 9 – mensen die alleen naar “Vogelverschrikker” keken.
11 – 6 = 5 – mensen die alleen naar ‘Above the Sky’ keken.

We krijgen:

Afb.7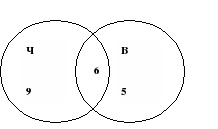

Antwoord. Vijf mensen keken alleen naar ‘Above the Sky’.

Taak nr. 4.

Van een groep van 80 toeristen die op excursie naar Moskou kwamen, willen 52 het Bolsjojtheater bezoeken, 30 willen het Kunsttheater bezoeken, 12 willen beide theaters bezoeken, de rest wil niet naar de theaters. Hoeveel mensen gaan niet naar het theater?

Oplossing.

Alleen het grote theater wordt bezocht door: 52-12=40 toeristen;

alleen het kunsttheater wordt bezocht

30-12=18 toeristen;

8
0-(40+18+12)=10 toeristen gaan niet naar het theater.

Afb.8

Antwoord: 10 personen.

Taak nr. 5.

Er lagen 26 magische boeken over spreuken op de plank. Hiervan werden er 4 gelezen door zowel Harry Potter als Ron. Hermelien las zeven boeken die noch Harry Potter noch Ron hadden gelezen, en twee boeken die Harry Potter had gelezen. In totaal heeft Harry Potter 11 boeken gelezen. Hoeveel boeken heeft Ron gelezen?

Oplossing.

Rekening houdend met de omstandigheden van het probleem, ziet de tekening er als volgt uit:

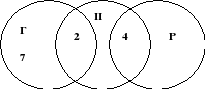
Afb.9

Omdat Harry Potter in totaal 11 boeken las, waarvan 4 boeken door Ron en 2 boeken door Hermelien, las alleen Harry 11 - 4 - 2 = 5 - boeken.

Daarom las Ron 26 – 7 – 2 – 5 – 4 = 8 – boeken.Antwoord. Ron heeft 8 boeken gelezen.

Taak nr. 6.

In een toeristengroep van 100 mensen kennen 75 mensen Duits, 65 mensen Engels en 10 mensen kennen noch Duits, noch Engels. Hoeveel toeristen spreken twee talen? Oplossing.

Laten we de probleemomstandigheden weergeven in de vorm van Euler-cirkels.

Het is gemakkelijk te zien dat 90 toeristen (100-10) minstens één taal kennen; Laat x toeristen zowel Engels als Duits kennen. Dan kennen (65e) toeristen alleen Engels, en (75e) mensen kennen alleen Duits. We krijgen de vergelijking 65's + 75's + x = 90, waaruit x = 50 - toeristen kennen beide talen. Antwoord: 50 toeristen.

Taak nr. 7.

Hoeveel mensen doen mee aan de wandeling als bekend is dat 16 van hen een broodje met ham namen, 24 met worst, 15 met kaas, 11 met zowel ham als worst, 8 met zowel ham als kaas, 12 met worst, en met kaas, 6 - allerlei soorten sandwiches, en 5 - taarten? Oplossing : Laten we de verzamelingen als volgt weergeven: Afb.11

16+24+15-11-8-12+6=30 (personen) - deden mee aan de wandeling en namen boterhammen mee of 3+2+6+5+7+6+1=30 (personen)

30+5=35 (personen) - namen deel aan de wandeling
Antwoord. 35 personen

Probleem nr. 8

In de 5e klas van onze school zijn er 22, in de 6e klas - 16, in de 7e klas - 23 kinderen. Het is bekend dat 4 mensen naar ski-, schaak- en sportclubs gaan. Elke twee secties worden bijgewoond door 9 personen. Hoeveel mensen gaan er van elke klas naar secties? Hoeveel studenten gaan niet naar een sportclub?

Oplossing. Als er in alle drie de clubs vier studenten zijn en in elke twee clubs negen mensen, dan worden twee secties uit groep 5 en 6, uit groep 6 en 7, en uit groep 5 en 7 door 5 personen bezocht.

Menselijk.

Afb.12

We zien dat 5+5+4=14 vijfdeklassers naar clubs gaan, 22-14=8 mensen gaan niet naar clubs. Ook redenerend: van de zesdeklassers gaan 16-14=2 leerlingen nergens heen, en van de zevendeklassers – 23-14=9 personen.

Antwoord: 14 leerlingen uit elke klas gaan naar clubs; 7 leerlingen uit de 5e, 2 uit de 6e, 9 uit de 7e gaan niet naar clubs.

Taak nr. 9.

Van de 100 kinderen die naar een gezondheidskamp voor kinderen gaan, kunnen 30 kinderen snowboarden, 28 kunnen skateboarden, 42 kunnen skaten. 8 kinderen kunnen skateboarden en snowboarden, 10 kunnen skateboarden en skaten, snowboarden en skaten – 5, en bij alle drie – 3. Hoeveel jongens weten niet hoe ze op een snowboard, skateboard of rolschaatsen moeten rijden?

Oplossing: IN Laten we Euler-cirkels gebruiken.

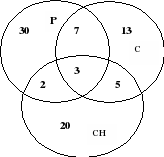
Afb.13

Drie mensen bezitten alle drie de sportartikelen, wat betekent dat we in het algemene deel van de cirkels het getal 3 betreden. 10 mensen kunnen skateboarden en rolschaatsen, en 3 van hen ook snowboarden. Bijgevolg kunnen 10-3=7 jongens alleen skateboarden en skeeleren. Op dezelfde manier ontdekken we dat slechts 8-3=5 jongens kunnen skateboarden en snowboarden, en slechts 5-3=2 mensen kunnen snowboarden en skaten. Wij zullen deze gegevens in de daarvoor bestemde delen invoeren. Laten we nu bepalen hoeveel mensen op slechts één sportuitrusting kunnen rijden. 30 mensen kunnen snowboarden, maar 5+3+2=10 van hen kennen ook andere uitrusting, dus 20 mensen kunnen alleen snowboarden. Op dezelfde manier zien we dat 13 kinderen alleen kunnen skateboarden, en 30 kinderen alleen kunnen rolschaatsen. Volgens de omstandigheden van het probleem zijn er slechts 100 jongens. 20+13+30+5+7+2+3=80 – de jongens weten hoe ze op minstens één sportuitrusting moeten rijden. Bijgevolg weten 20 mensen niet hoe ze met een sportuitrusting moeten rijden.
Antwoord. 20 mensen weten niet hoe ze op sportuitrusting moeten rijden.

Probleem nr. 10 .

Er zijn 70 kinderen in drie zevende klassen. Hiervan zijn er 27 betrokken bij de toneelclub, 32 zingen in het koor, 22 zijn dol op sport. Er zijn 10 jongens van het koor in de toneelclub, 6 atleten in het koor, 8 atleten in de toneelclub; 3 atleten bezoeken zowel de toneelclub als het koor. Hoeveel kinderen zingen niet in het koor, zijn niet geïnteresseerd in sport en zijn niet betrokken bij de toneelclub? Hoeveel jongens zijn alleen bezig met sporten?

Oplossing . D - toneelclub; X - koor; S-sport. In cirkel D - 27 kinderen, in cirkel X - 32 personen, in cirkel C - 22 studenten.Die 10 jongens van de toneelclub die in het koor zingen, zullen in het gemeenschappelijke deel van cirkels D en X zitten. Drie van hen zijn ook atleten, ze zullen in het gemeenschappelijke deel van alle drie de cirkels zitten. De overige zeven zijn niet geïnteresseerd in sport. Op dezelfde manier is 8-3=5

atleten die niet zingen in het koor en 6-3=3 die niet naar de toneelclub gaan. Het is gemakkelijk in te zien dat 5+3+3=11 atleten naar een koor of toneelclub gaan, terwijl 22-(5+3+3)=11 alleen maar aan sport doen; 70-(11+12+19+7+3+3+5)=10 - zing niet in een koor, neem niet deel aan een toneelclub, ben niet geïnteresseerd in sport.

Afb.14 Antwoord: 10 personen.

Probleem nr. 11 . Er zitten 30 mensen in de klas. 20 van hen gebruiken dagelijks de metro, 15 gebruiken de bus, 23 gebruiken de trolleybus, 10 gebruiken zowel de metro als de trolleybus, 12 gebruiken zowel de metro als de bus, 9 gebruiken zowel de trolleybus als de bus. Hoeveel mensen maken dagelijks gebruik van alle drie de vervoerswijzen?

Oplossing.

Afb.15

Laat x persoon alle drie de vervoerswijzen gebruiken. Vervolgens gebruiken ze alleen de metro en trolleybus - (10 − x) mensen, alleen de bus en trolleybus - (9 − x) mensen, alleen de metro en bus - (12 − x) mensen. Laten we eens kijken hoeveel mensen alleen de metro gebruiken:

20 − (12 − x) − (10 − x) − x = x − 2

Op dezelfde manier krijgen we: x − 6 - alleen met de bus en x + 4 - alleen met de trolleybus, aangezien er maar 30 mensen zijn, creëren we de vergelijking:

x + (12 − x) + (9 − x) + (10 − x) + (x + 4) + (x − 2) + (x − 6) = 30.

dus x = 3.

Antwoord: 3 personen.

Taak nr. 12.

Van de werknemers van het bedrijf bezochten er 16 Frankrijk, 10 Italië, 6 Engeland; in Engeland en Italië - 5; in Engeland en Frankrijk -6; in alle drie de landen - 5 werknemers. Hoeveel mensen hebben zowel Italië als Frankrijk bezocht als er in totaal 19 mensen in het bedrijf werken en elk van hen minstens één van de genoemde landen heeft bezocht?

Oplossing:

We weten dat er in alle drie de landen vijf werknemers waren. In Engeland en Italië zijn er ook 5, wat betekent dat dezelfde werknemers ook in Frankrijk zaten, en daarom zetten we 0 op het snijpunt van cirkels A en I. In Frankrijk en Italië weten we het niet, dus schrijven we x-5 bij het snijpunt van cirkels A en F. Omdat in Engeland waren er 6 mensen, dan 6-5-1=0 we schrijven 0, in Frankrijk zijn er 16+5-6 en in Italië 10+5-5 en in totaal zijn er 19 werknemers in het bedrijf, dan dat allemaal Wat overblijft is het maken en oplossen van de vergelijking: 1 +16x+5-6+5+x-5+10x+5-5=19, dus x=7, wat betekent dat 7-5=2 werknemers van het bedrijf Italië hebben bezocht en Frankrijk.

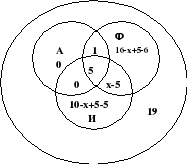
Afb.16

Antwoord: 2 medewerkers.

Taak nr. 13.

Er waren 10 jongens die verschillende soorten tijdschriften wilden uitwisselen. Onder hen zijn 6 mensen geabonneerd op K, 5 mensen op T, 5 mensen op Yu, 3 mensen op K en T, 2 mensen op T en Yu, 3 mensen op K en Yu, en één persoon is niet geabonneerd op een enkel tijdschrift maar leest al deze tijdschriften in de bibliotheek. We moeten uitzoeken hoeveel mensen zich op alle drie de tijdschriften abonneren, hoeveel op twee, en hoeveel op slechts één tijdschrift.

Oplossing. Laat een grote kring van 10 mensen de set zijn van alle jongens die tijdschriften uitwisselen. Binnen de grote cirkel tekenen we drie kleinere cirkels: K, T, Yu, die de jongens weergeven die zich hebben geabonneerd op de overeenkomstige tijdschriften. Het is bekend dat één persoon zich niet op één tijdschrift abonneert.

Laat x jongens zich abonneren op alle drie de tijdschriften, dan (3) jongens abonneren zich alleen op K en T, (2) op alleen T en Yu, (3) op alleen K en Yu. Dit betekent dat alleen tijdschrift K geabonneerd is op 6 - (3-x+x+3-x)=x mensen, T tijdschrift 5-(3-x+x+2-x)=x, Yu tijdschrift 5-(3-x+x+2-x)= X .

Afb.17

Laten we een vergelijking maken: x+3-x+3-x+x+x+x+x+2-x=9, 8+x=9,x=1

Dus 3 is het aantal jongens dat zich op slechts één tijdschrift heeft geabonneerd, 5 is het aantal jongens dat zich op twee tijdschriften heeft geabonneerd, en 1 is het aantal jongens dat zich op alle drie de tijdschriften heeft geabonneerd.

CONCLUSIE

Het onderwerp wiskunde is zo serieus

wat je niet mag missen

het is een beetje vermakelijk.

B.Pascal

Onder de wiskundige problemen nemen logische problemen een speciale plaats in. Het oplossen van dergelijke problemen draagt bij aan de ontwikkeling van wiskundig denken. Ze verschillen van de meeste wiskundige problemen doordat het oplossen ervan vaak geen speciale kennis vereist, maar in de regel intelligentie vereist. Een van de karakteristieke kenmerken van elke logica is dat ze, nadat ze wat informatie heeft ontvangen, de nieuwe kennis die erin zit kan extraheren (identificeren).

Het blijkt dat er verschillende technieken zijn waarmee je tekstlogische problemen kunt oplossen. Ze zijn divers en hebben elk hun eigen toepassingsgebied.

Mijn werk onderzoekt problemen die bestaan uit veel gegevens.De gevonden oplossingen volgen dezelfde werkwijze: maak een tekening; voer de initiële gegevens in cirkels in; analyserend en redenerend schrijven we de resultaten op in delen van de cirkels; We zoeken het antwoord en schrijven het op.Het weergeven van de omstandigheden van een probleem in de vorm van Euler-cirkels vereenvoudigt en vergemakkelijkt in de regel het pad naar de oplossing ervan. Bovendien kunt u met hun hulp veel vragen beantwoorden die betrekking hebben op één voorwaarde van het probleem.

Dit onderwerp verruimde mijn wiskundige horizon en verrijkte mijn arsenaal aan hulpmiddelen die worden gebruikt bij het oplossen van verschillende problemen.

Lijst met gebruikte bronnen:

1. Gavrilova T.D.. Vermakelijke wiskunde. 5 - 11 graden. Volgograd: Leraar, 2005.-96 p.

2. Germanovich P.Yu. "Verzameling van problemen in de wiskunde voor intelligentie."

3. Getmanova A.D. Logische grondslagen van de wiskunde, groep 10 – 11: leerboek. – M.: Trap, 2005.

4. Glazer G.I. . - M.: Onderwijs, 1964. - P. 232.

5. Gusev VA, Orlov AI, Rosenthal AL "Buitenschools werk in de wiskunde." M.: Onderwijs, 1984.

6. Nelin E.P., Dolgova OE. Leerboek van algebra en begin van analyse, graad 11.

Samenvattingen voor het werk

Het onderwerp van mijn onderzoekswerk is “Problemen oplossen met behulp van Euler-cirkels.” Bij de voorbereiding op de Olympiade kreeg ik te maken met taken waarbij veel data betrokken was. Het blijkt dat de zogenaamde Euler-cirkels de oplossing van dergelijke problemen helpen vereenvoudigen, met behulp waarvan je veel elementen kunt weergeven die een bepaalde eigenschap hebben. Het doel van dit werk is om deze methode te bestuderen en te kunnen toepassen om problemen op te lossen.

Het werk behandelt problemen waarvan de oplossing afhankelijk is van één algoritme: het maken van een tekening; We voeren de initiële gegevens in cirkels in, te beginnen met de voorwaarde die meer eigenschappen bevat; analyserend en redenerend schrijven we de resultaten op in delen van de cirkel; schrijf het antwoord op.

De relevantie ligt in het feit dat de taken van praktische aard zijn, wat belangrijk is in het moderne leven. Problemen dwingen je om na te denken, om de oplossing van een probleem vanuit een andere hoek te benaderen, om uit een verscheidenheid aan oplossingen te kunnen kiezen, op de eenvoudigste, gemakkelijkste manier. De methode die in het werk wordt besprokentoegankelijk en gemakkelijk te begrijpen, waardoor u het toepassingsbereik kunt uitbreiden. Euler-cirkels zijn te vinden in de geschiedenis, biologie en in de studie van andere onderwerpen.

Het materiaal dat in het werk werd bestudeerd, evenals het praktische gedeelte,kan worden gebruikt in aanvullende lessen ter voorbereiding op wiskundige olympiades.

Materiaaloverzicht

Wiskunde is een van mijn favoriete vakken op de middelbare school. Ik vind het leuk om verschillende wiskundige puzzels en logische problemen op te lossen. Op de wiskundeclub maken we kennis met verschillende manieren om problemen op te lossen. Op een dag kregen we tijdens een clubklas een huiswerkopdracht om het volgende probleem op te lossen: “Er zitten 35 leerlingen in de klas, 12 zitten in een wiskundeclub, 9 zitten in een biologieclub en 16 kinderen gaan niet naar deze clubs. . Hoeveel biologen zijn geïnteresseerd in wiskunde? Ik heb het zo opgelost:

35 - 16=19 (kinderen) - ga naar clubs

19- 9 = 10 (kinderen) – ga naar een wiskundeclub

12 - 10=2 (biologen) – zijn dol op wiskunde.

En ze vroeg me om de oplossing voor het probleem van mijn oudere broer te onderzoeken. Hij zei dat

Het probleem is correct opgelost, maar er is een handiger en snellere manier om het op te lossen. Het blijkt dat de zogenaamde Euler-cirkels de oplossing van dit probleem helpen vereenvoudigen, met behulp waarvan je veel elementen kunt weergeven die een bepaalde eigenschap hebben. Ik was geïnteresseerd in een nieuwe manier om het probleem op te lossen en besloot een onderzoekspaper te schrijven over het onderwerp: “Problemen oplossen met behulp van Euler-cirkels”

Ik stelde mezelf een doel: een nieuwe manier leren om niet-standaardproblemen op te lossen met behulp van Euler-cirkels.

Om het onderwerp van mijn onderzoekswerk duidelijk te maken, werden de volgende taken gesteld:

Leer wetenschappelijke literatuur gebruiken.

Leer wat Euler-cirkels zijn.

Creëer een algoritme voor het oplossen van problemen.

Leer problemen oplossen met behulp van Euler-cirkels.

Stel een selectie van problemen samen voor gebruik in wiskundelessen.

Onderzoeksmethoden:

Studie en analyse van wetenschappelijke literatuur;

Methode van inductieve generalisatie, specificatie.

Onderwerp van studie: Euler-cirkels

Onderwerp van onderzoek: het concept van een verzameling, de belangrijkste acties daarmee die nodig zijn bij het oplossen van problemen met behulp van Euler-cirkels

Studiedeelnemers: leerlingen in groep 5 t/m 9 van het gymnasium

Onderzoekshypothese: De methode van Euler vereenvoudigt het redeneren bij het oplossen van bepaalde problemen en vergemakkelijkt de weg naar de oplossing ervan.

De relevantie van het onderzoek ligt in het feit dat er veel technieken en manieren zijn om niet-standaard logische problemen op te lossen. Vaak wordt bij het oplossen van een probleem gebruik gemaakt van tekeningen, waardoor het oplossen van het probleem eenvoudiger en visueler wordt. Een van die visuele en handige manieren om problemen op te lossen is de Euler-cirkelmethode. Met deze methode kunt u problemen met lastige omstandigheden en met veel gegevens oplossen.

Problemen opgelost met behulp van Euler-cirkels worden vaak aangeboden op wiskundige Olympiades. Dergelijke taken zijn vaak van praktische aard, wat belangrijk is in het moderne leven. Ze laten je nadenken en het oplossen van een probleem vanuit verschillende invalshoeken benaderen. Ze leren je om uit verschillende methoden de eenvoudigste en gemakkelijkste te kiezen.

Theoretisch gedeelte

Korte historische achtergrond.

Leonhard Euler (1707-1783) – groot wiskundige van de Sint-Petersburg Academie van de 18e eeuw. Geboren in het Zwitserse Bazel. Hij ontdekte al vroeg wiskundige vaardigheden. Op 13-jarige leeftijd werd hij student aan de Faculteit der Letteren van de Universiteit van Basel, waar zowel wiskunde als astronomie werd onderwezen. Op 17-jarige leeftijd behaalde hij een masterdiploma. Op 20-jarige leeftijd werd Euler uitgenodigd om te werken aan de St. Petersburg Academie van Wetenschappen, en op 23-jarige leeftijd was hij al hoogleraar natuurkunde, en drie jaar later ontving hij de afdeling hogere wiskunde.

Tijdens zijn lange leven liet Leonhard Euler belangrijke werken na over verschillende takken van de wiskunde, mechanica, natuurkunde, astronomie en een aantal toegepaste wetenschappen, en schreef hij meer dan 850 wetenschappelijke artikelen. In een van hen verschenen deze cirkels.

Wat zijn Euler-cirkels?

Het antwoord op deze vraag heb ik gevonden door verschillende educatieve literatuur te lezen. Leonhard Euler geloofde dat “cirkels zeer geschikt zijn om ons denken te vergemakkelijken.” Bij het oplossen van een aantal problemen gebruikte hij het idee om verzamelingen weer te geven met behulp van cirkels. Daarom werden ze ‘Euleriaanse cirkels’ genoemd.

In de wiskunde is een set een verzameling, een verzameling van enkele objecten (objecten). De objecten waaruit een set bestaat, worden de elementen ervan genoemd. Het wordt conventioneel aanvaard dat een cirkel visueel het volume van één concept weergeeft. Ons vijfde leerjaar is bijvoorbeeld een set, en het aantal leerlingen in de klas is de elementen ervan.

In de wiskunde worden verzamelingen aangegeven met hoofdletters en hun elementen met hoofdletters. Vaak geschreven in de vorm A = (a, b, c, ...), waarbij de elementen van de verzameling A tussen accolades worden aangegeven.

Als elk element van set A tegelijkertijd een element van set B is, dan zeggen ze dat A een subset is van set B. De set leerlingen van groep 5 in ons gymnasium is bijvoorbeeld een subset van alle leerlingen in het gymnasium. .

Bij sets kun je, net als bij objecten, bepaalde acties (bewerkingen) uitvoeren. Om acties met sets duidelijker voor te stellen, worden speciale tekeningen gebruikt - Euler-diagrammen (cirkels). Laten we er een paar leren kennen.

De verzameling gemeenschappelijke elementen A en B wordt het snijpunt van de verzamelingen A en B genoemd en wordt aangegeven met het teken ∩.

A∩B = (m), C ∩B = (e, u).

Verzamelingen A en C hebben geen gemeenschappelijke elementen, dus het snijpunt van deze verzamelingen is de lege verzameling: A∩C =∅.

Als je een nieuwe set maakt uit de elementen van sets A en B, bestaande uit alle elementen van deze sets en geen andere elementen bevat, dan krijg je een vereniging van sets A en B, die wordt aangegeven met het teken ∪.

Beschouw een voorbeeld: Stel A = (t, o, h, k, a), B = (t, i, p, e), C = (d, e, f, u, s).

A∪B = (t, o, h, k, a, i, p, e), B∪ C = (t, i, p, e, d, f, s), A ∪ B ∪ C = (t , o, h, k, a, i, p, e, d, f, s).

Conclusies: Euler-cirkels zijn een geometrisch diagram waarmee je logische verbanden tussen verschijnselen en concepten duidelijker kunt maken. Het helpt ook om de relatie tussen een set en zijn onderdeel weer te geven.

U kunt dit verifiëren met behulp van een voorbeeldtaak.

Al mijn vrienden kweken wat bloemen in hun appartementen. Zes van hen kweken cactussen en vijf viooltjes. En slechts twee hebben zowel cactussen als viooltjes. Hoeveel vriendinnen heb ik?

Laten we bepalen hoeveel verzamelingen er in het probleem zitten (d.w.z. hoeveel cirkels we zullen tekenen bij het oplossen van het probleem).

Bij deze taak kweken de vrienden 2 soorten bloemen: cactussen en viooltjes.

Dit betekent de eerste set (1 cirkel is vrienden die cactussen kweken).

De tweede set (de 2e cirkel zijn vrienden die viooltjes kweken).

In de eerste cirkel zullen we de eigenaren van cactussen aanwijzen, en in de tweede cirkel de eigenaren van viooltjes.

We selecteren de voorwaarde die meer eigenschappen bevat om cirkels te tekenen. Sommige vrienden hebben beide bloemen, dus laten we cirkels tekenen zodat ze een gemeenschappelijk deel hebben.

Laten we de tekening maken.

In het algemene deel zetten we het getal 2, aangezien twee vrienden zowel cactussen als viooltjes hebben.

Volgens de omstandigheden van het probleem kweken 6 vrienden cactussen, en 2 bevinden zich al in het gemeenschappelijke deel, en vervolgens plaatsen we in het resterende deel van de cactussen het getal 4 (6-2 = 4).

5 vrienden kweken viooltjes, en 2 zitten al in het gemeenschappelijke deel, dan plaatsen we in het resterende deel van de viooltjes het getal 3 (5-2=3)

De afbeelding zelf vertelt ons het antwoord 4+2+3=9. Wij schrijven het antwoord op.

Antwoord: 9 vriendinnen

Praktisch gedeelte

Problemen oplossen met behulp van Euler-cirkels

Nadat ik op basis van het voorbeeld van het probleem en het bestudeerde materiaal had uitgezocht wat Euler-cirkels zijn, besloot ik verder te gaan met het opstellen van een algoritme voor het oplossen van problemen met behulp van deze methode.

2.1 Algoritme voor het oplossen van problemen

We bestuderen de voorwaarden van het probleem zorgvuldig en schrijven deze kort op.

We bepalen het aantal sets en wijzen deze aan.

Laten we de tekening maken. We construeren het snijpunt van verzamelingen.

We schrijven de initiële gegevens in cirkels.

Selecteer de voorwaarde die meer eigenschappen bevat.

We schrijven de ontbrekende gegevens in Euler-cirkels (redeneren en analyseren)

We controleren de oplossing voor het probleem en schrijven het antwoord op.

Nadat ik een algoritme had gemaakt voor het oplossen van problemen met behulp van Euler-cirkels, besloot ik het aan nog een aantal problemen te werken.

Problemen met betrekking tot de kruising en vereniging van twee sets

Taak 1.

Er zitten 15 leerlingen in mijn klas. Hiervan zijn er 9 betrokken bij de atletieksectie, 5 bij de zwemsectie en 3 bij beide secties. Hoeveel leerlingen in de klas volgen geen secties?

Oplossing.

Het probleem bestaat uit één verzameling en twee deelverzamelingen. 1 cirkel - totaal aantal studenten. 2e cirkel – aantal studenten dat betrokken is bij atletiek. 3 cirkel - het aantal studenten dat betrokken is bij zwemmen.

Laten we alle leerlingen vertegenwoordigen in een grotere cirkel. We plaatsen kleinere cirkels erin en tekenen ze zo dat ze een gemeenschappelijk deel hebben (aangezien drie jongens in beide secties studeren).

Totaal

Laten we de tekening maken.

Er staan 15 studenten in een grote cirkel. In het algemene deel van de kleinere cirkels plaatsen we het getal 3. In het resterende deel van de cirkel l/a plaatsen we het getal 6 (9-3=6). Plaats in het resterende deel van de cirkel n het getal 2 (5-3=2).

5. We noteren het antwoord uit de afbeelding: 15-(6+3+2) = 4 (leerlingen) zijn bij geen van deze onderdelen betrokken.

Probleem 2. (dat ik op een andere manier heb opgelost, maar nu zal ik het oplossen met behulp van Euler-cirkels)

Er zitten 35 leerlingen in de klas, 12 zitten in een wiskundeclub, 9 in een biologieclub, en 16 kinderen gaan niet naar deze clubs. Hoeveel biologen zijn geïnteresseerd in wiskunde?

Oplossing:

Het probleem bestaat uit één verzameling en twee deelverzamelingen. 1 cirkel - totaal aantal leerlingen in de klas. 2e cirkel het aantal studenten dat in een wiskundecirkel studeert (aangegeven met de letter M). 3e cirkel - het aantal studenten dat in de biologiecirkel studeert (aangegeven met de letter B).

Laten we de hele klas leerlingen weergeven met behulp van een grote cirkel. Binnenin plaatsen we kleinere cirkels die een gemeenschappelijk deel hebben, omdat Verschillende biologen zijn geïnteresseerd in wiskunde.

Laten we de tekening maken:

Er bevinden zich slechts 35 studenten in de grote cirkel. 35-16 = 19 (studenten) bezoeken deze clubs. Binnen cirkel M plaatsen we 12 studenten die studeren in een wiskundecirkel. Binnen cirkel B plaatsen we 9 studenten die studeren in de biologieclub.

Laten we het antwoord op de afbeelding schrijven: (12 + 9) – 19 = 2 (studenten) – ze zijn dol op biologie en wiskunde. Antwoord: 2 studenten.

2.3. Problemen met betrekking tot de kruising en vereniging van drie sets

Taak 3.

Er zitten 40 mensen in de klas. Hiervan hebben 19 mensen een “C”-graad in de Russische taal, 17 mensen in wiskunde en 22 mensen in geschiedenis. Slechts één vak heeft "C" -cijfers: in het Russisch - 4 personen, in wiskunde - 4 personen, in geschiedenis - 11 personen. Zeven leerlingen hebben een C-cijfer voor zowel wiskunde als geschiedenis, en vijf leerlingen hebben een C-cijfer voor alle vakken. Hoeveel mensen studeren zonder cijfers? Hoeveel mensen hebben C's in twee van de drie vakken?

Oplossing:

Het probleem bestaat uit één set en drie subsets. 1 grote cirkel - totaal aantal leerlingen in de klas. 2e cirkel is het aantal studenten met C-cijfers in wiskunde (aangeduid met de letter M), 3e cirkel is kleiner - het aantal studenten met C-cijfers in de Russische taal (aangeduid met de letter P), 4e cirkel is kleiner - de aantal studenten met C-cijfers in geschiedenis (aangeduid met de letter I)

Laten we Euler-cirkels tekenen. Binnen de grotere cirkel, die alle leerlingen in de klas afbeeldt, plaatsen we drie kleinere cirkels M, R, I, die respectievelijk wiskunde, Russische taal en geschiedenis betekenen, en alle drie de cirkels snijden elkaar, aangezien 5 leerlingen in totaal een “C”-cijfer hebben. onderwerpen.

Laten we de gegevens in cirkels schrijven, redeneren, analyseren en de nodige berekeningen uitvoeren. Aangezien het aantal studenten met “C”-cijfers in wiskunde en geschiedenis 7 is, is het aantal studenten met slechts twee “C”-cijfers – in wiskunde en geschiedenis – 7-5 = 2. Dan hebben 17-4-5-2=6 leerlingen twee “C”-cijfers – in wiskunde en de Russische taal, en 22-5-2-11=4 leerlingen hebben slechts twee “C”-cijfers – in geschiedenis en de Russische taal . In dit geval studeren 40-22-4-6-4 = 4 studenten zonder “C”. En ze hebben een “C”-cijfer voor twee van de drie vakken: 6+2+4=12 personen.

7-5=2 - het aantal studenten met slechts twee “C”-cijfers - M, I.

17-4-5-2=6 - het aantal studenten met slechts twee “C”-cijfers - M, R.

22-5-2-11=4 - het aantal studenten met slechts twee “C”-cijfers - I, R.

40-22-4-6-4=4 - het aantal studenten dat studeert zonder “C”

6+2+4=12 - het aantal studenten met een “C”-cijfer - in twee van de drie vakken

Antwoord: 4 studenten studeren zonder “C”-cijfers, 12 studenten hebben “C”-cijfers in twee van de drie vakken

Taak 4.

Er zitten 30 mensen in de klas. 20 van hen gebruiken dagelijks de metro, 15 gebruiken de bus, 23 gebruiken de trolleybus, 10 gebruiken zowel de metro als de trolleybus, 12 gebruiken zowel de metro als de bus, 9 gebruiken zowel de trolleybus als de bus. Hoeveel mensen maken dagelijks gebruik van alle drie de vervoerswijzen?

Oplossing. 1 manier. Om dit op te lossen, gebruiken we opnieuw Euler-cirkels:

20 − (12 − x) − (10 − x) − x = x − 2

Op dezelfde manier krijgen we: 15 –(12 − x) -(9 − x) - x = x − 6 - alleen met de bus en

23 - (9 − x) - (10 − x) – x = x + 4 - alleen met de trolleybus, aangezien er maar 30 mensen zijn, maken we de vergelijking:

X + (12 − x) + (9 − x) + (10 − x) + (x + 4) + (x − 2) + (x − 6) = 30. Dus x = 3.

Methode 2. Of je kunt dit probleem op een andere manier oplossen:

20+15+23-10-12-9+x=30, 27+x=30, x=3.

Antwoord: 3 personen maken dagelijks gebruik van alle drie de vervoerswijzen.

2.4. Voorbereiding van problemen van praktisch belang

Probleem 1. Er zitten 15 mensen in klas 5A. 5 mensen gaan naar de cirkel "Erudiete", 13 mensen gaan naar de cirkel "Pad naar het Woord", 3 mensen gaan naar de sportafdeling. Bovendien wonen 2 personen de cirkel “Erudiete” en de cirkel “Pad naar het Woord” bij, “Eruditie” en de sportsectie, de sportsectie en de “Pad naar het Woord”. Hoeveel mensen bezoeken alle drie de clubs?

Oplossing:

1. Laat dan x mensen naar alle drie de clubs gaan

2. 5+13+3-2-2-2+x=15, 13+x=15, x=2

Antwoord: Er gaan 2 mensen naar alle drie de clubs.

Probleem 2

Het is bekend dat studenten van groep 6B zijn geregistreerd op sociale netwerken: "VK", "Odnoklassniki", "Dating Galaxy". 2 studenten zijn op geen enkel sociaal netwerk geregistreerd, 7 studenten zijn geregistreerd op zowel Odnoklassniki als VK; 2 studenten alleen in Odnoklassniki en 1 alleen in VK; en 2 studenten zijn geregistreerd in alle 3 de sociale netwerken. Hoeveel mensen in de klas zijn geregistreerd op elk sociaal netwerk? Hoeveel mensen uit de klas hebben meegedaan aan het onderzoek?

Oplossing:

Met behulp van Euler-cirkels krijgen we:

Er zijn 1+5+2=8 mensen geregistreerd in VK,

In Odnoklassniki zijn er 2+5+2=9 mensen,

Er zijn slechts 2 mensen in de Dating Galaxy.

In totaal namen 1+5+2+2+2=12 mensen deel aan het onderzoek

2.5. Problemen voor gebruik in wiskundecirkellessen

Taak 1: "Harry Potter, Ron en Hermelien"

Er lagen 26 magische boeken over spreuken op de plank, ze waren allemaal gelezen. Hiervan werden er 4 gelezen door zowel Harry Potter als Ron. Hermelien las zeven boeken die noch Harry Potter noch Ron hadden gelezen, en twee boeken die Harry Potter had gelezen. In totaal heeft Harry Potter 11 boeken gelezen. Hoeveel boeken heeft Ron alleen gelezen?

Taak 2: “Pionierskamp”

Taak 3: “Extreem”

Taak 4: "Voetbalteam"

Het Spartak-voetbalteam heeft 30 spelers, waaronder 18 aanvallers, 11 middenvelders, 17 verdedigers en keepers. Het is bekend dat er drie aanvallers en verdedigers kunnen zijn, 10 verdedigers en middenvelders, 6 aanvallers en verdedigers, en 1 kan een aanvaller, een verdediger en een middenvelder zijn. Keepers zijn onvervangbaar. Hoeveel keepers zijn er in het team van Spartak?

Taak 5: “Winkel”

65 mensen bezochten de winkel. Het is bekend dat ze 35 koelkasten, 36 magnetrons en 37 televisies hebben gekocht. 20 van hen kochten zowel een koelkast als een magnetron, 19 kochten zowel een magnetron als een tv, 15 kochten een koelkast en een tv, en alle drie de aankopen werden door drie personen gedaan. Was er een bezoeker onder hen die niets kocht?

Taak 6: “Kleuterschool”

Er zijn 52 kinderen op de kleuterschool. Ze houden allemaal van cake of ijs, of allebei. De helft van de kinderen houdt van taart, en 20 mensen houden van taart en ijs. Hoeveel kinderen houden van ijs?

Taak 7: “Studentenbrigade”

Er zitten 86 middelbare scholieren in het studentenproductieteam. Acht van hen weten niet hoe ze een tractor of een maaidorser moeten bedienen. 54 studenten beheersten de tractor goed, 62 - de maaidorser. Hoeveel mensen uit dit team kunnen zowel aan een tractor als aan een maaidorser werken?

Onderzoeksgedeelte

Doel: gebruik van de Euler-methode door gymnasiumstudenten bij het oplossen van niet-standaard problemen.

Het experiment werd uitgevoerd met deelname van leerlingen uit de groepen 5 tot en met 9 die geïnteresseerd zijn in wiskunde. Hen werd gevraagd de volgende twee problemen op te lossen:

Zes leerlingen uit de klas gaan naar de muziekschool, tien zijn betrokken bij de voetbalafdeling en nog eens tien gaan naar een kunstatelier. Drie van hen gaan naar zowel de voetbal- als de muziekschool. Hoeveel mensen zitten er in de klas?

Van de 10 deelnemers (2 personen uit elke parallelle klas) van het experiment, losten slechts 4 mensen het eerste probleem op, en slechts twee het tweede probleem (leerlingen in groep 8 en 9). Nadat ik hen mijn onderzoekswerk had gepresenteerd, waarin ik over Euler-cirkels sprak, de oplossing van verschillende eenvoudige en voorgestelde problemen met behulp van deze methode analyseerde, konden de studenten eenvoudige problemen zelf oplossen.

Aan het einde van het experiment kregen de kinderen de volgende taak:

Er zijn 70 kinderen in het pionierskamp. Hiervan zijn er 27 betrokken bij de toneelclub, 32 zingen in het koor, 22 zijn dol op sport. Er zijn 10 jongens van het koor in de toneelclub, 6 atleten in het koor, 8 atleten in de toneelclub; 3 atleten bezoeken zowel de toneelclub als het koor. Hoeveel kinderen zingen niet, zijn niet geïnteresseerd in sport, nemen niet deel aan een toneelclub? Hoeveel jongens zijn alleen bezig met sporten?

Van de 10 deelnemers aan het experiment konden ze allemaal deze taak uitvoeren.

Conclusie: Het oplossen van problemen met behulp van Euler-cirkels ontwikkelt het logisch denken en maakt het mogelijk om problemen op te lossen die alleen op de gebruikelijke manier kunnen worden opgelost door een systeem van drie vergelijkingen met drie onbekenden samen te stellen. Leerlingen in de groepen 5 tot en met 7 weten niet hoe ze stelsels vergelijkingen moeten oplossen, maar ze kunnen wel dezelfde problemen oplossen. Dit betekent dat de kinderen deze methode voor het oplossen van problemen met behulp van Euler-cirkels moeten kennen.

Toepassingen