Теорема сложения вероятностей совместных событий доказательство. Теоремы сложения и умножения вероятностей
Изучение теории вероятности начинается с решения задач на сложение и умножение вероятностей. Стоит сразу упомянуть, что студент при освоении данной области знаний может столкнуться с проблемой: если физические или химические процессы можно представить визуально и понять эмпирически, то уровень математической абстракции очень высок, и понимание здесь приходит только с опытом.
Однако игра стоит свеч, ведь формулы - как рассматриваемые в данной статье, так и более сложные - используются сегодня повсеместно и вполне могут пригодиться в работе.
Происхождение
Как ни странно, толчком к развитию данного раздела математики стали… азартные игры. Действительно, игра в кости, бросание монетки, покер, рулетка - это типичные примеры, в которых используются сложение и умножение вероятностей. На примере задач в любом учебнике это можно увидеть наглядно. Людям было интересно узнать, как увеличить свои шансы на победу, и, надо сказать, некоторые в этом преуспели.
Например, уже в XXI веке один человек, чьего имени раскрывать мы не будем, использовал эти накопленные веками знания, чтобы буквально «обчистить» казино, выиграв в рулетку несколько десятков миллионов долларов.
Впрочем, несмотря на повышенный интерес к предмету, только к XX веку была разработана теоретическая база, делающая «теорвер» полноценной Сегодня же практически в любой науке можно встретить расчёты, использующие вероятностные методы.
Применимость
Важным моментом при использовании формул сложения и умножения вероятностей, условной вероятности является выполнимость центральной предельной теоремы. В противном случае хоть это и может и не осознаваться студентом, все вычисления, какими бы правдоподобными они ни казались, будут некорректны.
Да, у высокомотивированного учащегося возникает соблазн использовать новые знания при каждом удобном случае. Но в данном случае следует несколько притормозить и строго очертить рамки применимости.
Теория вероятности имеет дело со случайными событиями, которые в эмпирическом плане представляют собой результаты экспериментов: мы можем бросать кубик с шестью гранями, вытаскивать карту из колоды, предсказывать количество бракованных деталей в партии. Однако в некоторых вопросах использовать формулы из этого раздела математики категорически нельзя. Особенности рассмотрения вероятностей события, теорем сложения и умножения событий мы обсудим в конце статьи, а пока обратимся к примерам.
Основные понятия
Под случайным событием подразумевается некоторый процесс или результат, который может проявиться, а может и не проявиться в результате эксперимента. Например, мы подбрасываем бутерброд - он может упасть маслом вверх или маслом вниз. Любой из двух исходов будет являться случайным, и мы заранее не знаем, какой из них будет иметь место.

При изучении сложения и умножения вероятностей нам понадобятся ещё два понятия.
Совместными называются такие события, появление одного из которых не исключает появления другого. Скажем, два человека одновременно стреляют по мишени. Если один из них произведет успешный никак не отразится на возможности второго попасть в «яблочко» или промахнуться.
Несовместными будут такие события, появление которых одновременно является невозможным. Например, вытаскивая из коробки только один шарик, нельзя достать сразу и синий, и красный.
Обозначение
Понятие вероятности обозначается латинской заглавной буквой P. Далее в скобках следуют аргументы, обозначающие некоторые события.
В формулах теоремы сложения, условной вероятности, теоремы умножения вы увидите в скобках выражения, например: A+B, AB или A|B. Рассчитываться они будут различными способами, к ним мы сейчас и обратимся.
Сложение
Рассмотрим случаи, в которых используются формулы сложения и умножения вероятностей.
Для несовместных событий актуальна самая простая формула сложения: вероятность любого из случайных исходов будет равна сумме вероятностей каждого из этих исходов.

Предположим, что есть коробка с 2 синими, 3 красными и 5 жёлтыми шариками. Итого в коробке имеется 10 предметов. Какова доля истинности утверждения, что мы вытащим синий или красный шар? Она будет равна 2/10 + 3/10, т. е. пятьдесят процентов.
В случае же несовместных событий формула усложняется, поскольку добавляется дополнительное слагаемое. Вернемся к нему через один абзац, после рассмотрения ещё одной формулы.
Умножение
Сложение и умножение вероятностей независимых событий используются в разных случаях. Если по условию эксперимента нас устраивает любой из двух возможных исходов, мы посчитаем сумму; если же мы хотим получить два некоторых исхода друг за другом, мы прибегнем к использованию другой формулы.
Возвращаясь к примеру из предыдущего раздела, мы хотим вытащить сначала синий шарик, а затем - красный. Первое число нам известно - это 2/10. Что происходит дальше? Шаров остается 9, красных среди них всё столько же - три штуки. Согласно расчётам получится 3/9 или 1/3. Но что теперь делать с двумя числами? Правильный ответ - перемножать, чтобы получилось 2/30.
Совместные события
Теперь можно вновь обратиться к формуле суммы для совместных событий. Для чего мы отвлекались от темы? Чтобы узнать, как перемножаются вероятности. Сейчас нам это знание пригодится.

Мы уже знаем, какими будут первые два слагаемых (такие же, как и в рассмотренной ранее формуле сложения), теперь же потребуется вычесть произведение вероятностей, которое мы только что научились рассчитывать. Для наглядности напишем формулу: P(A+B) = P(A) + P(B) - P(AB). Получается, что в одном выражении используется и сложение, и умножение вероятностей.
Допустим, мы должны решить любую из двух задач, чтобы получить зачёт. Первую мы можем решить с вероятностью 0,3, а вторую - 0,6. Решение: 0,3 + 0,6 - 0,18 = 0,72. Заметьте, просто просуммировать числа здесь будет недостаточно.
Условная вероятность
Наконец, существует понятие условной вероятности, аргументы которой обозначаются в скобках и разделяются вертикальной чертой. Запись P(A|B) читается следующим образом: «вероятность события A при условии события B».
Посмотрим пример: друг дает вам некоторый прибор, пусть это будет телефон. Он может быть сломан (20 %) или исправен (80 %). Любой попавший в руки прибор вы в состоянии починить с вероятностью 0,4 либо не в состоянии этого сделать (0,6). Наконец, если прибор находится в рабочем состоянии, вы можете дозвониться до нужного человека с вероятностью 0,7.
Легко заметить, как в данном случае проявляется условная вероятность: вы не сможете дозвониться до человека, если телефон сломан, а если он исправен, вам не требуется его чинить. Таким образом, чтобы получить какие-либо результаты на «втором уровне», нужно узнать, какое событие выполнилось на первом.
Расчёты
Рассмотрим примеры решения задач на сложение и умножение вероятностей, воспользовавшись данными из предыдущего абзаца.
Для начала найдем вероятность того, что вы почините отданный вам аппарат. Для этого, во-первых, он должен быть неисправен, а во-вторых, вы должны справиться с починкой. Это типичная задача с использованием умножения: получаем 0,2*0,4 = 0,08.

Какова вероятность, что вы сразу дозвонитесь до нужного человека? Проще простого: 0,8*0,7 = 0,56. В этом случае вы обнаружили, что телефон исправен и успешно совершили звонок.
Наконец, рассмотрим такой вариант: вы получили сломанный телефон, починили его, после чего набрали номер, и человек на противоположном конце взял трубку. Здесь уже требуется перемножение трёх составляющих: 0,2*0,4*0,7 = 0,056.
А что делать, если у вас сразу два нерабочих телефона? С какой вероятностью вы почините хотя бы один из них? на сложение и умножение вероятностей, поскольку используются совместные события. Решение: 0,4 + 0,4 - 0,4*0,4 = 0,8 - 0,16 = 0,64. Таким образом, если вам в руки попадёт два сломанных аппарата, вы справитесь с починкой в 64% случаев.
Внимательное использование
Как говорилось в начале статьи, использование теории вероятности должно быть обдуманным и осознанным.
Чем больше серия экспериментов, тем ближе подходит теоретически предсказываемое значение к полученному на практике. Например, мы бросаем монетку. Теоретически, зная о существовании формул сложения и умножения вероятностей, мы можем предсказать, сколько раз выпадет «орёл» и «решка», если мы проведем эксперимент 10 раз. Мы провели эксперимент, и по стечению обстоятельств соотношение выпавших сторон составило 3 к 7. Но если провести серию из 100, 1000 и более попыток, окажется, что график распределения всё ближе подбирается к теоретическому: 44 к 56, 482 к 518 и так далее.

А теперь представьте, что данный эксперимент проводится не с монеткой, а с производством какого-нибудь новейшего химического вещества, вероятности получения которого мы не знаем. Мы провели бы 10 экспериментов и, не получив успешного результата, могли бы обобщить: «вещество получить невозможно». Но кто знает, проведи мы одиннадцатую попытку - достигли бы мы цели или нет?
Таким образом, если вы обращаетесь к неизведанному, к неисследованной области, теория вероятности может оказаться неприменима. Каждая последующая попытка в этом случае может оказаться успешной и обобщения типа «X не существует» или «X является невозможным» будут преждевременны.
Заключительное слово
Итак, мы рассмотрели два вида сложения, умножение и условные вероятности. При дальнейшем изучении данной области необходимо научиться различать ситуации, когда используется каждая конкретная формула. Кроме того, нужно представлять, применимы ли вообще вероятностные методы при решении вашей задачи.

Если вы будете практиковаться, то через некоторое время начнете осуществлять все требуемые операции исключительно в уме. Для тех, кто увлекается карточными играми, этот навык можно считать крайне ценным - вы значительно увеличите свои шансы на победу, всего лишь рассчитывая вероятность выпадения той или иной карты или масти. Впрочем, полученным знаниям вы без труда найдете применение и в других сферах деятельности.
Тип занятия:
изучение нового материала.
Учебно-воспитательные задачи:
- дать понятие о случайном событии, вероятности события;
- научить вычислять вероятности события; вероятности случайных событий по классическому определению;
- научить применять теоремы сложения и умножения вероятностей для решения задач;
- продолжать формировать интерес к математике посредством решения задач с применением классического определения вероятности для непосредственного подсчета вероятностей явлений;
- прививать интерес к математике, используя исторический материал;
- воспитывать осознанное отношение к процессу обучения, прививать чувство ответственности за качество знаний, осуществлять самоконтроль за процессом решения и оформления упражнений.
Обеспечение занятия:
- карточки-задания для индивидуального опроса;
- карточки-задания для проверочной работы;
- презентация.
Студент должен знать:
- определения и формулы числа перестановок, размещений и сочетаний;
- классическое определение вероятности;
- определения суммы событий, произведения событий; формулировки и формулы теорем сложения и умножения вероятностей.
Студент должен уметь:
- вычислять перестановки, размещения и сочетания;
- вычислять вероятность события используя классическое определение и формулы комбинаторики;
- решать задачи на применение теорем сложения и умножения вероятностей.
Мотивация познавательной деятельности студентов.
Преподаватель сообщает, что возникновение теории вероятностей относится к середине XVII в. и связанно с исследованием Б. Паскаля, П. Ферма и Х.Гюйгенса (1629-1695) . Крупный шаг в развитии теории вероятности связан с работами Я.Бернулли (1654-1705). Ему принадлежит первое доказательство одного из важнейших положений теории вероятностей - законом больших чисел. Следующий этап в развитии теории связан с именами А.Муавра (1667-1754) , К. Гаусса, П. Лапласа (1749-1827) , С.Пуассона (1781-1840). Среди ученых Петербургской школой следует назвать имена А.М. Ляпунова (1857-1918) и А.А Маркова (1856-1922) . После работ этих математиков во всем мире теорию вероятностей стали называть “Русской наукой”. В средине 20-х годов А.Я. Хинчин (1894-1959) и А.Н. Колмогорова создали Московскую школу теории вероятностей. Вклад акад. А.Н.Колмогоров – лауреата Ленинской премии, международной премии им. Б. Больцано, члена ряда зарубежных академиков – в современную математику огромен. Заслуга А.Н.Колмогорова состоит не только в разработке новых научных теорий, но и еще в большей степени в том, что он воспитал целую плеяду талантливых ученых (акад. АН УССР Б.В. Гнеденко, акад. Ю.В. Прохоров, Б.А. Севастьянов и др.).
Теория вероятностей – математическая наука, изучающая закономерности случайных величин,- за последнее десятилетие превратилась в один из основных методов современных науки и техники. Бурное развитие теории автоматического регулирования привело к необходимости решать многочисленные вопросы, связанные с выяснением возможного хода процессов, на которые влияют случайные факторы. Теория вероятностей необходима широкому кругу специалистов – физикам, биологам, врача, экономистам, инженерам, военным, организаторам производства и т.д.
Ход занятия.
I . Организационный момент.
II
. Проверка домашнего задания
Провести фронтальный опрос в виде ответов на вопросы:
Проверить решение упражнений:
- Сколькими способами можно составить список из 10 человек?
- Сколькими способами из 15 рабочих можно создать бригады по 5 человек в каждой?
- 30 учащихся обменялись друг с другом фотокарточками. Сколько всего было роздано фотокарточек?
III
. Изучение нового материала.
В толковом словаре С.И. Ожегова и Н.Ю. Шведовой читаем: «Вероятность – возможность исполнения, осуществимости чего-нибудь». Мы часто употребляем в повседневной жизни «вероятно», «вероятнее», «невероятно», вовсе не имея в виду конкретные количественные оценки этой возможности исполнения.
Основатель современной теории вероятностей А.Н. Колмогоров писал о вероятности так: «Вероятность математическая – это числовая характеристика степени возможности появления какого-либо определенного события в тех или иных определенных, могущих повторяться неограниченное число раз условиях».
Итак, в математике вероятность измеряется числом. Совсем скоро мы выясним, как именно это можно сделать. Но начнем мы с обсуждения того, у каких событий бывает «математическая вероятность» и что представляют собой эти «определенные, могущие повторяться неограниченное число раз условия». Именно поэтому рассмотрим случайные события и случайные эксперименты.
Нужно сказать, что теория вероятностей, как никакая другая область математики, полна противоречий и парадоксов. Объяснение этому очень простое – она слишком тесно связана с реальной, окружающей нас действительностью. Долгое время ее вместе с математической статистикой даже не хотели причислять к математическим дисциплинам, считая их сугубо прикладными науками.
Только в первой половине прошлого века, в основном благодаря трудам нашего великого соотечественника А.Н. Колмогорова, имя которого уже упоминалось выше, были построены математические основания теории вероятностей, которые позволили отделить собственно науку от ее приложений. Подход, предложенный Колмогоровым, теперь принято называть аксиоматическим, поскольку вероятность в нем (а точнее, вероятностное пространство) определяется как некая математическая структура, удовлетворяющая определенной системе аксиом.
Именно на этом подходе построен современный вузовский курс теории вероятностей, через который прошли в свое время все нынешние учителя математики. Однако в школе такой подход к изучению вероятности (да и математики в целом) вряд ли разумен. Если в вузе основной акцент делается на изучении математического аппарата для исследования вероятностных моделей, то в школе ученик должен научиться эти модели строить,
анализировать, проверять их адекватность реальным ситуациям. Такую точку зрения разделяют сегодня большинство ученых, занимающихся проблемами школьного математического образования
В современных школьных учебниках можно найти следующее определение: событие называется случайным
, если при одних и тех же условиях оно может как произойти, так и не произойти. Случайным будет, например, событие «При подбрасывании игрального кубика выпадет 6 очков».
В приведенном определении неявно подразумевается одно важное требование, которое необходимо подчеркнуть: мы должны иметь возможность неоднократно воспроизводить одни и те же условия, в которых наблюдается данное событие
(например, подбрасывать кубик),- иначе невозможно судить о его случайности.
Стало быть, говоря о любом случайном событии, мы всегда имеем в виду наличие определенных условий, без которых об этом событии вообще не имеет смысла говорить. Этот комплекс условий называют случайным опытом
или случайным экспериментом
.
В дальнейшем мы будем называть случайным любое событие, связанное со случайным экспериментом
. До эксперимента, как правило, невозможно точно сказать, произойдет данное событие, или не произойдет – это выясняется лишь после его завершения. Но неспроста мы сделали оговорку «как правило»: в теории вероятностей принято считать случайными все события, связанные со случайным экспериментом, в том числе:
- невозможные , которые никогда не могут произойти;
- достоверные, которые происходят при каждом таком эксперименте.
Например, событие «На игральном кубике выпадет 7 очков» - невозможное, а «На игральном кубике выпадет меньше семи очков» - достоверное. Разумеется, если речь идет о кубике, на гранях которого написаны числа от 1 до 6.
События называются несовместными,
если каждый раз возможно появление только одного из них. События называются совместными
, если в данных условиях появление одного из этих событий не исключает появление другого при том же испытании (В урне два шара – белый и черный, появление черного шара не исключает появление белого при том же испытании). События называются противоположными,
если в условиях испытания они, являясь единственными его исходами, несовместны. Вероятность события рассматривается как мера объективной возможности появления случайного события.
Обозначения:
Случайные события (большими буквами латинского алфавита): A,B,C,D,.. (или ). “Случайные” опускают и говорят просто “события”.
Число исходов, благоприятствующих наступлению данного события – m;
Число всех исходов (опытов) – n.
Классическое определение вероятности.
Вероятностью
события A называется отношение числа исходов m, благоприятствующих наступлению данного события к числу n всех исходов (несовместных, единственно возможных и равновозможных), т.е.
–
вероятность случайного события
Вероятность любого события не может быть меньше нуля и больше единицы, т.е. 0≤P(A)≤1
Невозможному событию соответствует вероятность P(A)=0, а достоверному – вероятность P(A)=1
Теоремы сложения вероятностей.
Теорема сложения вероятностей несовместных событий.
Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
P(A+B)=P(A)+P(B);
P(+ +…+=P(+P+…+P().
Теорема сложения вероятностей совместных событий.
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
P(A+B)=P(A)+P(B)-P(AB)
Для трех совместных событий имеет место формула:
P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)
Событие, противоположное событию A (т.е. ненаступление события A), обозначают . Сумма вероятностей двух противоположных событий равна единице: P(A)+P()=1
Вероятность наступления события A, вычисленная в предположении, что событие B уже произошло, называется условной вероятностью
события A при условии B и обозначается (A) или P(A/B).
Если A и B – независимые события, то
P(B)-(B)=(B).
События A,B,C,… называются независимыми в совокупности, если вероятность каждого из них не меняется в связи с наступлением или ненаступлением других событий по отдельности или в любой их комбинации.
Теоремы умножения вероятностей.
Теорема умножения вероятностей независимых событий.
Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
P(AB)=P(A) P(B)
Вероятность появления нескольких событий, независимых в совокупности, вычисляется по формуле:
P()=P() P()… P().
Теорема умножения вероятностей зависимых событий.
Вероятность совместного появления двух зависимых событий равна произведению одного из них на условную вероятность второго:
P(AB)=P(A) (B)=P(B) (A)
IV
. Применение знаний при решении типовых задач
Задача 1.
В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. Чему равна вероятность того, что этот билет выигрышный?
Решение:
Событие A-билет выигрышный. Общее число различных исходов есть n=1000
Число исходов, благоприятствующих получению выигрыша, составляет m=200. Согласно формуле P(A)=, получим P(A)== = 0,2 = 0,147
Задача 4
.
В ящике в случайном порядке разложены 20 деталей, причем 5 из них стандартные. Рабочий берет наудачу 3 детали. Найти вероятность того, что по крайней мере одна из взятых деталей окажется стандартной.
Задача 5.
Найти вероятность того, что наудачу взятое двухзначное число окажется кратным либо 3, либо 5, либо тому и другому одновременно
Задача 6.
В одной урне находятся 4 белых и 8 черных шаров, в другой – 3 белых и 9 черных. Из каждой урны вынули по шару. Найти вероятность того, что оба шара окажутся белыми.
Решение:
Пусть A - появление белого шара из первой урны, а B – появление белого шара из второй урны. Очевидно, что события A и B независимы. Найдем P(A)=4/12=1/3, P(B)=3/12=1/4, получим
P(AB)=P(A) P(B)=(1/3) (1/4)=1/12=0,083
Задача
7.
В ящике находится 12 деталей, из которых 8 стандартных. Рабочий берет наудачу одну за другой две детали. Найти вероятность того, что обе детали окажутся стандартными.
Решение:
Введем следующие обозначения: A – первая взятая деталь стандартная; B – вторая взятая деталь стандартная. Вероятность того, что первая деталь стандартная, составляет P(A)=8/12=2/3. Вероятность того, что вторая взятая деталь окажется стандартной при условии, что была стандартной первая деталь, т.е. условная вероятность события B, равна (B)=7/11.
Вероятность того, что обе детали окажутся стандартными, находим по теореме умножения вероятностей зависимых событий:
P(AB)=P(A) (B)=(2/3) (7/11)=14/33=0,424
Самостоятельное применение знаний, умений и навыков.
Вариант 1.
- Какова вероятность того, что наудачу выбранное целое число от 40 до 70 является кратным 6?
- Какова вероятность того, что при пяти бросаниях монеты она три раза упадет гербом к верху?
Вариант 2.
- Какова вероятность того, что наудачу выбранное целое число от 1 до 30 (включительно) является делителем числа 30?
- В НИИ работает 120 человек, из них 70 знают английский язык, 60 – немецкий, а 50 – знают оба. Какова вероятность того, что выбранный наудачу сотрудник не знает ни одного иностранного языка?
VI . Подведение итогов занятия.
VII
. Домашнее задание:
Г.Н. Яковлев, математика, книга 2, § 24.1, 24.2, стр. 365-386. Упражнения 24.11, 24.12, 24.17
Тема: 15. ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ
ВЕРОЯТНОСТЕЙ И ИХ СЛЕДСТВИЯ
1. Теорема сложения вероятностей совместных событий.
2. Теорема умножения вероятностей независимых событий.
3. Условная вероятность события. Теорема умножения вероятностей зависимых событий.
4. Теорема сложения вероятностей совместных событий.
5. Формула полной вероятности, формула Бейеса.
6. Повторение испытаний.
1. Теорема сложения вероятностей совместных событий.
Суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного из данных событий.
Если события А и В – совместные, то их сумма А+В обозначает наступление или события А, или события В, или обоих событий вместе. Если А и В – несовместные события, то их сумма А+В означает наступление или события А, или события В.
Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении этих событий.
Теорема: Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий
Р (А+В) = Р (А)+ Р(В).
Следствие: Сумма вероятностей несовместных событий А 1 ,...,А n , образующих полную группу, равна единице:
Р(А 1) + Р(А 2)+... +Р (А n) = 1
2. Теорема умножения вероятностей независимых
событий .
Два события называются независимыми, если вероятность появления одного из них не зависит от того, появилось или не появилось другое событие.
Несколько событий называются взаимно независимыми (или независимыми в совокупности), если каждое из них и любая комбинация, составленная из остальных (части или всех) событий, являются независимыми событиями.
Если события А 1 ,А 2 ,...,А n взаимно независимы, то и противоположные их события также взаимно независимы.
Теорема : Вероятность произведения нескольких взаимно независимых событий равна произведению вероятностей этих событий.
Р(А 1 А 2 ,...А n ) = Р(А 1 ) Р(А 2 ) ... Р(А n )
Для двух событий Р(АВ) = Р(А) Р(В)
Задача . Два товароведа работают независимо друг от друга. Вероятность пропустить бракованное изделие первым товароведом 0,1; вторым 0,2. Какова вероятность того, что при просмотре изделия оба товароведа не пропустят брак.
Решение : событие А - брак пропустил I товаровед, событие В - брак пропустил II товаровед.
Где событие А – брак не пропустит I товаровед,
событие В - брак не пропустит II товаровед.
Так как оба работают независимо друг от друга, то А и В независимые события.
3. Условная вероятность события. Теорема умножения вероятностей зависимых событий.
Событие В называют зависимым от события А, если появление события А изменяет вероятность появления события В.
Вероятность события В, найденная при условии, что событие А произошло, называется условной вероятностью события В и обозначается Р А (В).
Теорема : Вероятность совместного появления двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событиеуже наступило, т.е.
Р(АВ) = Р(А) Р А (В) или Р(АВ) = Р(В) Р В (А)
Теорема умножения вероятностей может быть распространена на любое число m зависимых событий А 1 А 2 ...А m .
Р(А 1 А 2 ..А m )=Р(А 1 )
причем вероятность последующего события вычисляется в предположении, что все предыдущие произошли.
Задача. В коробке 2 белых и 3 синих ручки. Из коробки вынимают подряд две ручки. Найти вероятность того, что обе ручки белые.
Решение: событие А - обе ручки белые, событие В - появление первой белой ручки, событие С - появление второй белой ручки.
Тогда А= В С.
Так как первая ручка не возвращается в коробку, т.е. состав коробки изменился, то события В и С зависимые.
Р (В) = 2/5; Вероятность события С находим в предположении, что В уже произошло, т.е. Р B (С) = ¼.
Искомая вероятность
Тип задания: 4
Условие
Вероятность того, что аккумулятор не заряжен, равна 0,15. Покупатель в магазине приобретает случайную упаковку, которая содержит два таких аккумулятора. Найдите вероятность того, что оба аккумулятора в этой упаковке окажутся заряжены.
Показать решениеРешение
Вероятность того, что аккумулятор заряжён, равна 1-0,15 = 0,85. Найдём вероятность события «оба аккумулятора заряжены». Обозначим через A и B события «первый аккумулятор заряжён» и «второй аккумулятор заряжён». Получили P(A) = P(B) = 0,85. Событие «оба аккумулятора заряжены» — это пересечение событий A \cap B, его вероятность равна P(A \cap B) = P(A)\cdot P(B) = 0,85\cdot 0,85 = 0,7225.
Ответ
Тип задания: 4
Тема:
Сложение и умножение вероятностей событий
Условие
Вероятность того, что ручка бракованная, равна 0,05 . Покупатель в магазине приобретает случайную упаковку, которая содержит две ручки. Найдите вероятность того, что обе ручки в этой упаковке окажутся исправными.
Показать решениеРешение
Вероятность того, что ручка исправная, равна 1-0,05 = 0,95. Найдём вероятность события «обе ручки исправны». Обозначим через A и B события «первая ручка исправна» и «вторая ручка исправна». Получили P(A) = P(B) = 0,95. Событие «обе ручки исправны» — это пересечение событий A\cap B, его вероятность равна P(A\cap B) = P(A)\cdot P(B) = 0,95\cdot 0,95 = 0,9025.
Ответ
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 4
Тема:
Сложение и умножение вероятностей событий
Условие
На рисунке изображён лабиринт. Жук заползает в лабиринт в точке «Вход». Развернуться и ползти в обратном направлении жук не может, поэтому на каждой развилке он выбирает один из путей, в котором еще не был. С какой вероятностью жук придет к выходу Д, если выбор дальнейшего пути является случайным.
Показать решениеРешение
Расставим на перекрёстках стрелки в направлениях, по которым может двигаться жук (см. рис.).

Выберем на каждом из перекрёстков одно направление из двух возможных и будем считать, что при попадании на перекрёсток жук будет двигаться по выбранному нами направлению.
Чтобы жук достиг выхода Д, нужно, чтобы на каждом перекрёстке было выбрано направление, обозначенное сплошной красной линией. Всего выбор направления делается 4 раза, каждый раз независимо от предыдущего выбора. Вероятность того, что каждый раз выбрана сплошная красная стрелка, равна \frac12\cdot\frac12\cdot\frac12\cdot\frac12= 0,5^4= 0,0625.
Ответ
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 4
Тема:
Сложение и умножение вероятностей событий
Условие
Стоянка освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,4. Найдите вероятность того, что за год хотя бы одна лампа не перегорит.
Показать решениеРешение
Сначала найдём вероятность события «обе лампы перегорели в течение года», противоположного событию из условия задачи. Обозначим через A и B события «первая лампа перегорела в течение года» и «вторая лампа перегорела в течение года». По условию P(A) = P(B) = 0,4. Событие «обе лампы перегорели в течение года» — это A \cap B, его вероятность равна P(A \cap B) = P(A) \cdot P(B) = 0,4 \cdot 0,4 = 0,16 (так как события A и B независимы).
Искомая вероятность равна 1 - P(A \cap B) = 1 - 0,16 = 0,84.
Ответ
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 4
Тема:
Сложение и умножение вероятностей событий
Условие
В гостинице стоят два кулера. Каждый из них может быть неисправен с вероятностью 0,2 независимо от другого кулера. Определите вероятность того, что хотя бы один из этих кулеров исправен.
Показать решениеРешение
Сначала найдём вероятность события «оба кулера неисправны», противоположного событию из условия задачи. Обозначим через A и B события «первый кулер неисправен» и «второй кулер неисправен». По условию P(A) = P(B) = 0,2. Событие «оба кулера неисправны» — это A \cap B , пересечение событий A и B , его вероятность равна P(A \cap B) = P(A)\cdot P(B) = 0,2\cdot 0,2 = 0,04 (так как события A и B независимы). Искомая вероятность равна 1-P(A \cap B)=1-0,04=0,96.
Ответ
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 4
Тема:
Сложение и умножение вероятностей событий
Условие
На экзамене по физике студент отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что этот вопрос на тему «Механика», равна 0,25 . Вероятность того, что этот вопрос на тему «Электричество», равна 0,3 . Вопросов, которые относились бы сразу к двум темам, нет. Найдите вероятность того, что студенту попадётся вопрос по одной из этих двух тем.
 Что произошло в Чернобыле – причины аварии, факты и теории
Что произошло в Чернобыле – причины аварии, факты и теории Гай юлий цезарь За что хвалили гая юлия цезаря
Гай юлий цезарь За что хвалили гая юлия цезаря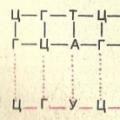 Что такое биосинтез в биологии?
Что такое биосинтез в биологии?