Y x знайти період функції. Періодичність функцій у = sin х, у = cos х - Гіпермаркет знань
Аргументу x, вона називається періодичної, якщо є число T, що з будь-якого x F(x + T) = F(x). Це число T називається періодом функції.
Періодів може бути кілька. Наприклад, функція F = const для будь-яких значень аргументу приймає одне й те саме значення, тому будь-яке число може вважатися її періодом.
Зазвичай цікавить найменший не рівний нулю період функції. Його для стислості і називають просто періодом.
Класичний приклад періодичних функцій – тригонометричні: синус, косинус та тангенс. Їх період однаковий і дорівнює 2π, тобто sin(x) = sin(x + 2π) = sin(x + 4π) тощо. Однак, зрозуміло, тригонометричні функції – не єдині періодичні.
Щодо простих, базових функцій єдиний спосіб встановити їх періодичність чи неперіодичність – обчислення. Для складних функцій вже є кілька простих правил.
Якщо F(x) - з періодом T, і для неї визначена похідна, то ця похідна f(x) = F′(x) - теж періодична функція з періодом T. у цій точці до осі абсцис, а оскільки первісна періодично повторюється, то має повторюватися і похідна. Наприклад, похідна від функції sin(x) дорівнює cos(x) і вона періодична. Беручи похідну cos(x), ви отримаєте –sin(x). Періодичність зберігається постійно.
Однак протилежне не завжди вірне. Так, функція f(x) = const періодична, та її первісна F(x) = const*x + C - немає.
Якщо F(x) - періодична функція з періодом T, то G(x) = a*F(kx + b), де a, b, і k - константи і k не дорівнює нулю - теж періодична функція, і її період дорівнює T/k. Наприклад sin(2x) - періодична функція, та її період дорівнює π. Наочно це можна уявити так: помножуючи x на якесь число, ви стискаєте графік функції по горизонталі саме в стільки разів
Якщо F1(x) і F2(x) - періодичні функції, та його періоди рівні T1 і T2 відповідно, то сума цих функцій також може бути періодичною. Однак її період не буде простою сумою періодів T1 та T2. Якщо результат розподілу T1/T2 - раціональне число, то сума функцій періодична, та її період дорівнює найменшому загальному кратному (НОК) періодів T1 і T2. Наприклад, якщо період першої функції дорівнює 12, а період другої - 15, то період їх суми дорівнюватиме НОК (12, 15) = 60.
Наочно це можна так: функції йдуть з різною «шириною кроку», але якщо відношення їх ширин раціонально, то рано чи пізно (а точніше, саме через НОК кроків), вони знову зрівняються, і їхня сума почне новий період.
Однак якщо співвідношення періодів ірраціональне, то сумарна функція не буде періодичною. Наприклад, нехай F1(x) = x mod 2 (залишок від поділу x на 2), а F2(x) = sin(x). T1 тут дорівнюватиме 2, а T2 дорівнює 2π. Співвідношення періодів дорівнює π - ірраціональному числу. Отже, функція sin(x) + x mod 2 не є періодичною.
Відеоурок «Періодичність функцій у = sin х, у = cos х» розкриває поняття періодичності функції, розглядає опис прикладів розв'язання задач, у яких використовується поняття періодичності функції. Цей відеоурок є наочним посібником для пояснення теми учням. Також цей посібник може стати самостійною частиною уроку, звільняючи вчителя для проведення індивідуальної роботи з учнями.
Наочність у поданні цієї теми дуже важлива. Щоб уявити поведінку функції, побудову графіка, її необхідно візуалізувати. Зробити побудови за допомогою класної дошки та крейди не завжди вдається так, щоб вони були зрозумілі всім учням. У відеоуроці є можливість при побудові виділяти частини малюнку кольором, робити перетворення за допомогою анімації. Таким чином, побудови стають більш зрозумілими для більшості учнів. Також можливості відеоуроку сприяють кращому запам'ятовування матеріалу.
Демонстрація починається з подання теми уроку, а також нагадування учням матеріалу, вивченого на минулих уроках. Зокрема, підсумовується перелік властивостей, виявлених у функціях у = sin х, і навіть у = cos х. Серед властивостей функцій, що розглядаються, відзначені область визначення, область значень, парність (непарність), інші особливості - обмеженість, монотонність, безперервність, точки найменшого (найбільшого) значення. Учням повідомляється, що на даному уроці вивчається ще одна властивість функції – періодичність.
Представлено визначення періодичної функції y=f(x), де xx, у якій виконується умова f(x-Т)= f(x)= f(x+Т) для деякого Т≠0. Інакше число Т називають період функції.
Для функцій синуса і косинуса, що розглядаються, виконання умови перевіряється, застосовуючи формули приведення. Очевидно, що вид тотожності sin(x-2π)=sinx=sin(x+2π) відповідає виду виразу визначального умова періодичності функції. Така ж рівність можна відзначити для косинуса cos (x-2π) = cos x = cos (x + 2π). Отже, ці тригонометричні функції є періодичними.
Далі наголошується, як властивість періодичності допомагає будувати графіки періодичних функцій. Розглядається функція у = sin x. На екрані будується координатна площина, де відзначені абсциси від -6π до 8π з кроком π. На поверхні будується частина графіка синуса, представлений однією хвилею на відрізку . На малюнку демонструється, як графік функції формується по всій області визначення зсувом побудованого фрагмента, і отримуючи довгу синусоїду.
Будується графік функції у = cos х, використовуючи властивість її періодичності. Для цього на малюнку будується координатна площина, де зображується фрагмент графіка. Зазначається, зазвичай такий фрагмент будується на відрізку [-π/2;3π/2]. Аналогічно графіку функції синуса, побудова графіка косинуса виконується зсувом фрагмента. В результаті побудови утворюється довга синусоїда.
Побудова графіка періодичної функції має особливості, які можна використовувати. Тому вони даються у узагальненому вигляді. Наголошується, що для побудови графіка такої функції спочатку будують гілка графіка на деякому проміжку довжиною Т. потім необхідно зрушити побудовану гілка вправо та вліво на Т, 2Т, 3Т і т.д. при цьому вказується ще на одну особливість періоду – для будь-якого цілого k≠0 число kТ також є періодом функції. Проте Т називається основним періодом, оскільки він найменших із усіх. Для тригонометричних функцій синуса та косинуса основним періодом є 2π. Однак також є періодами 4π, 6π тощо.
Далі пропонується розглянути знаходження основного періоду функції у = cos 5х. Рішення починається з припущенням, що Т – період функції. Отже, необхідне виконання умови f(x-Т)=f(x)=f(x+Т). У цьому тотожності f(x)= cos 5х, а f(x+Т)=cos 5(x+Т)= cos (5x+5Т). У цьому cos (5x+5Т)= cos 5х, отже 5Т=2πn. Тепер можна знайти Т = 2 / 5. Завдання вирішено.
У другому завданні необхідно знайти основний період функції y=sin(2x/7). Передбачається, що основний період функції Т. для цієї функції f(x)= sin(2x/7), а через період f(x+Т)=sin(2x/7)(х+Т)= sin(2x/7) + (2/7) Т). після приведення отримуємо (2/7)Т=2πn. Проте необхідно знайти основний період, тому беремо найменше значення (2/7)Т=2π, з якого знаходимо Т=7π. Завдання вирішено.
Наприкінці демонстрації результати прикладів узагальнюються, сформувавши правило визначення основного періоду функції. Зазначається, що з функцій у=sinkxи y=coskx основними періодами є 2π/k.
Відеоурок «Періодичність функцій у = sin х, у = cos х» може застосовуватися на традиційному уроці математики підвищення ефективності уроку. Також цей матеріал рекомендується використовувати вчителю, який здійснює дистанційне навчання для підвищення наочності пояснення. Відео може бути рекомендоване учню, що відстає, для поглиблення розуміння теми.
ТЕКСТОВЕ РОЗШИФРУВАННЯ:
"Періодичність функцій у = cos x, y = sin x".
Для побудови графіків функцій y = sin x та у = cos x були використані властивості функцій:
1 область визначення,
2 область значення,
3 парність або непарність,
4 монотонність,
5 обмеженість,
6 безперервність,
7 найбільше та найменше значення.
Сьогодні ми вивчимо ще одну властивість: періодичність функції.
ВИЗНАЧЕННЯ. Функцію у = f (x), де х ϵ Х(гравець дорівнює еф від ікс, де ікс належить множині ікс), називають періодичною, якщо існує відмінне від нуля число Т таке, що для будь-якого х із множини Х виконується подвійна рівність: f (x - Т) = f (x) = f (x + Т) (еф від ікс мінус те дорівнює еф від ікс і дорівнює еф від ікс плюс те). Число Т, яке задовольняє таку подвійну рівність, називають періодом функції
А так як синус і косинус визначені на всій числовій прямій і для будь-якого х виконуються рівності sin(x - 2π)= sin x= sin(x+ 2π) (синус від ікс мінус два пі дорівнює синусу ікс і дорівнює синусу від ікс плюс два пі ) та
cos (x - 2π) = cos x = cos (x + 2π) (косинус від ікс мінус два пі дорівнює косинус ікс і дорівнює косінус від ікс плюс два пі), то синус і косинус - це періодичні функції з періодом 2π.
Періодичність дозволяє швидко збудувати графік функції. Адже для того, щоб побудувати графік функції y = sin x досить побудувати одну хвилю (найчастіше на відрізку (від нуля до двох пі), а потім за допомогою зсуву побудованої частини графіка вздовж осі абсцис вправо і вліво на 2π, потім на 4π і так далі отримати синусоїду.
(показати зсув праворуч і ліворуч на 2π, 4π)
Аналогічно для графіка функції
у = cos x, тільки будуємо одну хвилю найчастіше на відрізку [; ] (від мінус пі на два до трьох пі на два).
Узагальнемо вище сказане і зробимо висновок: для побудови графіка періодичної функції з періодом Т спочатку потрібно побудувати гілка (або хвилю, або частину) графіка на будь-якому проміжку довжини Т (найчастіше це проміжок з кінцями в точках 0 і Т або - і (мінус е на два і те на два), а потім зрушити цю гілку вздовж осі х (ікс) вправо і вліво на Т, 2Т, 3Т і т.д.
Очевидно, що якщо функція періодична з періодом Т, то при будь-якому цілому k0(не рівному нулю) число виду kT(ка те) теж період цієї функції. Зазвичай намагаються виділити найменший позитивний період, який називають основним періодом.
Як період функцій у = cos x, y = sin x можна було б взяти - 4π, 4π, - 6π, 6π і т.д. (мінус чотири пі, чотири пі, мінус шість пі, шість пі і так далі). Але число 2 є основним періодом і тієї, і іншої функції.
Розглянемо приклади.
ПРИКЛАД 1. Знайти основний період функції у = сos5x (ігрок дорівнює косинус п'яти ікс).
Рішення. Нехай Т – основний період функції у = сos5x. Покладемо
f (x) = сos5x, тоді f (x + Т) = сos5(x + Т) = сos (5x + 5Т) (еф від ікс плюс те дорівнює косінусу п'яти, помноженого на суму ікса і те дорівнює косінусу від суми п'яти ікс та п'яти те).
сos (5x + 5Т) = сos5x. Звідси 5Т= 2πn (п'ять те дорівнює два пі ен), але за умовою потрібно знайти основний період, отже, 5Т= 2π. Отримуємо Т=
(Період цієї функції дорівнює два пі, поділене на п'ять).
Відповідь: Т =.
ПРИКЛАД 2. Знайти основний період функції у = sin (гравець дорівнює синус приватного двох ікс на сім).
Рішення. Нехай Т - основний період функції у = sin. Покладемо
f (x) = sin , тоді f (x + Т) = sin (x + Т) = sin (x + Т) (еф від ікс плюс те дорівнює синусу добутку двох сьомих і суми ікса і те дорівнює синусу від суми двох сьомих ікс та двох сьомих те).
Щоб число Т було періодом функції, має виконуватися тотожність
sin (x + Т) = sin. Звідси Т= 2πn (дві сьомі те дорівнює два пі ен), але за умовою потрібно знайти основний період, отже, Т= 2π. Отримуємо Т=7
(Період цієї функції дорівнює семи пі).
Відповідь: Т = 7.
Узагальнюючи результати, отримані в прикладах, можна зробити висновок: основний період функцій y = sin kx або у = cos kx (ігрок дорівнює синус ка ікс або гравець дорівнює косинус ка ікс) дорівнює (два пі, поділено на ка).
Мета: узагальнити та систематизувати знання учнів на тему “Періодичність функцій”; формувати навички застосування властивостей періодичної функції, знаходження найменшого позитивного періоду функції, побудови графіків періодичних функцій; сприяти підвищенню інтересу до вивчення математики; виховувати спостережливість, акуратність.
Обладнання: комп'ютер, мультимедійний проектор, картки із завданнями, слайди, годинники, таблиці орнаментів, елементи народного промислу
"Математика - це те, за допомогою чого люди керують природою і собою"
О.М. Колмогоров
Хід уроку
I. Організаційний етап.
Перевірка готовності учнів до уроку. Повідомлення теми та завдань уроку.
ІІ. Перевірка домашнього завдання.
Домашнє завдання перевіряємо за зразками, найскладніші моменти обговорюємо.
ІІІ. Узагальнення та систематизація знань.
1. Усна фронтальна робота.
Запитання теорії.
1) Сформуйте визначення періоду функції
2) Назвіть найменший позитивний період функцій y=sin(x), y=cos(x)
3). Назвіть найменший позитивний період функції y=tg(x), y=ctg(x)
4) Доведіть за допомогою кола вірність співвідношень:
y=sin(x) = sin(x+360º)
y=cos(x) = cos(x+360º)
y=tg(x) = tg(x+180º)
y=ctg(x) = ctg(x+180º)
tg(x+π n)=tgx, n € Z
ctg(x+π n)=ctgx, n € Z
sin(x+2π n)=sinx, n € Z
cos(x+2π n)=cosx, n € Z
5) Як побудувати графік періодичної функції?
Усні вправи.
1) Довести такі співвідношення
a) sin(740º ) = sin(20º )
b) cos(54º) = cos(-1026º)
c) sin(-1000º) = sin(80º )
2. Довести, що кут 540º є одним з періодів функції y=cos(2x)
3. Довести, що кут 360º є одним із періодів функції y=tg(x)
4. Дані вирази перетворити так, щоб кути, що входять до них, по абсолютній величині не перевищували 90º .
a) tg375º
b) ctg530º
c) sin1268º
d) cos(-7363º)
5. Де ви зустрічалися зі словами ПЕРІОД, ПЕРІОДІЧНІСТЬ?
Відповіді учнів: Період у музиці – побудова, у якому викладено більш менш завершена музична думка. Геологічний період – частина епохи і поділяється на епохи з періодом від 35 до 90 млн. років.
Період напіврозпаду радіоактивної речовини. Періодичний дріб. Періодична друк – друковані видання, що з'являються у певні терміни. Періодична система Менделєєва.
6. На малюнках зображено частини графіків періодичних функцій. Визначте період функції. Визначити період функції.
Відповідь: Т=2; Т=2; Т=4; Т = 8.
7. Де в житті ви зустрічалися з побудовою елементів, що повторюються?
Відповідь учнів: Елементи орнаментів, народна творчість.
IV. Колективне розв'язання задач.
(Розв'язання задач на слайдах.)
Розглянемо один із способів дослідження функції на періодичність.
При цьому способі обходяться труднощі, пов'язані з доказом того, що той чи інший період є найменшим, а також відпадає необхідність торкатися питань про арифметичні дії над періодичними функціями та про періодичність складної функції. Міркування спирається лише визначення періодичної функції і такий факт: якщо Т – період функції, те й nT(n?0) – її період.
Завдання 1. Знайдіть найменший позитивний період функції f(x)=1+3(x+q>5)
Рішення: Припустимо, що Т-період цієї функції. Тоді f(x+T)=f(x) всім x € D(f), тобто.
1+3(x+T+0,25)=1+3(x+0,25)
(x+T+0,25)=(x+0.25)
Покладемо x=-0,25 отримаємо
(T) = 0 T = n, n € Z
Ми отримали, що всі періоди цієї функції (якщо вони існують) знаходяться серед цілих чисел. Виберемо серед цих чисел найменше додатне число. Це 1 . Перевіримо, чи не буде воно і справді періодом 1 .
f(x+1) =3(x+1+0,25)+1
Оскільки (T+1)=(T) за будь-якого Т, то f(x+1)=3((x+0.25)+1)+1=3(x+0,25)+1=f(x ), тобто. 1 – період f. Оскільки 1 – найменше з усіх позитивних чисел, то T=1.
Завдання 2. Показати, що функція f(x)=cos 2 (x) періодична і визначити її основний період.
Завдання 3. Знайдіть основний період функції
f(x)=sin(1,5x)+5cos(0,75x)
Допустимо Т-період функції, тоді для будь-якого х справедливе співвідношення
sin1,5(x+T)+5cos0,75(x+T)=sin(1,5x)+5cos(0,75x)
Якщо х = 0, то
sin(1,5T)+5cos(0,75T)=sin0+5cos0
sin(1,5T)+5cos(0,75T)=5
Якщо х=-Т, то
sin0+5cos0=sin(-1,5Т)+5cos0,75(-Т)
5 = - sin (1,5 Т) + 5 cos (0,75 Т)
| sin(1,5Т)+5cos(0,75Т)=5 - sin (1,5 Т) + 5 cos (0,75 Т) = 5 |
Склавши, отримаємо:
10cos (0,75 Т) = 10
2π n, n € Z
Виберемо зі всіх “підозрілих” на період чисел найменше позитивне і перевіримо, чи воно періодом для f. Це число
f(x+)=sin(1,5x+4π )+5cos(0,75x+2π )= sin(1,5x)+5cos(0,75x)=f(x)
Отже – основний період функції f.
Завдання 4. Перевіримо, чи є періодичною функція f(x)=sin(x)
Нехай Т – період функції f. Тоді для будь-якого х
sin|x+Т|=sin|x|
Якщо х=0, то sin|Т|=sin0, sin|Т|=0 Т=π n, n € Z.
Припустимо. Що за деякого n число π n є періодом
розглянутої функції π n>0. Тоді sin|π n+x|=sin|x|
Звідси випливає, що n має бути одночасно і парним і непарним числом, а це неможливо. Тому ця функція не є періодичною.
Завдання 5. Перевірити, чи є періодичною функцією
f(x)= 
Нехай Т – період f, тоді
, Звідси sinT = 0, Т = π n, n € Z. Припустимо, що при деякому n число π n дійсно є періодом цієї функції. Тоді і число 2π n буде періодом
Оскільки чисельники рівні, то рівні та його знаменники, тому
Отже, функція f не періодична.
Робота у групах.
Завдання групи 1.
Завдання групи 2.
Перевірте, чи є функція f періодичною і знайдіть її основний період (якщо існує).
f(x)=cos(2x)+2sin(2x)
Завдання групи 3.
Після закінчення роботи гурту презентують свої рішення.
VI. Підбиття підсумків уроку.
Рефлексія.
Вчитель видає учням картки з малюнками і пропонує зафарбувати частину першого малюнка відповідно до того, в якому обсязі, як їм здається, вони оволоділи способами дослідження функції на періодичність, а в частині другого малюнка відповідно до свого внеску в роботу на уроці.
VII. Домашнє завдання
1). Перевірте, чи є функція f періодичною і знайдіть її основний період (якщо вона існує)
b). f(x)=x 2 -2x+4
c). f(x)=2tg(3x+5)
2). Функція y=f(x) має період Т=2 і f(x)=x 2 +2x при x [-2; 0]. Знайдіть значення виразу -2f(-3)-4f(3,5)
Література/
У липні 2020 року NASA запускає експедицію на Марс. Космічний апарат доставить на Марс електронний носій із іменами всіх зареєстрованих учасників експедиції.
Реєстрація учасників відкрита. Отримайте свій квиток на Марс за цим посиланням.
Якщо цей пост вирішив вашу проблему або просто сподобався вам, поділіться посиланням на нього зі своїми друзями у соціальних мережах.
Один з цих варіантів коду потрібно скопіювати і вставити в код вашої веб-сторінки, бажано між тегами або відразу після тега . За першим варіантом MathJax підвантажується швидше і менше гальмує сторінку. Натомість другий варіант автоматично відстежує та підвантажує свіжі версії MathJax. Якщо вставити перший код, його потрібно буде періодично оновлювати. Якщо вставити другий код, то сторінки завантажуватимуться повільніше, зате вам не потрібно буде постійно стежити за оновленнями MathJax.
Підключити MathJax найпростіше в Blogger або WordPress: в панелі керування сайтом додайте віджет, призначений для вставки стороннього коду JavaScript, скопіюйте в нього перший або другий варіант завантаженого коду, представленого вище, і розмістіть віджет ближче до початку шаблону (до речі, це зовсім не обов'язково , оскільки скрипт MathJax завантажується асинхронно). От і все. Тепер вивчіть синтаксис розмітки MathML, LaTeX та ASCIIMathML, і ви готові вставляти математичні формули на веб-сторінки свого сайту.
Черговий переддень Нового Року... морозна погода та сніжинки на шибці... Все це спонукало мене знову написати про... фрактали, і про те, що знає про це Вольфрам Альфа. Із цього приводу є цікава стаття, в якій є приклади двовимірних фрактальних структур. Тут же ми розглянемо складніші приклади тривимірних фракталів.
Фрактал можна наочно уявити (описати), як геометричну фігуру або тіло (маючи на увазі, що й те й інше є безліч, в даному випадку, безліч точок), деталі якої мають таку форму, як і сама вихідна фігура. Тобто це самоподібна структура, розглядаючи деталі якої при збільшенні, ми бачитимемо ту саму форму, що і без збільшення. Тоді як у випадку звичайної геометричної фігури (не фрактала), при збільшенні ми побачимо деталі, які мають простішу форму, ніж вихідна фігура. Наприклад, при досить великому збільшенні частина еліпса виглядає як відрізок прямий. З фракталами такого не відбувається: за будь-якого їх збільшення ми знову побачимо ту ж саму складну форму, яка з кожним збільшенням повторюватиметься знову і знову.
Бенуа Мандельброт (Benoit Mandelbrot), основоположник науки про фрактал, у своїй статті Фрактали і мистецтво в ім'я науки написав: "Фрактали - це геометричні форми, які однаково складні у своїх деталях, як і у своїй загальній формі. Тобто якщо частина фракталу буде збільшена до розміру цілого, вона виглядатиме, як ціле, або точно, або, можливо, з невеликою деформацією".
Тригонометричні функції періодичні, тобто повторюються через певний період. Внаслідок цього досить вивчати функцію на цьому інтервалі і поширити виявлені властивості на всі інші періоди.
Інструкція1. Якщо вам дано примітивний вираз, в якому присутня лише одна тригонометрична функція (sin, cos, tg, ctg, sec, cosec), причому кут всередині функції не помножений на якесь число, а вона сама не зведена в якусь кількість ступінь – скористайтеся визначенням. Для виразів, що містять sin, cos, sec, cosec відважно ставте період 2П, а якщо в рівнянні є tg, ctg – то П. Скажімо, для функції у=2 sinх+5 період дорівнюватиме 2П.
2. Якщо кут х під знаком тригонометричної функції помножений на якесь число, то, щоб виявити період цієї функції, поділіть типовий період на це число. Скажімо, вам дана функція = sin 5х. Типовий період для синуса - 2П, поділивши його на 5, ви отримаєте 2П/5 - це і є бажаний період цього виразу.
3. Щоб виявити період тригонометричної функції, зведеної на ступінь, оцініть парність ступеня. Для парної міри зменшіть типовий період удвічі. Скажімо, якщо вам дана функція у = 3 cos ^ 2х, то типовий період 2П зменшиться в 2 рази, таким чином, період дорівнюватиме П. Зверніть увагу, функції tg, ctg у всякій мірі періодичні П.
4. Якщо вам дано рівняння, що містить твір або приватне 2-х тригонометричних функцій, спочатку виявіть період для всієї їх окремо. Після цього виявіть мінімальне число, яке вміщало б у собі ціле число обох періодів. Скажімо, дана функція у = tgx * cos5x. Для тангенса період П, косинуса 5х – період 2П/5. Мінімальне число, в яке можна вмістити обидва ці періоди, це 2П, отже, бажаний період – 2П.
5. Якщо ви не можете робити запропонованим чином або сумніваєтеся в результаті, спробуйте робити за визначенням. Візьміть як період функції Т, він більший за нуль. Підставте в рівняння замість х вираз (х+Т) і розв'яжіть отриману рівність, якби Т було параметром чи числом. У результаті ви знайдете значення тригонометричної функції і зможете підібрати мінімальний період. Скажімо, у результаті полегшення вийшло тотожність sin (Т/2)=0. Мінімальне значення Т, у якому воно виконується, дорівнює 2П, і буде результат завдання.
Періодичною функцією називається функція, що повторює свої значення через якийсь ненульовий період. Періодом функції називається число, при додаванні якого до аргументу функції значення функції не змінюється.
Вам знадобиться
- Знання з елементарної математики та початків огляду.
1. Позначимо період функції f(x) через число К. Наше завдання виявити це значення К. Для цього уявімо, що функція f(x), користуючись визначенням періодичної функції, дорівнює f(x+K)=f(x).
2. Вирішуємо отримане рівняння щодо невідомої K, так як немов x - константа. Залежно від значення До вийде кілька варіантів.
3. Якщо K>0 – то це і є період вашої функції. Якщо K=0 – то функція f(x) не є періодичною. не рівному нулю, то така функція називається аперіодичною і в неї теж немає періоду.
Відео на тему
Зверніть увагу!
Усі тригонометричні функції є періодичними, проте поліноміальні зі ступенем більше 2 – апериодическими.
Корисна порада
Періодом функції, що складається з 2-х періодичних функцій, є найменше загальне кратне періодів цих функцій.
Тригонометричні рівняння – це рівняння, які містять у собі тригонометричні функції невідомого аргументу (наприклад: 5sinx-3cosx =7). Щоб навчитися вирішувати їх, необхідно знати деякі для цього способи.
1. Рішення таких рівняння складається з 2-х етапів. Перше – реформування рівняння для набуття його найпростішого виду. Найпростішими тригонометричними рівняннями називаються такі: Sinx = a; Cosx=a і т.д.
2. Друге – це рішення одержаного найпростішого тригонометричного рівняння. Існує основні способи вирішення рівнянь такого виду: Рішення методом алгебри. Цей спосіб класно відомий зі школи, з курсу алгебри. Інакше називають способом заміни змінної та підстановки. Застосовуючи формули приведення, перетворюємо, робимо заміну, після чого знаходимо коріння.
3. Розкладання рівняння на множники. Спочатку переносимо всі члени ліворуч і розкладаємо на множники.
4. Приведення рівняння до однорідного. Однорідними рівняннями називають рівняння, якщо всі члени одного і того ж ступеня і синус, косинус одного і того ж кута. Щоб його вирішити, слід: спочатку перенести всі його члени з правої частини до лівої частини; перенести всі загальні множники за дужки; прирівняти множники та дужки нулю; прирівняні дужки дають однорідне рівняння меншою мірою, що слід розділити на cos (або sin) старшого ступеня; вирішити отримане рівняння алгебри щодо tan.
5. Подальший спосіб – перехід до половинного кута. Скажімо, розв'язати рівняння: 3 sin x – 5 cos x = 7. Переходимо до половинного кута: 6 sin (x / 2) · cos (x / 2) – 5 cos ? (x / 2) + 5 sin? (x / 2) = 7 sin? (x / 2) + 7 cos? (x/ 2) , після чого всі члени зводимо в одну частину (відмінніше в праву) і розв'язуємо рівняння.
6. Вступ допоміжного кута. Коли ми замінюємо ціле значення cos(а) чи sin(а). Знак "а" - допоміжний кут.
7. Спосіб реформування твору на суму. Тут слід застосовувати відповідні формули. Скажімо дано: 2 sin x · sin 3x = cos 4x. Розв'яжемо її, перетворивши ліву частину в суму, тобто: cos 4x - cos 8x = cos 4x, cos 8x = 0,8 x = p / 2 + pk, x = p /16 + pk/8.
8. Кінцевий спосіб, званий багатофункціональною підстановкою. Ми перетворюємо вираз і робимо заміну, скажімо Cos(x/2)=u, потім вирішуємо рівняння з параметром u. При придбанні результату переводимо значення у зворотне.
Відео на тему
Якщо розглядати точки на колі, то точки x, x+2π, x+4π тощо. збігаються один з одним. Таким чином, тригонометричні функції на прямій періодично повторюють своє значення. Якщо знаменитий період функції , можна звести функцію у цьому періоді і повторити в інших.
1. Період – це число T, що f(x) = f(x+T). Щоб виявити період, вирішують відповідне рівняння, підставляючи як аргумент x і x+T. При цьому користуються вже відомими періодами для функцій. Для функцій синуса та косинуса період становить 2π, а для тангенсу та котангенсу – π.
2. Нехай дана функція f(x) = sin^2(10x). Розгляньте вираз sin^2(10x) = sin^2(10(x+T)). Скористайтеся формулою зниження ступеня: sin^2(x) = (1 – cos 2x)/2. Тоді отримаєте 1 – cos 20x = 1 – cos 20(x+T) чи cos 20x = cos (20x+20T). Знаючи, що період косинуса дорівнює 2?, 20T = 2?. Отже, T = π/10. Т - мінімальний правильний період, а функція повторюватиметься і через 2Т, і через 3Т, і в інший бік по осі: -T, -2T і т.д.
Корисна порада
Користуйтеся формулами зниження функцій. Якщо вам вже відомі періоди будь-яких функцій, спробуйте звести існуючу функцію до вестимим.
Пошук функції на парність і непарність допомагає будувати графік функції і осягати характер її поведінки. Для цього дослідження необхідно порівняти цю функцію, записану для аргументу "х" і для аргументу "-х".
1. Запишіть функцію, пошук якої потрібно провести, як y=y(x).
2. Замініть доказ функції на “-х”. Підставте цей аргумент у функціональний вираз.
3. Спростіть вираз.
4. Таким чином, ви отримали ту саму функцію, записану для доказів “х” та “-х”. Подивіться на ці дві записи.Якщо y(-x)=y(x), то це парна функція.Якщо y(-x)=-y(x), то це непарна функція.Якщо ж про функцію неможливо сказати, що y (-x) = y (x) або y (-x) = - y (x), то за якістю парності це функція загального вигляду. Тобто вона не є ні парною, ні непарною.
5. Запишіть зроблені вами результати. Тепер ви можете їх використовувати в побудові графіка функції або в майбутньому аналітичному дослідженні якостей функції.
6. Говорити про парності і непарності функції можна також у тому разі, коли вже заданий графік функції. Скажімо, графік послужив підсумком фізичного експерименту. Якщо графік функції симетричний щодо осі ординат, то y (x) - парна функція. Якщо графік функції симетричний щодо осі абсцис, то x (y) - парна функція. x(y) – функція, зворотна функції y(x). Якщо графік функції симетричний щодо початку координат (0,0), то y(x) – непарна функція. Непарною буде також обернена функція x(y).
7. Значно пам'ятати, що уявлення про парність і непарність функції має прямий зв'язок із областю визначення функції. Якщо, скажімо, парна чи непарна функція немає при х=5, вона немає і за х=-5, чого неможливо сказати про функцію загального виду. Під час встановлення парності та непарності звертайте увагу на область визначення функції.
8. Пошук функції на парність і непарність корелює зі знаходженням безлічі значень функції. Для знаходження безлічі значень парної функції досить розглянути половину функції, правіше чи лівіше нуля. Якщо при x>0 парна функція y(x) набуває значення від А до В, то ті ж значення вона прийматиме і при x0 непарна функція y(x) набуває діапазону значень від А до В, то при x sin^2 ? + cos^2? = 1.Третє і четверте тотожності отримує шляхом розподілу, відповідно, на b^2 і a^2:a^2/b^2 + 1 = c^2/b^2 => tg^2? + 1 = 1/cos^2 ?;1 + b^2/a^2 = c^2/a^2 => 1 + 1/tg^2 ? = 1/sin^? або 1 + ctg^2? = 1/sin^2 ?.П'яте і шосте основні тотожності доводяться через визначення суми гострих кутів прямокутного трикутника, яка дорівнює 90° або?/2. або добутку функцій, а також формули тригонометричної підстановки, а саме виразу основних тригонометричних функцій через tg половинного кута: sin? = (2 * tg? / 2) / (1 + tg ^ 2? / 2); cos? = (1 - tg ^ 2 ? / 2) / (1 = tg ^ 2 ? / 2); tg ? = (2 * tg? / 2) / (1 - tg ^ 2? / 2).
Необхідність виявити мінімальне значення математичної функції є фактичний інтерес у вирішенні прикладних завдань, скажімо, в економіці. Велике значення для підприємницької діяльності має мінімізація збитків.
1. Щоб виявити мінімальне значення функції , необхідно визначити, за якого значення доводу x0 виконуватиметься нерівність y(x0) ? y(x), де x? x0. Як правило, це завдання вирішується на певному проміжку або в кожній області значень функції , якщо така не задана. Одним із аспектів рішення є знаходження нерухомих точок.
2. Стаціонарною точкою називається значення аргументу, у якому похідна функції перетворюється на нуль. Відповідно до теореми Ферма, якщо функція, що диференціюється, набуває екстремального значення в деякій точці (в даному випадку – локальний мінімум), то ця точка є стаціонарною.
3. Мінімальне значення функція часто набуває саме у цій точці, проте її можна визначити не незмінно. Більше того, не завжди можна з точністю сказати, чому дорівнює мінімум функції або він приймає дуже мале значення. Тоді, як водиться, знаходять межу, до якої вона тяжіє при спаданні.
4. Щоб визначити мінімальне значення функції , необхідно виконати послідовність процесів, що з чотирьох етапів: знаходження області визначення функції , придбання нерухомих точок, огляд значень функції у цих точках і кінцях проміжку, виявлення мінімуму.
5. Виходить, нехай задана деяка функція y(x) на проміжку з межами в точках А та В. Виявіть область її визначення та дізнаєтеся, чи є проміжок її підмножиною.
6. Обчисліть похідну функції. Прирівняйте отриманий вираз нулю та виявіть коріння рівняння. Перевірте, чи ці стаціонарні точки потрапляють у проміжок. Якщо ні, то на подальшому етапі вони не враховуються.
7. Розгляньте проміжок щодо типу кордонів: відкриті, закриті, складові чи безмірні. Від цього залежить, як ви шукатимете мінімальне значення . Скажімо, відрізок [А, У] є закритим проміжком. Підставте їх у функцію та розрахуйте значення. Те саме проробіть зі стаціонарною точкою. Виберіть найменший результат.
8. З відкритими і безмірними проміжками справа дещо складніша. Тут доведеться шукати односторонні межі, які незмінно дають однозначний результат. Скажімо, для проміжку з однією закритою та однією виколотою кордоном [А, В) слід виявити функцію при х = А та односторонню межу lim y при х? В-0.
Штучна гравітація перестає бути фантастикою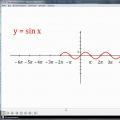
Періодичність функцій у = sin х, у = cos х - Гіпермаркет знань
Зведення ДНР та ЛНР: Потужні бої під Горлівкою, Обстріли Донецька з артилерії, бойові зіткнення по всій лінії фронту