Vòng tròn. Định lý cơ bản
Chúng ta hãy nhớ lại các trường hợp về vị trí tương đối của đường thẳng và đường tròn.
Cho đường tròn tâm O bán kính R. Đường thẳng P, khoảng cách từ tâm đến đường thẳng, tức là vuông góc với OM, bằng d.
Trường hợp 1- khoảng cách từ tâm đường tròn đến đường thẳng nhỏ hơn bán kính đường tròn:
Ta đã chứng minh trong trường hợp khoảng cách d nhỏ hơn bán kính đường tròn r thì đường thẳng và đường tròn chỉ có hai điểm chung (Hình 1).
Cơm. 1. Minh họa cho trường hợp 1
Trường hợp hai- khoảng cách từ tâm đường tròn đến đường thẳng bằng bán kính đường tròn:
Chúng tôi đã chứng minh rằng trong trường hợp này chỉ có một điểm chung (Hình 2).

Cơm. 2. Minh họa cho trường hợp 2
Trường hợp 3- khoảng cách từ tâm đường tròn đến đường thẳng lớn hơn bán kính đường tròn:
Chúng ta đã chứng minh rằng trong trường hợp này đường tròn và đường thẳng không có điểm chung (Hình 3).

Cơm. 3. Minh họa cho trường hợp 3
Trong bài học này chúng ta quan tâm đến trường hợp thứ hai, khi một đường thẳng và một đường tròn có một điểm chung.
Sự định nghĩa:
Đường thẳng có một điểm chung duy nhất với đường tròn gọi là tiếp tuyến của đường tròn; điểm chung gọi là điểm tiếp tuyến của đường thẳng và đường tròn.
Đường thẳng p là tiếp tuyến, điểm A là điểm tiếp tuyến (Hình 4).

Cơm. 4. Tiếp tuyến
Định lý:
Tiếp tuyến của đường tròn vuông góc với bán kính vẽ đến điểm tiếp xúc (Hình 5).

Cơm. 5. Minh họa định lý
Bằng chứng:
Ngược lại, cho OA không vuông góc với đường thẳng r. Trong trường hợp này, chúng ta hạ đường vuông góc từ điểm O xuống đường thẳng p, đó sẽ là khoảng cách từ tâm đường tròn đến đường thẳng:
Từ một tam giác vuông ta có thể nói cạnh huyền OH nhỏ hơn cạnh OA, nghĩa là đường thẳng và đường tròn có hai điểm chung, đường thẳng p là cát tuyến. Như vậy, ta thu được điều mâu thuẫn, nghĩa là định lý đã được chứng minh.

Cơm. 6. Minh họa định lý
Định lý ngược lại cũng đúng.
Định lý:
Nếu một đường thẳng đi qua điểm cuối của bán kính nằm trên một đường tròn và vuông góc với bán kính này thì đó là tiếp tuyến.
Bằng chứng:
Vì đường thẳng vuông góc với bán kính nên khoảng cách OA là khoảng cách từ đường thẳng đến tâm đường tròn và nó bằng bán kính: . Nghĩa là, và trong trường hợp này, như chúng tôi đã chứng minh trước đây, đường thẳng và đường tròn có điểm chung duy nhất - điểm A, do đó đường thẳng p tiếp xúc với đường tròn theo định nghĩa (Hình 7).

Cơm. 7. Minh họa định lý
Các định lý trực tiếp và nghịch đảo có thể được kết hợp như sau (Hình 8):
Cho đường tròn tâm O, đường thẳng p, bán kính OA

Cơm. 8. Minh họa định lý
Định lý:
Một đường thẳng tiếp tuyến với một đường tròn khi và chỉ khi bán kính vẽ tại điểm tiếp tuyến vuông góc với nó.
Định lý này có nghĩa là nếu một đường thẳng là tiếp tuyến thì bán kính vẽ tới điểm tiếp tuyến sẽ vuông góc với nó và ngược lại, từ đường vuông góc của OA và p suy ra p là tiếp tuyến, tức là đường thẳng và đường tròn có một điểm chung.
Xét hai tiếp tuyến từ một điểm đến một đường tròn.
Định lý:
Các đoạn tiếp tuyến của đường tròn vẽ từ một điểm thì bằng nhau và tạo thành các góc bằng nhau với đường thẳng đi qua điểm này và tâm của đường tròn.
Cho đường tròn tâm O, điểm A nằm ngoài đường tròn. Hai tiếp tuyến được vẽ từ điểm A, các điểm B và C là các điểm tiếp tuyến. Bạn cần chứng minh rằng góc 3 và 4 bằng nhau.

Cơm. 9. Minh họa định lý
Bằng chứng:
Chứng minh dựa trên sự đẳng thức của các tam giác ![]() . Hãy giải thích sự bằng nhau của các hình tam giác. Chúng có dạng hình chữ nhật vì bán kính vẽ tới điểm tiếp xúc vuông góc với tiếp tuyến. Điều này có nghĩa là các góc đều vuông và bằng nhau. Hai chân OB và OS bằng nhau vì chúng là bán kính của đường tròn. Cạnh huyền AO có tính tổng quát.
. Hãy giải thích sự bằng nhau của các hình tam giác. Chúng có dạng hình chữ nhật vì bán kính vẽ tới điểm tiếp xúc vuông góc với tiếp tuyến. Điều này có nghĩa là các góc đều vuông và bằng nhau. Hai chân OB và OS bằng nhau vì chúng là bán kính của đường tròn. Cạnh huyền AO có tính tổng quát.
Như vậy, các hình tam giác đều bằng nhau về độ bằng nhau của cạnh huyền và cạnh huyền. Từ đây rõ ràng hai chân AB và AC cũng bằng nhau. Ngoài ra, các góc đối diện với các cạnh bằng nhau thì bằng nhau, có nghĩa là các góc và , bằng nhau.
Định lý đã được chứng minh.
Như vậy, chúng ta đã làm quen với khái niệm tiếp tuyến của một đường tròn; trong bài học tiếp theo chúng ta sẽ xét độ đo của cung tròn.
Thư mục
- Alexandrov A.D. v.v. Hình học lớp 8. - M.: Giáo dục, 2006.
- Butuzov V.F., Kadomtsev S.B., Prasolov V.V. Hình học 8. - M.: Giáo dục, 2011.
- Merzlyak A.G., Polonsky V.B., Yakir S.M. Hình học lớp 8. - M.: VENTANA-GRAF, 2009.
- Đại học.omsk.su ().
- Oldskola1.narod.ru ().
- School6.aviel.ru ().
Bài tập về nhà
- Atanasyan L.S., Butuzov V.F., Kadomtsev S.B. và cộng sự, Hình học 7-9, Số 634-637, tr. 168.
Bài viết giải thích chi tiết các định nghĩa, ý nghĩa hình học của đạo hàm bằng ký hiệu đồ họa. Phương trình của đường tiếp tuyến sẽ được xem xét bằng các ví dụ, phương trình của đường tiếp tuyến với đường cong bậc 2 sẽ được tìm thấy.
Định nghĩa 1Góc nghiêng của đường thẳng y = k x + b gọi là góc α, được đo từ chiều dương của trục x đến đường thẳng y = k x + b theo chiều dương.
Trong hình, hướng x được biểu thị bằng mũi tên màu xanh lá cây và vòng cung màu xanh lá cây, và góc nghiêng được biểu thị bằng vòng cung màu đỏ. Đường màu xanh tượng trưng cho đường thẳng.
Định nghĩa 2
Độ dốc của đường thẳng y = k x + b gọi là hệ số k.
Hệ số góc bằng tiếp tuyến của đường thẳng, nói cách khác k = t g α.
- Góc nghiêng của một đường thẳng chỉ bằng 0 nếu nó song song với x và hệ số góc bằng 0, vì tiếp tuyến của 0 bằng 0. Điều này có nghĩa là dạng của phương trình sẽ là y = b.
- Nếu góc nghiêng của đường thẳng y = k x + b nhọn thì thỏa mãn điều kiện 0< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0 và có sự gia tăng trong biểu đồ.
- Nếu α = π 2 thì vị trí của đường thẳng vuông góc với x. Đẳng thức được xác định bởi x = c với giá trị c là số thực.
- Nếu góc nghiêng của đường thẳng y = k x + b tù thì ứng với điều kiện π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.
Cát tuyến là đường thẳng đi qua 2 điểm của hàm f(x). Nói cách khác, cát tuyến là một đường thẳng đi qua hai điểm bất kỳ trên đồ thị của hàm số đã cho.

Trên hình vẽ cho thấy A B là cát tuyến, f(x) là đường cong màu đen, α là cung màu đỏ biểu thị góc nghiêng của cát tuyến.
Khi hệ số góc của một đường thẳng bằng tiếp tuyến của góc nghiêng thì rõ ràng có thể tìm được tiếp tuyến của tam giác vuông A B C bằng tỉ số giữa cạnh đối diện và cạnh kề.
Định nghĩa 4
Ta có công thức tìm cát tuyến có dạng:
k = t g α = B C A C = f(x B) - f x A x B - x A, trong đó hoành độ của các điểm A và B lần lượt là các giá trị x A, x B, f(x A), f (x B) là các hàm giá trị tại các điểm này.
Rõ ràng hệ số góc của cát tuyến được xác định bằng đẳng thức k = f(x B) - f(x A) x B - x A hoặc k = f(x A) - f(x B) x A - x B , và phương trình phải được viết là y = f(x B) - f(x A) x B - x A x - x A + f (x A) hoặc
y = f(x A) - f(x B) x A - x B x - x B + f(x B) .
Đường cát tuyến chia đồ thị một cách trực quan thành 3 phần: bên trái điểm A, từ A đến B, bên phải B. Hình dưới đây cho thấy có ba đường cắt được coi là trùng nhau, tức là chúng được đặt bằng một phương trình tương tự.

Theo định nghĩa, rõ ràng đường thẳng và cát tuyến của nó trong trường hợp này trùng nhau.
Một cát tuyến có thể cắt đồ thị của một hàm đã cho nhiều lần. Nếu có phương trình dạng y = 0 đối với cát tuyến thì số giao điểm với đường sin là vô hạn.
Định nghĩa 5
Tiếp tuyến với đồ thị hàm số f(x) tại điểm x 0 ; f(x 0) là đường thẳng đi qua điểm x 0 cho trước; f(x 0), với sự có mặt của một đoạn có nhiều giá trị x gần với x 0.
ví dụ 1
Chúng ta hãy xem xét kỹ hơn ví dụ dưới đây. Khi đó rõ ràng đường thẳng xác định bởi hàm y = x + 1 được coi là tiếp tuyến với y = 2 x tại điểm có tọa độ (1; 2). Để rõ ràng, cần xét các đồ thị có giá trị gần (1; 2). Hàm y = 2 x được hiển thị bằng màu đen, đường màu xanh là đường tiếp tuyến và dấu chấm màu đỏ là điểm giao nhau.

Hiển nhiên, y = 2 x hợp nhất với đường thẳng y = x + 1.
Để xác định tiếp tuyến, chúng ta nên xem xét hành vi của tiếp tuyến A B khi điểm B tiến đến điểm A một cách vô hạn. Để rõ ràng, chúng ta trình bày một hình vẽ.

Đường cát tuyến A B, được biểu thị bằng đường màu xanh lam, hướng về vị trí của tiếp tuyến và góc nghiêng của đường cát tuyến α sẽ bắt đầu hướng về góc nghiêng của chính tiếp tuyến α x.
Định nghĩa 6
Tiếp tuyến của đồ thị hàm số y = f(x) tại điểm A được coi là vị trí giới hạn của cát tuyến A B khi B tiến về A, tức là B → A.
Bây giờ chúng ta chuyển sang xem xét ý nghĩa hình học của đạo hàm của hàm số tại một điểm.
Chúng ta hãy chuyển sang xét cát tuyến A B của hàm f (x), trong đó A và B có tọa độ x 0, f (x 0) và x 0 + ∆ x, f (x 0 + ∆ x), và ∆ x là được biểu thị là sự gia tăng của đối số. Bây giờ hàm sẽ có dạng ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . Để rõ ràng, hãy đưa ra một ví dụ về một bản vẽ.

Xét tam giác vuông A B C. Ta sử dụng định nghĩa tiếp tuyến để giải, tức là ta thu được hệ thức ∆ y ∆ x = t g α . Từ định nghĩa tiếp tuyến, ta suy ra lim ∆ x → 0 ∆ y ∆ x = t g α x . Theo quy tắc đạo hàm tại một điểm, ta có đạo hàm f(x) tại điểm x 0 được gọi là giới hạn của tỷ số giữa gia số của hàm số và gia số của đối số, trong đó ∆ x → 0 , thì chúng ta ký hiệu nó là f (x 0) = lim ∆ x → 0 ∆ y ∆ x .
Suy ra f " (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, trong đó k x được ký hiệu là hệ số góc của tiếp tuyến.
Nghĩa là, ta thấy f '(x) có thể tồn tại tại điểm x 0, và giống như tiếp tuyến của một đồ thị đã cho của hàm số tại điểm tiếp tuyến bằng x 0, f 0 (x 0), trong đó giá trị của hệ số góc của tiếp tuyến tại điểm bằng đạo hàm tại điểm x 0 . Sau đó, chúng ta nhận được k x = f " (x 0) .
Ý nghĩa hình học của đạo hàm của hàm số tại một điểm là nó đưa ra khái niệm về sự tồn tại của một tiếp tuyến với đồ thị tại cùng một điểm.
Để viết phương trình của một đường thẳng bất kỳ trên mặt phẳng cần có hệ số góc ứng với điểm mà nó đi qua. Ký hiệu của nó được lấy là x 0 tại giao điểm.
Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm x 0, f 0 (x 0) có dạng y = f"(x 0) x - x 0 + f(x 0).
Điều này có nghĩa là giá trị cuối cùng của đạo hàm f "(x 0) có thể xác định vị trí của tiếp tuyến, nghĩa là theo chiều dọc, với điều kiện lim x → x 0 + 0 f "(x) = ∞ và lim x → x 0 - 0 f "(x ) = ∞ hoặc hoàn toàn vắng mặt trong điều kiện lim x → x 0 + 0 f " (x) ≠ lim x → x 0 - 0 f " (x) .
Vị trí của tiếp tuyến phụ thuộc vào giá trị hệ số góc k x = f"(x 0). Khi song song với trục o x, ta thu được k k = 0, khi song song với o y - k x = ∞ và có dạng phương trình tiếp tuyến x = x 0 tăng khi k x > 0, giảm khi k x< 0 .
Ví dụ 2
Lập phương trình tiếp tuyến của đồ thị hàm số y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 tại điểm có tọa độ (1; 3) và xác định góc nghiêng.
Giải pháp
Theo điều kiện, ta có hàm được xác định cho mọi số thực. Ta thấy điểm có tọa độ xác định theo điều kiện (1; 3) là điểm tiếp tuyến thì x 0 = - 1, f(x 0) = - 3.
Cần tìm đạo hàm tại điểm có giá trị -1. Chúng tôi hiểu điều đó
y " = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = e x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = e x + 1 + x 2 - 6 - 3 3 y " (x 0) = y " (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3
Giá trị của f'(x) tại điểm tiếp tuyến là hệ số góc của tiếp tuyến, bằng tiếp tuyến của hệ số góc.
Khi đó k x = t g α x = y " (x 0) = 3 3
Suy ra rằng α x = a r c t g 3 3 = π 6
Trả lời: phương trình tiếp tuyến có dạng
y = f " (x 0) x - x 0 + f (x 0) y = 3 3 (x + 1) - 3 y = 3 3 x - 9 - 3 3
Để rõ ràng, chúng tôi đưa ra một ví dụ bằng hình ảnh minh họa.
Màu đen được sử dụng cho đồ thị của hàm số ban đầu, màu xanh lam là hình ảnh của tiếp tuyến và chấm màu đỏ là điểm tiếp tuyến. Hình bên phải hiển thị chế độ xem phóng to.

Ví dụ 3
Xác định sự tồn tại tiếp tuyến của đồ thị của hàm số đã cho
y = 3 · x - 1 5 + 1 tại điểm có tọa độ (1 ; 1) . Viết phương trình và xác định góc nghiêng.
Giải pháp
Theo điều kiện, ta có miền định nghĩa của hàm số cho trước được coi là tập hợp tất cả các số thực.
Hãy chuyển sang tìm đạo hàm
y " = 3 x - 1 5 + 1 " = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5
Nếu x 0 = 1 thì f'(x) không xác định, nhưng các giới hạn được viết dưới dạng lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 · 1 + 0 = + ∞ và lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , có nghĩa là tồn tại tiếp tuyến dọc tại điểm (1; 1).
Trả lời: phương trình sẽ có dạng x = 1, trong đó góc nghiêng sẽ bằng π 2.
Để rõ ràng, hãy mô tả nó bằng đồ họa.

Ví dụ 4
Tìm các điểm trên đồ thị của hàm số y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2, trong đó
- Không có tiếp tuyến;
- Tiếp tuyến song song với x;
- Tiếp tuyến song song với đường thẳng y = 8 5 x + 4.
Giải pháp
Cần phải chú ý đến phạm vi định nghĩa. Theo điều kiện, ta có hàm số được xác định trên tập hợp tất cả các số thực. Chúng tôi mở rộng mô-đun và giải hệ thống với các khoảng x ∈ - ∞ ; 2 và [ - 2 ; + ∞) . Chúng tôi hiểu điều đó
y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; + ∞)
Cần phân biệt chức năng. Chúng tôi có cái đó
y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12", x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; + ∞)
Khi x = − 2 thì đạo hàm không tồn tại vì giới hạn một phía không bằng tại điểm đó:
lim x → - 2 - 0 y " (x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y " (x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3
Chúng ta tính giá trị của hàm tại điểm x = - 2, nơi chúng ta nhận được giá trị đó
- y (- 2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2, tức là tiếp tuyến tại điểm ( - 2; - 2) sẽ không tồn tại.
- Tiếp tuyến song song với x khi hệ số góc bằng 0. Khi đó k x = t g α x = f "(x 0). Tức là cần tìm các giá trị của x đó khi đạo hàm của hàm biến nó về 0. Tức là các giá trị của f' (x) sẽ là các điểm tiếp tuyến, trong đó tiếp tuyến song song với x.
Khi x ∈ - ∞ ; - 2, khi đó - 1 5 (x 2 + 12 x + 35) = 0, và với x ∈ (- 2; + ∞) ta được 1 5 (x 2 - 4 x + 3) = 0.
1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞
Tính các giá trị hàm tương ứng
y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3
Do đó - 5; 8 5, - 4; 4 3, 1; 8 5, 3; 4 3 được coi là các điểm cần thiết của đồ thị hàm số.
Chúng ta hãy nhìn vào một biểu diễn đồ họa của giải pháp.

Đường màu đen là đồ thị của hàm số, các chấm màu đỏ là các điểm tiếp tuyến.
- Khi các đường thẳng song song thì các hệ số góc bằng nhau. Khi đó cần tìm kiếm các điểm trên đồ thị hàm số có độ dốc bằng giá trị 8 5. Để làm điều này, bạn cần giải phương trình dạng y "(x) = 8 5. Khi đó, nếu x ∈ - ∞; - 2, ta thu được - 1 5 (x 2 + 12 x + 35) = 8 5, và nếu x ∈ ( - 2 ; + ∞), thì 1 5 (x 2 - 4 x + 3) = 8 5.
Phương trình đầu tiên không có nghiệm vì biệt số nhỏ hơn 0. Hãy viết ra điều đó
1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0
Một phương trình khác có hai nghiệm thực thì
1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞
Hãy chuyển sang tìm các giá trị của hàm. Chúng tôi hiểu điều đó
y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3
Điểm có giá trị - 1; 4 15, 5; 8 3 là những điểm tại đó các tiếp tuyến song song với đường thẳng y = 8 5 x + 4.
Trả lời:đường màu đen – đồ thị của hàm số, đường màu đỏ – đồ thị của y = 8 5 x + 4, đường màu xanh – tiếp tuyến tại các điểm - 1; 4 15, 5; 8 3.

Có thể có vô số tiếp tuyến cho các hàm đã cho.
Ví dụ 5
Viết phương trình tất cả các tiếp tuyến sẵn có của hàm số y = 3 cos 3 2 x - π 4 - 1 3, vuông góc với đường thẳng y = - 2 x + 1 2.
Giải pháp
Để lập phương trình tiếp tuyến cần tìm hệ số và tọa độ của điểm tiếp tuyến dựa vào điều kiện vuông góc của các đường thẳng. Định nghĩa như sau: tích các hệ số góc vuông góc với đường thẳng bằng - 1, tức là viết là k x · k ⊥ = - 1. Từ điều kiện ta có hệ số góc nằm vuông góc với đường thẳng và bằng k ⊥ = - 2 thì k x = - 1 k ⊥ = - 1 - 2 = 1 2.
Bây giờ bạn cần tìm tọa độ của các điểm tiếp xúc. Bạn cần tìm x và sau đó tìm giá trị của nó cho một hàm nhất định. Lưu ý rằng từ ý nghĩa hình học của đạo hàm tại điểm
x 0 ta thu được k x = y"(x 0). Từ đẳng thức này ta tìm được các giá trị của x cho các điểm tiếp xúc.
Chúng tôi hiểu điều đó
y " (x 0) = 3 cos 3 2 x 0 - π 4 - 1 3 " = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 = - 9 2 sin 3 2 x 0 - π 4 ⇒ k x = y " (x 0) ⇔ - 9 2 sin 3 2 x 0 - π 4 = 1 2 ⇒ sin 3 2 x 0 - π 4 = - 1 9
Phương trình lượng giác này sẽ được sử dụng để tính tọa độ của các điểm tiếp tuyến.
3 2 x 0 - π 4 = arc sin - 1 9 + 2 πk hoặc 3 2 x 0 - π 4 = π - a arc sin - 1 9 + 2 πk
3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk hoặc 3 2 x 0 - π 4 = π + a arc sin 1 9 + 2 πk
x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk hoặc x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z
Z là tập hợp các số nguyên.
x điểm liên lạc đã được tìm thấy. Bây giờ bạn cần chuyển sang tìm kiếm các giá trị của y:
y 0 = 3 cos 3 2 x 0 - π 4 - 1 3
y 0 = 3 1 - sin 2 3 2 x 0 - π 4 - 1 3 hoặc y 0 = 3 - 1 - sin 2 3 2 x 0 - π 4 - 1 3
y 0 = 3 1 - - 1 9 2 - 1 3 hoặc y 0 = 3 - 1 - - 1 9 2 - 1 3
y 0 = 4 5 - 1 3 hoặc y 0 = - 4 5 + 1 3
Từ đó chúng ta thu được 2 3 π 4 - arc sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + arc sin 1 9 + 2 πk ; - 4 5 + 1 3 là các điểm tiếp tuyến.
Trả lời: các phương trình cần thiết sẽ được viết là
y = 1 2 x - 2 3 π 4 - arc sin 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + arc sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z
Để biểu diễn trực quan, hãy xem xét hàm số và tiếp tuyến trên đường tọa độ.
Hình vẽ cho thấy hàm số nằm trên khoảng [ - 10 ; 10 ], trong đó đường màu đen là đồ thị của hàm số, đường màu xanh là các tiếp tuyến, nằm vuông góc với đường thẳng đã cho có dạng y = - 2 x + 1 2. Các chấm đỏ là điểm tiếp xúc.

Các phương trình chính tắc của đường cong bậc 2 không phải là các hàm có một giá trị. Phương trình tiếp tuyến cho chúng được biên soạn theo sơ đồ đã biết.
Tiếp tuyến với đường tròn
Để xác định đường tròn có tâm tại điểm x c e n t e r ; y c e n t e r và bán kính R, áp dụng công thức x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 .
Đẳng thức này có thể được viết dưới dạng hợp của hai hàm:
y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r
Chức năng đầu tiên nằm ở trên cùng và chức năng thứ hai ở dưới cùng, như trong hình.

Lập phương trình đường tròn tại điểm x 0; y 0 , nằm ở hình bán nguyệt trên hoặc dưới, bạn cần tìm phương trình của đồ thị hàm số dạng y = R 2 - x - x c e n t e r 2 + y c e n t e r hoặc y = - R 2 - x - x c e n t e r 2 + y c e n t e tại điểm được chỉ định.
Khi tại các điểm x c n t e ; y c e n t e r + R và x c e n t e r ; Các tiếp tuyến y c e n t e r - R có thể được cho bởi các phương trình y = y c e n t e r + R và y = y c e n t e r - R và tại các điểm x c e n t e r + R ; y c e n t e r và
x c e n t e r - R ; y c e n t e r sẽ song song với o y, khi đó ta thu được các phương trình có dạng x = x c e n t e r + R và x = x c e n t e r - R .

Tiếp tuyến với một hình elip
Khi hình elip có tâm tại x c n t e ; y c e n t e r với các bán trục a và b thì có thể xác định bằng phương trình x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1.
Một hình elip và một hình tròn có thể được biểu thị bằng cách kết hợp hai hàm, đó là nửa hình elip trên và nửa dưới. Sau đó, chúng tôi nhận được điều đó
y = b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r

Nếu các tiếp tuyến nằm ở các đỉnh của hình elip thì chúng song song quanh x hoặc quanh y. Dưới đây, để rõ ràng, hãy xem xét hình ảnh.

Ví dụ 6
Viết phương trình tiếp tuyến của elip x - 3 2 4 + y - 5 2 25 = 1 tại các điểm có giá trị của x bằng x = 2.
Giải pháp
Cần tìm các điểm tiếp tuyến tương ứng với giá trị x = 2. Chúng ta thay thế vào phương trình hiện có của hình elip và tìm thấy rằng
x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5
Sau đó 2 ; 5 3 2 + 5 và 2; - 5 3 2 + 5 là các điểm tiếp tuyến của nửa elip trên và nửa elip dưới.
Chúng ta hãy chuyển sang tìm và giải phương trình elip đối với y. Chúng tôi hiểu điều đó
x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2
Rõ ràng, nửa hình elip trên được xác định bằng cách sử dụng hàm có dạng y = 5 + 5 2 4 - x - 3 2, và nửa hình elip dưới y = 5 - 5 2 4 - x - 3 2.
Hãy áp dụng một thuật toán chuẩn để tạo phương trình tiếp tuyến của đồ thị hàm số tại một điểm. Hãy viết phương trình tiếp tuyến thứ nhất tại điểm 2; 5 3 2 + 5 sẽ có dạng như sau
y " = 5 + 5 2 4 - x - 3 2 " = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y " (x 0) = y " (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5
Chúng ta thấy rằng phương trình của tiếp tuyến thứ hai có giá trị tại điểm
2 ; - 5 3 2 + 5 có dạng
y " = 5 - 5 2 4 - (x - 3) 2 " = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y " (x 0) = y " (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5
Tiếp tuyến đồ họa được chỉ định như sau:

Tiếp tuyến với cường điệu
Khi một hyperbol có tâm tại x c e n ter ; y c e n t e r và các đỉnh x c e n t e r + α ; y c e n t e r và x c e n t e r - α ; y c e n t e , bất đẳng thức x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 xảy ra nếu với các đỉnh x c e n ter ; y c e n t e r + b và x c e n t e r ; y c e n t e r - b , sau đó được xác định bằng bất đẳng thức x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

Một hyperbol có thể được biểu diễn dưới dạng hai hàm kết hợp có dạng
y = b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r hoặc y = b a · (x - x c e n t e r) 2 + a 2 + y c e n t e r y = - b a · (x - x c e n t e r) 2 + a 2 + y c e n t e r

Trong trường hợp đầu tiên, chúng ta có các tiếp tuyến song song với y và trong trường hợp thứ hai chúng song song với x.
Theo đó, để tìm phương trình tiếp tuyến của một hyperbol, cần phải tìm ra điểm tiếp tuyến thuộc hàm nào. Để xác định điều này, cần phải thế vào các phương trình và kiểm tra tính đồng nhất.
Ví dụ 7
Viết phương trình tiếp tuyến của hyperbol x - 3 2 4 - y + 3 2 9 = 1 tại điểm 7; - 3 3 - 3 .
Giải pháp
Cần chuyển đổi bản ghi lời giải để tìm hyperbol bằng 2 hàm. Chúng tôi hiểu điều đó
x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 và y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3
Cần xác định điểm cho trước có tọa độ 7 thuộc chức năng nào; - 3 3 - 3 .
Rõ ràng để kiểm tra hàm số thứ nhất cần y(7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3 thì điểm đó không thuộc đồ thị, vì sự bình đẳng không giữ được.
Đối với hàm thứ hai, chúng ta có y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3, có nghĩa là điểm thuộc đồ thị đã cho. Từ đây bạn sẽ tìm thấy độ dốc.
Chúng tôi hiểu điều đó
y " = - 3 2 (x - 3) 2 - 4 - 3 " = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y " (x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3
Trả lời: phương trình tiếp tuyến có thể được biểu diễn dưới dạng
y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3
Nó được mô tả rõ ràng như thế này:

Tiếp tuyến với một parabol
Để lập phương trình tiếp tuyến của parabol y = a x 2 + b x + c tại điểm x 0, y (x 0) các bạn phải dùng thuật toán chuẩn thì phương trình sẽ có dạng y = y"(x 0) x - x 0 + y ( x 0). Tiếp tuyến như vậy tại đỉnh song song với x.
Bạn nên xác định parabol x = a y 2 + b y + c là hợp của hai hàm số. Vì vậy, chúng ta cần giải phương trình cho y. Chúng tôi hiểu điều đó
x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a
Hãy mô tả nó bằng đồ họa như sau:

Để biết điểm x 0, y (x 0) có thuộc hàm nào hay không, hãy tiến hành nhẹ nhàng theo thuật toán chuẩn. Tiếp tuyến như vậy sẽ song song với o y so với parabol.
Ví dụ 8
Viết phương trình tiếp tuyến của đồ thị x - 2 y 2 - 5 y + 3 khi có góc tiếp tuyến bằng 150°.
Giải pháp
Chúng ta bắt đầu giải bằng cách biểu diễn parabol dưới dạng hai hàm số. Chúng tôi hiểu điều đó
2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4
Giá trị của hệ số góc bằng giá trị đạo hàm tại điểm x 0 của hàm số này và bằng tiếp tuyến của góc nghiêng.
Chúng tôi nhận được:
k x = y " (x 0) = tg α x = t g 150 ° = - 1 3
Từ đây chúng ta xác định giá trị x cho các điểm tiếp xúc.
Hàm đầu tiên sẽ được viết là
y " = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3
Rõ ràng là không có nghiệm thực vì chúng ta nhận được giá trị âm. Chúng ta kết luận rằng không có tiếp tuyến nào có góc 150° cho hàm số như vậy.
Hàm thứ hai sẽ được viết là
y " = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4
Ta có tiếp điểm là 23 4 ; - 5 + 3 4 .
Trả lời: phương trình tiếp tuyến có dạng
y = - 1 3 x - 23 4 + - 5 + 3 4
Hãy mô tả nó bằng đồ họa theo cách này:

Nếu bạn thấy văn bản có lỗi, vui lòng đánh dấu nó và nhấn Ctrl+Enter
Sự định nghĩa. Tiếp tuyến của một đường tròn là đường thẳng trong mặt phẳng có duy nhất một điểm chung với đường tròn đó.
Dưới đây là một vài ví dụ:
 Vòng tròn có tâm ồ chạm vào một đường thẳng tôi tại điểm MỘT
Vòng tròn có tâm ồ chạm vào một đường thẳng tôi tại điểm MỘT
 Từ bất cứ nơi nào M Vẽ được chính xác hai tiếp tuyến bên ngoài đường tròn
Từ bất cứ nơi nào M Vẽ được chính xác hai tiếp tuyến bên ngoài đường tròn  Sự khác biệt giữa tiếp tuyến tôi, đương căt BC và thẳng tôi, không có điểm chung với đường tròn
Sự khác biệt giữa tiếp tuyến tôi, đương căt BC và thẳng tôi, không có điểm chung với đường tròn Chúng ta có thể kết thúc ở đây, nhưng thực tế cho thấy rằng chỉ ghi nhớ định nghĩa là chưa đủ - bạn cần học cách nhìn các tiếp tuyến trong hình vẽ, biết các tính chất của chúng và ngoài ra, hãy thực hành đúng cách áp dụng các tính chất này bằng cách giải các bài toán thực tế. Chúng ta sẽ làm tất cả những điều này ngày hôm nay.
Tính chất cơ bản của tiếp tuyến
Để giải quyết bất kỳ vấn đề nào, bạn cần biết bốn thuộc tính chính. Hai trong số chúng được mô tả trong bất kỳ sách tham khảo/sách giáo khoa nào, nhưng hai cái cuối cùng bằng cách nào đó lại bị lãng quên nhưng vô ích.
1. Các đoạn tiếp tuyến vẽ từ một điểm đều bằng nhau
Cao hơn một chút chúng ta đã nói về hai tiếp tuyến vẽ từ một điểm M. Vậy:
Các đoạn tiếp tuyến của đường tròn vẽ từ một điểm thì bằng nhau.
 Phân đoạn LÀ. Và B.M. bình đẳng
Phân đoạn LÀ. Và B.M. bình đẳng 2. Tiếp tuyến vuông góc với bán kính vẽ tới điểm tiếp xúc
Chúng ta hãy nhìn vào hình ảnh trên một lần nữa. Hãy vẽ bán kính O.A. Và O.B., sau đó chúng ta thấy rằng các góc OAM Và O.B.M.- thẳng.
Bán kính vẽ tới điểm tiếp xúc vuông góc với tiếp tuyến.
Thực tế này có thể được sử dụng mà không cần bằng chứng trong bất kỳ vấn đề nào:
 Bán kính vẽ tới điểm tiếp tuyến vuông góc với các tiếp tuyến
Bán kính vẽ tới điểm tiếp tuyến vuông góc với các tiếp tuyến Nhân tiện, lưu ý: nếu bạn vẽ một đoạn ôi, khi đó ta được hai tam giác bằng nhau: OAM Và O.B.M..
3. Mối liên hệ giữa tiếp tuyến và cát tuyến
Nhưng đây là một thực tế nghiêm trọng hơn và hầu hết học sinh đều không biết điều đó. Xét một tiếp tuyến và một cát tuyến đi qua cùng một điểm chung M. Đương nhiên cát tuyến sẽ cho ta hai đoạn: bên trong đường tròn (đoạn BC- nó còn được gọi là hợp âm) và bên ngoài (đó là cách họ gọi nó - phần bên ngoài MC).
Tích của toàn bộ cát tuyến và phần bên ngoài của nó bằng bình phương của tiếp tuyến
 Mối liên hệ giữa sec và tang
Mối liên hệ giữa sec và tang 4. Góc giữa tiếp tuyến và dây cung
Một thực tế thậm chí còn cao cấp hơn thường được sử dụng để giải quyết các vấn đề phức tạp. Tôi thực sự khuyên bạn nên đưa nó vào sử dụng.
Góc giữa tiếp tuyến và dây cung bằng góc nội tiếp chắn bởi dây đó.

Điểm đến từ đâu? B? Trong các vấn đề thực tế, nó thường “bật lên” ở đâu đó trong tình trạng. Vì vậy, điều quan trọng là phải học cách nhận biết cấu hình này trong bản vẽ.
 Đôi khi nó quan trọng :)
Đôi khi nó quan trọng :) Bằng chứng
Nếu dây cung là đường kính thì định lý là hiển nhiên.
Hình 287 vẽ đường tròn tâm O, M là giao điểm của đường kính CD và dây AB, CD ⊥ AB. Ta cần chứng minh AM = MB.
Hãy vẽ bán kính OA và OB. Trong tam giác cân AOB (OA = OB), đoạn OM là chiều cao và do đó là đường trung tuyến, tức là AM = MB.
Định lý 20.2
Đường kính của đường tròn chia một dây không phải là đường kính làm đôi thì vuông góc với dây này.
Hãy tự mình chứng minh định lý này. Hãy xem xét liệu tuyên bố này có đúng nếu dây cung là đường kính hay không.
Hình 288 cho thấy tất cả các trường hợp có thể xảy ra về vị trí tương đối của đường thẳng và đường tròn. Trong Hình 288, a chúng không có điểm chung, trên Hình 288, b – chúng có hai điểm chung, trong Hình 288, c – một.
|
Cơm. 288 |
||
|
|
|
|
Sự định nghĩa
Đường thẳng chỉ có một điểm chung với đường tròn gọi là tiếp tuyến của đường tròn.
Tiếp tuyến của một đường tròn chỉ có một điểm chung với đường tròn giới hạn bởi đường tròn đó. Trên Hình 288, đường thẳng a tiếp xúc với đường tròn tâm tại điểm O, A là điểm tiếp tuyến.
Nếu một đoạn (tia) thuộc tiếp tuyến của một đường tròn và có một điểm chung với đường tròn này thì đoạn (tia) đó được gọi là tiếp tuyến với đường tròn. Ví dụ, Hình 289 cho thấy đoạn AB tiếp xúc với đường tròn tại điểm C.
Định lý 20.3
(tính chất tiếp tuyến)
Tiếp tuyến của một đường tròn vuông góc với bán kính vẽ tại điểm tiếp tuyến.
Bằng chứng
Hình 290 thể hiện một đường tròn tâm O, A là điểm tiếp tuyến của đường thẳng a và đường tròn. Ta cần chứng minh OA ⊥ a.
|
Cơm. 289 |
Cơm. 290 |
Cơm. 291 |
|
|
|
|
Giả sử điều này không xảy ra, tức là đoạn OA nghiêng với đường thẳng a. Sau đó từ điểm O chúng ta hạ đường vuông góc OM xuống đường thẳng a (Hình 291). Vì điểm A là điểm chung duy nhất của đường thẳng a và đường tròn tâm O nên điểm M không thuộc đường tròn này. Do đó OM = MB + OB, trong đó điểm B là giao điểm của đường tròn và đường vuông góc OM. Các đoạn OA và OB bằng bán kính của đường tròn. Do đó OM > OA. Ta thu được điều mâu thuẫn: OM vuông góc lớn hơn OA xiên. Do đó, OA ⊥ a.
Định lý 20.4
(dấu hiệu tiếp tuyến của đường tròn)
Nếu một đường thẳng đi qua một điểm trên đường tròn vuông góc với bán kính vẽ tại điểm này thì đường thẳng này tiếp xúc với đường tròn này.
Bằng chứng
|
Cơm. 292 |
|
|
Hình 290 vẽ đường tròn có tâm tại điểm O, đoạn OA là bán kính, điểm A thuộc đường thẳng a, OA ⊥ a. Chứng minh rằng đường thẳng a tiếp tuyến với đường tròn.
Giả sử đường thẳng a không phải là tiếp tuyến mà có một điểm chung B khác với đường tròn (Hình 292). Khi đó ∆ AOB là hình cân (OA = OB tính theo bán kính). Do đó ∠ OBA = ∠ OAB = 90°. Ta mâu thuẫn: tam giác AOB có hai góc vuông. Do đó, đường thẳng a tiếp xúc với đường tròn.
Kết quả
Nếu khoảng cách từ tâm đường tròn đến một đường thẳng nào đó bằng bán kính của đường tròn thì đường thẳng này tiếp xúc với đường tròn này.
|
Cơm. 293 |
|
|
Hãy tự mình chứng minh hệ quả này.
Nhiệm vụ. Chứng minh rằng nếu hai tiếp tuyến đi qua một điểm cho trước thành một đường tròn thì các đoạn tiếp tuyến nối điểm này với các điểm tiếp tuyến bằng nhau.
Giải pháp. Hình 293 cho thấy một đường tròn tâm O. Các đường thẳng AB và AC là các tiếp tuyến, các điểm B và C là các điểm tiếp tuyến. Ta cần chứng minh AB = AC.
Hãy vẽ bán kính OB và OC tại các điểm tiếp xúc. Theo tính chất tiếp tuyến, OB ⊥ AB và OC ⊥ AC. Trong các tam giác vuông AOB và AOC, hai chân OB và OC bằng bán kính của một đường tròn, AO là cạnh huyền chung. Do đó, tam giác AOB và AOC có cạnh huyền và cạnh bằng nhau. Do đó AB = AC.

- Đường kính vuông góc với nó chia dây như thế nào?
- Góc giữa dây cung ngoài đường kính và đường kính chia dây này làm đôi là bao nhiêu?
- Mô tả tất cả các trường hợp có thể xảy ra về vị trí tương đối của đường thẳng và đường tròn.
- Đường nào được gọi là tiếp tuyến của đường tròn?
- Bán kính vẽ tiếp điểm của đường thẳng và đường tròn có tính chất gì?
- Lập công thức kiểm tra tiếp tuyến của đường tròn.
- Các tiếp tuyến của đường tròn đi qua một điểm có tính chất gì?

Nhiệm vụ thực tế

507. Vẽ đường tròn tâm O, vẽ dây AB. Sử dụng một hình vuông, chia hợp âm này làm đôi.
508. Vẽ đường tròn tâm O, vẽ dây CD. Dùng thước kẻ vẽ đường kính vuông góc với dây cung CD.
509. Vẽ một đường tròn, đánh dấu các điểm A và B trên đó Dùng thước kẻ và hình vuông vẽ các đường thẳng tiếp xúc với đường tròn tại các điểm A và B.
510. Vẽ một đường thẳng a và đánh dấu điểm M trên đó. Dùng thước kẻ và compa vẽ một đường tròn bán kính 3 cm tiếp xúc với đường thẳng a tại điểm M. Có thể vẽ được bao nhiêu đường tròn như vậy?

Bài tập
511. Trên hình 294, điểm O là tâm đường tròn, đường kính CD vuông góc với dây AB. Chứng minh rằng ∠AOD = ∠BOD.
512. Chứng minh rằng các dây bằng nhau của một đường tròn cách đều tâm của nó.
513. Chứng minh rằng nếu các dây của một đường tròn cách đều tâm thì chúng bằng nhau.
514. Đường thẳng vuông góc với bán kính hình tròn có tiếp xúc với hình tròn này không?
515. Thẳng CD tiếp xúc với đường tròn tâm O tại điểm A, đoạn AB là dây cung của đường tròn, ∠ BAD = 35° (Hình 295). Tìm ∠AOB.
516. Thẳng CD tiếp xúc với đường tròn tâm O tại điểm A, đoạn AB là dây cung của đường tròn, ∠ AOB = 80° (xem Hình 295). Tìm ∠BAC.
517. Cho một đường tròn có đường kính là 6 cm, đường thẳng a cách tâm nó một đoạn: 1) 2 cm; 2) 3cm; 3) 6 cm trong trường hợp nào đường thẳng là tiếp tuyến của đường tròn?
518. Cho tam giác ABC biết ∠ C = 90°. Chứng minh rằng:
1) thẳng BC tiếp tuyến với đường tròn tâm A đi qua điểm C;
2) thẳng AB không tiếp xúc với đường tròn tâm C đi qua A.

519. Chứng minh rằng đường kính của một đường tròn lớn hơn bất kỳ dây cung nào khác ngoài đường kính.
520. Trong đường tròn tâm O kẻ dây AB đi qua tâm bán kính và vuông góc với nó. Chứng minh rằng ∠ AOB = 120°.
521. Tìm góc giữa bán kính OA và OB của đường tròn biết khoảng cách từ tâm O của đường tròn đến dây AB nhỏ hơn 2 lần: 1) độ dài dây AB; 2) bán kính của hình tròn.
522. Đường kính AB và các dây AC, CD vẽ trên đường tròn sao cho AC = 12 cm, ∠ BAC = 30°, AB ⊥ CD. Tìm độ dài của dây hợp âm CD.
523. Thông qua điểm M với đường tròn tâm O vẽ các tiếp tuyến MA và MB, A và B là các điểm tiếp tuyến ∠ OAB = 20°. Tìm ∠AMB.
524. Qua hai đầu dây AB bằng bán kính đường tròn vẽ hai đường tiếp tuyến cắt nhau tại điểm C. Tìm ∠ ACB.
525. Thông qua điểm Vẽ tiếp tuyến với đường tròn này từ đường tròn tâm O, AB là đường kính của đường tròn. Từ điểm A đường vuông góc AD hạ xuống một tiếp tuyến. Chứng minh tia AC là tia phân giác của góc BAD.
526. Thẳng AC tiếp xúc với đường tròn tâm O tại điểm A (Hình 296). Chứng minh góc BAC nhỏ hơn góc AOB 2 lần.
|
Cơm. 294 |
Cơm. 295 |
Cơm. 296 |
|
|
|
|
527. Phân đoạn AB và BC lần lượt là dây cung và đường kính của đường tròn, ∠ ABC = 30°. Qua điểm A kẻ tiếp tuyến của đường tròn cắt BC tại điểm D. Chứng minh ∆ ABD là cân.
528. Biết đường kính AB chia đôi dây CD nhưng không vuông góc với dây CD. Chứng minh rằng CD cũng là đường kính.

529. Tìm quỹ tích tâm của các đường tròn tiếp xúc với đường thẳng đã cho tại một điểm cho trước.
530. Tìm quỹ tích tâm các đường tròn tiếp xúc với cả hai cạnh của một góc cho trước.
531. Tìm quỹ tích tâm các đường tròn tiếp xúc với đường thẳng đã cho.
532. Các đường tiếp tuyến của đường tròn tâm O tại A và B cắt nhau tại điểm K, ∠ AKB = 120°. Chứng minh rằng AK + BK = OK.
533. Đường tròn tiếp xúc cạnh AB của tam giác ABC tại điểm M và tiếp xúc với phần kéo dài của hai cạnh còn lại. Chứng minh rằng tổng độ dài các đoạn thẳng BC và BM bằng nửa chu vi tam giác ABC.
|
Cơm. 297 |
|
|
534. Thông qua điểm C là các tiếp tuyến AC và BC với đường tròn, A và B là các điểm tiếp tuyến (Hình 297). Trên đường tròn ta lấy một điểm M tùy ý nằm trong cùng một nửa mặt phẳng với điểm C so với đường thẳng AB, và qua đó vẽ một tiếp tuyến của đường tròn cắt các đường thẳng AC và BC lần lượt tại các điểm D và E. Chứng minh rằng chu vi tam giác DEC không phụ thuộc vào việc chọn điểm M.
Bài tập lặp lại
535. Chứng minh rằng trung điểm M của đoạn thẳng có hai đầu thuộc hai đường thẳng song song là trung điểm của mọi đoạn thẳng đi qua điểm M và có hai đầu thuộc hai đường thẳng đó.
536. Phân đoạn AB và CD cùng nằm trên một đường thẳng và có chung trung điểm. Chọn điểm M sao cho tam giác AMB cân cạnh đáy AB. Chứng minh rằng ∆ CMD cũng cân xứng với CD cơ sở.
537. Ở bên cạnh MK của tam giác MPK đánh dấu hai điểm E và F sao cho điểm E nằm giữa hai điểm M và F, ME = EP, PF = FK. Tìm góc M nếu ∠ EPF = 92°, ∠ K = 26°.
538. Cho tam giác nhọn ABC kẻ đường phân giác BM, kẻ đường vuông góc MK từ điểm M đến cạnh BC, ∠ ABM = ∠ KMC. Chứng minh tam giác ABC cân.
Quan sát, vẽ, thiết kế, tưởng tượng
539. Thiết lập mẫu hình dạng của các hình như trong Hình 298. Tiếp theo nên đặt hình nào?
|
Cơm. 298 |
Khái niệm tiếp tuyến của đường tròn
Một đường tròn có ba vị trí tương đối có thể có so với một đường thẳng:
Nếu khoảng cách từ tâm đường tròn đến đường thẳng nhỏ hơn bán kính thì đường thẳng có hai điểm giao nhau với đường tròn.
Nếu khoảng cách từ tâm đường tròn đến đường thẳng bằng bán kính thì đường thẳng có hai điểm giao nhau với đường tròn.
Nếu khoảng cách từ tâm đường tròn đến đường thẳng lớn hơn bán kính thì đường thẳng có hai giao điểm với đường tròn.
Bây giờ chúng ta giới thiệu khái niệm tiếp tuyến của đường tròn.
Định nghĩa 1
Tiếp tuyến của một đường tròn là đường thẳng có một giao điểm với nó.
Điểm chung của đường tròn và tiếp tuyến gọi là điểm tiếp tuyến (Hình 1).
Hình 1. Tiếp tuyến của đường tròn
Các định lý liên quan đến khái niệm tiếp tuyến của đường tròn
Định lý 1
Định lý tính chất tang: tiếp tuyến của một đường tròn vuông góc với bán kính vẽ tại điểm tiếp tuyến.
Bằng chứng.
Xét một đường tròn có tâm $O$. Chúng ta vẽ tiếp tuyến $a$ tại điểm $A$. $OA=r$ (Hình 2).
Hãy chứng minh rằng $a\bot r$
Ta sẽ chứng minh định lý bằng phản chứng. Giả sử rằng tiếp tuyến $a$ không vuông góc với bán kính của đường tròn.

Hình 2. Minh họa Định lý 1
Nghĩa là $OA$ nghiêng về tiếp tuyến. Vì đường vuông góc với đường thẳng $a$ luôn nhỏ hơn đường vuông góc với đường thẳng đó nên khoảng cách từ tâm đường tròn đến đường thẳng nhỏ hơn bán kính. Như chúng ta đã biết, trong trường hợp này đường thẳng có hai điểm giao nhau với đường tròn. Điều này mâu thuẫn với định nghĩa của một tiếp tuyến.
Do đó, tiếp tuyến vuông góc với bán kính của đường tròn.
Định lý đã được chứng minh.
Định lý 2
Nghịch đảo của định lý tính chất tiếp tuyến: Nếu một đường thẳng đi qua điểm cuối bán kính của một đường tròn và vuông góc với bán kính thì đường thẳng này tiếp xúc với đường tròn này.
Bằng chứng.
Theo điều kiện của bài toán, bán kính là đường vuông góc kẻ từ tâm đường tròn đến một đường thẳng cho trước. Do đó, khoảng cách từ tâm đường tròn đến đường thẳng bằng độ dài bán kính. Như chúng ta đã biết, trong trường hợp này đường tròn chỉ có một điểm giao nhau với đường này. Theo Định nghĩa 1, chúng ta thấy rằng đường thẳng này tiếp tuyến với đường tròn.
Định lý đã được chứng minh.
Định lý 3
Các đoạn tiếp tuyến của đường tròn vẽ từ một điểm thì bằng nhau và tạo thành các góc bằng nhau với một đường thẳng đi qua điểm này và tâm của đường tròn.
Bằng chứng.
Cho một đường tròn có tâm tại điểm $O$. Hai tiếp tuyến khác nhau được vẽ từ điểm $A$ (nằm trên toàn bộ đường tròn). Từ điểm tiếp xúc $B$ và $C$ tương ứng (Hình 3).
Hãy chứng minh rằng $\angle BAO=\angle CAO$ và $AB=AC$.

Hình 3. Minh họa Định lý 3
Theo Định lý 1, ta có:
Do đó, các tam giác $ABO$ và $ACO$ là tam giác vuông. Vì $OB=OC=r$, và cạnh huyền $OA$ là chung, nên các tam giác này bằng nhau ở cạnh huyền và cạnh bên.
Do đó ta có $\angle BAO=\angle CAO$ và $AB=AC$.
Định lý đã được chứng minh.
Ví dụ về khái niệm tiếp tuyến của đường tròn
ví dụ 1
Cho một đường tròn có tâm tại điểm $O$ và bán kính $r=3\ cm$. Tiếp tuyến $AC$ có một điểm tiếp tuyến $C$. $AO=4\cm$. Tìm $AC$.
Giải pháp.
Trước tiên hãy mô tả mọi thứ trong hình (Hình 4).

Hinh 4.
Vì $AC$ là một tiếp tuyến và $OC$ là bán kính, nên theo Định lý 1, chúng ta thu được $\angle ACO=(90)^(()^\circ )$. Chúng ta thấy rằng tam giác $ACO$ là hình chữ nhật, có nghĩa là, theo định lý Pythagore, chúng ta có:
\[(AC)^2=(AO)^2+r^2\] \[(AC)^2=16+9\] \[(AC)^2=25\] \












 Báo cáo lịch sử Trung Quốc cổ đại, thông điệp Người Trung Quốc cổ đại sống ở đâu
Báo cáo lịch sử Trung Quốc cổ đại, thông điệp Người Trung Quốc cổ đại sống ở đâu Bài học hóa học Chúng tôi sẽ ngâm nó trong iốt một cách hào phóng để mọi thứ đều vô trùng.
Bài học hóa học Chúng tôi sẽ ngâm nó trong iốt một cách hào phóng để mọi thứ đều vô trùng.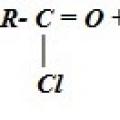 Tính chất hóa học. Biên lai. Điều chế axit cacboxylic Điều chế axit cacboxylic bằng quá trình oxy hóa hydrocarbon
Tính chất hóa học. Biên lai. Điều chế axit cacboxylic Điều chế axit cacboxylic bằng quá trình oxy hóa hydrocarbon