Формулата за дисперсията на случайна променлива. Дисперсия и стандартно отклонение в MS EXCEL

Само тази характеристика обаче не е достатъчна за изследване случайна величина. Представете си двама стрелци, които стрелят по мишена. Единият стреля точно и улучва близо до центъра, а другият ... просто се забавлява и дори не се прицелва. Но смешното е, че средно аритметичнорезултатът ще бъде абсолютно същият като при първия стрелец! Тази ситуация условно се илюстрира със следните случайни променливи:

"снайперист" очаквана стойносте равен обаче и интересна личност»: - също е нула!

Следователно е необходимо да се определи количествено докъде разпръснатикуршуми (стойности на случайна променлива) спрямо центъра на целта (очакване). добре и разсейванепреведено от латински само като дисперсия .

Нека да видим как се определя тази числена характеристика в един от примерите от 1-ва част на урока:

Там открихме разочароващо математическо очакване на тази игра и сега трябва да изчислим нейната дисперсия, която означенопрез .

Нека да разберем колко далеч са "разпръснати" печалбите/загубите спрямо средната стойност. Очевидно за това трябва да изчислим различиямежду стойности на случайна променливаи тя математическо очакване:

–5 – (–0,5) = –4,5
2,5 – (–0,5) = 3
10 – (–0,5) = 10,5

Сега изглежда е необходимо да се обобщят резултатите, но този начин не е добър - поради причината, че трептенията вляво ще се компенсират взаимно с трептенията вдясно. Така например "аматьорският" стрелец (пример по-горе)разликите ще са , и когато се добавят, те ще дадат нула, така че няма да получим никаква оценка за разсейването на неговата стрелба.

За да избегнете това раздразнение, помислете модулиразлики, но по технически причини подходът се е утвърдил, когато те са повдигнати на квадрат. По-удобно е решението да се подреди в таблица:

И тук е необходимо да се изчисли среднопретеглена стойностстойността на квадратните отклонения. Какво е? Тяхно е очаквана стойност, което е мярката за разсейване:

– определениедисперсия. Веднага става ясно от определението, че дисперсията не може да бъде отрицателна- вземете бележка за практика!

Нека си припомним как да намерим очакването. Умножете разликите на квадрат по съответните вероятности (Продължение на таблицата):
- образно казано, това е "теглителна сила",
и обобщете резултатите:

Не мислите ли, че на фона на печалбите резултатът се оказа твърде голям? Точно така – повдигахме на квадрат и за да се върнем към размерността на нашата игра, трябва да извадим корен квадратен. Тази стойностНаречен стандартно отклонение и се обозначава с гръцката буква "сигма":

Понякога това значение се нарича стандартно отклонение .

Какво е значението му? Ако се отклоним от математическото очакване наляво и надясно със средната стойност стандартно отклонение:

– тогава най-вероятните стойности на случайната променлива ще бъдат „концентрирани“ в този интервал. Какво всъщност виждаме:

Но така се случи, че при анализа на разсейването почти винаги се работи с концепцията за дисперсия. Нека да видим какво означава това във връзка с игрите. Ако при стрелците говорим за "точността" на попаденията спрямо центъра на мишената, то тук дисперсията характеризира две неща:

Първо, очевидно е, че с увеличаването на ставките дисперсията също се увеличава. Така например, ако увеличим 10 пъти, тогава математическото очакване ще се увеличи 10 пъти, а дисперсията ще се увеличи 100 пъти (щом е квадратична стойност). Но имайте предвид, че правилата на играта не са се променили! Само ставките се промениха, грубо казано, преди залагахме 10 рубли, сега 100.

Второ, повече интересен моменте, че дисперсията характеризира стила на играта. Мислено фиксирайте ставките на играта на някакво определено нивои вижте какво има тук:

Игра с ниска вариация е предпазлива игра. Играчът е склонен да избира най-надеждните схеми, при които не губи/печели твърде много наведнъж. Например системата червено/черно в рулетката (вижте Пример 4 от статията случайни променливи) .

Игра с висока вариация. Тя често се нарича дисперсияигра. Това е приключенски или агресивен стил на игра, при който играчът избира "адреналинови" схеми. Да си спомним поне "Мартингейл", в която заложените суми са с порядъци по-големи от „тихата“ игра от предходния параграф.

Ситуацията в покера е показателна: има т.нар стегнатииграчи, които са склонни да бъдат предпазливи и да "разклащат" средствата си за игра (банкрол). Не е изненадващо, че банкролът им не се колебае много (ниска вариация). Обратно, ако даден играч има висока вариация, тогава той е агресорът. Той често поема рискове, прави големи залози и може както да разбие огромна банка, така и да се разпадне.

Същото се случва във Форекс и т.н. - има много примери.

Освен това във всички случаи няма значение дали играта е за стотинка или за хиляди долари. Всяко ниво има играчи с ниска и висока вариация. Е, за средната победа, както си спомняме, "отговорен" очаквана стойност.

Вероятно сте забелязали, че намирането на дисперсията е дълъг и труден процес. Но математиката е щедра:

Формула за намиране на дисперсията

Тази формулаполучен директно от определението за дисперсия и ние веднага го пускаме в обращение. Ще копирам табелата с нашата игра отгоре:

и намереното очакване .

Изчисляваме дисперсията по втория начин. Първо, нека намерим математическото очакване - квадратът на случайната променлива. от дефиниция на математическото очакване:

AT този случай:

Така, според формулата:

Както се казва, усетете разликата. И на практика, разбира се, е по-добре да се прилага формулата (освен ако условието не изисква друго).

Ние владеем техниката на решаване и проектиране:

Пример 6

Намерете неговото математическо очакване, дисперсия и стандартно отклонение.

Тази задача се среща навсякъде и като правило остава без смислен смисъл.
Можете да си представите няколко крушки с цифри, които светят в лудница с определени вероятности :)

Решение: Удобно е основните изчисления да се обобщят в таблица. Първо записваме първоначалните данни в горните два реда. След това изчисляваме продуктите, след това и накрая сумите в дясната колона:

Всъщност почти всичко е готово. В третия ред беше начертано готово математическо очакване: .

Дисперсията се изчислява по формулата:

И накрая, стандартното отклонение:
- лично аз обикновено закръглявам до 2 знака след десетичната запетая.

Всички изчисления могат да се извършват на калкулатор, а още по-добре - в Excel:

Тук е трудно да сбъркаш :)

Отговор:

Тези, които желаят, могат да опростят живота си още повече и да се възползват от моите калкулатор (демонстрация), което не само незабавно ще реши тази задача, но и изграждат тематична графика (Ела скоро). Програмата може изтеглете в библиотеката– ако сте изтеглили поне един учебен материалили да получите друг начин. Благодаря за подкрепата на проекта!

Няколко задачи за независимо решение:

Пример 7

Изчислете дисперсията на случайната променлива от предишния пример по дефиниция.

И подобен пример:

Пример 8

Дискретна случайна променлива се дава от собствен закон за разпределение:

Да, стойностите на случайната променлива могат да бъдат доста големи (пример от истинска работа) , а тук по възможност използвайте Excel. Както, между другото, в пример 7 - той е по-бърз, по-надежден и по-приятен.

Решения и отговори в долната част на страницата.

В края на 2-ра част на урока ще анализираме още един типична задача, дори може да се каже, малък ребус:

Пример 9

Дискретна случайна променлива може да приема само две стойности: и , и . Известни са вероятността, математическото очакване и дисперсията.

Решение: Да започнем с неизвестна вероятност. Тъй като една случайна променлива може да приеме само две стойности, тогава сумата от вероятностите на съответните събития:

и тъй като , тогава .

Остава да намерим ..., лесно да се каже :) Но добре, започна се. По дефиниция на математическото очакване:
- заменете известните стойности:

- и нищо повече не може да се изтръгне от това уравнение, освен че можете да го пренапишете в обичайната посока:

или:

О следващи стъпкиМисля, че можете да познаете. Нека създадем и решим системата:

Десетични знаци- това, разбира се, е пълно безобразие; умножете двете уравнения по 10:

и разделете на 2:

Така е много по-добре. От първото уравнение изразяваме:
(това е по-лесният начин)- заместител във второто уравнение:

Ние строим на квадрати направете опростявания:

Умножаваме по:

Като резултат, квадратно уравнение, намерете неговия дискриминант:
- перфектно!

и получаваме две решения:

1) ако , тогава ;

2) ако , тогава .

Първата двойка стойности удовлетворява условието. С голяма вероятност всичко е правилно, но въпреки това записваме закона за разпределение:

и извършете проверка, а именно намерете очакването:

В много случаи става необходимо да се въведе друг числена характеристиказа измерване на степента дисперсия, разпространение на ценности, взета като случайна променлива ξ , около неговото математическо очакване.

Определение.Дисперсията на случайна променлива ξ нарече номер.

д= M(ξ-M ξ) 2 . (1)

С други думи, дисперсията е математическото очакване на квадратното отклонение на стойностите на случайна променлива от нейната средна стойност.

Наречен среден квадратотклонение

количества ξ .

Ако дисперсията характеризира средният размерквадратно отклонение ξ от Mξ, тогава числото може да се разглежда като някои средна характеристикасамото отклонение, по-точно големината на | ξ-Mξ |.

Определение (1) предполага следните две свойства на дисперсията.

1. Дисперсия постоянна стойносте равно на нула. Това е напълно в съответствие с визуалното значение на дисперсията като „мярка за разпространение“.

Наистина, ако

ξ \u003d C,тогава Mξ = Cа това означава Dξ = M(C-C) 2 = М 0 = 0.

2. При умножение на случайна величина ξ на постоянно числоС неговата дисперсия се умножава по C 2

D(Cξ) = ° С 2 Dξ . (3)

Наистина ли

D(Cξ) = M(C

= M(C .

3. Има следната формула за изчисляване на дисперсията:

. (4)

Доказателството на тази формула следва от свойствата на математическото очакване.

Ние имаме:

4. Ако стойностите ξ 1 и ξ 2 са независими, тогава дисперсията на тяхната сума е равна на сумата от техните дисперсии:

доказателство За доказателство използваме свойствата на математическото очакване. Позволявам Mξ 1 = m 1 , Mξ 2 = m 2 тогава.

Формула (5) е доказана.

Тъй като дисперсията на случайна променлива по дефиниция е математическото очакване на стойността ( ξ-m) 2 , където m = Mξ,тогава, за да изчислите дисперсията, можете да използвате формулите, получени в раздел 7, глава II.

Така че, ако ξ има ДСВ с разпределителен закон

х 1	х 2	...
стр 1	стр 2	...

тогава ще имаме:

. (7)

Ако ξ непрекъсната случайна променлива с плътност на разпределение p(x), тогава получаваме:

Dξ= . (8)

Ако се използва формула (4) за изчисляване на дисперсията, тогава могат да се получат други формули, а именно:

, (9)

ако стойността ξ дискретни и

Dξ= , (10)

ако ξ разпределени с плътност стр(х).

Пример 1 . Нека стойността ξ е равномерно разпределен върху сегмента [ а,б]. Използвайки формула (10), получаваме:

Може да се покаже, че дисперсията на случайна променлива, разпределена според нормалния закон с плътност

p(x)= , (11)

е равно на σ 2 .

Това изяснява значението на параметъра σ, включен в израза за плътност (11) за нормален закон; σ има средно стандартно отклонениеколичества ξ.

Пример 2 . Намерете дисперсията на случайна променлива ξ разпределени по биномния закон.

Решение . Използвайки представянето на ξ във формата

ξ = ξ 1 + ξ 2 + н(виж пример 2 §7 гл. II) и прилагане на формулата за добавяне на вариации за независими променливи, получаваме

Dξ = Dξ 1 + Dξ 2 + Dξn .

Разсейване на всяко от количествата ξ i (аз= 1,2, н) се изчислява директно:

Dξi = M(ξi) 2 - (Mξ i) 2 = 0 2 р+ 1 2 стр- стр 2 = стр(1-стр) = pq.

Накрая получаваме

Dξ= npq, където q = 1 -стр.

За групирани данни остатъчна дисперсия - средно от вътрешногрупови отклонения:

Където σ 2 j е вътрешногруповата дисперсия на j -тата група.

За негрупирани данни остатъчна дисперсияе мярка за точността на приближението, т.е. приближаване на регресионната линия към оригиналните данни:
където y(t) е прогнозата според уравнението на тенденцията; y t – начална серия от динамика; n е броят на точките; p е броят на коефициентите на регресионното уравнение (броят на обяснителните променливи).
В този пример се нарича безпристрастна оценка на дисперсията.

Пример #1. Разпределението на работниците от три предприятия от една асоциация по тарифни категории се характеризира със следните данни:

Категория на заплатата на работника	Броят на работниците в предприятието
Категория на заплатата на работника	предприятие 1	предприятие 2	предприятие 3
1	50	20	40
2	100	80	60
3	150	150	200
4	350	300	400
5	200	150	250
6	150	100	150

Определете:
1. дисперсия за всяко предприятие (вътрешногрупова дисперсия);
2. средна стойност на вътрешногруповите дисперсии;
3. междугрупова дисперсия;
4. обща дисперсия.

Решение.
Преди да се пристъпи към решаване на проблема, е необходимо да се установи коя характеристика е ефективна и коя факторна. В разглеждания пример действащият признак е "Тарифна категория", а факторният признак е "Номер (име) на предприятието".
След това имаме три групи (предприятия), за които е необходимо да се изчисли средната групова и вътрешногруповата дисперсия:

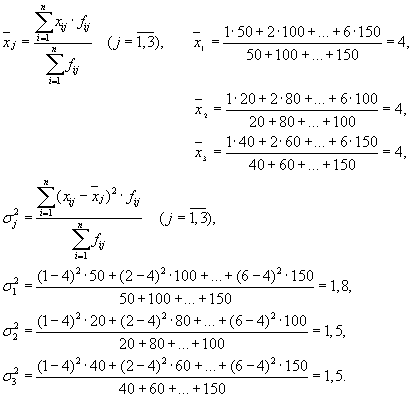
Търговско дружество	средна група,	дисперсия в рамките на групата,
1	4	1,8

Средната стойност на вътрешногруповите дисперсии ( остатъчна дисперсия), изчислено по формулата:

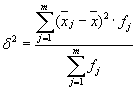
където можете да изчислите:

или:

тогава:
Общата дисперсия ще бъде равна на: s 2 \u003d 1,6 + 0 \u003d 1,6.
Общата дисперсия може също да се изчисли с помощта на една от следните две формули:

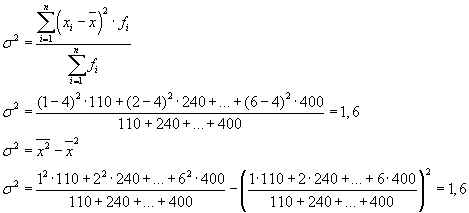
Когато решавате практически проблеми, често трябва да се справяте със знак, който приема само две алтернативни стойности. В този случай те не говорят за тежестта на определена стойност на характеристика, а за нейния дял в съвкупността. Ако съотношението единици на популацията, които притежават изследваната характеристика, се означи с " Р", а не притежаване - чрез" р”, тогава дисперсията може да се изчисли по формулата:
s 2 = p×q

Пример #2. Според данните за развитието на шестима работници от бригадата, определете междугруповата вариация и оценете влиянието на работната смяна върху тяхната производителност на труда, ако общата вариация е 12,2.

No на работната бригада	Работна мощност, бр.
No на работната бригада	в първа смяна	на 2-ра смяна
1	18	13
2	19	14
3	22	15
4	20	17
5	24	16
6	23	15

Решение. Изходни данни

х	f1	f2	е 3	f4	f5	f6	Обща сума
1	18	19	22	20	24	23	126
2	13	14	15	17	16	15	90
Обща сума	31	33	37	37	40	38

След това имаме 6 групи, за които е необходимо да се изчисли груповата средна и вътрешногруповата дисперсия.
1. Намерете средните стойности на всяка група.

2. Намерете средния квадрат на всяка група.

Обобщаваме резултатите от изчислението в таблица:

Номер на групата	Групово средно	Вътрешногрупова дисперсия
1	1.42	0.24
2	1.42	0.24
3	1.41	0.24
4	1.46	0.25
5	1.4	0.24
6	1.39	0.24

3. Вътрешногрупова дисперсияхарактеризира промяната (вариацията) на изследваната (резултатна) черта в рамките на групата под влияние на всички фактори, с изключение на фактора, който е в основата на групирането:
Изчисляваме средната стойност на вътрешногруповите дисперсии по формулата:

4. Междугрупова дисперсияхарактеризира промяната (вариацията) на изследваната (резултатна) черта под влиянието на фактор (факторна черта), лежащ в основата на групирането.
Междугруповата дисперсия се определя като:

където

Тогава

Обща дисперсияхарактеризира промяната (вариацията) на изследваната (резултатна) черта под въздействието на всички фактори (факторни черти) без изключение. По условието на задачата то е равно на 12,2.
Емпирична корелационна връзкаизмерва каква част от общата флуктуация на резултантния атрибут е причинена от изследвания фактор. Това е съотношението на факторната дисперсия към общата дисперсия:

Определяме емпиричната корелационна връзка:

Връзките между характеристиките могат да бъдат слаби или силни (близки). Техните критерии се оценяват по скалата на Chaddock:
0,1 0,3 0,5 0,7 0,9 В нашия пример връзката между функция Y фактор X е слаба
Коефициент на определяне.

Нека да определим коефициента на детерминация:

По този начин 0,67% от вариацията се дължи на разлики между признаците, а 99,37% се дължи на други фактори.
Заключение: в този случай продукцията на работниците не зависи от работата в определена смяна, т.е. влиянието на работната смяна върху тяхната производителност на труда не е значително и се дължи на други фактори.

Пример #3. Въз основа на средната стойност заплатии квадратни отклонения от неговата стойност за две групи работници, намерете общата дисперсия, като приложите правилото за добавяне на дисперсии:

Решение:
Средна стойност на дисперсиите в рамките на групата

Междугруповата дисперсия се определя като:

Общата дисперсия ще бъде: 480 + 13824 = 14304

Основните обобщаващи показатели за вариация в статистиката са дисперсията и стандартното отклонение.

дисперсия то средноаритметично квадратни отклонения на всяка стойност на характеристиката от общата средна стойност. Дисперсията обикновено се нарича среден квадрат на отклоненията и се означава с  2 . В зависимост от първоначалните данни дисперсията може да се изчисли от средната аритметична, проста или претеглена:

 непретеглена (проста) дисперсия;

 претеглена дисперсия.

Стандартно отклонение е обобщаваща характеристика на абсолютните размери вариации черта в съвкупността. Изразява се в същите единици като знака (в метри, тонове, проценти, хектари и т.н.).

Стандартното отклонение е корен квадратен от дисперсията и се означава с :

 непретеглено стандартно отклонение;

 претеглено стандартно отклонение.

Стандартното отклонение е мярка за надеждността на средната стойност. Колкото по-малко е стандартното отклонение, толкова по-добре средното аритметично отразява цялата представена популация.

Изчисляването на стандартното отклонение се предшества от изчисляването на дисперсията.

Процедурата за изчисляване на претеглената дисперсия е следната:

1) определяне на средното аритметично претеглено:

2) изчислете отклоненията на опциите от средната стойност:

3) повдигнете на квадрат отклонението на всяка опция от средната стойност:

4) умножете отклоненията на квадрат по тегла (честоти):

5) обобщете получените произведения:

6) получената сума се разделя на сумата от теглата:

Пример 2.1

Изчислете среднопретеглената аритметична стойност:

Стойностите на отклоненията от средната стойност и техните квадрати са представени в таблицата. Нека дефинираме дисперсията:

Стандартното отклонение ще бъде равно на:

Ако изходните данни са представени като интервал серия за разпространение , тогава първо трябва да определите дискретната стойност на характеристиката и след това да приложите описания метод.

Пример 2.2

Нека покажем изчисляването на дисперсията за интервалната серия върху данните за разпределението на посевната площ на колективното стопанство по добив на пшеница.

Средната аритметична стойност е:

Нека изчислим дисперсията:

6.3. Изчисляване на дисперсията по формулата за индивидуални данни

Изчислителна техника дисперсия сложно и големи стойностиопциите и честотите могат да бъдат тромави. Изчисленията могат да бъдат опростени с помощта на дисперсионните свойства.

Дисперсията има следните свойства.

1. Намаляването или увеличаването на теглата (честотите) на променлива характеристика с определен брой пъти не променя дисперсията.

2. Намаляване или увеличаване на стойността на всяка характеристика със същата постоянна стойност НОдисперсията не се променя.

3. Намаляване или увеличаване на стойността на всяка характеристика с определен брой пъти ксъответно намалява или увеличава дисперсията в к 2 пъти стандартно отклонение  в кведнъж.

4. Дисперсията на признак спрямо произволна стойност винаги е по-голяма от дисперсията спрямо средната аритметична с квадрата на разликата между средната и произволната стойност:

Ако НО 0, тогава стигаме до следното равенство:

т.е. дисперсията на характеристика е равна на разликата между средния квадрат на стойностите на характеристиката и квадрата на средната стойност.

Всяко свойство може да се използва самостоятелно или в комбинация с други при изчисляване на дисперсията.

Процедурата за изчисляване на дисперсията е проста:

1) определям средноаритметично :

2) повдигнете на квадрат средното аритметично:

3) повдигнете на квадрат отклонението на всеки вариант на серията:

х аз 2 .

4) намерете сумата от квадратите на опциите:

5) разделете сумата от квадратите на опциите на техния брой, т.е. определете средния квадрат:

6) определете разликата между средния квадрат на характеристиката и квадрата на средната стойност:

Пример 3.1Имаме следните данни за производителността на работниците:

Нека направим следните изчисления:

Дисперсията на случайна променлива е мярка за разпространението на стойностите на тази променлива. Малката вариация означава, че стойностите са групирани близо една до друга. Голямото отклонение показва силно разсейване на стойностите. Концепцията за дисперсията на случайна променлива се използва в статистиката. Например, ако сравните дисперсията на стойностите на две величини (като резултатите от наблюденията на пациенти мъже и жени), можете да тествате значимостта на някаква променлива. Дисперсията се използва и при конструирането статистически модели, тъй като малката дисперсия може да е знак, че превишавате стойностите.

стъпки

Примерно изчисляване на дисперсията

Запишете пробните стойности.В повечето случаи само извадки от определени популации са достъпни за статистиците. Например, като правило, статистиците не анализират разходите за поддръжка на съвкупността от всички автомобили в Русия - те анализират произволна извадкаот няколко хиляди коли. Такава извадка ще помогне да се определи средната цена на автомобил, но най-вероятно получената стойност ще бъде далеч от реалната.
- Например, нека анализираме броя на кифлите, продадени в кафене за 6 дни, взети в произволен ред. Пробата има следващ изглед: 17, 15, 23, 7, 9, 13. Това е извадка, а не съвкупност, защото нямаме данни за продадени кифли за всеки ден, в който кафенето е отворено.
- Ако ви е дадена популация, а не извадка от стойности, преминете към следващия раздел.
Запишете формулата за изчисляване на дисперсията на извадката.Дисперсията е мярка за разпространението на стойностите на някакво количество. Колкото по-близо е стойността на дисперсията до нула, толкова по-близо са групирани стойностите. Когато работите с извадка от стойности, използвайте следната формула, за да изчислите дисперсията:
- s 2 (\displaystyle s^(2)) = ∑[(x i (\displaystyle x_(i))-х) 2 (\displaystyle ^(2))] / (n - 1)
- s 2 (\displaystyle s^(2))е дисперсията. Дисперсията се измерва в квадратни единициизмервания.
- x i (\displaystyle x_(i))- всяка стойност в извадката.
- x i (\displaystyle x_(i))трябва да извадите x̅, да го повдигнете на квадрат и след това да добавите резултатите.
- x̅ – извадкова средна (извадкова средна).
- n е броят на стойностите в извадката.
Изчислете средната стойност на извадката.Означава се като x̅. Средната стойност на извадката се изчислява като нормална средна аритметична стойност: добавете всички стойности в извадката и след това разделете резултата на броя на стойностите в извадката.
- В нашия пример добавете стойностите в извадката: 15 + 17 + 23 + 7 + 9 + 13 = 84
  Сега разделете резултата на броя на стойностите в извадката (в нашия пример има 6): 84 ÷ 6 = 14.
  Примерна средна x̅ = 14.
- Средната стойност на извадката е централната стойност, около която се разпределят стойностите в извадката. Ако стойностите в клъстера на извадката около извадката са средни, тогава дисперсията е малка; в противен случай дисперсията е голяма.
Извадете средната стойност на извадката от всяка стойност в извадката.Сега изчислете разликата x i (\displaystyle x_(i))- x̅, където x i (\displaystyle x_(i))- всяка стойност в извадката. Всеки получен резултат показва степента, до която определена стойност се отклонява от средната стойност на извадката, тоест колко далеч е тази стойност от средната стойност на извадката.
- В нашия пример:
  x 1 (\displaystyle x_(1))- x̅ = 17 - 14 = 3
  x 2 (\displaystyle x_(2))- x̅ = 15 - 14 = 1
  x 3 (\displaystyle x_(3))- x̅ = 23 - 14 = 9
  x 4 (\displaystyle x_(4))- x̅ = 7 - 14 = -7
  x 5 (\displaystyle x_(5))- x̅ = 9 - 14 = -5
  x 6 (\displaystyle x_(6))- x̅ = 13 - 14 = -1
- Правилността на получените резултати е лесна за проверка, тъй като тяхната сума трябва да е равна на нула. Това е свързано с определянето на средната стойност, тъй като отрицателни стойности(разстояния от средната стойност до по-малки стойности) са напълно компенсирани положителни стойности(разстояния от средни до големи стойности).
Както беше отбелязано по-горе, сумата от разликите x i (\displaystyle x_(i))- x̅ трябва да е равно на нула. Означава, че средна дисперсиявинаги е равно на нула, което не дава никаква представа за разпространението на стойностите на определена величина. За да разрешите тази задача, повдигнете на квадрат всяка разлика x i (\displaystyle x_(i))- х. Това ще доведе до получаване само на положителни числа, което при добавяне никога няма да даде 0.
- В нашия пример:
  (x 1 (\displaystyle x_(1))-х) 2 = 3 2 = 9 (\displaystyle ^(2)=3^(2)=9)
  (x 2 (\displaystyle (x_(2))-х) 2 = 1 2 = 1 (\displaystyle ^(2)=1^(2)=1)
  9 2 = 81
  (-7) 2 = 49
  (-5) 2 = 25
  (-1) 2 = 1
- Намерихте квадрата на разликата - x̅) 2 (\displaystyle ^(2))за всяка стойност в извадката.
Изчислете сумата на квадратите на разликите.Тоест намерете частта от формулата, която е написана така: ∑[( x i (\displaystyle x_(i))-х) 2 (\displaystyle ^(2))]. Тук знакът Σ означава сумата от квадратните разлики за всяка стойност x i (\displaystyle x_(i))в пробата. Вече намерихте разликите на квадрат (x i (\displaystyle (x_(i))-х) 2 (\displaystyle ^(2))за всяка стойност x i (\displaystyle x_(i))в пробата; сега просто добавете тези квадратчета.
- В нашия пример: 9 + 1 + 81 + 49 + 25 + 1 = 166 .
Разделете резултата на n - 1, където n е броят на стойностите в извадката.Преди време, за да изчислят дисперсията на извадката, статистиците просто разделиха резултата на n; в този случай ще получите средната стойност на квадратната дисперсия, която е идеална за описание на дисперсията на дадена проба. Но не забравяйте, че всяка проба е само малка част. населениестойности. Ако вземете различна проба и направите същите изчисления, ще получите различен резултат. Както се оказа, деленето на n - 1 (а не само n) дава повече точна оценкавариация на населението, което е това, което ви интересува. Деленето на n - 1 е станало обичайно, така че е включено във формулата за изчисляване на дисперсията на извадката.
- В нашия пример извадката включва 6 стойности, тоест n = 6.
  Дисперсия на извадката = s 2 = 166 6 − 1 = (\displaystyle s^(2)=(\frac (166)(6-1))=) 33,2
Разликата между дисперсията и стандартното отклонение.Имайте предвид, че формулата съдържа експонента, така че дисперсията се измерва в квадратни единици на анализираната стойност. Понякога такава стойност е доста трудна за работа; в такива случаи използвайте стандартното отклонение, което е равно на корен квадратенот дисперсия. Ето защо дисперсията на извадката се означава като s 2 (\displaystyle s^(2)), а стандартно отклонениепроби - как s (\displaystyle s).
- В нашия пример примерното стандартно отклонение е: s = √33,2 = 5,76.
Изчисляване на дисперсията на популацията
1. Анализирайте някакъв набор от стойности.Комплектът включва всички стойности на разглежданото количество. Например, ако изследвате възрастта на жителите Ленинградска област, тогава населението включва възрастта на всички жители на тази област. В случай на работа с агрегат се препоръчва да създадете таблица и да въведете стойностите на агрегата в нея. Разгледайте следния пример:
  - В дадена стая има 6 аквариума. Всеки аквариум съдържа следния брой риби:
    x 1 = 5 (\displaystyle x_(1)=5)
    x 2 = 5 (\displaystyle x_(2)=5)
    x 3 = 8 (\displaystyle x_(3)=8)
    x 4 = 12 (\displaystyle x_(4)=12)
    x 5 = 15 (\displaystyle x_(5)=15)
    x 6 = 18 (\displaystyle x_(6)=18)
2. Запишете формулата за изчисляване на дисперсията на съвкупността.Тъй като популацията включва всички стойности на определено количество, следната формула ви позволява да получите точната стойност на дисперсията на популацията. За да разграничат вариацията на популацията от вариацията на извадката (която е само приблизителна), статистиците използват различни променливи:
  - σ 2 (\displaystyle ^(2)) = (∑(x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / н
  - σ 2 (\displaystyle ^(2))- дисперсия на популацията (разчетена като "сигма на квадрат"). Дисперсията се измерва в квадратни единици.
  - x i (\displaystyle x_(i))- всяка стойност в съвкупността.
  - Σ е знакът на сумата. Тоест за всяка стойност x i (\displaystyle x_(i))извадете μ, повдигнете го на квадрат и след това добавете резултатите.
  - μ е средната популация.
  - n е броят на стойностите в общата съвкупност.
3. Изчислете средната стойност на населението.Когато се работи с генералната съвкупност, нейната средна стойност се означава като μ (mu). Средната популация се изчислява като обичайната средна аритметична стойност: добавете всички стойности в популацията и след това разделете резултата на броя на стойностите в популацията.
  - Имайте предвид, че средните стойности не винаги се изчисляват като средно аритметично.
  - В нашия пример населението означава: μ = 5 + 5 + 8 + 12 + 15 + 18 6 (\displaystyle (\frac (5+5+8+12+15+18)(6))) = 10,5
4. Извадете средната популация от всяка стойност в популацията.Колкото по-близо е стойността на разликата до нула, толкова по-близо е конкретната стойност до средната за съвкупността. Намерете разликата между всяка стойност в популацията и нейната средна стойност и ще получите първи поглед върху разпределението на стойностите.
  - В нашия пример:
    x 1 (\displaystyle x_(1))- μ = 5 - 10,5 = -5,5
    x 2 (\displaystyle x_(2))- μ = 5 - 10,5 = -5,5
    x 3 (\displaystyle x_(3))- μ = 8 - 10,5 = -2,5
    x 4 (\displaystyle x_(4))- μ = 12 - 10,5 = 1,5
    x 5 (\displaystyle x_(5))- μ = 15 - 10,5 = 4,5
    x 6 (\displaystyle x_(6))- μ = 18 - 10,5 = 7,5
5. Квадратирайте всеки получен резултат.Стойностите на разликата ще бъдат както положителни, така и отрицателни; ако поставите тези стойности на числова ос, тогава те ще лежат отдясно и отляво на средната стойност на съвкупността. Това не е подходящо за изчисляване на дисперсията, тъй като положителни и отрицателни числавзаимно се компенсират. Затова повдигнете на квадрат всяка разлика, за да получите изключително положителни числа.
  - В нашия пример:
    (x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))за всяка стойност на популацията (от i = 1 до i = 6):
    (-5,5)2 (\displaystyle ^(2)) = 30,25
    (-5,5)2 (\displaystyle ^(2)), където x n (\displaystyle x_(n)) – последна стойноств общата популация.
  - За да изчислите средната стойност на получените резултати, трябва да намерите тяхната сума и да я разделите на n: (( x 1 (\displaystyle x_(1)) - μ) 2 (\displaystyle ^(2)) + (x 2 (\displaystyle x_(2)) - μ) 2 (\displaystyle ^(2)) + ... + (x n (\displaystyle x_(n)) - μ) 2 (\displaystyle ^(2))) / н
  - Сега нека напишем горното обяснение с помощта на променливи: (∑( x i (\displaystyle x_(i)) - μ) 2 (\displaystyle ^(2))) / n и получете формула за изчисляване на дисперсията на съвкупността.