Намерете матрици, обратни на дадената матрица a. Намиране на обратната матрица онлайн

Намиране на обратната матрица- проблем, който най-често се решава по два метода:

• методът на алгебричните допълнения, при който се изисква намиране на детерминанти и транспониране на матрици;
• методът на елиминиране на Гаус, който изисква елементарни трансформации на матрици (събиране на редове, умножаване на редове по едно и също число и т.н.).

За тези, които са особено любопитни, има и други методи, например методът на линейните трансформации. В този урок ще анализираме трите споменати метода и алгоритмите за намиране на обратната матрица чрез тези методи.

обратна матрица НО, такава матрица се нарича

НО
. (1)

обратна матрица , което се изисква да се намери за дадена квадратна матрица НО, такава матрица се нарича

продуктът, чрез който матриците НОвдясно е матрицата на идентичността, т.е.
. (1)

Идентификационната матрица е диагонална матрица, в която всички диагонални записи са равни на единица.

Теорема.За всяка неособена (неособена, неособена) квадратна матрица може да се намери обратна матрица и освен това само една. За специална (изродена, сингулярна) квадратна матрица обратната матрица не съществува.

Квадратната матрица се нарича неспециални(или неизродени, неединствен), ако неговата детерминанта не е равна на нула, и специален(или изродени, единствено число), ако неговата детерминанта е нула.

Обратната матрица може да се намери само за квадратна матрица. Естествено, обратната матрица също ще бъде квадратна и от същия ред като дадената матрица. Матрица, за която може да се намери обратна матрица, се нарича обратима матрица.

За обратна матрица има подходяща аналогия с реципрочната стойност на число. За всяко число а, което не е равно на нула, съществува число bче работата аи bравно на едно: аб= 1. Номер bсе нарича реципрочна стойност на число b. Например за числото 7 обратното е числото 1/7, тъй като 7*1/7=1.

Намиране на обратната матрица по метода на алгебричните допълнения (матрица на обединение)

За неособена квадратна матрица НОобратното е матрицата

където е матричната детерминанта НО, а е матрицата, свързана с матрицата НО.

В съюз с квадратна матрица Ае матрица от същия ред, чиито елементи са алгебричните допълнения на съответните елементи на детерминантата на матрицата, транспонирана по отношение на матрицата A. Така, ако

тогава

и

Алгоритъм за намиране на обратната матрица по метода на алгебричните събирания

1. Намерете детерминантата на тази матрица А. Ако детерминантата е равна на нула, намирането на обратната матрица спира, тъй като матрицата е изродена и за нея няма обратна.

2. Намерете матрица, транспонирана по отношение на А.

3. Изчислете елементите на обединителната матрица като алгебричните допълнения на марита, намерени в стъпка 2.

4. Приложете формула (2): умножете реципрочната стойност на детерминантата на матрицата А, към матрицата на обединение, намерена в стъпка 4.

5. Проверете резултата, получен в стъпка 4, като умножите тази матрица Акъм обратната матрица. Ако произведението на тези матрици е равно на единичната матрица, тогава обратната матрица е намерена правилно. В противен случай стартирайте процеса на решение отново.

Пример 1За матрица

намерете обратната матрица.

Решение. За да се намери обратната матрица, е необходимо да се намери детерминантата на матрицата НО. Намираме по правилото на триъгълниците:

Следователно матрицата НОе неединично (неизродено, неединично) и има обратно за него.

Нека намерим матрицата, свързана с дадената матрица НО.

Нека намерим матрицата, транспонирана по отношение на матрицата А:

Ние изчисляваме елементите на обединителната матрица като алгебрични допълнения на матрицата, транспонирани по отношение на матрицата А:

Следователно, матрицата, конюгирана с матрицата А, има формата

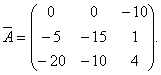
Коментирайте.Редът на изчисляване на елементите и транспонирането на матрицата може да бъде различен. Първо могат да се изчислят алгебричните допълнения на матрицата А, и след това транспонирайте матрицата от алгебрични допълнения. Резултатът трябва да бъде същите елементи на обединителната матрица.

Прилагайки формула (2), намираме матрицата, обратна на матрицата НО:

Намиране на обратната матрица чрез елиминиране на неизвестните по Гаус

Първата стъпка за намиране на обратната матрица чрез елиминиране на Гаус е да се присвои на матрицата Аидентификационна матрица от същия ред, като ги разделя с вертикална черта. Получаваме двойна матрица. Умножете двете части на тази матрица по , тогава получаваме

,

Алгоритъм за намиране на обратната матрица чрез елиминиране на неизвестните по Гаус

1. Към матрицата Азадайте идентична матрица от същия ред.

2. Трансформирайте получената двойна матрица, така че матрицата за идентичност да се получи в лявата й част, след което обратната матрица автоматично ще бъде получена в дясната част на мястото на матрицата за идентичност. Матрица Аот лявата страна се преобразува в матрицата на идентичност чрез елементарни трансформации на матрицата.

2. Ако в процеса на матрична трансформация Ав матрицата за идентичност във всеки ред или във всяка колона ще има само нули, тогава детерминантата на матрицата е равна на нула и следователно матрицата Аще бъде изродена и няма обратна матрица. В този случай по-нататъшното намиране на обратната матрица спира.

Пример 2За матрица

намерете обратната матрица.

и ще го трансформираме така, че матрицата на идентичност да се получи от лявата страна. Да започнем трансформацията.

Умножете първия ред на лявата и дясната матрица по (-3) и го добавете към втория ред, след което умножете първия ред по (-4) и го добавете към третия ред, след което получаваме

.

Така че, ако е възможно, да няма дробни числа по време на следващите трансформации, първо ще създадем единица във втория ред от лявата страна на двойната матрица. За да направите това, умножете втория ред по 2 и извадете третия ред от него, тогава получаваме

.

Нека добавим първия ред към втория и след това да умножим втория ред по (-9) и да го добавим към третия ред. Тогава получаваме

.

След това разделете третия ред на 8

.

Умножете третия ред по 2 и го добавете към втория ред. Оказва се:

.

Разменяйки местата на втория и третия ред, накрая получаваме:

.

Виждаме, че матрицата на идентичността се получава от лявата страна, следователно обратната матрица се получава от дясната страна. По този начин:

.

Можете да проверите правилността на изчисленията, като умножите оригиналната матрица по намерената обратна матрица:

Резултатът трябва да бъде обратна матрица.

Пример 3За матрица

намерете обратната матрица.

Решение. Съставяне на двойна матрица

и ние ще го трансформираме.

Умножаваме първия ред по 3, а втория по 2 и изваждаме от втория, след което умножаваме първия ред по 5 и третия по 2 и изваждаме от третия ред, тогава получаваме

.

Умножаваме първия ред по 2 и го добавяме към втория, след което изваждаме втория от третия ред, след което получаваме

.

Виждаме, че в третия ред от лявата страна всички елементи се оказаха равни на нула. Следователно матрицата е изродена и няма обратна матрица. Спираме по-нататъшното намиране на обратната мария.

Методи за намиране на обратната матрица, . Помислете за квадратна матрица

Означаваме Δ = det A.

Квадратната матрица A се нарича неизроден,или неспециалниако неговата детерминанта е различна от нула, и изроден,или специален, акоΔ = 0.

Квадратна матрица B съществува за квадратна матрица A от същия ред, ако техният продукт A B = B A = E, където E е матрицата на идентичност от същия ред като матриците A и B.

Теорема . За да има матрицата A обратна матрица, е необходимо и достатъчно нейната детерминанта да е различна от нула.

Обратна матрица към матрица A, означена с A- 1, така че B = A - 1 и се изчислява по формулата

, (1)

където А i j - алгебрични добавки на елементите a i j на матрицата A..

Изчисляването на A -1 по формула (1) за матрици от висок ред е много трудоемко, така че на практика е удобно да се намери A -1 с помощта на метода на елементарните трансформации (EP). Всяка неособена матрица A може да бъде намалена чрез EP само на колони (или само редове) към матрицата за идентичност E. Ако EP, изпълнени върху матрицата A, се прилагат в същия ред към матрицата за идентичност E, тогава резултатът е обратна матрица. Удобно е да се извърши EP върху матриците A и E едновременно, като се изпишат двете матрици една до друга през линията. Още веднъж отбелязваме, че когато търсите каноничната форма на матрица, за да я намерите, можете да използвате трансформации на редове и колони. Ако трябва да намерите обратната матрица, трябва да използвате само редове или само колони в процеса на трансформация.

Пример 2.10. За матрица намерете A -1 .

Решение.Първо намираме детерминантата на матрицата A
така че обратната матрица съществува и можем да я намерим по формулата: , където A i j (i,j=1,2,3) - алгебрични допълнения на елементи a i j от оригиналната матрица.

Където .

Пример 2.11. Използвайки метода на елементарните трансформации, намерете A -1 за матрицата: A=.

Решение.Присвояваме идентична матрица от същия ред на оригиналната матрица вдясно: . С помощта на елементарни трансформации на колони ние редуцираме лявата „половина“ до идентичността, като едновременно с това извършваме точно такива трансформации на дясната матрица.
За да направите това, разменете първата и втората колона: ~ . Добавяме първата към третата колона и първата, умножена по -2, към втората: . От първата колона изваждаме удвоената секунда, а от третата - втората, умножена по 6; . Нека добавим третата колона към първата и втората: . Умножете последната колона по -1: . Квадратната матрица, получена вдясно от вертикалната лента, е обратната матрица на дадената матрица A. И така,
.

В първата част беше разгледан метод за намиране на обратната матрица с алгебрични добавки. Тук описваме друг метод за намиране на обратни матрици: използване на трансформациите на Гаус и Гаус-Джордан. Често този метод за намиране на обратната матрица се нарича метод на елементарни трансформации.

Метод на елементарните преобразувания

За да се приложи този метод, дадената матрица $A$ и матрицата за идентичност $E$ се записват в една матрица, т.е. образуват матрица от формата $(A|E)$ (тази матрица се нарича още разширена матрица). След това, с помощта на елементарни трансформации, извършени с редовете на разширената матрица, матрицата отляво на линията става единица, а разширената матрица приема формата $\left(E| A^(-1) \right )$. Елементарните трансформации в тази ситуация включват следните действия:

1. Замяна на два реда.
2. Умножаване на всички елементи на низ по някакво различно от нула число.
3. Добавяне към елементите на един ред на съответните елементи на друг ред, умножени по произволен коефициент.

Тези елементарни трансформации могат да се прилагат по различни начини. Обикновено се избира методът на Гаус или методът на Гаус-Джордан. Като цяло методите на Гаус и Гаус-Джордан са предназначени за решаване на системи от линейни алгебрични уравнения, а не за намиране на обратни матрици. Изразът „прилагане на метода на Гаус за намиране на обратната на матрица“ трябва да се разбира тук като „прилагане на операциите, присъщи на метода на Гаус за намиране на обратната на матрица“.

Номерирането на примерите продължава от първата част. В примерите се разглежда използването на метода на Гаус за намиране на обратната матрица, а в примерите се анализира използването на метода на Гаус-Джордан. Трябва да се отбележи, че ако по време на решението всички елементи на някакъв ред или колона на матрицата, разположени преди линията, са нулирани, тогава обратната матрица не съществува.

Пример #5

Намерете матрица $A^(-1)$, ако $A=\left(\begin(array) (ccc) 7 & 4 & 6 \\ 2 & 5 & -4 \\ 1 & -1 & 3 \end( масив )\вдясно)$.

В този пример обратната матрица ще бъде намерена с помощта на метода на Гаус. Разширената матрица, която обикновено е $(A|E)$, в този пример приема следната форма: $ \left(\begin(array) (ccc|ccc) 7 & 4 & 6 & 1 & 0 & 0 \\ 2 & 5 & -4 & 0 & 1 & 0 \\ 1 & -1 & 3 & 0 & 0 & 1 \end(array) \right)$.

Цел: използвайки елементарни трансформации, приведете разширената матрица до формата $\left(E|A^(-1) \right)$. Прилагаме същите операции, които се използват при решаване на системи от линейни уравнения по метода на Гаус. За да приложите метода на Гаус, е удобно, когато първият елемент от първия ред на разширената матрица е един. За да постигнем това, разменяме първия и третия ред на разширената матрица, което става: $ \left(\begin(array) (ccc|ccc) 1 & -1 & 3 & 0 & 0 & 1 \\ 2 & 5 & - 4 & 0 & 1 & 0 \\ 7 & 4 & 6 & 1 & 0 & 0 \end(array) \right)$.

Сега да преминем към решението. Методът на Гаус е разделен на два етапа: напред и назад (подробно описание на този метод за решаване на системи от уравнения е дадено в примерите на съответната тема). Същите две стъпки ще бъдат приложени в процеса на намиране на обратната матрица.

удар напред

Първа стъпка

С помощта на първия ред нулираме елементите на първата колона, разположена под първия ред:

Нека коментирам малко какво направих. Нотацията $II-2\cdot I$ означава, че съответните елементи на първия ред, предварително умножени по две, са били извадени от елементите на втория ред. Това действие може да се напише отделно, както следва:

Действието $III-7\cdot I$ се изпълнява по абсолютно същия начин. Ако има затруднения при извършването на тези операции, те могат да бъдат извършени отделно (подобно на действието $II-2\cdot I$, показано по-горе), и след това резултатът се въвежда в разширената матрица.

Втора стъпка

С помощта на втория ред нулираме елемента от втората колона, разположен под втория ред:

Разделете третия ред на 5:

Правото бягане приключи. Всички елементи, разположени под главния диагонал на матрицата до линията, бяха нулирани.

Обратен

Първа стъпка

С помощта на третия ред нулираме елементите на третата колона, разположена над третия ред:

Преди да преминете към следващата стъпка, разделете втория ред на $7$:

Втора стъпка

С помощта на втория ред нулираме елементите на втората колона, разположени над втория ред:

Трансформациите са завършени, обратната матрица се намира по метода на Гаус: $A^(-1)=\left(\begin(array) (ccc) -11/5 & 18/5 & 46/5 \\ 2 & -3 & -8 \ \ 7/5 & -11/5 & -27/5 \end(array) \right)$. Проверката, ако е необходимо, може да се извърши по същия начин, както в предишните примери. Ако пропуснете всички обяснения, тогава решението ще приеме формата:

Отговор: $A^(-1)=\left(\begin(array) (ccc) -11/5 & 18/5 & 46/5 \\ 2 & -3 & -8 \\ 7/5 & -11/ 5 & ​​​​-27/5 \end(array) \right)$.

Пример #6

Намерете матрица $A^(-1)$, ако $A=\left(\begin(array) (cccc) -5 & 4 & 1 & 0 \\ 2 & 3 & -2 & 1 \\ 0 & 7 & - 4 & -3 \\ 1 & 4 & 0 & 6 \end(array) \right)$.

За да намерим обратната матрица в този пример, ще използваме същите операции, които се използват при решаването на системи от линейни уравнения с помощта на метода на Гаус. Дадени са подробни обяснения, но тук се ограничаваме до кратки коментари. Нека напишем разширената матрица: $\left(\begin(array) (cccc|cccc) -5 & 4 & 1 & 0 & 1 & 0 & 0 & 0 \\ 2 & 3 & -2 & 1 &0 &1&0 &0 \ \ 0 & 7 & -4 & -3 &0 & 0 & 1 & 0\\ 1 & 4 & 0 & 6 &0 &0 & 0 & 1 \end(array) \right)$. Разменете първия и четвъртия ред на тази матрица: $\left(\begin(array) (cccc|cccc) 1 & 4 & 0 & 6 &0 &0 & 0 & 1 \\ 2 & 3 & -2 & 1 &0 &1&0 &0 \ \ 0 & 7 & -4 & -3 &0 & 0 & 1 & 0\\ -5 & 4 & 1 & 0 & 1 & 0 & 0 & 0 \end(array) \right)$.

удар напред

Трансформациите напред са завършени. Всички елементи, разположени под главния диагонал на матрицата вляво от линията, са нулирани.

Обратен

Намерено обратно на Гаус, $A^(-1)=\left(\begin(array) (cccc) -13/14 & -75/8 & 31/8 & 7/2 \\ -19/8 & - 117/ 16 & 49/16 & 11/4 \\ -23/4 & -141/8 & 57/8 & 13/2 \\ 17/8 & 103/6 & -43/16 & -9/4 \ край ( масив)\десен)$. Проверката, ако е необходимо, се извършва по същия начин, както в примери № 2 и № 3.

Отговор: $A^(-1)=\left(\begin(array) (cccc) -13/14 & -75/8 & 31/8 & 7/2 \\ -19/8 & -117/16 & 49 /16 & 11/4 \\ -23/4 & -141/8 & 57/8 & 13/2 \\ 17/8 & 103/6 & -43/16 & -9/4 \край (масив) \ надясно)$.

Пример #7

Намерете матрица $A^(-1)$, ако $A=\left(\begin(array) (ccc) 2 & 3 & 4 \\ 7 & 1 & 9 \\ -4 & 5 & -2 \end( масив )\вдясно)$.

За да намерим обратната матрица, прилагаме операциите, характерни за метода на Гаус-Джордан. Разликата от метода на Гаус, разгледан в предишните примери и , е, че решението се извършва на един етап. Позволете ми да ви напомня, че методът на Гаус е разделен на 2 етапа: движение напред („ние правим“ нули под главния диагонал на матрицата към лентата) и обратно движение (ние нулираме елементите над главния диагонал на матрицата до бара). За изчисляване на обратната матрица по метода на Гаус-Джордан не са необходими два етапа на решение. Първо, нека направим разширена матрица: $(A|E)$:

$$ (A|E)=\left(\begin(array) (ccc|ccc) 2 & 3 & 4 & 1 & 0 & 0\\ 7 & 1 & 9 & 0 & 1 & 0\\ -4 & 5 & ​​​​-2 &0 & 0 & 1 \end(array) \right) $$

Първа стъпка

Задайте всички елементи на първата колона на нула, с изключение на един. В първата колона всички елементи са различни от нула, така че можем да изберем всеки елемент. Вземете например $(-4)$:

Избраният елемент $(-4)$ е в третия ред, така че използваме третия ред, за да нулираме избраните елементи от първата колона:

Нека направим първия елемент от третия ред равен на единица. За да направим това, разделяме елементите на третия ред на разширената матрица на $(-4)$:

Сега нека започнем да нулираме съответните елементи от първата колона:

В следващите стъпки вече няма да е възможно да използвате третия ред, защото вече сме го приложили в първата стъпка.

Втора стъпка

Нека изберем някакъв ненулев елемент от втората колона и да занулим всички останали елементи от втората колона. Можем да изберем един от два елемента: $\frac(11)(2)$ или $\frac(39)(4)$. Елементът $\left(-\frac(5)(4) \right)$ не може да бъде избран, защото се намира в третия ред, който използвахме в предишната стъпка. Нека изберем елемента $\frac(11)(2)$, който е в първия ред. Нека променим $\frac(11)(2)$ на едно в първия ред:

Сега нека занулим съответните елементи на втората колона:

При по-нататъшно разсъждение първият ред не може да се използва.

Трета стъпка

Необходимо е да нулирате всички елементи на третата колона с изключение на един. Трябва да изберем някакъв ненулев елемент от третата колона. Въпреки това не можем да вземем $\frac(6)(11)$ или $\frac(13)(11)$, защото тези елементи са в първия и третия ред, които използвахме по-рано. Изборът е малък: остава само елементът $\frac(2)(11)$, който е във втория ред. Разделете всички елементи на втория ред на $\frac(2)(11)$:

Сега нека занулим съответните елементи на третата колона:

Трансформациите по метода на Гаус-Йордан са завършени. Остава само матрицата до линията да стане единица. За да направите това, трябва да промените реда на редовете. Първо разменете първия и третия ред:

$$ \left(\begin(array) (ccc|ccc) 1 & 0 & 0 & 47/4 & -13/2 & -23/4 \\ 0 & 0 & 1 & -39/4 & 11/2 & 19/4 \\ 0 & 1 & 0 & 11/2 & -3 & -5/2 \end(array) \right) $$

Сега нека разменим втория и третия ред:

$$ \left(\begin(array) (ccc|ccc) 1 & 0 & 0 & 47/4 & -13/2 & -23/4 \\ 0 & 1 & 0 & 11/2 & -3 & - 5/2 \\ 0 & 0 & 1 & -39/4 & 11/2 & 19/4 \end(array) \right) $$

Така че $A^(-1)=\left(\begin(array) (ccc) 47/4 & -13/2 & -23/4 \\ 11/2 & -3 & -5/2 \\ - 39 /4 & 11/2 & 19/4 \end(array) \right)$. Естествено, решението може да се извърши по различен начин, като се избират елементите на главния диагонал. Обикновено те правят точно това, защото в този случай в края на решението няма да се налага редовете да се разменят. Дадох предишното решение само с една цел: да покажа, че изборът на ред на всяка стъпка не е фундаментален. Ако избираме диагонални елементи на всяка стъпка, тогава решението ще бъде както следва.

Нека е дадена квадратна матрица. Необходимо е да се намери обратната матрица.

Първи начин. В теорема 4.1 за съществуването и единствеността на обратната матрица е посочен един от начините за нейното намиране.

1. Изчислете детерминантата на дадената матрица. Ако, тогава обратната матрица не съществува (матрицата е изродена).

2. Съставете матрица от алгебричните допълнения на матричните елементи.

3. Транспониране на матрицата, получаване на свързаната матрица .

4. Намерете обратната матрица (4.1), като разделите всички елементи на асоциираната матрица на детерминантата

Вторият начин. За намиране на обратната матрица могат да се използват елементарни трансформации.

1. Съставете блокова матрица, като присвоите на дадената матрица идентификационна матрица от същия ред.

2. С помощта на елементарни трансформации, извършени върху редовете на матрицата, приведете левия й блок до най-простата форма. В този случай блоковата матрица се редуцира до формата, където е квадратна матрица, получена в резултат на трансформации от матрицата на идентичността.

3. Ако , тогава блокът е равен на обратната матрица, т.е. ако, тогава матрицата няма обратна.

Наистина, с помощта на елементарни трансформации на редовете на матрицата, нейният ляв блок може да бъде намален до опростен вид (виж фиг. 1.5). В този случай блоковата матрица се трансформира във формата, където е елементарна матрица, която удовлетворява равенството. Ако матрицата е неособена, тогава, съгласно точка 2 от забележки 3.3, нейната опростена форма съвпада с матрицата на идентичността. Тогава от равенството следва, че. Ако матрицата е изродена, тогава нейната опростена форма се различава от матрицата на идентичността и матрицата няма обратна.

11. Матрични уравнения и тяхното решение. Матрична нотация на SLAE. Матричен метод (метод на обратната матрица) за решаване на СЛАУ и условия за неговата приложимост.

Матричните уравнения са уравнения от вида: A*X=C; X*A=C; A*X*B=C където матрицата A, B, C са известни, матрицата X не е известна, ако матриците A и B не са изродени, тогава решенията на оригиналните матрици ще бъдат записани в съответната форма: X=A -1 *C; X=C*A -1; X \u003d A -1 * C * B -1 Матрична форма на запис на системи от линейни алгебрични уравнения.Няколко матрици могат да бъдат свързани с всеки SLAE; освен това самият SLAE може да бъде написан като матрично уравнение. За SLAE (1) разгледайте следните матрици:

Матрицата А се нарича системна матрица. Елементите на тази матрица са коефициентите на дадената SLAE.

Матрицата A˜ се нарича разширена матрична система. Получава се чрез добавяне към системната матрица на колона, съдържаща свободни членове b1,b2,...,bm. Обикновено тази колона е разделена с вертикална линия за по-голяма яснота.

Столбната матрица B се нарича матрица от свободни условия, а колонната матрица X е матрица на неизвестните.

Използвайки въведената по-горе нотация, SLAE (1) може да се запише под формата на матрично уравнение: A⋅X=B.

Забележка

Матриците, свързани със системата, могат да бъдат записани по различни начини: всичко зависи от реда на променливите и уравненията на разглеждания SLAE. Но във всеки случай редът на неизвестните във всяко уравнение на дадена SLAE трябва да бъде еднакъв.

Матричният метод е подходящ за решаване на SLAE, в които броят на уравненията съвпада с броя на неизвестните променливи и детерминантата на основната матрица на системата е различна от нула. Ако системата съдържа повече от три уравнения, тогава намирането на обратната матрица изисква значителни изчислителни усилия, следователно в този случай е препоръчително да се използва за решаване Метод на Гаус.

12. Хомогенни СЛАУ, условия за съществуване на ненулевите им решения. Свойства на частични решения на хомогенни СЛАУ.

Едно линейно уравнение се нарича хомогенно, ако неговият свободен член е равен на нула, и нехомогенно в противен случай. Система, състояща се от хомогенни уравнения, се нарича хомогенна и има общ вид:

13 .Концепцията за линейна независимост и зависимост на частни решения на хомогенна СЛАУ. Фундаментална система за вземане на решения (FSR) и нейното намиране. Представяне на общото решение на хомогенен SLAE по отношение на FSR.

Функционална система г 1 (х ), г 2 (х ), …, г н (х ) е наречен линейно зависимина интервала ( а , b ), ако има набор от постоянни коефициенти, които не са равни на нула едновременно, така че линейната комбинация от тези функции е идентично равна на нула на ( а , b ): за . Ако равенството за е възможно само за , системата от функции г 1 (х ), г 2 (х ), …, г н (х ) е наречен линейно независимина интервала ( а , b ). С други думи, функциите г 1 (х ), г 2 (х ), …, г н (х ) линейно зависимина интервала ( а , b ), ако съществува нула на ( а , b ) тяхната нетривиална линейна комбинация. Функции г 1 (х ),г 2 (х ), …, г н (х ) линейно независимина интервала ( а , b ), ако само тяхната тривиална линейна комбинация е идентично равна на нула на ( а , b ).

Фундаментална система за вземане на решения (FSR)хомогенна SLAE е основата на тази система от колони.

Броят на елементите в FSR е равен на броя на неизвестните в системата минус ранга на системната матрица. Всяко решение на оригиналната система е линейна комбинация от решения на FSR.

Теорема

Общото решение на нехомогенната SLAE е равно на сумата от частното решение на нехомогенната SLAE и общото решение на съответната хомогенна SLAE.

1 . Ако колоните са решения на хомогенна система от уравнения, тогава всяка линейна комбинация от тях също е решение на хомогенна система.

Наистина, от равенствата следва, че

тези. линейна комбинация от решения е решение на хомогенна система.

2. Ако рангът на матрицата на хомогенна система е , тогава системата има линейно независими решения.

Наистина, чрез формулите (5.13) на общото решение на хомогенната система можем да намерим конкретни решения, като присвоим следното на свободните променливи набори от стойности по подразбиране (всеки път се приема, че една от свободните променливи е равна на единица, а останалите са равни на нула):

които са линейно независими. Всъщност, ако една матрица се формира от тези колони, тогава нейните последни редове формират матрицата за идентичност. Следователно минорът, намиращ се в последните редове, не е равен на нула (равен е на единица), т.е. е основен. Следователно рангът на матрицата ще бъде равен. Следователно всички колони на тази матрица са линейно независими (виж теорема 3.4).

Всяка колекция от линейно независими решения на хомогенна система се нарича фундаментална система (множество) от решения .

14 Минор от ти порядък, основен минор, матричен ранг. Изчисляване на матричен ранг.

Редът k минор на матрица A е детерминантата на някои от нейните квадратни подматрица от ред k.

В m x n матрица A минор от порядък r се нарича основен, ако е различен от нула, а всички минори от по-голям порядък, ако съществуват, са равни на нула.

Колоните и редовете на матрицата A, в пресечната точка на които има базис минор, се наричат ​​базисни колони и редове на A.

Теорема 1. (За ранга на матрица). За всяка матрица второстепенният ранг е равен на ранга на реда и равен на ранга на колоната.

Теорема 2. (За основния минор). Всяка колона на матрицата се разлага на линейна комбинация от нейните основни колони.

Рангът на матрица (или второстепенен ранг) е редът на основния минор или, с други думи, най-големият ред, за който съществуват ненулеви минори. Рангът на нулева матрица по дефиниция се счита за 0.

Отбелязваме две очевидни свойства от второстепенен ранг.

1) Рангът на матрица не се променя при транспониране, тъй като когато една матрица се транспонира, всички нейни подматрици се транспонират и второстепенните не се променят.

2) Ако A' е подматрица на матрица A, тогава рангът на A' не надвишава ранга на A, тъй като ненулевият минор, включен в A', също е включен в A.

15. Концепцията за -мерен аритметичен вектор. Векторно равенство. Действия върху вектори (събиране, изваждане, умножение с число, умножение с матрица). Линейна комбинация от вектори.

Поръчана колекция нреални или комплексни числа се нарича n-мерен вектор. Извикват се номерата векторни координати.

Два (ненулеви) вектора аи bса равни, ако са равнопосочни и имат еднакъв модул. Всички нулеви вектори се считат за равни. Във всички останали случаи векторите не са равни.

Добавяне на вектори. Има два начина за добавяне на вектори.1. правило на успоредник. За да добавим векторите и, поставяме началото на двата в една и съща точка. Завършваме успоредника и изчертаваме диагонала на успоредника от същата точка. Това ще бъде сумата от векторите.

2. Вторият начин за добавяне на вектори е правилото на триъгълника. Нека вземем същите вектори и . Добавяме началото на втория към края на първия вектор. Сега нека свържем началото на първия и края на втория. Това е сумата от векторите и . По същото правило можете да добавите няколко вектора. Прикрепяме ги един по един и след това свързваме началото на първия с края на последния.

Изваждане на вектори. Векторът е насочен противоположно на вектора. Дължините на векторите са равни. Сега е ясно какво е изваждане на вектори. Разликата на векторите и е сумата от вектора и вектора .

Умножете вектор по число

Умножаването на вектор по число k води до вектор, чиято дължина е k пъти различна от дължината. Той е съпосочен с вектора, ако k е по-голямо от нула, и насочен противоположно, ако k е по-малко от нула.

Скаларното произведение на векторите е произведението на дължините на векторите и косинуса на ъгъла между тях.Ако векторите са перпендикулярни, точковият им продукт е нула. И ето как скаларното произведение се изразява по отношение на координатите на векторите и .

Линейна комбинация от вектори

Линейна комбинация от вектори вектор на повикване

където - линейни комбинирани коефициенти. Ако комбинацията се нарича тривиална, ако е нетривиална.

16 .Скаларно произведение на аритметични вектори. Дължината на вектора и ъгълът между векторите. Концепцията за ортогоналност на векторите.

Скаларното произведение на векторите a и b е числото

Скаларният продукт се използва за изчисляване на: 1) намиране на ъгъла между тях; 2) намиране на проекцията на вектори; 3) изчисляване на дължината на вектор; 4) условието за перпендикулярност на векторите.

Дължината на отсечката AB е разстоянието между точките A и B. Ъгълът между векторите A и B се нарича ъгъл α = (a, c), 0≤ α ≤П. С което е необходимо да се завърти 1 вектор, така че посоката му да съвпадне с друг вектор. При условие, че началото им съвпада.

Orth a е вектор a с единична дължина и посока a.

17. Системата от вектори и нейната линейна комбинация. Концепцията за линейна зависимост и независимост на система от вектори. Теорема за необходимите и достатъчни условия за линейна зависимост на система от вектори.

Система от вектори a1,a2,...,an се нарича линейно зависима, ако има числа λ1,λ2,...,λn такива, че поне едно от тях е различно от нула и λ1a1+λ2a2+...+λnan=0 . В противен случай системата се нарича линейно независима.

Два вектора a1 и a2 се наричат ​​колинеарни, ако посоките им са еднакви или противоположни.

Три вектора a1,a2 и a3 се наричат ​​компланарни, ако са успоредни на някаква равнина.

Геометрични критерии за линейна зависимост:

а) системата (a1,a2) е линейно зависима тогава и само тогава, когато векторите a1 и a2 са колинеарни.

б) системата (a1,a2,a3) е линейно зависима тогава и само тогава, когато векторите a1,a2 и a3 са копланарни.

теорема. (Необходимо и достатъчно условие за линейна зависимост системивектори.)

Векторна система вектор пространствое линейнозависим тогава и само ако един от векторите на системата е линейно изразен по отношение на останалите вектортази система.

Следствие.1. Система от вектори във векторно пространство е линейно независима тогава и само ако нито един от векторите на системата не е линейно изразен чрез други вектори на тази система.2. Векторна система, съдържаща нулев вектор или два равни вектора, е линейно зависима.

За всяка неособена матрица A съществува уникална матрица A -1, такава че

A*A -1 =A -1 *A = E,

където E е матрицата на идентичност от същия ред като A. Матрицата A -1 се нарича обратна на матрица A.

Ако някой е забравил, в матрицата за идентичност, с изключение на диагонала, запълнен с единици, всички останали позиции са запълнени с нули, пример за матрица за идентичност:

Намиране на обратната матрица чрез метода на присъединената матрица

Обратната матрица се определя от формулата:

където A ij - елементи a ij .

Тези. За да изчислите обратното на матрица, трябва да изчислите детерминантата на тази матрица. След това намерете алгебрични добавки за всички негови елементи и направете нова матрица от тях. След това трябва да транспортирате тази матрица. И разделяме всеки елемент от новата матрица на детерминантата на оригиналната матрица.

Нека да разгледаме няколко примера.

Намерете A -1 за матрица

Решение Намерете A -1 чрез метода на присъединената матрица. Имаме det A = 2. Нека намерим алгебричните допълнения на елементите на матрицата A. В този случай алгебричните допълнения на матричните елементи ще бъдат съответните елементи на самата матрица, взети със знак в съответствие с формула

Имаме A 11 = 3, A 12 = -4, A 21 = -1, A 22 = 2. Формираме присъединената матрица

Транспортираме матрицата A*:

Намираме обратната матрица по формулата:

Получаваме:

Използвайте метода на свързаната матрица, за да намерите A -1 if

Решение Първо, изчисляваме дадената матрица, за да се уверим, че обратната матрица съществува. Ние имаме

Тук добавихме към елементите на втория ред елементите на третия ред, умножени преди това по (-1), и след това разширихме детерминантата с втория ред. Тъй като дефиницията на тази матрица е различна от нула, тогава матрицата, обратна на нея, съществува. За да построим присъединената матрица, намираме алгебричните допълнения на елементите на тази матрица. Ние имаме

Според формулата

транспортираме матрицата A*:

След това по формулата

Намиране на обратната матрица чрез метода на елементарните трансформации

В допълнение към метода за намиране на обратната матрица, който следва от формулата (методът на свързаната матрица), съществува метод за намиране на обратната матрица, наречен метод на елементарни трансформации.

Елементарни матрични трансформации

Следните трансформации се наричат ​​елементарни матрични трансформации:

1) пермутация на редове (колони);

2) умножаване на ред (колона) с ненулево число;

3) добавяне към елементите на ред (колона) на съответните елементи на друг ред (колона), предварително умножени по определено число.

За да намерим матрицата A -1, ние конструираме правоъгълна матрица B \u003d (A | E) от поръчки (n; 2n), присвоявайки на матрицата A отдясно матрицата на идентичност E през разделителната линия:

Помислете за пример.

Използвайки метода на елементарните трансформации, намерете A -1 if

Решение Формираме матрицата B:

Означаваме редовете на матрицата B през α 1 , α 2 , α 3 . Нека извършим следните трансформации на редовете на матрицата B.