Разгънете периодичната функция в ред на Фурие 2n. Редици на Фурие в примери и задачи

Редица на Фурие от периодични функции с период 2π.

Серията на Фурие ви позволява да изучавате периодични функции, като ги разлагате на компоненти. Променливите токове и напрежения, преместванията, скоростта и ускорението на коляно-мотовилковите механизми и акустичните вълни са типични практически примери за приложението на периодични функции в инженерните изчисления.

Разширяването на реда на Фурие се основава на предположението, че всички функции с практическо значение в интервала -π ≤ x ≤ π могат да бъдат изразени като сходящи тригонометрични редове (серията се счита за сходяща, ако последователността от частични суми, съставена от нейните членове, се сближава) :

Стандартна (=обичайна) нотация чрез сумата от sinx и cosx

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,

където a o , a 1 ,a 2 ,...,b 1 ,b 2 ,.. са реални константи, т.е.

Където за диапазона от -π до π коефициентите на реда на Фурие се изчисляват по формулите:

Коефициентите a o ,a n и b n се наричат Коефициенти на Фурие, и ако те могат да бъдат намерени, тогава се извиква серия (1). близо до Фурие,съответстваща на функцията f(x). За ред (1) членът (a 1 cosx+b 1 sinx) се нарича първо или основна хармоника,

Друг начин да напишете серия е да използвате релацията acosx+bsinx=csin(x+α)

f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)

Където a o е константа, c 1 \u003d (a 1 2 +b 1 2) 1/2, c n \u003d (a n 2 +b n 2) 1/2 са амплитудите на различните компоненти и е равно на a n \ u003d arctg a n /b n.

За серия (1) терминът (a 1 cosx + b 1 sinx) или c 1 sin (x + α 1) се нарича първи или основна хармоника,(a 2 cos2x+b 2 sin2x) или c 2 sin(2x+α 2) се нарича втори хармоники така нататък.

За да се представи точно сложен сигнал, обикновено се изисква безкраен брой членове. Въпреки това, в много практически задачи е достатъчно да се разгледат само първите няколко члена.

Редица на Фурие от непериодични функции с период 2π.

Разлагане на непериодични функции.

Ако функцията f(x) е непериодична, тогава тя не може да бъде разширена в серия на Фурие за всички стойности на x. Въпреки това е възможно да се дефинира серия на Фурие, представляваща функция във всеки диапазон с ширина 2π.

Като се има предвид непериодична функция, човек може да състави нова функция, като избере f(x) стойности в определен диапазон и ги повтори извън този диапазон на интервали от 2π. Тъй като новата функция е периодична с период от 2π, тя може да бъде разширена в ред на Фурие за всички стойности на x. Например функцията f(x)=x не е периодична. Въпреки това, ако е необходимо да се разшири в серия на Фурие в интервала от 0 до 2π, тогава периодична функция с период от 2π се конструира извън този интервал (както е показано на фигурата по-долу).

За непериодични функции като f(x)=x, сумата от реда на Фурие е равна на стойността на f(x) във всички точки в дадения диапазон, но не е равна на f(x) за точки извън диапазона. За да се намери редът на Фурие на непериодична функция в диапазона 2π, се използва същата формула на коефициентите на Фурие.

Четни и нечетни функции.

Те казват, че функцията y=f(x) дориако f(-x)=f(x) за всички стойности на x. Графиките на четните функции винаги са симетрични спрямо оста y (т.е. те са огледални). Два примера за четни функции: y=x 2 и y=cosx.

Те казват, че функцията y=f(x) странно,ако f(-x)=-f(x) за всички стойности на x. Графиките на нечетните функции винаги са симетрични спрямо началото.

Много функции не са нито четни, нито нечетни.

Разлагане в ред на Фурие по косинуси.

Редът на Фурие на четна периодична функция f(x) с период 2π съдържа само косинусови членове (т.е. не съдържа синусови членове) и може да включва постоянен член. Следователно,

където са коефициентите на реда на Фурие,

Редът на Фурие на нечетна периодична функция f(x) с период 2π съдържа само членове със синуси (т.е. не съдържа членове с косинуси).

Следователно,

където са коефициентите на реда на Фурие,

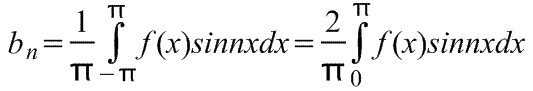
Ред на Фурие на полупериод.

Ако дадена функция е дефинирана за диапазон, да речем от 0 до π, а не само от 0 до 2π, тя може да бъде разширена в серия само по отношение на синусите или само по отношение на косинусите. Полученият ред на Фурие се нарича близо до Фурие на половин цикъл.

Ако искате да получите разлагане Фурие върху полупериод в косинусифункции f(x) в диапазона от 0 до π, тогава е необходимо да се състави четна периодична функция. На фиг. по-долу е функцията f(x)=x, построена върху интервала от x=0 до x=π. Тъй като четната функция е симетрична спрямо оста f(x), начертаваме линията AB, както е показано на фиг. По-долу. Ако приемем, че извън разглеждания интервал, получената триъгълна форма е периодична с период от 2π, тогава крайната графика има формата, display. на фиг. По-долу. Тъй като се изисква да се получи разширението на Фурие в косинуси, както преди, ние изчисляваме коефициентите на Фурие a o и a n

Ако трябва да получите разширение на Фурие за полупериод по синусфункция f(x) в диапазона от 0 до π, тогава е необходимо да се състави нечетна периодична функция. На фиг. по-долу е функцията f(x)=x, построена върху интервала от x=0 до x=π. Тъй като нечетната функция е симетрична спрямо началото, ние конструираме правата CD, както е показано на фиг. Ако приемем, че извън разглеждания интервал, полученият трионообразен сигнал е периодичен с период от 2π, тогава крайната графика има формата, показана на фиг. Тъй като се изисква да се получи разширението на Фурие върху полупериод по отношение на синусите, както преди, ние изчисляваме коефициента на Фурие. b

Редица на Фурие за произволен интервал.

Разгъване на периодична функция с период L.

Периодичната функция f(x) се повтаря, когато x нараства с L, т.е. f(x+L)=f(x). Преходът от разгледаните по-рано функции с период 2π към функции с период L е доста прост, тъй като може да се направи с промяна на променлива.

За да намерим реда на Фурие на функцията f(x) в диапазона -L/2≤x≤L/2, въвеждаме нова променлива u, така че функцията f(x) да има период от 2π по отношение на u. Ако u=2πx/L, тогава x=-L/2 за u=-π и x=L/2 за u=π. Нека също f(x)=f(Lu/2π)=F(u). Редът на Фурие F(u) има формата

(Границите на интегриране могат да бъдат заменени с всеки интервал с дължина L, например от 0 до L)

Редици на Фурие върху полуцикъл за функции, дадени в интервала L≠2π.

За заместването u=πx/L, интервалът от x=0 до x=L съответства на интервала от u=0 до u=π. Следователно функцията може да бъде разширена в редица само по косинуси или само по синуси, т.е. в Ред на Фурие на половин цикъл.

Разширението в косинуси в диапазона от 0 до L има формата

Как да вмъквам математически формули в сайта?

Ако някога трябва да добавите една или две математически формули към уеб страница, тогава най-лесният начин да направите това е както е описано в статията: математическите формули лесно се вмъкват в сайта под формата на снимки, които Wolfram Alpha автоматично генерира. В допълнение към простотата, този универсален метод ще помогне за подобряване на видимостта на сайта в търсачките. Работи отдавна (и мисля, че ще работи завинаги), но е морално остарял.

Ако постоянно използвате математически формули на вашия сайт, тогава ви препоръчвам да използвате MathJax, специална JavaScript библиотека, която показва математически нотации в уеб браузъри, използвайки MathML, LaTeX или ASCIIMathML маркиране.

Има два начина да започнете да използвате MathJax: (1) като използвате прост код, можете бързо да свържете MathJax скрипт към вашия сайт, който ще бъде автоматично зареден от отдалечен сървър в точното време (списък със сървъри); (2) качете скрипта MathJax от отдалечен сървър на вашия сървър и го свържете към всички страници на вашия сайт. Вторият метод е по-сложен и отнема много време и ще ви позволи да ускорите зареждането на страниците на вашия сайт, а ако родителският MathJax сървър стане временно недостъпен по някаква причина, това няма да засегне собствения ви сайт по никакъв начин. Въпреки тези предимства избрах първия метод, тъй като е по-прост, по-бърз и не изисква технически умения. Следвайте примера ми и след 5 минути ще можете да използвате всички функции на MathJax на вашия сайт.

Можете да свържете скрипта на библиотеката MathJax от отдалечен сървър, като използвате две опции за код, взети от основния уебсайт на MathJax или от страницата с документация:

Една от тези опции за код трябва да бъде копирана и поставена в кода на вашата уеб страница, за предпочитане между таговете иили веднага след етикета . Според първата опция MathJax се зарежда по-бързо и забавя страницата по-малко. Но втората опция автоматично проследява и зарежда най-новите версии на MathJax. Ако поставите първия код, той ще трябва да се актуализира периодично. Ако поставите втория код, тогава страниците ще се зареждат по-бавно, но няма да е необходимо постоянно да наблюдавате актуализациите на MathJax.

Най-лесният начин да свържете MathJax е в Blogger или WordPress: в контролния панел на сайта добавете изпълним модул, предназначен да вмъква JavaScript код на трета страна, копирайте първата или втората версия на кода за зареждане по-горе в него и поставете изпълнимия модул по-близо до началото на шаблона (между другото, това изобщо не е необходимо, тъй като скриптът MathJax се зарежда асинхронно). Това е всичко. Сега научете синтаксиса за маркиране на MathML, LaTeX и ASCIIMathML и сте готови да вграждате математически формули във вашите уеб страници.

Всеки фрактал се изгражда според определено правило, което се прилага последователно неограничен брой пъти. Всяко такова време се нарича итерация.

Итеративният алгоритъм за конструиране на гъба на Менгер е доста прост: оригиналният куб със страна 1 е разделен от равнини, успоредни на лицата му, на 27 равни куба. От него се отстраняват един централен куб и 6 куба, съседни на него по стените. Получава се комплект, състоящ се от 20 останали по-малки кубчета. Като направим същото с всяко от тези кубчета, получаваме комплект, състоящ се от 400 по-малки кубчета. Продължавайки този процес за неопределено време, получаваме гъбата Menger.

Много процеси, протичащи в природата и технологиите, имат свойството да се повтарят на равни интервали. Такива процеси се наричат периодични и се описват математически чрез периодични функции. Тези функции включват грях(х) , cos(х) , грях(wx), cos(wx) . Сумата от две периодични функции, например функция на формата , като цяло вече не е периодично. Но може да се покаже, че ако връзката w 1 / w 2 е рационално число, тогава тази сума е периодична функция.

Най-простите периодични процеси - хармоничните трептения - се описват с периодични функции грях(wx) и cos(wx). По-сложните периодични процеси се описват от функции, които са съставени или от краен, или от безкраен брой членове на формата грях(wx) и cos(wx).

3.2. тригонометрични серии. Коефициенти на Фурие

Помислете за функционална серия от формата:

Този ред се нарича тригонометричен; числа а 0 , b 0 , а 1 , b 1 ,а 2 , b 2 …, а н , b н ,… Наречен коефициентитригонометрични серии. Серия (1) често се записва по следния начин:

. (2)

Тъй като членовете на тригонометричната редица (2) имат общ период
, тогава сумата от редицата, ако се събира, също е периодична функция с период
.

Да приемем, че функцията f(х) е сумата от тази серия:

. (3)

В този случай се казва, че функцията е f(х) се разширява в тригонометричен ред. Ако приемем, че този ред се събира равномерно в интервала
, можете да определите неговите коефициенти по формулите:

,
,
. (4)

Коефициентите на редицата, определени по тези формули, се наричат Коефициенти на Фурие.

Тригонометричните редове (2), чиито коефициенти се определят от формулите на Фурие (4), се наричат близо до Фуриесъответстващ на функцията f(х).

Така, ако периодичната функция f(х) е сумата от сходящ се тригонометричен ред, тогава този ред е неговият ред на Фурие.

3.3. Конвергенция на редове на Фурие

Формули (4) показват, че коефициентите на Фурие могат да бъдат изчислени за всеки интегрируем интервал

-периодична функция, т.е. за такава функция винаги може да се състави ред на Фурие. Но дали този ред ще се сближи с функцията f(х) и при какви условия?

Припомнете си, че функцията f(х), определени на сегмента [ а; b] , се нарича частично гладка, ако тя и нейната производна имат най-много краен брой точки на прекъсване от първи род.

Следващата теорема дава достатъчни условия за разлагане на функция в ред на Фурие.

Теорема на Дирихле. Позволявам
-периодична функция f(х) е гладка на части
. Тогава неговият ред на Фурие се събира до f(х) във всяка от неговите точки на непрекъснатост и до стойността 0,5(f(х+0)+ f(х-0)) в точката на счупване.

Пример1.

Разгънете функцията в ред на Фурие f(х)= х, дадени на интервала
.

Решение.Тази функция удовлетворява условията на Дирихле и следователно може да бъде разширена в ред на Фурие. Прилагане на формули (4) и метода на интегриране по части
, намираме коефициентите на Фурие:

По този начин редът на Фурие за функцията f(х) има поглед.

препис

1 МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА НА РУСКАТА ФЕДЕРАЦИЯ НОВОСИБИРСКИ ДЪРЖАВЕН УНИВЕРСИТЕТ ФИЗИЧЕСКИ ФАКУЛТЕТ Р. К. Белхеева РЕДОВЕ НА ФУРИЕ В ПРИМЕРИ И ЗАДАЧИ Урок Новосибирск 211

2 UDC BBK V161 B44 B44 Белхеева Р. К. Серии на Фурие в примери и задачи: Учебник / Новосиб. състояние un-t. Новосибирск, с. ISBN Урокът предоставя основна информация за редовете на Фурие, дава примери за всяка изучавана тема. Подробно е анализиран пример за прилагане на метода на Фурие за решаване на задачата за напречните трептения на струна. Даден е илюстративен материал. Има задачи за самостоятелно решаване. Предназначен е за студенти и преподаватели от Физическия факултет на Новосибирския държавен университет. Публикува се с решение на Методическата комисия на Физическия факултет на НГУ. Рецензент д-р физ.-мат. науки. В. А. Александров ISBN c Новосибирски държавен университет, 211 c Белхеева Р. К., 211

3 1. Разлагане в ред на Фурие на 2π-периодична функция Определение. Редът на Фурие на функцията f(x) е функционалният ред a 2 + (a n cosnx + b n sin nx), (1) където коефициентите a n, b n се изчисляват по формулите: a n = 1 π b n = 1 π f (x) cosnxdx, n = , 1,..., (2) f(x) sin nxdx, n = 1, 2,.... (3) Формулите (2) (3) се наричат формули на Ойлер на Фурие . Фактът, че функцията f(x) съответства на реда на Фурие (1), се записва като формула f(x) a 2 + (a n cosnx + b n sin nx) (4) и те казват, че дясната страна на формулата ( 4) е формален ред функции на Фурие f(x). С други думи, формула (4) означава само, че коефициентите a n, b n се намират по формули (2), (3). 3

4 Определение. 2π-периодична функция f(x) се нарича частично гладка, ако интервалът [, π] съдържа краен брой точки = x< x 1 <... < x n = π таких, что в каждом открытом промежутке (x j, x j+1) функция f(x) непрерывно дифференцируема, а в каждой точке x j существуют конечные пределы слева и справа: f(x j) = lim h + f(x j h), f(x j +) = lim h + f(x j + h), (5) f(x j h) f(x j) f(x j + h) f(x j +) lim, lim. h + h h + h (6) Отметим, что последние два предела превратятся в односторонние производные после замены предельных значений f(x j) и f(x j +) значениями f(x j). Теорема о представимости кусочно-гладкой функции в точке своим рядом Фурье (теорема о поточечной сходимости). Ряд Фурье кусочно-гладкой 2π-периодической функции f(x) сходится в каждой точке x R, а его сумма равна числу f(x), если x точка непрерывности функции f(x), f(x +) + f(x) и равна числу, если x точка разрыва 2 функции f(x). ПРИМЕР 1. Нарисуем график, найдем ряд Фурье функции, заданной на промежутке [, π] формулой, f(x) = x, предполагая, что она имеет период 2π, и вычислим суммы 1 1 числовых рядов (2n + 1) 2, n 2. n= Решение. Построим график функции f(x). Получим кусочно-линейную непрерывную кривую с изломами в точках x = πk, k целое число (рис. 1). 4

5 Фиг. 1. Графика на функцията f(x) nx + π n n 2 = 2 π (1) n 1 n 2 = b n = 1 π π = 2 π f(x) cosnxdx = cos nx cos n 2 = 4 πn2, за нечетно n, за четно n, f(x ) sin nxdx = защото функцията f(x) е четна. Записваме официалния ред на Фурие за функцията f(x): f(x) π 2 4 π k= 5 cos (2k + 1)x (2k + 1) 2.

6 Разберете дали функцията f(x) е частично гладка. Тъй като е непрекъснат, ние изчисляваме само границите (6) в крайните точки на интервала x = ±π и в точката на прекъсване x = : и f(π h) f(π) π h π lim = lim h + h h + h = 1, f(+ h) f(+) + h () lim = lim h + h h + h f(+ h) f(+) + h lim = lim = 1, h + h h + h = 1 , f(h) f () h () lim = lim = 1. h + h h + h Границите съществуват и са крайни, следователно функцията е частично гладка. Съгласно теоремата за поточкова конвергенция, неговият ред на Фурие се сближава към числото f(x) във всяка точка, т.е. f(x) = π 2 4 π k= cos (2k + 1) + x (2k + 1) 2 = = π 2 4 (cosx + 19 π cos 3x) cos 5x (7) Фигури 2 и 3 показват характера на апроксимацията на частичните суми от реда на Фурие S n (x), където S n (x) = a n 2 + (a k coskx + b k sin kx), k=1, към функцията f(x) в интервала [, π] . 6

7 Фиг. Фиг. 2. Графика на функцията f(x) с насложени графики на частични суми S (x) = a 2 и S 1(x) = a 2 + a 1 cos x 3. Графика на функцията f (x) с графика на частична сума, насложена върху нея S 99 (x) \u003d a 2 + a 1 cos x + + a 99 cos 99x 7

8 Замествайки в (7) x = получаваме: = π 2 4 π k= 1 (2k + 1) 2, откъдето намираме сумата на редицата от числа: = π2 8. Като знаем сумата на тази редица, тя е лесно да намерим следната сума. Имаме: S = ( ) S = ()= π S, следователно S = π2 6, т.е. 1 n = π Сумата от тази известна серия е намерена за първи път от Леонхард Ойлер. Често се среща в математическия анализ и неговите приложения. ПРИМЕР 2. Начертайте графика, намерете реда на Фурие на функцията, дадена по формулата f(x) = x за x< π, предполагая, что она имеет период 2π, и вычислим суммы числовых (1) n) рядов + n= ((2n + 1,) (k k + 1) Решение. График функции f(x) приведен на рис. 4. 8

9 Фиг. 4. Графика на функцията f(x) Функцията f(x) е непрекъснато диференцируема на интервала (, π). В точките x = ±π той има крайни граници (5): f() =, f(π) = π. Освен това има крайни граници (6): f(+ h) f(+) lim = 1 и h + h f(π h) f(π +) lim = 1. h + h Следователно f(x) е частично гладка функция. Тъй като функцията f(x) е нечетна, тогава a n =. Коефициентите b n се намират чрез интегриране по части: b n = 1 π f(x) sin πnxdx= 1 [ x cosnx π πn + 1 n = 1 πn [(1)n π + (1) n π] = 2(1 )n+ едно. n Нека съставим формалния ред на Фурие на функцията 2(1) n+1 f(x) sin nx. n 9 cosnxdx ] =

10 Съгласно теоремата за поточкова конвергенция за частично гладка 2π-периодична функция, редът на Фурие на функцията f(x) се свежда до сумата: 2(1) n+1 sin nx = n f(x) = x ако π< x < π, = f(π) + f(π +) 2 =, если x = π, (8) f() + f(+) =, если x =. 2 На рис. 5 8 показан характер приближения частичных сумм S n (x) ряда Фурье к функции f(x). Рис. 5. График функции f(x) с наложенным на него графиком частичной суммы S 1 (x) = a 2 + a 1 cos x 1

11 Фиг. Фиг. 6. Графика на функцията f(x) с насложена върху нея графика на частичната сума S 2 (x). 7. Графика на функцията f(x) с насложена върху нея графика на частичната сума S 3 (x) 11

12 Фиг. 8. Графика на функцията f(x) с насложена върху нея графика на частичната сума S 99 (x) Използваме получените редове на Фурие, за да намерим сумите на две числови редове. Поставяме в (8) x = π/2. Тогава 2 () +... = π 2, или = n= (1) n 2n + 1 = π 4. Лесно намерихме сумата на добре познатата редица на Лайбниц. Поставяйки x = π/3 в (8), намираме () +... = π 2 3, или (1+ 1) () (k) 3π +...= 3k

13 ПРИМЕР 3. Начертайте графика, намерете реда на Фурие на функцията f(x) = sin x, като приемете, че има период 2π, и 1 изчислете сумата от редицата от числа 4n 2 1. Решение. Графиката на функцията f(x) е показана на фиг. 9. Очевидно f(x) = sin x е непрекъсната четна функция с период π. Но 2π също е периодът на функцията f(x). Ориз. 9. Графика на функцията f(x) Нека изчислим коефициентите на Фурие. Всички b n = защото функцията е четна. Използвайки тригонометрични формули, ние изчисляваме a n за n 1: a n = 1 π = 1 π sin x cosnxdx = 2 π sin x cosnxdx = (sin(1 + n)x sin(1 n)x) dx = = 1 () π cos( 1 + n)x cos(1 n)x + = 2 () 1 + (1) n = π 1 + n 1 n π 1 n 2 ( 4 1 ако n = 2k, = π n 2 1 ако n = 2k

14 Това изчисление не ни позволява да намерим коефициента a 1, тъй като при n = 1 знаменателят отива на нула. Следователно изчисляваме директно коефициента a 1: a 1 = 1 π sin x cosxdx =. Тъй като f(x) е непрекъснато диференцируем върху (,) и (, π) и в точките kπ, (k е цяло число), има крайни граници (5) и (6), редът на Фурие на функцията се сближава до то във всяка точка: = 2 π 4 π sinx = 2 π 4 π cos 2nx 4n 2 1 = (1 1 cos 2x cos 4x + 1) cos 6x 1. Графика на функцията f(x) с насложена върху нея графика на частичната сума S(x) 14

15 Фиг. Фиг. 11. Графика на функцията f(x) с насложена върху нея графика на частичната сума S 1 (x). Фиг. 12. Графика на функцията f(x) с насложена върху нея графика на частичната сума S 2 (x). 13. Графика на функцията f(x) с насложена върху нея графика на частичната сума S 99 (x) 15

16 1 Пресметнете сбора на редицата от числа. За да направим това, поставяме 4n 2 1 в (9) x =. Тогава cosnx = 1 за всички n = 1, 2,... и следователно 2 π 4 π 1 4n 2 1 =. 1 4n 2 1 = = 1 2. ПРИМЕР 4. Нека докажем, че ако една гладка непрекъсната функция f(x) удовлетворява условието f(x π) = f(x) за всички x (т.е. е π-периодична) , тогава a 2n 1 = b 2n 1 = за всички n 1, и обратно, ако a 2n 1 = b 2n 1 = за всички n 1, тогава f(x) е π-периодична. Решение. Нека функцията f(x) е π-периодична. Нека изчислим неговите коефициенти на Фурие a 2n 1 и b 2n 1: = 1 π (a 2n 1 = 1 π f(x) cos(2n 1)xdx + f(x) cos(2n 1)xdx =) f(x ) cos (2n 1)xdx. В първия интеграл правим промяната на променливата x = t π : f(x) cos(2n 1)xdx = f(t π) cos(2n 1)(t + π) dt. 16

17 Използвайки факта, че cos(2n 1)(t + π) = cos(2n 1)t и f(t π) = f(t), получаваме: a 2n 1 = 1 π (f(x) cos( 2n 1)x dx+) f(x) cos(2n 1)x dx =. По подобен начин се доказва, че b 2n 1 =. Обратно, нека a 2n 1 = b 2n 1 =. Тъй като функцията f(x) е непрекъсната, тогава, съгласно теоремата за представимостта на функция в точка чрез нейния ред на Фурие, имаме Тогава f(x π) = f(x) = (a 2n cos 2nx + b 2n sin 2nx). (a2n cos 2n(x π) + b 2n sin 2n(x π)) = (a2n cos 2nx + b 2n sin 2nx) = f(x), което означава, че f(x) е π-периодична функция. ПРИМЕР 5. Нека докажем, че ако гладка на части функция f(x) удовлетворява условието f(x) = f(x) за всички x, тогава a = и a 2n = b 2n = за всички n 1, и обратно , ако a = a 2n = b 2n =, тогава f(x π) = f(x) за всички x. Решение. Нека функцията f(x) удовлетворява условието f(x π) = f(x). Нека изчислим неговите коефициенти на Фурие: 17

18 = 1 π (a n = 1 π f(x) cos nxdx + f(x) cosnxdx =) f(x) cosnxdx. В първия интеграл правим промяната на променливата x = t π. Тогава f(x) cosnxdx = f(t π) cosn(t π) dt. Използвайки факта, че cos n(t π) = (1) n cosnt и f(t π) = f(t), получаваме: a n = 1 π ((1) n) f(t) cosnt dt = ако n четно, = 2 π f(t) cos nt dt, ако n е нечетно. π По подобен начин се доказва, че b 2n =. Обратно, нека a = a 2n = b 2n = за всички n 1. Тъй като функцията f(x) е непрекъсната, тогава, съгласно теоремата за представимостта на функция в точка, нейният ред на Фурие удовлетворява равенството f( x) = (a 2n 1 cos ( 2n 1)x + b 2n 1 sin (2n 1)x). осемнадесет

19 Тогава = f(x π) = = = f(x). ПРИМЕР 6. Нека да проучим как да разширим функцията f(x), интегрируема в интервала [, π/2] до интервала [, π], така че нейният ред на Фурие да има формата: a 2n 1 cos(2n 1) х. (1) Решение. Нека графиката на функцията има формата, показана на фиг. 14. Тъй като в редица (1) a = a 2n = b 2n = за всички n, от пример 5 следва, че функцията f(x) трябва да удовлетворява равенството f(x π) = f(x) за всички x. Това наблюдение дава начин за разширяване на функцията f(x) до интервала [, /2] : f(x) = f(x+π), фиг. 15. От факта, че редица (1) съдържа само косинуси, заключаваме, че непрекъснатата функция f (x) трябва да бъде четна (т.е. нейната графика трябва да е симетрична спрямо оста Oy), Фиг.

20 Фиг. 14. Графика на функцията f(x) 15. Графика на продължението на функцията f(x) на интервала [, /2] 2

21 И така, желаната функция има формата, показана на фиг. 16. Фиг. 16. Графика на продължението на функцията f(x) на интервала [, π] Обобщавайки, заключаваме, че функцията трябва да бъде продължена, както следва: f(x) = f(x), f(π x) = f(x), което е интервал [π/2, π], графиката на функцията f(x) е централно симетрична спрямо точката (π/2,), а на интервала [, π] нейната графика е симетричен спрямо оста Oy. 21

22 ОБОБЩЕНИЕ НА ПРИМЕРИ 3 6 Нека l >. Разгледайте две условия: a) f(l x) = f(x); b) f(l + x) = f(x), x [, l/2]. От геометрична гледна точка условие (a) означава, че графиката на функцията f(x) е симетрична по отношение на вертикалната линия x = l/2, а условие (b) че графиката f(x) е централно симетричен спрямо точката (l/2;) на абсцисната ос. Тогава следните твърдения са верни: 1) ако функцията f(x) е четна и условие (a) е изпълнено, тогава b 1 = b 2 = b 3 =... =, a 1 = a 3 = a 5 = ... = ; 2) ако функцията f(x) е четна и условие (b) е изпълнено, тогава b 1 = b 2 = b 3 =... =, a = a 2 = a 4 =... = ; 3) ако функцията f(x) е нечетна и условие (a) е изпълнено, тогава a = a 1 = a 2 =... =, b 2 = b 4 = b 6 =... = ; 4) ако функцията f(x) е нечетна и условие (b) е изпълнено, тогава a = a 1 = a 2 =... =, b 1 = b 3 = b 5 =... =. ЗАДАЧИ В задачи 1 7 начертайте графики и намерете редовете на Фурие за функциите (ако приемем, че имат период от 2π: ако< x <, 1. f(x) = 1, если < x < π. 1, если < x < /2, 2. f(x) =, если /2 < x < π/2, 1, если π/2 < x < π. 3. f(x) = x 2 (< x < π). 4. f(x) = x 3 (< x < π). { π/2 + x, если < x <, 5. f(x) = π/2 x, если < x < π. 22

23 (1 ако /2< x < π/2, 6. f(x) = 1, если π/2 < x < 3π/2. {, если < x <, 7. f(x) = sin x, если < x < π. 8. Как следует продолжить интегрируемую на промежутке [, π/2] функцию f(x) на промежуток [, π], чтобы ее ряд Фурье имел вид: b 2n 1 sin (2n 1)x? Ответы sin(2n 1)x sin(2n + 1)x. π 2n 1 π 2n + 1 n= 3. 1 (1) n () 12 3 π2 + 4 cosnx. 4. (1) n n 2 n 2π2 sin nx. 3 n 5. 4 cos(2n + 1)x π (2n + 1) (1) n cos(2n + 1)x. π 2n + 1 n= n= 7. 1 π sin x 2 cos 2nx. 8. Функцию следует продолжить следующим образом: f(x) = f(x), f(π x) = f(x), π 4n 2 1 то есть на промежутке [, π], график функции f(x) будет симметричен относительно вертикальной прямой x = π/2, на промежутке [, π] ее график центрально симметричен относительно точки (,). 23

24 2. Разгъване на функция, дадена в интервала [, π] само по синуси или само по косинуси Нека функция f е дадена в интервала [, π]. За да го разширим в този интервал в ред на Фурие, първо разширяваме f в интервала [, π] по произволен начин и след това използваме формулите на Ойлер на Фурие. Произволът в продължението на функция води до факта, че за една и съща функция f: [, π] R можем да получим различни редове на Фурие. Но е възможно да се използва този произвол по такъв начин, че да се получи разширение само по синуси или само по косинуси: в първия случай е достатъчно да продължим f по нечетен начин, а във втория по четен начин. Алгоритъм за решение 1. Продължете функцията по нечетен (четен) начин върху (,), и след това периодично с период от 2π продължете функцията към цялата ос. 2. Изчислете коефициентите на Фурие. 3. Съставете ред на Фурие на функцията f(x). 4. Проверете условията за сходимост на редицата. 5. Посочете функцията, към която тази серия ще се сближи. ПРИМЕР 7. Разгънете функцията f(x) = cosx,< x < π, в ряд Фурье только по синусам. Решение. Продолжим функцию нечетным образом на (,) (т. е. так, чтобы равенство f(x) = f(x) выполнялось для всех x (, π)), а затем периодически с периодом 2π на всю ось. Получим функцию f (x), график которой приведен на рис

25 Фиг. 17. Графика на продължителната функция Очевидно функцията f (x) е късично гладка. Нека изчислим коефициентите на Фурие: a n = за всички n, тъй като функцията f (x) е нечетна. Ако n 1, тогава b n = 2 π f(x) sin πnxdx = 2 π cosx sin nxdx = = 2 π dx = = 2 π cos (n + 1) x cos (n 1) x + = π n + 1 n 1 = 1 (1) n (1)n 1 1 = π n + 1 n 1 = 1 ако n = 2 k + 1, (1)n+1 (n 1) + (n + 1) = π ( n + 1)(n 1) 2 2n ако n = 2k. π n 2 1 За n = 1 в предишните изчисления, знаменателят се нулира, така че коефициентът b 1 може да се изчисли директно.

26 По същество: b 1 = 2 π cosx sin xdx =. Съставете реда на Фурие на функцията f (x) : f (x) 8 π k=1 k 4k 2 1 sin 2kx. Тъй като функцията f (x) е частично гладка, тогава, съгласно теоремата за точкова конвергенция, редът на Фурие на функцията f (x) се сближава към сумата cosx, ако π< x <, S(x) =, если x =, x = ±π, cosx, если < x < π. В результате функция f(x) = cosx, заданная на промежутке (, π), выражена через синусы: cosx = 8 π k=1 k 4k 2 1 sin 2kx, x (, π). Рис демонстрируют постепенное приближение частичных сумм S 1 (x), S 2 (x), S 3 (x) к разрывной функции f (x). 26

27 Фиг. Фиг. 18. Графика на функцията f (x) с насложена върху нея графика на частичната сума S 1 (x). 19. Графика на функцията f(x) с насложена върху нея графика на частичната сума S 2 (x) 27

28 Фиг. Фиг. 2. Графика на функцията f (x) с насложена върху нея графика на частичната сума S 3 (x). 21 показва графики на функцията f (x) и нейната частична сума S 99 (x). Ориз. 21. Графика на функцията f (x) с насложена върху нея графика на частичната сума S 99 (x) 28

29 ПРИМЕР 8. Нека разложим функцията f(x) = e ax, a >, x [, π], в ред на Фурие само по косинуси. Решение. Продължаваме функцията по четен начин до (,) (т.е. така че равенството f(x) = f(x) да е в сила за всички x (, π)), а след това периодично с период от 2π до цялото реално ос. Получаваме функцията f (x), чиято графика е показана на фиг. 22. Функция f (x) в точки 22. Графиката на продължителната функция f (x) x = kπ, k е цяло число, има извивки. Нека изчислим коефициентите на Фурие: b n =, тъй като f (x) е четно. Интегрирайки по части, получаваме 29

30 a n = 2 π a = 2 π = 2 cosnxd(e ax) = 2 πa e ax dx = 2 π a (eaπ 1), f(x) cos πnxdx = 2 π πa eax cosnx = 2 πa (eaπ cosnπ 1) ) + 2n πa 2 π e ax cos nxdx = + 2n e ax sin nxdx = πa sin nxde ax = = 2 π a (eaπ cos n π 1) + 2n π sin nx π a 2eax 2n2 e ax cos nxdx = 2 π a 2 π a (eaπ cos n π 1) n2 a a n. 2 Следователно a n = 2a e aπ cos n π 1. π a 2 + n 2 Тъй като f (x) е непрекъснато, съгласно теоремата за поточкова конвергенция, неговият ред на Фурие се събира към f (x). Следователно за всички x [, π] имаме f(x) = 1 π a (eaπ 1)+ 2a π k=1 e aπ (1) k 1 a 2 + k 2 coskx (x π). Фигурите демонстрират постепенното приближаване на частичните суми от реда на Фурие до дадена прекъсната функция. 3

31 Фиг. 23. Графики на функции f (x) и S (x) 24. Графики на функции f (x) и S 1 (x) 25. Графики на функции f (x) и S 2 (x) 26. Графики на функции f (x) и S 3 (x) 31

32 Фиг. 27. Графики на функции f (x) и S 4 (x) 28. Графики на функциите f (x) и S 99 (x) ЗАДАЧА 9. Разгънете функцията f (x) = cos x, x π в ред на Фурие само по косинуси. 1. Разгънете функцията f (x) \u003d e ax, a >, x π, в серия на Фурие само по отношение на синусите. 11. Разгънете функцията f (x) \u003d x 2, x π, в серия на Фурие само в синуси. 12. Разгънете функцията f (x) \u003d sin ax, x π, в ред на Фурие само по косинуси. 13. Разгънете функцията f (x) \u003d x sin x, x π, в серия на Фурие само в синуси. Отговори 9. cosx = cosx. 1. e ax = 2 [ 1 (1) k e aπ] k sin kx. π a 2 + k2 k=1 11. x 2 2 [ π 2 (1) n 1 π n + 2 ] n 3 ((1)n 1) sin nx. 32

33 12. Ако a не е цяло число, тогава sin ax = 1 cosaπ (1 + +2a cos 2nx ) + π a 2 (2n) 2 +2a 1 + cosaπ cos(2n 1)x π a 2 (2n 1) 2; ако a = 2m е четно число, тогава sin 2mx = 8m cos(2n 1)x π (2m) 2 (2n 1) 2; ако a = 2m 1 е положително нечетно число, тогава sin(2m 1)x = 2 ( cos 2nx ) 1 + 2(2m 1). π (2m 1) 2 (2n) π 16 n sin x sin 2nx. 2 π (4n 2 1) 2 3. Ред на Фурие от функция с произволен период Да приемем, че функцията f(x) е дефинирана в интервала [ l, l], l >. Като заместим x = ly, y π, получаваме функцията g(y) = f(ly/π), дефинирана в интервала π [, π]. Тази функция g(y) съответства на (формалния) ред на Фурие () ly f = g(y) a π 2 + (a n cosny + b n sin ny), чиито коефициенти се намират по формулите на Ойлер на Фурие: a n = 1 π g(y) cosny dy = 1 π f (ly π) cos ny dy, n =, 1, 2,..., 33

34 b n = 1 π g(y) sinny dy = 1 π f () ly sin ny dy, n = 1, 2,.... π l, получаваме леко модифициран тригонометричен ред за функцията f(x): където f(x) a 2 + a n = 1 l b n = 1 l l l l l (a n cos πnx l f(x) cos πnx l f(x) sin πnx l + b n sin πnx), (11) l dx, n =, 1, 2 ,..., (12) dx, n = 1, 2,.... (13) За формули (11) (13) се казва, че дефинират разширение в ред на Фурие на функция с произволен период. ПРИМЕР 9. Намерете реда на Фурие на функцията, дадена в интервала (l, l) с израза ( A if l< x, f(x) = B, если < x < l, считая, что она периодична с периодом 2l. Решение. Продолжим функцию периодически, с периодом 2l, на всю ось. Получим функцию f (x), кусочно-постоянную в промежутках (l + 2kl, l + 2kl), и претерпевающую разрывы первого рода в точках x = lk, k целое число. Ее коэффициенты Фурье вычисляются по формулам (12) и (13): 34

35 a = 1 l l f(x) dx = 1 l A dx + 1 l l B dx = A + B, l l a n = 1 l l l f(x) cos πnx l dx = = 1 l = 1 l l A cos πnx l = A + B π n l b n = 1 l dx + 1 l l B cos πnx l sin πn = ако n, l l A sin πnx l f(x) sin πnx l dx + 1 l l dx = B sin πnx l = B A (1 cosπn). πn Съставете реда на Фурие на функцията f (x) : f(x) A + B π (B A Тъй като cosπn = (1) n, то n dx = dx = (1 cosπn) sin πnx). l за n = 2k получаваме b n = b 2k =, за n = 2k 1 b n = b 2k 1 = 35 2(B A) π(2k 1).

36 Следователно f(x) A + B (B A) π (sin πx + 1 3πx sin + 1 5πx sin +... l 3 l 5 l Според теоремата за поточкова конвергенция, редът на Фурие на функцията f(x) се сближава към сумата A, ако l< x, S(x) = A + B, если x =, x = ±l, 2 B, если < x < l. Придавая параметрам l, A, B конкретные значения получим разложения в ряд Фурье различных функций. Пусть l = π, A =, B = 3π. На рис. 29 приведены графики первых пяти членов ряда, функции f (x) и частичной суммы S 7 (x) = a 2 + b 1 sin x b 7 sin 7x. Величина a является средним значением функции на промежутке. Обратим внимание на то, что с возрастанием ча- 2 стоты гармоники ее амплитуда уменьшается. Для наглядности графики трех высших гармоник сдвинуты по вертикали. На рис. 3 приведен график функции f(x) и частичной суммы S 99 (x) = a 2 + b 1 sin x b 99 sin 99x. Для наглядности на рис. 31 приведен тот же график в другом масштабе. Последние два графика иллюстрируют явление Гиббса. 36).

37 Фиг. 29. Графика на функцията f (x) с насложени графики на хармониците S (x) = a 2 и S 1 (x) = b 1 sinx. За по-голяма яснота графиките на трите висши хармоника S 3 (x) = b 3 sin 3πx, S l 5 (x) = b 5 sin 5πx l и S 7 (x) = b 7 sin 7πx се изместват вертикално нагоре l 37

38 Фиг. Фиг. 3. Графика на функцията f(x) с насложена върху нея графика на частичната сума S 99 (x). 31. Фрагмент от фиг. 3 в друга скала 38

39 ЗАДАЧИ В задачите разгънете посочените функции в редове на Фурие в дадени интервали. 14. f(x) = x 1, (1, 1). 15. f(x) = ch2x, (2, 2] f(x) = x (1 x), (1, 1]. 17. f(x) = cos π x, [ 1, 1] f(x ) = sin π x, (1, 1).( 2 1 ако 1< x < 1, 19. f(x) = 2l = 4., если 1 < x < 3; x, если x 1, 2. f(x) = 1, если 1 < x < 2, 2l = 3. { 3 x, если 2 x < 3;, если ωx, 21. f(x) = 2l = 2π/ω. sin ωx, если ωx π; Разложить в ряды Фурье: а) только по косинусам; б) только по синусам указанные функции в заданных промежутках (, l) { 22. f(x) = { 23. f(x) = ax, если < x < l/2, a(l x), если l/2 < x < l. 1, если < x 1, 2 x, если 1 x 2. Ответы 14. f(x) = 4 cos(2n 1)πx. π 2 (2n 1) f(x) = sh sh4 (1) n nπx cos 16 + π 2 n f(x) = cos 2nπx. π 2 n f(x) = 2 π + 8 π (1) n n 1 4n 2 cosnπx. 39

40 18. f(x) = 8 (1) n n sin nπx. π 1 4n (1) n 2n + 1 cos πx. π 2n πn 2πnx π 2 sin2 cos n π sin ωx 2 cos 2nωx π 4n 2 1. (l 22. a) f(x) = al 4 2) 1 (4n 2)πx cos, π 2 (2n 1) 2 l b) f(x) = 4al (1) n 1 (2n 1) πx sin. π 2 (2n 1) 2 l 23. a) f(x) = (cos π π 2 2 x 2 2 cos 2π 2 2 x cos 3π 2 2 x cos 5π), 2 2 x... b) f( x) = 4 (sin π π 2 2 x 1 3 sin 3π)+ 2 2 x (sin π π 2 x cos 2π) 2 x Комплексна форма на реда на Фурие Разлагане f(x) = c n e inx, където c n = 1 2π f (x)e inx dx, n = ±1, ±2,..., се нарича комплексна форма на реда на Фурие. Функцията се разширява в сложен ред на Фурие при същите условия, при които се разширява в реален ред на Фурие. четири

41 ПРИМЕР 1. Намерете реда на Фурие в комплексната форма на функцията, дадена с формулата f(x) = e ax в интервала [, π), където a е реално число. Решение. Нека изчислим коефициентите: = c n = 1 2π f(x)e inx dx = 1 2π e (a in)x dx = 1 ((1) n e aπ (1) n e aπ) = (1)n sh aπ. 2π(a in) π(a in) Комплексният ред на Фурие на функцията f има формата f(x) sh aπ π n= (1) n a in einx. Нека проверим, че функцията f(x) е частично гладка: в интервала (, π) тя е непрекъснато диференцируема, а в точките x = ±π има крайни граници (5), (6) lim h + ea( +h) = e aπ, lim h + ea(π h) = e aπ, e a(+h) e a(+) lim h + h = ae aπ e a(π h) e a(π), lim h + h = ae aπ. Следователно функцията f(x) може да бъде представена чрез редица на Фурие sh aπ π n= (1) n a в einx, която се свежда до сумата: ( e S(x) = ax ако π< x < π, ch a, если x = ±π. 41

42 ПРИМЕР 11. Намерете реда на Фурие в комплексна и реална форма на функцията, дадена с формулата f(x) = 1 a 2 1 2a cosx + a2, където a< 1, a R. Решение. Функция f(x) является четной, поэтому для всех n b n =, а a n = 2 π f(x) cosnxdx = 2 (1 a2) π cos nxdx 1 2a cosx + a 2. Не будем вычислять такой сложный интеграл, а применим следующий прием: 1. используя формулы Эйлера sin x = eix e ix 2i = z z 1, cosx = eix + e ix 2i 2 = z + z 1, 2 где z = e ix, преобразуем f(x) к рациональной функции комплексной переменной z; 2. полученную рациональную функцию разложим на простейшие дроби; 3. разложим простейшую дробь по формуле геометрической прогрессии; 4. упростим полученную формулу. Итак, по формулам Эйлера получаем = f(x) = 1 a 2 1 a(z + z 1) + a 2 = (a 2 1)z (z a)(z a 1) = a z a az. (14) 42

43 Спомнете си, че сумата от безкрайна геометрична прогресия със знаменател q (q< 1) вычисляется по формуле: + n= q n = 1 1 q. Эта формула верна как для вещественных, так и для комплексных чисел. Поскольку az = a < 1 и a/z = a < 1, то az = + a n z n = a n e inx, a z a = a z 1 1 a/z = a z n= + n= a n z = + n n= n= a n+1 z = + a n+1 e i(n+1)x. n+1 После замены переменной (n + 1) = k, < k < 1, получим: 1 a z a = a k e ikx. Следовательно, f(x) + n= k= c n e inx, где c n = n= { a n, если n, a n, если n <, то есть c n = a n. Поскольку функция f(x) непрерывна, то в силу теоремы о поточечной сходимости имеет место равенство: f(x) = + n= a n e inx. Тем самым мы разложили функцию f(x) в ряд Фурье в комплексной форме. 43

44 Сега нека намерим реда на Фурие в реална форма. За да направим това, групираме членовете с числа n и n за n: a n e inx + a n e inx = 2a neinx + e inx Тъй като c = 1, тогава 2 = 2a n cos nx. f(x) = 1 a 2 1 2a cosx + a = a n cosnx. 2 Това е ред на Фурие в реалната форма на функцията f(x). Така, без да изчисляваме нито един интеграл, намерихме реда на Фурие на функцията. По този начин изчислихме твърд интеграл в зависимост от параметъра cos nxdx 1 2a cosx + a = 2 π an 2 1 a2, a< 1. (15) ПРИМЕР 12. Найдем ряд Фурье в комплексной и вещественной форме функции, заданной формулой a sin x f(x) = 1 2a cosx + a2, a < 1, a R. Решение. Функция f(x) является нечетной, поэтому для всех n a n = и b n = 2 π f(x) sin nxdx = 2a π sin x sin nxdx 1 2a cosx + a 2. Чтобы записать ряд Фурье нужно вычислить сложные интегралы или воспользоваться приемом, описанным выше. Поступим вторым способом: 44

45 a(z z 1) f(x) = 2i (1 a(z z 1) + a 2) = i 2 + i (a + a 1)z 2 2 (z a)(z a 1) = = i 2 + i () a 2 z a + a 1. z a 1 Развиваме всяка от простите дроби според формулата на геометричната прогресия: + a z a = a 1 z 1 a = a a n z z n, n= z a 1 z a = az = a n z n. n= Това е възможно, защото az = a/z = a< 1. Значит + ia n /2, если n <, f(x) c n e inx, где c n =, если n =, n= ia n /2, если n >, или по-накратко, c n = 1 2i a n sgnn. Така се намира редът на Фурие в сложна форма. Групирайки членове с числа n и n, получаваме реда на Фурие на функцията в реална форма: = f(x) = + a sin x 1 2a cosx + a + 2 (1 2i an e inx 1 2i an e inx n= +) = c n e inx = a n sin nx. Отново успяхме да изчислим следния комплексен интеграл: sin x sin nxdx 1 2a cosx + a 2 = π an 1. (16) 45

46 ЗАДАЧА 24. Използвайки (15), изчислете интеграла cos nxdx 1 2a cosx + a 2 за реално a, a > Като използвате (16), изчислете интеграла sin x sin nxdx за реално a, a > a cosx + a2 В задачи , намерете редицата на Фурие в сложна форма за функции. 26. f(x) = sgn x, π< x < π. 27. f(x) = ln(1 2a cosx + a 2), a < 1. 1 a cosx 28. f(x) = 1 2a cosx + a2, a < Докажите, что функция f, определенная в промежутке [, π], вещественнозначна, если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n =, ±1, ±2, Докажите, что функция f, определенная в промежутке [, π], является четной (т. е. удовлетворяет соотношению f(x) = f(x)), если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n = ±1, ±2, Докажите, что функция f, определенная в промежутке [, π], является нечетной (т. е. удовлетворяет соотношению f(x) = f(x)), если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n =, ±1, ±2,.... Ответы 1 2π 24. a n a π a n i + e 2inx, где подразумевается, что слагаемое, соответствующее n =, пропущено. π n n= a n n cosnx. 28. a n cosnx. n= 46

47 5. Теорема за равенство на Ляпунов (равенство на Ляпунов). Нека функция f: [, π] R е такава, че f 2 (x) dx< +, и пусть a n, b n ее коэффициенты Фурье. Тогда справедливо равенство, a (a 2 n + b2 n) = 1 π называемое равенством Ляпунова. f 2 (x) dx, ПРИМЕР 13. Напишем равенство Ляпунова для функции { 1, если x < a, f(x) =, если a < x < π и найдем с его помощью суммы числовых рядов + sin 2 na n 2 и + Решение. Очевидно, 1 (2n 1) 2. 1 π f 2 (x) dx = 1 π a a dx = 2a π. Так как f(x) четная функция, то для всех n имеем b n =, a = 2 π f(x) dx = 2 π a dx = 2a π, 47

48 a n = 2 π f(x) cosnxdx = 2 π a cos nxdx = 2 sin na πn. Следователно равенството на Ляпунов за функцията f(x) приема формата: 2 a 2 π + 4 sin 2 na = 2a 2 π 2 n 2 π. От последното равенство за a π намираме sin 2 na n 2 = a(π a) 2 Ако приемем a = π 2, получаваме sin2 na = 1 за n = 2k 1 и sin 2 na = за n = 2k. Следователно k=1 1 (2k 1) 2 = π2 8. ПРИМЕР 14. Нека напишем равенството на Ляпунов за функцията f(x) = x cosx, x [, π] и да го използваме, за да намерим сумата на числото редица (4n 2 + 1) 2 (4n 2 1) 4. 1 π Решение. Преките изчисления дават = π π f 2 (x) dx = 1 π x 2 cos 2 xdx = 1 π x sin 2xdx = π π x cos x = π x 21 + cos 2x dx = 2 π 1 4π cos 2xdx =

49 Тъй като f(x) е четна функция, тогава за всички n имаме b n =, a n = 2 π = 1 π 1 = π(n + 1) = f(x) cosnxdx = 2 π 1 cos(n + 1 )x π (n + 1) 2 x cosxcosnxdx = x (cos(n + 1)x + cos(n 1)x) dx = 1 π sin(n + 1)xdx sin(n 1)xdx = π(n 1) π π 1 + cos(n 1)x = π(n 1) 2 1 (= (1) (n+1) 1) 1 (+ (1) (n+1) 1) = π(n + 1) 2 π(n 1) 2 () = (1)(n+1) 1 1 π (n + 1) + 1 = 2 (n 1) 2 = 2 (1)(n+1) 1 n k π (n 2 1) = π (4k 2 1) 2 ако n = 2k, 2 ако n = 2k + 1. Коефициентът a 1 трябва да се изчисли отделно, тъй като в общата формула за n = 1 знаменателят на дробта се нулира . = 1 π a 1 = 2 π f(x) cosxdx = 2 π x(1 + cos 2x)dx = π 2 1 2π 49 x cos 2 xdx = sin 2xdx = π 2.

50 Така равенството на Ляпунов за функцията f(x) има формата: 8 π + π (4n 2 + 1) 2 π 2 (4n 2 1) = π 2 1) = π π ЗАДАЧА 32. Напишете равенството на Ляпунов за функцията ( x f(x) = 2 πx, ако x< π, x 2 πx, если π < x. 33. Напишите равенства Ляпунова для функций f(x) = cos ax и g(x) = sin ax, x [, π]. 34. Используя результат предыдущей задачи и предполагая, что a не является целым числом, выведите следующие классические разложения функций πctgaπ и (π/ sin aπ) 2 по рациональным функциям: πctgaπ = 1 a + + 2a a 2 n 2, (π) = sin aπ (a n) 2. n= 35. Выведите комплексную форму обобщенного равенства Ляпунова. 36. Покажите, что комплексная форма равенства Ляпунова справедлива не только для вещественнозначных функций, но и для комплекснозначных функций. 5

51 π (2n + 1) = π sin 2απ 2απ = 2sin2 απ α 2 π 2 Отговори + 4 sin2 απ π 2 α 2 (α 2 n 2) 2; sin 2απ 1 2απ = απ n 2 4sin2 π 2 (α 2 n 2) 2. 1 π 35. f(x)g(x) dx= c n d n, където c n е коефициентът на Фурие 2π на f(x) и d n е функцията на коефициента на Фурие g(x). 6. Диференциране на редове на Фурие Нека f: R R е непрекъснато диференцируема 2π-периодична функция. Неговият ред на Фурие има формата: f(x) = a 2 + (a n cos nx + b n sin nx). Производната f (x) на тази функция ще бъде непрекъсната и 2π-периодична функция, за която може да се запише формален ред на Фурие: f (x) a 2 + (a n cos nx + b n sin nx), където a, a n , b n, n = 1 , 2,... Коефициенти на Фурие на функцията f (x). 51

52 Теорема (за почленно диференциране на редове на Фурие). При горните предположения са верни равенствата a =, a n = nb n, b n = na n, n 1. ПРИМЕР 15. Нека частично гладка функция f(x) е непрекъсната в интервала [, π]. Нека докажем, че когато условието f(x)dx = е изпълнено, неравенството 2 dx 2 dx, наречено неравенство на Стеклов, е в сила и ще проверим, че равенството в него се реализира само за функции от вида f(x) = A cosx. С други думи, неравенството на Стеклов дава условия, при които малкостта на производната (в средноквадратична стойност) предполага малкостта на функцията (в средноквадратична стойност). Решение. Нека разширим равномерно функцията f(x) до интервала [, ]. Означете разширената функция със същия символ f(x). Тогава продължителната функция ще бъде непрекъсната и късово гладка на интервала [, π]. Тъй като функцията f(x) е непрекъсната, тогава f 2 (x) е непрекъсната на интервала и 2 dx< +, следовательно, можно применить теорему Ляпунова, согласно которой имеет место равенство 1 π 2 dx = a () a 2 n + b 2 n. 52

53 Тъй като продължителната функция е четна, тогава b n =, a = по условие. Следователно равенството на Ляпунов приема формата 1 π 2 dx = a 2 π n. (17) Нека се уверим, че f (x) удовлетворява заключението на теоремата за диференцирането член по член на реда на Фурие, тоест, че a =, a n = nb n, b n = na n, n 1. Нека производната f (x) претърпи прекъсвания в точките x 1, x 2,..., x N в интервала [, π]. Означаваме x =, x N+1 = π. Нека разделим интервала на интегриране [, π] на N +1 интервала (x, x 1),..., (x N, x N+1), на всеки от които f(x) е непрекъснато диференцируем. След това, използвайки свойството за адитивност на интеграла и след това интегрирайки по части, получаваме: b n = 1 π = 1 π = 1 π f (x) sin nxdx = 1 π N f(x) sin nx j= N f(x ) sin nx j= x j+1 x j x j+1 x j n n π N j= x j+1 x j x j+1 x j f (x) sin nxdx = f(x) cosnxdx = f(x) cosnxdx = = 1 π [( f(x 1) sin nx 1 f(x) sin nx) + + (f(x 2) sinnx 2 f(x 1) sin nx 1)

54 + (f(x N+1) sin nx N+1 f(x N) sin nx N)] na n = = 1 π na n = = 1 π na n = na n. x j+1 a = 1 f (x)dx = 1 N f (x)dx = π π j= x j = 1 N x j+1 f(x) π = 1 (f(π) f()) = . x j π j= По същия начин получаваме a n = nb n. Показахме, че теоремата за почленно диференциране на редове на Фурие за непрекъсната късично-гладка 2π-периодична функция, чиято производна в интервала [, π] претърпява прекъсвания от първи вид, е вярна. Така че f (x) a 2 + (a n cosnx + b n sin nx) = (na n)sin nx, тъй като a =, a n = nb n =, b n = na n, n = 1, 2,... Тъй като 2dx< +, то по равенству Ляпунова 1 π 2 dx = 54 n 2 a 2 n. (18)

55 Тъй като всеки член на редицата в (18) е по-голям или равен на съответния член на редицата в (17), тогава 2 dx 2 dx. Припомняйки си, че f(x) е четно продължение на оригиналната функция, имаме 2 dx 2 dx. Което доказва равенството на Стеклов. Сега нека разгледаме за кои функции се отнася равенството в неравенството на Стеклов. Ако за поне едно n 2 коефициентът a n е различен от нула, тогава a 2 n< na 2 n. Следовательно, равенство a 2 n = n 2 a 2 n возможно только если a n = для n 2. При этом a 1 = A может быть произвольным. Значит в неравенстве Стеклова равенство достигается только на функциях вида f(x) = A cosx. Отметим, что условие πa = f(x)dx = (19) существенно для выполнения неравенства Стеклова, ведь если условие (19) нарушено, то неравенство примет вид: a a 2 n n 2 a 2 n, а это не может быть верно при произвольном a. 55

56 ЗАДАЧИ 37. Нека късично-гладка функция f(x) е непрекъсната в интервала [, π]. Докажете, че при условието f() = f(π) = неравенството 2 dx 2 dx, наричано още неравенство на Стеклов, е в сила и се уверете, че равенството в него е в сила само за функции от вида f(x) = B sin x . 38. Нека функция f е непрекъсната в интервала [, π] и има в нея (с възможно изключение само на краен брой точки) квадратно интегрируема производна f(x). Докажете, че ако условията f() = f(π) и f(x) dx = са изпълнени, то неравенството 2 dx 2 dx, наречено неравенство на Виртингер, е в сила и равенството в него има място само за функциите на форма f(x) = A cosx + B sinx. 56

57 7. Приложение на редовете на Фурие за решаване на частични диференциални уравнения При изучаване на реален обект (природно явление, производствен процес, система за управление и т.н.) два фактора се оказват значими: нивото на натрупаните знания за изследвания обект и степента на развитие на математическия апарат. На съвременния етап от научните изследвания е разработена следната верига: явление - физически модел - математически модел. Физическата постановка (модел) на проблема е следната: идентифицират се условията за развитие на процеса и основните фактори, влияещи върху него. Математическата формулировка (модел) се състои в описание на факторите и условията, избрани във физическата формулировка под формата на система от уравнения (алгебрични, диференциални, интегрални и др.). Проблемът се нарича добре поставен, ако в определено функционално пространство решението на проблема съществува, еднозначно и непрекъснато зависи от началните и граничните условия. Математическият модел не е идентичен на разглеждания обект, а е негово приблизително описание.Извеждане на уравнението на свободните малки напречни трептения на струната.Ще следваме учебника. Нека краищата на връвта са фиксирани, а самата връв да е опъната. Ако струната бъде извадена от равновесие (например чрез издърпване или удар), тогава струната ще започне 57

58 колебайте се. Ще приемем, че всички точки на струната се движат перпендикулярно на нейното равновесно положение (напречни вибрации) и във всеки момент от време струната лежи в една и съща равнина. Нека вземем система от правоъгълни координати xou в тази равнина. Тогава, ако в началния момент t = струната е била разположена по оста Ox, тогава u ще означава отклонението на струната от равновесното положение, т.е. позицията на точката на струната с абсцисата x в произволен момент t съответства на стойността на функцията u(x, t). За всяка фиксирана стойност на t, графиката на функцията u(x, t) представлява формата на вибриращата струна в момент t (фиг. 32). При постоянна стойност на x функцията u(x, t) дава закона за движение на точка с абсцисата x по права линия, успоредна на оста Ou, производната u t е скоростта на това движение, а втората производна 2 u t 2 е ускорението. Ориз. 32. Сили, приложени към безкрайно малък участък от низ Нека напишем уравнение, на което трябва да отговаря функцията u(x, t). За да направим това, правим някои по-опростени предположения. Ще приемем, че низът е абсолютно гъвкав.

59 coy, тоест ще приемем, че струната не се съпротивлява на огъване; това означава, че напреженията, възникващи в струната, винаги са насочени тангенциално към нейния моментен профил. Приема се, че струната е еластична и се подчинява на закона на Хук; това означава, че промяната в големината на силата на опън е пропорционална на промяната в дължината на струната. Да приемем, че низът е хомогенен; това означава, че неговата линейна плътност ρ е постоянна. Пренебрегваме външните сили. Това означава, че разглеждаме свободни трептения. Ще изучаваме само малки вибрации на струна. Ако означим с ϕ(x, t) ъгъла между абсцисната ос и допирателната към струната в точката с абсцисата x в момента t, тогава условието за малки колебания е, че стойността на ϕ 2 (x, t) може да се пренебрегне в сравнение с ϕ (x, t), т.е. ϕ 2. Тъй като ъгълът ϕ е малък, тогава cos ϕ 1, ϕ sin ϕ tg ϕ u, следователно стойността (u x x,) 2 може също бъдете пренебрегнати. От това веднага следва, че в процеса на трептене можем да пренебрегнем промяната в дължината на който и да е участък от струната. Наистина, дължината на парче низ M 1 M 2, проектирана в интервала на оста x, където x 2 = x 1 + x, е равна на l = x 2 x () 2 u dx x. x Нека покажем, че при нашите предположения стойността на силата на опън T ще бъде постоянна по протежение на цялата струна. За да направим това, ние вземаме част от низа M 1 M 2 (фиг. 32) в момент t и заместваме действието на изхвърлените части

60 kov от силите на опън T 1 и T 2. Тъй като според условието всички точки на струната се движат успоредно на оста Ou и няма външни сили, сумата от проекциите на силите на опън върху оста Ox трябва да бъде равно на нула: T 1 cosϕ(x 1, t) + T 2 cosϕ(x 2, t) =. Следователно, поради малките ъгли ϕ 1 = ϕ(x 1, t) и ϕ 2 = ϕ(x 2, t), заключаваме, че T 1 = T 2. Означаваме общата стойност на T 1 = T 2 по T. Сега изчисляваме сумата от проекциите F u на същите сили върху оста Ou: F u = T sin ϕ(x 2, t) T sin ϕ(x 1, t). (2) Тъй като за малки ъгли sin ϕ(x, t) tg ϕ(x, t) и tg ϕ(x, t) u(x, t)/ x, уравнение (2) може да бъде пренаписано като F u T (tan ϕ(x 2, t) tan ϕ(x 1, t)) (u T x (x 2, t) u) x (x 1, t) x x T 2 u x 2(x 1, t) x . Тъй като точката x 1 е избрана произволно, тогава F u T 2 u x2(x, t) x. След като бъдат намерени всички сили, действащи върху сечението M 1 M 2, ние прилагаме към него втория закон на Нютон, според който произведението на масата и ускорението е равно на сумата от всички действащи сили. Масата на парче връв M 1 M 2 е равна на m = ρ l ρ x, а ускорението е равно на 2 u(x, t). Уравнението t 2 на Нютон приема формата: 2 u t (x, t) x = u 2 α2 2 x2(x, t) x, където α 2 = T ρ е постоянно положително число. 6

61 Намалявайки с x, получаваме 2 u t (x, t) = u 2 α2 2 x2(x, t). (21) В резултат на това получихме линейно хомогенно частично диференциално уравнение от втори ред с постоянни коефициенти. Нарича се уравнение на вибрациите на струната или уравнение на едномерната вълна. Уравнение (21) по същество е преформулиране на закона на Нютон и описва движението на струна. Но във физическата формулировка на проблема имаше изисквания краищата на струната да са фиксирани и позицията на струната в даден момент от времето да е известна. Ще запишем тези условия в уравнения, както следва: а) ще приемем, че краищата на низа са фиксирани в точките x = и x = l, т.е. ще приемем, че за всички t отношенията u(, t) = , u(l, t ) = ; (22) b) ще приемем, че в момента t = позицията на низа съвпада с графиката на функцията f(x), т.е. ще приемем, че за всички x [, l] равенството u(x, ) = f( x); (23) c) ще приемем, че в момента t = на точката на струната с абсцисата x е дадена скорост g(x), т.е. ще приемем, че u (x,) = g(x). (24) t Съотношенията (22) се наричат гранични условия, а отношенията (23) и (24) се наричат начални условия. Математически модел на свободен малък напречен 61

62 вибрации на струната е, че е необходимо да се реши уравнение (21) с гранични условия (22) и начални условия (23) и (24) Решение на уравнението на свободните малки напречни вибрации на струната по метода на Фурие< t <, удовлетворяющие граничным условиям (22) и начальным условиям (23) и (24), будем искать методом Фурье (называемым также методом разделения переменных). Метод Фурье состоит в том, что частные решения ищутся в виде произведения двух функций, одна из которых зависит только от x, а другая только от t. То есть мы ищем решения уравнения (21), которые имеют специальный вид: u(x, t) = X(x)T(t), (25) где X дважды непрерывно дифференцируемая функция от x на [, l], а T дважды непрерывно дифференцируемая функция от t, t >. Замествайки (25) в (21), получаваме: X T = α 2 X T, (26) или T (t) α 2 T(t) = X (x) X(x). (27) Твърди се, че е имало разделяне на променливите. Тъй като x и t не зависят едно от друго, лявата страна в (27) не зависи от x, но дясната страна не зависи от t и общата стойност на тези съотношения е 62

63 трябва да бъде константа, която означаваме с λ: T (t) α 2 T(t) = X (x) X(x) = λ. Оттук получаваме две обикновени диференциални уравнения: X (x) λx(x) =, (28) T (t) α 2 λt(t) =. (29) В този случай граничните условия (22) приемат формата X()T(t) = и X(l)T(t) =. Тъй като те трябва да бъдат изпълнени за всички t, t >, тогава X() = X(l) =. (3) Нека намерим решения на уравнение (28), удовлетворяващи гранични условия (3). Нека разгледаме три случая. Случай 1: λ >. Означаваме λ = β 2. Уравнение (28) приема формата X (x) β 2 X(x) =. Неговото характеристично уравнение k 2 β 2 = има корени k = ±β. Следователно общото решение на уравнение (28) има формата X(x) = C e βx + De βx. Трябва да изберем константите C и D така, че да са изпълнени граничните условия (3), т.е. X() = C + D =, X(l) = C e βl + De βl =. Тъй като β, тогава тази система от уравнения има уникално решение C = D =. Следователно X(x) и 63

64 u(x, t). Така в случай 1 получихме тривиално решение, което няма да разглеждаме по-нататък. Случай 2: λ =. Тогава уравнение (28) приема формата X (x) = и неговото решение очевидно е дадено по формулата: X(x) = C x+d. Замествайки това решение в граничните условия (3), получаваме X() = D = и X(l) = Cl =, следователно C = D =. Следователно X(x) и u(x, t), и отново имаме тривиално решение. Случай 3: λ<. Обозначим λ = β 2. Уравнение (28) принимает вид: X (x)+β 2 X(x) =. Его характеристическое уравнение имеет вид k 2 + β 2 =, а k = ±βi являются его корнями. Следовательно, общее решение уравнения (28) в этом случае имеет вид X(x) = C sin βx + D cosβx. В силу граничных условий (3) имеем X() = D =, X(l) = C sin βl =. Поскольку мы ищем нетривиальные решения (т. е. такие, когда C и D не равны нулю одновременно), то из последнего равенства находим sin βl =, т. е. βl = nπ, n = ±1, ±2,..., n не равно нулю, так как сейчас мы рассматриваем случай 3, в котором β. Итак, если β = nπ (nπ) 2, l, т. е. λ = то существуют l решения X n (x) = C n sin πnx, (31) l C n произвольные постоянные, уравнения (28), не равные тождественно нулю. 64

65 По-нататък ще присвоим на n само положителни стойности n = 1, 2,..., тъй като за отрицателни n ще се получат решения от същата форма (nπ).Стойностите λ n = са наречени собствени стойности, а функциите X n (x) = C n sin πnx собствени функции на диференциално уравнение (28) с гранични условия (3). Сега нека решим уравнение (29). За него характеристичното уравнение има вида k 2 α 2 λ =. (32) l 2 Тъй като открихме по-горе, че нетривиалните решения X(x) на уравнение (28) съществуват само за отрицателно λ равно на λ = n2 π 2, именно тези λ ще разгледаме по-долу. Корените на уравнение (32) са k = ±iα λ, а решенията на уравнение (29) имат формата: T n (t) = A n sin πnαt + B n cos πnαt, (33) l l където A n и B n са произволни константи. Замествайки формули (31) и (33) в (25), намираме конкретни решения на уравнение (21), които отговарят на гранични условия (22): (u n (x, t) = B n cos πnαt + A n sin πnαt) C n грях pnx. l l l Въвеждайки фактора C n в скоби и въвеждайки обозначението C n A n = b n и B n C n = a n, записваме u n (X, T) като (u n (x, t) = a n cos πnαt + b n sin πnαt ) грях pnx. (34) l l l 65

66 Трептенията на струната, съответстващи на решенията u n (x, t), се наричат собствени вибрации на струната. Тъй като уравнение (21) и гранични условия (22) са линейни и хомогенни, тогава линейна комбинация от решения (34) (u(x, t) = a n cos πnαt + b n sin πnαt) sin πnx (35) l l l ще бъде a решение на уравнение (21), удовлетворяващо граничните условия (22) със специален избор на коефициентите a n и b n, което осигурява равномерната сходимост на реда. Сега избираме коефициентите a n и b n на решение (35), така че то да отговаря не само на граничните условия, но и на началните условия (23) и (24), където f(x), g(x) са дадени функции ( освен това, f() = f (l) = g() = g(l) =). Приемаме, че функциите f(x) и g(x) удовлетворяват условията за разлагане на Фурие. Като заместим стойността t = в (35), получаваме u(x,) = a n sin πnx l = f(x). Диференцирайки ред (35) по отношение на t и замествайки t =, получаваме u t (x,) = πnα b n sin πnx l l = g(x) и това е разширението на функциите f(x) и g(x) в редове на Фурие. Следователно a n = 2 l l f(x) sin πnx l dx, b n = 2 l g(x) sin πnx dx. πnα l (36) 66

67 Замествайки изразите за коефициентите a n и b n в редица (35), получаваме решение на уравнение (21), което удовлетворява гранични условия (22) и начални условия (23) и (24). Така решихме проблема със свободните малки напречни вибрации на струна. Нека изясним физическия смисъл на собствените функции u n (x, t) на задачата за свободните трептения на струна, определени с формула (34). Нека го пренапишем като където u n (x, t) = α n cos πnα l α n = a 2 n + b2 n, (t + δ n) sin πnx, (37) l πnα δ n = arctg b n. l a n Формула (37) показва, че всички точки на струната извършват хармонични трептения с еднаква честота ω n = πnα и фаза πnα δ n. Амплитудата на трептене зависи от l l абсцисата x на точката на струната и е равна на α n sin πnx. При такова трептене всички точки на струната едновременно достигат своето l максимално отклонение в една или друга посока и едновременно преминават равновесното положение. Такива трептения се наричат стоящи вълни. Една стояща вълна ще има n + 1 фиксирани точки, дадени от корените на уравнението sin πnx = в интервала [, l]. Фиксираните точки се наричат възли на стоящата вълна. В средата между възлите - l mi са точките, в които отклоненията достигат максимум; такива точки се наричат антивъзли. Всяка струна може да има свои собствени трептения със строго определени честоти ω n = πnα, n = 1, 2,.... Тези честоти се наричат собствени честоти на струната. Най-ниският l тон, който една струна може да произведе, се определя от самата нея 67

68 ниска естествена честота ω 1 = π T и се нарича основен тон на струната. Останалите тонове, съответстващи на l ρ честоти ω n, n = 2, 3,..., се наричат обертонове или хармоници. За по-голяма яснота ще изобразим типичните профили на струна, излъчваща основния тон (фиг. 33), първия обертон (фиг. 34) и втория обертон (фиг. 35). Ориз. Фиг. 33. Профил на струната, която излъчва основния тон. Фиг. 34. Профил на струна, излъчваща първия обертон. Фиг. 35. Профил на струна, излъчваща втори обертон Ако струната извършва свободни вибрации, определени от началните условия, тогава функцията u(x, t) се представя, както се вижда от формула (35), като сума от индивидуални хармоници. Така произволно трептене 68

69-та струна е суперпозиция на стоящи вълни. В този случай естеството на звука на струната (тон, сила на звука, тембър) ще зависи от съотношението между амплитудите на отделните хармоници Сила, височина и тембър на звука Вибриращата струна възбужда въздушни вибрации, възприемани от човека ухо като звук, издаван от струна. Силата на звука се характеризира с енергията или амплитудата на вибрациите: колкото по-голяма е енергията, толкова по-голяма е силата на звука. Височината на звука се определя от неговата честота или период на трептене: колкото по-висока е честотата, толкова по-висок е звукът. Тембърът на звука се определя от наличието на обертонове, разпределението на енергията върху хармониците, т.е. методът на възбуждане на трептенията. Амплитудите на обертоновете са, най-общо казано, по-малки от амплитудата на основния тон, а фазите на обертоновете могат да бъдат произволни. Нашето ухо не е чувствително към фазата на трептенията. Сравнете, например, двете криви на фиг. 36, заимствано от . Това е запис на звук със същия основен тон, извлечен от кларинет (a) и пиано (b). И двата звука не са прости синусоидални трептения. Основната честота на звука и в двата случая е една и съща и това създава същия тон. Но моделите на кривите са различни, защото върху основния тон се наслагват различни обертонове. В известен смисъл тези рисунки показват какво е тембър. 69

МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА НА РУСИЯ Федерална държавна бюджетна образователна институция за висше професионално образование МАТИ Руски държавен технологичен университет на името на К. Е. Циолковски

Федерална агенция за образование Федерална държавна образователна институция за висше професионално образование ЮЖЕН ФЕДЕРАЛЕН УНИВЕРСИТЕТ Р. М. Гаврилова, Г. С. Костецкая Методическа

Министерство на образованието на Република Беларус Витебски държавен технологичен университет Тема. Катедра "Редове" по теоретична и приложна математика. разработен от ст.н.с. Е.Б. Дунина. Основен

Лекция 4. Хармоничен анализ. Редове на Фурие Периодични функции. Хармоничен анализ В науката и технологиите често трябва да се работи с периодични явления, т.е. такива, които се повтарят през

МОСКОВСКИЯТ ДЪРЖАВЕН ТЕХНИЧЕСКИ УНИВЕРСИТЕТ ЗА ГРАЖДАНСКА АВИАЦИЯ V.M. Любимов, Е.А. Жукова, В.А. Ухова, Ю.А. Шуринов

СЪДЪРЖАНИЕ Ред на Фурие 4 Понятието за периодична функция 4 Тригонометричен полином 6 3 Ортогонални системи от функции 4 Тригонометричен ред на Фурие 3 5 Ред на Фурие за четни и нечетни функции 6 6 Разлагане

ОПРЕДЕЛЕН ИНТЕГРАЛ. Интегрални суми и определен интеграл Нека функция y = f (), дефинирана на сегмента [, b], където< b. Разобьём отрезок [, b ] с помощью точек деления на n элементарных

ТЕОРИЯ НА РЕДИЦИТЕ Теорията на редовете е най-важният компонент на математическия анализ и намира както теоретични, така и множество практически приложения. Разграничете числови и функционални редове.

ТЕМА V РЕДИЦИ НА ФУРИЕ ЛЕКЦИЯ 6 Разгъване на периодична функция в редица на Фурие Много процеси, протичащи в природата и технологията, имат свойствата да се повтарят на определени интервали Такива процеси

6 Редица на Фурие 6 Ортогонални системи от функции Редица на Фурие по отношение на ортогонална система от функции Функциите ϕ () и ψ (), дефинирани и интегрируеми на сегмента [, ], се наричат ортогонални на този сегмент, ако

Федерална агенция за железопътен транспорт Уралски държавен университет по железопътен транспорт Катедра "Висша и приложна математика" Н. П. Чуев Елементи на хармоничния анализ Методичен

БЕЛОРУСКИ ДЪРЖАВЕН УНИВЕРСИТЕТ ФАКУЛТЕТ ПО ПРИЛОЖНА МАТЕМАТИКА И ИНФОРМАЦИОННИ НАУКИ Катедра по висша математика Учебно помагало за студенти от Факултета по приложна математика и информатика

Пояснения към текста: знакът се чете като "еквивалентен" и означава, че уравненията отдясно на знака и отляво на знака имат едно и също множество от решения, знакът IR означава множеството от реални числа, знакът IN

УРАВНЕНИЯ НА МАТЕМАТИЧЕСКАТА ФИЗИКА 1. Частни диференциални уравнения

1 2 Съдържание 1 Ред на Фурие 5 1.1 Тригонометричен ред на Фурие 5 1.2 Само sin & cos ............. ............ 7 1.3 Редица на Фурие в сложна форма............. 11 1.4 f(x) = c k?......... ......

82 4. Раздел 4. Функционални и степенни редове 4.2. Урок 3 4.2. Урок 3 4.2.. Разширение на Тейлър на функция ДЕФИНИЦИЯ 4.2.. Нека функцията y = f(x) е безкрайно диференцируема в някакво съседство

Лекция 8 4 Проблем на Щурм-Лиувил

МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА НА РУСИЯ ФЕДЕРАЛНА ДЪРЖАВНА БЮДЖЕТНА ОБРАЗОВАТЕЛНА ИНСТИТУЦИЯ ЗА ВИСШЕ ПРОФЕСИОНАЛНО ОБРАЗОВАНИЕ "САМАРСКИ ДЪРЖАВЕН ТЕХНИЧЕСКИ УНИВЕРСИТЕТ" Катедра по приложна математика

Интегрируемост на функция (според Риман) и определен интеграл Примери за решаване на задачи 1. Постоянната функция f(x) = C е интегрируема върху , тъй като за всякакви дялове и всеки избор на точки ξ i интегралът

МЕТОДИЧЕСКИ УКАЗАНИЯ ЗА ИЗЧИСЛИТЕЛНИ ЗАДАЧИ ПО КУРСА ПО ВИСША МАТЕМАТИКА "ОБИКНОВЕНИ ДИФЕРЕНЦИАЛНИ УРАВНЕНИЯ, ДВОЙНИ ИНТЕГРАЛИ" ЧАСТ III ТЕМАТИЧНА ПОРЕДИЦА Съдържание Поредица Числова поредица Сходимост и дивергенция

РЕДОВЕ. Числови редове. Основни дефиниции Нека е дадена безкрайна последователност от числа. Изразът (безкрайна сума) a, a 2,..., a n,... a i = a + a 2 + + a n +... () i= се нарича a числова серия. Числа

Заглавие Въведение. Основни понятия.... 4 1. Интегрални уравнения на Волтера... 5 Варианти за домашна работа.... 8 2. Резолвента на интегралното уравнение на Волтера. 10 опции за домашна работа.... 11

Лекция 3 Редици на Тейлър и Маклорен Приложение на степенни редове Разгъване на функции в редове на степен Тейлър и Маклорен За приложения е важно да можете да разширите дадена функция в степенни редове, тези функции

35 7 Тригонометричен ред на Фурие Ред на Фурие за периодични функции с период T. Нека f(x) е непрекъсната периодична функция с период T. Разгледайте основната тригонометрична система

ЯЖТЕ. РУДЕН МАТЕМАТИЧЕСКИ АНАЛИЗ. ЦИФРОВИ И ФУНКЦИОНАЛНИ ПОРЕДИ НОВОСИБИРСК 200 2 МИНИСТЕРСТВО НА ОБРАЗОВАНИЕТО И НАУКАТА НА РУСКАТА СФЕРА SEI HPE "НОВОСИБИРСК ДЪРЖАВЕН ПЕДАГОГИЧЕСКИ УНИВЕРСИТЕТ" E.M. Рудой МАТЕМАТИЧЕСКИ АНАЛИЗ.

I курс, задача. Докажете, че функцията на Риман, ако 0, m m R(), ако, m, m 0 и дробта е несводима, 0, ако е ирационална, е прекъсната във всяка рационална точка и непрекъсната във всяка ирационална. Решение.

1. Електростатика 1 1. Електростатика Урок 6 Разделяне на променливи в декартови координати 1.1. (Задача 1.49) Равнината z = е заредена с плътност σ (x, y) = σ sin (αx) sin (βy), където σ, α, β са константи.

Ch Степенен ред a a a Серия от формата a a a a a () се нарича степенна редица, където a са константи, наречени коефициенти на редицата. Понякога се разглежда степенна редица от по-обща форма: a a (a) a ( a) a (a) (), където

S A Lavrenchenko wwwwrckoru Лекция Преобразуване на Фурие Концепция за интегрална трансформация Методът на интегралните трансформации е един от мощните методи на математическата физика и е мощно решение

Диференциално смятане Въведение в математическия анализ Последователност и граница на функцията. Разкриване на несигурности в рамките. Производна на функция. Правила за диференциране. Приложение на производната

ЛЕКЦИЯ N 7 .Власт

Металургичен факултет Катедра Висша математика

9. Първопроизводна и неопределен интеграл 9.. Нека функцията f() е дадена на интервала I R. Функцията F () се нарича първоизводна функция f () на интервала I, ако F () = f () за всеки I и първоизводната

Московски физико-технологичен институт (държавен университет) O.V. Бесов ТРИГОНОМЕТРИЧНИ РЕДОВЕ НА ФУРИЕ Учебно помагало Москва, 004 Съставител О.В.Бесов УДК 517. Тригонометрични редове

8. Степенен ред 8.. Функционален ред от вида c n (z) n, (8.) n= където c n е числова последователност, R е фиксирано число и z R се нарича степенен ред с коефициенти c n . Чрез промяна на променливите

Катедра Математика и информатика Елементи на висшата математика Учебно-методически комплекс за ученици от средното професионално образование, обучаващи се с дистанционни технологии Модул Диференциално смятане Съставител:

1. Определен интеграл 1.1. Нека f е ограничена функция, дефинирана върху сегмента [, b] R. Разделение на сегмента [, b] е набор от точки τ = (x, x 1,..., x n 1, x n ) [, b ] така че = x< x 1 < < x n 1

ВЪПРОСИ И ТИПОВИ ЗАДАЧИ за финален изпит по дисциплината "Математически анализ" Приложна математика На устния изпит студентът получава два теоретични въпроса и две задачи Общо 66 въпроса за година

Модул Тема Функционални последователности и серии Свойства на равномерна конвергенция на последователности и серии Степенен ред Лекция Дефиниции на функционални последователности и серии Равномерно

~ ~ Неопределени и определени интеграли Понятието първоизводен и неопределен интеграл. Определение: Функция F се нарича първоизводна по отношение на функция f, ако тези функции са свързани както следва

Министерство на образованието и науката на Руската федерация Федерална държавна бюджетна образователна институция за висше професионално образование "Сибирски държавен индустриален университет"

КВАДРАТНИ УРАВНЕНИЯ

ВОЕНЕН ОБРАЗОВАТЕЛЕН И НАУЧЕН ЦЕНТЪР НА ВЪЗДУШНИТЕ СИЛИ "ВОЕННА АКАДЕМИЯ на името на професор Н. Е. ЖУКОВСКИ и Ю. А. ГАГАРИН" ПРИМЕРИ

ФЕДЕРАЛНА АГЕНЦИЯ ПО ОБРАЗОВАНИЕТО ДЪРЖАВНА ОБРАЗОВАТЕЛНА ИНСТИТУЦИЯ ЗА ВИСШЕ ПРОФЕСИОНАЛНО ОБРАЗОВАНИЕ Московски държавен университет по приборостроене и информатика Катедра по висше

Глава 5. Ред на Фурие 5 .. Урок 5 5 ... Основни дефиниции Функционален ред от формата a 2 + (a k cos x + b k si x) (5 ..) се нарича тригонометричен

Серии на Фурие Ортогонални системи от функции От гледна точка на алгебрата, равенството където са функции от даден клас и са коефициенти от R или C просто означава, че векторът е линейна комбинация от вектори B

3724 ПОРЕДИЦА ОТ МНОЖЕСТВЕНИ И КРИВОЛИНЕЙНИ ИНТЕГРАЛИ 1 РАБОТНА ПРОГРАМА НА РАЗДЕЛИ "ПОРЕДИЦА ОТ МНОЖЕСТВЕНИ И КРИВОЛИНЕЙНИ ИНТЕГРАЛИ" 11 Числови серии Концепцията за числови серии Свойства на числови серии Необходим критерий за сходимост

ДИФЕРЕНЦИАЦИЯ НА ФУНКЦИИ НА ЕДНА ПРОМЕНЛИВА Концепцията за производна, нейното геометрично и физическо значение Проблеми, водещи до концепцията за производна Определение на допирателната S към правата y f (x) в точка A x ; е(

ДИФЕРЕНЦИАЛНИ УРАВНЕНИЯ 1. Основни понятия Диференциално уравнение по отношение на някаква функция е уравнение, което свързва тази функция с нейните независими променливи и с нейните производни.

ОБИКНОВЕНИ ДИФЕРЕНЦИАЛНИ УРАВНЕНИЯ ОТ ПЪРВИ РЯД.Основни понятия Диференциално уравнение е уравнение, в което под производна или диференциален знак влиза неизвестна функция.

ДИФЕРЕНЦИАЛНИ УРАВНЕНИЯ Общи понятия Диференциалните уравнения имат многобройни и много разнообразни приложения в механиката, физиката, астрономията, технологиите и в други клонове на висшата математика (напр.

Функционална серия Функционална серия нейната сума и площ на функционален o Нека последователност от функции k (k 1) е дадена в областта Δ на реални или комплексни числа

СИСТЕМИ ОТ ОРТОГОНАЛНИ ПОЛИНОМИ И ТЕХНИТЕ ПРИЛОЖЕНИЯ Полиноми на А. Чебишев-Ермит

Лекции, подготвени от доц. Мусина М. В. Определение Израз на формата Числова и функционална серия Числова серия: основни понятия (), където се нарича числова серия (или просто серия) Числа, членове на серия (зависят от

Редица на Фурие от периодични функции с период 2π.

Стандартна (=обичайна) нотация чрез сумата от sinx и cosx

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,

където a o , a 1 ,a 2 ,...,b 1 ,b 2 ,.. са реални константи, т.е.

Където за диапазона от -π до π коефициентите на реда на Фурие се изчисляват по формулите:

Друг начин да напишете серия е да използвате релацията acosx+bsinx=csin(x+α)

f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)

Редица на Фурие от непериодични функции с период 2π.

Разлагане на непериодични функции.

Четни и нечетни функции.

Много функции не са нито четни, нито нечетни.

Разлагане в ред на Фурие по косинуси.

където са коефициентите на реда на Фурие,

Следователно,

където са коефициентите на реда на Фурие,

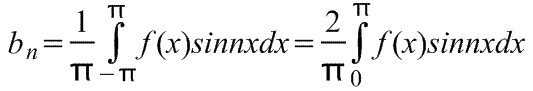
Ред на Фурие на полупериод.

Редица на Фурие за произволен интервал.

Разгъване на периодична функция с период L.

(Границите на интегриране могат да бъдат заменени с всеки интервал с дължина L, например от 0 до L)

Редици на Фурие върху полуцикъл за функции, дадени в интервала L≠2π.

Разширението в косинуси в диапазона от 0 до L има формата