What are Euler circles for? Euler circle

Euler circles are a geometric diagram. With its help, you can depict the relationships between subsets (concepts) for a visual representation.

The way of depicting concepts in the form of circles allows you to develop imagination and logical thinking not only for children, but also for adults. Starting from 4-5 years old, children can solve simple problems with Euler circles, first with explanations from adults, and then independently. Mastering the method of solving problems using Euler circles develops the child’s ability to analyze, compare, generalize and group their knowledge for wider application.

Example

The picture shows a variety of all possible toys. Some of the toys are construction sets - they are highlighted in a separate oval. This is part of a large set of “toys” and at the same time a separate set (after all, a construction set can be “Lego” or primitive construction sets made from blocks for kids). Some part of the large variety of “toys” may be wind-up toys. They are not constructors, so we draw a separate oval for them. The yellow oval “wind-up car” refers both to the set “toy” and is part of the smaller set “wind-up toy”. Therefore, it is depicted inside both ovals at once.

Here are some logical thinking tasks for young children:

Identify the circles that fit the description of the object. In this case, it is advisable to pay attention to those qualities that the object possesses permanently and that it has temporarily. For example, a glass glass with juice always remains glass, but there is not always juice in it. Or there is some kind of broad definition that includes different concepts; such a classification can also be depicted using Euler circles. For example, a cello is a musical instrument, but not every musical instrument is a cello.

For older children, you can offer options for problems with calculations - from fairly simple to very complex. Moreover, independently coming up with these tasks for children will provide parents with a very good workout for the mind.

1. Of the 27 fifth-graders, all are studying foreign languages - English and German. 12 are studying German and 19 are studying English. It is necessary to determine how many fifth-graders are studying two foreign languages; how many people don’t study German; how many people don’t study English; How many study only German and only English?

At the same time, the first question of the problem hints in general at the path to solving this problem, informing that some students study both languages, in which case the use of the diagram also makes it easier for children to understand the problem.

By the way, if you can’t decide which profession to choose, try drawing a diagram in the form of Euler circles. Perhaps a drawing like this will help you make your choice:

Those options that will be at the intersection of all three circles are the profession that will not only be able to feed you, but will also please you.

And one more sign...

If you think that you know nothing about such a concept as Euler circles, then you are deeply mistaken. Even from elementary school, schematic images, or circles, are known that allow one to visually comprehend the relationships between concepts and elements of the system.

The method, invented by Leonhard Euler, was used by the scientist to solve complex mathematical problems. He depicted sets in circles and made this diagram the basis of such a concept as symbolic. The method is designed to simplify as much as possible the reasoning aimed at solving a particular problem, which is why the technique is actively used both in primary school and in the academic environment. Interestingly, a similar approach was previously used by the German philosopher Leibniz, and was later taken up and applied in various modifications by famous minds in the field of mathematics. For example, rectangular diagrams of the Czech Bolzano, Schroeder, Venn, famous for creating a popular diagram based on this simple but surprisingly effective method.

Circles are the basis of the so-called “visual Internet memes,” which are based on the similarity of characteristics of individual sets. It’s funny, visual, and most importantly, understandable.

Circles of thought

Circles allow you to clearly describe the conditions of a problem and instantly make the right decision, or identify the direction of movement towards the correct answer. Typically, Euler circles are used to solve logical-mathematical problems involving sets, their unions, or partial superpositions. The intersection of circles includes objects that have the properties of each of the sets depicted in a circle. Objects not included in the set are located outside of one or another circle. If the concepts are absolutely equivalent, they are denoted by one circle, which is the union of two sets that have equal properties and volumes.

Logic of relationships

Using Euler circles, you can solve a number of everyday problems and even decide on the choice of a future profession, you just need to analyze your capabilities and desires and choose their maximum intersection.

Now it becomes clear that Euler’s circles are not at all an abstract mathematical and philosophical concept from the category of theoretical knowledge, they have a very applied and practical significance, allowing you to deal not only with the simplest mathematical problems, but also to solve important life dilemmas in a visual and understandable way for everyone.

Each object or phenomenon has certain properties (signs).

It turns out that forming a concept about an object means, first of all, the ability to distinguish it from other objects similar to it.

We can say that a concept is the mental content of a word.

Concept - it is a form of thought that displays objects in their most general and essential characteristics.

A concept is a form of thought, and not a form of a word, since a word is only a label with which we mark this or that thought.

Words can be different, but still mean the same concept. In Russian - “pencil”, in English - “pencil”, in German - bleistift. The same thought has different verbal expressions in different languages.

RELATIONS BETWEEN CONCEPTS. EULER CIRCLES.

Concepts that have common features in their content are called COMPARABLE(“lawyer” and “deputy”; “student” and “athlete”).

Otherwise, the concepts are considered INCOMPARABLE(“crocodile” and “notebook”; “man” and “steamboat”).

If, in addition to common features, concepts also have common elements of volume, then they are called COMPATIBLE.

There are six types of relationships between comparable concepts. It is convenient to denote relationships between the scopes of concepts using Euler circles (circular diagrams where each circle denotes the scope of a concept).

KIND OF RELATIONSHIP BETWEEN CONCEPTS	IMAGE USING EULER CIRCLES
EQUIVALITY (IDENTITY) The scopes of the concepts completely coincide. Those. These are concepts that differ in content, but the same elements of volume are thought of in them.	1) A - Aristotle B - founder of logic 2) A - square B - equilateral rectangle
SUBORDINATION (SUBORDINATION) The scope of one concept is completely included in the scope of another, but does not exhaust it.	1) A - person B - student 2) A - animal B - elephant
INTERSECTION (CROSSING) The volumes of two concepts partially coincide. That is, concepts contain common elements, but also include elements that belong to only one of them.	1) A - lawyer B - deputy 2) A - student B - athlete
COORDINATION (COORDINATION) Concepts that do not have common elements are completely included in the scope of the third, broader concept.	1) A - animal B - cat; C - dog; D - mouse 2) A - precious metal B - gold; C - silver; D - platinum
OPPOSITE (CONTRAPARITY) The concepts A and B are not simply included in the scope of the third concept, but seem to be at its opposite poles. That is, concept A has in its content such a feature, which in concept B is replaced by the opposite one.	1) A - white cat; B - red cat (cats are both black and gray) 2) A - hot tea; iced tea (tea can also be warm) I.e. concepts A and B do not exhaust the entire scope of the concept they are included in.
CONTRADITION (CONTRADITIONALITY) The relationship between concepts, one of which expresses the presence of some characteristics, and the other - their absence, that is, it simply denies these characteristics, without replacing them with any others.	1) A - tall house B - low house 2) A - winning ticket B - non-winning ticket I.e. the concepts A and not-A exhaust the entire scope of the concept into which they are included, since no additional concept can be placed between them.

Exercise : Determine the type of relationship based on the scope of the concepts below. Draw them using Euler circles.

1) A - hot tea; B - iced tea; C - tea with lemon

Hot tea (B) and iced tea (C) are in an opposite relationship.

Tea with lemon (C) can be either hot,

so cold, but it can also be, for example, warm.

2)A- wood; IN- stone; WITH- structure; D- house.

Is every building (C) a house (D)? - No.

Is every house (D) a building (C)? - Yes.

Something wooden (A) is it necessarily a house (D) or a building (C) - No.

But you can find a wooden structure (for example, a booth),

You can also find a wooden house.

Something made of stone (B) is not necessarily a house (D) or building (C).

But there may be a stone building or a stone house.

3)A- Russian city; IN- capital of Russia;

WITH- Moscow; D- city on the Volga; E- Uglich.

The capital of Russia (B) and Moscow (C) are the same city.

Uglich (E) is a city on the Volga (D).

At the same time, Moscow, Uglich, like any city on the Volga,

are Russian cities (A)

Ministry of Education, Science and Youth of the Republic of Crimea Small Academy of Sciences "Iskatel"

Direction: mathematics

G. Krasnoperekopsk– 2017

Work completed:

Shumilina Maria Sergeevna,

student of class 7-A of the municipal budget general education institutions "Secondary general education School No. 5" municipal formation city district Krasnoperekopsk

Scientific adviser:

Sheina Elena Nikolaevna, municipal budget mathematics teacher general education institutions "Secondary general education school No. 5 » municipal formation city district Krasnoperekopsk

INTRODUCTION …………………………………………………………… 3

CHAPTER 1. A little bit of history…………………………………. 5

CHAPTER 2. From set theory…………………………………….7

2.1. The concept of set.……………………………………………………..8

2.2. Operations on sets.…………………………..9

CHAPTER 3.Solving problems using Euler circles………………..10

CONCLUSION………………………………………………………..22

LIST OF SOURCES USED………………….23

INTRODUCTION

Nothing helps

formation of a mental culture,

as a solution to logical problems. Mathematics-

not dry and boring science, but complete

unusual and interesting discoveries

Solving logic problems is very exciting. There are people for whom solving a logic problem is an exciting, but not difficult task. Their brain, like a spotlight, immediately illuminates all the ingenious constructions, and they come to the correct answer unusually quickly. It’s great that they can’t explain how they came to the decision.

Logical problems constitute a large class of non-standard problems. This includes, first of all, word problems in which it is necessary to recognize objects or arrange them in a certain order according to existing properties.

There are many techniques that are used to solve text logic problems. Very often the solution helps to find a drawing. Using a picture makes solving the problem simple and clear. Depicting the conditions of a problem in the form of Euler circles, as a rule, simplifies and facilitates the path to its solution.

Relevance is that the tasks are of a practical nature, which is important in modern life. Problems force you to think, to approach the solution of a problem from a different angle, to be able to choose from a variety of solutions, the simplest, easiest way.

Goal of the work:

Get acquainted with Euler–Venn circles;

Learn to apply the method of solving problems using Euler circles;

Create tasks with practical content.

Chapter 1. A little history

Leonhard Euler, the greatest mathematicianXVIIIc., born in Switzerland in 1707.In 1727, at the invitation of the St. Petersburg Academy of Sciences, he came to Russia. In St. Petersburg, Euler found himself in a circle of outstanding scientists: mathematicians, physicists, astronomers, and received great opportunities to create and publish his works. He worked with passion and soon became, according to the unanimous recognition of his contemporaries, the first mathematician in the world. Euler's scientific legacy is striking in its volume and versatility. The list of his works includes more than 800 titles. The complete collected works of the scientist occupy 72 volumes. Among his works are the first textbooks on differential and integral calculus. In number theory, Euler continued the work of the French mathematician P. Fermat.

Euler works a lot in the field of mathematical analysis. The scientist was the first to develop a general doctrine of the logarithmic function. In geometry, Euler laid the foundation for a completely new field of research, which later grew into an independent science - topology.

Euler’s name is given to a formula that connects the number of vertices (B), edges (P) and faces (G) of a convex polyhedron: B -P + G = 2. Even the main results of Euler’s scientific work are difficult to list. Here is the geometry of curves and surfaces, and the first presentation of the calculus of variations with numerous new concrete results. He wrote works on hydraulics, shipbuilding, artillery, geometric optics, and even music theory. For the first time, he gives an analytical presentation of mechanics instead of Newton's geometric presentation, and constructs the mechanics of a solid body, and not just a material point or a solid plate. One of Euler's most remarkable achievements is related to astronomy and celestial mechanics. He constructed an accurate theory of the movement of the Moon, taking into account the attraction of not only the Earth, but also the Sun. This is an example of solving a very difficult problem.

The last 17 years of Euler's life were marred by almost complete loss of vision. But he continued to create as intensely as in his youth. Only now he no longer wrote himself, but dictated to his students, who carried out the most cumbersome calculations for him.

From 1761 to 1768, he wrote the famous “Letters to a German Princess,” where Euler talked about his method, about depicting sets in the form of circles. That is why drawings in the form of circles are usually called “Eulerian circles”. Euler noted that the representation of sets as circles “is very suitable to facilitate our reasoning.”

After Euler, the same method was developed by the Czech mathematician Bernard Bolzano (1781 – 1848). Only, unlike Euler, he drew not circular, but rectangular diagrams. Euler's circle method was also used by the German mathematician Ernst Schroeder (1841 – 1902). This method is widely used in his book Algebra Logic. But graphical methods reached their greatest flowering in the works of the English logician John Venn (1843 - 1923). He outlined this method most fully in his book “Symbolic Logic,” published in London in 1881. In honor of Venn, instead of Euler circles, the corresponding drawings are sometimes called Venn diagrams; in some books they are also called Euler–Venn diagrams (or circles).

Chapter 2. From set theory

2.1. The concept of set.

One of the main concepts used in mathematics is the concept of set. No definition is given for it. It can be explained that a set is an arbitrary collection of objects, and the objects themselves are the elements of a given set. So, we can talk about a set of students in a class (elements are students), a set of days of the week (elements are days of the week), a set of natural divisors of the number 6 (elements are numbers 1, 2, 3, 6), etc.

In algebra and algebra courses, the beginning of analysis most often consider sets whose elements are numbers, and therefore they are called number sets.

As a rule, sets are denoted by capital letters of the Latin alphabet. For example, if the setMconsists of numbers 1; 2; 3, then it is designated as follows:M= (1; 2; 3). The fact that the number 2 is included in this set

(is an element of this setM) is recorded using a special icon as follows: 2M; and the fact that the number 5 is not included in this set (is not an element of this setM), written like this: 5 M.

We can also consider a set that does not contain a single element - the empty set. For example: the set of prime factors of the number 1 is an empty set.

For some sets there are special notations. Thus, the empty set is denoted by the symbol , the set of all natural numbers – a letterN, the set of all integers – a letterZ, the set of all rational numbers – the letterQ, and the set of all real numbers is the letterR. Using Euler–Venn circles, this can be depicted as follows:

Fig.1

If each element of the setAis an element of the setB, then they say that the setAis a subset of the setB.

This is written as follows:A B.

Fig.2

2.2. Operations on sets.

You can perform certain actions on sets: find their intersection, union. Let us define these operations and illustrate them using circles.

Intersection of sets A And B call their common part, that is, the setCall elements belonging to both the setA, and manyB

The intersection of sets is denoted by the sign∩ and write downA∩ B .

Fig.3

Union of sets A And B call a setC, consisting of all elements belonging to at least one of these sets (AorB). The union of sets is indicated by the sign
and write down A
B

Chapter 3. Solving Problems Using Euler Circles

Task No. 1.

Of the 52 schoolchildren, 23 collect badges, 35 collect stamps, and 16 collect both badges and stamps.

The rest are not interested in collecting. How many schoolchildren are not interested in collecting?

Solution.

The conditions of this problem are not so easy to understand. If you add 23 and 35, you get more than 52. This is explained by the fact that we counted some schoolchildren twice here, namely those who collect both badges and stamps.

To make it easier to solve the problem, let’s present its data in the following diagram

Fig.5

In this diagram, the large circle represents all the schoolchildren in question. CircleZ depicts schoolchildren collecting badges (23 in total), and the circleM - schoolchildren collecting stamps (35 in total). At the intersection of circlesZ And M The number 16 is worth - these are those who collect both badges and stamps. This means that 23 - 16 = 7 people collect only badges, 35 - 16 = 19 people collect only stamps. In total, stamps and badges are collected by 19 + 7 + 16 = 42 people. That leaves 52 - 42 = 10 people who are not keen on collecting. This number can be entered into the free field of the circle. Answer: 10 people.

Task 2.

There are 15 boys in the class. Of these, 10 people play volleyball and 9 basketball. How many boys do both?

Solution.

Let us depict the condition using Euler circles. This figure gives us some reasoning. Let's analyze this reasoning and enter the required number into each of the parts formed on the diagram.

Let x boys play all kinds of sports. Then only (10th) boys play volleyball, and only (9th) boys play basketball. Let's make an equation: 10's + x+ 9's = 15, from which x = 4

10's B

x 9's

Fig.6

Answer: 4 people.

Task No. 3.

Some guys from our class like to go to the movies. It is known that 15 children watched the film “Scarecrow”, 11 people watched the film “Above the Sky”, of which 6 watched both “Scarecrow” and"Above the sky". How many people have only watched the movie “Above the Sky”?

Solution:Let's draw two sets like this: We place 6 people who watched the films “Scarecrow” and “Above the Sky” at the intersection of sets.

15 – 6 = 9 – people who watched only “Scarecrow”.
11 – 6 = 5 – people who watched only “Above the Sky.”

We get:

Fig.7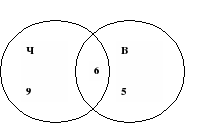

Answer. 5 people only watched “Above the Sky.”

Task No. 4.

In a group of 80 tourists who came on an excursion to Moscow, 52 want to visit the Bolshoi Theater, 30 want to visit the Art Theater, 12 want to visit both theaters, the rest do not want to go to the theaters. How many people are not going to go to the theater?

Solution.

Only the big theater will be visited by: 52-12=40 tourists;

only the art theater will be visited

30-12=18 tourists;

8
0-(40+18+12)=10 tourists are not going to go to the theater.

Fig.8

Answer: 10 people.

Task No. 5.

There were 26 magic books on spells on the shelf. Of these, 4 were read by both Harry Potter and Ron. Hermione read 7 books that neither Harry Potter nor Ron had read, and two books that Harry Potter had read. In total, Harry Potter read 11 books. How many books has Ron read?

Solution.

Considering the conditions of the problem, the drawing will be as follows:

Fig.9

Since Harry Potter read 11 books in total, of which 4 books were read by Ron and 2 books by Hermione, then only Harry read 11 - 4 - 2 = 5 - books.

Therefore, Ron read 26 – 7 – 2 – 5 – 4 = 8 – books.Answer. Ron read 8 books.

Task No. 6.

In a tourist group of 100 people, 75 people know German, 65 people know English, and 10 people know neither German nor English. How many tourists speak two languages? Solution.

Let us depict the problem conditions in the form of Euler circles.

It is easy to see that 90 tourists (100-10) know at least one language; Let x tourists know both English and German. Then (65th) tourists only know English, and (75th) people only know German. We get the equation 65's + 75's + x = 90, from which x = 50 - tourists know both languages. Answer: 50 tourists.

Task No. 7.

How many people are participating in the walk if it is known that 16 of them took a sandwich with ham, 24 with sausage, 15 with cheese, 11 with both ham and sausage, 8 with both ham and cheese, 12 with sausage , and with cheese, 6 - sandwiches of all kinds, and 5 - took pies? Solution : Let us represent the sets as follows: Fig.11

16+24+15-11-8-12+6=30 (persons) - participated in the walk and took sandwiches with them or 3+2+6+5+7+6+1=30 (persons)

30+5=35 (persons) - took part in the walk
Answer. 35 people

Problem No. 8

In the 5th grade of our school there are 22, in the 6th grade - 16, in the 7th grade - 23 children. It is known that 4 people attend skiing, chess and sports clubs. Every two sections are attended by 9 people. How many people go from each class to sections? How many students do not go to any sports club?

Solution. If there are 4 students in all three clubs, and 9 people in every two, then two sections from grades 5 and 6, from grades 6 and 7, and from grades 5 and 7 are attended by 5

Human.

Fig.12

We get 5+5+4=14 fifth-graders attend clubs, 22-14=8 people do not attend any clubs. Reasoning also, of the sixth-graders, 16-14=2 students do not go anywhere, and of the seventh-graders – 23-14=9 people.

Answer: 14 students from each class attend clubs; 7 students from the 5th, 2 from the 6th, 9 from the 7th do not attend clubs.

Task No. 9.

Out of 100 kids going to a children's health camp, 30 kids can snowboard, 28 can skateboard, 42 can rollerblade. 8 kids can skateboard and snowboard, 10 can skateboard and rollerblade, snowboard and rollerblade – 5, and on all three – 3. How many guys don’t know how to ride a snowboard, a skateboard, or roller skates?

Solution: IN Let's use Euler circles.

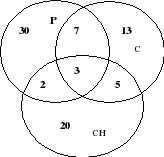
Fig.13

Three people own all three sports equipment, which means that in the general part of the circles we enter the number 3. 10 people can skateboard and roller skate, and 3 of them also snowboard. Consequently, 10-3=7 guys can only skateboard and rollerblade. Similarly, we find that only 8-3=5 guys can skateboard and snowboard, and only 5-3=2 people can ride snowboards and rollerblades. We will enter this data in the appropriate parts. Let us now determine how many people can ride only one sports equipment. 30 people know how to snowboard, but 5+3+2=10 of them also know other equipment, therefore, 20 people know how to snowboard only. Similarly, we find that 13 children know how to skateboard only, and 30 children know how to roller skate only. According to the conditions of the problem, there are only 100 guys. 20+13+30+5+7+2+3=80 – the guys know how to ride at least one sports equipment. Consequently, 20 people do not know how to ride any sports equipment.
Answer. 20 people do not know how to ride any sports equipment.

Problem No. 10 .

There are 70 children in three seventh grades. Of these, 27 are involved in the drama club, 32 sing in the choir, 22 are fond of sports. There are 10 guys from the choir in the drama club, 6 athletes in the choir, 8 athletes in the drama club; 3 athletes attend both the drama club and the choir. How many kids don’t sing in the choir, aren’t interested in sports, and aren’t involved in the drama club? How many guys are only involved in sports?

Solution . D - drama club; X - choir; S - sport. In circle D - 27 children, in circle X - 32 people, in circle C - 22 students.Those 10 guys from the drama club who sing in the choir will be in the common part of circles D and X. Three of them are also athletes, they will be in the common part of all three circles. The remaining seven are not interested in sports. Likewise, 8-3=5

athletes who do not sing in the choir and 6-3=3 who do not attend the drama club. It is easy to see that 5+3+3=11 athletes attend a choir or drama club, 22-(5+3+3)=11 are engaged only in sports; 70-(11+12+19+7+3+3+5)=10 - do not sing in a choir, do not participate in a drama club, are not interested in sports.

Fig.14 Answer: 10 people.

Problem No. 11 . There are 30 people in the class. 20 of them use the metro every day, 15 use the bus, 23 use the trolleybus, 10 use both the metro and trolleybus, 12 use both the metro and bus, 9 use both trolleybus and bus. How many people use all three modes of transport every day?

Solution.

Fig.15

Let x person use all three modes of transport. Then they use only the metro and trolleybus - (10 − x) people, only the bus and trolleybus - (9 − x) people, only the metro and bus - (12 − x) people. Let's find how many people use the metro alone:

20 − (12 − x) − (10 − x) − x = x − 2

Similarly, we get: x − 6 - only by bus and x + 4 - only by trolleybus, since there are only 30 people, we create the equation:

x + (12 − x) + (9 − x) + (10 − x) + (x + 4) + (x − 2) + (x − 6) = 30.

hence x = 3.

Answer: 3 people.

Task No. 12.

Of the company’s employees, 16 visited France, 10 Italy, 6 England; in England and Italy - 5; in England and France -6; in all three countries - 5 employees. How many people visited both Italy and France, if a total of 19 people work in the company, and each of them visited at least one of the named countries?

Solution:

We know that there were 5 employees in all three countries. In England and Italy there are also 5, which means these same employees were also in France, and therefore we put 0 at the intersection of circles A and I. In France and Italy we don’t know, so we write x-5 at the intersection of circles A and F. Because in England there were 6 people, then 6-5-1=0 we write 0, in France there are 16+5-6 and in Italy 10+5-5 and in total there are 19 employees in the company, then all that remains is to create and solve the equation: 1 +16x+5-6+5+x-5+10x+5-5=19, hence x=7, which means 7-5=2 employees of the company visited Italy and France.

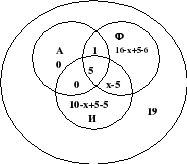
Fig.16

Answer: 2 employees.

Task No. 13.

There were 10 guys who wanted to exchange various kinds of magazines. Among them, 6 people subscribe to K, 5 people to T, 5 people to Yu, 3 people to K and T, 2 people to T and Yu, 3 people to K and Yu, and one person does not subscribe to a single magazine. but reads all these magazines in the library. We need to find out how many people subscribe to all three magazines, how many subscribe to two, and how many subscribe to only one magazine.

Solution. Let a large circle of 10 people be the set of all the guys exchanging magazines. Inside the large circle we will draw three smaller circles: K, T, Yu, which depict the guys who have subscribed to the corresponding magazines.. It is known that one person does not subscribe to a single magazine.

Let x guys subscribe to all three magazines, then (3) guys subscribe only to K and T, (2) to only T and Yu, (3) to only K and Yu. This means that only magazine K is subscribed to 6 -(3-x+x+3-x)=x people, T magazine 5-(3-x+x+2-x)=x, Yu magazine 5-(3-x+x+2-x)= X.

Fig.17

Let's make an equation: x+3-x+3-x+x+x+x+x+2-x=9, 8+x=9,x=1

So, 3 is the number of guys who subscribed to only one magazine, 5 is the number of guys who subscribed to two magazines, and 1 is the number of guys who subscribed to all three magazines.

CONCLUSION

The subject of mathematics is so serious

what you can't miss an opportunity to do

its a bit entertaining.

B. Pascal

Among mathematical problems, logical problems occupy a special place. Solving such problems contributes to the development of mathematical thinking. They differ from most mathematical problems in that solving them often does not require a stock of any special knowledge, but, as a rule, requires intelligence. One of the characteristic features of any logic is that it allows, having received some information, to extract (identify) the new knowledge contained in it.

It turns out there are several techniques with which you can solve text logic problems. They are diverse and each of them has its own area of application.

My work examines problems that consist of a lot of data.The solutions found follow the same method: make a drawing; enter the initial data in circles; analyzing and reasoning, we write down the results in parts of the circles; We look for and write down the answer.Depicting the conditions of a problem in the form of Euler circles, as a rule, simplifies and facilitates the path to its solution. In addition, with their help you can answer many questions posed to one condition of the problem.

This topic expanded my mathematical horizons and enriched my arsenal of tools used in solving various problems.

List of sources used:

1. Gavrilova T.D.. Entertaining mathematics. 5 - 11 grades. Volgograd: Teacher, 2005.-96 p.

2. Germanovich P.Yu. "Collection of problems in mathematics for intelligence."

3. Getmanova A.D. Logical foundations of mathematics, grades 10 – 11: textbook. – M.: Bustard, 2005.

4. Glazer G.I. . - M.: Education, 1964. - P. 232.

5. Gusev V.A., Orlov A.I., Rosenthal A.L. "Extracurricular work in mathematics." M.: Education, 1984.

6. Nelin E.P., Dolgova O.E.. Textbook of algebra and beginnings of analysis, grade 11.

Abstracts for the work

The topic of my research work is “Solving problems using Euler circles.” When preparing for the Olympiad, I was faced with tasks that involved a large amount of data. It turns out that the so-called Euler circles help to simplify the solution of such problems, with the help of which you can depict many elements that have a certain property. The purpose of this work is to study this method and be able to apply it to solve problems.

The work considers problems whose solution is subject to one algorithm: making a drawing; We enter the initial data in circles, starting with the condition that contains more properties; analyzing and reasoning, we write down the results in parts of the circle; write down the answer.

The relevance lies in the fact that the tasks are of a practical nature, which is important in modern life. Problems force you to think, to approach the solution of a problem from a different angle, to be able to choose from a variety of solutions, the simplest, easiest way. The method discussed in the workaccessible and easy to understand, which allows you to expand the range of its application. Euler circles can be found in history, biology, and in the study of other subjects.

The material that was studied in the work, as well as the practical part,can be used in additional classes in preparation for mathematical Olympiads.

Material overview

Mathematics is one of my favorite subjects in high school. I like to solve various mathematical puzzles and logical problems. At the math club we get acquainted with different ways of solving problems. One day during a club class, we were given a homework assignment to solve the following problem: “There are 35 students in the class, 12 are in a math club, 9 are in a biology club, and 16 kids do not attend these clubs. How many biologists are interested in mathematics? I solved it this way:

35 - 16=19 (children) - attend clubs

19- 9 = 10 (children) – attend a math club

12 - 10=2 (biologists) – are fond of mathematics.

And she asked me to check the solution to my older brother’s problem. He said that

The problem was solved correctly, but there is a more convenient and faster way to solve it. It turns out that the so-called Euler circles help to simplify the solution of this problem, with the help of which you can depict many elements that have a certain property. I was interested in a new way to solve the problem and I decided to write a research paper on the topic: “Solving problems using Euler circles”

I set a goal for myself: to learn a new way to solve non-standard problems using Euler circles.

To reveal the topic of my research work, the following tasks were set:

Learn to use scientific literature.

Learn what Euler circles are.

Create an algorithm for solving problems.

Learn to solve problems using Euler circles.

Compile a selection of problems for use in math circle classes.

Research methods:

Study and analysis of scientific literature;

Method of inductive generalization, specification.

Object of study: Euler circles

Subject of research: the concept of a set, the main actions with them necessary when solving problems using Euler circles

Study participants: students in grades 5-9 at the gymnasium

Research hypothesis: Euler's method simplifies reasoning when solving certain problems and facilitates the path to its solution.

The relevance of the study lies in the fact that there are many techniques and ways to solve non-standard logical problems. Often, when solving a problem, drawings are used, which makes solving the problem simpler and more visual. One such visual and convenient way to solve problems is the Euler circle method. This method allows you to solve problems with cumbersome conditions and with many data.

Problems solved using Euler circles are often offered at mathematical Olympiads. Such tasks are often of a practical nature, which is important in modern life. They make you think and approach solving a problem from different angles. They teach you to choose the simplest and easiest one from a variety of methods.

Theoretical part

Brief historical background.

Leonhard Euler (1707-1783) – great mathematician of the St. Petersburg Academy of the 18th century. Born in the Swiss town of Basel. He discovered mathematical abilities early. At the age of 13, he became a student at the Faculty of Arts at the University of Basel, where both mathematics and astronomy were taught. At the age of 17 he was awarded a master's degree. At the age of 20, Euler was invited to work at the St. Petersburg Academy of Sciences, and at the age of 23 he was already a professor of physics, and three years later he received the department of higher mathematics.

During his long life, Leonhard Euler left important works on various branches of mathematics, mechanics, physics, astronomy and a number of applied sciences, and wrote more than 850 scientific papers. In one of them these circles appeared.

What are Euler circles?

I found the answer to this question by reading various educational literature. Leonhard Euler believed that “circles are very suitable for facilitating our thinking.” When solving a number of problems, he used the idea of representing sets using circles, which is why they were called “Eulerian circles.”

In mathematics, a set is a collection, a collection of some objects (objects). The objects that make up a set are called its elements. It is conventionally accepted that a circle visually depicts the volume of one concept. For example, our 5th grade is a set, and the number of students in the class is its elements.

In mathematics, sets are denoted by capital letters and their elements by capital letters. Often written in the form A = (a, b, c, ...), where the elements of the set A are indicated in curly brackets.

If each element of set A is at the same time an element of set B, then they say that A is a subset of set B. For example, the set of 5th grade students in our gymnasium is a subset of all students in the gymnasium.

With sets, as with objects, you can perform certain actions (operations). In order to more clearly imagine actions with sets, special drawings are used - Euler diagrams (circles). Let's get to know some of them.

The set of common elements A and B is called the intersection of the sets A and B and is denoted by the sign ∩.

A∩B = (m), C ∩B = (e, u).

Sets A and C do not have common elements, so the intersection of these sets is the empty set: A∩C =∅.

If you create a new set from the elements of sets A and B, consisting of all the elements of these sets and not containing other elements, then you get a union of sets A and B, which is denoted by the sign ∪.

Consider an example: Let A = (t, o, h, k, a), B = (t, i, p, e), C = (d, e, f, u, s).

A∪B = (t, o, h, k, a, i, p, e), B∪ C = (t, i, p, e, d, f, s), A ∪ B ∪ C = (t , o, h, k, a, i, p, e, d, f, s).

Conclusions: Euler circles are a geometric diagram that allows you to make logical connections between phenomena and concepts more clear. It also helps to depict the relationship between a set and its part.

You can verify this using an example task.

All my friends grow some flowers in their apartments. Six of them grow cacti, and five grow violets. And only two have both cacti and violets. How many girlfriends do I have?

Let’s determine how many sets there are in the problem (i.e., how many circles we will draw when solving the problem).

In the task, the friends grow 2 types of flowers: cacti and violets.

This means the first set (1 circle is friends who grow cacti).

The second set (the 2nd circle are friends who grow violets).

In the first circle we will designate the owners of cacti, and in the second circle the owners of violets.

We select the condition that contains more properties to draw circles. Some friends have both flowers, so let's draw circles so that they have a common part.

Let's do the drawing.

In the general part we put the number 2, since two friends have both cacti and violets.

According to the conditions of the problem, 6 friends breed cacti, and 2 are already in the common part, then in the remaining part of the cacti we put the number 4 (6-2 = 4).

5 friends grow violets, and 2 are already in the common part, then in the remaining part of the violets we put the number 3 (5-2=3)

The picture itself tells us the answer 4+2+3=9. We write down the answer.

Answer: 9 girlfriends

Practical part

Solving problems using Euler circles

Having figured out what Euler circles are based on the example of the problem and the material studied, I decided to move on to drawing up an algorithm for solving problems using this method.

2.1 Algorithm for solving problems

We carefully study and briefly write down the conditions of the problem.

We determine the number of sets and designate them.

Let's do the drawing. We construct the intersection of sets.

We write the initial data in circles.

Select the condition that contains more properties.

We write the missing data in Euler circles (reasoning and analyzing)

We check the solution to the problem and write down the answer.

Having created an algorithm for solving problems using Euler circles, I decided to work it on several more problems.

Problems involving the intersection and union of two sets

Task 1.

There are 15 students in my class. Of these, 9 are involved in the athletics section, 5 in the swimming section and 3 in both sections. How many students in the class do not attend sections?

Solution.

The problem has one set and two subsets. 1 circle - total students. 2nd circle – number of students involved in athletics. 3 circle - the number of students involved in swimming.

Let us represent all the students using a larger circle. We’ll place smaller circles inside, and draw them so that they have a common part (since three guys study in both sections).

Total

Let's do the drawing.

There are 15 students inside a large circle. In the general part of the smaller circles we put the number 3. In the remaining part of the circle l/a we put the number 6 (9-3=6). In the remaining part of the circle n - put the number 2 (5-3=2).

5. We write down the answer from the picture: 15-(6+3+2) = 4 (students) are not engaged in any of these sections.

Problem 2. (which I solved in a different way, but now I’ll solve it using Euler circles)

There are 35 students in the class, 12 are in a math club, 9 in a biology club, and 16 kids do not attend these clubs. How many biologists are interested in mathematics?

Solution:

The problem has one set and two subsets. 1 circle - total students in the class. 2nd circle the number of students studying in a math circle (denoted by the letter M). 3rd circle - the number of students studying in the biology circle (denoted by the letter B).

Let us depict the entire class of students using a large circle. Inside we will place smaller circles that have a common part, because Several biologists are interested in mathematics.

Let's do the drawing:

There are only 35 students inside the large circle. 35-16 = 19 (students) attend these clubs. Inside circle M we put 12 students studying in a math circle. Inside circle B we put 9 students studying in the biology club.

Let's write the answer from the picture: (12 + 9) – 19 = 2 (students) – they are fond of biology and mathematics. Answer: 2 students.

2.3. Problems involving the intersection and union of three sets

Task 3.

There are 40 people in the class. Of these, 19 people have “C” grades in the Russian language, 17 people in mathematics and 22 people in history. Only one subject has “C” grades: in Russian - 4 people, in mathematics - 4 people, in history - 11 people. Seven students have “C” grades in both mathematics and history, and 5 students have “C” grades in all subjects. How many people study without grades? How many people have C's in two out of three subjects?

Solution:

The problem has one set and three subsets. 1 large circle - total number of students in the class. 2nd circle is the number of students with C grades in mathematics (denoted by the letter M), 3rd circle is smaller - the number of students with C grades in the Russian language (denoted by the letter P), 4th circle is smaller - the number of students with C grades in history (denoted by the letter I)

Let's draw Euler circles. Inside the larger circle depicting all the students in the class, we will place three smaller circles M, R, I, meaning mathematics, Russian language and history, respectively, and all three circles intersect, since 5 students have “C” grades in all subjects.

Let's write the data in circles, reasoning, analyzing and performing the necessary calculations. Since the number of students with “C” grades in mathematics and history is 7, the number of students with only two “C” grades - in mathematics and history - is 7-5 = 2. Then 17-4-5-2=6 students have two “C” grades - in mathematics and the Russian language, and 22-5-2-11=4 students have only two “C” grades - in history and the Russian language. In this case, 40-22-4-6-4 = 4 students study without a “C”. And they have “C” grades in two subjects out of three 6+2+4=12 people.

7-5=2 - the number of students with only two “C” grades - M, I.

17-4-5-2=6 - the number of students with only two “C” grades - M, R.

22-5-2-11=4 - the number of students with only two “C” grades - I, R.

40-22-4-6-4=4 - the number of students studying without a “C”

6+2+4=12 - the number of students with “C” grades - in two out of three subjects

Answer: 4 students study without “C” grades, 12 students have “C” grades in two out of three subjects

Task 4.

There are 30 people in the class. 20 of them use the metro every day, 15 use the bus, 23 use the trolleybus, 10 use both the metro and trolleybus, 12 use both the metro and bus, 9 use both trolleybus and bus. How many people use all three modes of transport every day?

Solution. 1 way. To solve, we again use Euler circles:

20 − (12 − x) − (10 − x) − x = x − 2

Similarly we get: 15 –(12 − x) -(9 − x) - x = x − 6 - only by bus and

23 - (9 − x) - (10 − x) – x = x + 4 - only by trolleybus, since there are only 30 people, we create the equation:

X + (12 − x) + (9 − x) + (10 − x) + (x + 4) + (x − 2) + (x − 6) = 30. Hence x = 3.

Method 2. Or you can solve this problem in another way:

20+15+23-10-12-9+x=30, 27+x=30, x=3.

Answer: 3 people use all three modes of transport every day.

2.4. Preparation of problems of practical importance

Problem 1. There are 15 people in class 5A. 5 people go to the “Erudite” circle, 13 people go to the “Path to the Word” circle, 3 people attend the sports section. Moreover, 2 people attend the “Erudite” circle and the “Path to the Word” circle, “Erudition” and the sports section, the sports section and the “Path to the Word”. How many people attend all three clubs?

Solution:

1. Let x people attend all three clubs, then

2. 5+13+3-2-2-2+x=15, 13+x=15, x=2

Answer: 2 people attend all three clubs.

Problem 2

It is known that students of grade 6B are registered on social networks: “VK”, “Odnoklassniki”, “Dating Galaxy”. 2 students are not registered on any social network, 7 students are registered on both Odnoklassniki and VK; 2 students only in Odnoklassniki and 1 only in VK; and 2 students are registered in all 3 social networks. How many people in the class are registered on each social network? How many people in the class took part in the survey?

Solution:

Using Euler circles we get:

There are 1+5+2=8 people registered in VK,

In Odnoklassniki there are 2+5+2=9 people,

There are only 2 people in the Dating Galaxy.

A total of 1+5+2+2+2=12 people took part in the survey

2.5. Problems for use in math circle classes

Task 1: "Harry Potter, Ron and Hermione"

There were 26 magic books on spells on the shelf, all of them had been read. Of these, 4 were read by both Harry Potter and Ron. Hermione read 7 books that neither Harry Potter nor Ron had read, and two books that Harry Potter had read. In total, Harry Potter read 11 books. How many books has Ron alone read?

Task 2: “Pioneer camp”

Task 3: “Extreme”

Task 4: "Football Team"

The Spartak football team has 30 players, including 18 forwards, 11 midfielders, 17 defenders and goalkeepers. It is known that three can be forwards and defenders, 10 defenders and midfielders, 6 forwards and defenders, and 1 can be an attacker, a defender, and a midfielder. Goalkeepers are irreplaceable. How many goalkeepers are there in the Spartak team?

Task 5: “Shop”

65 people visited the store. It is known that they bought 35 refrigerators, 36 microwaves, 37 televisions. 20 of them bought both a refrigerator and a microwave, 19 bought both a microwave and a TV, 15 bought a refrigerator and a TV, and all three purchases were made by three people. Was there a visitor among them who did not buy anything?

Task 6: “Kindergarten”

There are 52 children in the kindergarten. Each of them loves either cake or ice cream, or both. Half of the children like cake, and 20 people like cake and ice cream. How many children love ice cream?

Task 7: “Student Brigade”

There are 86 high school students in the student production team. 8 of them do not know how to operate either a tractor or a combine. 54 students mastered the tractor well, 62 - the combine. How many people from this team can work on both a tractor and a combine?

Research part

Goal: use of the Euler method by gymnasium students when solving non-standard problems.

The experiment was conducted with the participation of students in grades 5-9 who are interested in mathematics. They were asked to solve the following two problems:

Six students from the class go to music school, ten are involved in the football section, and another ten attend an art studio. Three of them attend both football and music school. How many people are in the class?

Out of 10 participants (2 people from each parallel class) of the experiment, only 4 people solved the first problem, only two solved the second problem (students in grades 8 and 9). After I presented them with my research work, in which I talked about Euler circles, analyzed the solution of several simple and proposed problems using this method, the students could solve simple problems themselves.

At the end of the experiment, the children were given the following task:

There are 70 children in the pioneer camp. Of these, 27 are involved in the drama club, 32 sing in the choir, 22 are fond of sports. There are 10 guys from the choir in the drama club, 6 athletes in the choir, 8 athletes in the drama club; 3 athletes attend both the drama club and the choir. How many kids don’t sing, aren’t interested in sports, don’t participate in a drama club? How many guys are only involved in sports?

Of the 10 participants in the experiment, all coped with this task.

Conclusion: Solving problems using Euler circles develops logical thinking and makes it possible to solve problems that can be solved in the usual way only by composing a system of three equations with three unknowns. Students in grades 5-7 do not know how to solve systems of equations, but they can solve the same problems. This means that the children need to know this method of solving problems using Euler circles.

Applications