Inverse matrix examples with 2x2 solution. Inverse matrix and its properties

Matrix algebra - Inverse matrix

inverse matrix

Inverse matrix is called a matrix which, when multiplied both on the right and on the left by this matrix gives the identity matrix.
Let us denote the inverse matrix of the matrix A through , then according to definition we get:

Where E – identity matrix.
Square matrix called not special (non-degenerate) if its determinant is not zero. Otherwise it is called special (degenerate) or singular.

The theorem holds: Every non-singular matrix has an inverse matrix.

The operation of finding the inverse matrix is called appeal matrices. Let's consider the matrix inversion algorithm. Let a non-singular matrix be given n-th order:

where Δ = det A ≠ 0.

Algebraic addition of an element matrices n-th order A is called the determinant of a matrix taken with a certain sign ( n–1)th order obtained by deleting i-th line and j th matrix column A:

Let's create the so-called attached matrix:

where are the algebraic complements of the corresponding elements of the matrix A.
Note that algebraic additions of matrix row elements A are placed in the corresponding columns of the matrix Ã , that is, the matrix is transposed at the same time.
By dividing all the elements of the matrix Ã by Δ – the value of the matrix determinant A, we get the inverse matrix as a result:

Let's note the row special properties inverse matrix:
1) for a given matrix A her inverse matrix is the only one;
2) if there is an inverse matrix, then right reverse And left reverse the matrices coincide with it;
3) a singular (singular) square matrix does not have an inverse matrix.

Basic properties of an inverse matrix:
1) the determinant of the inverse matrix and the determinant of the original matrix are reciprocals;
2) the inverse matrix of the product of square matrices is equal to the product of the inverse matrix of factors, taken in reverse order:

3) the transposed inverse matrix is equal to the inverse matrix of the given transposed matrix:

EXAMPLE Calculate the inverse of the given matrix.

Definition 1: a matrix is called singular if its determinant is zero.

Definition 2: a matrix is called non-singular if its determinant is not equal to zero.

Matrix "A" is called inverse matrix, if the condition A*A-1 = A-1 *A = E (unit matrix) is satisfied.

A square matrix is invertible only if it is non-singular.

Scheme for calculating the inverse matrix:

1) Calculate the determinant of matrix "A" if ∆ A = 0, then the inverse matrix does not exist.

2) Find all algebraic complements of matrix "A".

3) Create a matrix of algebraic additions (Aij)

4) Transpose the matrix of algebraic complements (Aij )T

5) Multiply the transposed matrix by the number, inverse of the determinant of this matrix.

6) Perform check:

At first glance it may seem complicated, but in fact everything is very simple. All solutions are based on simple arithmetic operations, the main thing when deciding is not to get confused with the “-” and “+” signs and not to lose them.

Now let's decide together practical task, calculating the inverse matrix.

Task: find the inverse matrix "A" shown in the picture below:

We solve everything exactly as indicated in the plan for calculating the inverse matrix.

1. The first thing to do is to find the determinant of matrix "A":

Explanation:

We have simplified our determinant using its basic functions. First, we added to the 2nd and 3rd lines the elements of the first line, multiplied by one number.

Secondly, we changed the 2nd and 3rd columns of the determinant, and according to its properties, we changed the sign in front of it.

Thirdly, we took out the common factor (-1) of the second line, thereby changing the sign again, and it became positive. We also simplified line 3 in the same way as at the very beginning of the example.

We have obtained a triangular determinant whose elements below the diagonal are equal to zero, and by property 7 it equal to the product diagonal elements. In the end we got ∆ A = 26, therefore the inverse matrix exists.

A11 = 1*(3+1) = 4

A12 = -1*(9+2) = -11

A13 = 1*1 = 1

A21 = -1*(-6) = 6

A22 = 1*(3-0) = 3

A23 = -1*(1+4) = -5

A31 = 1*2 = 2

A32 = -1*(-1) = -1

A33 = 1+(1+6) = 7

3. The next step is to compile a matrix from the resulting additions:

5. Multiply this matrix by the inverse of the determinant, that is, by 1/26:

6. Now we just need to check:

During the test, we received an identity matrix, therefore, the solution was carried out absolutely correctly.

2 way to calculate the inverse matrix.

1. Elementary matrix transformation

2. Inverse matrix through an elementary converter.

Elementary matrix transformation includes:

1. Multiplying a string by a number that is not equal to zero.

2. Adding to any line another line multiplied by a number.

3. Swap the rows of the matrix.

4. Applying a chain elementary transformations, we get another matrix.

A -1 = ?

1. (A|E) ~ (E|A -1 )

2.A -1 * A = E

Let's look at this practical example with real numbers.

Exercise: Find the inverse matrix.

Solution:

Let's check:

A little clarification on the solution:

First, we rearranged rows 1 and 2 of the matrix, then multiplied the first row by (-1).

After that, we multiplied the first row by (-2) and added it with the second row of the matrix. Then we multiplied line 2 by 1/4.

The final stage The transformations were multiplication of the second line by 2 and addition from the first. As a result, we have the identity matrix on the left, therefore, the inverse matrix is the matrix on the right.

After checking, we were convinced that the decision was correct.

As you can see, calculating the inverse matrix is very simple.

At the end of this lecture, I would also like to spend a little time on the properties of such a matrix.

Finding the inverse matrix- a problem that is often solved by two methods:

the method of algebraic additions, which requires finding determinants and transposing matrices;
by elimination unknown Gauss, in which it is necessary to perform elementary transformations of matrices (add rows, multiply rows by the same number, etc.).

For those who are especially curious, there are other methods, for example, the method of linear transformations. In this lesson we will analyze the three mentioned methods and algorithms for finding the inverse matrix using these methods.

Inverse matrix A, such a matrix is called

A
. (1)

Inverse matrix , which needs to be found for a given square matrix A, such a matrix is called

the product of which the matrices A on the right is the identity matrix, i.e.
. (1)

An identity matrix is a diagonal matrix in which all diagonal elements are equal to one.

Theorem.For every non-singular (non-degenerate, non-singular) square matrix, one can find an inverse matrix, and only one. For a special (degenerate, singular) square matrix, the inverse matrix does not exist.

The square matrix is called not special(or non-degenerate, non-singular), if its determinant is not zero, and special(or degenerate, singular) if its determinant is zero.

The inverse of a matrix can only be found for a square matrix. Naturally, the inverse matrix will also be square and of the same order as the given matrix. A matrix for which an inverse matrix can be found is called an invertible matrix.

For inverse matrix There is a relevant analogy with the inverse of a number. For every number a, not equal to zero, there is such a number b that the work a And b equals one: ab= 1 . Number b called the inverse of a number b. For example, for the number 7 the reciprocal is 1/7, since 7*1/7=1.

Finding the inverse matrix using the method of algebraic additions (allied matrix)

For a non-singular square matrix A the inverse is the matrix

where is the determinant of the matrix A, a is a matrix allied with the matrix A.

Allied with a square matrix A is a matrix of the same order, the elements of which are the algebraic complements of the corresponding elements of the determinant of the matrix transposed with respect to the matrix A. Thus, if

That

And

Algorithm for finding the inverse matrix using the method of algebraic additions

1. Find the determinant of this matrix A. If the determinant is equal to zero, finding the inverse matrix stops, since the matrix is singular and its inverse does not exist.

2. Find the matrix transposed with respect to A.

3. Calculate the elements of the union matrix as algebraic complements of the maritz found in step 2.

4. Apply formula (2): multiply the inverse of the matrix determinant A, to the union matrix found in step 4.

5. Check the result obtained in step 4 by multiplying this matrix A to the inverse matrix. If the product of these matrices is equal to the identity matrix, then the inverse matrix was found correctly. Otherwise, start the solution process again.

Example 1. For matrix

find the inverse matrix.

Solution. To find the inverse matrix, you need to find the determinant of the matrix A. We find by the rule of triangles:

Therefore, the matrix A– non-singular (non-degenerate, non-singular) and there is an inverse for it.

Let's find a matrix allied to this matrix A.

Let's find the matrix transposed with respect to the matrix A:

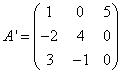
We calculate the elements of the allied matrix as algebraic complements of the matrix transposed with respect to the matrix A:

Therefore, the matrix allied to the matrix A, has the form

Comment. The order in which the elements are calculated and the matrix is transposed may be different. You can first calculate the algebraic complements of the matrix A, and then transpose the algebraic complement matrix. The result should be the same elements of the union matrix.

Applying formula (2), we find the matrix inverse to the matrix A:

Finding the inverse matrix using the Gaussian unknown elimination method

The first step to find the inverse of a matrix using the Gaussian elimination method is to assign to the matrix A identity matrix of the same order, separating them with a vertical bar. We will get a dual matrix. Let's multiply both sides of this matrix by , then we get

Algorithm for finding the inverse matrix using the Gaussian unknown elimination method

1. To the matrix A assign an identity matrix of the same order.

2. Transform the resulting dual matrix so that on its left side you get a unit matrix, then on the right side, in place of the identity matrix, you automatically get an inverse matrix. Matrix A on the left side is transformed into the identity matrix by elementary matrix transformations.

2. If in the process of matrix transformation A in the identity matrix there will be only zeros in any row or in any column, then the determinant of the matrix is equal to zero, and, consequently, the matrix A will be singular, and it does not have an inverse matrix. In this case, further determination of the inverse matrix stops.

Example 2. For matrix

find the inverse matrix.

and we will transform it so that on the left side we get an identity matrix. We begin the transformation.

Multiply the first row of the left and right matrix by (-3) and add it to the second row, and then multiply the first row by (-4) and add it to the third row, then we get

So that if possible there is no fractional numbers during subsequent transformations, we will first create a unit in the second row on the left side of the dual matrix. To do this, multiply the second line by 2 and subtract the third line from it, then we get

Let's add the first line with the second, and then multiply the second line by (-9) and add it with the third line. Then we get

Divide the third line by 8, then

Multiply the third line by 2 and add it to the second line. It turns out:

Let's swap the second and third lines, then we finally get:

We see that on the left side we have the identity matrix, therefore, on the right side we have the inverse matrix. Thus:

You can check the correctness of the calculations by multiplying the original matrix by the found inverse matrix:

The result should be an inverse matrix.

Example 3. For matrix

find the inverse matrix.

Solution. Compiling a dual matrix

and we will transform it.

We multiply the first line by 3, and the second by 2, and subtract from the second, and then we multiply the first line by 5, and the third by 2 and subtract from the third line, then we get

We multiply the first line by 2 and add it to the second, and then subtract the second from the third line, then we get

We see that in the third line on the left side all elements are equal to zero. Therefore, the matrix is singular and has no inverse matrix. We stop further finding the inverse maritz.

The matrix $A^(-1)$ is called the inverse of the square matrix $A$ if the condition $A^(-1)\cdot A=A\cdot A^(-1)=E$ is satisfied, where $E $ is the identity matrix, the order of which is equal to the order of the matrix $A$.

A non-singular matrix is a matrix whose determinant is not equal to zero. Accordingly, a singular matrix is one whose determinant is equal to zero.

The inverse matrix $A^(-1)$ exists if and only if the matrix $A$ is non-singular. If the inverse matrix $A^(-1)$ exists, then it is unique.

There are several ways to find the inverse of a matrix, and we will look at two of them. This page will discuss the adjoint matrix method, which is considered standard in most courses. higher mathematics. The second method of finding the inverse matrix (the method of elementary transformations), which involves using the Gauss method or the Gauss-Jordan method, is discussed in the second part.

Adjoint matrix method

Let the matrix $A_(n\times n)$ be given. In order to find the inverse matrix $A^(-1)$, three steps are required:

Find the determinant of the matrix $A$ and make sure that $\Delta A\neq 0$, i.e. that matrix A is non-singular.
Compose algebraic complements $A_(ij)$ of each element of the matrix $A$ and write the matrix $A_(n\times n)^(*)=\left(A_(ij) \right)$ from the found algebraic complements.
Write the inverse matrix taking into account the formula $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$.

The matrix $(A^(*))^T$ is often called adjoint (reciprocal, allied) to the matrix $A$.

If the solution is done manually, then the first method is good only for matrices of relatively small orders: second (), third (), fourth (). To find the inverse of a matrix higher order, other methods are used. For example, the Gaussian method, which is discussed in the second part.

Example No. 1

Find the inverse of matrix $A=\left(\begin(array) (cccc) 5 & -4 &1 & 0 \\ 12 &-11 &4 & 0 \\ -5 & 58 &4 & 0 \\ 3 & - 1 & -9 & 0 \end(array) \right)$.

Since all elements of the fourth column are equal to zero, then $\Delta A=0$ (i.e. the matrix $A$ is singular). Since $\Delta A=0$, there is no inverse matrix to matrix $A$.

Example No. 2

Find the inverse of matrix $A=\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right)$.

We use the adjoint matrix method. First let's find the determinant given matrix$A$:

$$ \Delta A=\left| \begin(array) (cc) -5 & 7\\ 9 & 8 \end(array)\right|=-5\cdot 8-7\cdot 9=-103. $$

Since $\Delta A \neq 0$, then the inverse matrix exists, therefore we will continue the solution. Finding algebraic complements

\begin(aligned) & A_(11)=(-1)^2\cdot 8=8; \; A_(12)=(-1)^3\cdot 9=-9;\\ & A_(21)=(-1)^3\cdot 7=-7; \; A_(22)=(-1)^4\cdot (-5)=-5.\\ \end(aligned)

We compose a matrix of algebraic additions: $A^(*)=\left(\begin(array) (cc) 8 & -9\\ -7 & -5 \end(array)\right)$.

We transpose the resulting matrix: $(A^(*))^T=\left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right)$ (the resulting matrix is often is called the adjoint or allied matrix to the matrix $A$). Using the formula $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, we have:

$$ A^(-1)=\frac(1)(-103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right) =\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right) $$

So, the inverse matrix is found: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right) $. To check the truth of the result, it is enough to check the truth of one of the equalities: $A^(-1)\cdot A=E$ or $A\cdot A^(-1)=E$. Let's check the equality $A^(-1)\cdot A=E$. In order to work less with fractions, we will substitute the matrix $A^(-1)$ not in the form $\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \ end(array)\right)$, and in the form $-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array )\right)$:

Answer: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right)$.

Example No. 3

Find the inverse matrix for the matrix $A=\left(\begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right)$.

Let's start by calculating the determinant of the matrix $A$. So, the determinant of the matrix $A$ is:

$$ \Delta A=\left| \begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right| = 18-36+56-12=26. $$

Since $\Delta A\neq 0$, then the inverse matrix exists, therefore we will continue the solution. We find the algebraic complements of each element of a given matrix:

We compose a matrix of algebraic additions and transpose it:

$$ A^*=\left(\begin(array) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37\end(array) \right); \; (A^*)^T=\left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right) $$

Using the formula $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, we get:

$$ A^(-1)=\frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37\end(array) \right)= \left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \end(array) \right) $$

So $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6/13 & -3/26 & 37/26 \end(array) \right)$. To check the truth of the result, it is enough to check the truth of one of the equalities: $A^(-1)\cdot A=E$ or $A\cdot A^(-1)=E$. Let's check the equality $A\cdot A^(-1)=E$. In order to work less with fractions, we will substitute the matrix $A^(-1)$ not in the form $\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end(array) \right)$, and in the form $\frac(1)(26)\cdot \left( \begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right)$:

The check was successful, the inverse matrix $A^(-1)$ was found correctly.

Answer: $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 /13 & -3/26 & 37/26 \end(array) \right)$.

Example No. 4

Find the matrix inverse of matrix $A=\left(\begin(array) (cccc) 6 & -5 & 8 & 4\\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7\\ -4 & 8 & -8 & -3 \end(array) \right)$.

For a fourth-order matrix, finding the inverse matrix using algebraic additions is somewhat difficult. However, such examples in tests meet.

To find the inverse of a matrix, you first need to calculate the determinant of the matrix $A$. The best way to do this in this situation is by decomposing the determinant along a row (column). We select any row or column and find the algebraic complements of each element of the selected row or column.

Finding the inverse matrix.

In this article we will understand the concept of an inverse matrix, its properties and methods of finding. Let us dwell in detail on solving examples in which it is necessary to construct an inverse matrix for a given one.

Page navigation.

Inverse matrix - definition.

Finding the inverse matrix using a matrix from algebraic complements.

Properties of an inverse matrix.

Finding the inverse matrix using the Gauss-Jordan method.

Finding the elements of the inverse matrix by solving the corresponding systems of linear algebraic equations.

Inverse matrix - definition.

The concept of an inverse matrix is introduced only for square matrices whose determinant is nonzero, that is, for non-singular square matrices.

Definition.

Matrixcalled the inverse of a matrix, whose determinant is different from zero if the equalities are true , Where E– unit order matrix n on n.

Finding the inverse matrix using a matrix from algebraic complements.

How to find the inverse matrix for a given one?

First, we need the concepts transposed matrix, matrix minor and algebraic complement of a matrix element.

Definition.

Minorkth order matrices A order m on n is the determinant of the order matrix k on k, which is obtained from the matrix elements A located in the selected k lines and k columns. ( k does not exceed the smallest number m or n).

Minor (n-1)th order, which is composed of elements of all rows except i-th, and all columns except jth, square matrix A order n on n let's denote it as .

In other words, the minor is obtained from a square matrix A order n on n by crossing out elements i-th lines and jth column.

For example, let's write, minor 2nd order, which is obtained from the matrix selecting elements of its second, third rows and first, third columns . We will also show the minor, which is obtained from the matrix by crossing out the second line and third column . Let us illustrate the construction of these minors: and .

Definition.

Algebraic complement element of a square matrix is called minor (n-1)th order, which is obtained from the matrix A, crossing out elements of it i-th lines and jth column multiplied by .

The algebraic complement of an element is denoted as . Thus, .

For example, for the matrix the algebraic complement of an element is .

Secondly, we will need two properties of the determinant, which we discussed in the section calculating the determinant of a matrix:

Based on these properties of the determinant, the definition operations of multiplying a matrix by a number and the concept of an inverse matrix is true: , where is a transposed matrix whose elements are algebraic complements.

Matrix is indeed the inverse of the matrix A, since the equalities are satisfied . Let's show it

Let's compose algorithm for finding the inverse matrix using equality .

Let's look at the algorithm for finding the inverse matrix using an example.

Example.

Given a matrix . Find the inverse matrix.

Solution.

Let's calculate the determinant of the matrix A, decomposing it into the elements of the third column:

The determinant is nonzero, so the matrix A reversible.

Let's find a matrix of algebraic additions:

That's why

Let's transpose the matrix from algebraic additions:

Now we find the inverse matrix as :

Let's check the result:

Equalities are satisfied, therefore, the inverse matrix is found correctly.

Properties of an inverse matrix.

The concept of an inverse matrix, equality , definitions of operations on matrices and properties of the determinant of a matrix make it possible to justify the following properties of inverse matrix:

Finding the elements of the inverse matrix by solving the corresponding systems of linear algebraic equations.

Let's consider another way to find the inverse matrix for a square matrix A order n on n.

This method is based on the solution n systems of linear inhomogeneous algebraic equations with n unknown. The unknown variables in these systems of equations are the elements of the inverse matrix.

The idea is very simple. Let us denote the inverse matrix as X, that is, . Since by definition of the inverse matrix, then

Equating the corresponding elements by columns, we get n systems of linear equations

We solve them in any way and form an inverse matrix from the found values.

Let's look at this method with an example.

Example.

Given a matrix . Find the inverse matrix.

Solution.

Let's accept . Equality gives us three systems of linear inhomogeneous algebraic equations:

We will not describe the solution to these systems; if necessary, refer to the section solving systems of linear algebraic equations.

From the first system of equations we have, from the second - , from the third - . Therefore, the required inverse matrix has the form . We recommend checking it to make sure the result is correct.

Summarize.

We looked at the concept of an inverse matrix, its properties, and three methods for finding it.

Example of solutions using the inverse matrix method

Exercise 1. Solve SLAE using the inverse matrix method. 2 x 1 + 3x 2 + 3x 3 + x 4 = 1 3 x 1 + 5x 2 + 3x 3 + 2x 4 = 2 5 x 1 + 7x 2 + 6x 3 + 2x 4 = 3 4 x 1 + 4x 2 + 3x 3 + x 4 = 4

Beginning of the form

End of form

Solution. Let's write the matrix in the form: Vector B: B T = (1,2,3,4) Main determinant Minor for (1,1): = 5 (6 1-3 2)-7 (3 1-3 2)+4 ( 3 2-6 2) = -3 Minor for (2,1): = 3 (6 1-3 2)-7 (3 1-3 1)+4 (3 2-6 1) = 0 Minor for (3 ,1): = 3 (3 1-3 2)-5 (3 1-3 1)+4 (3 2-3 1) = 3 Minor for (4,1): = 3 (3 2-6 2) -5 (3 2-6 1)+7 (3 2-3 1) = 3 Determinant of minor ∆ = 2 (-3)-3 0+5 3-4 3 = -3

Transposed matrix Algebraic additions ∆ 1,1 = 5 (6 1-2 3)-3 (7 1-2 4)+2 (7 3-6 4) = -3 ∆ 1,2 = -3 (6 1-2 3) -3 (7 1-2 4)+1 (7 3-6 4) = 0 ∆ 1.3 = 3 (3 1-2 3)-3 (5 1-2 4)+1 (5 3-3 4 ) = 3 ∆ 1.4 = -3 (3 2-2 6)-3 (5 2-2 7)+1 (5 6-3 7) = -3 ∆ 2.1 = -3 (6 1-2 3)-3 (5 1-2 4)+2 (5 3-6 4) = 9 ∆ 2.2 = 2 (6 1-2 3)-3 (5 1-2 4)+1 (5 3- 6 4) = 0 ∆ 2.3 = -2 (3 1-2 3)-3 (3 1-2 4)+1 (3 3-3 4) = -6 ∆ 2.4 = 2 (3 2- 2 6)-3 (3 2-2 5)+1 (3 6-3 5) = 3 ∆ 3.1 = 3 (7 1-2 4)-5 (5 1-2 4)+2 (5 4 -7 4) = -4 ∆ 3.2 = -2 (7 1-2 4)-3 (5 1-2 4)+1 (5 4-7 4) = 1 ∆ 3.3 = 2 (5 1 -2 4)-3 (3 1-2 4)+1 (3 4-5 4) = 1 ∆ 3.4 = -2 (5 2-2 7)-3 (3 2-2 5)+1 ( 3 7-5 5) = 0 ∆ 4.1 = -3 (7 3-6 4)-5 (5 3-6 4)+3 (5 4-7 4) = -12 ∆ 4.2 = 2 ( 7 3-6 4)-3 (5 3-6 4)+3 (5 4-7 4) = -3 ∆ 4.3 = -2 (5 3-3 4)-3 (3 3-3 4) +3 (3 4-5 4) = 9 ∆ 4.4 = 2 (5 6-3 7)-3 (3 6-3 5)+3 (3 7-5 5) = -3 Inverse matrix Results vector X X = A -1 ∙ B X T = (2,-1,-0.33,1) x 1 = 2 x 2 = -1 x 3 = -0.33 x 4 = 1

see also solutions of SLAEs using the inverse matrix method online. To do this, enter your data and receive a solution with detailed comments.

Task 2. Write the system of equations in matrix form and solve it using the inverse matrix. Check the resulting solution. Solution:xml:xls

Example 2. Write the system of equations in matrix form and solve using the inverse matrix. Solution:xml:xls

Example. A system of three linear equations with three unknowns is given. Required: 1) find its solution using Cramer formulas; 2) write the system in matrix form and solve it using matrix calculus. Guidelines. After solving by Cramer's method, find the "Solving by inverse matrix method for source data" button. You will receive the appropriate solution. Thus, you will not have to fill in the data again. Solution. Let us denote by A the matrix of coefficients for unknowns; X - matrix-column of unknowns; B - matrix-column of free members:

Vector B: B T =(4,-3,-3) Taking into account these notations, this system of equations takes the following matrix form: A*X = B. If matrix A is non-singular (its determinant is non-zero, then it has an inverse matrix A -1... Multiplying both sides of the equation by A -1, we get: A -1 *A*X = A -1 *B, A -1 *A = E. This equality is called matrix notation of the solution to a system of linear equations. To find a solution to the system of equations, it is necessary to calculate the inverse matrix A -1. The system will have a solution if the determinant of the matrix A is nonzero. Let's find the main determinant. ∆=-1 (-2 (-1)-1 1)-3 (3 (-1)-1 0)+2 (3 1-(-2 0))=14 So, determinant 14 ≠ 0, so we continue solution. To do this, we find the inverse matrix through algebraic additions. Let us have a non-singular matrix A:

We calculate algebraic complements.

∆ 1,1 =(-2 (-1)-1 1)=1

∆ 1,2 =-(3 (-1)-0 1)=3

∆ 1,3 =(3 1-0 (-2))=3

∆ 2,1 =-(3 (-1)-1 2)=5

∆ 2,2 =(-1 (-1)-0 2)=1

∆ 2,3 =-(-1 1-0 3)=1

∆ 3,1 =(3 1-(-2 2))=7

∆ 3,2 =-(-1 1-3 2)=7

X T =(-1,1,2) x 1 = -14 / 14 =-1 x 2 = 14 / 14 =1 x 3 = 28 / 14 =2 Examination. -1 -1+3 1+0 2=4 3 -1+-2 1+1 2=-3 2 -1+1 1+-1 2=-3 doc:xml:xls Answer: -1,1,2.