Как решать примеры с неправильными дробями. Положительные и отрицательные дроби
С дробями мы сталкиваемся в жизни гораздо раньше, чем начинается их изучение в школе. Если разрезать целое яблоко пополам, то мы получим часть фрукта - ½. Разрежем ещё раз - будет ¼. Это и есть дроби. И все, казалось бы, просто. Для взрослого человека. Для ребенка же (а данную тему начинают изучать в конце младшей школы) абстрактные математические понятия ещё пугающе непонятны, и преподаватель должен доступно объяснить, что такое правильная дробь и неправильная, обыкновенная и десятичная, какие операции можно с ними совершать и, главное, для чего всё это нужно.
Какие бывают дроби
Знакомство с новой темой в школе начинается с обыкновенных дробей. Их легко узнать по горизонтальной черте, разделяющей два числа - сверху и снизу. Верхнее называется числителем, нижнее - знаменателем. Существует и строчный вариант написания неправильных и правильных обыкновенных дробей - через косую черту, например: ½, 4/9, 384/183. Такой вариант используется, когда высота строки ограничена и нет возможности применить «двухэтажную» форму записи. Почему? Да потому что она удобнее. Чуть позже мы в этом убедимся.
Помимо обыкновенных, существуют также десятичные дроби. Различить их очень просто: если в одном случае используется горизонтальная или наклонная черта, то в другом - запятая, разделяющая последовательности цифр. Посмотрим пример: 2,9; 163,34; 1,953. Мы намеренно воспользовались точкой с запятой в качестве разделителя, чтобы разграничить числа. Первое из них будет читаться так: «две целых, девять десятых».
Новые понятия
Вернемся к обыкновенным дробям. Они бывают двух видов.
Определение правильной дроби звучит следующим образом: это такая дробь, числитель которой меньше знаменателя. Почему это важно? Сейчас увидим!
У вас есть несколько яблок, разделенных на половинки. Всего - 5 частей. Как вы скажете: у вас «два с половиной» или «пять вторых» яблока? Конечно, первый вариант звучит естественнее, и при разговоре с друзьями мы воспользуемся им. А вот если потребуется посчитать, сколько фруктов достанется каждому, если в компании пять человек, мы запишем число 5/2 и разделим его на 5 - с точки зрения математики это будет нагляднее.

Итак, для наименования правильных и неправильных дробей правило таково: если в дроби можно выделить целую часть (14/5, 2/1, 173/16, 3/3), то она является неправильной. Если этого сделать нельзя, как в случае с ½, 13/16, 9/10, она будет правильной.
Основное свойство дроби
Если числитель и знаменатель дроби одновременно умножить или разделить на одно и то же число, её величина не изменится. Представьте: торт порезали на 4 равные части и дали вам одну. Такой же торт порезали на восемь частей и дали вам две. Не всё ли равно? Ведь ¼ и 2/8 - это одно и то же!
Сокращение
Авторы задач и примеров в учебниках по математике зачастую стремятся запутать учеников, предлагая громоздкие в написании дроби, которые на самом деле можно сократить. Вот пример правильной дроби: 167/334, который, казалось бы, выглядит очень «страшно». Но на самом деле мы можем записать его как ½. Число 334 делится на 167 без остатка - проделав такую операцию, мы получим 2.
Смешанные числа
Неправильную дробь можно представить в форме смешанного числа. Это когда целая часть вынесена вперед и записана на уровне горизонтальной черты. Фактически выражение принимает вид суммы: 11/2 = 5 + ½; 13/6 = 2 + 1/6 и так далее.

Чтобы вынести целую часть, нужно разделить числитель на знаменатель. Остаток от деления записать сверху, над чертой, а целую часть - перед выражением. Таким образом, мы получаем две структурные части: целые единицы + правильную дробь.
Можно осуществить и обратную операцию - для этого нужно целую часть умножить на знаменатель и прибавить полученное значение к числителю. Ничего сложного.
Умножение и деление
Как ни странно, умножать дроби проще, чем складывать. Всего-то и требуется - продлить горизонтальную черту: (2/3) * (3/5) = 2*3 / 3*5 = 2/5.
С делением тоже всё просто: нужно перемножить дроби крест-накрест: (7/8) / (14/15) = 7*15 / 8*14 = 15/16.
Сложение дробей
Что делать, если требуется осуществить сложение или а в знаменателе у них разные числа? Поступить так же, как с умножением, не получится - здесь следует понимать определение правильной дроби и её сущность. Нужно привести слагаемые к общему знаменателю, то есть в нижней части обеих дробей должны оказаться одинаковые числа.

Чтобы это осуществить, следует воспользоваться основным свойством дроби: умножить обе части на одно и то же число. Например, 2/5 + 1/10 = (2*2)/(5*2) + 1/10 = 5/10 = ½.
Как же выбрать, к какому знаменателю приводить слагаемые? Это должно быть минимальное число, кратное обоим числам, стоящим в знаменателях дробей: для 1/3 и 1/9 это будет 9; для ½ и 1/7 - 14, потому что меньшего значения, делящегося без остатка на 2 и 7, не существует.
Использование
Для чего нужны неправильные дроби? Ведь гораздо удобнее сразу выделить целую часть, получить смешанное число - и дело с концом! Оказывается, если требуется выполнить умножение или деление двух дробей, выгоднее воспользоваться именно неправильными.
Возьмем следующий пример: (2 + 3/17) / (37 / 68).

Казалось бы, сократить и вовсе нечего. Но что, если записать результат сложения в первых скобках в виде неправильной дроби? Посмотрите: (37/17) / (37/68)
Теперь всё встает на свои места! Запишем пример таким образом, чтобы всё стало очевидно: (37*68) / (17*37).
Сократим 37 в числителе и знаменателе и, наконец, разделим верхнюю и нижнюю части на 17. Вы же помните основное правило для правильной и неправильной дроби? Мы можем умножать и делить их на любое число, если делаем это одновременно для числителя и знаменателя.
Итак, получаем ответ: 4. Пример выглядел сложным, а ответ содержит всего одну цифру. В математике так часто происходит. Главное - не бояться и следовать простым правилам.
Распространенные ошибки
При осуществлении учащийся может легко совершить одну из популярных ошибок. Обычно они происходят из-за невнимательности, а иногда - из-за того, что изученный материал ещё не отложился в голове как следует.
Нередко сумма чисел, стоящая в числителе, вызывает желание сократить отдельные её компоненты. Допустим, в примере: (13 + 2) / 13, написанном без скобок (с горизонтальной чертой), многие ученики по неопытности зачеркивают 13 сверху и снизу. Но так делать нельзя ни в коем случае, ведь это грубая ошибка! Если бы вместо сложения стоял знак умножения, мы получили бы в ответе число 2. Но при осуществлении сложения никакие операции с одним из слагаемых не позволительны, только со всей суммой целиком.

Ещё ребята часто ошибаются при делении дробей. Возьмем две правильные несократимые дроби и разделим друг на друга: (5/6) / (25/33). Ученик может перепутать и записать результирующее выражение как (5*25) / (6*33). Но так бы получилось при умножении, а в нашем случае всё будет несколько иначе: (5*33) / (6*25). Сокращаем то, что возможно, и в ответе увидим 11/10. Получившуюся неправильную дробь запишем как десятичную - 1,1.
Скобки
Помните, что в любых математических выражениях порядок действий определяется приоритетом знаков операций и наличием скобок. При прочих равных отсчёт очередности выполнения действий происходит слева направо. Это актуально и для дробей - выражение в числителе или знаменателе рассчитывается строго по этому правилу.
Ведь Это результат деления одного числа на другое. Если они не делятся нацело, получается дробь - вот и всё.
Как записать дробь на компьютере
Поскольку стандартные средства не всегда позволяют создать дробь, состоящую из двух «ярусов», ученики порой идут на различные ухищрения. Например, копируют числители и знаменатели в графический редактор «Пейнт» и склеивают их воедино, рисуя между ними горизонтальную линию. Конечно, есть более простой вариант, который, кстати, предоставляет и массу дополнительных возможностей, которые станут полезны вам в будущем.
Откройте «Майкрософт Ворд». Одна из панелей в верхней части экрана носит называние «Вставка» - нажмите её. Справа, в той стороне, где расположены значки закрытия и сворачивания окна, есть кнопка «Формула». Это именно то, что нам нужно!

Если вы воспользуетесь данной функцией, на экране появится прямоугольная область, в которой можно использовать любые математические знаки, отсутствующие на клавиатуре, а также писать дроби в классическом виде. То есть разделяя числитель и знаменатель горизонтальной чертой. Вы даже можете удивиться, что такую правильную дробь настолько легко записать.
Изучайте математику
Если вы учитесь в 5-6 классе, то уже скоро знание математики (в том числе - умение работать с дробями!) потребуется во многих школьных предметах. Практически в любой задаче по физике, при измерении массы веществ в химии, в геометрии и тригонометрии без дробей никак не обойтись. Уже скоро вы научитесь вычислять всё в уме, даже не записывая выражения на бумаге, но будут появляться всё более и более сложные примеры. Поэтому выучите, что такое правильная дробь и как с ней работать, не отставайте по учебной программе, своевременно делайте домашние задания, и тогда вы преуспеете.
Дробь в математике — число, состоящее из одной или нескольких частей (долей) единицы. Дроби являются частью поля рациональных чисел. По способу записи дроби делятся на 2 формата: обыкновенные вида и десятичные .
Числитель дроби — число, показывающее количество взятых долей (находится в верхней части дроби - над чертой). Знаменатель дроби — число, показывающее, на сколько долей разделена единица (находится под чертой - в нижней части). , в свою очередь делятся на: правильные и неправильные , смешанные и составные тесно связаны с единицами измерения. 1 метр содержит в себе 100 см. Что означает, что 1 м разделён на 100 равных долей. Таким образом, 1 см = 1/100 м (один сантиметр равен одной сотой метра).
или 3/5 (три пятых), здесь 3 — числитель, 5 — знаменатель. Если числитель меньше знаменателя, то дробь меньше единицы и называется правильной :
Если числитель равен знаменателю, дробь равна единице. Если числитель больше знаменателя, дробь больше единицы. В обоих последних случаях дробь называется неправильной :

Чтобы выделить наибольшее целое число , содержащееся в неправильной дроби, нужно разделить числитель на знаменатель. Если деление выполняется без остатка, то взятая неправильная дробь равна частному:

Если деление выполняется с остатком, то (неполное) частное дает искомое целое число, остаток же становится числителем дробной части; знаменатель дробной части остается прежним.

Число, содержащее целую и дробную части, называется смешанным . Дробная часть смешанного числа может быть и неправильной дробью . Тогда можно из дробной части выделить наибольшее целое число и представить смешанное число в таком виде, чтобы дробная часть стала правильной дробью (или вовсе исчезла).
При слове "дроби" у многих бегут мурашки. Потому что вспоминается школа и задания, которые решались на математике. Это являлось обязанностью, которую необходимо было выполнить. А что если относиться к заданиям, содержащим правильные и неправильные дроби, как к головоломке? Ведь многие взрослые решают цифровые и японские кроссворды. Разобрались в правилах, и все. Так же и здесь. Стоит только вникнуть в теорию - и все встанет на свои места. А примеры превратятся в способ потренировать мозг.
Какие виды дробей существуют?
Для начала о том, что это такое. Дробь — число, которое имеет некоторую часть от единицы. Ее можно записать в двух видах. Первый носит название обыкновенной. То есть такая, у которой есть горизонтальная или наклонная черта. Она приравнивается к знаку деления.
В такой записи число, стоящее над черточкой, называется числителем, а под ней — знаменателем.
Среди обыкновенных выделяют правильные и неправильные дроби. У первых числитель по модулю всегда меньше знаменателя. Неправильные потому так и называются, что у них все наоборот. Значение правильной дроби всегда меньше единицы. В то время как неправильная всегда больше этого числа.
Есть еще смешанные числа, то есть такие у которых имеются целая и дробная части.
Второй вид записи — десятичная дробь. О ней отдельный разговор.
Чем отличаются неправильные дроби от смешанных чисел?
По своей сути, ничем. Это просто разная запись одного и того же числа. Неправильные дроби после несложных действий легко становятся смешанными числами. И наоборот.
Все зависит от конкретной ситуации. Иногда в заданиях удобнее использовать неправильную дробь. А порой необходимо перевести ее в смешанное число и тогда пример решится очень легко. Поэтому, что использовать: неправильные дроби, смешанные числа, - зависит от наблюдательности решающего задачу.
Смешанное число еще сравнивают с суммой целой части и дробной. Причем вторая всегда меньше единицы.

Как представить смешанное число в виде неправильной дроби?
Если требуется выполнить какое-либо действие с несколькими числами, которые записаны в разных видах, то нужно сделать их одинаковыми. Один из методов — представить числа в виде неправильных дробей.
Для этой цели потребуется выполнить действия по такому алгоритму:
- умножить знаменатель на целую часть;
- прибавить к результату значение числителя;
- записать ответ над чертой;
- знаменатель оставить тем же.
Вот примеры того, как записать неправильные дроби из смешанных чисел:
- 17 ¼ = (17 х 4 + 1) : 4 = 69/4;
- 39 ½ = (39 х 2 + 1) : 2 = 79/2.

Как записать неправильную дробь в виде смешанного числа?
Следующий прием противоположен рассмотренному выше. То есть когда все смешанные числа заменяются на неправильные дроби. Алгоритм действий будет таким:
- разделить числитель на знаменатель до получения остатка;
- записать частное на месте целой части смешанного;
- остаток следует разместить над чертой;
- делитель будет знаменателем.
Примеры такого преобразования:
76/14; 76:14 = 5 с остатком 6; ответом будет 5 целых и 6/14; дробную часть в этом примере нужно сократить на 2, получится 3/7; итоговый ответ — 5 целых 3/7.
108/54; после деления получается частное 2 без остатка; это значит, что не все неправильные дроби удается представить в виде смешанного числа; ответом будет целое — 2.
Как целое число превратить в неправильную дробь?
Бывают ситуации, когда необходимо и такое действие. Чтобы получить неправильные дроби с заранее известным знаменателем, потребуется выполнить такой алгоритм:
- умножить целое число на нужный знаменатель;
- записать это значение над чертой;
- разместить под ней знаменатель.
Самый простой вариант, когда знаменатель равен единице. Тогда ничего умножать не нужно. Достаточно просто написать целое число, которое дано в примере, а под чертой расположить единицу.
Пример : 5 сделать неправильной дробью со знаменателем 3. После умножения 5 на 3 получается 15. Это число будет знаменателем. Ответ задания дробь: 15/3.

Два подхода к решению заданий с разными числами
В примере требуется вычислить сумму и разность, а также произведение и частное двух чисел: 2 целых 3/5 и 14/11.
В первом подходе смешанное число будет представлено в виде неправильной дроби.
После выполнения действий, описанных выше, получится такое значение: 13/5.
Для того чтобы узнать сумму, нужно привести дроби к одинаковому знаменателю. 13/5 после умножения на 11 станет 143/55. А 14/11 после умножения на 5 примет вид: 70/55. Для вычисления суммы нужно только сложить числители: 143 и 70, а потом записать ответ с одним знаменателем. 213/55 — эта неправильная дробь ответ задачи.
При нахождении разности эти же числа вычитаются: 143 - 70 = 73. Ответом будет дробь: 73/55.
При умножении 13/5 и 14/11 не нужно приводить к общему знаменателю. Достаточно перемножить попарно числители и знаменатели. Получится ответ: 182/55.
Так же и при делении. Для правильного решения нужно заменить деление на умножение и перевернуть делитель: 13/5: 14/11 = 13/5 х 11/14 = 143/70.
Во втором подходе неправильная дробь обращается в смешанное число.
После выполнения действий алгоритма 14/11 обратится в смешанное число с целой частью 1 и дробной 3/11.
Во время вычисления суммы нужно сложить целые и дробные части по отдельности. 2 + 1 = 3, 3/5 + 3/11 = 33/55 + 15/55 = 48/55. Итоговый ответ получается 3 целых 48/55. В первом подходе была дробь 213/55. Проверить правильность можно, переведя его в смешанное число. После деления 213 на 55 получается частное 3 и остаток 48. Нетрудно заметить, что ответ правильный.
При вычитании знак «+» заменяется на «-». 2 - 1 = 1, 33/55 - 15/55 = 18/55. Для проверки ответ из предыдущего подхода нужно перевести в смешанное число: 73 делится на 55 и получается частное 1 и остаток 18.
Для нахождения произведения и частного пользоваться смешанными числами неудобно. Здесь всегда рекомендуется переходить к неправильным дробям.
Эта статья про обыкновенные дроби . Здесь мы познакомимся с понятием доли целого, которое приведет нас к определению обыкновенной дроби. Дальше остановимся на принятых обозначениях для обыкновенных дробей и приведем примеры дробей, скажем про числитель и знаменатель дроби. После этого дадим определения правильных и неправильных, положительных и отрицательных дробей, а также рассмотрим положение дробных чисел на координатном луче. В заключение перечислим основные действия с дробями.
Навигация по странице.
Доли целого
Сначала введем понятие доли .
Предположим, что у нас есть некоторый предмет, составленный из нескольких абсолютно одинаковых (то есть, равных) частей. Для наглядности можно представить, например, яблоко, разрезанное на несколько равных частей, или апельсин, состоящий из нескольких равных долек. Каждую из этих равных частей, составляющих целый предмет, называют долей целого или просто долей .
Заметим, что доли бывают разные. Поясним это. Пусть у нас есть два яблока. Разрежем первое яблоко на две равные части, а второе – на 6 равных частей. Понятно, что доля первого яблока будет отличаться от доли второго яблока.
В зависимости от количества долей, составляющих целый предмет, эти доли имеют свои названия. Разберем названия долей . Если предмет составляют две доли, любая из них называется одна вторая доля целого предмета; если предмет составляют три доли, то любая из них называется одна третья доля, и так далее.
Одна вторая доля имеет специальное название – половина . Одна третья доля называется третью , а одна четверная доля – четвертью .
Для краткости записи были введены следующие обозначения долей . Одну вторую долю обозначают как или 1/2 , одну третью долю – как или 1/3 ; одну четвертую долю – как или 1/4 , и так далее. Отметим, что запись с горизонтальной чертой употребляется чаще. Для закрепления материала приведем еще один пример: запись обозначает одну сто шестьдесят седьмую долю целого.
Понятие доли естественным образом распространяется с предметов на величины. Например, одной из мер измерения длины является метр. Для измерения длин меньших, чем метр, можно использовать доли метра. Так можно воспользоваться, например, половиной метра или десятой или тысячной долей метра. Аналогично применяются доли других величин.
Обыкновенные дроби, определение и примеры дробей
Для описания количества долей используются обыкновенные дроби . Приведем пример, который позволит нам подойти к определению обыкновенных дробей.
Пусть апельсин состоит из 12 долей. Каждая доля в этом случае представляет одну двенадцатую долю целого апельсина, то есть, . Две доли обозначим как , три доли – как , и так далее, 12 долей обозначим как . Каждую из приведенных записей называют обыкновенной дробью.
Теперь дадим общее определение обыкновенных дробей .
Озвученное определение обыкновенных дробей позволяет привести примеры обыкновенных дробей
: 5/10
, , 21/1
, 9/4
, . А вот записи  не подходят под озвученное определение обыкновенных дробей, то есть, не являются обыкновенными дробями.
не подходят под озвученное определение обыкновенных дробей, то есть, не являются обыкновенными дробями.
Числитель и знаменатель
Для удобства в обыкновенной дроби различают числитель и знаменатель .
Определение.
Числитель обыкновенной дроби (m/n ) – это натуральное число m .
Определение.
Знаменатель обыкновенной дроби (m/n ) – это натуральное число n .
Итак, числитель расположен сверху над чертой дроби (слева от наклонной черты), а знаменатель – снизу под чертой дроби (справа от наклонной черты). Для примера приведем обыкновенную дробь 17/29 , числителем этой дроби является число 17 , а знаменателем – число 29 .
Осталось обговорить смысл, заключенный в числителе и знаменателе обыкновенной дроби. Знаменатель дроби показывает, из скольких долей состоит один предмет, числитель в свою очередь указывает количество таких долей. Например, знаменатель 5 дроби 12/5 означает, что один предмет состоит из пяти долей, а числитель 12 означает, что взято 12 таких долей.
Натуральное число как дробь со знаменателем 1
Знаменатель обыкновенной дроби может быть равен единице. В этом случае можно считать, что предмет неделим, иными словами, представляет собой нечто целое. Числитель такой дроби указывает, сколько целых предметов взято. Таким образом, обыкновенная дробь вида m/1 имеет смысл натурального числа m . Так мы обосновали справедливость равенства m/1=m .
Перепишем последнее равенство так: m=m/1 . Это равенство дает нам возможность любое натуральное число m представлять в виде обыкновенной дроби. Например, число 4 – это дробь 4/1 , а число 103 498 равно дроби 103 498/1 .
Итак, любое натуральное число m можно представить в виде обыкновенной дроби со знаменателем 1 как m/1 , а любую обыкновенную дробь вида m/1 можно заменить натуральным числом m .
Черта дроби как знак деления
Представление исходного предмета в виде n долей представляет собой не что иное как деление на n равных частей. После того как предмет разделен на n долей, мы его можем разделить поровну между n людьми – каждый получит по одной доле.
Если же у нас есть изначально m одинаковых предметов, каждый из которых разделен на n долей, то эти m предметов мы можем поровну разделить между n людьми, раздав каждому человеку по одной доле от каждого из m предметов. При этом у каждого человека будет m долей 1/n , а m долей 1/n дает обыкновенную дробь m/n . Таким образом, обыкновенную дробь m/n можно применять для обозначения деления m предметов между n людьми.
Так мы получили явную связь между обыкновенными дробями и делением (смотрите общее представление о делении натуральных чисел). Эта связь выражается в следующем: черту дроби можно понимать как знак деления, то есть, m/n=m:n .
С помощью обыкновенной дроби можно записать результат деления двух натуральных чисел, для которых не выполняется деление нацело. Например, результат деления 5 яблок на 8 человек можно записать как 5/8 , то есть, каждому достанется пять восьмых долей яблока: 5:8=5/8 .
Равные и неравные обыкновенные дроби, сравнение дробей
Достаточно естественным действием является сравнение обыкновенных дробей , ведь понятно, что 1/12 апельсина отличается от 5/12 , а 1/6 доля яблока такая же, как другая 1/6 доля этого яблока.
В результате сравнения двух обыкновенных дробей получается один из результатов: дроби либо равны, либо не равны. В первом случае мы имеем равные обыкновенные дроби , а во втором – неравные обыкновенные дроби . Дадим определение равных и неравных обыкновенных дробей.
Определение.
равны , если справедливо равенство a·d=b·c .
Определение.
Две обыкновенные дроби a/b и c/d не равны , если равенство a·d=b·c не выполняется.
Приведем несколько примеров равных дробей. Например, обыкновенная дробь 1/2 равна дроби 2/4 , так как 1·4=2·2 (при необходимости смотрите правила и примеры умножения натуральных чисел). Для наглядности можно представить два одинаковых яблока, первое разрезано пополам, а второе – на 4 доли. При этом очевидно, что две четвертых доли яблока составляют 1/2 долю. Другими примерами равных обыкновенных дробей являются дроби 4/7 и 36/63 , а также пара дробей 81/50 и 1 620/1 000 .
А обыкновенные дроби 4/13 и 5/14 не равны, так как 4·14=56 , а 13·5=65 , то есть, 4·14≠13·5 . Другим примером неравных обыкновенных дробей являются дроби 17/7 и 6/4 .
Если при сравнении двух обыкновенных дробей выяснилось, что они не равны, то возможно потребуется узнать, какая из этих обыкновенных дробей меньше другой, а какая – больше . Чтобы это выяснить, используется правило сравнения обыкновенных дробей, суть которого сводится к приведению сравниваемых дробей к общему знаменателю и последующему сравнению числителей. Детальная информация по этой теме собрана в статье сравнение дробей: правила, примеры, решения .
Дробные числа
Каждая дробь является записью дробного числа . То есть, дробь – это всего лишь «оболочка» дробного числа, его внешний вид, а вся смысловая нагрузка содержится именно в дробном числе. Однако для краткости и удобства понятие дроби и дробного числа объединяют и говорят просто дробь. Здесь уместно перефразировать известное изречение: мы говорим дробь – подразумеваем дробное число, мы говорим дробное число – подразумеваем дробь.
Дроби на координатном луче
Все дробные числа, отвечающие обыкновенным дробям, имеют свое уникальное место на , то есть, существует взаимно однозначное соответствие между дробями и точками координатного луча.
Чтобы на координатном луче попасть в точку, соответствующую дроби m/n нужно от начала координат в положительном направлении отложить m отрезков, длина которых составляет 1/n долю единичного отрезка. Такие отрезки можно получить, разделив единичный отрезок на n равных частей, что всегда можно сделать с помощью циркуля и линейки.
Для примера покажем точку М на координатном луче, соответствующую дроби 14/10 . Длина отрезка с концами в точке O и ближайшей к ней точке, отмеченной маленьким штрихом, составляет 1/10 долю единичного отрезка. Точка с координатой 14/10 удалена от начала координат на расстояние 14 таких отрезков.

Равным дробям отвечает одно и то же дробное число, то есть, равные дроби являются координатами одной и той же точки на координатном луче. Например, координатам 1/2 , 2/4 , 16/32 , 55/110 на координатном луче соответствует одна точка, так как все записанные дроби равны (она расположена на расстоянии половины единичного отрезка, отложенного от начала отсчета в положительном направлении).
На горизонтальном и направленном вправо координатном луче точка, координатой которой является большая дробь, располагается правее точки, координатой которой является меньшая дробь. Аналогично, точка с меньшей координатой лежит левее точки с большей координатой.
Правильные и неправильные дроби, определения, примеры
Среди обыкновенных дробей различают правильные и неправильные дроби . Это разделение в своей основе имеет сравнение числителя и знаменателя.
Дадим определение правильных и неправильных обыкновенных дробей.
Определение.
Правильная дробь
– это обыкновенная дробь, числитель которой меньше знаменателя, то есть, если m Определение.
Неправильная дробь
– это обыкновенная дробь, в которой числитель больше или равен знаменателю, то есть, если m≥n
, то обыкновенная дробь является неправильной.
Приведем несколько примеров правильных дробей: 1/4
, , 32 765/909 003
. Действительно, в каждой из записанных обыкновенных дробей числитель меньше знаменателя (при необходимости смотрите статью сравнение натуральных чисел), поэтому они правильные по определению. А вот примеры неправильных дробей: 9/9
, 23/4
, . Действительно, числитель первой из записанных обыкновенных дробей равен знаменателю, а в остальных дробях числитель больше знаменателя. Также имеют место определения правильных и неправильных дробей, базирующиеся на сравнении дробей с единицей. Определение.
правильной
, если она меньше единицы.
Определение.
Обыкновенная дробь называется неправильной
, если она либо равна единице, либо больше 1
.
Так обыкновенная дробь 7/11
– правильная, так как 7/11<1
, а обыкновенные дроби 14/3
и 27/27
– неправильные, так как 14/3>1
, а 27/27=1
. Давайте поразмыслим, чем же обыкновенные дроби с числителем, превосходящим или равным знаменателю, заслужили такое название – «неправильные». Для примера возьмем неправильную дробь 9/9
. Эта дробь означает, что взято девять долей предмета, который состоит из девяти долей. То есть, из имеющихся девяти долей мы можем составить целый предмет. То есть, неправильная дробь 9/9
по сути дает целый предмет, то есть, 9/9=1
. Вообще, неправильные дроби с числителем равным знаменателю обозначают один целый предмет, и такую дробь может заменить натуральное число 1
. Теперь рассмотрим неправильные дроби 7/3
и 12/4
. Достаточно очевидно, что из этих семи третьих долей мы можем составить два целых предмета (один целый предмет составляют 3
доли, тогда для составления двух целых предметов нам потребуется 3+3=6
долей) и еще останется одна третья доля. То есть, неправильная дробь 7/3
по сути означает 2
предмета да еще 1/3
долю такого предмета. А из двенадцати четвертых долей мы можем составить три целых предмета (три предмета по четыре доли в каждом). То есть, дробь 12/4
по сути означает 3
целых предмета. Рассмотренные примеры приводят нас к следующему выводу: неправильные дроби, могут быть заменены либо натуральными числами, когда числитель делится нацело на знаменатель (например, 9/9=1
и 12/4=3
), либо суммой натурального числа и правильной дроби, когда числитель не делится нацело на знаменатель (например, 7/3=2+1/3
). Возможно, именно этим и заслужили неправильные дроби такое название – «неправильные». Отдельный интерес вызывает представление неправильной дроби в виде суммы натурального числа и правильной дроби (7/3=2+1/3
). Этот процесс называется выделением целой части из неправильной дроби , и заслуживает отдельного и более внимательного рассмотрения. Также стоит заметить, что существует очень тесная связь между неправильными дробями и смешанными числами . Каждая обыкновенная дробь отвечает положительному дробному числу (смотрите статью положительные и отрицательные числа). То есть, обыкновенные дроби являются положительными дробями
. К примеру, обыкновенные дроби 1/5
, 56/18
, 35/144
– положительные дроби. Когда нужно особо выделить положительность дроби, то перед ней ставится знак плюс, например, +3/4
, +72/34
. Если перед обыкновенной дробью поставить знак минус, то эта запись будет соответствовать отрицательному дробному числу. В этом случае можно говорить об отрицательных дробях
. Приведем несколько примеров отрицательных дробей: −6/10
, −65/13
, −1/18
. Положительная и отрицательная дроби m/n
и −m/n
являются противоположными числами . К примеру, дроби 5/7
и −5/7
– противоположные дроби. Положительные дроби, как и положительные числа в целом, обозначают прибавление, доход, изменение какой-либо величины в сторону увеличения и т.п. Отрицательные дроби отвечают расходу, долгу, изменению какой-либо величины в сторону уменьшения. Например, отрицательную дробь −3/4
можно трактовать как долг, величина которого равна 3/4
. На горизонтальной и направленной вправо отрицательные дроби располагаются левее начала отсчета. Точки координатной прямой, координатами которых являются положительная дробь m/n
и отрицательная дробь −m/n
расположены на одинаковом расстоянии от начала координат, но по разные стороны от точки O
. Здесь же стоит сказать о дробях вида 0/n
. Эти дроби равны числу нуль, то есть, 0/n=0
. Положительные дроби, отрицательные дроби, а также дроби 0/n
объединяются в рациональные числа . Одно действие с обыкновенными дробями – сравнение дробей - мы уже рассмотрели выше. Определены еще четыре арифметических действия с дробями
– сложение, вычитание, умножение и деление дробей. Остановимся на каждом из них. Общая суть действий с дробями аналогична сути соответствующих действий с натуральными числами. Проведем аналогию. Умножение дробей
можно рассматривать как действие, при котором находится дробь от дроби. Для пояснения приведем пример. Пусть у нас есть 1/6
часть яблока и нам нужно взять 2/3
части от нее. Нужная нам часть является результатом умножения дробей 1/6
и 2/3
. Результатом умножения двух обыкновенных дробей является обыкновенная дробь (которая в частном случае равна натуральному числу). Дальше рекомендуем к изучению информацию статьи умножение дробей – правила, примеры и решения . Список литературы.
Изучая царицу всех наук - математику, в определенный момент все сталкиваются с дробями. Хотя это понятие (как и сами виды дробей или математические действия с ними) совсем несложное, к нему нужно относиться внимательно, ведь в реальной жизни за пределами школы оно очень пригодится. Итак, давайте освежим свои знания о дробях: что это, для чего нужно, какие виды их бывают и как совершать с ними различные арифметические действия. Дробями в математике называются числа, каждое из которых состоит из одной или более частей единицы. Такие дроби еще называют обыкновенными, либо простыми. Как правило, они записываются в виде двух чисел, которые разделены горизонтальной или слеш-чертой, она называется «дробной». Например: ½, ¾. Верхнее, или первое из этих чисел - это числитель (показывает, сколько взято долей от числа), а нижнее, или второе - знаменатель (демонстрирует, на столько частей разделена единица). Дробная черта фактически выполняет функции знака деления. К примеру, 7:9=7/9 Традиционно обыкновенные дроби меньше единицы. В то время как десятичные могут быть больше ее. Для чего нужны дроби? Да для всего, ведь в реальном мире далеко не все числа целые. К примеру, две школьницы в столовой купили в складчину одну вкусную шоколадку. Когда они уже собрались делить десерт, встретили подружку и решили угостить и и ее. Однако теперь необходимо правильно разделить шоколадку, если учесть, что она состоит из 12 квадратиков. Поначалу девчонки хотели разделить все поровну, и тогда каждой бы досталось по четыре кусочка. Но, раздумав, они решили угостить подружку, не 1/3, а 1/4 шоколадки. А поскольку школьницы плохо изучали дроби, то они не учли, что при подобном раскладе в результате у них останется 9 кусочков, которые очень плохо делятся на двоих. Этот довольно простой пример показывает, насколько важно уметь правильно находить часть от числа. А ведь в жизни подобных случаев гораздо больше. Все математические дроби делятся на два больших разряда: обыкновенные и десятичные. Об особенностях первого из них было рассказано в предыдущем пункте, так что теперь стоит уделить внимание второму. Десятичной называют позиционную запись дроби числа, которая фиксируется на письме через запятую, без черточки или слеша. Например: 0,75, 0,5. Фактически десятичная дробь идентична обыкновенной, однако, в ее знаменателе всегда единица с последующими нулями - отсюда произошло и ее название. Число, предшествующее запятой, - это целая часть, а все находящееся после - дробная. Любую простую дробь можно перевести в десятичную. Так, указанные в предыдущем примере десятичные дроби можно записать как обычные: ¾ и ½. Стоит отметить, что и десятичные, и обыкновенные дроби могут быть как положительными, так и отрицательными. Если перед ними стоит знак "-", данная дробь отрицательная, если "+" - то положительная. Есть такие виды дробей простых. В отличие от простой, десятичная дробь делится всего на 2 вида. Проводить различные арифметические манипуляции с дробями немного сложнее, чем с обычными числами. Однако, если усвоить основные правила, решить любой пример с ними не составит особого труда. Например: 2/3+3/4. Наименьшим общим кратным для них будет 12, следовательно, необходимо, чтобы в каждом знаменателе стояло это число. Для этого числитель и знаменатель первой дроби умножаем на 4, получается 8/12, аналогично поступаем со вторым слагаемым, но только множим на 3 - 9/12. Теперь можно легко решить пример: 8/12+9/12= 17/12. Получившаяся дробь - это неправильная величина, поскольку числитель больше знаменателя. Ее можно и нужно пребразовать в правильную смешанную, разделив 17:12= 1 и 5/12. В случае, если слагаются смешанные дроби, сначала действия совершаются с целыми числами, а потом с дробными. Если в примере присутствует десятичная дробь и обычная, необходимо, чтобы обе стали простыми, потом привести их к одному знаменателю и сложить. К примеру 3,1+1/2. Число 3,1 можно записать как смешанную дробь 3 и 1/10 или как неправильную - 31/10. Общим знаменателем для слагаемых будет 10, поэтому нужно умножить поочередно числитель и знаменатель 1/2 на 5, получается 5/10. Далее можно легко все высчитать: 31/10+5/10=35/10. Полученный результат - неправильная сократимая дробь, приводим ее в нормальный вид, сократив на 5: 7/2=3 и 1/2, или десятичной - 3,5. Если слагать 2 десятичные дроби, важно, чтобы после запятой было одинаковое количество цифр. Если это не так, нужно просто дописать необходимое количество нулей, ведь в десятичной дроби это можно сделать безболезненно. Например, 3,5+3,005. Чтобы решить это задание, нужно к первому числу прибавить 2 ноля и далее поочередно слагать: 3,500+3,005=3,505. Вычитая дроби, стоит поступать так же, как и при сложении: свести к общему знаменателю, отнять один числитель от другого, при необходимости перевести результат в смешанную дробь. Например: 16/20-5/10. Общим знаменателем будет 20. Нужно привести вторую дробь к этому знаменателю, умножив обе ее части на 2, получается 10/20. Теперь можно решать пример: 16/20-10/20= 6/20. Однако этот результат относится к сократимым дробям, поэтому стоит поделить обе части на 2 и получается результат - 3/10. Деление и умножение дробей - значительно более простые действия, нежели сложение и вычитание. Дело в том, что, выполняя эти задания, нет необходимости искать общий знаменатель. Чтобы умножить дроби, нужно просто поочередно перемножить между собою оба числителя, а затем и оба знаменателя. Получившийся результат сократить, если дробь - это сократимая величина. Например: 4/9х5/8. После поочередного умножения получается такой результат 4х5/9х8=20/72. Такая дробь сократима на 4, поэтому конечный ответ в примере - 5/18. Деление дробей - тоже несложное действие, фактически оно все равно сводится к их умножению. Чтобы разделить одну дробь на другую, нужно вторую перевернуть и умножить на первую. Например, деление дробей 5/19 и 5/7. Чтобы решить пример, нужно поменять местами знаменатель и числитель второй дроби и умножить: 5/19х7/5=35/95. Результат можно сократить на 5 - получается 7/19. В случае, если необходимо разделить дробь на простое число, методика немного отличается. Изначально стоит записать это число как неправильную дробь, а потом делить по той же схеме. Например, 2/13:5 нужно записать как 2/13: 5/1. Теперь нужно перевернуть 5/1 и умножить получившиеся дроби: 2/13х1/5= 2/65. Иногда приходится совершать деление дробей смешанных. С ними нужно поступать, как и с целыми числами: превратить в неправильные дроби, перевернуть делитель и умножить все. Например, 8 ½: 3. Превращаем все в неправильные дроби: 17/2: 3/1. Далее следует переворот 3/1 и умножение: 17/2х1/3= 17/6. Теперь следует перевести неправильную дробь в правильную - 2 целых и 5/6. Итак, разобравшись с тем, что такое дроби и как можно с ними совершать различные арифметические действия, нужно постараться не забывать об этом. Ведь люди всегда более склонны делить что-то на части, нежели прибавлять, поэтому нужно уметь делать это правильно.Положительные и отрицательные дроби
Действия с дробями
Ее величество дробь: это что такое

Виды дробей: обыкновенные и десятичные

Подвиды обыкновенных дробей

Подвиды десятичной дроби
Сложение дробей
Вычитание дробей

Умножение дробей

Как делить дроби

 Воля: функции, понятие, основные признаки
Воля: функции, понятие, основные признаки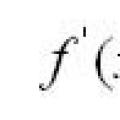 Геометрический и механический смысл производной
Геометрический и механический смысл производной Свойства степеней при сложении
Свойства степеней при сложении