المصفوفة المعكوسة وخصائصها. مصفوفة معكوسة

إيجاد معكوس المصفوفة- مشكلة يتم حلها غالبًا بطريقتين:

طريقة الإضافات الجبرية ، حيث يلزم إيجاد المحددات وتبديل المصفوفات ؛
طريقة القضاء جاوس غير معروف، حيث يلزم إجراء تحويلات أولية للمصفوفات (إضافة صفوف ، وضرب الصفوف بنفس العدد ، وما إلى ذلك).

بالنسبة لأولئك الذين لديهم فضول بشكل خاص ، هناك طرق أخرى ، على سبيل المثال ، طريقة التحولات الخطية. في هذا الدرس ، سنقوم بتحليل الطرق الثلاثة المذكورة والخوارزميات لإيجاد معكوس المصفوفة بهذه الطرق.

مصفوفة معكوسة لكن، تسمى هذه المصفوفة

لكن
. (1)

مصفوفة معكوسة ، المطلوب إيجاده لمصفوفة مربعة معينة لكن، تسمى هذه المصفوفة

المنتج الذي بواسطته المصفوفات لكنعلى اليمين مصفوفة الهوية ، أي
. (1)

مصفوفة الوحدة هي مصفوفة قطرية تكون فيها جميع الإدخالات القطرية مساوية لواحد.

نظرية.لكل مصفوفة مربعة غير مفردة (غير مفردة ، غير مفردة) ، يمكن للمرء أن يجد مصفوفة معكوسة ، وعلاوة على ذلك ، مصفوفة واحدة فقط. بالنسبة لمصفوفة مربعة خاصة (منحطة ، مفردة) ، لا توجد مصفوفة معكوسة.

تسمى المصفوفة المربعة غير خاص(أو غير منحط, غير مفرد) إذا كان محدده لا يساوي صفرًا ، و خاص(أو تتدهور, صيغة المفرد) إذا كان المحدد هو صفر.

مصفوفة معكوسةيمكن إيجاده فقط لمصفوفة مربعة. بطبيعة الحال ، ستكون المصفوفة العكسية أيضًا مربعة ومن نفس ترتيب المصفوفة المعطاة. تسمى المصفوفة التي يمكن إيجاد مصفوفة معكوسة بها مصفوفة عكسية.

إلى عن على مصفوفة معكوسة هناك تشابه مناسب مع مقلوب الرقم. لكل رقم أ، الذي لا يساوي الصفر ، يوجد رقم بهذا العمل أو بيساوي واحد: أب= 1. رقم بيسمى مقلوب الرقم ب. على سبيل المثال ، بالنسبة للرقم 7 ، المعكوس هو الرقم 1/7 ، حيث أن 7 * 1/7 = 1.

إيجاد معكوس المصفوفة بطريقة الجمع الجبرية (مصفوفة الاتحاد)

لمصفوفة مربعة غير مفردة لكنالمعكوس هو المصفوفة

أين محدد المصفوفة لكن، а هي المصفوفة المرتبطة بالمصفوفة لكن.

متحالف مع مصفوفة مربعة أهي مصفوفة من نفس الترتيب تكون عناصرها الإضافات الجبريةتم تحويل العناصر المقابلة لمحدد المصفوفة فيما يتعلق بالمصفوفة أ. وهكذا ، إذا

ومن بعد

خوارزمية لإيجاد معكوس المصفوفة بطريقة الجمع الجبرية

1. أوجد محدد هذه المصفوفة أ. إذا كان المحدد يساوي صفرًا ، فإن إيجاد معكوس المصفوفة يتوقف ، لأن المصفوفة تتدهور ولا يوجد معكوس لها.

2. البحث عن مصفوفة منقول بالنسبة ل أ.

3. احسب عناصر مصفوفة الاتحاد كمكملات جبرية لماريتا الموجودة في الخطوة 2.

4. طبِّق الصيغة (2): اضرب الرقم ، محدد عكسيالمصفوفات أ، إلى مصفوفة الاتحاد الموجودة في الخطوة 4.

5. تحقق من النتيجة التي تم الحصول عليها في الخطوة 4 عن طريق الضرب مصفوفة معينة أإلى معكوس المصفوفة. إذا كان حاصل ضرب هذه المصفوفات يساوي مصفوفة الوحدة ، فسيتم إيجاد معكوس المصفوفة بشكل صحيح. وإلا ابدأ عملية الحل مرة أخرى.

مثال 1للمصفوفة

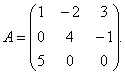
أوجد معكوس المصفوفة.

المحلول. لإيجاد معكوس المصفوفة ، من الضروري إيجاد محدد المصفوفة لكن. نجد من خلال قاعدة المثلثات:

لذلك ، المصفوفة لكنهو غير مفرد (غير منحط ، غير مفرد) وهناك معكوس له.

لنجد المصفوفة المرتبطة بالمصفوفة المعطاة لكن.

لنجد المصفوفة المنقولة بالنسبة إلى المصفوفة أ:

نحسب عناصر مصفوفة الاتحاد كمكملات جبرية للمصفوفة المنقولة فيما يتعلق بالمصفوفة أ:

لذلك ، فإن المصفوفة مترافقة مع المصفوفة أ، له الشكل

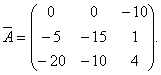
تعليق.قد يختلف ترتيب حساب العناصر وتبديل المصفوفة. يمكن للمرء أن يحسب أولا المكملات الجبرية للمصفوفة أ، ثم بدّل مصفوفة التكميلات الجبرية. يجب أن تكون النتيجة نفس عناصر مصفوفة الاتحاد.

بتطبيق الصيغة (2) ، نجد معكوس المصفوفة على المصفوفة لكن:

إيجاد المصفوفة المعكوسة عن طريق القضاء على المجهول

الخطوة الأولى لإيجاد معكوس المصفوفة بالحذف الغاوسي هي إسناد المصفوفة أ مصفوفة الهويةمن نفس الترتيب ، مع فصلها بشريط عمودي. نحصل على مصفوفة مزدوجة. اضرب كلا الجزأين في هذه المصفوفة ، ثم نحصل على

خوارزمية لإيجاد معكوس المصفوفة من خلال القضاء الغاوسي على المجهول

1. إلى المصفوفة أتخصيص مصفوفة هوية من نفس الترتيب.

2. قم بتحويل المصفوفة المزدوجة الناتجة بحيث يتم الحصول على مصفوفة الوحدة في الجزء الأيسر منها ، ثم يتم الحصول على المصفوفة العكسية تلقائيًا في الجزء الأيمن بدلاً من مصفوفة الوحدة. مصفوفة أعلى الجانب الأيسر يتم تحويلها إلى مصفوفة الوحدة بواسطة التحولات الأوليةالمصفوفات.

2. إذا كان في عملية تحويل مصفوفة أفي مصفوفة الوحدة في أي صف أو في أي عمود سيكون هناك فقط أصفار ، ثم محدد المصفوفة يساوي صفرًا ، وبالتالي ، المصفوفة أسوف تتدهور ، وليس لها مصفوفة معكوسة. في هذه الحالة ، يتوقف العثور على معكوس المصفوفة.

مثال 2للمصفوفة

أوجد معكوس المصفوفة.

وسنقوم بتحويله بحيث يتم الحصول على مصفوفة الوحدة على الجانب الأيسر. لنبدأ التحول.

اضرب الصف الأول من المصفوفة اليسرى واليمنى في (-3) وأضفه إلى الصف الثاني ، ثم اضرب الصف الأول في (-4) وأضفه إلى الصف الثالث ، ثم نحصل على

لتجنب ، إذا كان ذلك ممكنا أعداد كسريةفي التحويلات اللاحقة ، سننشئ أولاً وحدة في الصف الثاني على الجانب الأيسر من المصفوفة المزدوجة. للقيام بذلك ، اضرب الصف الثاني في 2 واطرح منه الصف الثالث ، ثم نحصل عليه

لنضيف الصف الأول إلى الصف الثاني ، ثم نضرب الصف الثاني في (-9) ونضيفه إلى الصف الثالث. ثم نحصل

اقسم الصف الثالث على 8 ، ثم

اضرب الصف الثالث في 2 وأضفه إلى الصف الثاني. اتضح:

تبديل أماكن الخطين الثاني والثالث ، ثم نحصل أخيرًا على:

نرى أن مصفوفة الوحدة تم الحصول عليها من الجانب الأيسر ، لذلك تم الحصول على معكوس المصفوفة في الجانب الأيمن. في هذا الطريق:

يمكنك التحقق من صحة العمليات الحسابية بضرب المصفوفة الأصلية في معكوس المصفوفة:

يجب أن تكون النتيجة معكوس المصفوفة.

مثال 3للمصفوفة

أوجد معكوس المصفوفة.

المحلول. تجميع مصفوفة مزدوجة

وسوف نقوم بتحويله.

نضرب الصف الأول في 3 ، والثاني في 2 ، ونطرح من الثاني ، ثم نضرب الصف الأول في 5 ، والثالث في 2 ونطرح من الصف الثالث ، ثم نحصل على

نضرب الصف الأول في 2 ونضيفه إلى الثاني ، ثم نطرح الثاني من الصف الثالث ، ثم نحصل على

نرى أنه في السطر الثالث على الجانب الأيسر ، تبين أن جميع العناصر تساوي صفرًا. لذلك ، فإن المصفوفة متدهورة وليس لها مصفوفة معكوسة. نتوقف عن المزيد من العثور على ماريا العكسية.

هذا الموضوع هو واحد من أكثر المواضيع مكروهًا بين الطلاب. الأسوأ ، على الأرجح ، المحددات فقط.

الحيلة هي أن مفهوم العنصر العكسي (وأنا لا أتحدث فقط عن المصفوفات الآن) يحيلنا إلى عملية الضرب. حتى في المناهج الدراسيةيعتبر الضرب عملية معقدة، وعادة ما يكون ضرب المصفوفات موضوعًا منفصلاً ، ولدي فقرة كاملة ومقطع فيديو تعليمي مخصص له.

اليوم لن ندخل في تفاصيل حسابات المصفوفة. فقط تذكر: كيف يتم الإشارة إلى المصفوفات ، وكيف يتم ضربها وما يلي ذلك.

مراجعة: مصفوفة الضرب

بادئ ذي بدء ، دعنا نتفق على التدوين. المصفوفة $ A $ of size $ \ left [m \ times n \ right] $ هي ببساطة جدول أرقام يحتوي بالضبط على $ m $ من الصفوف و $ n $ من الأعمدة:

\ = \ underbrace (\ left [\ begin (matrix) ((a) _ (11)) & ((a) _ (12)) & ... & ((a) _ (1n)) \\ (( أ) _ (21)) & ((أ) _ (22)) & ... & ((أ) _ (2 ن)) \\ ... & ... & ... & ... ((a) _ (m1)) & ((a) _ (m2)) & ... & ((a) _ (mn)) \\\ end (matrix) \ right]) _ (n) \]

من أجل عدم الخلط بين الصفوف والأعمدة عن طريق الخطأ في الأماكن (صدقني ، في الاختبار يمكنك الخلط بين أحدهما وشيطان - ماذا يمكننا أن نقول عن بعض السطور هناك) ، ما عليك سوى إلقاء نظرة على الصورة:

تحديد الفهارس لخلايا المصفوفة

ماذا يحدث؟ إذا وضعنا نظام الإحداثيات القياسي $ OXY $ في اليسار الزاوية العلويةوتوجيه المحاور بحيث تغطي المصفوفة بأكملها ، ثم يمكن ربط كل خلية من هذه المصفوفة بشكل فريد بالإحداثيات $ \ left (x ؛ y \ right) $ - سيكون هذا هو رقم الصف ورقم العمود.

لماذا تم وضع نظام الإحداثيات بالضبط في الزاوية اليسرى العليا؟ نعم ، لأنه من هناك نبدأ في قراءة أي نصوص. من السهل جدًا تذكرها.

لماذا يشير المحور $ x $ إلى الأسفل وليس إلى اليمين؟ مرة أخرى ، الأمر بسيط: خذ نظام الإحداثيات القياسي (المحور $ x $ يذهب إلى اليمين ، المحور $ y $ لأعلى) وقم بتدويره بحيث يحيط بالمصفوفة. هذا دوران بزاوية 90 درجة في اتجاه عقارب الساعة - نرى نتيجته في الصورة.

بشكل عام ، توصلنا إلى كيفية تحديد مؤشرات عناصر المصفوفة. الآن دعونا نتعامل مع الضرب.

تعريف. المصفوفات $ A = \ left [m \ times n \ right] $ و $ B = \ left [n \ times k \ right] $ ، عندما يتطابق عدد الأعمدة في الأول مع عدد الصفوف في الثانية ، يكون يسمى متسقة.

إنه بهذا الترتيب. يمكن للمرء أن يكون غامضًا ويقول إن المصفوفتين $ A $ و $ B $ يشكلان زوجًا مرتبًا $ \ left (A؛ B \ right) $: إذا كانا متسقين بهذا الترتيب ، فليس من الضروري على الإطلاق أن يكون $ B $ و $ A $ ، هؤلاء. الزوج $ \ left (B؛ A \ right) $ هو أيضًا ثابت.

يمكن ضرب المصفوفات المتسقة فقط.

تعريف. حاصل ضرب المصفوفات المتسقة $ A = \ left [m \ times n \ right] $ و $ B = \ left [n \ times k \ right] $ هو المصفوفة الجديدة $ C = \ left [m \ times k \ right ] $ ، الذي يتم حساب عناصره $ ((c) _ (ij)) $ بواسطة الصيغة:

\ [((c) _ (ij)) = \ sum \ limits_ (k = 1) ^ (n) (((a) _ (ik))) \ cdot ((b) _ (kj)) \]

بمعنى آخر: للحصول على العنصر $ ((c) _ (ij)) $ من المصفوفة $ C = A \ cdot B $ ، عليك أن تأخذ صف $ i $ من المصفوفة الأولى ، $ j $ -العمود الثاني من المصفوفة الثانية ، ثم اضرب في أزواج العناصر من هذا الصف والعمود. اجمع النتائج.

نعم ، هذا تعريف صارم. عدة حقائق تليها على الفور:

يعتبر ضرب المصفوفة بشكل عام غير تبادلي: $ A \ cdot B \ ne B \ cdot A $؛
ومع ذلك ، فإن عملية الضرب ترابطية: $ \ left (A \ cdot B \ right) \ cdot C = A \ cdot \ left (B \ cdot C \ right) $؛
وحتى التوزيعية: $ \ left (A + B \ right) \ cdot C = A \ cdot C + B \ cdot C $؛
والتوزيع مرة أخرى: $ A \ cdot \ left (B + C \ right) = A \ cdot B + A \ cdot C $.

يجب وصف توزيعية الضرب بشكل منفصل لمجموع المضاعف الأيمن والأيسر فقط بسبب عدم تبادلية عملية الضرب.

ومع ذلك ، إذا اتضح أن $ A \ cdot B = B \ cdot A $ ، تسمى هذه المصفوفات قابلة للتبادل.

من بين جميع المصفوفات التي يتم ضربها في شيء ما هناك ، هناك مصفوفات خاصة - تلك التي ، عند ضربها في أي مصفوفة $ A $ ، تعطي مرة أخرى $ A $:

تعريف. تسمى المصفوفة $ E $ الهوية إذا كان $ A \ cdot E = A $ أو $ E \ cdot A = A $. في حالة المصفوفة المربعة $ A $ يمكننا كتابة:

مصفوفة الهوية ضيف متكرر في الحل معادلات المصفوفة. وبشكل عام ضيف متكرر في عالم المصفوفات. :)

وبسبب هذا $ E $ ، ابتكر شخص ما كل اللعبة التي سيتم كتابتها بعد ذلك.

ما هي معكوس المصفوفة

نظرًا لأن ضرب المصفوفة عملية تستغرق وقتًا طويلاً (يجب عليك مضاعفة مجموعة من الصفوف والأعمدة) ، فإن مفهوم المصفوفة العكسية ليس أيضًا أقل أهمية. ويحتاج إلى بعض الشرح.

التعريف الرئيسي

حسنًا ، حان الوقت لمعرفة الحقيقة.

تعريف. تسمى المصفوفة $ B $ معكوس المصفوفة $ A $ if

يتم الإشارة إلى المصفوفة المعكوسة بواسطة $ ((A) ^ (- 1)) $ (يجب عدم الخلط بينه وبين الدرجة!) ، لذلك يمكن إعادة كتابة التعريف على النحو التالي:

يبدو أن كل شيء بسيط للغاية وواضح. ولكن عند تحليل مثل هذا التعريف ، تظهر عدة أسئلة على الفور:

هل توجد مصفوفة معكوسة دائمًا؟ وإذا لم يكن الأمر كذلك دائمًا ، فكيف تحدد: متى توجد ومتى لا توجد؟
ومن قال أن مثل هذه المصفوفة هي بالضبط واحدة؟ ماذا لو كان هناك حشد كامل من الانعكاسات بالنسبة لبعض المصفوفات الأصلية $ A $؟
كيف تبدو كل هذه "الانعكاسات"؟ وكيف تحسبهم في الواقع؟

بالنسبة لخوارزميات الحساب - سنتحدث عن هذا بعد قليل. لكننا سنجيب على بقية الأسئلة الآن. دعونا نرتبهم في شكل تأكيدات منفصلة.

الخصائص الأساسية

لنبدأ بالشكل الذي يجب أن تبدو عليه المصفوفة $ A $ حتى يكون لها $ ((A) ^ (- 1)) $. الآن سوف نتأكد من أن كلا المصفوفتين يجب أن تكون مربعة ومن نفس الحجم: $ \ left [n \ times n \ right] $.

ليما 1. بإعطاء مصفوفة $ A $ ومعكوسها $ ((A) ^ (- 1)) $. ثم تكون كلتا المصفوفتين مربعتين ولها نفس الترتيب $ n $.

دليل - إثبات. كل شيء بسيط. دع المصفوفة $ A = \ left [m \ times n \ right] $، $ ((A) ^ (- 1)) = \ left [a \ times b \ right] $. نظرًا لأن المنتج $ A \ cdot ((A) ^ (- 1)) = E $ موجود بالتعريف ، فإن المصفوفات $ A $ و $ ((A) ^ (- 1)) $ متسقة بهذا الترتيب:

\ [\ start (align) & \ left [m \ times n \ right] \ cdot \ left [a \ times b \ right] = \ left [m \ times b \ right] \\ & n = a \ end ( محاذاة) \]

هذه نتيجة مباشرة لخوارزمية ضرب المصفوفة: المعامِلات $ n $ و $ a $ "عبور" ويجب أن تكون متساوية.

في نفس الوقت ، يتم تعريف الضرب العكسي أيضًا: $ ((A) ^ (- 1)) \ cdot A = E $ ، لذا فإن المصفوفات $ ((A) ^ (- 1)) $ و $ A $ هي متسقة أيضًا في هذا الترتيب:

\ [\ start (align) & \ left [a \ times b \ right] \ cdot \ left [m \ times n \ right] = \ left [a \ times n \ right] \\ & b = m \ end ( محاذاة) \]

وبالتالي ، بدون فقدان العمومية ، يمكننا أن نفترض أن $ A = \ left [m \ times n \ right] $ ، $ ((A) ^ (- 1)) = \ left [n \ times m \ right] $. ومع ذلك ، وفقًا لتعريف $ A \ cdot ((A) ^ (- 1)) = ((A) ^ (- 1)) \ cdot A $ ، فإن أبعاد المصفوفات هي نفسها تمامًا:

\ [\ start (align) & \ left [m \ times n \ right] = \ left [n \ times m \ right] \\ & m = n \ end (align) \]

لذلك اتضح أن جميع المصفوفات الثلاث - $ A $ و $ ((A) ^ (- 1)) $ و $ E $ - هي الحجم المربع$ \ left [n \ times n \ right] $. ثبت أن اللمة.

حسنًا ، هذا جيد بالفعل. نرى أن المصفوفات المربعة فقط هي التي يمكن عكسها. لنتأكد الآن من أن معكوس المصفوفة هو نفسه دائمًا.

ليما 2. بإعطاء مصفوفة $ A $ ومعكوسها $ ((A) ^ (- 1)) $. إذن هذه المصفوفة المعكوسة فريدة من نوعها.

دليل - إثبات. لنبدأ من العكس: دع المصفوفة $ A $ لها مثيلين على الأقل من المقلوبات - $ B $ و $ C $. ثم ، وفقًا للتعريف ، فإن المساواة التالية صحيحة:

\ [\ start (align) & A \ cdot B = B \ cdot A = E ؛ \\ & A \ cdot C = C \ cdot A = E. \\ \ end (محاذاة) \]

من Lemma 1 نستنتج أن جميع المصفوفات الأربعة $ A $ و $ B $ و $ C $ و $ E $ مربعة من نفس الترتيب: $ \ left [n \ times n \ right] $. لذلك ، يتم تعريف المنتج:

نظرًا لأن عملية ضرب المصفوفة ترابطية (ولكنها ليست تبادلية!) ، فيمكننا كتابة:

\ [\ start (align) & B \ cdot A \ cdot C = \ left (B \ cdot A \ right) \ cdot C = E \ cdot C = C ؛ \\ & B \ cdot A \ cdot C = B \ cdot \ left (A \ cdot C \ right) = B \ cdot E = B ؛ \\ & B \ cdot A \ cdot C = C = B \ Rightarrow B = C. \\ \ end (محاذاة) \]

استلمت فقط متغير ممكن: مثيلين من معكوس المصفوفة متساويان. ثبت أن اللمة.

يكرر الاستدلال أعلاه حرفيًا تقريبًا إثبات تفرد العنصر العكسي للجميع أرقام حقيقية$ b \ ne 0 $. الإضافة المهمة الوحيدة هي مراعاة أبعاد المصفوفات.

ومع ذلك ، ما زلنا لا نعرف أي شيء عما إذا كان هناك أي شيء مصفوفة مربعةقابل للعكس. هنا يأتي المحدد لمساعدتنا - هذه سمة رئيسية لجميع المصفوفات المربعة.

ليما 3. إعطاء مصفوفة $ A $. إذا كانت المصفوفة $ ((A) ^ (- 1)) $ معكوسًا ، فإن محدد المصفوفة الأصلية لا يساوي صفرًا:

\ [\ اليسار | أ \ صحيح | \ ني 0 \]

دليل - إثبات. نعلم بالفعل أن $ A $ و $ ((A) ^ (- 1)) $ مصفوفتان مربعتان بالحجم $ \ left [n \ times n \ right] $. لذلك ، من الممكن حساب المحدد لكل منهم: $ \ left | أ \ يمين | $ و $ \ يسار | ((A) ^ (- 1)) \ right | $. ومع ذلك ، فإن المنتج المحدد يساوي المنتجالمحددات:

\ [\ اليسار | أ \ cdot ب \ يمين | = \ يسار | أ \ يمين | \ cdot \ يسار | ب \ يمين | \ يمين \ يسار | أ \ cdot ((أ) ^ (- 1)) \ يمين | = \ يسار | أ \ يمين | \ cdot \ يسار | ((أ) ^ (- 1)) \ حق | \]

ولكن وفقًا لتعريف $ A \ cdot ((A) ^ (- 1)) = E $ ، ومحدد $ E $ يساوي دائمًا 1 ، لذلك

\ [\ start (align) & A \ cdot ((A) ^ (- 1)) = E ؛ \\ & \ اليسار | أ \ cdot ((أ) ^ (- 1)) \ يمين | = \ يسار | ه \ الحق | ؛ \\ & \ اليسار | أ \ يمين | \ cdot \ يسار | ((A) ^ (- 1)) \ right | = 1. \\ \ end (محاذاة) \]

حاصل ضرب عددين يساوي واحدًا فقط إذا كان كل رقم من هذه الأرقام مختلفًا عن الصفر:

\ [\ اليسار | أ \ يمين | \ ne 0 ؛ \ رباعي \ يسار | ((A) ^ (- 1)) \ right | \ ne 0. \]

لذلك اتضح أن $ \ left | أ \ صحيح | \ ne 0 $. تم إثبات اللمة.

في الواقع ، هذا المطلب منطقي تمامًا. سنقوم الآن بتحليل الخوارزمية لإيجاد معكوس المصفوفة - وسوف يتضح تمامًا لماذا ، من حيث المبدأ ، لا يمكن أن توجد مصفوفة عكسية ذات محدد صفري.

لكن أولاً ، لنقم بصياغة تعريف "مساعد":

تعريف. المصفوفة المتدهورة هي مصفوفة مربعة حجمها $ \ left [n \ times n \ right] $ التي يكون محددها صفر.

وبالتالي ، يمكننا أن نؤكد أن أي مصفوفة عكسية غير متولدة.

كيفية إيجاد معكوس المصفوفة

الآن سننظر في خوارزمية عالمية لإيجاد المصفوفات المعكوسة. بشكل عام ، هناك نوعان من الخوارزميات المقبولة عمومًا ، وسننظر أيضًا في الثانية اليوم.

التي سيتم النظر فيها الآن فعالة للغاية للمصفوفات ذات الحجم $ \ left [2 \ times 2 \ right] $ و - جزئيًا - من الحجم $ \ left [3 \ times 3 \ right] $. لكن بدءًا من الحجم $ \ left [4 \ times 4 \ right] $ فمن الأفضل عدم استخدامه. لماذا - الآن سوف تفهم كل شيء.

الإضافات الجبرية

إستعد. الآن سيكون هناك ألم. لا ، لا تقلقي: ممرضة جميلة في تنورة ، جوارب من الدانتيل لا تأتي إليك ولن تعطيك حقنة في الأرداف. كل شيء أكثر تعقيدًا: الإضافات الجبرية وصاحبة الجلالة "مصفوفة الاتحاد" تأتي إليك.

لنبدأ بالأمر الرئيسي. يجب أن تكون هناك مصفوفة مربعة بحجم $ A = \ left [n \ times n \ right] $ التي تسمى عناصرها $ ((a) _ (ij)) $. بعد ذلك ، لكل عنصر من هذا القبيل ، يمكن للمرء تحديد مكمل جبري:

تعريف. المكمل الجبري $ ((A) _ (ij)) $ للعنصر $ ((a) _ (ij)) $ في الصف $ i $ والعمود $ j $ من المصفوفة $ A = \ left [n \ times n \ right] $ هو بناء النموذج

\ [((A) _ (ij)) = ((\ left (-1 \ right)) ^ (i + j)) \ cdot M_ (ij) ^ (*) \]

حيث $ M_ (ij) ^ (*) $ هو محدد المصفوفة التي تم الحصول عليها من $ A $ الأصلي عن طريق حذف نفس الصف $ i $ والعمود $ j $.

ثانية. يُشار إلى المكمل الجبري لعنصر المصفوفة بالإحداثيات $ \ left (i؛ j \ right) $ على أنه $ ((A) _ (ij)) $ ويتم حسابه وفقًا للمخطط:

أولاً ، نحذف العمود $ i $ -row والعمود $ j $ -th من المصفوفة الأصلية. نحصل على مصفوفة مربعة جديدة ، ونشير إلى محددها $ M_ (ij) ^ (*) $.
ثم نضرب هذا المحدد في $ ((\ left (-1 \ right)) ^ (i + j)) $ - في البداية قد يبدو هذا التعبير مذهلًا ، لكننا في الحقيقة اكتشفنا العلامة أمام $ M_ (ij) ^ (*) $.
نحن نعول - نحصل رقم محدد. أولئك. الجمع الجبري هو مجرد رقم ، وليس مصفوفة جديدة ، وهكذا.

المصفوفة $ M_ (ij) ^ (*) $ نفسها تسمى القاصر التكميلي للعنصر $ ((a) _ (ij)) $. وبهذا المعنى ، فإن التعريف أعلاه للمكمل الجبري هو حالة خاصة لما هو أكثر تعريف معقد- ما رأيناه في الدرس عن المحدد.

ملاحظة مهمة. في الواقع ، في الرياضيات "للبالغين" ، يتم تعريف الإضافات الجبرية على النحو التالي:

نأخذ $ k $ من الصفوف و $ k $ في الأعمدة في مصفوفة مربعة. عند تقاطعهم ، نحصل على مصفوفة بحجم $ \ left [k \ times k \ right] $ - المحدد لها يسمى أمر ثانوي $ k $ ويشار إليه بـ $ ((M) _ (k)) $.

ثم نقوم بشطب هذه الصفوف "المحددة" $ k $ وأعمدة $ k $. مرة أخرى ، نحصل على مصفوفة مربعة - محددها يسمى الصغرى التكميلية ويُرمز لها بـ $ M_ (k) ^ (*) $.

اضرب $ M_ (k) ^ (*) $ في $ ((\ left (-1 \ right)) ^ (t)) $ ، حيث $ t $ هو (الانتباه الآن!) مجموع أرقام كل الصفوف المحددة والأعمدة. ستكون هذه الإضافة الجبرية.

ألق نظرة على الخطوة الثالثة: هناك مبلغ 2k $ حد! شيء آخر هو أنه بالنسبة إلى $ k = 1 $ ، نحصل على مصطلحين فقط - ستكون هذه هي نفس $ i + j $ - "إحداثيات" العنصر $ ((a) _ (ij)) $ ، والتي نحن من أجلها تبحث عن مكمل جبري.

لذلك نستخدم اليوم تعريفًا مبسطًا بعض الشيء. ولكن كما سنرى لاحقًا ، سيكون هذا أكثر من كافٍ. الأهم من ذلك هو ما يلي:

تعريف. مصفوفة الاتحاد $ S $ إلى المصفوفة المربعة $ A = \ left [n \ times n \ right] $ مصفوفة جديدة بحجم $ \ left [n \ times n \ right] $ ، والتي تم الحصول عليها من $ A $ باستبدال $ ((a) _ (ij)) $ بالمكملات الجبرية $ ((A) _ (ij)) $:

\\ Rightarrow S = \ left [\ begin (matrix) ((A) _ (11)) & ((A) _ (12)) & ... & ((A) _ (1n)) \\ (( أ) _ (21)) & ((أ) _ (22)) & ... & ((أ) _ (2 ن)) \\ ... & ... & ... & ... \\ ((A) _ (n1)) & ((A) _ (n2)) & ... & ((A) _ (nn)) \\\ end (matrix) \ right] \]

الفكرة الأولى التي ظهرت في لحظة إدراك هذا التعريف هي "هذا هو مقدار ما عليك أن تحسبه إجمالاً!" استرخ: عليك أن تعد ، لكن ليس كثيرًا. :)

حسنًا ، كل هذا جميل جدًا ، لكن لماذا هو ضروري؟ لكن لماذا.

النظرية الرئيسية

دعنا نعود قليلا. تذكر أن Lemma 3 ذكر أن المصفوفة المعكوسة $ A $ تكون دائمًا غير مفردة (أي أن محددها ليس صفريًا: $ \ left | A \ right | \ ne 0 $).

لذا ، فإن العكس صحيح أيضًا: إذا لم تكن المصفوفة $ A $ متدهورة ، فهي دائمًا قابلة للعكس. بل ويوجد مخطط بحث $ ((A) ^ (- 1)) $. تحقق من ذلك:

نظرية المصفوفة العكسية. دع المصفوفة المربعة $ A = \ left [n \ times n \ right] $ تُعطى ، ومحددها غير صفري: $ \ left | أ \ صحيح | \ ne 0 $. ثم المصفوفة العكسية $ ((A) ^ (- 1)) $ موجودة وتحسب بالصيغة:

\ [((A) ^ (- 1)) = \ frac (1) (\ left | A \ right |) \ cdot ((S) ^ (T)) \]

والآن - كل نفس ، ولكن بخط يد مقروء. لإيجاد معكوس المصفوفة ، تحتاج إلى:

احسب المحدد $ \ left | A \ right | $ وتأكد من أنه غير صفري.
قم بتجميع مصفوفة الاتحاد $ S $ ، أي عد 100500 الإضافات الجبرية $ ((A) _ (ij)) $ وضعها في مكانها $ ((a) _ (ij)) $.
انقل هذه المصفوفة $ S $ ثم اضربها في عدد ما $ q = (1) / (\ left | A \ right |) \؛ $.

وهذا كل شيء! تم إيجاد المصفوفة المعكوسة $ ((A) ^ (- 1)) $. لنلقِ نظرة على الأمثلة:

\ [\ يسار [\ ابدأ (مصفوفة) 3 & 1 \ 5 & 2 \ نهاية (مصفوفة) \ يمين] \]

المحلول. دعنا نتحقق من الانعكاس. دعنا نحسب المحدد:

\ [\ اليسار | أ \ يمين | = \ يسار | \ start (matrix) 3 & 1 \\ 5 & 2 \\\ end (matrix) \ right | = 3 \ cdot 2-1 \ cdot 5 = 6-5 = 1 \]

المحدد يختلف عن الصفر. لذا فإن المصفوفة قابلة للعكس. لنقم بإنشاء مصفوفة اتحاد:

لنحسب الإضافات الجبرية:

\ [\ start (align) & ((A) _ (11)) = ((\ left (-1 \ right)) ^ (1 + 1)) \ cdot \ left | 2 \ حق | = 2 ؛ \\ & ((A) _ (12)) = ((\ left (-1 \ right)) ^ (1 + 2)) \ cdot \ left | 5 \ حق | = -5 ؛ \\ & ((A) _ (21)) = ((\ left (-1 \ right)) ^ (2 + 1)) \ cdot \ left | 1 \ حق | = -1 ؛ \\ & ((A) _ (22)) = ((\ left (-1 \ right)) ^ (2 + 2)) \ cdot \ left | 3 \ صحيح | = 3. \\ \ end (محاذاة) \]

انتبه: المحددات | 2 | ، | 5 | ، | 1 | و | 3 | هي محددات مصفوفات الحجم $ \ left [1 \ times 1 \ right] $ ، وليست وحدات. أولئك. إذا كانت المحددات أرقام سالبة، ليس من الضروري إزالة "ناقص".

في المجموع ، تبدو مصفوفة الاتحاد الخاصة بنا كما يلي:

\ [((A) ^ (- 1)) = \ frac (1) (\ left | A \ right |) \ cdot ((S) ^ (T)) = \ frac (1) (1) \ cdot ( (\ left [\ start (array) (* (35) (r)) 2 & -5 \\ -1 & 3 \\\ end (array) \ right]) ^ (T)) = \ left [\ begin (مجموعة) (* (35) (r)) 2 & -1 \\ -5 & 3 \\\ end (array) \ right] \]

حسنًا ، انتهى كل شيء الآن. تم حل المشكلة.

إجابه. $ \ left [\ start (array) (* (35) (r)) 2 & -1 \\ -5 & 3 \\\ end (array) \ right] $

مهمة. أوجد معكوس المصفوفة:

\ [\ left [\ start (array) (* (35) (r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\ end (array) \ right] \]

المحلول. مرة أخرى ، نعتبر المحدد:

\ [\ ابدأ (محاذاة) & \ يسار | \ start (array) (* (35) (r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\ end (array) \ right | = \ begin (matrix) ) \ يسار (1 \ cdot 2 \ cdot 1+ \ يسار (-1 \ يمين) \ cdot \ يسار (-1 \ يمين) \ cdot 1 + 2 \ cdot 0 \ cdot 0 \ right) - \\ - \ يسار (2 \ cdot 2 \ cdot 1+ \ يسار (-1 \ يمين) \ cdot 0 \ cdot 1 + 1 \ cdot \ يسار (-1 \ يمين) \ cdot 0 \ يمين) \ نهاية (مصفوفة) = \ \ & = \ يسار (2 + 1 + 0 \ يمين) - \ يسار (4 + 0 + 0 \ يمين) = - 1 \ ني 0. \ \ نهاية (محاذاة) \]

المحدد يختلف عن الصفر - المصفوفة قابلة للعكس. ولكن الآن سيكون الأكثر صغرًا: عليك أن تحسب ما يصل إلى 9 إضافات جبرية (تسعة ، اللعنة!). وسيحتوي كل منهم على المؤهل $ \ left [2 \ times 2 \ right] $. طار:

\ [\ start (matrix) ((A) _ (11)) = ((\ left (-1 \ right)) ^ (1 + 1)) \ cdot \ left | \ start (matrix) 2 & -1 \\ 0 & 1 \\\ end (matrix) \ right | = 2؛ \\ ((A) _ (12)) = ((\ left (-1 \ right)) ^ (1 + 2)) \ cdot \ left | \ start (matrix) 0 & -1 \\ 1 & 1 \\\ end (matrix) \ right | = -1؛ \\ ((A) _ (13)) = ((\ left (-1 \ right)) ^ (1 + 3)) \ cdot \ left | \ start (matrix) 0 & 2 \\ 1 & 0 \\\ end (matrix) \ right | = -2؛ \\ ... \\ ((A) _ (33)) = ((\ left (-1 \ right)) ^ (3 + 3)) \ cdot \ left | \ start (matrix) 1 & -1 \\ 0 & 2 \\\ end (matrix) \ right | = 2؛ \\ \ end (matrix) \]

باختصار ، ستبدو مصفوفة الاتحاد كما يلي:

لذلك ، سيكون معكوس المصفوفة:

\ [((A) ^ (- 1)) = \ frac (1) (- 1) \ cdot \ left [\ begin (matrix) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\ end (matrix) \ right] = \ left [\ start (array) (* (35) (r)) - 2 & -1 & 3 \\ 1 & 1 & -1 \ \ 2 & 1 & -2 \\\ end (مجموعة) \ يمين] \]

حسنا هذا كل شيء. هنا الجواب.

إجابه. $ \ left [\ start (array) (* (35) (r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\ end (array) \ right ] $

كما ترى ، في نهاية كل مثال ، قمنا بإجراء فحص. في هذا الصدد ، ملاحظة مهمة:

لا تكن كسولًا للتحقق. اضرب المصفوفة الأصلية في المعكوس الموجود - يجب أن تحصل على $ E $.

إن إجراء هذا الفحص أسهل وأسرع بكثير من البحث عن خطأ في عمليات حسابية أخرى ، عندما تقوم ، على سبيل المثال ، بحل معادلة مصفوفة.

طريقة بديلة

كما قلت ، تعمل نظرية المصفوفة العكسية بشكل جيد للأحجام $ \ left [2 \ times 2 \ right] $ و $ \ left [3 \ times 3 \ right] $ (in الحالة الأخيرة- لم تعد "مثالية" بعد الآن) ، ولكن بالنسبة للمصفوفات كبيرة الحجم ، يبدأ الحزن.

لكن لا تقلق: هناك خوارزمية بديلة يمكن استخدامها لإيجاد المعكوس بهدوء حتى لمصفوفة $ \ left [10 \ times 10 \ right] $. ولكن ، كما هو الحال غالبًا ، للنظر في هذه الخوارزمية ، نحتاج إلى القليل من الخلفية النظرية.

التحولات الأولية

من بين التحولات المختلفة للمصفوفة ، هناك العديد من التحولات الخاصة - يطلق عليها الابتدائية. هناك ثلاثة تحولات بالضبط:

عمليه الضرب. يمكنك أن تأخذ الصف (العمود) $ i $ وتضربه بأي رقم $ k \ ne 0 $؛
إضافة. أضف إلى الصف $ i $ -th (العمود) أي صف آخر $ j $ -th (عمود) مضروبًا في أي رقم $ k \ ne 0 $ (بالطبع ، $ k = 0 $ ممكن أيضًا ، ولكن ما هي الفائدة؟ من ذلك؟؟ لن يتغير شيء رغم ذلك).
التقليب. خذ الصفين $ i $ -th و $ j $ -th (الأعمدة) وقم بتبديلهما.

لماذا تسمى هذه التحولات الابتدائية (بالنسبة للمصفوفات الكبيرة فهي لا تبدو أولية جدًا) ولماذا لا يوجد سوى ثلاثة منها - هذه الأسئلة خارج نطاق درس اليوم. لذلك ، لن نخوض في التفاصيل.

شيء آخر مهم: علينا القيام بكل هذه الانحرافات في المصفوفة المرتبطة. نعم ، نعم ، لقد سمعت جيدًا. الآن سيكون هناك تعريف آخر - آخر تعريف في درس اليوم.

المصفوفة المرفقة

بالتأكيد في المدرسة قمت بحل أنظمة المعادلات باستخدام طريقة الجمع. حسنًا ، هناك ، اطرح آخرًا من سطر واحد ، واضرب سطرًا ما في رقم - هذا كل شيء.

لذلك: الآن كل شيء سيكون كما هو ، ولكن بالفعل "بطريقة الكبار". مستعد؟

تعريف. دع المصفوفة $ A = \ left [n \ times n \ right] $ ومصفوفة الهوية $ E $ من نفس الحجم $ n $ تُعطى. ثم المصفوفة المرتبطة $ \ left [A \ left | هـ \ حق. \ right] $ مصفوفة $ \ يسار جديدة [n \ مرات 2n \ right] $ مصفوفة تبدو كالتالي:

\ [\ اليسار [أ \ اليسار | هـ \ حق. \ right] = \ left [\ start (array) (rrrr | rrrr) ((a) _ (11)) & ((a) _ (12)) & ... & ((a) _ (1n)) & 1 & 0 & ... & 0 \\ ((a) _ (21)) & ((a) _ (22)) & ... & ((a) _ (2n)) & 0 & 1 & ... & 0 \\ ... & ... & ... & ... & ... & ... & ... & ... \\ ((a) _ (n1)) & ((a) _ (n2)) & ... & ((a) _ (nn)) & 0 & 0 & ... & 1 \\\ end (array) \ right] \]

باختصار ، نأخذ المصفوفة $ A $ ، على اليمين نخصص لها مصفوفة الهوية $ E $ بالحجم المطلوب ، ونفصل بينها بشريط رأسي للجمال - ها هو المرفق. :)

ما الفائدة؟ وإليك ما يلي:

نظرية. اجعل المصفوفة $ A $ قابلة للعكس. ضع في اعتبارك المصفوفة المرافقة $ \ left [A \ left | هـ \ حق. \ حق] $. في حالة استخدام تحويلات السلسلة الأوليةأحضره إلى النموذج $ \ left [E \ left | لامع. \ right] $ ، أي بضرب الصفوف وطرحها وإعادة ترتيبها للحصول على المصفوفة $ E $ على اليمين من $ A $ ، ثم المصفوفة $ B $ التي تم الحصول عليها على اليسار هي معكوس $ A $:

\ [\ اليسار [أ \ اليسار | هـ \ حق. \ يمين] \ إلى \ يسار [E \ يسار | لامع. \ right] \ Rightarrow B = ((A) ^ (- 1)) \]

بكل بساطة! باختصار ، تبدو خوارزمية إيجاد معكوس المصفوفة كما يلي:

اكتب المصفوفة المرتبطة $ \ left [A \ left | هـ \ حق. \ حق] $؛
قم بإجراء تحويلات السلسلة الأولية حتى يظهر اليمين بدلاً من $ A $ $ E $؛
بالطبع ، سيظهر أيضًا شيء ما على اليسار - مصفوفة معينة $ B $. سيكون هذا هو العكس.
الأرباح! :)

بالطبع ، القول أسهل بكثير من الفعل. لنلق نظرة على مثالين: للأحجام $ \ left [3 \ times 3 \ right] $ و $ \ left [4 \ times 4 \ right] $.

مهمة. أوجد معكوس المصفوفة:

\ [\ يسار [\ يبدأ (مجموعة) (* (35) (r)) 1 & 5 & 1 \ 3 & 2 & 1 \ 6 & -2 & 1 \ نهاية (مجموعة) \ يمين] \ ]

المحلول. نؤلف المصفوفة المرفقة:

\ [\ يسار [\ ابدأ (مجموعة) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\ end (مجموعة) \ يمين] \]

بما أن العمود الأخير من المصفوفة الأصلية مملوء بآحاد ، اطرح الصف الأول من الباقي:

\ [\ start (align) & \ left [\ start (array) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \\\ end (array) \ right] \ start (matrix) \ downarrow \\ -1 \\ -1 \\\ end (matrix) \ to \\ & \ to \ left [\ start (مجموعة) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\ end (مجموعة) \ يمين] \\ \ end (محاذاة) \]

لا يوجد المزيد من الوحدات باستثناء السطر الأول. لكننا لا نلمسها ، وإلا فإن الوحدات التي تمت إزالتها حديثًا ستبدأ في "التكاثر" في العمود الثالث.

لكن يمكننا طرح السطر الثاني مرتين من السطر الأخير - نحصل على وحدة في الزاوية اليسرى السفلية:

\ [\ start (محاذاة) & \ يسار [\ start (array) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\ end (array) \ right] \ start (matrix) \ \\ \ downarrow \\ -2 \\\ end (matrix) \ to \\ & \ left [\ start (مجموعة) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\ end (مجموعة) \ يمين] \\ \ end (محاذاة) \]

الآن يمكننا طرح الصف الأخير من الصف الأول ومرتين من الثاني - بهذه الطريقة سنقوم "بإخراج" الصفر من العمود الأول:

\ [\ start (align) & \ left [\ start (array) (rrr | rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\ end (array) \ right] \ start (matrix) -1 \\ -2 \\ \ uparrow \\\ end (matrix) \ to \\ & \ إلى \ يسار [\ start (array) (rrr | rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\ end (مجموعة) \ يمين] \\ \ end (محاذاة) \]

اضرب الصف الثاني في −1 ثم اطرحه 6 مرات من الأول وأضف مرة واحدة إلى الأخيرة:

\ [\ start (align) & \ left [\ begin (array) (rrr | rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\\ نهاية (مجموعة) \ يمين] \ ابدأ (مصفوفة) \ \\ \ يسار | \ cdot \ يسار (-1 \ يمين) \ يمين. \\ \ \\\ end (matrix) \ to \\ & \ to \ left [\ start (array) (rrr | rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\ end (array) \ right] \ begin (matrix) -6 \\ updownarrow \\ +1 \\\ end (مصفوفة) \ to \\ & \ to \ left [\ start (array) (rrr | rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\ end (مجموعة) \ يمين] \\ \ end (محاذاة) \]

يبقى فقط تبديل الخطين 1 و 3:

\ [\ يسار [\ ابدأ (مجموعة) (rrr | rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 & 32 & -13 \\\ end (مجموعة) \ يمين] \]

مستعد! على اليمين المصفوفة العكسية المطلوبة.

إجابه. $ \ left [\ start (array) (* (35) (r)) 4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\ end (array) \ right ] $

مهمة. أوجد معكوس المصفوفة:

\ [\ يسار [\ ابدأ (مصفوفة) 1 & 4 & 2 & 3 \ 1 & -2 & 1 & -2 \ 1 & -1 & 1 & 1 \ 0 & -10 & -2 & -5 \\\ end (matrix) \ right] \]

المحلول. مرة أخرى نؤلف المرفق:

\ [\ يسار [\ ابدأ (مجموعة) (rrrr | rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\ end (مجموعة) \ يمين] \]

دعنا نستعير قليلاً ، ونقلق بشأن مقدار ما يجب أن نحسبه الآن ... ونبدأ العد. بادئ ذي بدء ، "لا نخرج" العمود الأول بطرح الصف 1 من الصفين 2 و 3:

\ [\ start (align) & \ left [\ begin (array) (rrrr | rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\ end (مجموعة) \ right] \ start (matrix) \ downarrow \\ -1 \\ -1 \\ \ \\\ end (matrix) \ to \\ & \ to \ left [\ begin (array) (rrrr | rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\ end (array) \ right] \\ \ end (align) \]

نلاحظ الكثير من "العيوب" في السطور 2-4. اضرب الصفوف الثلاثة كلها في −1 ، ثم احرق العمود الثالث بطرح الصف 3 من الباقي:

\ [\ start (align) & \ left [\ begin (array) (rrrr | rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\ \ end (array) \ right] \ start (matrix) \ \\ \ left | \ cdot \ يسار (-1 \ يمين) \ يمين. \\ \ اليسار | \ cdot \ يسار (-1 \ يمين) \ يمين. \\ \ اليسار | \ cdot \ يسار (-1 \ يمين) \ يمين. \\\ end (matrix) \ to \\ & \ to \ left [\ start (array) (rrrr | rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & 1 & -1 & 0 & 0 \ 0 & 5 & 1 & 2 & 1 & 0 & 1 & 0 \ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \ \ end (array) \ right] \ start (matrix) -2 \\ -1 \\ \ updownarrow \\ -2 \\\ end (matrix) \ to \\ & \ to \ left [\ start (array) ( rrrr | rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 & 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ end (مجموعة) \ يمين] \\ \ end (محاذاة) \]

حان الآن وقت "تقلي" العمود الأخير من المصفوفة الأصلية: اطرح الصف 4 من الباقي:

\ [\ start (align) & \ left [\ start (array) (rrrr | rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ end (مجموعة ) \ right] \ start (matrix) +1 \\ -3 \\ -2 \\ \ uparrow \\\ end (matrix) \ to \\ & \ to \ left [\ begin (array) (rrrr | rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ end (مجموعة) \ يمين] \\ \ end (محاذاة) \]

اللف النهائي: "احترق" العمود الثاني بطرح الصف 2 من الصفين 1 و 3:

\ [\ start (align) & \ left [\ begin (array) (rrrr | rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \ نهاية ( صفيف) \ يمين] \ تبدأ (مصفوفة) 6 \\ \ updownarrow \\ -5 \ \ \\\ end (matrix) \ to \\ & \ to \ left [\ start (array) (rrrr | rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ end (مجموعة) \ يمين] \\ \ end (محاذاة) \]

ومرة أخرى ، مصفوفة الهوية على اليسار ، وبالتالي معكوس على اليمين. :)

إجابه. $ \ left [\ start (matrix) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\ end (matrix) \ right] $

التعريف 1:تسمى المصفوفة متدهورة إذا كان محددها صفرًا.

التعريف 2:تسمى المصفوفة غير المفرد إذا كان محددها لا يساوي الصفر.

يسمى مصفوفة "أ" مصفوفة معكوسة، إذا تم استيفاء الشرط A * A-1 = A-1 * A = E (مصفوفة الهوية).

تكون المصفوفة المربعة قابلة للعكس فقط إذا كانت غير أحادية.

مخطط لحساب معكوس المصفوفة:

1) احسب محدد المصفوفة "أ" إذا ∆ A = 0 ، إذن لا يوجد معكوس المصفوفة.

2) أوجد كل التكميلات الجبرية للمصفوفة "أ".

3) يؤلف مصفوفة من الإضافات الجبرية (Aij)

4) قلب مصفوفة المكملات الجبرية (Aij) T

5) اضرب المصفوفة المنقولة بمقلوب محدد هذه المصفوفة.

6) قم بإجراء فحص:

للوهلة الأولى قد يبدو الأمر صعبًا ، لكن في الحقيقة كل شيء بسيط للغاية. كل الحلول مبنية على أساس بسيط عمليات حسابية، الشيء الرئيسي عند الحل هو عدم الخلط بين علامات "-" و "+" ، وعدم فقدانها.

الآن دعونا نقرر معا مهمة عملية، حساب معكوس المصفوفة.

المهمة: إيجاد معكوس المصفوفة "أ" الموضحة في الصورة أدناه:

نحل كل شيء تمامًا كما هو موضح في خطة حساب معكوس المصفوفة.

1. أول شيء يجب فعله هو إيجاد محدد المصفوفة "أ":

تفسير:

لقد بسطنا المحدد باستخدام وظائفه الرئيسية. أولاً ، أضفنا إلى الصف الثاني والثالث عناصر الصف الأول مضروبة في رقم واحد.

ثانيًا ، قمنا بتغيير العمودين الثاني والثالث من المحدد ، ووفقًا لخصائصه ، قمنا بتغيير العلامة الموجودة أمامه.

ثالثًا ، استخرجنا العامل المشترك (-1) للصف الثاني ، وبالتالي غيرنا الإشارة مرة أخرى ، وأصبحت موجبة. قمنا أيضًا بتبسيط السطر 3 بنفس الطريقة كما في بداية المثال.

لدينا محدد مثلث ، حيث العناصر الموجودة أسفل القطر تساوي صفرًا ، وبخاصية 7 ، يساوي حاصل ضرب عناصر القطر. نتيجة لذلك ، وصلنا ∆ أ = 26 ، ومن هنا توجد المصفوفة العكسية.

أ 11 = 1 * (3 + 1) = 4

A12 = -1 * (9 + 2) = -11

أ 13 = 1 * 1 = 1

أ 21 = -1 * (- 6) = 6

أ 22 = 1 * (3-0) = 3

A23 = -1 * (1 + 4) = -5

أ 31 = 1 * 2 = 2

أ 32 = -1 * (- 1) = -1

أ 33 = 1+ (1 + 6) = 7

3. الخطوة التالية هي تجميع مصفوفة من الإضافات الناتجة:

5. نضرب هذه المصفوفة في مقلوب المحدد ، أي في 1/26:

6. حسنًا ، نحتاج الآن فقط إلى التحقق مما يلي:

أثناء التحقق ، تلقينا مصفوفة هوية ، وبالتالي ، تم اتخاذ القرار بشكل صحيح تمامًا.

2 طريقة لحساب معكوس المصفوفة.

1. التحول الأولي للمصفوفات

2. مصفوفة معكوسة من خلال محول أولي.

يتضمن تحويل المصفوفة الأولية:

1. ضرب سلسلة في عدد غير صفري.

2. إضافة إلى أي سطر من سطر آخر ، مضروبًا في رقم.

3. تبديل صفوف المصفوفة.

4. بتطبيق سلسلة من التحولات الأولية ، نحصل على مصفوفة أخرى.

لكن -1 = ?

1. (أ | هـ) ~ (هـ | أ -1 )

2. أ -1 * أ = هـ

النظر في الأمر مثال عمليبأرقام حقيقية.

ممارسه الرياضه:أوجد معكوس المصفوفة.

المحلول:

دعونا تحقق:

القليل من التوضيح حول الحل:

قمنا أولاً بتبديل الصفين 1 و 2 من المصفوفة ، ثم ضربنا الصف الأول في (-1).

بعد ذلك ، تم ضرب الصف الأول في (-2) وإضافته إلى الصف الثاني من المصفوفة. ثم قمنا بضرب الصف الثاني في 1/4.

المرحلة الأخيرةكانت التحويلات هي ضرب الصف الثاني في 2 والجمع من الأول. نتيجة لذلك ، لدينا مصفوفة وحدة على اليسار ، وبالتالي ، فإن معكوس المصفوفة هو المصفوفة الموجودة على اليمين.

بعد التدقيق ، اقتنعنا بصحة القرار.

كما ترى ، حساب معكوس المصفوفة بسيط للغاية.

في ختام هذه المحاضرة ، أود أيضًا تخصيص بعض الوقت لخصائص مثل هذه المصفوفة.

طرق إيجاد معكوس المصفوفة. اعتبر مصفوفة مربعة

دلالة Δ = det A.

تسمى المصفوفة المربعة أ غير منحطأو غير خاصإذا كان محدده غير صفري ، و منحطأو خاص، إذاΔ = 0.

توجد مصفوفة مربعة B لمصفوفة مربعة A من نفس الترتيب إذا كان منتجها A B = B A = E ، حيث E هي مصفوفة الوحدة من نفس ترتيب المصفوفتين A و B.

نظرية . لكي يكون للمصفوفة A مصفوفة معكوسة ، من الضروري والكافي أن يكون محددها غير صفري.

مصفوفة معكوسة للمصفوفة A ، يُرمز إليها بالرمز A- 1 لذا ب = أ - 1 وتحسب بالصيغة

, (1)

حيث А i j - المكملات الجبرية للعناصر a i j من المصفوفة A ..

حساب أ -1 بالصيغة (1) للمصفوفات ترتيب عاليشاق للغاية ، لذلك من الملائم عمليًا العثور على A -1 باستخدام طريقة التحولات الأولية (EP). أي مصفوفة غير مفردة A يمكن اختزالها بواسطة EP للأعمدة فقط (أو الصفوف فقط) إلى مصفوفة الهوية E. إذا تم تطبيق EPs على المصفوفة A بنفس الترتيب على مصفوفة الهوية E ، فإن النتيجة هي مصفوفة معكوسة. من الملائم إجراء EP على المصفوفتين A و E في وقت واحد ، وكتابة كلتا المصفوفتين جنبًا إلى جنب عبر السطر. نلاحظ مرة أخرى أنه عند البحث عن الشكل الأساسي لمصفوفة ، من أجل العثور عليها ، يمكن للمرء استخدام تحويلات الصفوف والأعمدة. إذا كنت بحاجة إلى العثور على المصفوفة المعكوسة ، فيجب عليك استخدام الصفوف فقط أو الأعمدة فقط في عملية التحويل.

المثال 2.10. للمصفوفة تجد A -1.

المحلول.نجد أولًا محدد المصفوفة A
لذلك توجد المصفوفة العكسية ويمكننا إيجادها بالصيغة: ، حيث A i j (i ، j = 1،2،3) - المكملات الجبرية للعناصر a i j من المصفوفة الأصلية.

أين .

المثال 2.11. باستخدام طريقة التحويلات الأولية ، أوجد A -1 للمصفوفة: A =.

المحلول.نخصص مصفوفة هوية من نفس الترتيب للمصفوفة الأصلية الموجودة على اليمين: . بمساعدة تحويلات العمود الأولي ، نقوم بتقليص "النصف" الأيسر إلى هوية واحدة ، ونقوم في نفس الوقت بإجراء مثل هذه التحويلات بالضبط على المصفوفة اليمنى.
للقيام بذلك ، قم بتبديل العمودين الأول والثاني: ~ . نضيف الأول إلى العمود الثالث ، ونضرب الأول في -2 إلى الثاني: . من العمود الأول نطرح الثانية المضاعفة ، ومن الثالث - الثاني مضروبًا في 6 ؛ . دعنا نضيف العمود الثالث إلى الأول والثاني: . اضرب العمود الأخير في -1: . المصفوفة المربعة التي تم الحصول عليها على يمين الشريط العمودي هي معكوس المصفوفة للمصفوفة المعطاة أ.
.

لأي مصفوفة غير مولدةوهناك ، علاوة على ذلك ، مصفوفة فريدة من نوعها A -1 من هذا القبيل

أ * أ -1 = أ -1 * أ = ه ،

حيث E هي مصفوفة الوحدة من نفس الرتب مثل A. تسمى المصفوفة A -1 معكوس المصفوفة A.

إذا نسي شخص ما ، في مصفوفة الهوية ، باستثناء المائل المملوء بالواحد ، فإن جميع المواضع الأخرى مملوءة بالأصفار ، مثال على مصفوفة الهوية:

إيجاد معكوس المصفوفة بطريقة المصفوفة المجاورة

يتم تعريف المصفوفة المعكوسة بالصيغة:

حيث A ij - عناصر ij.

أولئك. لحساب معكوس المصفوفة ، عليك حساب محدد هذه المصفوفة. ثم ابحث عن الإضافات الجبرية لجميع عناصرها واصنع منها مصفوفة جديدة. بعد ذلك ، تحتاج إلى نقل هذه المصفوفة. وقسم كل عنصر من عناصر المصفوفة الجديدة على محدد المصفوفة الأصلية.

لنلقِ نظرة على بعض الأمثلة.

ابحث عن A -1 للمصفوفة

الحل: أوجد A -1 بطريقة المصفوفة المجاورة. اكتشفنا A = 2. أوجد المكملات الجبرية لعناصر المصفوفة A. In هذه القضيةستكون المكملات الجبرية لعناصر المصفوفة هي العناصر المقابلة للمصفوفة نفسها ، مأخوذة بعلامة وفقًا للصيغة

لدينا A 11 = 3 ، A 12 = -4 ، A 21 = -1 ، A 22 = 2. نشكل المصفوفة المساعدة

نقوم بنقل المصفوفة A *:

نوجد معكوس المصفوفة بالصيغة:

نحن نحصل:

استخدم طريقة المصفوفة المرافقة لإيجاد A -1 إذا

الحل: أولًا ، نحسب المصفوفة المعطاة للتأكد من وجود معكوس المصفوفة. نملك

هنا أضفنا إلى عناصر الصف الثاني عناصر الصف الثالث ، مضروبة مسبقًا في (-1) ، ثم فكنا المحدد في الصف الثاني. نظرًا لأن تعريف هذه المصفوفة يختلف عن الصفر ، فإن معكوس المصفوفة موجود. لإنشاء المصفوفة المساعدة ، نجد المكملات الجبرية لعناصر هذه المصفوفة. نملك

حسب الصيغة

نقوم بنقل المصفوفة A *:

ثم حسب الصيغة

إيجاد معكوس المصفوفة بطريقة التحويلات الأولية

بالإضافة إلى طريقة إيجاد المصفوفة المعكوسة ، والتي تتبع الصيغة (طريقة المصفوفة المرتبطة) ، هناك طريقة لإيجاد معكوس المصفوفة ، تسمى طريقة التحويلات الأولية.