Косинус на ъгъла между две равнини. Намиране на ъгъл между равнините (двустенен ъгъл)

Цели:

развиват способността да разглеждат различни подходи за решаване на проблеми и да анализират „ефекта“ от прилагането на тези методи за решаване;
развиват способността на ученика да избира метод за решаване на задача в съответствие с математическите си предпочитания, въз основа на по-солидни знания и уверени умения;
развиват способността да съставят план от последователни етапи за постигане на резултата;
развийте способността да обосновавате всички предприети стъпки и изчисления;
повторете и поправете различни темии въпроси на стереометрията и планиметрията, характерни стереометрични структури, свързани с решаване на текущи проблеми;
развиват пространственото мислене.

анализ различни методирешаване на задачи: метод на координатния вектор, приложение на косинусовата теорема, приложение на теоремата за трите перпендикуляра;
сравняване на предимствата и недостатъците на всеки метод;
повторение на свойствата на куб, триъгълна призма, правилен шестоъгълник;
подготовка за полагане на изпит;
развитие на самостоятелност при вземане на решения.

Конспект на урока

На кубчета ABCDA 1 B 1 C 1 D 1с ръб 1 точка O - лице център ABCD.

а) ъгълът между правите A 1 Dи BO;

б) разстояние от точката бдо средата на разреза A 1 D.

Решение точка а).

Нека поставим нашия куб правоъгълна системакоординати, както е показано на фигурата, върхове A 1 (1; 0; 1), D (1; 1; 0), B 1 (0; 0; 1), O (½; ½; 0).

Насочващи вектори на прави A 1 Dи B1O:

(0; 1; -1) и (½; ½; -1);

желаният ъгъл φ между тях се намира по формулата:

cos∠φ = ,
откъдето ∠φ = 30°.

2 начина. Използваме косинусовата теорема.

1) Начертайте права линия На 1 Суспоредна на права линия A 1 D. Ъгъл CB1Oще бъде желано.

2) От правоъгълен триъгълник BB 1Oспоред Питагоровата теорема:

3) По закона за косинусите от триъгълник CB1Oизчислете ъгъла CB1O:

cos CB 1 O = , желаният ъгъл е 30°.

Коментирайте. При решаването на задачата по 2-ри начин се вижда, че според теоремата за три перпендикуляра COB 1 = 90°, така че от правоъгълника ∆ CB1Oсъщо така е лесно да се изчисли косинусът на желания ъгъл.

Точка на решение б).

1 начин. Нека използваме формулата за разстоянието между две точки

Нека точката д- средно A 1 D, след това координатите E (1; 1/2; ½), B (0; 0; 0).

B.E.= .

2 начина. Според Питагоровата теорема

От правоъгълник ∆ BAEс директен BAEнамирам БЪДА = .

В дясно триъгълна призма ABCA 1 B 1 C 1всички ръбове са равни а. Намерете ъгъла между линиите ABи A 1 C.

1 начин. Метод на координатния вектор

Координатите на върховете на призмата в правоъгълна система, когато призмата е разположена, както е на фигурата: A (0; 0; 0), B (a; ; 0), A 1 (0; 0; a), C (0; a; 0).

Насочващи вектори на прави A 1 Cи AB:

(0; а; -а)и (а; ; 0} ;

cos φ = ;

2 начина. Използваме закона на косинусите

Разглеждаме ∆ A 1 B 1 C, при което A 1 B 1 || AB. Ние имаме

cos φ = .

(От сборника на Единния държавен изпит-2012. Математика: типичен опции за изпитизд. А. Л. Семенова, И. В. Ященко)

В правилна шестоъгълна призма ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, чиито ръбове са равни на 1, намерете разстоянието от точката днаправо B 1 C 1.

1 начин. Метод на координатния вектор

1) Поставете призмата в правоъгълна координатна система, като поставите координатните оси, както е показано на фигурата. SS 1, SWи CEса по двойки перпендикулярни, така че координатните оси могат да бъдат насочени по тях. Получаваме координатите:

C 1 (0; 0; 1), E (; 0; 0), B 1 (0; 1; 1).

2) Намерете координатите на насочващите вектори за линиите От 1 до 1и C 1 E:

(0;1;0), (;0;-1).

3) Намерете косинуса на ъгъла между От 1 до 1и C 1 Eизползвайки скаларно произведениевектори и:

cos β = = 0 => β = 90° => C 1 E е желаното разстояние.

4)C 1 E \u003d \u003d 2.

Извод: знание различни подходиза решаване на стереометрични проблеми ви позволява да изберете предпочитания метод за всеки ученик, т.е. такъв, в който студентът е уверен, помага да се избегнат грешки, води до успешно решаване на проблема и получаване на добър резултат на изпита. координатен методима предимство пред други методи, тъй като изисква по-малко стереометрични съображения и визия и се основава на използването на формули, които имат много планиметрични и алгебрични аналогии, по-познати на учениците.

Формата на урока е комбинация от обяснението на учителя с фронталната колективна работа на учениците.

Разглежданите полиедри се показват на екрана с помощта на видео проектор, което позволява сравнението различни начинирешения.

Домашна работа: решете задача 3 по различен начин, например като използвате теоремата за трите перпендикуляра .

Литература

1. Ершова А.П., Голобородко В.В. Независими и тестови работипо геометрия за 11 клас. - М .: ИЛЕКСА, - 2010. - 208 с.

2. Геометрия, 10-11: учебник за образователни институции: основно и профилно ниво / Л. С. Атанасян, В. Ф. Бутузов, С.Б. Кадомцев и др. - М .: Образование, 2007. - 256 с.

3. УПОТРЕБА-2012. Математика: типични изпитни варианти: 10 варианта / изд. A.L. Семенова, I.V. Yashchenko. – М.: национално образование, 2011. - 112 с. - (USE-2012. FIPI - школа).

Статията говори за намирането на ъгъла между равнините. След като представим определението, ще зададем графична илюстрация, помислете многословен начиннамиране по метода на координатите. Получаваме формула за пресичащи се равнини, която включва координатите нормални вектори.

Yandex.RTB R-A-339285-1

Материалът ще използва данни и концепции, които преди това са били изучавани в статии за равнината и линията в пространството. Като начало е необходимо да се премине към разсъждения, които позволяват да има определен подход за определяне на ъгъла между две пресичащи се равнини.

Дадени са две пресичащи се равнини γ 1 и γ 2. Тяхното пресичане ще приеме обозначението c . Конструкцията на равнината χ е свързана с пресичането на тези равнини. Равнината χ минава през точка M като права c. Равнините γ 1 и γ 2 ще бъдат пресечени с помощта на равнината χ. Приемаме обозначенията на правата, пресичаща γ 1 и χ за права a, и пресичаща γ 2 и χ за права b. Получаваме, че пресечната точка на правите a и b дава точката M .

Местоположението на точка M не влияе на ъгъла между пресичащите се прави a и b, а точката M се намира на правата c, през която минава равнината χ.

Необходимо е да се построи равнина χ 1 , перпендикулярна на правата c и различна от равнината χ . Пресечната точка на равнините γ 1 и γ 2 с помощта на χ 1 ще приеме обозначението на правите a 1 и b 1 .

Вижда се, че при построяването на χ и χ 1 правите a и b са перпендикулярни на правата c, след това a 1, b 1 са перпендикулярни на правата c. Намирането на прави a и a 1 в равнината γ 1 с перпендикулярност към правата c, тогава те могат да се считат за успоредни. По същия начин разположението на b и b 1 в равнината γ 2 с перпендикулярността на правата c показва техния паралелизъм. Това означава, че е необходимо да се направи успореден пренос на равнината χ 1 в χ, при което се получават две съвпадащи прави a и a 1 , b и b 1 . Получаваме, че ъгълът между пресичащите се прави a и b е 1 равен на ъгълапресичащи прави a и b.

Разгледайте фигурата по-долу.

Това съждение се доказва от факта, че между пресичащите се прави a и b има ъгъл, който не зависи от местоположението на точката M, тоест точката на пресичане. Тези прави се намират в равнините γ 1 и γ 2 . Всъщност полученият ъгъл може да се разглежда като ъгъл между две пресичащи се равнини.

Нека да преминем към определяне на ъгъла между съществуващите пресичащи се равнини γ 1 и γ 2 .

Определение 1

Ъгълът между две пресичащи се равнини γ 1 и γ 2наричаме ъгъла, образуван от пресичането на линии a и b, където равнините γ 1 и γ 2 се пресичат с равнината χ, перпендикулярна на правата c.

Разгледайте фигурата по-долу.

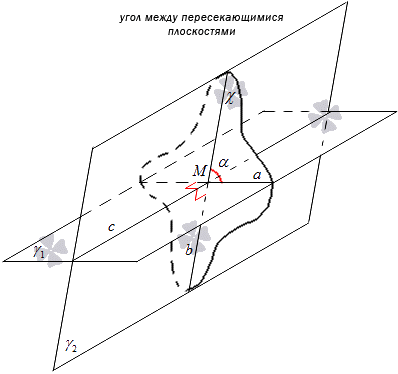
Определението може да бъде представено и в друга форма. В пресечната точка на равнините γ 1 и γ 2, където c е линията, на която те се пресичат, маркирайте точката M, през която начертайте правите a и b, перпендикулярни на правата c и лежащи в равнините γ 1 и γ 2, тогава ъгълът между правите a и b ще бъде ъгълът между равнините. На практика това е приложимо при построяването на ъгъл между равнините.

В пресечната точка се образува ъгъл, чиято стойност е по-малка от 90 градуса, т.е. степенна мяркаъгълът е валиден за интервал от този вид (0, 90] . В същото време тези равнини се наричат перпендикулярни, ако в пресечната точка се образува прав ъгъл. Ъгълът между успоредните равнини се счита за нула.

Обичайният начин за намиране на ъгъла между пресичащите се равнини е извършването на допълнителни конструкции. Това помага да се определи с точност и това може да стане с помощта на знаците за равенство или подобие на триъгълника, синусите, косинусите на ъгъла.

Помислете за решаване на проблеми, като използвате пример от ИЗПОЛЗВАЙТЕ задачиблок C 2 .

Пример 1

Попитан кубоид A B C D A 1 B 1 C 1 D 1, където страната A B = 2, A D = 3, A A 1 = 7, точка E разделя страната A A 1 в съотношение 4: 3. Намерете ъгъла между равнините A B C и B E D 1 .

Решение

За по-голяма яснота трябва да направите чертеж. Разбираме това

Необходимо е визуално представяне, за да е по-удобно да се работи с ъгъла между равнините.

Даваме дефиницията на права линия, по която се пресичат равнините A B C и B E D 1. Точка B е обща точка. Трябва да намеря друг обща точкакръстовища. Да разгледаме правите D A и D 1 E , които се намират в една и съща равнина A D D 1 . Разположението им не показва успоредност, което означава, че имат обща пресечна точка.

Обаче правата D A се намира в равнината A B C, а D 1 E в B E D 1 . Следователно получаваме тези линии Д Аи D 1 Eимат обща пресечна точка, която е обща и за равнините A B C и B E D 1 . Показва точката на пресичане на линиите Д Аи D 1 E буква F. От тук получаваме, че B F е права, по която се пресичат равнините A B C и B E D 1.

Разгледайте фигурата по-долу.

За да се получи отговор, е необходимо да се построят прави линии, разположени в равнините A B C и B E D 1 с преминаване през точка, разположена на правата B F и перпендикулярна на нея. Тогава полученият ъгъл между тези линии се счита за желания ъгъл между равнините A B C и B E D 1.

От това се вижда, че точката A е проекцията на точката E върху равнината A B C. Необходимо е да се начертае права, пресичаща правата B F под прав ъгъл в точката M. Вижда се, че правата A M е проекцията на правата E M върху равнината A B C въз основа на теоремата за тези перпендикуляри A M ⊥ B F . Разгледайте фигурата по-долу.

∠ A M E е търсеният ъгъл, образуван от равнините A B C и B E D 1 . От получения триъгълник A E M можем да намерим синуса, косинуса или тангенса на ъгъла, след което и самия ъгъл, само с двете му известни страни. По условие имаме, че дължината на A E се намира по този начин: линията A A 1 е разделена на точката E в съотношение 4: 3, което означава, че общата дължина на линията е 7 части, тогава A E \u003d 4 части. Намираме A.M.

Трябва да се вземе предвид правоъгълен триъгълник A B F . Имаме прав ъгъл A с височина A M. От условието A B \u003d 2, тогава можем да намерим дължината A F по сходството на триъгълници D D 1 F и A E F. Получаваме, че A E D D 1 = A F D F ⇔ A E D D 1 = A F D A + A F ⇒ 4 7 = A F 3 + A F ⇔ A F = 4

Необходимо е да се намери дължината на страната B F от триъгълника A B F с помощта на Питагоровата теорема. Получаваме, че B F = A B 2 + A F 2 = 2 2 + 4 2 = 2 5 . Дължината на страната A M се намира през площта на триъгълника A B F. Имаме, че площта може да бъде равна както на S A B C = 1 2 · A B · A F, така и на S A B C = 1 2 · B F · A M.

Получаваме, че A M = A B A F B F = 2 4 2 5 = 4 5 5

Тогава можем да намерим стойността на тангенса на ъгъла на триъгълника A E M. Получаваме:

t g ∠ A M E = A E A M = 4 4 5 5 = 5

Желаният ъгъл, получен от пресичането на равнините A B C и B E D 1, е равен на a r c t g 5, тогава, когато се опрости, получаваме a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .

Отговор: a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .

Дадени са някои случаи на намиране на ъгъла между пресичащите се прави координатна равнинаОтносно x y z и метода на координатите. Нека разгледаме по-подробно.

Ако е дадена задача, където е необходимо да се намери ъгълът между пресичащите се равнини γ 1 и γ 2, ние означаваме желания ъгъл с α.

Тогава дадена системакоординати показва, че имаме координатите на нормалните вектори на пресичащите се равнини γ 1 и γ 2 . След това означаваме, че n 1 → = n 1 x , n 1 y , n 1 z е нормален вектор на равнината γ 1 и n 2 → = (n 2 x , n 2 y , n 2 z) - за равнина γ 2 . Помислете за подробно намиране на ъгъла, разположен между тези равнини, според координатите на векторите.

Необходимо е да обозначите правата линия, по която се пресичат равнините γ 1 и γ 2, с буквата c. На правата с имаме точка M, през която прекарваме равнина χ, перпендикулярна на c. Равнината χ по правата a и b пресича равнините γ 1 и γ 2 в точка M . от определението следва, че ъгълът между пресичащите се равнини γ 1 и γ 2 е равен на ъгъла на пресичащите се линии a и b, принадлежащи съответно на тези равнини.

В равнината χ отделяме нормалните вектори от точката M и ги обозначаваме с n 1 → и n 2 →. Вектор n 1 → е разположен на права, перпендикулярна на права a, а вектор n 2 → на права, перпендикулярна на права b. Следователно получаваме това дадена равнинаχ има нормален вектор на правата a равен на n 1 → и за правата b равен на n 2 → . Разгледайте фигурата по-долу.

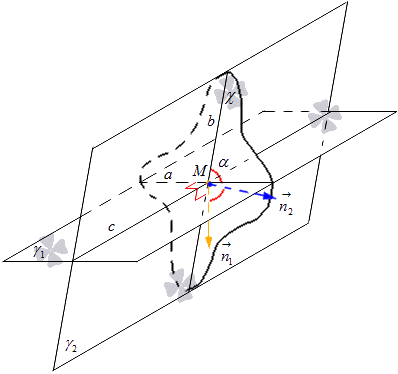
От тук получаваме формула, чрез която можем да изчислим синуса на ъгъла на пресичащите се прави, като използваме координатите на векторите. Установихме, че косинусът на ъгъла между правите a и b е същият като косинуса между пресичащите се равнини γ 1 и γ 2, получен от cos формулиα = cos n 1 → , n 2 → ^ = n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2 , където имаме, че n 1 → = (n 1 x , n 1 y , n 1 z) и n 2 → = (n 2 x , n 2 y , n 2 z) са координатите на векторите на представените равнини.

Ъгълът между пресичащите се линии се изчислява по формулата

α = a r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2

Пример 2

По условие е даден паралелепипед А В С D A 1 B 1 C 1 D 1 , където A B = 2, A D = 3, A A 1 = 7, а точка E разделя страната A A 1 4: 3. Намерете ъгъла между равнините A B C и B E D 1 .

Решение

От условието се вижда, че страните му са по двойки перпендикулярни. Това означава, че е необходимо да се въведе координатна система O x y z с връх в точка C и координатни оси O x, O y, O z. Необходимо е да поставите посоката на съответните страни. Разгледайте фигурата по-долу.

Пресичащи се равнини A B Cи B E D 1образуват ъгъл, който може да се намери по формулата 2 x 2 + n 2 y 2 + n 2 z 2 , където n 1 → = (n 1 x , n 1 y , n 1 z) и n 2 → = (n 2 x , n 2 y , n 2 z ) са нормални вектори на тези равнини. Необходимо е да се определят координатите. От фигурата виждаме това координатна осОколо x y съвпада в равнината A B C, което означава, че координатите на нормалния вектор k → равни на стойността n 1 → = k → = (0, 0, 1) .

Нормалният вектор на равнината B E D 1 е векторното произведение на B E → и B D 1 → , където техните координати се намират от координатите крайни точки B, E, D 1 , които се определят въз основа на условието на задачата.

Получаваме, че B (0 , 3 , 0) , D 1 (2 , 0 , 7) . Тъй като A E E A 1 = 4 3 , от координатите на точките A 2 , 3 , 0 , A 1 2 , 3 , 7 намираме E 2 , 3 , 4 . Получаваме, че B E → = (2 , 0 , 4) , B D 1 → = 2 , - 3 , 7 n 2 → = B E → × B D 1 = i → j → k → 2 0 4 2 - 3 7 = 12 i → - 6 j → - 6 k → ⇔ n 2 → = (12, - 6, - 6)

Необходимо е да замените намерените координати във формулата за изчисляване на ъгъла през аркосинуса. Получаваме

α = a r c cos 0 12 + 0 (- 6) + 1 (- 6) 0 2 + 0 2 + 1 2 12 2 + (- 6) 2 + (- 6) 2 = a r c cos 6 6 6 = a r c cos 6 6

Координатният метод дава подобен резултат.

Отговор: a r c cos 6 6 .

Последната задача се разглежда, за да се намери ъгълът между пресичащите се равнини с наличните известни уравнения на равнините.

Пример 3

Изчислете синуса, косинуса на ъгъла и стойността на ъгъла, образуван от две пресичащи се прави, които са определени в координатната система O x y z и дадени от уравненията 2 x - 4 y + z + 1 = 0 и 3 y - z - 1 = 0 .

Решение

При изучаване на тема общо уравнениелиния под формата A x + B y + C z + D = 0 разкри, че A, B, C са коефициенти, равни на координатите на нормалния вектор. Следователно, n 1 → = 2 , - 4 , 1 и n 2 → = 0 , 3 , - 1 са нормални вектори на дадени прави.

Необходимо е да замените координатите на нормалните вектори на равнините във формулата за изчисляване на желания ъгъл на пресичащите се равнини. Тогава разбираме това

α = a r c cos 2 0 + - 4 3 + 1 (- 1) 2 2 + - 4 2 + 1 2 = a r c cos 13 210

Оттук имаме, че косинусът на ъгъла приема формата cos α = 13 210 . Тогава ъгълът на пресичащите се прави не е тъп. Заместване в тригонометрична идентичност, получаваме, че стойността на синуса на ъгъла е равна на израза. Изчисляваме и получаваме това

sin α = 1 - cos 2 α = 1 - 13 210 = 41 210

Отговор: sin α = 41 210, cos α = 13 210, α = a r c cos 13 210 = a r c sin 41 210.

Ако забележите грешка в текста, моля, маркирайте я и натиснете Ctrl+Enter

В задача C2 по математика най-често трябва да решите задача, в която трябва да определите:

Разстояние между две точки
Разстояние от точка до линия
Разстояние от точка до равнина
Разстояние между пресичащите се линии
Ъгъл между две прави
Ъгъл между права и равнина
Ъгъл между равнините

Задачите са елементарни, ако следвате алгоритъма за решаване на C2 и запомните основното тригонометрични свойства, като свойствата на диагоналите или повърхността на полиедър. Помощните задачи ще ви помогнат да запомните тези основни свойства.

Сега да преминем към алгоритмите.

1. За да определим разстоянието между две точки A и B, използваме един от двата метода:

Включваме AB в някакъв триъгълник и намираме неговата дължина като страна на триъгълника
Според формулата

Освен това методът на координатите според мен е най-простият, необходимо е само точно да се определят координатите на всяка точка.

2. За да определите разстоянието от точка до права, изчислете

като дължината на перпендикулярен сегмент, ако е възможно този сегмент да се включи в някакъв триъгълник като една от височините

с помощта на координатния метод с помощта на формули за изчисляване на площта, в която необходимото разстояние ще бъде височината и

3. Разстоянието от точка до равнина е

дължината на перпендикуляра, паднал от тази точка към равнината. За да направите това, внимателно изградете разрез, който е перпендикулярен на равнината и минава през нея дадена точка. Желаното разстояние ще бъде равно на височината на получения нов полиедър.
Използване на метода на координатите

Уравнението се намира чрез заместване на координатите на три точки, принадлежащи на тази равнина

Използване на векторния метод

За да направите това, трябва да запомните правилата за добавяне и изваждане на вектори, че продуктът перпендикулярни векторие равно на нула.

Използвайки метода на обема, ако има пирамида ABCM, тогава разстоянието от точка M до равнината, съдържаща триъгълника ABC, се изчислява по формулата

По метода на справочните задачи, които могат да се видят

4. Разстоянието между пресичащите се линии може да се определи с помощта на

4.1. Метод на изчисление стъпка по стъпка:

построяват общ перпендикуляр на две пресичащи се прави и намират дължината му;
построете равнина, съдържаща една от правите и успоредна на другата. Тогава желаното разстояние ще бъде равно на разстоянието от точката до правата линия, построена в равнината;
оградете дадените прави в успоредни равнини, минаващи през дадените коси прави, намерете разстоянието между тези равнини
конструирайте равнина, перпендикулярна на една от тези линии и конструирайте ортогонална проекция на втората линия

4.2. Векторно-координатен метод

Намерете координатите на краищата на отсечка, която е общ перпендикуляр на две пресичащи се прави
Намиране на разстоянието между две точки

4.3. векторен метод
Свеждаме проблема до определяне на дължината на вектор, принадлежащ на перпендикуляр, който е общ перпендикуляр на две пресичащи се прави

6. Ъгъл между права и равнинасе определя чрез включването му в правоъгълен триъгълник като един от острите ъгли или чрез метода на векторния координатор

Или

Как се определя ъгълът между равнините ще разгледаме в следващия урок. Тези алгоритми за решаване на C2 допринасят за цялостното разбиране на метода за решаване на проблема. „В помощ на студентското списание за студенти и техните родители“. Прочетете повече: http://education-club.ru/#ixzz2IXf5GOJU

7. Ъгъл между равнините(геометричен метод)

1. Намерете правата, по която се пресичат равнините.
2. Изберете точка на тази права и начертайте два перпендикуляра към нея, лежащи в тези равнини. Или начертайте равнина, перпендикулярна на линията на пресичане на равнините.
3. Намерете тригонометричната функция на ъгъла, образуван от перпендикулярите към пресечната линия на равнините. Като правило, ние правим това чрез триъгълник, който включва желания ъгъл.
4. В отговора запишете стойността на ъгъла или тригонометрична функцияъгъл.

Ъгъл между равнините. координатен метод. Задача C2

Две пресичащи се равнини образуват две двойки равни двустенни ъгли:

Стойността на двустенния ъгъл се измерва със стойността на съответния линеен ъгъл.

За да изградите линеен ъгъл на двустенен ъгъл, трябва да вземете линията на пресичане на равнините произволна точка, и във всяка равнина начертайте лъч до тази точка, перпендикулярен на линията на пресичане на равнините. Ъгълът, образуван от тези лъчи, е линейният ъгъл на двустенния ъгъл:

Стойността на ъгъла между равнините е стойността на по-малкия от една година двустенен ъгъл.

Нека нашите равнини и са дадени от уравненията:

Косинусът на ъгъла между равнините се намира по следната формула:

В отговора пишем , тъй като стойността на ъгъла между равнините е стойността на по-малкия двустенен ъгъл.

В правилна четириъгълна призма с основа страна от 12 и височина от 21, точка M се взема на ръба, така че . Точка K се взема на ръба, така че . Намерете ъгъла между равнина и равнина.

Да направим рисунка. Тъй като ще използваме координатния метод, веднага ще въведем координатната система: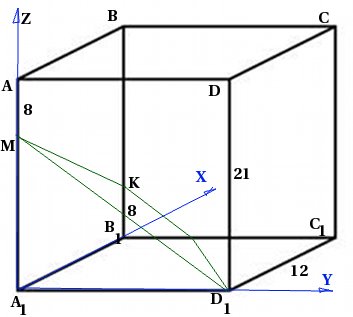

Сега сме изправени пред задачата да напишем уравненията на равнината и равнината.

Описах подробен алгоритъм за намиране на уравнението на равнина с помощта на три точки.

След като намерим коефициентите в равнината и уравненията на равнината, заместваме ги във формулата за намиране на косинуса на ъгъла между равнините и намираме ъгъла.

Предлагам ви да гледате подробно видео решение на този проблем:

Още една задача от Инна Владимировна Фелдман

Видео уроци "Координатен метод за решаване на задачи c-2"

Урок 2 http://youtu.be/dKQWG8OZRGo
урок 3 http://youtu.be/ddgr0PnbFno
урок 4 http://youtu.be/n6yx2pQC0Lo
урок 5 http://youtu.be/JkWbxAw1YLI
урок 6 http://youtu.be/gybIqCMKBiI
урок 7 http://youtu.be/_LpARpYxp5g
урок 8 http://youtu.be/XJhyZQoofD8

Ъгълът между две различни равнини може да се определи за всеки относителна позициясамолети.

Тривиалният случай е, ако равнините са успоредни. Тогава ъгълът между тях се счита за равен на нула.

Нетривиален случай, ако равнините се пресичат. Този случай е обект на по-нататъшно обсъждане. Първо се нуждаем от понятието двустенен ъгъл.

9.1 Двустенен ъгъл

Двустенен ъгъл са две полуравнини с обща права линия (която се нарича ръб на двустенен ъгъл). На фиг. 50 показва двустенен ъгъл, образуван от полуравнини и; ръбът на този двустенен ъгъл е правата a, обща за дадените полуравнини.

Ориз. 50. Двустенен ъгъл

Двустенният ъгъл може да бъде измерен в градуси или радиани с една дума, въведете ъгловата стойност на двустенния ъгъл. Това става по следния начин.

На ръба на двустенния ъгъл, образуван от полуравнините и, вземаме произволна точка M. Нека начертаем лъчите MA и MB, лежащи съответно в тези полуравнини и перпендикулярни на ръба (фиг. 51).

Ориз. 51. Линеен ъгъл двустенен ъгъл

Полученият ъгъл AMB е линейният ъгъл на двустенния ъгъл. Ъгълът " = \AMB е точно ъгловата стойност на нашия двустенен ъгъл.

Определение. Ъгловата величина на двустенния ъгъл е големината на линейния ъгъл на даден двустенен ъгъл.

Всички линейни ъгли на двустенен ъгъл са равни един на друг (в крайна сметка те се получават един от друг чрез паралелно изместване). Ето защо това определениеправилно: стойността "не зависи от специфичен изборточка М на ръба на двустенния ъгъл.

9.2 Определяне на ъгъла между равнините

При пресичане на две равнини се получават четири двустенни ъгъла. Ако всички имат същата стойност(с 90), тогава равнините се наричат перпендикулярни; тогава ъгълът между равнините е 90 .

Ако не всички двустенни ъгли са еднакви (т.е. има два остри и два тъпи), тогава ъгълът между равнините е стойността на острия двустенен ъгъл (фиг. 52).

Ориз. 52. Ъгъл между равнините

9.3 Примери за решаване на проблеми

Нека разгледаме три задачи. Първият е прост, вторият и третият са приблизително на ниво C2 на изпита по математика.

Задача 1. Намерете ъгъла между две страни на правилен тетраедър.

Решение. Нека ABCD е правилен тетраедър. Нека начертаем медианите AM и DM на съответните лица, както и височината на тетраедъра DH (фиг. 53).

Ориз. 53. Към задача 1

Тъй като са медиани, AM и DM също са височини на равностранен триъгълници ABCи DBC. Следователно ъгълът " = \AMD е линейният ъгъл на двустенния ъгъл, образуван от лицата ABC и DBC. Намираме го от триъгълника DHM:

			1 сутринта

Отговор: arccos 1 3 .

Задача 2. В правилна четириъгълна пирамида SABCD (с връх S) страничният ръб е равен на страната на основата. Точка K е средата на ръба SA. Намерете ъгъла между равнините

Решение. Правата BC е успоредна на AD и следователно е успоредна на равнината ADS. Следователно равнината KBC пресича равнината ADS по правата KL, успоредна на BC (фиг. 54).

Ориз. 54. Към задача 2

В този случай KL също ще бъде успореден на правата AD; следователно KL средна линиятриъгълник ADS, а точката L е средата на DS.

Начертайте височината на пирамидата SO. Нека N е средата на DO. Тогава LN е средната линия на триъгълника DOS и следователно LN k SO. Така че LN е перпендикулярна на равнината ABC.

От точката N пускаме перпендикуляра NM на правата BC. Правата NM ще бъде проекцията на наклонената LM върху равнината ABC. Тогава от теоремата за трите перпендикуляра следва, че LM също е перпендикулярна на BC.

Така ъгълът " = \LMN е линейният ъгъл на двустенния ъгъл, образуван от полуравнините KBC и ABC. Ще търсим този ъгъл от правоъгълния триъгълник LMN.

Нека ръбът на пирамидата е a. Първо намерете височината на пирамидата:

SO=p

Решение. Нека L е пресечната точка на правите A1 K и AB. Тогава равнината A1 KC пресича равнината ABC по правата CL (фиг.55).

А ° С

Ориз. 55. Задача 3

Триъгълниците A1 B1 K и KBL са равни по катет и остър ъгъл. Следователно другите катети също са равни: A1 B1 = BL.

Помислете за триъгълник ACL. В него BA = BC = BL. Ъгълът CBL е 120; така че \BCL = 30 . Също така \BCA = 60 . Следователно \ACL = \BCA + \BCL = 90 .

Така че LC? AC. Но правата AC е проекцията на правата A1 C върху равнината ABC. По теоремата за трите перпендикуляра тогава заключаваме, че LC ? A1C.

Така ъгълът A1 CA е линейният ъгъл на двустенния ъгъл, образуван от полуравнините A1 KC и ABC. Това е необходимият ъгъл. От равнобедрения правоъгълен триъгълник A1 AC виждаме, че той е равен на 45 .

\(\blacktriangleright\) Двустенният ъгъл е ъгълът, образуван от две полуравнини и правата линия \(a\), която е тяхната обща граница.

\(\blacktriangleright\) За да намерите ъгъла между равнините \(\xi\) и \(\pi\) , трябва да намерите линейния ъгъл пикантенили прав) на двустенния ъгъл, образуван от равнините \(\xi\) и \(\pi\) :

Стъпка 1: нека \(\xi\cap\pi=a\) (линията на пресичане на равнините). В равнината \(\xi\) маркираме произволна точка \(F\) и чертаем \(FA\perp a\) ;

Стъпка 2: изчертайте \(FG\perp \pi\) ;

Стъпка 3: според TTP (\(FG\) - перпендикуляр, \(FA\) - наклонен, \(AG\) - проекция) имаме: \(AG\perp a\) ;

Стъпка 4: Ъгълът \(\angle FAG\) се нарича линеен ъгъл на двустенния ъгъл, образуван от равнините \(\xi\) и \(\pi\) .

Обърнете внимание, че триъгълникът \(AG\) е правоъгълен триъгълник.
Забележете също, че равнината \(AFG\), конструирана по този начин, е перпендикулярна на двете равнини \(\xi\) и \(\pi\) . Следователно може да се каже по друг начин: ъгъл между равнините\(\xi\) и \(\pi\) е ъгълът между две пресичащи се прави \(c\in \xi\) и \(b\in\pi\) , образуващи равнина, перпендикулярна на \(\xi\ ) и \(\pi\) .

Задача 1 #2875

Ниво на задачата: По-трудно от изпита

Дана четириъгълна пирамида, като всички ръбове са равни, а основата е квадрат. Намерете \(6\cos \alpha\) , където \(\alpha\) е ъгълът между неговите съседни странични стени.

Нека \(SABCD\) е дадена пирамида (\(S\) е връх), чиито ръбове са равни на \(a\) . Следователно всички странични лицаса еднакви равностранни триъгълници. Намерете ъгъла между лицата \(SAD\) и \(SCD\) .

Нека начертаем \(CH\perp SD\) . защото \(\триъгълник SAD=\триъгълник SCD\), тогава \(AH\) също ще бъде височина на \(\триъгълник SAD\) . Следователно по дефиниция \(\angle AHC=\alpha\) е линейният двустенен ъгъл между лицата \(SAD\) и \(SCD\) .
Тъй като основата е квадрат, тогава \(AC=a\sqrt2\) . Обърнете внимание също, че \(CH=AH\) е височината равностранен триъгълниксъс страна \(a\) , следователно \(CH=AH=\frac(\sqrt3)2a\) .
Тогава по косинусовата теорема от \(\триъгълник AHC\) : \[\cos \alpha=\dfrac(CH^2+AH^2-AC^2)(2CH\cdot AH)=-\dfrac13 \quad\Rightarrow\quad 6\cos\alpha=-2.\]

Отговор: -2

Задача 2 #2876

Ниво на задачата: По-трудно от изпита

Равнините \(\pi_1\) и \(\pi_2\) се пресичат под ъгъл, чийто косинус е равен на \(0,2\) . Равнините \(\pi_2\) и \(\pi_3\) се пресичат под прав ъгъл, а пресечната линия на равнините \(\pi_1\) и \(\pi_2\) е успоредна на пресечната линия на равнините \(\pi_2\) и \(\ pi_3\) . Намерете синуса на ъгъла между равнините \(\pi_1\) и \(\pi_3\) .

Нека пресечната линия на \(\pi_1\) и \(\pi_2\) е правата \(a\) , пресечната линия на \(\pi_2\) и \(\pi_3\) е правата \ (b\) , а пресечната линия \(\pi_3\) и \(\pi_1\) са правата линия \(c\) . Тъй като \(a\паралел b\) , то \(c\паралел а\паралел b\) (според теоремата от раздела на теоретичния справочник „Геометрия в пространството“ \(\rightarrow\) „Въведение в стереометрията, паралелизъм”).

Маркирайте точките \(A\in a, B\in b\), така че \(AB\perp a, AB\perp b\) (това е възможно, защото \(a\паралел b\) ). Забележете \(C\in c\), така че \(BC\perp c\) , следователно \(BC\perp b\) . След това \(AC\perp c\) и \(AC\perp a\) .
Наистина, тъй като \(AB\perp b, BC\perp b\) , тогава \(b\) е перпендикулярен на равнината \(ABC\) . Тъй като \(c\паралел a\паралел b\) , тогава правите \(a\) и \(c\) също са перпендикулярни на равнината \(ABC\) и следователно всяка права от тази равнина, в частност, линията \ (AC\) .

Оттук следва, че \(\ъгъл BAC=\ъгъл (\pi_1, \pi_2)\), \(\ъгъл ABC=\ъгъл (\pi_2, \pi_3)=90^\circ\), \(\ъгъл BCA=\ъгъл (\pi_3, \pi_1)\). Оказва се, че \(\триъгълник ABC\) е правоъгълен, което означава \[\sin \angle BCA=\cos \angle BAC=0,2.\]

Отговор: 0,2

Задача 3 #2877

Ниво на задачата: По-трудно от изпита

Дадени са прави \(a, b, c\), пресичащи се в една точка и ъгълът между всеки две от тях е равен на \(60^\circ\) . Намерете \(\cos^(-1)\alpha\) , където \(\alpha\) е ъгълът между равнината, образувана от правите \(a\) и \(c\) и равнината, образувана от правите \(b\ ) и \(c\) . Дайте отговора си в градуси.

Нека правите се пресичат в точка \(O\) . Тъй като ъгълът между всеки две от тях е равен на \(60^\circ\) , тогава и трите прави не могат да лежат в една и съща равнина. Нека маркираме точка \(A\) на правата \(a\) и начертаем \(AB\perp b\) и \(AC\perp c\) . Тогава \(\триъгълник AOB=\триъгълник AOC\)като правоъгълник в хипотенуза и остър ъгъл. Следователно \(OB=OC\) и \(AB=AC\) .
Нека направим \(AH\perp (BOC)\) . Тогава по теоремата за трите перпендикуляра \(HC\perp c\) , \(HB\perp b\) . Тъй като \(AB=AC\) , тогава \(\триъгълник AHB=\триъгълник AHC\)като правоъгълник по дължината на хипотенузата и крака. Следователно \(HB=HC\) . Следователно \(OH\) е ъглополовящата на ъгъла \(BOC\) (тъй като точката \(H\) е на еднакво разстояние от страните на ъгъла).

Обърнете внимание, че по този начин ние също конструирахме линейния ъгъл на двустенния ъгъл, образуван от равнината, образувана от правите \(a\) и \(c\), и равнината, образувана от правите \(b\) и \( ° С\) . Това е ъгълът \(ACH\) .

Нека намерим този ъгъл. Тъй като избрахме точката \(A\) произволно, тогава нека я изберем така, че \(OA=2\) . След това в правоъгълник \(\триъгълник AOC\): \[\sin 60^\circ=\dfrac(AC)(OA) \quad\Rightarrow\quad AC=\sqrt3 \quad\Rightarrow\quad OC=\sqrt(OA^2-AC^2)=1.\ ]Тъй като \(OH\) е ъглополовяща, тогава \(\angle HOC=30^\circ\) , следователно, в правоъгълник \(\триъгълник HOC\) : \[\mathrm(tg)\,30^\circ=\dfrac(HC)(OC)\quad\Rightarrow\quad HC=\dfrac1(\sqrt3).\]След това от правоъгълник \(\триъгълник ACH\) : \[\cos\angle \alpha=\cos\angle ACH=\dfrac(HC)(AC)=\dfrac13 \quad\Rightarrow\quad \cos^(-1)\alpha=3.\]

Отговор: 3

Задача 4 #2910

Ниво на задачата: По-трудно от изпита

Равнините \(\pi_1\) и \(\pi_2\) се пресичат по правата \(l\) , която съдържа точките \(M\) и \(N\) . Отсечките \(MA\) и \(MB\) са перпендикулярни на правата \(l\) и лежат съответно в равнините \(\pi_1\) и \(\pi_2\) и \(MN = 15 \) , \(AN = 39\) , \(BN = 17\) , \(AB = 40\) . Намерете \(3\cos\alpha\) , където \(\alpha\) е ъгълът между равнините \(\pi_1\) и \(\pi_2\) .

Триъгълникът \(AMN\) е правоъгълен, \(AN^2 = AM^2 + MN^2\) , откъдето \ Триъгълникът \(BMN\) е правоъгълен, \(BN^2 = BM^2 + MN^2\) , откъдето \ Записваме косинусовата теорема за триъгълника \(AMB\): \ Тогава \ Тъй като ъгълът \(\alpha\) между равнините е остър ъгъли \(\angle AMB\) е тъп, тогава \(\cos\alpha=\dfrac5(12)\) . Тогава \

Отговор: 1,25

Задача 5 #2911

Ниво на задачата: По-трудно от изпита

\(ABCDA_1B_1C_1D_1\) е паралелепипед, \(ABCD\) е квадрат със страна \(a\) , точка \(M\) е основата на перпендикуляра, пуснат от точката \(A_1\) към равнината \ ((ABCD)\) , освен това \(M\) е пресечната точка на диагоналите на квадрата \(ABCD\) . Известно е, че \(A_1M = \dfrac(\sqrt(3))(2)a\). Намерете ъгъла между равнините \((ABCD)\) и \((AA_1B_1B)\) . Дайте отговора си в градуси.

Построяваме \(MN\) перпендикулярно на \(AB\), както е показано на фигурата.

Тъй като \(ABCD\) е квадрат със страна \(a\) и \(MN\perp AB\) и \(BC\perp AB\) , тогава \(MN\паралел BC\) . Тъй като \(M\) е пресечната точка на диагоналите на квадрата, тогава \(M\) е средната точка на \(AC\) , следователно \(MN\) е средната линия и \(MN=\frac12BC=\frac(1)(2)a\).
\(MN\) е проекцията на \(A_1N\) върху равнината \((ABCD)\) и \(MN\) е перпендикулярна на \(AB\) , тогава, съгласно теоремата за трите перпендикуляра, \( A_1N\) е перпендикулярна на \(AB \) и ъгълът между равнините \((ABCD)\) и \((AA_1B_1B)\) е \(\ъгъл A_1NM\) .
\[\mathrm(tg)\, \angle A_1NM = \dfrac(A_1M)(NM) = \dfrac(\frac(\sqrt(3))(2)a)(\frac(1)(2)a) = \sqrt(3)\qquad\Rightarrow\qquad\angle A_1NM = 60^(\circ)\]

Отговор: 60

Задача 6 #1854

Ниво на задачата: По-трудно от изпита

В квадрата \(ABCD\) : \(O\) е пресечната точка на диагоналите; \(S\) не е в равнината на квадрата, \(SO \perp ABC\) . Намерете ъгъла между равнините \(ASD\) и \(ABC\), ако \(SO = 5\) и \(AB = 10\) .

Правоъгълните триъгълници \(\триъгълник SAO\) и \(\триъгълник SDO\) са равни по две страни и ъгълът между тях (\(SO \perp ABC\) \(\Rightarrow\) \(\ъгъл SOA = \ъгъл SOD = 90^\circ\); \(AO = DO\) , защото \(O\) е пресечната точка на диагоналите на квадрата, \(SO\) е обща страна) \(\Rightarrow\) \(AS = SD\) \(\Rightarrow\) \(\триъгълник ASD\) е равнобедрен. Точката \(K\) е средата на \(AD\) , тогава \(SK\) е височината в триъгълника \(\triangle ASD\) и \(OK\) е височината в триъгълника \ (AOD\) \(\ Rightarrow\) равнина \(SOK\) е перпендикулярна на равнините \(ASD\) и \(ABC\) \(\Rightarrow\) \(\angle SKO\) е линеен ъгъл, равен до необходимия двустенен ъгъл.

В \(\триъгълник SKO\): \(OK = \frac(1)(2)\cdot AB = \frac(1)(2)\cdot 10 = 5 = SO\)\(\Rightarrow\) \(\triangle SOK\) е равнобедрен правоъгълен триъгълник \(\Rightarrow\) \(\angle SKO = 45^\circ\) .

Отговор: 45

Задача 7 #1855

Ниво на задачата: По-трудно от изпита

В квадрата \(ABCD\) : \(O\) е пресечната точка на диагоналите; \(S\) не е в равнината на квадрата, \(SO \perp ABC\) . Намерете ъгъла между равнините \(ASD\) и \(BSC\), ако \(SO = 5\) и \(AB = 10\) .

Правоъгълните триъгълници \(\триъгълник SAO\) , \(\триъгълник SDO\) , \(\триъгълник SOB\) и \(\триъгълник SOC\) са равни по две страни и ъгълът между тях (\(SO \perp ABC \) \(\Стрелка надясно\) \(\angle SOA = \angle SOD = \angle SOB = \angle SOC = 90^\circ\); \(AO = OD = OB = OC\) , защото \(O\) е пресечната точка на диагоналите на квадрата, \(SO\) е общата страна) \(\Rightarrow\) \(AS = DS = BS = CS\) \(\Rightarrow\) \(\триъгълник ASD\) и \(\триъгълник BSC\) са равнобедрени. Точката \(K\) е средата на \(AD\) , тогава \(SK\) е височината в триъгълника \(\triangle ASD\) и \(OK\) е височината в триъгълника \ (AOD\) \(\ Стрелка надясно\) равнината \(SOK\) е перпендикулярна на равнината \(ASD\) . Точката \(L\) е средата на \(BC\) , тогава \(SL\) е височината в триъгълника \(\triangle BSC\) и \(OL\) е височината в триъгълника \ (BOC\) \(\ Rightarrow\) равнината \(SOL\) (известна още като равнината \(SOK\) ) е перпендикулярна на равнината \(BSC\) . Така получаваме, че \(\angle KSL\) е линеен ъгъл, равен на желания двустенен ъгъл.

\(KL = KO + OL = 2\cdot OL = AB = 10\)\(\Стрелка надясно\) \(OL = 5\) ; \(SK = SL\) – равни височини равнобедрени триъгълници, което може да се намери с помощта на Питагоровата теорема: \(SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50\). Вижда се, че \(SK^2 + SL^2 = 50 + 50 = 100 = KL^2\)\(\Rightarrow\) за триъгълник \(\triangle KSL\) обратна теоремаПитагор \(\Rightarrow\) \(\triangle KSL\) – правоъгълен триъгълник \(\Rightarrow\) \(\angle KSL = 90^\circ\) .

Отговор: 90

Подготовката на учениците за изпита по математика като правило започва с повторение на основните формули, включително тези, които ви позволяват да определите ъгъла между равнините. Въпреки факта, че този раздел от геометрията е разгледан достатъчно подробно в рамките на училищна програма, много възпитаници трябва да повторят основния материал. Разбирайки как да намерят ъгъла между равнините, учениците от гимназията ще могат бързо да изчислят правилния отговор в хода на решаването на задачата и да разчитат на получаване на прилични резултати въз основа на единния държавен изпит.

Основни нюанси

За да не създава трудности въпросът как да намерите двустенния ъгъл, препоръчваме ви да следвате алгоритъма за решение, който ще ви помогне да се справите със задачите на изпита.

Първо трябва да определите линията, по която се пресичат равнините.

След това на тази линия трябва да изберете точка и да нарисувате два перпендикуляра към нея.

Следващата стъпка е да се намери тригонометричната функция на двустенния ъгъл, който се образува от перпендикулярите. Най-удобно е да направите това с помощта на получения триъгълник, част от който е ъгълът.

Отговорът ще бъде стойността на ъгъла или неговата тригонометрична функция.

Подготовката за изпитния тест заедно с Школково е ключът към вашия успех

По време на час предишния ден преминаване на изпитамного студенти са изправени пред проблема с намирането на определения и формули, които ви позволяват да изчислите ъгъла между 2 равнини. Училищният учебник не винаги е под ръка точно когато е необходим. И да намериш необходимите формулии примери за тяхното правилно приложение, включително намиране на ъгъла между равнините в интернет онлайн, понякога отнема много време.

Математически портал "Школково" предлага нов подходза подготовка за държавен изпит. Класовете на нашия уебсайт ще помогнат на учениците да идентифицират най-трудните секции за себе си и да запълнят пропуските в знанията.

Подготвихме и ясно представихме всички необходими материали. Основни определенияи формулите са представени в раздела "Теоретичен справочник".

За по-добро усвояване на материала предлагаме също да практикувате съответните упражнения. Голям избор от задачи различни степенисложност, например на, е представена в раздела "Каталог". Всички задачи съдържат подробен алгоритъм за намиране на верния отговор. Списъкът с упражнения на сайта непрекъснато се допълва и актуализира.

Упражнявайки се в решаването на задачи, в които се изисква да се намери ъгъл между две равнини, учениците имат възможност да запазят всяка задача онлайн в „Любими“. Благодарение на това те ще могат да се върнат при него. необходимо количествопъти и обсъдете хода на своето решение с учител в училищеили учител.