Основни теореми на динамиката. Общи теореми на динамиката

Лекция 3 Общи теореми на динамиката

Динамика на системата от материални точкие важен раздел на теоретичната механика. Тук основно разглеждаме проблемите на движението на механични системи (системи от материални точки) с крайно числостепени на свобода - максималният брой независими параметри, които определят положението на системата. основната задачасистемна динамика - изследване на законите на движение на твърдо тяло и механични системи.

Най-простият подход за изследване на движението на система, състоящ се от нматериални точки, се свежда до разглеждане на движенията на всяка отделна точка от системата. В този случай трябва да се определят всички сили, действащи върху всяка точка на системата, включително силите на взаимодействие между точките.

Определяйки ускорението на всяка точка в съответствие с втория закон на Нютон (1.2), получаваме за всяка точка три скаларни диференциални закона на движение от втори ред, т.е. 3 н диференциален закон на движение за цялата система.

Да се намерят уравненията на движението механична системаполучени зададени сили и начални условия за всяка точка от системата диференциални законитрябва да се интегрира. Тази задача е трудна дори в случай на две материални точки, които се движат само под действието на сили на взаимодействие съгласно закона за всеобщото привличане (задача на две тела), и изключително трудна в случай на три взаимодействащи точки (задача на три тела ).

Следователно е необходимо да се намерят такива методи за решаване на проблеми, които да доведат до разрешими уравнения и да дадат представа за движението на механична система. Общите теореми на динамиката, като следствие от диференциалните закони на движение, позволяват да се избегне сложността, която възниква по време на интегрирането, и да се получат необходимите резултати.

3.1 Общи бележки

Точките на механичната система ще бъдат номерирани с индекси аз, й, ки т.н., които преминават през всички стойности 1, 2, 3… н, където н е броят на системните точки. Физически величини, свързани с кточката се обозначават със същия индекс като точката. Например те изразяват съответно радиус вектора и скоростта к-та точка.

Във всяка една от точките на системата действат сили с два произхода: първо, сили, чиито източници са извън системата, т.нар. външенсили и се обозначава с ; второ, сили от други точки на тази система, т.нар вътрешнисили и се обозначава с . Вътрешните сили отговарят на третия закон на Нютон. Помислете за най-простите свойства на вътрешните сили, действащи върху цялата механична система във всяко от нейните състояния.

Първи имот. Геометричната сума на всички вътрешни сили на системата (основният вектор на вътрешните сили) е равна на нула.

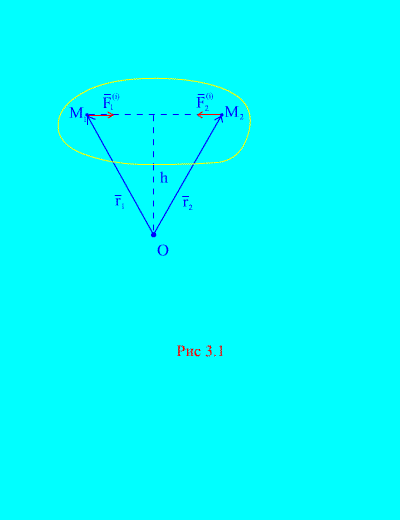
Наистина, ако разгледаме произволни две точки от системата, например и (фиг. 3.1), тогава за тях , защото силите на действие и противодействие винаги са равни по абсолютна стойност, действат по една линия на действие в противоположна посока, която свързва взаимодействащите точки. Следователно основният вектор на вътрешните сили се състои от двойки сили на взаимодействащи точки

(3.1)

Втори имот. Геометричната сума на моментите на всички вътрешни сили спрямо произволна точка в пространството е нула.

Разгледайте системата от моменти на силите и по отношение на точката О(фиг. 3.1). от (фиг. 3.1). това е ясно

защото и двете сили имат еднакви рамена и противоположни посоки на векторни моменти. Основният момент на вътрешните сили около точката Осе състои от векторната сума на такива изрази и е равна на нула. Следователно,

Нека външни и вътрешни силидействащи върху механична система, състояща се от нточки (фиг. 3.2). Ако резултантната на външни сили и резултантната на всички вътрешни сили се приложат към всяка точка на системата, тогава за всяка кточка на системата, могат да се съставят диференциални уравнения на движение. Общо такива уравнения ще бъдат н:

и в проекции върху фиксирани координатни оси 3 н:

(3.4)

Векторни уравнения (3.3) или еквивалентни скаларни уравнения (3.4) представляват диференциалните закони на движение на материалните точки на цялата система. Ако всички точки се движат успоредно на една равнина или една права линия, тогава броят на уравненията (3.4) в първия случай ще бъде 2 н, във втория н.

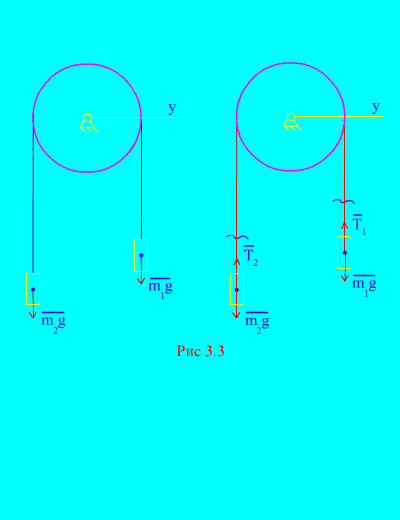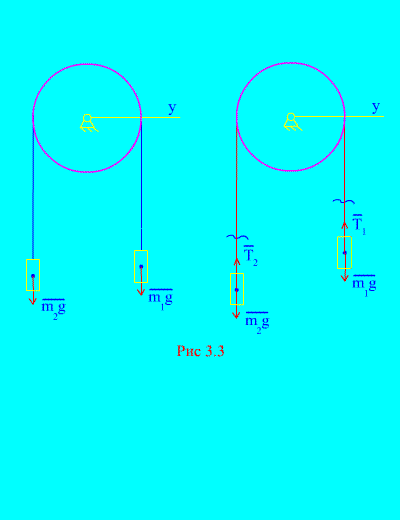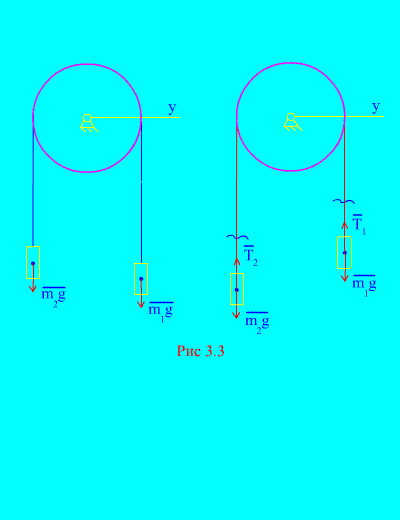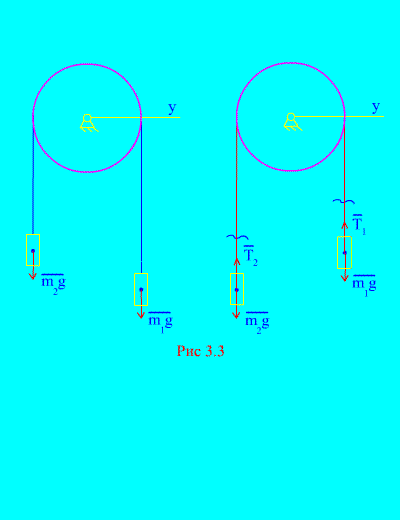
Пример 1Два товара с маса и са свързани помежду си с неразтеглив кабел, хвърлен върху блок (фиг. 3.3). Пренебрегвайки силите на триене, както и масата на блока и кабела, определят закона за движение на стоките и напрежението на кабела.

Решение. Системата се състои от две материални тела (свързани с неразтеглив кабел), движещи се успоредно на една ос Х.Нека запишем диференциалните закони на движение в проекции върху оста хза всеки.

Оставете дясната тежест да се спусне с ускорение, след което лявата тежест ще се издигне с ускорение. Мислено се освобождаваме от връзката (кабела) и я заместваме с реакции и (фиг. 3.3). Приемайки, че телата са свободни, ще съставим диференциалните закони на движение в проекцията върху оста х(което означава, че напреженията на нишката са вътрешни сили, а теглото на товарите са външни):

Тъй като и (телата са свързани с неразтеглив кабел), получаваме

Решаване на тези уравнения за ускорението и опъна на въжето T, получаваме

Обърнете внимание, че напрежението на кабела при не е равно на гравитацията на съответния товар.

3. 2. Теоремата за движението на центъра на масата

Известно е, че твърдо тяло и механична система в равнина могат да се движат доста трудно. До първата теорема за движението на тяло и механична система може да се стигне по следния начин: изпуснете в.-л. обект, състоящ се от много твърди тела, закрепени заедно. Ясно е, че ще лети по парабола. Това беше разкрито при изучаване на движението на точка. Сега обаче обектът не е точка. Той се върти, люлее се в процеса на летене около някакъв ефективен център, който се движи по парабола. Първа теорема за движение трудни предметиказва, че определен ефективен център е центърът на масата на движещ се обект. Центърът на масата не е задължително да се намира в самото тяло, той може да лежи някъде извън него.

Теорема. Центърът на масата на механична система се движи като материална точка с маса равна на масатацялата система, към която се прилагат всички външни сили, действащи върху системата.

За да докажем теоремата, пренаписваме диференциалните закони на движение (3.3) в следната форма:

(3.5)

където н е броят на системните точки.

Нека съберем уравненията заедно член по член:

(а)

Положението на центъра на масата на механичната система спрямо избраната координатна система се определя по формула (2.1): където Ме масата на системата. След това се записва лявата страна на равенството (a).

Първата сума, стояща от дясната страна на равенството (а), е равна на главния вектор на външните сили, а последната, по свойството на вътрешните сили, е равна на нула. Тогава равенството (a), като се вземе предвид (b), ще бъде пренаписано

, (3.6)

тези. произведението на масата на системата и ускорението на нейния център на маса е равно на геометрична сумавсички външни сили, действащи върху системата.

От уравнение (3.6) следва, че вътрешните сили не влияят пряко на движението на центъра на масата. Въпреки това, в някои случаи те са причина за появата на външни сили, приложени към системата. По този начин вътрешните сили, които въртят задвижващите колела на автомобила, причиняват действието върху него на външна сила на сцепление, приложена към джантата.

Пример 2Механизмът, разположен във вертикална равнина, е монтиран върху хоризонтална гладка равнина и е прикрепен към нея с пръти, здраво закрепени към повърхността. Да сеи Л (фиг. 3.4).

Диск 1 радиус Рнеподвижен. Диск 2 маса ми радиус r закопчава се с манивела, дълж Р+ rв точката От 2. Манивела се върти постоянно

ъглова скорост. AT начален моментманивелата заема правилното хоризонтално положение. Пренебрегвайки масата на манивелата, определете максималните хоризонтални и вертикални сили, действащи върху прътите, ако общо теглолегло и колело 1 е равно на М.Също така вземете предвид поведението на механизма при липса на решетки.

Решение. Системата се състои от две маси ( н=2 ): неподвижен диск 1 с рамка и подвижен диск 2. Нека насочим оста припрез центъра на тежестта на неподвижния диск вертикално нагоре, оста х- заедно хоризонтална равнина.

Записваме теоремата за движението на центъра на масата (3.6) в координатна форма

Външните сили на тази система са: теглото на рамката и неподвижния диск - мг, тегло на подвижния диск мг, - общата хоризонтална реакция на болтовете, - нормалната обща реакция на самолета. Следователно,

След това законите на движение (b) се пренаписват

Нека изчислим координатите на центъра на масата на механичната система:

; (G)

както се вижда от (фиг. 3.4), , , (ъгъл на въртене на манивелата), . Заместване на тези изрази в (r) и изчисляване на вторите производни по отношение на времето Tот , , получаваме това

д)

Замествайки (c) и (e) в (b), намираме

Хоризонталното налягане, действащо върху прътите, има най-голямо и най-малка стойност, кога cos = 1 съответно, т.е.

Налягането на механизма върху хоризонталната равнина има най-високи и най-ниски стойности, когато грях съответно, т.е.

Всъщност първият проблем на динамиката е решен: съгласно известните уравнения на движение на центъра на масата на системата (e), силите, участващи в движението, се възстановяват.

При липса на решетки Ки Л (фиг. 3.4), механизмът може да започне да подскача над хоризонталната равнина. Това ще стане, когато , т.е. когато , следва, че ъгловата скорост на въртене на манивелата, при която механизмът отскача, трябва да удовлетворява равенството

3. 3. Закон за запазване на движението на центъра на масата

Ако главният вектор на външните сили, действащи върху системата, е равен на нула, т.е. , след това от(3.6)следва, че ускорението на центъра на масата е нула, следователно скоростта на центъра на масата е постоянна по големина и посока. Ако, по-специално, в началния момент центърът на масата е в покой, то той е в покой през цялото време, докато главният вектор на външните сили стане равен на нула.

От тази теорема следват няколко следствия.

· Вътрешните сили сами по себе си не могат да променят характера на движението на центъра на масата на системата.

· Ако главният вектор на външните сили, действащи върху системата, е равен на нула, тогава центърът на масата е в покой или се движи равномерно и праволинейно.

· Ако проекцията на главния вектор на външните сили на системата върху някаква фиксирана ос е равна на нула, тогава проекцията на скоростта на центъра на масата на системата върху тази ос не се променя.

· Няколко сили, приложени към твърдо тяло, не могат да променят движението на неговия център на масата (те могат само да накарат тялото да се върти около центъра на масата).

Нека разгледаме пример, илюстриращ закона за запазване на движението на центъра на масата.

Пример 3Две тежести с маси и са свързани с неразтеглива нишка, хвърлена върху блок (фиг. 3.5), фиксирани на клин с маса М.Клинът лежи върху гладка хоризонтална равнина. Първоначално системата беше в покой. Намерете изместването на клина по равнината, когато първият товар се спусне на височина Н.Игнорирайте масата на блока и нишката.

Решение.Външните сили, действащи върху клина заедно с тежестите, са силите на гравитацията и мг, както и нормална реакциягладка хоризонтална повърхност N. Следователно,

Тъй като системата е била в покой в началния момент, имаме .

Нека изчислим координатата на центъра на масата на системата в и в момента T 1 когато теглото на товара жспуснете се на височина з.

За момент:

където , , Х- съответно координатите на центъра на масата на товари с тегло g, g и тегло на клин Мж.

Да приемем, че клинът в момента се движи в положителната посока на оста волпо количеството Лако теглото на товара падне на височина Н.След това за момент

защото товарите заедно с клина ще се преместят към Лнадясно, тежестта ще се премести на разстояние нагоре по клина. Тъй като , след изчисления получаваме

3.4. Количество на системата за движение

3.4.1. Изчисляване на импулса на система

Инерцията на материална точка е векторна величина, равно на произведениетомаса на точка върху нейния вектор на скоростта

Единица за измерване на количеството движение -

Импулсът на механичната система се нарича векторна сума от импулсите на отделните точки на системата, т.е.

където н е броят на системните точки.

Импулсът на механична система може да бъде изразен чрез масата на системата Ми скоростта на центъра на масата. Наистина ли,

тези. импулсът на системата е равен на произведението от масата на цялата система и скоростта на нейния център на масата.Посоката е същата като посоката (фиг. 3.6)

В проекции върху правоъгълни оси имаме

където , , - проекции на скоростта на центъра на масата на системата.

Тук Ме масата на механичната система; не се променя, докато системата се движи.

Особено удобно е тези резултати да се използват при изчисляване на моментите на твърди тела.

От формула (3.7) може да се види, че ако една механична система се движи по такъв начин, че нейният център на масата остава неподвижен, тогава импулсът на системата остава равен на нула.

3.4.2. Елементарен и пълен импулс

Действието на сила върху материална точка във времето дтможе да се характеризира с елементарен импулс. Общ импулс на сила във времето T, или импулс на сила , се определя по формулата

или в проекции върху координатите на оста

(3.8a)

Единицата импулс на сила е.

3.4.3. Теорема за промяната на импулса на системата

Нека към точките на системата са приложени външни и вътрешни сили. Тогава за всяка точка от системата можем да приложим диференциалните закони на движение (3.3), като имаме предвид, че :

Сумирайки всички точки на системата, получаваме

По свойството на вътрешните сили и по определение ние имаме

(3.9)

Умножавайки двете страни на това уравнение по дт, получаваме теорема за промяната на импулса в диференциална форма:

, (3.10)

тези. диференциалът на импулса на механичната система е равен на векторната сума на елементарните импулси на всички външни сили, действащи върху точките на механичната система.

Изчисляване на интеграла на двете части на (3.10) за време от 0 до T, получаваме теоремата в крайна или интегрална форма

(3.11)

В проекции върху координатните оси ще имаме

Промяна в импулса на механична система във времетоT, е равна на векторната сума на всички импулси на външни сили, действащи върху точките на механичната система за едно и също време.

Пример 4Натоварване на маса м слизане на наклонена равнинаот покой под действието на сила Е, пропорционално на времето: , където (фиг. 3.7). Каква е скоростта на тялото след T секунди след началото на движението, ако коефициентът на триене при плъзгане на товара върху наклонената равнина е равен на f.

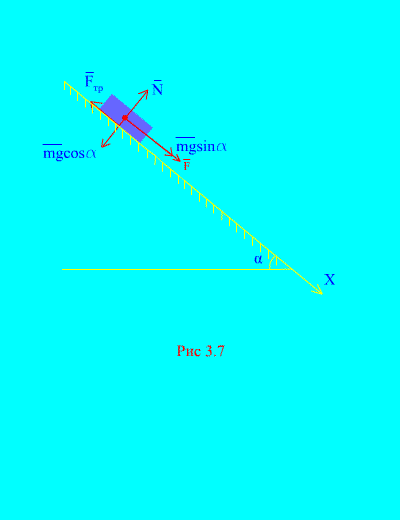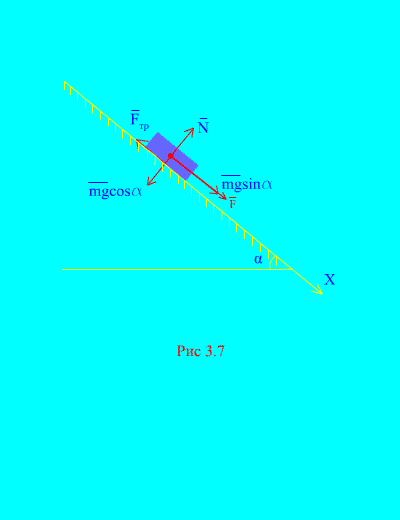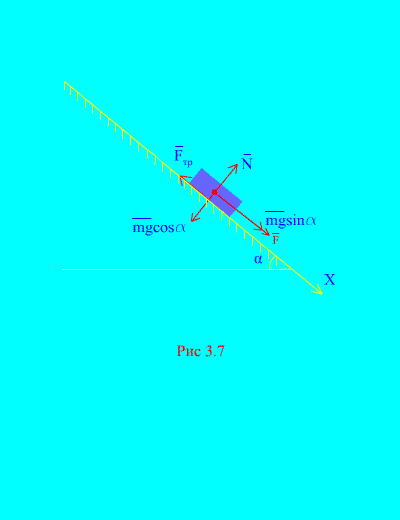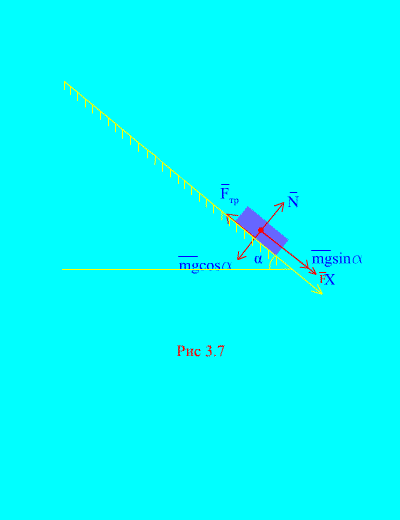
Решение.Нека изобразим силите, приложени към товара: мг - тежестта на товара, не нормалната реакция на равнината, е силата на триене при плъзгане на товара върху равнината и . Посоката на всички сили е показана в (фиг. 3.7).

Нека насочим оста хнадолу по наклонена равнина. Нека напишем теоремата за промяната на импулса (3.11) в проекцията върху оста х:

(а)

По условие, защото в началния момент товарът е бил в покой. Сумата от проекциите на импулсите на всички сили върху оста x е

Следователно,

3.4.4. Закони за запазване на импулса

Законите за запазване се получават като специални случаи на теоремата за промяна на импулса. Възможни са два специални случая.

· Ако векторната сума на всички външни сили, приложени към системата, е равна на нула, т.е. , то следва от теоремата (3.9) , Какво ,

тези. ако главният вектор на външните сили на системата е равен на нула, тогава импулсът на системата е постоянен по големина и посока.

· Ако проекцията на главния вектор на външните сили върху който и да е координатна осе равно на нула, например О, т.е. , тогава проекцията на количеството движение върху тази ос е постоянна.

Помислете за пример за прилагане на закона за запазване на импулса.

Пример 5Балистичното махало е тяло с маса, окачено на дълга нишка (фиг. 3.8).

Куршум от маса, движещ се със скорост Vи попадайки в неподвижно тяло, се забива в него и тялото се отклонява. Каква беше скоростта на куршума, ако тялото се издигна на височина ч ?

Решение.Оставете тялото със заседналия куршум да придобие скорост. След това, използвайки закона за запазване на импулса при взаимодействието на две тела, можем да напишем .

Скоростта може да се изчисли с помощта на закона за запазване механична енергия . Тогава . В резултат на това намираме

Пример 6. Водата влиза в фиксиран канал (фиг. 3.9)променлив участък със скорост под ъгъл спрямо хоризонта; квадрат напречно сечениеканал на входа; скоростта на водата при изхода на канала и сключва ъгъл с хоризонта.

Определете хоризонталния компонент на реакцията, която водата упражнява върху стените на канала. Плътност на водата .

Решение.Ще определим хоризонталния компонент на реакцията, упражнявана от стените на канала върху водата. Тази сила е равна по абсолютна стойност и противоположен по знак на желаната сила. Имаме, съгласно (3.11a),

. (а)

Изчисляваме масата на обема на течността, влизаща в канала за времето t:

Извиква се стойността на rAV 0 втора маса - масата на течността, протичаща през който и да е участък на тръбата за единица време.

Едно и също количество вода напуска канала за същото време. В условието са дадени началната и крайната скорост.

Изчислете правилната странаравенство (а), което определя сумата от проекциите върху хоризонталната ос на външни сили, приложени към системата (вода). Единствената хоризонтална сила е хоризонталният компонент на резултантната реакция на стените R x. Тази сила е постоянна по време на равномерното движение на водата. Ето защо

. (в)

Замествайки (b) и (c) в (a), получаваме

3.5. Кинетичен момент на системата

3.5.1. Главен момент на импулса на системата

Нека е радиус вектор на точка с масата на системата спрямо някаква точка A, наречена център (фиг. 3.10).

Момент на импулса (кинетичен момент) на точка спрямо центъра Анаречен вектор , определена по формулата

. (3.12)

В този случай векторът насочена перпендикулярно на равнината, минаваща през центъра НОи вектор .

Момент на импулс (кинетичен момент) на точка около оссе нарича проекция върху тази ос на ъгловия момент на точката спрямо който и да е център, избран на тази ос.

Основният момент на импулса (кинетичен момент) на системата спрямо центъра Асе нарича количеството

(3.13)

Основният момент на импулса (кинетичен момент) на системата около остасе нарича проекцията върху тази ос на главния момент на импулса на системата спрямо всеки избран върху дадения централна ос.

3.5.2. Импулс на въртящо се твърдо тяло около оста на въртене

Съвместима фиксирана точка Отяло, лежащо върху оста на въртене Оz, с началото на координатната система Охуz, чиито оси ще се въртят с тялото (фиг. 3.11). Нека е радиус-вектор на точката на тялото спрямо началото на координатите, неговите проекции върху осите ще бъдат означени с , , . Векторни проекции ъглова скоросттела на същите оси ще бъдат означени с 0, 0, ().

Доста често е възможно да се разграничи важни характеристикидвижение на механична система, без да се прибягва до интегриране на системата от диференциални уравнения на движение. Това се постига чрез прилагане на общите теореми на динамиката.

5.1. Основни понятия и определения

Външни и вътрешни сили.Всяка сила, действаща върху точка в механична система, непременно е едно от двете активна сила, или реакция на връзка. Целият набор от сили, действащи върху точките на системата, може да бъде разделен на два класа по различен начин: на външни сили и вътрешни сили (долни индекси e и i - от латински думи externus – външен и internus – вътрешен). Външни сили се наричат сили, действащи върху точки на системата от точки и тела, които не са част от разглежданата система. Силите на взаимодействие между точките и телата на разглежданата система се наричат вътрешни.

Това разделение зависи от това какви материални точки и тела са включени от изследователя в разглежданата механична система. Ако съставът на системата се разшири, за да включва допълнителни точки и тела, тогава някои сили, които са били външни за предишната система, могат да станат вътрешни за разширената система.

Свойства на вътрешните сили.Тъй като тези сили са сили на взаимодействие между частите на системата, те са включени в цялостната система от вътрешни сили в "две", организирани в съответствие с аксиомата действие-реакция. Всяко такова "две" сили

главен вектор и Основната точкаспрямо произволен център са равни на нула. Тъй като цялостната система от вътрешни сили се състои само от "двойки", тогава

1) основният вектор на системата от вътрешни сили е равен на нула,

2) основният момент на системата от вътрешни сили спрямо произволна точка е равен на нула.

Масата на системата е аритметична сумамаса mk на всички точки и тела, образуващи системата:

център на тежестта(център на инерция) на механична система се нарича геометрична точка C, чийто радиус вектор и координати се определят по формулите

където са радиус-векторите и координатите на точките, които образуват системата.

За твърдо тяло в еднородно гравитационно поле позициите на центъра на масата и центъра на тежестта съвпадат, в други случаи това са различни геометрични точки.

Заедно с инерциалната отправна система, често се разглежда едновременно неинерциална отправна система, движеща се напред. Неговите координатни оси (оси на Koenig) са избрани така, че референтната точка C винаги да съвпада с центъра на масата на механичната система. В съответствие с дефиницията центърът на масата е фиксиран в осите на Koenig и се намира в началото на координатите.

Инерционният момент на систематаоколо оста се нарича скаларен равно на суматапроизведенията на масите mk на всички точки от системата по квадратите на техните разстояния до оста:

Ако механичната система е твърдо тяло, за да намерите 12, можете да използвате формулата

където е плътността, обемът, зает от тялото.

Да разгледаме движението на определена система от материални обеми спрямо фиксирана координатна система.Когато системата не е свободна, тогава тя може да се счита за свободна, ако отхвърлим ограниченията, наложени на системата и заменим тяхното действие със съответните реакции.

Нека разделим всички сили, приложени към системата, на външни и вътрешни; и двете могат да включват реакции на изхвърляне

връзки. Означаваме с и главния вектор и главния момент на външните сили спрямо точка А.

1. Теорема за промяната на импулса.Ако е импулсът на системата, тогава (вижте)

т.е. теоремата е валидна: производната по време на импулса на системата е равна на главния вектор на всички външни сили.

Заменяйки вектора чрез неговия израз, където е масата на системата, е скоростта на центъра на масата, на уравнение (4.1) може да се даде различна форма:

Това равенство означава, че центърът на масата на системата се движи като материална точка, чиято маса е равна на масата на системата и към която е приложена сила, геометрично равна на главния вектор на всички външни сили на системата. Последното твърдение се нарича теорема за движението на центъра на масата (центъра на инерцията) на системата.

Ако тогава от (4.1) следва, че векторът на импулса е постоянен по големина и посока. Проектирайки го върху координатната ос, получаваме три скаларни първи интеграла на диференциалните уравнения на двойната верига на системата:

Тези интеграли се наричат интеграли на импулса. Когато скоростта на центъра на масата е постоянна, т.е. той се движи равномерно и праволинейно.

Ако проекцията на главния вектор на външните сили върху която и да е ос, например върху оста, е равна на нула, тогава имаме един първи интеграл или ако две проекции на главния вектор са равни на нула, тогава има два интеграла на импулса.

2. Теорема за изменението на кинетичния момент.Нека A е произволна точка в пространството (движеща се или неподвижна), която не е задължително да съвпада с някоя конкретна материална точка на системата през цялото време на движение. Неговата скорост във фиксирана система от координати ще бъде обозначена с Теорема за промяната на ъгловия момент материална системапо отношение на точка А има формата

Ако точка А е фиксирана, тогава равенството (4.3) приема по-проста форма:

Това равенство изразява теоремата за промяната на ъгловия момент на системата по отношение на фиксирана точка: производната по време на ъгловия момент на системата, изчислена по отношение на някаква фиксирана точка, е равна на главния момент на всички външни сили по отношение на тази точка.

Ако тогава, съгласно (4.4), векторът на ъгловия момент е постоянен по големина и посока. Проектирайки го върху координатната ос, получаваме скаларните първи интеграли на диференциалните уравнения на движението на системата:

Тези интеграли се наричат интеграли на ъгловия момент или интеграли на площите.

Ако точка А съвпада с центъра на масата на системата, тогава първият член от дясната страна на равенството (4.3) изчезва и теоремата за промяната на ъгловия момент има същия вид (4.4), както в случая на фиксирана точка A. Забележете (вижте 4 § 3), че в разглеждания случай абсолютният ъглов импулс на системата от лявата страна на равенство (4.4) може да бъде заменен с равен ъглов импулс на системата при нейното движение спрямо центъра на масата.

Нека е някаква постоянна ос или ос с постоянна посока, минаваща през центъра на масата на системата, и нека е ъгловият импулс на системата спрямо тази ос. От (4.4) следва, че

където е моментът на външните сили спрямо оста. Ако през цялото време на движение, тогава имаме първия интеграл

В трудовете на С. А. Чаплигин бяха получени няколко обобщения на теоремата за промяната на ъгловия момент, които след това бяха приложени при решаването на редица проблеми за търкалянето на топки. Допълнителни обобщения на теоремата за промяната на кпнетологичния момент и техните приложения в проблемите на динамиката на твърдо тяло се съдържат в трудовете. Основните резултати от тези работи са свързани с теоремата за промяната на ъгловия момент спрямо движещия се, постоянно преминаващ през някаква движеща се точка А. Нека - единичен векторнасочена по тази ос. Умножавайки скаларно по двете страни на равенството (4.3) и добавяйки члена към двете му части, получаваме

Когато кинематичното условие е изпълнено

уравнение (4.5) следва от (4.7). И ако условието (4.8) е изпълнено през цялото време на движение, тогава първият интеграл (4.6) съществува.

Ако връзките на системата са идеални и позволяват въртене на системата като твърдо тяло около оста и в броя на виртуалните премествания, тогава основният момент на реакциите около оста и е равен на нула, а след това стойността на дясната страна на уравнение (4.5) е главният момент на всички външни активни сили около оста и . Равенството на нула на този момент и изпълнимостта на отношението (4.8) ще бъде в разглеждания случай достатъчни условияза съществуването на интеграла (4.6).

Ако посоката на оста и е непроменена, тогава условието (4.8) може да се запише като

Това равенство означава, че проекциите на скоростта на центъра на масата и скоростта на точка А върху оста и върху равнината, перпендикулярна на нея, са успоредни. В работата на С. А. Чаплигин вместо (4.9) се изисква по-малко от общо състояниекъдето X е произволна константа.

Забележете, че условие (4.8) не зависи от избора на точка върху . Наистина, нека P е произволна точка на оста. Тогава

и следователно

В заключение отбелязваме геометричната интерпретация на Resal на уравнения (4.1) и (4.4): векторите абсолютни скоростикраищата на векторите и са равни съответно на главния вектор и главния момент на всички външни сили спрямо точка А.

МИНИСТЕРСТВО НА ЗЕМЕДЕЛИЕТО И ХРАНИТЕ НА РЕПУБЛИКА БЕЛАРУС

Образователна институция „БЕЛОРУСКИ ДЪРЖАВЕН АГРАР

ТЕХНИЧЕСКИ УНИВЕРСИТЕТ"

Катедра "Теоретична механика и теория на механизмите и машините".

ТЕОРЕТИЧНА МЕХАНИКА

методически комплекс за студенти от групата специалности

74 06 Аграрна техника

В 2 части Част 1

UDC 531.3(07) LBC 22.213ya7 T 33

съставен от:

Кандидат на физико-математическите науки, доцент Ю. С. Биза, канд технически науки, доц. Н. Л. Ракова, старши преподавателI. А. Тарасевич

Рецензенти:

Катедрата по теоретична механика на образователната институция „Беларуски национален Технически университет" (глава

Катедра "Теоретична механика" БНТУ Доктор на физико-математическите науки, професор А. В. Чигарев);

Водещ научен сътрудник на лаборатория "Виброзащита на механични системи" Държавна научна институция "Съединен институт по машиностроене

Национална академия на науките на Беларус”, кандидат на техническите науки, доцент А. М. Гоман

Теоретична механика. Раздел "Динамика": образователен

Метод Т33. комплекс. В 2 ч. Част 1 / съст.: Ю. С. Биза, Н. Л. Ракова, И. А. Тарасевич. - Минск: BGATU, 2013. - 120 с.

ISBN 978-985-519-616-8.

AT учебно-методически комплекспредставя материали за изучаване на раздел "Динамика", част 1, който е част от дисциплината "Теоретична механика". Включва курс от лекции, основни материали за изпълнение практически упражнения, задачи и образци на задачи за самостоятелна работа и контрол учебни дейностина пълен работен ден и формуляри за кореспонденцияизучаване на.

УДК 531.3(07) LBC 22.213я7


ВЪВЕДЕНИЕ ................................................. .........................................
1. НАУЧНО-ТЕОРЕТИЧНО СЪДЪРЖАНИЕ НА ОБРАЗОВАНИЕТО
НА МЕТОДИЧЕСКИЯ КОМПЛЕКС .............................................. ..
1.1. Терминологичен речник................................................. ................................
1.2. Теми на лекциите и тяхното съдържание ............................................ .. ..
Глава 1. Въведение в динамиката. Основни понятия
класическа механика ................................................. .................. ....................
Тема 1. Динамика на материална точка..................................... ....
1.1. Закони на динамиката на материалната точка
(закони на Галилей - Нютон) ............................................ ... ..........
1.2. Диференциални уравнениядвижения

1.3. Две основни задачи на динамиката ............................................. .............


Тема 2. Динамика на относителното движение
материална точка ................................................ ................ .........................
Въпроси за преглед ................................................ .................. .............
Тема 3. Динамика на механична система ............................................ ....
3.1. Геометрия на масата. Център на масата на механична система......
3.2. Вътрешни сили ................................................. .................. .................
Въпроси за преглед ................................................ .................. .............
Тема 4. Инерционни моменти на твърдо тяло .......................................
4.1. Инерционни моменти на твърдо тяло
спрямо оста и полюса ............................................. ...................... .....
4.2. Теорема за инерционните моменти на твърдо тяло
относно успоредните оси
(теорема на Хюйгенс-Щайнер) ............................................ .. ....
4.3. Центробежни инерционни моменти ................................................. .
Въпроси за преглед ................................................ .................. ............
Глава 2

Тема 5. Теорема за движението на центъра на масата на системата ...............................
Въпроси за преглед ................................................ .................. .............
Задачи за самоподготовка ............................................. .......
Тема 6. Количеството на движение на материална точка
и механична система ............................................. ................ ...................
6.1. Количество на движение на материална точка 43
6.2. Импулс на сила ................................................. .........................
6.3. Теорема за промяната на импулса
материална точка ................................................ ................ ....................
6.4. Теорема за промяна на главния вектор
импулс на механична система .............................................
Въпроси за преглед ................................................ .................. .............
Задачи за самоподготовка ............................................. .......
Тема 7. Инерционен момент на материална точка
и механична система спрямо центъра и оста .................................
7.1. Момент на импулс на материална точка
спрямо центъра и оста ............................................. .................. ..........
7.2. Теорема за промяната на ъгловия момент
материална точка спрямо центъра и оста .......................
7.3. Теорема за промяната на кинетичния момент
механична система спрямо центъра и оста .................................
Въпроси за преглед ................................................ .................. .............
Задачи за самоподготовка ............................................. .......
Тема 8. Работа и сила на силите ............................................ ... .........
Въпроси за преглед ................................................ .................. .............
Задачи за самоподготовка ............................................. .......
Тема 9. Кинетична енергия на материална точка
и механична система ............................................. ................ ...................
9.1. Кинетична енергия на материална точка
и механична система. Теорема на Кьониг.....................................
9.2. Кинетична енергия на твърдо тяло
с различни движения ................................................. ................... .............
9.3. Теорема за промяна кинетична енергия
материална точка ................................................ ................ ....................

9.4. Теорема за промяна на кинетичната енергия
механична система ................................................ .................. ................
Въпроси за преглед ................................................ .................. .............
Задачи за самоподготовка ............................................. .......
Тема 10. Потенциално силово поле
и потенциална енергия ................................................. ................ .................
Въпроси за преглед ................................................ .................. .............
Тема 11. Динамика на твърдо тяло.................................................. .......... .........
Въпроси за преглед ................................................ .................. .............
2. МАТЕРИАЛИ ЗА КОНТРОЛ
ПО МОДУЛ................................................ ... ...................................

САМОСТОЯТЕЛНА РАБОТА НА УЧЕНИЦИТЕ ..............................
4. ИЗИСКВАНИЯ КЪМ ПРОЕКТИРАНЕТО НА УПРАВЛЕНИЕТО
РАБОТИ ЗА СТУДЕНТИ РЕДОВНА И ЗАДОННА
ФОРМИ НА ОБУЧЕНИЕ ................................................. ................. .........................
5. СПИСЪК С ПОДГОТОВИТЕЛНИ ВЪПРОСИ
КЪМ ИЗПИТ (УЧЕНИЕ) НА СТУДЕНТИ
РЕДОВНА И ЗАДОСТНА ОБУЧЕНИЕ................................................. ......
6. СПИСЪК НА ЛИТЕРАТУРАТА .................................................. .. ............

ВЪВЕДЕНИЕ

Теоретична механика - наука за общите закони механично движение, равновесие и взаимодействие на материалните тела.

Това е една от фундаменталните общонаучни физико-математически дисциплини. Това е теоретичната основа на съвременната технология.

Изучаването на теоретичната механика, заедно с други физико-математически дисциплини, допринася за разширяване на научните хоризонти, формира способността за конкретизиране и абстрактно мисленеи допринася за повишаване на общата техническа култура на бъдещия специалист.

Теоретичната механика е научната основа на всичко технически дисциплини, допринася за развитието на уменията рационални решения инженерни задачисвързани с експлоатацията, ремонта и проектирането на селскостопански и мелиоративни машини и съоръжения.

Според характера на разглежданите задачи механиката се разделя на статика, кинематика и динамика. Динамиката е раздел от теоретичната механика, който изучава движението на материалните тела под действието на приложени сили.

AT учебно-методическикомплекс (UMK) представя материали за изучаване на раздела "Динамика", който включва курс от лекции, основни материали за провеждане практическа работа, задачи и образци на изпълнение за самостоятелна работаи контрол на учебната дейност на редовните задочни студенти.

AT в резултат на изучаването на раздела "Динамика" ученикът трябва да научи теоретична основадинамика и овладяване на основните методи за решаване на проблеми на динамиката:

Познава методи за решаване на задачи от динамиката, общи теореми на динамиката, принципи на механиката;

Да може да определя законите на движение на тялото в зависимост от силите, действащи върху него; прилагат законите и теоремите на механиката за решаване на проблеми; определят статичните и динамичните реакции на връзките, които ограничават движението на телата.

В учебния план на дисциплината „Теоретична механика” е предвиден общ хорариум – 136 часа, в т. ч. 36 часа за изучаване на раздел „Динамика”.

1. НАУЧНО И ТЕОРЕТИЧНО СЪДЪРЖАНИЕ НА УЧЕБНО-МЕТОДИЧЕСКИ КОМПЛЕКС

1.1. Терминологичен речник

Статиката е раздел от механиката, който очертава общото учение за силите, изучава се намаляването сложни системисили до най-проста форма и се установяват условията на равновесие различни системисили.

Кинематиката е дял от теоретичната механика, в който се изучава движението на материални обекти, независимо от причините, които причиняват това движение, т.е. независимо от силите, действащи върху тези обекти.

Динамиката е раздел от теоретичната механика, който изучава движението на материални тела (точки) под действието на приложени сили.

Материална точка- материално тяло, чиято разлика в движението на точките е незначителна.

Масата на тялото е скаларна положителна стойност, която зависи от количеството материя, съдържащо се в дадено тяло, и определя неговата мярка за инерция при движение напред.

Референтна система - координатна система, свързана с тялото, по отношение на която се изучава движението на друго тяло.

инерционна система- система, в която са изпълнени първият и вторият закон на динамиката.

Импулсът на силата е векторна мярка за действието на силата за известно време.

Количество движение на материална точка е векторната мярка на нейното движение, която е равна на произведението на масата на точката и вектора на нейната скорост.

Кинетична енергияе скаларна мярка за механично движение.

Елементарна работа на силатае безкрайно малка скаларна стойност, равна на точков продуктвектор на силата към вектора на безкрайно малкото преместване на точката на приложение на силата.

Кинетична енергияе скаларна мярка за механично движение.

Кинетичната енергия на материална точка е скалар

положителна стойност, равна на половината от произведението на масата на точка и квадрата на нейната скорост.

Кинетичната енергия на механична система е аритме-

кинетичната сума на кинетичните енергии на всички материални точки на тази система.

Силата е мярка за механичното взаимодействие на телата, характеризираща неговата интензивност и посока.

1.2. Теми на лекциите и тяхното съдържание

Раздел 1. Въведение в динамиката. Основни понятия

класическа механика

Тема 1. Динамика на материална точка

Законите на динамиката на материалната точка (законите на Галилей - Нютон). Диференциални уравнения на движение на материална точка. Две основни задачи на динамиката за материална точка. Решение на втората задача на динамиката; интеграционни константи и тяхното определяне от начални условия.

Литература:, с. 180-196, , с. 12-26.

Тема 2. Динамика на относителното движение на материала

Относително движение на материална точка. Диференциални уравнения на относително движение на точка; преносими и Кориолисови инерционни сили. Принципът на относителността в класическата механика. Случай на относителна почивка.

Литература: , с. 180-196, , с. 127-155.

Тема 3. Геометрия на масите. Център на масата на механична система

Маса на системата. Центърът на масата на системата и неговите координати.

Литература:, с. 86-93, с. 264-265

Тема 4. Инерционни моменти на твърдо тяло

Инерционни моменти на твърдо тяло спрямо оста и полюса. Радиус на инерция. Теорема за инерционните моменти относно успоредни оси. Осови моменти на инерция на някои тела.

Центробежните инерционни моменти като характеристика на асиметрията на тялото.

Литература: , с. 265-271, , с. 155-173.

Раздел 2. Общи теореми за динамиката на материална точка

и механична система

Тема 5. Теорема за движението на центъра на масата на системата

Теорема за движението на центъра на масата на системата. Следствия от теоремата за движението на центъра на масата на системата.

Литература: , с. 274-277, , с. 175-192.

Тема 6. Количеството на движение на материална точка

и механична система

Количеството на движение на материална точка и механична система. Елементарен импулс и импулс на сила за краен период от време. Теорема за изменението на импулса на точка и система в диференциална и интегрална форма. Закон за запазване на импулса.

Литература: , с. 280-284, , с. 192-207.

Тема 7. Инерционен момент на материална точка

и механична система спрямо центъра и оста

Моментът на импулса на точка спрямо центъра и оста. Теорема за промяната на ъгловия момент на точка. Кинетичен момент на механична система спрямо центъра и оста.

Ъгловият импулс на въртящо се твърдо тяло около оста на въртене. Теорема за промяната на кинетичния момент на системата. Закон за запазване на импулса.

Литература: , с. 292-298, , с. 207-258.

Тема 8. Работа и мощност на силите

Елементарна работа на силата, нейното аналитично изражение. Работата на силата на окончателен път. Работа на гравитацията, еластична сила. Равенство на нула на сумата от работата на вътрешните сили, действащи в твърдо тяло. Работата на силите, приложени към твърдо тяло, въртящо се около фиксирана ос. Мощност. Ефективност.

Литература: , с. 208-213, , с. 280-290.

Тема 9. Кинетична енергия на материална точка

и механична система

Кинетична енергия на материална точка и механична система. Изчисляване на кинетичната енергия на твърдо тяло в различни случаи на неговото движение. Теорема на Кьониг. Теорема за изменението на кинетичната енергия на точка в диференциална и интегрална форма. Теорема за изменението на кинетичната енергия на механична система в диференциална и интегрална форма.

Литература: , с. 301-310, , с. 290-344.

Тема 10. Потенциално силово поле и потенциал

Концепцията за силово поле. Потенциално силово поле и силова функция. Работата на сила върху окончателното преместване на точка в потенциално силово поле. Потенциална енергия.

Литература: , с. 317-320, , с. 344-347.

Тема 11. Динамика на твърдото тяло

Диференциални уравнения на постъпателното движение на твърдо тяло. Диференциално уравнение въртеливо движениетвърдо тяло около фиксирана ос. физическо махало. Диференциални уравнения на равнинно движение на твърдо тяло.

Литература: , с. 323-334, , с. 157-173.

Раздел 1. Въведение в динамиката. Основни понятия

класическа механика

материално тяло- тяло, което има маса.

Материална точка- материално тяло, чиято разлика в движението на точките е незначителна. Това може да бъде или тяло, чиито размери могат да бъдат пренебрегнати по време на движението му, или тяло с крайни размери, ако се движи напред.

Частиците се наричат още материални точки, на които мислено се разделя твърдото тяло при определяне на някои от неговите динамични характеристики. Примери за материални точки (фиг. 1): а - движението на Земята около Слънцето. Земята е материална точка; b е постъпателното движение на твърдо тяло. Твърди- майка-

al точка, тъй като V B \u003d V A; a B = a A; c - въртене на тялото около оста.

Частицата на тялото е материална точка.

Инерцията е свойството на материалните тела да променят по-бързо или по-бавно скоростта на своето движение под действието на приложени сили.

Масата на тялото е скаларна положителна стойност, която зависи от количеството материя, съдържащо се в дадено тяло, и определя неговата мярка за инерция по време на транслационно движение. В класическата механика масата е константа.

Сила - количествена мяркамеханично взаимодействие между телата или между тяло (точка) и поле (електрическо, магнитно и др.).

Силата е векторна величина, характеризираща се с големина, точка на приложение и посока (линия на действие) (фиг. 2: A - точка на приложение; AB - линия на действие на силата).

Ориз. 2

В динамиката, наред с постоянните сили, има и променливи сили, които могат да зависят от времето t, скоростта ϑ, разстоянието r или от комбинация от тези величини, т.е.

F = const;

F = F(t);

F = F(ϑ) ;

F = F(r);

F = F(t, r, ϑ ) .


Примери за такива сили са показани на фиг. 3: а			- телесно тегло;
	(ϑ) – сила на съпротивление на въздуха; b −	Т =	- теглителна сила

електрически локомотив; c − F = F (r) е силата на отблъскване от центъра O или привличане към него.

Инерциална система е система, в която са изпълнени първият и вторият закон на динамиката. Това е неподвижна координатна система или система, движеща се равномерно и праволинейно.

Движението в механиката е промяна в положението на тялото в пространството и времето по отношение на други тела.

Пространството в класическата механика е триизмерно, подчинявайки се на евклидовата геометрия.

Времето е скаларна величина, която тече по един и същ начин във всяка референтна система.

Система от единици е набор от мерни единици физични величини. За измерване на всички механични величини са достатъчни три основни единици: единици за дължина, време, маса или сила.




Механични	Измерение	Нотация	Измерение	Нотация
величина
			сантиметър



	килограм-

Всички други мерни единици на механични величини са производни на тях. Използват се два вида системи от единици: международна система SI единици (или по-малки - CGS) и техническата система от единици - MKGSS.

Тема1. Динамика на материалната точка

1.1. Законите на динамиката на материалната точка (законите на Галилей - Нютон)

Първият закон (на инерцията).

изолиран от външни влиянияматериалната точка поддържа състоянието си на покой или се движи равномерно и праволинейно, докато приложените сили не я принудят да промени това състояние.

Движението, извършено от точка при липса на сили или под действието на балансирана система от сили, се нарича движение по инерция.

Например движението на тяло по гладка (силата на триене е нула) движение-

хоризонтална повърхност (фиг. 4: G - телесно тегло; N - нормална реакция на самолета).

Тъй като G = − N , тогава G + N = 0.

Когато ϑ 0 ≠ 0 тялото се движи със същата скорост; при ϑ 0 = 0 тялото е в покой (ϑ 0 е началната скорост).

Втори закон (основен закон на динамиката).

Произведението от масата на дадена точка и ускорението, което тя получава под действието на дадена сила, е равно по абсолютна стойност на тази сила, а посоката й съвпада с посоката на ускорението.

а б

Математически този закон се изразява чрез векторно равенство

За F = const,

a = const - движението на точката е равномерно. ЕС-

дали a ≠ const, α

- бавно движение (фиг. 5, но);

a ≠ const,

а -

– ускорено движение (фиг. 5, б) m – точкова маса;

вектор на ускорението;

– векторна сила; ϑ 0 е векторът на скоростта).

При F = 0,a 0 = 0 = ϑ 0 = const - точката се движи равномерно и праволинейно или при ϑ 0 = 0 - тя е в покой (законът за инерцията). Второ

законът ви позволява да установите връзка между масата m на тяло, разположено в близост земната повърхност, а теглото му G .G = mg , където g е

ускорение на гравитацията.

Третият закон (законът за равенството на действието и реакцията). Две материални точки действат една върху друга с равни по големина сили, насочени по правата, свързваща ги

тези точки в противоположни посоки.

Тъй като силите F 1 = − F 2 са приложени към различни точки, тогава системата от сили (F 1 , F 2 ) не е уравновесена, т.е. (F 1 , F 2 )≈ 0 (фиг. 6).

На свой ред

m a = m a

- поведение

масите на взаимодействащите точки са обратно пропорционални на техните ускорения.

Четвъртият закон (законът за независимостта на действието на силите). Ускорението, получено от точка под действието на едновременно

но няколко сили, е равна на геометричната сума от тези ускорения, които една точка би получила при действието на всяка сила поотделно върху нея.

Обяснение (фиг. 7).

t a n

a 1 a kF n

Резултантните R сили (F 1 ,...F k ,...F n ) .

Тъй като ma = R ,F 1 = ma 1 , ...,F k = ma k , ...,F n = ma n , тогава

a = a 1 + ...+ a k + ...+ a n = ∑ a k , т.е. четвъртият закон е еквивалентен на

k = 1

правилото за добавяне на сили.

1.2. Диференциални уравнения на движение на материална точка

Нека няколко сили действат едновременно върху материална точка, сред които има както постоянни, така и променливи.

Записваме втория закон на динамиката във формата

= ∑

(T ,

k = 1

, ϑ=

r е радиус векторът на движението

точка, тогава (1.2) съдържа производни на r и е диференциално уравнение на движението на материална точка във векторна форма или основното уравнение на динамиката на материална точка.

Проекции на векторно равенство (1.2): - върху оста на декартовите координати (фиг. 8, а)

max=md
max=md	= ∑Fkx;
	k = 1
май=мр
май=мр	= ∑Fky;	(1.3)
	k = 1

maz=m	= ∑Fkz;
maz=m	= ∑Fkz;
	k = 1

По естествената ос (фиг. 8, б)


мат				= ∑ Fk τ ,
мат				= ∑ Fk τ ,
				k = 1

				= ∑ F k n ;
				k = 1

mab = m0 = ∑ Fk b

k = 1

M t oM oa

b на o

Уравнения (1.3) и (1.4) са диференциални уравнения на движение на материална точка в декартовите координатни оси и естествените оси, съответно, т.е. естествени диференциални уравнения, които обикновено се използват за криволинейно движение на точка, ако траекторията на точката и неговият радиус на кривина е известен.

1.3. Два основни проблема на динамиката за материална точка и тяхното решение

Първата (пряка) задача.

Познавайки закона за движение и масата на точката, определете силата, действаща върху точката.

За да разрешите тази задача, трябва да знаете ускорението на точката. В задачи от този тип може да се уточни директно или да се уточни законът за движение на точка, в съответствие с който тя да се определи.

1. Така че, ако движението на точка е дадено в декартови координати

x \u003d f 1 (t) , y \u003d f 2 (t) и z \u003d f 3 (t), тогава се определят проекциите на ускорението

върху координатната ос x =

d2x

d2y

d2z

И тогава - проект-

F x , F y и F z сили върху тези оси:

,k ) = F F z . (1.6)

2. Ако точката се ангажира криволинейно движениеи законът на движение е известен s = f (t), траекторията на точката и нейният радиус на кривина ρ, тогава

удобно е да се използват естествени оси, а проекциите на ускорението върху тези оси се определят от добре известните формули:

Тангенциална ос

a τ = d ϑ = d 2 2 s – тангенциално ускорение;dt dt

HomeNormal

ds 2

a n = ϑ 2 = dt е нормално ускорение.

Проекцията на ускорението върху бинормалата е нула. След това проекциите на силата върху естествените оси

F=m			F=m

Модулът и посоката на силата се определят по формулите:

F \u003d F τ 2 + F n 2; защото (

; защото (

Втората (обратна) задача.

Познавайки силите, действащи върху точката, нейната маса и начални условиядвижение, определят закона на движение на точка или всяка друга нейна кинематична характеристика.

Началните условия за движение на точка в декартовите оси са координатите на точката x 0, y 0, z 0 и проекцията на началната скорост ϑ 0 върху тях

оси ϑ 0 x \u003d x 0, ϑ 0 y \u003d y 0 и ϑ 0 z \u003d z 0 в момента, съответстващ на

дава началото на движението на точката и се приема за нула. Решаването на задачи от този тип се свежда до съставяне на диференциал

диференциални уравнения (или едно уравнение) на движението на материална точка и тяхното последващо решение чрез директна интеграцияили използване на теорията на диференциалните уравнения.

Въпроси за преглед

1. Какво изучава динамиката?

2. Какъв вид движение се нарича инерционно?

3. При какво условие една материална точка ще бъде в покой или ще се движи равномерно и праволинейно?

4. Каква е същността на първия основен проблем за динамиката на материална точка? Втора задача?

5. Запишете естествените диференциални уравнения на движението на материална точка.

Задачи за самоподготовка

1. Точка с маса m = 4 kg се движи по хоризонтална права с ускорение a = 0,3 t. Определете модула на силата, действаща върху точката по посока на нейното движение в момент t = 3 s.

2. Част с маса m = 0,5 kg се плъзга по тавата. Под какъв ъгъл спрямо хоризонталната равнина трябва да бъде разположена тавата, така че частта да се движи с ускорение a = 2 m / s 2? Ъгъл експрес

в градуси.

3. Точка с маса m = 14 kg се движи по оста Ox с ускорение a x = 2 t . Определете модула на силата, действаща върху точката по посока на движението в момент t = 5 s.

(МЕХАНИЧНИ СИСТЕМИ) - IV вариант

1. Основното уравнение на динамиката на материална точка, както е известно, се изразява с уравнението . Диференциални уравнения на движението произволни точкина несвободна механична система според два начина на разделяне на силите може да се запише в две форми:

(1) , където k=1, 2, 3, … , n е броят точки на материалната система.

(2)

където е масата на k-тата точка; - радиус-вектор на k-та точка, - дадена (активна) сила, действаща върху k-та точка, или резултат от всички активни сили, действащи върху k-та точка. - резултантната на силите на реакция на връзките, действащи в k-та точка; - равностойна на вътрешни сили, действащи върху k-та точка; - резултантната на външните сили, действащи върху k-тата точка.

Уравнения (1) и (2) могат да се използват за решаване както на първия, така и на втория проблем на динамиката. Решението на втория проблем на динамиката на системата обаче става много сложно не само с математическа точкавизия, но и защото сме изправени пред фундаментални трудности. Те се състоят в това, че както за система (1), така и за система (2) броят на уравненията е значителен по-малко от числонеизвестен.

Така че, ако използваме (1), тогава известното за втората (обратна) задача на динамиката ще бъде и , а неизвестните ще бъдат и . Векторните уравнения ще бъдат " н“, а неизвестен – „2n”.

Ако изхождаме от системата от уравнения (2), тогава известните и част от външните сили . Защо част? Факт е, че броят на външните сили включва външни реакциивръзки, които са неизвестни. Освен това ще има и неизвестни.

Така и системата (1), и системата (2) са ОТВОРЕНИ. Трябва да добавим уравнения, като вземем предвид уравненията на отношенията и може би все още трябва да наложим някои ограничения на самите отношения. Какво да правя?

Ако изхождаме от (1), тогава можем да следваме пътя на съставяне на уравненията на Лагранж от първи вид. Но този начин не е рационален, защото по-лесна задача(по-малко степени на свобода), толкова по-трудно е да се реши от гледна точка на математиката.

Тогава нека обърнем внимание на системата (2), където - винаги са неизвестни. Първата стъпка в решаването на системата е да се премахнат тези неизвестни. Трябва да се има предвид, че по правило не се интересуваме от вътрешните сили по време на движението на системата, тоест когато системата се движи, не е необходимо да знаем как се движи всяка точка от системата, но е достатъчно, за да знаете как се движи системата като цяло.

По този начин, ако различни начиниизключване от системата (2) неизвестни сили, тогава получаваме някои отношения, т.е. някои Основни характеристикиза системата, чието познаване позволява да се прецени как се движи системата като цяло. Тези характеристики се въвеждат с помощта на т.нар общи теореми на динамиката. Има четири такива теореми:

1. Теорема за движение на центъра на масата на механичната система;

2. Теорема за промяна в импулса на механична система;

3. Теорема за промяна в ъгловия момент на механична система;

4. Теорема за промяна в кинетичната енергия на механична система.