Площта на триъгълник е Питагоровата теорема. Различни начини за доказване на Питагоровата теорема: примери, описание и прегледи
Кога за първи път сте започнали да изучавате квадратни корени и как да ги решавате ирационални уравнения(равенства, съдържащи неизвестното под знака за корен), вероятно сте получили първата представа за тях практическа употреба. Възможността за извличане Корен квадратенна числата е необходим и за решаване на задачи по прилагането на Питагоровата теорема. Тази теорема свързва дължините на страните на всеки правоъгълен триъгълник.
Нека дължините на катетите на правоъгълен триъгълник (тези две страни, които се събират под прав ъгъл) се обозначават с буквите и , а дължината на хипотенузата (най-дългата страна на триъгълника срещу прав ъгъл) ще бъдат обозначени с буквата . Тогава съответните дължини са свързани със следната връзка:
Това уравнение ви позволява да намерите дължината на страната на правоъгълен триъгълник, когато е известна дължината на другите му две страни. В допълнение, той ви позволява да определите дали разглежданият триъгълник е правоъгълен триъгълник, при условие че дължините на всички три партииизвестен предварително.
Решаване на задачи с помощта на Питагоровата теорема
За да консолидираме материала, ще решим следните задачи за приложението на Питагоровата теорема.

Така дадено:
- Дължината на един от краката е 48, хипотенузата е 80.
- Дължината на крака е 84, хипотенузата е 91.
Да стигнем до решението:
а) Заместването на данните в горното уравнение дава следните резултати:
48 2 + b 2 = 80 2
2304 + b 2 = 6400
b 2 = 4096
b= 64 или b = -64
Тъй като дължината на една страна на триъгълник не може да бъде изразена отрицателно число, втората опция автоматично се отхвърля.
Отговор на първата снимка: b = 64.
б) Дължината на катета на втория триъгълник се намира по същия начин:
84 2 + b 2 = 91 2
7056 + b 2 = 8281
b 2 = 1225
b= 35 или b = -35
Както в предишния случай, отрицателното решение се отхвърля.
Отговор на втората снимка: b = 35

Дадено ни е:
- Дължините на по-малките страни на триъгълника са съответно 45 и 55, а на по-големите са 75.
- Дължините на по-малките страни на триъгълника са съответно 28 и 45, а на по-големите са 53.
Решаваме проблема:
а) Необходимо е да се провери дали сумата от квадратите на дължините на по-малките страни на даден триъгълник е равна на квадрата на дължината на по-голямата:
45 2 + 55 2 = 2025 + 3025 = 5050
Следователно първият триъгълник не е правоъгълен.
б) Извършва се същата операция:
28 2 + 45 2 = 784 + 2025 = 2809
Следователно вторият триъгълник е правоъгълен триъгълник.
Първо намираме дължината най-дългия сегмент, образувана от точки с координати (-2, -3) и (5, -2). За това използваме известна формулаза намиране на разстоянието между точките в правоъгълна системакоординати:
По същия начин намираме дължината на отсечката, затворена между точките с координати (-2, -3) и (2, 1):
Накрая определяме дължината на сегмента между точки с координати (2, 1) и (5, -2):
Тъй като има равенство:
тогава съответният триъгълник е правоъгълен триъгълник.
По този начин можем да формулираме отговора на проблема: тъй като сумата от квадратите на страните с най-малка дължина е равна на квадрата на страната с най-голяма дължина, точките са върховете на правоъгълен триъгълник.
Основата (разположена строго хоризонтално), преградата (разположена строго вертикално) и кабелът (опънат диагонално) образуват съответно правоъгълен триъгълник, теоремата на Питагор може да се използва за намиране на дължината на кабела:
Така дължината на кабела ще бъде приблизително 3,6 метра.
Дадено: разстоянието от точка R до точка P (катета на триъгълника) е 24, от точка R до точка Q (хипотенуза) - 26.
И така, ние помагаме на Витя да реши проблема. Тъй като се предполага, че страните на триъгълника, показан на фигурата, образуват правоъгълен триъгълник, можете да използвате Питагоровата теорема, за да намерите дължината на третата страна:
И така, ширината на езерото е 10 метра.
Сергей Валериевич
Питагорова теорема
Питагорова теорема- една от основните теореми на евклидовата геометрия, установяваща връзката
между страните на правоъгълен триъгълник.
Смята се, че е доказано от гръцкия математик Питагор, на когото е кръстена.
Геометрична формулировка на Питагоровата теорема.
Първоначално теоремата е формулирана по следния начин:
В правоъгълен триъгълник площта на квадрата, построен върху хипотенузата, е равна на сумата от площите на квадратите,
изградени върху катетри.
Алгебрична формулировка на Питагоровата теорема.
В правоъгълен триъгълник квадратът на дължината на хипотенузата е равен на сумата от квадратите на дължините на катетите.
Тоест, обозначавайки дължината на хипотенузата на триъгълника през ° С, и дължините на краката през аи b:
И двете формулировки питагорови теоремиса еквивалентни, но втората формулировка е по-елементарна, не е така
изисква концепцията за площ. Тоест второто твърдение може да се провери, без да се знае нищо за района и
чрез измерване само на дължините на страните на правоъгълен триъгълник.
Обратната теорема на Питагор.
Ако квадратът на едната страна на триъгълник е равен на сумата от квадратите на другите две страни, тогава
триъгълникът е правоъгълен.
Или с други думи:
За всяка тройка положителни числа а, bи ° С, така че
има правоъгълен триъгълник с катети аи bи хипотенуза ° С.
Питагоровата теорема за равнобедрен триъгълник.

Питагорова теорема за равностранен триъгълник.

Доказателства на Питагоровата теорема.
Към момента в научната литература са записани 367 доказателства на тази теорема. Вероятно теоремата
Питагоровата теорема е единствената теорема с толкова впечатляващ брой доказателства. Такова разнообразие
може да се обясни само с фундаменталното значение на теоремата за геометрията.
Разбира се, концептуално всички те могат да бъдат разделени на малък брой класове. Най-известните от тях:
доказателство за метод на площта, аксиоматичени екзотични доказателства(например,
като се използва диференциални уравнения).
1. Доказателство на Питагоровата теорема от гледна точка на подобни триъгълници.
Следното доказателство на алгебричната формулировка е най-простото от конструираните доказателства
директно от аксиомите. По-специално, той не използва концепцията за площта на фигурата.
Позволявам ABCима правоъгълен триъгълник ° С. Нека начертаем височина от ° Си обозначават
нейната основа чрез з.
Триъгълник ACHподобен на триъгълник AB C на два ъгъла. По същия начин, триъгълникът CBHподобен ABC.
Чрез въвеждане на нотацията:

получаваме:
![]() ,
,
което съвпада -
Като фолдна а 2 и b 2, получаваме:
или , което трябваше да се докаже.
2. Доказателство на Питагоровата теорема по метода на площта.
Следващите доказателства, въпреки привидната си простота, изобщо не са толкова прости. Всички тях
използвайте свойствата на областта, чието доказателство е по-сложно от доказателството на самата питагорова теорема.
- Доказателство чрез равнодопълване.
 Подредете четири еднакви правоъгълни
Подредете четири еднакви правоъгълни
триъгълник, както е показано на снимката
на дясно.
Четириъгълник със страни ° С- квадрат,
тъй като сумата от два остри ъгъла е 90°, и
развитият ъгъл е 180°.
Площта на цялата фигура е, от една страна,
площ на квадрат със страна ( a+b), а от друга страна, сумата от площите четири триъгълникаи
![]()
![]()
Q.E.D.
3. Доказателство на Питагоровата теорема по метода на безкрайно малките.

Като се има предвид чертежът, показан на фигурата, и
гледам как се сменя странатаа, ние можем
напишете следната връзка за безкрайност
малък странични увеличенияси а(използвайки прилика
триъгълници):
Използвайки метода за разделяне на променливи, намираме:
По-общ израз за промяна на хипотенузата в случай на нарастване на двата крака:
Интегриране дадено уравнениеи използвайки началните условия, получаваме:
Така стигаме до желания отговор:
Както е лесно да се види, квадратичната зависимост в крайната формула се появява поради линейната
пропорционалност между страните на триъгълника и увеличенията, докато сумата е свързана с независимата
приноси от нарастването на различни крака.
Може да се получи по-просто доказателство, ако приемем, че един от краката не изпитва нарастване
(във този случайкрак b). Тогава за интеграционната константа получаваме:
(според папирус 6619 от Берлинския музей). Според Кантор арпедонаптите или „обтегачи на струни“ изграждат прави ъгли, използвайки правоъгълни триъгълници със страни 3, 4 и 5.
Много е лесно да се възпроизведе техният метод на изграждане. Нека вземем въже с дължина 12 m и го завържем за него по цветна лента на разстояние 3 m от единия край и 4 метра от другия. Между страните с дължина 3 и 4 метра ще бъде ограден прав ъгъл. Може да се възрази на харпедонаптите, че техният метод на конструиране става излишен, ако например се използва дървеният квадрат, използван от всички дърводелци. Наистина са известни египетски рисунки, в които се намира такъв инструмент - например рисунки, изобразяващи дърводелска работилница.
Сред вавилонците се знае малко повече за Питагоровата теорема. В един текст, датиращ от времето на Хамурапи, тоест до 2000 г. пр.н.е. д. , е дадено приблизително изчисление на хипотенузата на правоъгълен триъгълник. От това можем да заключим, че в Месопотамия са умеели да извършват изчисления с правоъгълни триъгълници, поне в някои случаи. Въз основа, от една страна, на сегашното ниво на познания за египетската и вавилонската математика, а от друга страна, на критично изследване на гръцките източници, ван дер Ваерден (холандски математик) заключава, че има голяма вероятност, че теоремата за квадрата на хипотенузата е известна в Индия още около 18 век пр.н.е. д.
Около 400 г. пр.н.е. д., според Прокъл, Платон дава метод за намиране на питагорови тройки, комбинирайки алгебра и геометрия. Около 300 г. пр.н.е. д. Елементите на Евклид съдържат най-старото аксиоматично доказателство на Питагоровата теорема.
Формулировка
Геометрична формулировка:
Първоначално теоремата е формулирана по следния начин:
Алгебрична формулировка:
Тоест, обозначавайки дължината на хипотенузата на триъгълника през и дължините на краката през и:
И двете формулировки на теоремата са еквивалентни, но втората формулировка е по-елементарна, не изисква понятието площ. Тоест, второто твърдение може да се провери, без да се знае нищо за площта и чрез измерване само на дължините на страните на правоъгълен триъгълник.
Обратна теорема на Питагор:
Доказателство за
Към момента в научната литература са записани 367 доказателства на тази теорема. Вероятно Питагоровата теорема е единствената теорема с толкова впечатляващ брой доказателства. Такова разнообразие може да се обясни само с фундаменталното значение на теоремата за геометрията.
Разбира се, концептуално всички те могат да бъдат разделени на малък брой класове. Най-известните от тях: доказателства по метода на площта, аксиоматични и екзотични доказателства (например с помощта на диференциални уравнения).
Чрез подобни триъгълници
Следното доказателство на алгебричната формулировка е най-простото от доказателствата, изградени директно от аксиомите. По-специално, той не използва понятието площ на фигурата.

Позволявам ABCима правоъгълен триъгълник ° С. Нека начертаем височина от ° Си обозначаваме основата му с з. Триъгълник ACHподобен на триъгълник ABCна два ъгъла. По същия начин, триъгълникът CBHподобен ABC. Въвеждане на нотацията
получаваме
Какво е еквивалентно
Добавяйки, получаваме
, което трябваше да се докажеПлощни доказателства
Следващите доказателства, въпреки привидната си простота, изобщо не са толкова прости. Всички те използват свойствата на площта, чието доказателство е по-сложно от доказателството на самата Питагорова теорема.
Доказателство чрез еквивалентност
- Подредете четири равни правоъгълни триъгълника, както е показано на фигура 1.
- Четириъгълник със страни ° Се квадрат, защото сборът от два остри ъгъла е 90°, а правият ъгъл е 180°.
- Площта на цялата фигура е равна, от една страна, на площта на квадрат със страна (a + b), а от друга страна, сумата от площите на четири триъгълника и площта на вътрешния квадрат.
Q.E.D.
Доказателството на Евклид
Идеята на доказателството на Евклид е следната: нека се опитаме да докажем, че половината от площта на квадрата, построен върху хипотенузата, е равна на сбора от половините площи на квадратите, построени върху краката, и след това площите на големият и двата малки квадрата са равни.
Разгледайте рисунката вляво. Върху него построихме квадрати от страните на правоъгълен триъгълник и начертахме лъч s от върха на прав ъгъл C, перпендикулярен на хипотенузата AB, той разрязва квадрата ABIK, построен върху хипотенузата, на два правоъгълника - BHJI и HAKJ , съответно. Оказва се, че площите на тези правоъгълници са точно равни на площите на квадратите, построени върху съответните крака.
Нека се опитаме да докажем, че площта на квадрата DECA е равна на площта на правоъгълника AHJK. За да направим това, използваме спомагателно наблюдение: Площта на триъгълник със същата височина и основа като дадената правоъгълник е равен на половината от площта на дадения правоъгълник. Това е следствие от определянето на площта на триъгълник като половината от произведението на основата и височината. От това наблюдение следва, че площта на триъгълника ACK е равна на площта на триъгълника AHK (не е показан), който от своя страна е равен на половината от площта на правоъгълника AHJK.
Нека сега докажем, че площта на триъгълника ACK също е равна на половината от площта на квадрата DECA. Единственото нещо, което трябва да се направи за това, е да се докаже равенството на триъгълниците ACK и BDA (тъй като площта на триъгълника BDA е равна на половината от площта на квадрата по горното свойство). Това равенство е очевидно: триъгълниците са равни по двете страни и ъгъла между тях. А именно - AB=AK, AD=AC - равенството на ъглите CAK и BAD е лесно да се докаже чрез метода на движението: нека завъртим триъгълника CAK на 90 ° обратно на часовниковата стрелка, тогава е очевидно, че съответните страни на двата разглеждани триъгълника ще съвпаднат (поради факта, че ъгълът при върха на квадрата е 90°).
Аргументът за равенството на лицата на квадрата BCFG и правоъгълника BHJI е напълно аналогичен.
Така доказахме, че площта на квадрата, построен върху хипотенузата, е сумата от площите на квадратите, построени върху краката. Идея това доказателстводопълнително илюстрирано с анимацията по-горе.
Доказателство за Леонардо да Винчи
Основните елементи на доказателството са симетрия и движение.
Помислете за чертежа, както се вижда от симетрията, сегментът разрязва квадрата на две еднакви части (тъй като триъгълниците и са равни по конструкция).
Използвайки завъртане обратно на часовниковата стрелка на 90 градуса около точката, виждаме равенството на защрихованите фигури и .
Сега е ясно, че площта на фигурата, която сме засенчили, е равна на сумата от половината площи на малки квадратчета (построени върху краката) и площта на оригиналния триъгълник. От друга страна, той е равен на половината от площта на големия квадрат (построен върху хипотенузата) плюс площта на оригиналния триъгълник. Така половината от сумата от площите на малките квадрати е равна на половината от площта на големия квадрат и следователно сумата от площите на квадратите, изградени върху краката, е равна на площта на квадрата, построен върху хипотенузата.
Доказателство по метода на безкрайно малките
Следното доказателство с помощта на диференциални уравнения често се приписва на добре познатите Английски математикХарди, живял през първата половина на 20 век.
Разглеждайки чертежа, показан на фигурата, и наблюдавайки промяната на страната а, можем да напишем следната връзка за безкрайно малки странични увеличения си а(с помощта на подобни триъгълници):
Използвайки метода на разделяне на променливите, намираме
По-общ израз за промяна на хипотенузата в случай на нарастване на двата катета
Интегрирайки това уравнение и използвайки началните условия, получаваме
Така стигаме до желания отговор
Както е лесно да се види, квадратичната зависимост в крайната формула се появява поради линейната пропорционалност между страните на триъгълника и увеличенията, докато сумата се дължи на независимите приноси от нарастването на различните катети.
Може да се получи по-просто доказателство, ако приемем, че един от краката не изпитва увеличение (в този случай кракът). Тогава за константата на интегриране, която получаваме
Вариации и обобщения
Подобни геометрични фигури от три страни
Обобщение за подобни триъгълници, площ на зелени фигури A + B = площ на сини C
Питагорова теорема, използваща подобни правоъгълни триъгълници
Обобщение на Питагоровата теорема е направено от Евклид в неговия труд Наченки, разширявайки площите на квадратите отстрани до площите на подобни геометрични форми :
Ако изградим подобни геометрични фигури (виж Евклидовата геометрия) върху страните на правоъгълен триъгълник, тогава сумата от двете по-малки фигури ще бъде равна на площта на по-голямата фигура.
Основната идея на това обобщение е, че площта на такава геометрична фигура е пропорционална на квадрата на всяко от нейните линейни измерения и по-специално на квадрата на дължината на всяка страна. Следователно, за подобни фигури с области А, би ° Сизградени от страни с дълж а, bи ° С, ние имаме:
Но според Питагоровата теорема, а 2 + b 2 = ° С 2, тогава А + б = ° С.
Обратно, ако можем да докажем това А + б = ° Сза три подобни геометрични фигури, без да използваме Питагоровата теорема, тогава можем да докажем самата теорема, преминавайки към обратна посока. Например началният централен триъгълник може да се използва повторно като триъгълник ° Свърху хипотенузата и два подобни правоъгълни триъгълника ( Аи б), построени върху другите две страни, които се образуват в резултат на разделянето на централния триъгълник по неговата височина. Сумата от двете по-малки площи на триъгълниците тогава очевидно е равна на площта на третата, по този начин А + б = ° Си, следвайки предишните доказателства в обратен ред, получаваме Питагоровата теорема a 2 + b 2 = c 2 .
Косинусова теорема
Питагоровата теорема е специален случайПовече ▼ обща теоремакосинус, който свързва дължините на страните в произволен триъгълник:
където θ е ъгълът между страните аи b.
Ако θ е 90 градуса, тогава cos θ = 0 и формулата е опростена до обичайната Питагорова теорема.
Произволен триъгълник
Към всеки избран ъгъл на произволен триъгълник със страни a, b, cвпишете равнобедрен триъгълник по такъв начин, че равни ъглив основата си θ е равно на избрания ъгъл. Да приемем, че избраният ъгъл θ е разположен срещу посочената страна ° С. В резултат на това получихме триъгълник ABD с ъгъл θ, който се намира срещу страната аи партита r. Вторият триъгълник е образуван от ъгъла θ, който е срещу страната bи партита сдълго с, както е показано на снимката. Сабит Ибн Кура твърди, че страните в тези три триъгълника са свързани по следния начин:
Когато ъгълът θ се доближи до π/2, основата равнобедрен триъгълникнамалява и двете страни r и s се припокриват все по-малко. Когато θ = π/2, ADB се превръща в правоъгълен триъгълник, r + с = ° Си получаваме първоначалната Питагорова теорема.
Нека да разгледаме един от аргументите. Триъгълник ABCима същите ъгли като триъгълник ABD, но в обратен ред. (Двата триъгълника имат общ ъгъл при върха B, и двата имат ъгъл θ и също имат същия трети ъгъл, чрез сумата от ъглите на триъгълника) Съответно ABC е подобно на отражението ABD на триъгълник DBA, както е показано в долната фигура. Нека напишем връзката между противоположни странии съседен на ъгъла θ,
Същото е и отражението на друг триъгълник,
Умножете дробите и добавете тези две съотношения:
Q.E.D.
Обобщение за произволни триъгълници чрез успоредници
Обобщение за произволни триъгълници,
зона на зелено парцел = площсин
Доказателство за тезата, че на фигурата по-горе
Нека направим по-нататъшно обобщение за неправоъгълни триъгълници, като използваме успоредници от три страни вместо квадрати. (квадратите са специален случай.) Горната фигура показва, че за остроъгълен триъгълникплощта на успоредника от дългата страна е равна на сбора от успоредниците от другите две страни, при условие че успоредникът от дългата страна е построен, както е показано на фигурата (размерите, отбелязани със стрелки, са еднакви и определете страните на долния успоредник). Тази замяна на квадрати с успоредници има ясна прилика с първоначалната Питагорова теорема и се смята, че е формулирана от Папус от Александрия през 4 г. сл. н. е. д.
Долната фигура показва напредъка на доказателството. Нека погледнем лявата страна на триъгълника. Левият зелен успоредник има същата площ като лявата страна на синия успоредник, защото имат една и съща основа bи височина ч. Освен това лявата зелена кутия има същата площ като лявата зелена кутия в горната снимка, защото те имат общо основание(горен лявата странатриъгълник) и общата височина, перпендикулярна на тази страна на триъгълника. Като се аргументираме по подобен начин за дясната страна на триъгълника, доказваме, че долният успоредник има същата площ като двата зелени успоредника.
Комплексни числа
Теоремата на Питагор се използва за намиране на разстоянието между две точки в декартова координатна система и тази теорема е вярна за всички истински координати: разстояние смежду две точки ( а, б) и ( c, d) се равнява
Няма проблеми с формулата, ако комплексните числа се третират като вектори с реални компоненти х + аз г = (х, г). . Например разстоянието смежду 0 + 1 ази 1 + 0 азизчислете като модул на вектора (0, 1) − (1, 0) = (−1, 1), или
Въпреки това, за операции с вектори със сложни координати е необходимо да се направи известно подобрение на формулата на Питагор. Разстояние между точки с комплексни числа (а, b) и ( ° С, д); а, b, ° С, и двсички са сложни, формулираме с помощта на абсолютни стойности. Разстояние сна база векторна разлика (а − ° С, b − д) в следната форма: нека разликата а − ° С = стр+i р, където стре истинската част от разликата, ре имагинерната част и i = √(−1). По същия начин нека b − д = r+i с. Тогава:
където е комплексно спрегнатото на . Например разстоянието между точките (а, b) = (0, 1) и (° С, д) = (аз, 0) , изчислете разликата (а − ° С, b − д) = (−аз, 1) и резултатът ще бъде 0, ако не се използват комплексни конюгати. Следователно, използвайки подобрената формула, получаваме
Модулът е дефиниран така:
Стереометрия
Значително обобщение на Питагоровата теорема за тримерното пространство е теоремата на де Гуа, наречена на J.-P. де Гуа: ако тетраедърът има прав ъгъл (както в куб), тогава квадратът на площта на лицето срещу правия ъгъл е равен на сумата от квадратите на площите на другите три лица. Това заключение може да се обобщи като " н-измерна питагорова теорема":
Теорема на Питагор триизмерно пространствосвързва диагонала AD с три страни.
Друго обобщение: Питагоровата теорема може да се приложи към стереометрията в следната форма. Обмисли кубоид, както е показано на снимката. Намерете дължината на диагонала BD, като използвате Питагоровата теорема:
където три страни образуват правоъгълен триъгълник. Използвайте хоризонталния диагонал BD и вертикалния ръб AB, за да намерите дължината на диагонала AD, като отново използвате Питагоровата теорема:
или, ако всичко е написано в едно уравнение:
Този резултат е 3D израз за определяне на големината на вектора v(диагонал AD), изразен чрез неговите перпендикулярни компоненти ( v k) (три взаимно перпендикулярни страни):
Това уравнение може да се разглежда като обобщение на Питагоровата теорема за многомерно пространство. Резултатът обаче всъщност не е нищо повече от многократното прилагане на Питагоровата теорема към поредица от правоъгълни триъгълници в последователно перпендикулярни равнини.
векторно пространство
В случай на ортогонална система от вектори има равенство, което се нарича още Питагорова теорема:
Ако е проекцията на вектора върху координатни оси, тогава тази формула съвпада с евклидовото разстояние - и означава, че дължината на вектора е равна на корена квадратна сумаквадрати на неговите компоненти.
Аналог на това равенство в случая безкрайна системавектори се нарича равенство на Парсевал.
Неевклидова геометрия
Питагоровата теорема е извлечена от аксиомите на евклидовата геометрия и всъщност не е валидна за неевклидовата геометрия във формата, в която е написана по-горе. (Тоест Питагоровата теорема се оказва един вид еквивалент на постулата на Евклид за паралелизъм) С други думи, в неевклидовата геометрия отношението между страните на триъгълника задължително ще бъде във форма, различна от Питагоровата теорема . Например в сферичната геометрия и трите страни на правоъгълен триъгълник (да речем а, bи ° С), които ограничават октанта (една осма) от единичната сфера, имат дължина π/2, което противоречи на Питагоровата теорема, защото а 2 + b 2 ≠ ° С 2 .
Разгледайте тук два случая на неевклидова геометрия - сферична и хиперболична геометрия; и в двата случая, както и за евклидовото пространство за правоъгълни триъгълници, резултатът, който замества Питагоровата теорема, следва от косинусовата теорема.
Питагоровата теорема обаче остава валидна за хиперболична и елиптична геометрия, ако изискването триъгълникът да е правоъгълен се замени с условието, че сборът от два ъгъла на триъгълника трябва да бъде равен на третия, да речем А+б = ° С. Тогава съотношението между страните изглежда така: сумата от площите на кръгове с диаметри аи bравна на площта на кръг с диаметър ° С.
сферична геометрия
За всеки правоъгълен триъгълник върху сфера с радиус Р(например, ако ъгълът γ в триъгълника е прав) със страни а, b, ° Сотношенията между страните ще изглеждат така:
Това равенство може да се изведе като специален случайсферична косинусова теорема, която е валидна за всички сферични триъгълници:
където cosh е хиперболичният косинус. Тази формула е специален случай на хиперболичната косинусова теорема, която е валидна за всички триъгълници:
където γ е ъгълът, чийто връх е срещу страната ° С.
където ж ijсе нарича метричен тензор. Може да бъде функция на позицията. Такива криволинейни пространства включват риманова геометрия като общ пример. Тази формулировка е подходяща и за евклидово пространство, когато се използват криволинейни координати. Например за полярни координати:
векторен продукт
Питагоровата теорема свързва два израза за големината на векторно произведение. Един подход за дефиниране на кръстосано произведение изисква той да отговаря на уравнението:
тази формула използва точковия продукт. Дясната страна на уравнението се нарича детерминанта на Грам за аи b, което е равно на площта на успоредника, образуван от тези два вектора. Въз основа на това изискване, както и на изискването векторното произведение да е перпендикулярно на неговите компоненти аи bследва, че с изключение на тривиалните случаи на 0- и 1-мерно пространство, векторният продукт е дефиниран само в три и седем измерения. Използваме дефиницията на ъгъла в н-измерително пространство:
това свойство на векторното произведение дава неговата стойност в следната форма:
Чрез основното тригонометрична идентичностПитагор, получаваме различна форма на запис на неговата стойност:
Алтернативен подход за дефиниране на кръстосано произведение използва израз за неговата величина. След това, аргументирайки се в обратен ред, получаваме връзка с скаларно произведение:
Вижте също
Бележки
- Историческа тема: Теоремата на Питагор във вавилонската математика
- ( , стр. 351) стр. 351
- ( , том I, стр. 144)
- Дискусия исторически фактидадено в (, стр. 351) стр. 351
- Курт фон Фриц (април 1945 г.). „Откриването на несъизмеримостта от Хипас от Метапонт“. Анали на математиката, втора серия(Анали на математиката) 46 (2): 242–264.
- Луис Карол, "Историята с възли", М., Мир, 1985 г., стр. 7
- Асгер АбоеЕпизоди от ранната история на математиката. - Mathematical Association of America, 1997. - P. 51. - ISBN 0883856131
- Предложение на Питагорот Елиша Скот Лумис
- на Евклид Елементи: Книга VI, Твърдение VI 31: „В правоъгълните триъгълници фигурата от страната, обхващаща правия ъгъл, е равна на подобните и подобно описани фигури от страните, съдържащи правия ъгъл.“
- Лорънс С. Леф цитиран труд. - Образователна поредица на Barron.- P. 326. - ISBN 0764128922
- Хауърд Уитли Ивс§4.8:...обобщение на Питагоровата теорема // Велики моменти в математиката (преди 1650) . - Mathematical Association of America, 1983. - P. 41. - ISBN 0883853108
- Tâbit ibn Qorra (пълно име Thābit ibn Qurra ibn Marwan Al-Ṣābiʾ al-Ḥarrānī) (826-901 г. сл. н. е.) е лекар, живеещ в Багдад, който пише много за Елементите на Евклид и другиматематически предмети.
- Айдън Сайили (март 1960 г.). „Обобщението на Питагоровата теорема от Thâbit ibn Qurra“. Изида 51 (1): 35–37. DOI:10.1086/348837.
- Джудит Д. Сали, Пол СалиУпражнение 2.10(ii) // Цитирана работа . - С. 62. - ISBN 0821844032
- За подробности за такава конструкция вж Джордж ДженингсФигура 1.32: Обобщена Питагорова теорема // Съвременна геометрия с приложения: със 150 фигури . - 3-то. - Springer, 1997. - P. 23. - ISBN 038794222X
- Арлен Браун, Карл М. Пиърсивещ ° С: Норма за произволно н-кортеж ... // Въведение в анализа. - Springer, 1995. - P. 124. - ISBN 0387943692Вижте също страници 47-50.
- Алфред Грей, Елза Абена, Саймън СаламонСъвременна диференциална геометрия на криви и повърхнини с Mathematica. - 3-то. - CRC Press, 2006. - С. 194. - ISBN 1584884487
- Раджендра Бхатияматричен анализ. - Springer, 1997. - P. 21. - ISBN 0387948465
- Стивън У. Хокинг цитиран труд. - 2005. - С. 4. - ISBN 0762419229
- Ерик У. Вайсщайн CRC кратка енциклопедия по математика. - 2-ро. - 2003. - С. 2147. - ISBN 1584883472
- Александър Р. Прус
Средно ниво
Правоъгълен триъгълник. Пълно илюстрирано ръководство (2019)
ПРАВИЛЕН ТРИЪГЪЛНИК. ПЪРВО НИВО.
В задачите прав ъгъл изобщо не е необходим - долният ляв, така че трябва да се научите как да разпознавате правоъгълен триъгълник в тази форма,

и в такива

и в такива 
Какво е добро за правоъгълен триъгълник? Ами... първо, има специални красиви именаза неговите страни.
Внимание към чертежа!

Запомнете и не бъркайте: крака - два, а хипотенузата - само един(единствен, неповторим и най-дълъг)!
Е, обсъдихме имената, сега най-важното: Питагоровата теорема.
Питагорова теорема.
Тази теорема е ключът към решаването на много задачи, свързани с правоъгълен триъгълник. Доказано е от Питагор в незапомнени времена и оттогава донесе много ползи на онези, които го познават. А най-хубавото в нея е, че е проста.
Така, Питагорова теорема:
Спомняте ли си вица: „Питагоровите панталони са равни от всички страни!“?
Нека да нарисуваме тези много питагорейски панталони и да ги разгледаме. 
Наистина ли прилича на шорти? Е, от кои страни и къде са равни? Защо и откъде дойде шегата? И тази шега е свързана именно с Питагоровата теорема, по-точно с начина, по който самият Питагор е формулирал своята теорема. И той го формулира така:
„Сума площ на квадратите, построен върху краката, е равен на квадратна площпостроен върху хипотенузата.
Не звучи ли малко по-различно, нали? И така, когато Питагор нарисува твърдението на своята теорема, се получи точно такава картина.

На тази снимка сумата от площите на малките квадрати е равна на площта на големия квадрат. И за да запомнят децата по-добре, че сумата от квадратите на катетите е равна на квадрата на хипотенузата, някой остроумен измисли тази шега за Питагоровите панталони.
Защо сега формулираме Питагоровата теорема
Питагор страдал ли е и говорил за квадрати?
Виждате ли, в древността не е имало ... алгебра! Нямаше табели и т.н. Нямаше никакви надписи. Представяте ли си колко ужасно е било за горките древни ученици да запомнят всичко с думи??! И можем да се радваме, че имаме проста формулировка на Питагоровата теорема. Нека го повторим отново, за да запомним по-добре:
Сега трябва да е лесно:
| Квадратът на хипотенузата е равен на сумата от квадратите на катетите. |
Е, най-важната теорема за правоъгълен триъгълник беше обсъдена. Ако се чудите как е доказано, прочетете нататък. следващи ниватеория, а сега да продължим ... към тъмна гора... тригонометрия! Към ужасните думи синус, косинус, тангенс и котангенс.
Синус, косинус, тангенс, котангенс в правоъгълен триъгълник.
Всъщност всичко изобщо не е толкова страшно. Разбира се, "истинското" определение на синус, косинус, тангенс и котангенс трябва да се разгледа в статията. Но ти наистина не искаш, нали? Можем да се радваме: за да решите задачи за правоъгълен триъгълник, можете просто да попълните следните прости неща:
Защо всичко е около ъгъла? Къде е ъгълът? За да разберете това, трябва да знаете как се пишат твърдения 1 - 4 с думи. Вижте, разберете и запомнете!
1.
Всъщност звучи така:
Какво ще кажете за ъгъла? Има ли крак, който е срещу ъгъла, тоест противоположният крак (за ъгъла)? Разбира се, че има! Това е катет!
Но какво да кажем за ъгъла? Вгледай се по-внимателно. Кой крак е в съседство с ъгъла? Разбира се, котката. И така, за ъгъла катетът е съседен и
А сега внимание! Вижте какво имаме:
Вижте колко е страхотен:
Сега да преминем към тангенса и котангенса.
Как да го изразя с думи сега? Какъв е кракът спрямо ъгъла? Отсреща, разбира се - "лежи" срещу ъгъла. А катетът? В непосредствена близост до ъгъла. И така, какво получихме?
Вижте как числителят и знаменателят са обърнати?
И сега отново ъглите и направи размяната:
Резюме
Нека накратко запишем какво сме научили.
 |
Питагорова теорема: |
Основната теорема за правоъгълния триъгълник е теоремата на Питагор.
Питагорова теорема
Между другото, помните ли добре какво представляват катетите и хипотенузата? Ако не, тогава погледнете снимката - опреснете знанията си

Възможно е вече да сте използвали Питагоровата теорема много пъти, но замисляли ли сте се защо такава теорема е вярна. Как ще го докажеш? Да направим като древните гърци. Нека начертаем квадрат със страна.

Виждате ли колко хитро разделихме страните му на сегменти с дължини и!
Сега нека свържем маркираните точки

Тук обаче отбелязахме нещо друго, но вие сами погледнете снимката и се замислете защо.
Каква е площта на по-големия квадрат? Правилно, . Какво ще кажете за по-малката площ? Разбира се, . Общата площ на четирите ъгъла остава. Представете си, че сме взели две от тях и сме ги облегнали една на друга с хипотенузи. Какво стана? Два правоъгълника. Така че площта на "резниците" е равна.
Нека да го съберем сега.
Нека трансформираме:
Така посетихме Питагор - доказахме теоремата му по древен начин.
Правоъгълен триъгълник и тригонометрия
За правоъгълен триъгълник важат следните отношения:

синусите остър ъгълравно на отношението на противоположния катет към хипотенузата
Косинусът на остър ъгъл е равен на отношението на съседния катет към хипотенузата.
Тангенсът на остър ъгъл е равен на отношението на срещуположния катет към съседния катет.
Котангенсът на остър ъгъл е равен на отношението на съседния катет към противоположния катет.
И отново всичко това под формата на чиния:
Много е удобно!
Признаци за равенство на правоъгълни триъгълници
I. На два крака

II. По катет и хипотенуза

III. Чрез хипотенуза и остър ъгъл

IV. По крака и остър ъгъл
а) 
б) 
внимание! Тук е много важно краката да са "съответстващи". Например, ако стане така:

ТОГАВА ТРИЪГЪЛНИЦИТЕ НЕ СА РАВНИ, въпреки факта, че имат един идентичен остър ъгъл.
Трябва да и в двата триъгълника катетът беше съседен, или в двата - срещуположен.
Забелязали ли сте как знаците за равенство на правоъгълни триъгълници се различават от обичайните знаци за равенство на триъгълници? Погледнете темата "и обърнете внимание на факта, че за равенството на "обикновените" триъгълници е необходимо равенството на трите им елемента: две страни и ъгъл между тях, два ъгъла и страна между тях или три страни. Но за равенството на правоъгълни триъгълници са достатъчни само два съответстващи елемента. Страхотно е, нали?
Приблизително същата ситуация със знаци за сходство на правоъгълни триъгълници.
Признаци за подобие на правоъгълни триъгълници
I. Остър ъгъл

II. На два крака

III. По катет и хипотенуза

Медиана в правоъгълен триъгълник
Защо е така?
Помислете за цял правоъгълник вместо правоъгълен триъгълник.
Нека начертаем диагонал и разгледаме точка - пресечната точка на диагоналите. Какво знаете за диагоналите на правоъгълник?
И какво следва от това?
Така се случи така
- - Медиана:
Запомнете този факт! Помага много!
Още по-изненадващо е, че обратното също е вярно.
Какво добро може да се спечели от факта, че медианата, прекарана към хипотенузата, е равна на половината от хипотенузата? Нека погледнем снимката
Вгледай се по-внимателно. Имаме: , т.е. разстоянията от точката до трите върха на триъгълника се оказаха равни. Но в триъгълника има само една точка, разстоянията от която около трите върха на триъгълника са равни и това е ЦЕНТЪРЪТ НА ОПИСАНАТА ОКРУЖНА ОКРУГА. И какво стана?
Така че нека започнем с това "освен...".
Нека да разгледаме i.
Но в подобни триъгълници всички ъгли са равни!
Същото може да се каже и за и
Сега нека го нарисуваме заедно:
Каква полза може да се извлече от това "тройно" сходство.
Е, например - две формули за височина на правоъгълен триъгълник.
Пишем отношенията на съответните страни:

За да намерим височината, решаваме пропорцията и получаваме първа формула "Височина в правоъгълен триъгълник":
И така, нека приложим приликата: .

Какво ще стане сега?
Отново решаваме пропорцията и получаваме втората формула:
И двете формули трябва да се запомнят много добре и тази, която е по-удобна за прилагане. Нека ги запишем отново.
Питагорова теорема:
В правоъгълен триъгълник квадратът на хипотенузата е равен на сумата от квадратите на катетите:.

Признаци за равенство на правоъгълни триъгълници:
- на два крака:
- по крака и хипотенузата: или
- по крака и прилежащия остър ъгъл: или
- по крака и срещуположния остър ъгъл: или
- чрез хипотенуза и остър ъгъл: или.
Признаци за сходство на правоъгълни триъгълници:
- един остър ъгъл: или
- от пропорционалността на двата крака:
- от пропорционалността на катета и хипотенузата: или.
Синус, косинус, тангенс, котангенс в правоъгълен триъгълник
- Синусът на остър ъгъл на правоъгълен триъгълник е отношението на срещуположния катет към хипотенузата:
- Косинусът на остър ъгъл на правоъгълен триъгълник е отношението на съседния катет към хипотенузата:
- Тангенсът на остър ъгъл на правоъгълен триъгълник е отношението на срещуположния катет към съседния:
- Котангенсът на остър ъгъл на правоъгълен триъгълник е отношението на съседния катет към противоположния:.
Височина на правоъгълен триъгълник: или.
В правоъгълен триъгълник медианата, изтеглена от върха на правия ъгъл, е равна на половината от хипотенузата: .
Площ на правоъгълен триъгълник:
- през катетри:
 По същия начин, триъгълник CBH е подобен на ABC. Въвеждане на нотацията
По същия начин, триъгълник CBH е подобен на ABC. Въвеждане на нотацията  1. Подредете четири равни правоъгълни триъгълника, както е показано на фигурата.
1. Подредете четири равни правоъгълни триъгълника, както е показано на фигурата. 
 Идеята на доказателството на Евклид е следната: нека се опитаме да докажем, че половината от площта на квадрата, построен върху хипотенузата, е равна на сбора от половините площи на квадратите, построени върху краката, и след това площите на големият и двата малки квадрата са равни. Разгледайте рисунката вляво. Върху него построихме квадрати от страните на правоъгълен триъгълник и начертахме лъч s от върха на прав ъгъл C, перпендикулярен на хипотенузата AB, той разрязва квадрата ABIK, построен върху хипотенузата, на два правоъгълника - BHJI и HAKJ , съответно. Оказва се, че площите на тези правоъгълници са точно равни на площите на квадратите, построени върху съответните крака. Нека се опитаме да докажем, че площта на квадрата DECA е равна на площта на правоъгълника AHJK. За да направим това, използваме спомагателно наблюдение: Площта на триъгълник със същата височина и основа като дадената правоъгълник е равен на половината от площта на дадения правоъгълник. Това е следствие от определянето на площта на триъгълник като половината от произведението на основата и височината. От това наблюдение следва, че площта на триъгълника ACK е равна на площта на триъгълника AHK (не е показан), който от своя страна е равен на половината от площта на правоъгълника AHJK. Нека сега докажем, че площта на триъгълника ACK също е равна на половината от площта на квадрата DECA. Единственото нещо, което трябва да се направи за това, е да се докаже равенството на триъгълниците ACK и BDA (тъй като площта на триъгълника BDA е равна на половината от площта на квадрата по горното свойство). Това равенство е очевидно, триъгълниците са равни по двете страни и ъгъла между тях. А именно - AB=AK,AD=AC - равенството на ъглите CAK и BAD е лесно да се докаже чрез метода на движението: нека завъртим триъгълника CAK на 90 ° обратно на часовниковата стрелка, тогава е очевидно, че съответните страни на двата разглеждани триъгълника ще съвпадат (поради факта, че ъгълът при върха на квадрата е 90°). Аргументът за равенството на лицата на квадрата BCFG и правоъгълника BHJI е напълно аналогичен. Така доказахме, че площта на квадрата, построен върху хипотенузата, е сумата от площите на квадратите, построени върху краката.
Идеята на доказателството на Евклид е следната: нека се опитаме да докажем, че половината от площта на квадрата, построен върху хипотенузата, е равна на сбора от половините площи на квадратите, построени върху краката, и след това площите на големият и двата малки квадрата са равни. Разгледайте рисунката вляво. Върху него построихме квадрати от страните на правоъгълен триъгълник и начертахме лъч s от върха на прав ъгъл C, перпендикулярен на хипотенузата AB, той разрязва квадрата ABIK, построен върху хипотенузата, на два правоъгълника - BHJI и HAKJ , съответно. Оказва се, че площите на тези правоъгълници са точно равни на площите на квадратите, построени върху съответните крака. Нека се опитаме да докажем, че площта на квадрата DECA е равна на площта на правоъгълника AHJK. За да направим това, използваме спомагателно наблюдение: Площта на триъгълник със същата височина и основа като дадената правоъгълник е равен на половината от площта на дадения правоъгълник. Това е следствие от определянето на площта на триъгълник като половината от произведението на основата и височината. От това наблюдение следва, че площта на триъгълника ACK е равна на площта на триъгълника AHK (не е показан), който от своя страна е равен на половината от площта на правоъгълника AHJK. Нека сега докажем, че площта на триъгълника ACK също е равна на половината от площта на квадрата DECA. Единственото нещо, което трябва да се направи за това, е да се докаже равенството на триъгълниците ACK и BDA (тъй като площта на триъгълника BDA е равна на половината от площта на квадрата по горното свойство). Това равенство е очевидно, триъгълниците са равни по двете страни и ъгъла между тях. А именно - AB=AK,AD=AC - равенството на ъглите CAK и BAD е лесно да се докаже чрез метода на движението: нека завъртим триъгълника CAK на 90 ° обратно на часовниковата стрелка, тогава е очевидно, че съответните страни на двата разглеждани триъгълника ще съвпадат (поради факта, че ъгълът при върха на квадрата е 90°). Аргументът за равенството на лицата на квадрата BCFG и правоъгълника BHJI е напълно аналогичен. Така доказахме, че площта на квадрата, построен върху хипотенузата, е сумата от площите на квадратите, построени върху краката.  Разгледайте чертежа, както се вижда от симетрията, сегментът CI разрязва квадрата ABHJ на две еднакви части (тъй като триъгълниците ABC и JHI са равни по конструкция). Използвайки завъртане на 90 градуса обратно на часовниковата стрелка, виждаме равенството на защрихованите фигури CAJI и GDAB. Сега е ясно, че площта на фигурата, засенчена от нас, е равна на сумата от половината от площите на квадратите, построени върху краката, и площта на оригиналния триъгълник. От друга страна, той е равен на половината от площта на квадрата, построен върху хипотенузата, плюс площта на оригиналния триъгълник. Последната стъпка в доказателството е оставена на читателя.
Разгледайте чертежа, както се вижда от симетрията, сегментът CI разрязва квадрата ABHJ на две еднакви части (тъй като триъгълниците ABC и JHI са равни по конструкция). Използвайки завъртане на 90 градуса обратно на часовниковата стрелка, виждаме равенството на защрихованите фигури CAJI и GDAB. Сега е ясно, че площта на фигурата, засенчена от нас, е равна на сумата от половината от площите на квадратите, построени върху краката, и площта на оригиналния триъгълник. От друга страна, той е равен на половината от площта на квадрата, построен върху хипотенузата, плюс площта на оригиналния триъгълник. Последната стъпка в доказателството е оставена на читателя.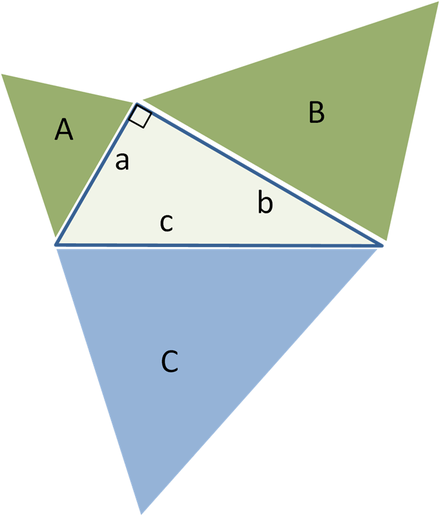




 Ораторското изкуство като първообраз на журналистиката
Ораторското изкуство като първообраз на журналистиката Цитати за Наполеон - dslinkov — LiveJournal
Цитати за Наполеон - dslinkov — LiveJournal Аз отмъщение Човекът на булдозера унищожи града
Аз отмъщение Човекът на булдозера унищожи града