Γραμμική εξάρτηση δύο διανυσμάτων. Γραμμικά εξαρτώμενα και γραμμικά ανεξάρτητα διανύσματα

Για να ελέγξετε εάν ένα σύστημα διανυσμάτων εξαρτάται γραμμικά, είναι απαραίτητο να συνθέσετε έναν γραμμικό συνδυασμό αυτών των διανυσμάτων και να ελέγξετε εάν μπορεί να είναι μηδέν εάν τουλάχιστον ένας συντελεστής είναι μηδέν.

Περίπτωση 1. Το σύστημα των διανυσμάτων δίνεται από διανύσματα

Κάνουμε έναν γραμμικό συνδυασμό

Αποκτήσαμε ένα ομοιογενές σύστημα εξισώσεων. Αν έχει μη μηδενική λύση, τότε η ορίζουσα πρέπει να είναι ίση με μηδέν. Ας κάνουμε έναν προσδιορισμό και ας βρούμε την αξία του.

Η ορίζουσα είναι μηδέν, επομένως, τα διανύσματα εξαρτώνται γραμμικά.

Περίπτωση 2. Το σύστημα των διανυσμάτων δίνεται από αναλυτικές συναρτήσεις:

ένα)
, εάν η ταυτότητα είναι αληθής, τότε το σύστημα εξαρτάται γραμμικά.

Ας κάνουμε έναν γραμμικό συνδυασμό.

Είναι απαραίτητο να ελέγξουμε αν υπάρχουν τέτοια a, b, c (τουλάχιστον ένα από τα οποία δεν είναι ίσο με μηδέν) για τα οποία η δοθείσα έκφραση είναι ίση με μηδέν.

Γράφουμε τις υπερβολικές συναρτήσεις

,
, έπειτα

τότε ο γραμμικός συνδυασμός διανυσμάτων θα πάρει τη μορφή:

Οπου
, πάρτε, για παράδειγμα, τότε ο γραμμικός συνδυασμός είναι ίσος με μηδέν, επομένως, το σύστημα εξαρτάται γραμμικά.

Απάντηση: Το σύστημα εξαρτάται γραμμικά.

σι)
, συνθέτουμε έναν γραμμικό συνδυασμό

Ένας γραμμικός συνδυασμός διανυσμάτων, πρέπει να είναι μηδέν για οποιεσδήποτε τιμές του x.

Ας ελέγξουμε για ειδικές περιπτώσεις.

Ένας γραμμικός συνδυασμός διανυσμάτων είναι μηδέν μόνο εάν όλοι οι συντελεστές είναι μηδέν.

Επομένως, το σύστημα είναι γραμμικά ανεξάρτητο.

Απάντηση: Το σύστημα είναι γραμμικά ανεξάρτητο.

5.3. Βρείτε κάποια βάση και προσδιορίστε τη διάσταση του γραμμικού χώρου των λύσεων.

Ας σχηματίσουμε έναν εκτεταμένο πίνακα και ας τον φέρουμε σε μορφή τραπεζοειδούς χρησιμοποιώντας τη μέθοδο Gauss.

Για να έχουμε κάποια βάση, αντικαθιστούμε αυθαίρετες τιμές:

Πάρτε τις υπόλοιπες συντεταγμένες

Απάντηση:

5.4. Να βρείτε τις συντεταγμένες του διανύσματος Χ στη βάση, αν αυτό δίνεται στη βάση.

Η εύρεση των συντεταγμένων του διανύσματος στη νέα βάση περιορίζεται στην επίλυση του συστήματος των εξισώσεων

Μέθοδος 1. Εύρεση χρησιμοποιώντας τον πίνακα μετάβασης

Συνθέστε τον πίνακα μετάβασης

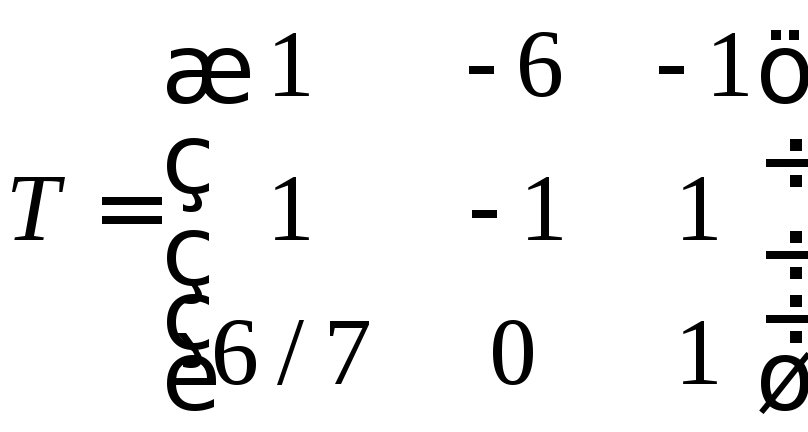
Ας βρούμε το διάνυσμα στη νέα βάση με τον τύπο

Βρείτε τον αντίστροφο πίνακα και κάντε τον πολλαπλασιασμό

,

Μέθοδος 2. Εύρεση με σύνταξη συστήματος εξισώσεων.

Να συνθέσετε τα διανύσματα βάσης από τους συντελεστές της βάσης

,
,

Η εύρεση ενός διανύσματος σε νέα βάση έχει τη μορφή

, όπου ρεαυτό είναι δεδομένο διάνυσμα Χ.

Η εξίσωση που προκύπτει μπορεί να λυθεί με οποιονδήποτε τρόπο, η απάντηση θα είναι η ίδια.

Απάντηση: διάνυσμα σε νέα βάση
.

5.5. Έστω x = (Χ 1 , Χ 2 , Χ 3 ) . Είναι γραμμικοί οι παρακάτω μετασχηματισμοί.

Ας συνθέσουμε πίνακες γραμμικών τελεστών από τους συντελεστές δεδομένων διανυσμάτων.

Ας ελέγξουμε την ιδιότητα των γραμμικών πράξεων για κάθε πίνακα ενός γραμμικού τελεστή.

Η αριστερή πλευρά βρίσκεται με πολλαπλασιασμό πίνακα ΑΛΛΑανά διάνυσμα

Βρίσκουμε τη δεξιά πλευρά πολλαπλασιάζοντας το δεδομένο διάνυσμα με ένα βαθμωτό
.

Το βλέπουμε αυτό
οπότε ο μετασχηματισμός δεν είναι γραμμικός.

Ας ελέγξουμε άλλα διανύσματα.

, ο μετασχηματισμός δεν είναι γραμμικός.

, ο μετασχηματισμός είναι γραμμικός.

Απάντηση: Ω- δεν γραμμικός μετασχηματισμός, Vx- όχι γραμμικό Cx- γραμμικός.

Σημείωση.Μπορείτε να ολοκληρώσετε αυτήν την εργασία πολύ πιο εύκολα κοιτάζοντας προσεκτικά τα δεδομένα διανύσματα. ΣΤΟ Ωβλέπουμε ότι υπάρχουν όροι που δεν περιέχουν στοιχεία Χ, το οποίο δεν ήταν δυνατό να ληφθεί ως αποτέλεσμα μιας γραμμικής πράξης. ΣΤΟ Vxυπάρχει ένα στοιχείο Χστην τρίτη δύναμη, η οποία επίσης δεν μπορούσε να ληφθεί πολλαπλασιάζοντας με ένα διάνυσμα Χ.

5.6. Δεδομένος Χ = { Χ 1 , Χ 2 , Χ 3 } , Τσεκούρι = { Χ 2 – Χ 3 , Χ 1 , Χ 1 + Χ 3 } , bx = { Χ 2 , 2 Χ 3 , Χ 1 } . Εκτελέστε τη δεδομένη λειτουργία: ( ΕΝΑ ( σι – ΕΝΑ )) Χ .

Ας γράψουμε τους πίνακες των γραμμικών τελεστών.

Ας εκτελέσουμε μια πράξη σε πίνακες

Πολλαπλασιάζοντας τον προκύπτοντα πίνακα με Χ, παίρνουμε

Απάντηση:

Εργασία 1.Μάθετε εάν το σύστημα των διανυσμάτων είναι γραμμικά ανεξάρτητο. Το σύστημα των διανυσμάτων θα οριστεί από τον πίνακα του συστήματος, οι στήλες του οποίου αποτελούνται από τις συντεταγμένες των διανυσμάτων.

.

Λύση.Αφήστε τον γραμμικό συνδυασμό ισούται με μηδέν. Έχοντας γράψει αυτή την ισότητα σε συντεταγμένες, λαμβάνουμε το ακόλουθο σύστημα εξισώσεων:

.

Ένα τέτοιο σύστημα εξισώσεων ονομάζεται τριγωνικό. Έχει τη μόνη λύση. . Εξ ου και τα διανύσματα είναι γραμμικά ανεξάρτητα.

Εργασία 2.Μάθετε εάν το σύστημα των διανυσμάτων είναι γραμμικά ανεξάρτητο.

.

Λύση.Διανύσματα είναι γραμμικά ανεξάρτητες (βλ. Πρόβλημα 1). Ας αποδείξουμε ότι το διάνυσμα είναι ένας γραμμικός συνδυασμός διανυσμάτων . Διανυσματικοί συντελεστές επέκτασης καθορίζονται από το σύστημα των εξισώσεων

.

Αυτό το σύστημα, όπως ένα τριγωνικό, έχει μια μοναδική λύση.

Επομένως, το σύστημα των διανυσμάτων γραμμικά εξαρτώμενη.

Σχόλιο. Οι πίνακες όπως στο πρόβλημα 1 καλούνται τριγωνικός και στο πρόβλημα 2 - κλιμακωτό τριγωνικό . Το ζήτημα της γραμμικής εξάρτησης ενός συστήματος διανυσμάτων λύνεται εύκολα εάν ο πίνακας που αποτελείται από τις συντεταγμένες αυτών των διανυσμάτων είναι σταδιακά τριγωνικός. Εάν ο πίνακας δεν το κάνει ιδιαίτερο είδος, στη συνέχεια χρησιμοποιώντας στοιχειώδεις μετασχηματισμοί χορδών , διατηρώντας τις γραμμικές σχέσεις μεταξύ των στηλών, μπορεί να μειωθεί σε μια βαθμιδωτή τριγωνική μορφή.

Στοιχειώδεις μεταμορφώσειςγραμμέςΠίνακες (EPS) ονομάζονται οι ακόλουθες πράξεις στον πίνακα:

1) μετάθεση γραμμών.

2) πολλαπλασιασμός μιας συμβολοσειράς με έναν μη μηδενικό αριθμό.

3) προσθέτοντας στη συμβολοσειρά μια άλλη συμβολοσειρά, πολλαπλασιασμένη με έναν αυθαίρετο αριθμό.

Εργασία 3.Βρείτε το μέγιστο γραμμικά ανεξάρτητο υποσύστημα και υπολογίστε την κατάταξη του συστήματος των διανυσμάτων

.

Λύση.Ας μειώσουμε τη μήτρα του συστήματος με τη βοήθεια του EPS σε μια κλιμακωτή-τριγωνική μορφή. Για να εξηγηθεί η διαδικασία, η γραμμή με τον αριθμό του πίνακα που θα μετασχηματιστεί θα συμβολίζεται με το σύμβολο . Η στήλη μετά το βέλος δείχνει τις ενέργειες που πρέπει να εκτελεστούν στις σειρές του πίνακα που έχει μετατραπεί για να ληφθούν οι σειρές του νέου πίνακα.

.

Προφανώς, οι δύο πρώτες στήλες του προκύπτοντος πίνακα είναι γραμμικά ανεξάρτητες, η τρίτη στήλη είναι ο γραμμικός συνδυασμός τους και η τέταρτη δεν εξαρτάται από τις δύο πρώτες. Διανύσματα ονομάζονται βασικά. Αποτελούν το μέγιστο γραμμικά ανεξάρτητο υποσύστημα του συστήματος , και η κατάταξη του συστήματος είναι τρεις.

Βάση, συντεταγμένες

Εργασία 4.Βρείτε τη βάση και τις συντεταγμένες των διανυσμάτων σε αυτή τη βάση στο σύνολο γεωμετρικά διανύσματα, του οποίου οι συντεταγμένες ικανοποιούν την προϋπόθεση .

Λύση. Το σετ είναι ένα αεροπλάνο που διέρχεται από την αρχή. Μια αυθαίρετη βάση στο επίπεδο αποτελείται από δύο μη γραμμικά διανύσματα. Οι συντεταγμένες των διανυσμάτων στην επιλεγμένη βάση καθορίζονται με την επίλυση του αντίστοιχου συστήματος γραμμικών εξισώσεων.

Υπάρχει ένας άλλος τρόπος για να λύσετε αυτό το πρόβλημα, όταν μπορείτε να βρείτε τη βάση με συντεταγμένες.

Συντεταγμένες Οι χώροι δεν είναι συντεταγμένες στο επίπεδο, αφού σχετίζονται με τη σχέση , δηλαδή δεν είναι ανεξάρτητα. Οι ανεξάρτητες μεταβλητές και (ονομάζονται ελεύθερες) καθορίζουν μοναδικά το διάνυσμα στο επίπεδο και, επομένως, μπορούν να επιλεγούν ως συντεταγμένες στο . Στη συνέχεια η βάση αποτελείται από διανύσματα που βρίσκονται μέσα και αντιστοιχούν σε σύνολα ελεύθερων μεταβλητών και , αυτό είναι .

Εργασία 5.Βρείτε τη βάση και τις συντεταγμένες των διανυσμάτων σε αυτή τη βάση στο σύνολο όλων των διανυσμάτων του χώρου , των οποίων οι περιττές συντεταγμένες είναι ίσες μεταξύ τους.

Λύση. Επιλέγουμε, όπως και στο προηγούμενο πρόβλημα, συντεταγμένες στο διάστημα .

Επειδή , μετά τις ελεύθερες μεταβλητές ορίζουν μοναδικά ένα διάνυσμα από και, επομένως, είναι συντεταγμένες. Η αντίστοιχη βάση αποτελείται από διανύσματα .

Εργασία 6.Βρείτε τη βάση και τις συντεταγμένες των διανυσμάτων σε αυτή τη βάση στο σύνολο όλων των πινάκων της φόρμας , όπου είναι αυθαίρετοι αριθμοί.

Λύση. Κάθε πίνακας από μπορεί να αναπαρασταθεί μοναδικά ως:

Αυτή η σχέση είναι η επέκταση του διανύσματος από ως προς τη βάση
με συντεταγμένες .

Εργασία 7.Να βρείτε τη διάσταση και τη βάση του γραμμικού ανοίγματος ενός συστήματος διανυσμάτων

.

Λύση.Χρησιμοποιώντας το EPS, μετατρέπουμε τον πίνακα από τις συντεταγμένες των διανυσμάτων του συστήματος σε μια κλιμακωτή τριγωνική μορφή.

.

στήλες του τελευταίου πίνακα είναι γραμμικά ανεξάρτητες και οι στήλες εκφράζονται γραμμικά μέσα από αυτά. Εξ ου και τα διανύσματα αποτελούν τη βάση , και .

Σχόλιο. Βάση σε επιλεγεί διφορούμενα. Για παράδειγμα, διανύσματα αποτελούν επίσης τη βάση .

ένα 1 = { 3, 5, 1 , 4 }, ένα 2 = { –2, 1, -5 , -7 }, ένα 3 = { -1, –2, 0, –1 }.

Λύση.Ψάχνουν για κοινή απόφασησυστήματα εξισώσεων

ένα 1 Χ 1 + ένα 2 Χ 2 + ένα 3 Χ 3 = Θ

Γκαουσιανή μέθοδος. Για να γίνει αυτό, γράφουμε αυτό το ομοιογενές σύστημα σε συντεταγμένες:

Σύστημα Matrix

Το επιτρεπόμενο σύστημα μοιάζει με: (r Α = 2, n= 3). Το σύστημα είναι συνεπές και απροσδιόριστο. Η γενική του λύση ( Χ 2 - δωρεάν μεταβλητή): Χ 3 = 13Χ 2 ; 3Χ 1 – 2Χ 2 – 13Χ 2 = 0 => Χ 1 = 5Χ 2 => Χ o = . Η παρουσία μιας μη μηδενικής ιδιωτικής λύσης, για παράδειγμα, δείχνει ότι τα διανύσματα ένα 1 , ένα 2 , ένα 3 γραμμικά εξαρτώμενη.

Παράδειγμα 2

Μάθετε αν είναι αυτό το σύστημαδιανύσματα γραμμικά εξαρτώμενα ή γραμμικά ανεξάρτητα:

1. ένα 1 = { -20, -15, - 4 }, ένα 2 = { –7, -2, -4 }, ένα 3 = { 3, –1, –2 }.

Λύση.Θεωρήστε το ομοιογενές σύστημα εξισώσεων ένα 1 Χ 1 + ένα 2 Χ 2 + ένα 3 Χ 3 = Θ

ή επεκτείνεται (κατά συντεταγμένες)

Το σύστημα είναι ομοιογενές. Αν είναι μη εκφυλισμένο, τότε έχει μοναδική λύση. Πότε ομοιογενές σύστημαείναι η μηδενική (τετριμμένη) λύση. Επομένως, σε αυτή την περίπτωση το σύστημα των διανυσμάτων είναι ανεξάρτητο. Εάν το σύστημα είναι εκφυλισμένο, τότε έχει μη μηδενικές λύσεις και, επομένως, είναι εξαρτημένο.

Έλεγχος του συστήματος για εκφυλισμό:

= –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.

Το σύστημα είναι μη εκφυλισμένο και, επομένως, τα διανύσματα ένα 1 , ένα 2 , ένα 3 είναι γραμμικά ανεξάρτητα.

Καθήκοντα.Βρείτε αν το δεδομένο σύστημα διανυσμάτων είναι γραμμικά εξαρτώμενο ή γραμμικά ανεξάρτητο:

1. ένα 1 = { -4, 2, 8 }, ένα 2 = { 14, -7, -28 }.

2. ένα 1 = { 2, -1, 3, 5 }, ένα 2 = { 6, -3, 3, 15 }.

3. ένα 1 = { -7, 5, 19 }, ένα 2 = { -5, 7 , -7 }, ένα 3 = { -8, 7, 14 }.

4. ένα 1 = { 1, 2, -2 }, ένα 2 = { 0, -1, 4 }, ένα 3 = { 2, -3, 3 }.

5. ένα 1 = { 1, 8 , -1 }, ένα 2 = { -2, 3, 3 }, ένα 3 = { 4, -11, 9 }.

6. ένα 1 = { 1, 2 , 3 }, ένα 2 = { 2, -1 , 1 }, ένα 3 = { 1, 3, 4 }.

7. ένα 1 = {0, 1, 1 , 0}, ένα 2 = {1, 1 , 3, 1}, ένα 3 = {1, 3, 5, 1}, ένα 4 = {0, 1, 1, -2}.

8. ένα 1 = {-1, 7, 1 , -2}, ένα 2 = {2, 3 , 2, 1}, ένα 3 = {4, 4, 4, -3}, ένα 4 = {1, 6, -11, 1}.

9. Να αποδείξετε ότι ένα σύστημα διανυσμάτων θα εξαρτάται γραμμικά αν περιέχει:

α) δύο ίσα διανύσματα.

β) δύο αναλογικά διανύσματα.

Τα διανύσματα, οι ιδιότητές τους και οι ενέργειες μαζί τους

Διανύσματα, ενέργειες με διανύσματα, γραμμικός διανυσματικός χώρος.

Τα διανύσματα είναι μια διατεταγμένη συλλογή ενός πεπερασμένου αριθμού πραγματικών αριθμών.

Ενέργειες: 1. Πολλαπλασιασμός ενός διανύσματος με έναν αριθμό: λάμδα * διάνυσμα x \u003d (λάμδα * x 1, λάμδα * x 2 ... λάμδα * x n). (3.4, 0. 7) * 3 \u003d (9, 12,0.21 )

2. Προσθήκη διανυσμάτων (ανήκουν στον ίδιο διανυσματικό χώρο) διάνυσμα x + διάνυσμα y \u003d (x 1 + y 1, x 2 + y 2, ... x n + y n,)

3. Διάνυσμα 0=(0,0…0)---n E n – n-διάστατο (γραμμικός χώρος) διάνυσμα x + διάνυσμα 0 = διάνυσμα x

Θεώρημα. Για να είναι γραμμικά εξαρτημένο ένα σύστημα n διανυσμάτων σε γραμμικό χώρο n διαστάσεων, είναι απαραίτητο και αρκετό ένα από τα διανύσματα να είναι γραμμικός συνδυασμός των άλλων.

Θεώρημα. Οποιοδήποτε σύνολο n+ 1ου διανύσματος n-διάστατου γραμμικού χώρου yavl. γραμμικά εξαρτώμενη.

Πρόσθεση διανυσμάτων, πολλαπλασιασμός διανυσμάτων με αριθμούς. Αφαίρεση διανυσμάτων.

Το άθροισμα δύο διανυσμάτων είναι το διάνυσμα που κατευθύνεται από την αρχή του διανύσματος έως το τέλος του διανύσματος, με την προϋπόθεση ότι η αρχή συμπίπτει με το τέλος του διανύσματος. Εάν τα διανύσματα δίνονται από τις επεκτάσεις τους ως διανύσματα βάσης, τότε προσθέτοντας τα διανύσματα αθροίζονται οι αντίστοιχες συντεταγμένες τους.

Ας το εξετάσουμε χρησιμοποιώντας το παράδειγμα ενός καρτεσιανού συστήματος συντεταγμένων. Αφήνω

Ας το δείξουμε

Το σχήμα 3 δείχνει ότι

Το ποσό οποιουδήποτε πεπερασμένος αριθμόςτα διανύσματα μπορούν να βρεθούν χρησιμοποιώντας τον κανόνα του πολυγώνου (Εικ. 4): για να δημιουργήσετε το άθροισμα ενός πεπερασμένου αριθμού διανυσμάτων, αρκεί να συνδυάσετε την αρχή κάθε επόμενου διανύσματος με το τέλος του προηγούμενου και να κατασκευάσετε ένα διάνυσμα που συνδέει την αρχή του πρώτου διανύσματος με το τέλος του τελευταίου.

Ιδιότητες της πράξης πρόσθεσης διανύσματος:

Σε αυτές τις παραστάσεις τα m, n είναι αριθμοί.

Η διαφορά των διανυσμάτων ονομάζεται διάνυσμα Ο δεύτερος όρος είναι ένα διάνυσμα αντίθετο προς το διάνυσμα ως προς τη διεύθυνση, αλλά ίσο με αυτό σε μήκος.

Έτσι, η πράξη αφαίρεσης του διανύσματος αντικαθίσταται από την πράξη πρόσθεσης

Το διάνυσμα του οποίου η αρχή βρίσκεται στην αρχή των συντεταγμένων και το τέλος του στο σημείο Α (x1, y1, z1), ονομάζεται διάνυσμα ακτίνας του σημείου Α και συμβολίζεται ή απλά. Δεδομένου ότι οι συντεταγμένες του συμπίπτουν με τις συντεταγμένες του σημείου Α, η επέκτασή του ως προς τα διανύσματα έχει τη μορφή

Ένα διάνυσμα που ξεκινά από το σημείο A(x1, y1, z1) και τελειώνει στο σημείο B(x2, y2, z2) μπορεί να γραφτεί ως

όπου r 2 είναι το διάνυσμα ακτίνας του σημείου Β. r 1 - διάνυσμα ακτίνας του σημείου Α.

Επομένως, η επέκταση του διανύσματος ως προς τα orts έχει τη μορφή

Το μήκος του είναι ίσο με την απόσταση μεταξύ των σημείων Α και Β

ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ

Έτσι σε περίπτωση πρόβλημα αεροπλάνουτο γινόμενο ενός διανύσματος με a = (ax; ay) και έναν αριθμό b βρίσκεται από τον τύπο

a b = (ax b; ay b)

Παράδειγμα 1. Βρείτε το γινόμενο του διανύσματος a = (1; 2) επί 3.

3 a = (3 1; 3 2) = (3; 6)

Έτσι σε περίπτωση χωροταξικό πρόβληματο γινόμενο του διανύσματος a = (ax; ay; az) και ο αριθμός b βρίσκεται από τον τύπο

a b = (ax b; ay b; az b)

Παράδειγμα 1. Βρείτε το γινόμενο του διανύσματος a = (1; 2; -5) επί 2.

2 a = (2 1; 2 2; 2 (-5)) = (2; 4; -10)

Τελική γινόμενο διανυσμάτων και πού είναι η γωνία μεταξύ των διανυσμάτων και ? αν ένα, τότε

Από τον ορισμό του βαθμωτού γινομένου, προκύπτει ότι

όπου, για παράδειγμα, είναι η τιμή της προβολής του διανύσματος στην κατεύθυνση του διανύσματος .

Κλιμακωτό τετράγωνο ενός διανύσματος:

Ιδιότητες προϊόντος Dot:

Το προϊόν με τελείες σε συντεταγμένες

Αν ένα έπειτα

Γωνία μεταξύ των διανυσμάτων

Γωνία μεταξύ διανυσμάτων - η γωνία μεταξύ των κατευθύνσεων αυτών των διανυσμάτων (μικρότερη γωνία).

Διανυσματικό γινόμενο (Το διανυσματικό γινόμενο δύο διανυσμάτων.)-αυτός είναι ένας ψευδοδέκτορας, κάθετο στο επίπεδο, που χτίζεται από δύο παράγοντες, που είναι το αποτέλεσμα της δυαδικής πράξης «διανυσματικός πολλαπλασιασμός» σε διανύσματα στον τρισδιάστατο Ευκλείδειο χώρο. Το γινόμενο δεν είναι ούτε αντιμεταθετικό ούτε συνειρμικό (είναι αντιμεταθετικό) και διαφέρει από το γινόμενο κουκίδων των διανυσμάτων. Σε πολλά προβλήματα μηχανικής και φυσικής, είναι απαραίτητο να μπορούμε να δημιουργήσουμε ένα διάνυσμα κάθετο σε δύο ήδη υπάρχοντα - το διανυσματικό γινόμενο παρέχει αυτή την ευκαιρία. Το εγκάρσιο γινόμενο είναι χρήσιμο για τη "μέτρηση" της καθετότητας των διανυσμάτων - το μήκος του εγκάρσιου γινομένου δύο διανυσμάτων είναι ίσο με το γινόμενο των μηκών τους εάν είναι κάθετα και μειώνεται στο μηδέν εάν τα διανύσματα είναι παράλληλα ή αντιπαράλληλα.

Το διανυσματικό προϊόν ορίζεται μόνο σε τρισδιάστατους και επταδιάστατους χώρους. Το αποτέλεσμα του διανυσματικού γινόμενου, όπως και του βαθμωτό γινόμενο, εξαρτάται από τη μετρική του Ευκλείδειου χώρου.

Σε αντίθεση με τον τύπο για τον υπολογισμό του γινόμενου κουκίδων από τις συντεταγμένες των διανυσμάτων σε ένα τρισδιάστατο ορθογώνιο σύστημα συντεταγμένων, ο τύπος για το διασταυρούμενο γινόμενο εξαρτάται από τον προσανατολισμό ορθογώνιο σύστημασυντεταγμένες ή, με άλλα λόγια, η «χειρικότητα» του

Συγγραμμικότητα διανυσμάτων.

Δύο μη μηδενικά (όχι ίσα με 0) διανύσματα ονομάζονται συγγραμμικά αν βρίσκονται σε παράλληλες ευθείες ή στην ίδια ευθεία. Επιτρέπουμε, αλλά δεν συνιστούμε, ένα συνώνυμο - «παράλληλα» διανύσματα. Συγγραμμικά διανύσματαμπορεί να κατευθυνθεί προς την ίδια κατεύθυνση («συν-σκηνοθεσία») ή αντίθετα (σε τελευταία περίπτωσημερικές φορές ονομάζονται «αντιγραμμικά» ή «αντιπαράλληλα»).

Μικτό γινόμενο διανυσμάτων( αλφάβητο)- κλιμακωτό γινόμενο του διανύσματος a και διανυσματικό γινόμενο των διανυσμάτων b και c:

(a,b,c)=a ⋅(b×c)

μερικές φορές ονομάζεται τριπλή κλιμακωτό προϊόνδιανύσματα, προφανώς λόγω του γεγονότος ότι το αποτέλεσμα είναι βαθμωτό (ακριβέστερα, ψευδοκλιμακωτή).

γεωμετρική αίσθηση: Ο συντελεστής του μικτού προϊόντος είναι αριθμητικά ίσος με τον όγκο του παραλληλεπίπεδου που σχηματίζουν τα διανύσματα (αλφάβητο) .

Ιδιότητες

Ένα μικτό γινόμενο είναι λοξό-συμμετρικό ως προς όλα τα επιχειρήματά του: δηλαδή, ε. μια μετάθεση οποιωνδήποτε δύο παραγόντων αλλάζει το πρόσημο του προϊόντος. Από αυτό προκύπτει ότι το μικτό προϊόν στα δεξιά Καρτεσιανό σύστημασυντεταγμένες (σε ορθοκανονική βάση) ισούται με την ορίζουσα ενός πίνακα που αποτελείται από διανύσματα και:

Το μικτό γινόμενο στο αριστερό καρτεσιανό σύστημα συντεταγμένων (σε ορθοκανονική βάση) είναι ίσο με την ορίζουσα ενός πίνακα που αποτελείται από διανύσματα και λαμβάνεται με πρόσημο μείον:

Συγκεκριμένα,

Εάν οποιαδήποτε δύο διανύσματα είναι παράλληλα, τότε με οποιοδήποτε τρίτο διάνυσμα σχηματίζουν ένα μικτό γινόμενο ίσο με μηδέν.

Εάν τρία διανύσματα είναι γραμμικά εξαρτώμενα (δηλαδή, συνεπίπεδα, βρίσκονται στο ίδιο επίπεδο), τότε το μικτό γινόμενο τους είναι μηδέν.

Γεωμετρική αίσθηση - Μικτό προϊόν από απόλυτη τιμήισούται με τον όγκο του παραλληλεπίπεδου (βλ. σχήμα) που σχηματίζεται από τα διανύσματα και? το πρόσημο εξαρτάται από το αν αυτή η τριάδα των διανυσμάτων είναι δεξιά ή αριστερά.

Συγκρισιμότητα διανυσμάτων.

Τρία διανύσματα (ή περισσότερο) ονομάζονται συνεπίπεδα εάν, αν μειωθούν σε κοινή αρχή, ξαπλώστε στο ίδιο επίπεδο

Ιδιότητες συμβατότητας

Αν τουλάχιστον ένα από τα τρία διανύσματα- μηδέν, τότε τα τρία διανύσματα θεωρούνται επίσης συνεπίπεδα.

Ένα τριπλό διανυσμάτων που περιέχει ένα ζεύγος συγγραμμικών διανυσμάτων είναι συνεπίπεδο.

Μικτό γινόμενο συνεπίπεδων διανυσμάτων. Αυτό είναι ένα κριτήριο για την ομοεπίπεδη τριών διανυσμάτων.

Τα συνεπίπεδα διανύσματα εξαρτώνται γραμμικά. Αυτό είναι επίσης ένα κριτήριο για την ομοεπίπεδη.

Στον τρισδιάστατο χώρο, 3 μη ομοεπίπεδα διανύσματα αποτελούν τη βάση

Γραμμικά εξαρτώμενα και γραμμικά ανεξάρτητα διανύσματα.

Γραμμικά εξαρτώμενα και ανεξάρτητα συστήματα διανυσμάτων.Ορισμός. Το σύστημα των διανυσμάτων ονομάζεται γραμμικά εξαρτώμενη, εάν υπάρχει τουλάχιστον ένας μη τετριμμένος γραμμικός συνδυασμός αυτών των διανυσμάτων ίσος με το μηδενικό διάνυσμα. Διαφορετικά, δηλ. αν μόνο ένας τετριμμένος γραμμικός συνδυασμός δεδομένων διανυσμάτων είναι ίσος με το μηδενικό διάνυσμα, τα διανύσματα ονομάζονται γραμμικά ανεξάρτητη.

Θεώρημα (κριτήριο γραμμικής εξάρτησης). Για να είναι γραμμικά εξαρτημένο ένα σύστημα διανυσμάτων σε έναν γραμμικό χώρο, είναι απαραίτητο και αρκετό τουλάχιστον ένα από αυτά τα διανύσματα να είναι ένας γραμμικός συνδυασμός των άλλων.

1) Εάν υπάρχει τουλάχιστον ένα μηδενικό διάνυσμα μεταξύ των διανυσμάτων, τότε ολόκληρο το σύστημα των διανυσμάτων εξαρτάται γραμμικά.

Πράγματι, αν, για παράδειγμα, , τότε, υποθέτοντας , έχουμε έναν μη τετριμμένο γραμμικό συνδυασμό .▲

2) Εάν μερικά από τα διανύσματα σχηματίζουν ένα γραμμικά εξαρτώμενο σύστημα, τότε ολόκληρο το σύστημα είναι γραμμικά εξαρτημένο.

Πράγματι, αφήστε τα διανύσματα , , να είναι γραμμικά εξαρτημένα. Επομένως, υπάρχει ένας μη τετριμμένος γραμμικός συνδυασμός ίσος με το μηδενικό διάνυσμα. Στη συνέχεια όμως, υποθέτοντας , λαμβάνουμε επίσης έναν μη τετριμμένο γραμμικό συνδυασμό ίσο με το μηδενικό διάνυσμα.

2. Βάση και διάσταση. Ορισμός. Σύστημα γραμμικά ανεξάρτητων διανυσμάτων διανυσματικός χώροςπου ονομάζεται βάσηαυτός ο χώρος, εάν οποιοδήποτε διάνυσμα από μπορεί να αναπαρασταθεί ως ένας γραμμικός συνδυασμός των διανυσμάτων αυτού του συστήματος, δηλ. για κάθε διάνυσμα υπάρχουν πραγματικούς αριθμούς τέτοια που ισχύει η ισότητα.Αυτή η ισότητα ονομάζεται διάνυσμα αποσύνθεσηςσύμφωνα με τη βάση και τους αριθμούς που ονομάζεται διανυσματικές συντεταγμένες σε σχέση με τη βάση(ή στη βάση) .

Θεώρημα (σχετικά με τη μοναδικότητα της επέκτασης ως προς τη βάση). Κάθε διάνυσμα χώρου μπορεί να επεκταθεί ως προς τη βάση με μοναδικό τρόπο, δηλ. συντεταγμένες κάθε διανύσματος στη βάση ορίζονται ξεκάθαρα.

Το σύστημα των διανυσμάτων ονομάζεται γραμμικά εξαρτώμενη, εάν υπάρχουν τέτοιοι αριθμοί , μεταξύ των οποίων τουλάχιστον ένας είναι διαφορετικός από το μηδέν, ότι η ισότητα https://pandia.ru/text/78/624/images/image004_77.gif" width="57" height="24 src =" >.

Αν αυτή η ισότητα ισχύει μόνο αν όλα , τότε καλείται το σύστημα των διανυσμάτων γραμμικά ανεξάρτητη.

Θεώρημα.Το σύστημα των διανυσμάτων θα γραμμικά εξαρτώμενηαν και μόνο αν τουλάχιστον ένα από τα διανύσματά του είναι γραμμικός συνδυασμός των άλλων.

Παράδειγμα 1Πολυώνυμος είναι ένας γραμμικός συνδυασμός πολυωνύμων https://pandia.ru/text/78/624/images/image010_46.gif" width="88 height=24" height="24">. Τα πολυώνυμα αποτελούν ένα γραμμικά ανεξάρτητο σύστημα, αφού το https πολυώνυμο: //pandia.ru/text/78/624/images/image012_44.gif" width="129" height="24">.

Παράδειγμα 2Το σύστημα μήτρας , , https://pandia.ru/text/78/624/images/image016_37.gif" width="51" height="48 src="> είναι γραμμικά ανεξάρτητο, αφού ο γραμμικός συνδυασμός είναι ίσος με το μηδενικός πίνακας μόνο όταν https://pandia.ru/text/78/624/images/image019_27.gif" width="69" height="21">, , https://pandia.ru/text/78/ 624 /images/image022_26.gif" width="40" height="21"> γραμμικά εξαρτώμενο.

Λύση.

Συνθέστε έναν γραμμικό συνδυασμό αυτών των διανυσμάτων https://pandia.ru/text/78/624/images/image023_29.gif" width="97" height="24">=0..gif" width="360" ύψος =" 22">.

Εξίσωση των συντεταγμένων με το ίδιο όνομα ίσα διανύσματα, έχουμε https://pandia.ru/text/78/624/images/image027_24.gif" width="289" height="69">

Τελικά παίρνουμε

και

Το σύστημα έχει μόνο ένα ασήμαντη λύση, άρα ο γραμμικός συνδυασμός αυτών των διανυσμάτων είναι ίσος με μηδέν μόνο στην περίπτωση που όλοι οι συντελεστές είναι ίσοι με μηδέν. Επομένως, αυτό το σύστημα διανυσμάτων είναι γραμμικά ανεξάρτητο.

Παράδειγμα 4Τα διανύσματα είναι γραμμικά ανεξάρτητα. Ποια θα είναι τα συστήματα των διανυσμάτων

ένα).;

σι).?

Λύση.

ένα).Συνθέστε έναν γραμμικό συνδυασμό και εξισώστε τον με μηδέν

Χρησιμοποιώντας τις ιδιότητες των πράξεων με διανύσματα σε γραμμικό χώρο, ξαναγράφουμε την τελευταία ισότητα στη μορφή

Δεδομένου ότι τα διανύσματα είναι γραμμικά ανεξάρτητα, οι συντελεστές για πρέπει να είναι ίσοι με μηδέν, δηλαδή.gif" width="12" height="23 src=">

Το προκύπτον σύστημα εξισώσεων έχει μια μοναδική ασήμαντη λύση .

Από την ισότητα (*) εκτελείται μόνο στη διεύθυνση https://pandia.ru/text/78/624/images/image031_26.gif" width="115 height=20" height="20"> – γραμμικά ανεξάρτητο.

σι).Συνθέστε την ισότητα https://pandia.ru/text/78/624/images/image039_17.gif" width="265" height="24 src="> (**)

Εφαρμόζοντας παρόμοιο σκεπτικό, παίρνουμε

Λύνοντας το σύστημα εξισώσεων με τη μέθοδο Gauss, παίρνουμε

ή

Το τελευταίο σύστημα έχει άπειρο σύνολολύσεις https://pandia.ru/text/78/624/images/image044_14.gif" width="149" height="24 src=">. Έτσι, υπάρχει ένα μη μηδενικό σύνολο συντελεστών για τους οποίους η ισότητα (**) . Επομένως, το σύστημα των διανυσμάτων εξαρτάται γραμμικά.

Παράδειγμα 5Το διανυσματικό σύστημα είναι γραμμικά ανεξάρτητο και το διανυσματικό σύστημα εξαρτάται γραμμικά..gif" width="80" height="24">.gif" width="149 height=24" height="24"> (***)

Ανισότητα (***) . Πράγματι, για το , το σύστημα θα ήταν γραμμικά εξαρτημένο.

Από τη σχέση (***) παίρνουμε ή Σημαίνω .

Παίρνω

Καθήκοντα για ανεξάρτητη λύση(στο κοινό)

1. Ένα σύστημα που περιέχει μηδενικό διάνυσμα εξαρτάται γραμμικά.

2. Ενιαίο διανυσματικό σύστημα ένα, εξαρτάται γραμμικά αν και μόνο αν, a=0.

3. Ένα σύστημα που αποτελείται από δύο διανύσματα εξαρτάται γραμμικά αν και μόνο εάν τα διανύσματα είναι ανάλογα (δηλαδή, το ένα από αυτά προκύπτει από το άλλο πολλαπλασιάζοντας με έναν αριθμό).

4. Αν το k είναι γραμμικό εξαρτημένο σύστημαπροσθέστε ένα διάνυσμα, παίρνετε ένα γραμμικά εξαρτώμενο σύστημα.

5. Αν από γραμμικό ανεξάρτητο σύστημαδιαγράψετε ένα διάνυσμα, τότε το προκύπτον σύστημα διανυσμάτων είναι γραμμικά ανεξάρτητο.

6. Εάν το σύστημα μικρόγραμμικά ανεξάρτητο, αλλά γίνεται γραμμικά εξαρτώμενο όταν προστεθεί ένα διάνυσμα σι, μετά το διάνυσμα σιεκφράζεται γραμμικά ως προς τα διανύσματα του συστήματος μικρό.

ντο).Το σύστημα πινάκων , , στο χώρο πινάκων δεύτερης τάξης.

10. Αφήστε το σύστημα των διανυσμάτων ένα,σι,ντοΟ διανυσματικός χώρος είναι γραμμικά ανεξάρτητος. Αποδεικνύω γραμμική ανεξαρτησία τα ακόλουθα συστήματαφορείς:

ένα).α+β, β, γ.

σι).α+https://pandia.ru/text/78/624/images/image062_13.gif" width="15" height="19">–αυθαίρετος αριθμός

ντο).α+β, α+γ, β+γ.

11. Αφήνω ένα,σι,ντοείναι τρία διανύσματα στο επίπεδο που μπορούν να χρησιμοποιηθούν για να σχηματίσουν ένα τρίγωνο. Αυτά τα διανύσματα θα εξαρτώνται γραμμικά;

12. Δίνονται δύο διανύσματα a1=(1, 2, 3, 4),a2=(0, 0, 0, 1). Σηκώστε δύο ακόμη 4D διανύσματα α3 καια4ώστε το σύστημα Α'1,Α2,α3,α4ήταν γραμμικά ανεξάρτητη .