Αποσύνθεση αριθμών σε πρώτους παράγοντες, μεθόδους και παραδείγματα αποσύνθεσης. Λάβετε την κανονική αποσύνθεση ενός αριθμού σε πρώτους παράγοντες

Διάλεξη 14 Τυχαίες διεργασίες Κανονική επέκταση τυχαίων διεργασιών. Φασματική αποσύνθεσηακίνητος τυχαία διαδικασία. Διάλεξη 14
Τυχαίες διαδικασίες
Κανονική επέκταση τυχαίων διεργασιών.
Φασματική αποσύνθεση ακίνητης τυχαίας
επεξεργάζομαι, διαδικασία. Τυχαίες διαδικασίες με ανεξάρτητες
ενότητες. Διεργασίες Markov και αλυσίδες Markov.
Κανονικές τυχαίες διαδικασίες. Περιοδικά
μη στάσιμες τυχαίες διεργασίες
(Akhmetov S.K.)

Κανονική επέκταση τυχαίων διεργασιών

Οποιοδήποτε SP X(t) m.b. παρουσιάζονται σε
τη μορφή της αποσύνθεσής του, δηλ. ως άθροισμα
στοιχειώδεις διαδικασίες:
Vk - τυχαίες μεταβλητές
φk(t) – μη τυχαίες συναρτήσεις (ημιτονοειδείς, εκθετικές, ισχύς
λειτουργίες, κλπ.)
Μια ειδική περίπτωση τέτοιας αποσύνθεσης είναι η Canonical
αποσύνθεση
SP X(t), που έχει τη μορφή
mx(t) = M – μαθηματική προσδοκία του SP X(t)
V1, V2…Vk – μη συσχετισμένα και κεντραρισμένα SV
D1, D2…Dk- Διασπορές SW V1, V2…Vk
φk(t) – μη τυχαίες συναρτήσεις του ορίσματος t
Οι τυχαίες μεταβλητές V1, V2…Vk ονομάζονται συντελεστές του κανονικού
αποσύνθεση,
και μη τυχαίες συναρτήσεις φ1(t), φ2(t) φk(t) - συναρτήσεις συντεταγμένων
κανονική επέκταση

Κύρια χαρακτηριστικά του SP που ορίζονται από την κανονική αποσύνθεση

M – μαθηματική προσδοκία του SP X(t)
Kx(t,t') - συνάρτηση συσχέτισης SP X(t)
Εκφραση
- κανονική επέκταση του συσχετισμού
λειτουργίες
Αν t=t’, τότε σύμφωνα με το πρώτο
ιδιότητα της συνάρτησης συσχέτισης
Εκφραση
Dk(t) -
διασπορά
κανονική επέκταση της διακύμανσης του SP X(t)

Φασματική αποσύνθεση ενός ακίνητου SP

Σταθερή κοινοπραξία m.b. αντιπροσωπεύεται από την κανονική αποσύνθεση
Vk και Uk – μη συσχετισμένα και κεντραρισμένα SV με διασπορές
D = D = Dk
ω – μη τυχαία τιμή (συχνότητα)
Σε αυτή την περίπτωση, η κανονική επέκταση της συνάρτησης συσχέτισης
καθορίζεται από την έκφραση
Υποβλήθηκε
κανονικός
αποσύνθεση
JV
X(t)
που ονομάζεται
φασματική αποσύνθεση του SP και
εκφράστηκε ώς
Θk - φάση αρμονική δόνησηστοιχειώδες σταθερό SP,
είναι ένα ΝΔ ομοιόμορφα κατανεμημένο στο διάστημα (0, 2π).
Zk – SV, που είναι το πλάτος της αρμονικής ταλάντωσης
στοιχειώδες σταθερό ΣΠ

Φασματική αποσύνθεση σταθερού SP (2)

Οι τυχαίες μεταβλητές Θk και Zk είναι εξαρτημένες και ισχύουν τα ακόλουθα για αυτές:
Vk = Zk cos Θk
Uk = Zk sin Θk
Σταθερή κοινοπραξία m.b. παρουσιάζεται ως άθροισμα αρμονικών
ταλαντώσεις με τυχαία πλάτη Zk και τυχαίες φάσεις Θk on
διάφορες μη τυχαίες συχνότητες ωκ
Η συνάρτηση συσχέτισης του στατικού SP X(t) είναι άρτια
συνάρτηση του επιχειρήματός του, δηλ. kx(τ) = kx(-τ). Επομένως, στο διάστημα (-T,
T) μπορεί να επεκταθεί σε μια σειρά Fourier σε άρτιες (συνημίτονες) αρμονικές:
Η διακύμανση του ακίνητου SP X(t) είναι ίση με
ποσό
αποκλίσεις
Ολοι
αρμονικές
του
φασματική αποσύνθεση
Η εξάρτηση Dk = f(wk) ονομάζεται διακριτό φάσμα διασποράς ή
διακριτό φάσμα ενός ακίνητου SP.

Φασματική αποσύνθεση σταθερού SP (3)

Στο ∆ω
→ 0 θα υπάρξει μετάβαση σε ένα συνεχές φάσμα
Sx(ω) - φασματική πυκνότητα
Έτσι, η συνάρτηση συσχέτισης και η φασματική πυκνότητα
συνδεδεμένο με συνημίτονο – μετασχηματισμό Fourier. Επομένως, το φασματικό
πυκνότητα σταθερής κοινοπραξίας μ.β. εκφράζεται μέσω συσχέτισης
συνάρτηση κατά τύπο

Τυχαίες διεργασίες με ανεξάρτητες διατομές

Στην υδρολογία, πιστεύεται ότι η σειρά αντιστοιχεί σε ένα τυχαίο μοντέλο
τιμές, εάν δεν υπάρχει σημαντική συσχέτιση μεταξύ των μελών αυτής της σειράς
για οποιαδήποτε βάρδια τ.
Μια τυχαία διαδικασία με ανεξάρτητες διατομές είναι μια SP για την οποία
στις τιμές t και t
mx(t) = mx
Dx(t) = Dx
Kx(t,t’) = kx(τ) = (Dx για τ = 0 και 0 για τ ≠ 0)
Μια τέτοια διαδικασία είναι στατική και έχει εργοδοτική
ιδιοκτησία
Για τέτοιες διαδικασίες, τα χαρακτηριστικά του νόμου της μονοδιάστατης κατανομής
μπορεί να αξιολογηθεί τόσο για οποιαδήποτε ενότητα όσο και για οποιαδήποτε (αρκετά
μακροπρόθεσμη) υλοποίηση
Τέτοιες διαδικασίες δεν έχουν καμία συσχέτιση μεταξύ των μελών σε κανένα
εκτέλεση
Αποδεχόμενοι ένα τέτοιο μοντέλο, υποτίθεται ότι ένας αριθμός υδρολογικών μεγεθών
αντιπροσωπεύει μία υλοποίηση της κοινής επιχείρησης
Μερικές φορές ονομάζεται μια τυχαία διαδικασία με ανεξάρτητες διατομές
"λευκός θόρυβος" κατ' αναλογία με λευκό φως

Διεργασίες Markov και αλυσίδες Markov

Τυχαία διαδικασία
λέγεται Μαρκοβιανός αν υπάρχει
τη χρονική στιγμή t την πιθανότητα κάθε κατάστασης του συστήματος στο μέλλον
(στο t > t0) εξαρτάται μόνο από την κατάστασή του στο παρόν (στο t = t0) και όχι
εξαρτάται από την κατάστασή του στο παρελθόν (στο t< t0)
Markov αλυσίδα ή απλό Αλυσίδα Markovπου ονομάζεται
Διαδικασία Markov με διακριτή κατάσταση και διακριτό χρόνο
Ο Markov SP περιγράφεται πλήρως από έναν δισδιάστατο νόμο
διανομές. Αν διαδικασία Markovείναι ακίνητο και
εργοδοτικό, τότε τα χαρακτηριστικά του μπορούν να εκτιμηθούν βάσει ενός
εκτέλεση.
Το κύκλωμα στο οποίο υπό όρους πιθανότητεςκράτη στο μέλλον εξαρτώνται
από την κατάστασή του σε πολλά προηγούμενα βήματα ονομάζεται σύνθετη
Αλυσίδα Markov.

Κανονικές (Gaussian) τυχαίες διεργασίες

Μια κανονική (Gaussian) τυχαία διαδικασία X(t) ονομάζεται
SP, στο οποίο σε όλα τα τμήματα το SP X(ti) έχει κανονικό
διανομή
Περιοδικά μη στάσιμες κοινοπραξίες
Όταν μελετάτε ετήσια, μηνιαία, ημερήσια κ.λπ. διαδικασίες είναι συνήθως
παρατηρείται ενδοετησίως κ.λπ. διακυμάνσεις. Στην περίπτωση αυτή, όπως
μαθηματικό μοντέλο, μπορείτε να χρησιμοποιείτε το μοντέλο περιοδικά
μη σταθερή τυχαία διαδικασία (NSRP)
Μια τυχαία διαδικασία ονομάζεται περιοδικά μη στάσιμη αν
Τα πιθανοτικά χαρακτηριστικά του είναι αμετάβλητα σε σχέση με τις μετατοπίσεις κατά
θετικός αριθμός Τ. Για παράδειγμα, με ένα διακριτό βήμα ενός μήνα
Η αμετάβλητη πρέπει να διατηρηθεί για βάρδιες 12, 24, 36 κ.λπ.

Αυτό το άρθρο δίνει απαντήσεις στο ερώτημα της παραγοντοποίησης ενός αριθμού σε ένα φύλλο. Ας σκεφτούμε γενική ιδέασχετικά με την αποσύνθεση με παραδείγματα. Ας το τακτοποιήσουμε κανονική μορφήαποσύνθεση και ο αλγόριθμός της. Όλες οι εναλλακτικές μέθοδοι θα εξεταστούν χρησιμοποιώντας πρόσημα διαιρετότητας και πίνακες πολλαπλασιασμού.

Yandex.RTB R-A-339285-1

Τι σημαίνει να συνυπολογίζουμε έναν αριθμό σε πρώτους παράγοντες;

Ας δούμε την έννοια πρωταρχικούς παράγοντες. Είναι γνωστό ότι κάθε πρώτος παράγοντας είναι πρώτος αριθμός. Σε ένα γινόμενο της μορφής 2 · 7 · 7 · 23 έχουμε ότι έχουμε 4 πρώτους παράγοντες στη μορφή 2, 7, 7, 23.

Η παραγοντοποίηση περιλαμβάνει την αναπαράστασή της με τη μορφή προϊόντων πρώτων. Αν χρειαστεί να αποσυνθέσουμε τον αριθμό 30, τότε παίρνουμε 2, 3, 5. Η καταχώρηση θα έχει τη μορφή 30 = 2 · 3 · 5. Είναι πιθανό οι πολλαπλασιαστές να επαναληφθούν. Ένας αριθμός όπως το 144 έχει 144 = 2 2 2 2 3 3.

Δεν είναι όλοι οι αριθμοί επιρρεπείς στη φθορά. Οι αριθμοί που είναι μεγαλύτεροι από 1 και είναι ακέραιοι μπορούν να παραγοντοποιηθούν. Οι πρώτοι αριθμοί, όταν συνυπολογίζονται, διαιρούνται μόνο με το 1 και τον εαυτό τους, επομένως είναι αδύνατο να αναπαραστήσουμε αυτούς τους αριθμούς ως γινόμενο.

Όταν το z αναφέρεται σε ακέραιους αριθμούς, αναπαρίσταται ως γινόμενο των a και b, όπου το z διαιρείται με το a και το b. Οι σύνθετοι αριθμοί παράγονται χρησιμοποιώντας το θεμελιώδες θεώρημα της αριθμητικής. Αν ο αριθμός είναι μεγαλύτερος από 1, τότε η παραγοντοποίησή του p 1, p 2, ..., p n παίρνει τη μορφή a = p 1 , p 2 , … , p n . Η αποσύνθεση θεωρείται ότι είναι σε μία μόνο παραλλαγή.

Κανονική παραγοντοποίηση ενός αριθμού σε πρώτους παράγοντες

Κατά τη διάρκεια της επέκτασης, οι παράγοντες μπορούν να επαναληφθούν. Είναι γραμμένα συμπαγή χρησιμοποιώντας μοίρες. Αν, κατά την αποσύνθεση του αριθμού a, έχουμε έναν παράγοντα p 1, ο οποίος εμφανίζεται s 1 φορές και ούτω καθεξής p n – s n φορές. Έτσι η επέκταση θα πάρει τη μορφή a=p 1 s 1 · a = p 1 s 1 · p 2 s 2 · … · p n s n. Αυτή η καταχώρηση ονομάζεται κανονική παραγοντοποίηση ενός αριθμού σε πρώτους παράγοντες.

Όταν επεκτείνουμε τον αριθμό 609840, παίρνουμε ότι 609 840 = 2 2 2 2 3 3 5 7 11 11, η κανονική του μορφή θα είναι 609 840 = 2 4 3 2 5 7 11 2. Χρησιμοποιώντας την κανονική επέκταση, μπορείτε να βρείτε όλους τους διαιρέτες ενός αριθμού και τον αριθμό τους.

Για να παραγοντοποιήσετε σωστά, πρέπει να κατανοήσετε τους πρώτους και τους σύνθετους αριθμούς. Το θέμα είναι να ληφθεί ένας διαδοχικός αριθμός διαιρετών της μορφής p 1, p 2, ..., p n αριθμοί a , a 1 , a 2 , ... , a n - 1, αυτό καθιστά δυνατή την απόκτηση a = p 1 a 1, όπου a 1 = a: p 1 , a = p 1 · a 1 = p 1 · p 2 · a 2 , όπου a 2 = a 1: p 2 , … , a = p 1 · p 2 · … · p n · a n , όπου a n = a n - 1: p n. Κατά την παραλαβή a n = 1, μετά η ισότητα a = p 1 · p 2 · … · p nλαμβάνουμε την απαιτούμενη αποσύνθεση του αριθμού α σε πρώτους παράγοντες. σημειώσε ότι p 1 ≤ p 2 ≤ p 3 ≤ … ≤ p n.

Να βρεις το μικρότερο κοινούς διαιρέτεςπρέπει να χρησιμοποιήσετε έναν πίνακα πρώτων αριθμών. Αυτό γίνεται χρησιμοποιώντας το παράδειγμα εύρεσης του μικρότερου πρώτου διαιρέτη του αριθμού z. Όταν παίρνουμε πρώτους αριθμούς 2, 3, 5, 11 και ούτω καθεξής, και διαιρούμε τον αριθμό z με αυτούς. Αφού το z δεν είναι πρώτος αριθμός, θα πρέπει να ληφθεί υπόψη ότι ο μικρότερος πρώτος διαιρέτης δεν θα είναι μεγαλύτερος από z. Μπορεί να φανεί ότι δεν υπάρχουν διαιρέτες του z, τότε είναι σαφές ότι το z είναι πρώτος αριθμός.

Παράδειγμα 1

Ας δούμε το παράδειγμα του αριθμού 87. Όταν διαιρεθεί με το 2, έχουμε ότι 87: 2 = 43 με υπόλοιπο 1. Επομένως, το 2 δεν μπορεί να είναι διαιρέτης· η διαίρεση πρέπει να γίνει εξ ολοκλήρου. Όταν διαιρεθεί με το 3, παίρνουμε ότι 87: 3 = 29. Ως εκ τούτου, το συμπέρασμα είναι ότι το 3 είναι ο μικρότερος πρώτος διαιρέτης του αριθμού 87.

Όταν συνυπολογίζετε τους πρώτους παράγοντες, πρέπει να χρησιμοποιείτε έναν πίνακα πρώτων αριθμών, όπου α. Κατά την παραγοντοποίηση 95, θα πρέπει να χρησιμοποιήσετε περίπου 10 πρώτους αριθμούς και κατά την παραγοντοποίηση 846653, περίπου 1000.

Ας εξετάσουμε τον αλγόριθμο αποσύνθεσης σε πρώτους παράγοντες:

• βρίσκοντας τον μικρότερο παράγοντα του διαιρέτη p 1 ενός αριθμού έναμε τον τύπο a 1 = a: p 1, όταν a 1 = 1, τότε ο a είναι πρώτος αριθμός και περιλαμβάνεται στην παραγοντοποίηση, όταν δεν ισούται με 1, τότε a = p 1 · a 1 και ακολουθήστε το παρακάτω σημείο.
• βρίσκοντας τον πρώτο διαιρέτη p 2 ενός αριθμού a 1 με τη διαδοχική απαρίθμηση πρώτων αριθμών χρησιμοποιώντας a 2 = a 1: p 2 , όταν a 2 = 1 , τότε η επέκταση θα πάρει τη μορφή a = p 1 p 2 , όταν a 2 = 1, τότε a = p 1 p 2 a 2 , και προχωράμε στο επόμενο βήμα.
• ψάχνοντας στους πρώτους αριθμούς και βρίσκοντας πρώτο διαιρέτη σελ 3αριθμοί Α2σύμφωνα με τον τύπο a 3 = a 2: p 3 όταν a 3 = 1 , τότε παίρνουμε ότι a = p 1 p 2 p 3 , όταν δεν είναι ίσο με 1, τότε a = p 1 p 2 p 3 a 3 και προχωρήστε στο επόμενο βήμα.
• βρίσκεται ο πρώτος διαιρέτης p nαριθμοί α ν - 1με την απαρίθμηση πρώτων αριθμών με pn - 1, και a n = a n - 1: p n, όπου a n = 1, το βήμα είναι τελικό, ως αποτέλεσμα παίρνουμε ότι a = p 1 · p 2 · … · p n .

Το αποτέλεσμα του αλγορίθμου γράφεται με τη μορφή πίνακα με τους αποσυντεθειμένους συντελεστές με μια κάθετη ράβδο διαδοχικά σε μια στήλη. Σκεφτείτε το παρακάτω σχήμα.

Ο αλγόριθμος που προκύπτει μπορεί να εφαρμοστεί με την αποσύνθεση των αριθμών σε πρώτους παράγοντες.

Κατά την παραγοντοποίηση σε πρώτους παράγοντες, θα πρέπει να ακολουθείται ο βασικός αλγόριθμος.

Παράδειγμα 2

Παράγοντας τον αριθμό 78 σε πρώτους παράγοντες.

Λύση

Για να βρείτε τον μικρότερο πρώτο διαιρέτη, πρέπει να διαβάσετε όλους τους πρώτους αριθμούς του 78. Δηλαδή 78: 2 = 39. Διαίρεση χωρίς υπόλοιπο σημαίνει ότι αυτός είναι ο πρώτος απλός διαιρέτης, τον οποίο συμβολίζουμε ως p 1. Παίρνουμε ότι a 1 = a: p 1 = 78: 2 = 39. Φτάσαμε σε μια ισότητα της μορφής a = p 1 · a 1 , όπου 78 = 2 39. Τότε a 1 = 39, δηλαδή, πρέπει να προχωρήσουμε στο επόμενο βήμα.

Ας επικεντρωθούμε στην εύρεση του πρώτου διαιρέτη p2αριθμοί a 1 = 39. Θα πρέπει να περάσετε από τους πρώτους αριθμούς, δηλαδή, 39: 2 = 19 (υπόλοιπο 1). Εφόσον διαίρεση με υπόλοιπο, το 2 δεν είναι διαιρέτης. Όταν επιλέγουμε τον αριθμό 3, παίρνουμε ότι 39: 3 = 13. Αυτό σημαίνει ότι ο p 2 = 3 είναι ο μικρότερος πρώτος διαιρέτης του 39 με ένα 2 = a 1: p 2 = 39: 3 = 13. Λαμβάνουμε μια ισότητα της μορφής a = p 1 p 2 a 2με τη μορφή 78 = 2 3 13. Έχουμε ότι ένα 2 = 13 δεν είναι ίσο με 1, τότε πρέπει να προχωρήσουμε.

Ο μικρότερος πρώτος διαιρέτης του αριθμού a 2 = 13 βρίσκεται αναζητώντας αριθμούς, ξεκινώντας από το 3. Παίρνουμε ότι 13: 3 = 4 (υπόλοιπο 1). Από αυτό μπορούμε να δούμε ότι το 13 δεν διαιρείται με το 5, το 7, το 11, επειδή 13: 5 = 2 (υπόλοιπο 3), 13: 7 = 1 (υπόλοιπο 6) και 13: 11 = 1 (υπόλοιπο 2) . Μπορεί να φανεί ότι το 13 είναι πρώτος αριθμός. Σύμφωνα με τον τύπο μοιάζει με αυτό: a 3 = a 2: p 3 = 13: 13 = 1. Βρήκαμε ότι a 3 = 1, που σημαίνει την ολοκλήρωση του αλγορίθμου. Τώρα οι συντελεστές γράφονται ως 78 = 2 · 3 · 13 (a = p 1 · p 2 · p 3) .

Απάντηση: 78 = 2 3 13.

Παράδειγμα 3

Συνυπολογίστε τον αριθμό 83.006 σε πρώτους παράγοντες.

Λύση

Το πρώτο βήμα περιλαμβάνει την παραγοντοποίηση p 1 = 2Και a 1 = a: p 1 = 83.006: 2 = 41.503, όπου 83.006 = 2 · 41.503.

Το δεύτερο βήμα προϋποθέτει ότι το 2, το 3 και το 5 δεν είναι πρώτοι διαιρέτες για τον αριθμό a 1 = 41.503, αλλά το 7 είναι πρώτος διαιρέτης, επειδή 41.503: 7 = 5.929. Παίρνουμε ότι p 2 = 7, a 2 = a 1: p 2 = 41.503: 7 = 5.929. Προφανώς, 83.006 = 2 7 5 929.

Η εύρεση του μικρότερου πρώτου διαιρέτη του p 4 στον αριθμό a 3 = 847 είναι 7. Μπορεί να φανεί ότι a 4 = a 3: p 4 = 847: 7 = 121, άρα 83 006 = 2 7 7 7 121.

Για να βρούμε τον πρώτο διαιρέτη του αριθμού a 4 = 121, χρησιμοποιούμε τον αριθμό 11, δηλαδή p 5 = 11. Τότε παίρνουμε μια έκφραση της φόρμας a 5 = a 4: p 5 = 121: 11 = 11και 83.006 = 2 7 7 7 11 11.

Για τον αριθμό a 5 = 11αριθμός p 6 = 11είναι ο μικρότερος πρώτος διαιρέτης. Ως εκ τούτου a 6 = a 5: p 6 = 11: 11 = 1. Τότε ένα 6 = 1. Αυτό υποδηλώνει την ολοκλήρωση του αλγορίθμου. Οι συντελεστές θα γραφτούν ως 83 006 = 2 · 7 · 7 · 7 · 11 · 11.

Ο κανονικός συμβολισμός της απάντησης θα έχει τη μορφή 83 006 = 2 · 7 3 · 11 2.

Απάντηση: 83 006 = 2 7 7 7 11 11 = 2 7 3 11 2.

Παράδειγμα 4

Υπολογίστε τον αριθμό 897.924.289.

Λύση

Για να βρείτε τον πρώτο πρώτο παράγοντα, αναζητήστε τους πρώτους αριθμούς, ξεκινώντας από το 2. Το τέλος της αναζήτησης εμφανίζεται στον αριθμό 937. Τότε p 1 = 937, a 1 = a: p 1 = 897 924 289: 937 = 958 297 και 897 924 289 = 937 958 297.

Το δεύτερο βήμα του αλγορίθμου είναι η επανάληψη σε μικρότερους πρώτους αριθμούς. Δηλαδή ξεκινάμε με τον αριθμό 937. Ο αριθμός 967 μπορεί να θεωρηθεί πρώτος επειδή είναι πρώτος διαιρέτης του αριθμού a 1 = 958.297. Από εδώ παίρνουμε ότι p 2 = 967, μετά a 2 = a 1: p 1 = 958 297: 967 = 991 και 897 924 289 = 937 967 991.

Το τρίτο βήμα λέει ότι το 991 είναι πρώτος αριθμός, αφού δεν έχει ούτε έναν πρώτο παράγοντα που να μην υπερβαίνει το 991. Η κατά προσέγγιση τιμή της έκφρασης ρίζας είναι 991< 40 2 . Иначе запишем как 991 < 40 2 . Αυτό δείχνει ότι p 3 = 991 και a 3 = a 2: p 3 = 991: 991 = 1. Βρίσκουμε ότι η αποσύνθεση του αριθμού 897 924 289 σε πρώτους παράγοντες προκύπτει ως 897 924 289 = 937 967 991.

Απάντηση: 897 924 289 = 937 967 991.

Χρησιμοποιώντας τεστ διαιρετότητας για παραγοντοποίηση πρώτων

Για να συνυπολογίσετε έναν αριθμό σε πρώτους παράγοντες, πρέπει να ακολουθήσετε έναν αλγόριθμο. Όταν υπάρχουν μικροί αριθμοί, επιτρέπεται η χρήση του πίνακα πολλαπλασιασμού και των σημάτων διαιρετότητας. Ας το δούμε αυτό με παραδείγματα.

Παράδειγμα 5

Εάν είναι απαραίτητο να παραγοντοποιήσετε το 10, τότε ο πίνακας δείχνει: 2 · 5 = 10. Οι αριθμοί 2 και 5 που προκύπτουν είναι πρώτοι αριθμοί, επομένως είναι πρώτοι παράγοντες για τον αριθμό 10.

Παράδειγμα 6

Εάν είναι απαραίτητο να αποσυντεθεί ο αριθμός 48, τότε ο πίνακας δείχνει: 48 = 6 8. Αλλά το 6 και το 8 δεν είναι πρώτοι παράγοντες, αφού μπορούν επίσης να επεκταθούν ως 6 = 2 3 και 8 = 2 4. Επειτα πλήρης αποσύνθεσηεπομένως προκύπτει ως 48 = 6 8 = 2 3 2 4. Ο κανονικός συμβολισμός θα έχει τη μορφή 48 = 2 4 · 3.

Παράδειγμα 7

Κατά την αποσύνθεση του αριθμού 3400, μπορείτε να χρησιμοποιήσετε τα σημάδια της διαιρετότητας. ΣΕ σε αυτήν την περίπτωσηΤα κριτήρια διαιρετότητας με το 10 και το 100 είναι σχετικά. Από εδώ παίρνουμε ότι 3.400 = 34 · 100, όπου το 100 μπορεί να διαιρεθεί με το 10, δηλαδή να γράφεται ως 100 = 10 · 10, που σημαίνει ότι 3.400 = 34 · 10 · 10. Με βάση το τεστ διαιρετότητας, βρίσκουμε ότι 3 400 = 34 10 10 = 2 17 2 5 2 5. Όλοι οι παράγοντες είναι πρωταρχικοί. Η κανονική επέκταση παίρνει τη μορφή 3 400 = 2 3 5 2 17.

Όταν βρίσκουμε πρώτους παράγοντες, πρέπει να χρησιμοποιούμε τεστ διαιρετότητας και πίνακες πολλαπλασιασμού. Εάν φανταστείτε τον αριθμό 75 ως γινόμενο παραγόντων, τότε πρέπει να λάβετε υπόψη τον κανόνα της διαιρετότητας με το 5. Παίρνουμε ότι 75 = 5 15 και 15 = 3 5. Δηλαδή, η επιθυμητή επέκταση είναι ένα παράδειγμα της μορφής του προϊόντος 75 = 5 · 3 · 5.

Εάν παρατηρήσετε κάποιο σφάλμα στο κείμενο, επισημάνετε το και πατήστε Ctrl+Enter

Καλείται η τυχαία μεταβλητή V κεντραρισμένος , αν η μαθηματική της προσδοκία είναι ίση με 0. Μια στοιχειώδης κεντραρισμένη τυχαία διαδικασία είναι το γινόμενο μιας κεντραρισμένης τυχαίας μεταβλητής V και μιας μη τυχαίας συνάρτησης φ(t):X(t)=Vφ(t). Μια στοιχειώδης επικεντρωμένη τυχαία διαδικασία έχει τα ακόλουθα χαρακτηριστικά:

Έκφραση της φόρμας
, όπου φ κ ( t ), κ =1;2;…-μη τυχαίες συναρτήσεις; , κ =1;2;…-μη συσχετισμένες κεντραρισμένες τυχαίες μεταβλητές, που ονομάζονται κανονική επέκταση της τυχαίας διαδικασίαςΧ ( t ), ενώ οι τυχαίες μεταβλητές ονομάζονται συντελεστές της κανονικής επέκτασης. και μη τυχαίες συναρτήσεις φ κ ( t ) - συντεταγμένες συναρτήσεις της κανονικής επέκτασης.

Ας εξετάσουμε τα χαρακτηριστικά μιας τυχαίας διαδικασίας

Αφού κατά συνθήκη
Οτι

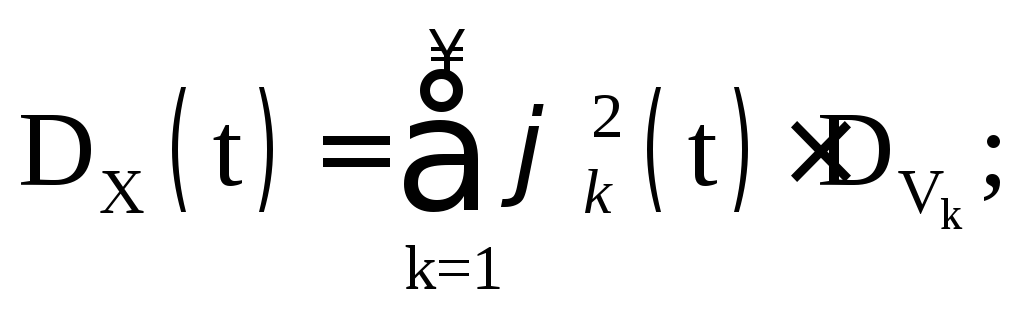
Προφανώς, η ίδια τυχαία διαδικασία έχει διαφορετικά είδηκανονική επέκταση ανάλογα με την επιλογή των συναρτήσεων συντεταγμένων. Επιπλέον, ακόμη και με την επιλογή των συναρτήσεων συντεταγμένων, υπάρχει αυθαιρεσία στην κατανομή των τυχαίων μεταβλητών V k. Στην πράξη, με βάση τα αποτελέσματα των πειραμάτων, λαμβάνονται εκτιμήσεις για τη μαθηματική προσδοκία και τη συνάρτηση συσχέτισης:
. Μετά την αποσύνθεση
σε διπλή σειρά Fourier στις συντεταγμένες φ έως (t):

λάβετε τιμές διακύμανσης
τυχαίες μεταβλητές V k .

4.2. Η έννοια της γενικευμένης συνάρτησης. Συνάρτηση δέλτα Dirac. Ολοκληρωμένη κανονική αναπαράσταση τυχαίων διεργασιών.

Γενικευμένη λειτουργία ονομάζεται όριο μιας ακολουθίας μιας μονοπαραμετρικής οικογένειας συνεχών συναρτήσεων.

Συνάρτηση δέλτα Dirac
- αυτή είναι μια γενικευμένη συνάρτηση που προκύπτει από τη μετάβαση στο όριο στο
σε μια οικογένεια λειτουργιών

Ανάμεσα στα ακίνητα -συναρτήσεις σημειώνουμε τα εξής:

2.

3. Αν f(t)- συνεχής λειτουργία, Οτι

Τυχαία διαδικασία X( t ), η συνάρτηση συσχέτισης της οποίας έχει τη μορφή που ονομάζεται μη στάσιμος «λευκός θόρυβος». Αν W ( t 1 )= W - συνθ , μετά Χ( t )-στάσιμος «λευκός θόρυβος».

Όπως προκύπτει από τον ορισμό, δεν συσχετίζονται δύο, όσο στενά κι αν είναι, τμήματα «λευκού θορύβου». Η έκφραση W(t) ονομάζεται ένταση «λευκού θορύβου».

Ολοκληρωμένη κανονική αναπαράσταση της τυχαίας διαδικασίας X( t ) ονομάζεται έκφραση της μορφής
Οπου
- τυχαία κεντραρισμένη συνάρτηση.
- μη τυχαία συνάρτηση συνεχών ορισμάτων

Η συνάρτηση συσχέτισης μιας τέτοιας τυχαίας διαδικασίας έχει τη μορφή:

Μπορεί να φανεί ότι υπάρχει μια μη τυχαία συνάρτηση G(λ) τέτοια ώστε

όπου G(λ 1) είναι η πυκνότητα διασποράς. Το δ(x) είναι η συνάρτηση δέλτα Dirac. Παίρνουμε

Επομένως, η διακύμανση της τυχαίας διαδικασίας X(t):

.

4.3. Γραμμικοί και μη γραμμικοί μετασχηματισμοί τυχαίων διεργασιών

Εξετάζεται το ακόλουθο πρόβλημα: ένα «σήμα εισόδου» που έχει τη φύση μιας τυχαίας διεργασίας X(t) παρέχεται στην είσοδο του συστήματος (συσκευή, μετατροπέας) S. Το σύστημα το μετατρέπει σε «σήμα εξόδου» Y(t):

.

Τυπικά, ο μετασχηματισμός μιας τυχαίας διαδικασίας X(t) σε Y(t) μπορεί να περιγραφεί χρησιμοποιώντας τον λεγόμενο χειριστή συστήματος A t:

Y(t)=A t (X(t)).

Ο δείκτης t υποδεικνύει ότι αυτός ο τελεστής εκτελεί μια χρονική μετατροπή. Οι ακόλουθες διατυπώσεις του προβλήματος του μετασχηματισμού μιας τυχαίας διαδικασίας είναι δυνατές.

Οι νόμοι της διανομής είναι γνωστοί ή Γενικά χαρακτηριστικάτυχαία διαδικασία X(t) στην είσοδο του συστήματος S, δίνεται ο τελεστής A t του συστήματος S, είναι απαραίτητο να προσδιοριστεί ο νόμος κατανομής ή τα γενικά χαρακτηριστικά της τυχαίας διαδικασίας Y(t) στην έξοδο του συστήματος ΜΙΚΡΟ.

Οι νόμοι κατανομής (γενικά χαρακτηριστικά) της τυχαίας διεργασίας X(t) και οι απαιτήσεις για την τυχαία διαδικασία Y(t) είναι γνωστοί. είναι απαραίτητο να προσδιοριστεί ο τύπος χειριστή A t του συστήματος S που ικανοποιεί καλύτερα τις δεδομένες απαιτήσεις kY(t).

Οι νόμοι κατανομής (γενικά χαρακτηριστικά) της τυχαίας διαδικασίας Y(t) είναι γνωστοί και δίνεται ο τελεστής A t του συστήματος S. απαιτείται να καθοριστούν οι νόμοι κατανομής ή τα γενικά χαρακτηριστικά της τυχαίας διαδικασίας X(t).

Π rinyata επόμενη ταξινόμησηχειριστές A t του συστήματος S:

Χειριστές Συστήματος

Γραμμικό LΜη ΓραμμικόΝ

Γραμμική ομοιογενής L 0 Γραμμική ανομοιογενής L n

Ας εξετάσουμε την επίδραση ενός γραμμικού ανομοιογενούς συστήματος

L n (...)=L 0 (...)+φ(t)

σε μια τυχαία διεργασία X(t) που έχει την ακόλουθη κανονική επέκταση:

.

Παίρνουμε:

ας εισαγάγουμε τη σημειογραφία

τότε η κανονική επέκταση του Y(t) παίρνει τη μορφή:

.

Μαθηματική προσδοκία της τυχαίας διαδικασίας Y(t):

συνάρτηση συσχέτισης της τυχαίας διαδικασίας Y(t):

ως εκ τούτου,

Στην άλλη πλευρά

Διακύμανση της τυχαίας διαδικασίας Y(t):

Συμπερασματικά αυτής της παραγράφου, σημειώνουμε ότι οι τελεστές διαφοροποίησης και ολοκλήρωσης τυχαίων διεργασιών είναι γραμμικά ομοιογενείς.

2. Ο τετραγωνικός μετασχηματισμός θεωρείται:

Y(t)=(X(t)) 2,

V k-κεντρικές τυχαίες μεταβλητές που έχουν συμμετρική κατανομή περίπου μηδέν. οποιαδήποτε τέσσερα από αυτά είναι από κοινού ανεξάρτητα. Επειτα

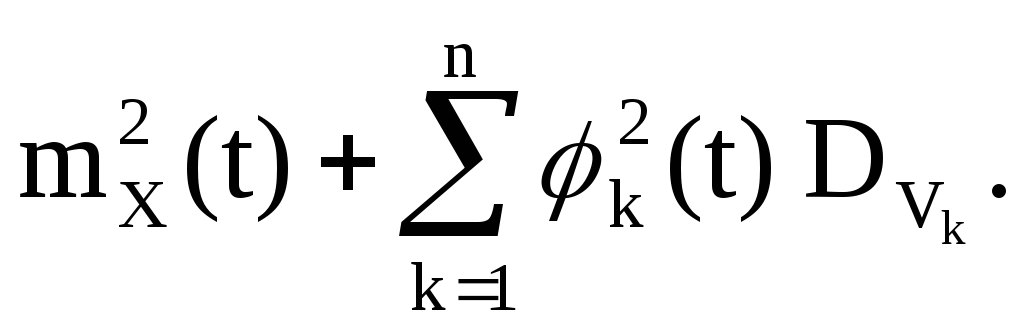
Ας εισάγουμε μη τυχαίες συναρτήσεις

και τυχαίες μεταβλητές

τότε η τυχαία διαδικασία Y(t) παίρνει τη μορφή

Λαμβάνεται μια κανονική επέκταση της τυχαίας διαδικασίας Y(t). Συνάρτηση συσχέτισηςY(t):

Διατύπωση.Δεδομένος φυσικός αριθμός n(n > 1). Λάβετε την κανονική αποσύνθεσή του σε απλούς παράγοντες, παρουσιάζετέ τον δηλαδή ως προϊόν απλών παραγόντων. Σε αυτήν την περίπτωση, επιτρέπεται η ένδειξη συντελεστή 1 στην επέκταση. Για παράδειγμα, 264 = 2 * 2 * 2 * 3 * 11 (το πρόγραμμα μπορεί να παράγει την απάντηση 264 = 1 * 2 * 2 * 2 * 3 * 11).

Λύση. Αυτή η εργασίαέχει μια πολύ ωραία λύση.

Από θεμελιώδες θεώρημα της αριθμητικήςΕίναι γνωστό ότι για οποιονδήποτε φυσικό αριθμό μεγαλύτερο από 1 υπάρχει μια κανονική αποσύνθεση σε πρώτους παράγοντες, και αυτή η αποσύνθεση είναι μοναδική μέχρι την τάξη των παραγόντων. Δηλαδή, για παράδειγμα, 12 = 2 * 2 * 2 και 12 = 3 * 2 * 2 είναι οι ίδιες επεκτάσεις.

Εξετάστε την κανονική μορφή οποιουδήποτε αριθμού επάνω συγκεκριμένο παράδειγμα. Για παράδειγμα, 264 = 2 * 2 * 2 * 3 * 11. Πώς μπορεί να αναγνωριστεί αυτή η δομή; Για να απαντήσουμε σε αυτό το ερώτημα, ας θυμηθούμε αυτά που αναφέρονται σε οποιαδήποτε σχολικό μάθημαΚανόνες άλγεβρας για τη διαίρεση μονωνύμων, φανταζόμαστε ότι οι αριθμοί στην κανονική επέκταση είναι μεταβλητοί. Όπως γνωρίζετε, εάν διαιρέσετε μια παράσταση σε μια μεταβλητή σε κάποιο βαθμό που περιέχεται σε αυτήν την έκφραση στον ίδιο βαθμό, διαγράφεται στη σημειογραφία της.

Δηλαδή, αν διαιρέσουμε το 264 με το 2, τότε στην κανονική του επέκταση θα είναι ένα δύο. Τότε μπορούμε να ελέγξουμε αν το πηλίκο που προκύπτει διαιρείται ξανά με το 2. Η απάντηση θα είναι ναι, αλλά την τρίτη φορά η διαίρεση θα δώσει υπόλοιπο. Στη συνέχεια, πρέπει να λάβετε υπόψη τον επόμενο φυσικό αριθμό 3 - το πηλίκο θα διαιρεθεί με αυτό μία φορά. Ως αποτέλεσμα, περνώντας την αριθμητική γραμμή προς τη θετική κατεύθυνση, θα φτάσουμε στον αριθμό 11 και αφού διαιρέσουμε με το 11 nθα γίνει ίσο με 1, το οποίο θα υποδεικνύει την ανάγκη ολοκλήρωσης της διαδικασίας.

Γιατί, με τέτοια «διαγραφή» των παραγόντων που βρέθηκαν, δεν παίρνουμε διαιρετότητα σε σύνθετους αριθμούς; Στην πραγματικότητα, όλα είναι απλά εδώ - κάθε σύνθετος αριθμός είναι το γινόμενο πρώτων παραγόντων μικρότερων από αυτόν. Ως αποτέλεσμα, αποδεικνύεται ότι θα διαγράψουμε nόλους τους παράγοντες οποιουδήποτε σύνθετου αριθμού, μέχρι να τον φτάσουμε ο ίδιος στην αλυσίδα των διαιρέσεων. Για παράδειγμα, με μια τόσο εξαντλητική αναζήτηση nδεν θα διαιρεθεί ποτέ με το 4, αφού "στο δρόμο" προς αυτόν τον αριθμό θα διαγράψουμε από nόλοι οι παράγοντες είναι δύο.

Αλγόριθμος σε φυσική γλώσσα:

1) Εισαγωγή n;

2) Ανάθεση σε μεταβλητή Παριθμοί 2;

3) Πληκτρολογήστε τον αριθμό n, σύμβολο ίσου και μονάδα για την επισημοποίηση της επέκτασης.

4) Έναρξη βρόχου με προϋπόθεση n< > 1 . Σε βρόχο:

1. Αν Μmodp = 0, μετά εμφανίστε το πρόσημο πολλαπλασιασμού και τη μεταβλητή p και μετά διαιρέστε nεπί Π, διαφορετικά αυξήστε την τιμή Εγώμε 1?

1. πρόγραμμα PrimeFactors?
2. n, p: λέξη;
3. αρχίζουν
4. p:= 2;
5. readln(n);
6. write(n, ' = 1');
7. ενώ n<>1 ξεκινήστε
8. αν (n mod p) = 0 τότε ξεκινήστε
9. write(' * ', p);
10. n:= n div p
11. αλλιως αρχιζουν
12. inc(p)