Sample from m to n. Placements with repetitions
COMBINATORICS
Combinatorics is a branch of mathematics that studies the problems of selecting and arranging elements from a certain basic set in accordance with given rules. Formulas and principles of combinatorics are used in probability theory to calculate probability random events and, accordingly, obtaining distribution laws random variables. This, in turn, allows us to study the patterns of mass random phenomena, which is very important for a correct understanding of the statistical patterns that manifest themselves in nature and technology.
Rules for addition and multiplication in combinatorics
Sum rule. If two actions A and B are mutually exclusive, and action A can be performed in m ways, and B in n ways, then one of these actions (either A or B) can be performed in n + m ways.
Example 1.
There are 16 boys and 10 girls in the class. In how many ways can you assign one duty officer?
Solution
Either a boy or a girl can be assigned to duty, i.e. the duty officer can be any of the 16 boys or any of the 10 girls.
Using the sum rule, we find that one duty officer can be assigned in 16+10=26 ways.
Product rule. Let there be k actions required to be performed sequentially. If the first action can be performed in n 1 ways, the second action in n 2 ways, the third in n 3 ways, and so on until the kth action that can be performed in n k ways, then all k actions together can be performed:
ways.
Example 2.
There are 16 boys and 10 girls in the class. In how many ways can two duty officers be appointed?
Solution
Either a boy or a girl can be appointed as the first person on duty. Because There are 16 boys and 10 girls in the class, then you can appoint the first person on duty in 16+10=26 ways.
After we have chosen the first duty officer, we can choose the second one from the remaining 25 people, i.e. 25 ways.
According to the multiplication theorem, two attendants can be selected in 26*25=650 ways.
Combinations without repetition. Combinations with repetitions
A classic problem in combinatorics is the problem of the number of combinations without repetitions, the content of which can be expressed by the question: how many ways Can choose m from n various items ?
![]()
Example 3.
You must choose 4 out of 10 different books available as a gift. In how many ways can this be done?
Solution
We need to choose 4 books out of 10, and the order of choice does not matter. Thus, you need to find the number of combinations of 10 elements of 4:
![]() .
.
Consider the problem of the number of combinations with repetitions: there are r identical items each of n various types; how many ways Can choose m() from these (n*r) items?
![]() .
.
Example 4.
The pastry shop sold 4 types of cakes: Napoleons, eclairs, shortbread and puff pastries. In how many ways can you buy 7 cakes?
Solution
Because Among 7 cakes there may be cakes of the same type, then the number of ways in which 7 cakes can be bought is determined by the number of combinations with repetitions of 7 to 4.
![]() .
.
Placements without repetition. Placements with repetitions
A classic problem in combinatorics is the problem of the number of placements without repetitions, the content of which can be expressed by the question: how many ways Can choose And post By m different places m from n different items?
![]()
Example 5.
Some newspaper has 12 pages. It is necessary to place four photographs on the pages of this newspaper. In how many ways can this be done if no page of the newspaper should contain more than one photograph?
Solution.
In this task, we do not just select photographs, but place them on certain pages of the newspaper, and each page of the newspaper should contain no more than one photograph. Thus, the problem is reduced to the classical problem of determining the number of placements without repetitions of 12 elements of 4 elements:
Thus, 4 photos on 12 pages can be arranged in 11,880 ways.
Also classic problem combinatorics is the problem of the number of placements with repetitions, the content of which can be expressed by the question: how many ways Can Youbarmy And post By m different places m from n items,Withready which There is the same?
Example 6.
The boy still had stamps with the numbers 1, 3 and 7 from his board game set. He decided to use these stamps to put five-digit numbers on all the books to create a catalogue. How many different five-digit numbers can a boy make?
Permutations without repetition. Permutations with repetitions
A classic problem in combinatorics is the problem of the number of permutations without repetition, the content of which can be expressed by the question: how many ways Can post n various items on n different places?
Example 7.
How many four-letter “words” can you make from the letters of the word “marriage”?
Solution
The general population is the 4 letters of the word “marriage” (b, p, a, k). The number of “words” is determined by the permutations of these 4 letters, i.e.
![]()
For the case when among the selected n elements there are identical ones (selection with return), the problem of the number of permutations with repetitions can be expressed by the question: In how many ways can n objects located in n different places be rearranged if among n objects there are k different types (k< n), т. е. есть одинаковые предметы.

Example 8.
How many different letter combinations can be made from the letters of the word "Mississippi"?
Solution
There is 1 letter "m", 4 letters "i", 3 letters "c" and 1 letter "p", for a total of 9 letters. Therefore, the number of permutations with repetitions is equal to
![]()
BACKGROUND SUMMARY FOR THE SECTION "COMBINATORICS"
Plan:
1. Elements of combinatorics.
2. General rules of combinatorics.
4. Application of graphs (schemes) in solving combinatorial problems.
1. Combinatorics and its origins.Combinatorics- this is an area of mathematics in which questions are studied about how many different combinations, subject to certain conditions, can be made from elements belonging to this set.
Combinatorics originated in the 16th century. Gambling (cards, dice) occupied a large place in the life of the privileged layers of society at that time. Lotteries were widespread. Initially, combinatorial problems concerned mainly gambling: in how many ways can you get given number points by throwing 2 or 3 dice or how many ways can you get 2 kings in a certain card game. These and other gambling problems were driving force in the development of combinatorics and further in the development of probability theory.
One of the first to count the number of different combinations when playing dice was the Italian mathematician Tartaglia. He compiled tables (the number of ways of getting k points on r dice). However, he did not take into account that the same amount of points may appear different ways, so his tables contained a large number of errors.
Theoretical study of combinatorics issues was undertaken in the 17th century French mathematicians Blaise Pascal and Fermat. The starting point of their research was also gambling problems.
The further development of combinatorics is associated with the names of J. Bernoulli, G. Leibniz, L. Euler. However, in their work, applications to various games played a major role.
Today, combinatorial methods are used to solve transport tasks, in particular tasks for drawing up schedules, for drawing up plans for production and sales of products, etc.
2. General rules of combinatorics.Sum rule: If some object A can be chosen in m ways, and an object B in k ways, then the object “either A or B” can be chosen in m + k ways.
Examples:
1. Let's assume that there are n different-colored balls in a box. 1 ball is randomly taken out. In how many ways can this be done?
Answer: n ways.
Let's distribute these n balls into two boxes: the first contains m balls, the second contains k balls. 1 ball is randomly drawn from a randomly selected box. In how many ways can this be done?
Solution: The ball can be removed from the first box in m ways, and from the second in k ways. Then the total number of ways is m+k=n.
2. Marine semaphore.In maritime semaphore, each letter of the alphabet corresponds to a certain position of two flags relative to the signalman’s body. How many such signals can there be?
Solution: The total number is the sum of the positions when both flags are located along different sides from the signalman's body and positions when they are located on one side of the signalman's body. When counting the number of possible positions, the sum rule is applied.
Product rule: If object A can be selected in m ways, and after each such choice another object B can be selected (regardless of the choice of object A) in k ways, then pairs of objects “A and B” can be selected in m * k ways.
Examples:
1. How many double digit numbers exists?Solution: The number of tens can be denoted by any number from 1 to 9. The number of ones can be denoted by any number from 0 to 9. If the number of tens is 1, then the number of ones can be any number (from 0 to 9). Thus, there are 10 two-digit numbers, with the number of tens being 1. We reason similarly for any other number of tens. Then we can calculate that there are 9 *10 = 90 two-digit numbers.
2. There are 2 drawers. One contains m multi-colored cubes, and the other contains k multi-colored balls. In how many ways can you choose the “Cube-Ball” pair?
Solution: The choice of ball does not depend on the choice of cube, and vice versa. Therefore, the number of ways in which a given pair can be selected is m *k .
3. Population without repetition and sample without repetition.Population without repetitions is a set of some finite number various elements a 1 , a 2 , a 3 , ..., a n .
Example: Set of n multi-colored shreds.
Sampling volumek (kn) is a group of m elements of a given population.
Example: A variegated ribbon sewn from m multi-colored scraps selected from the given n .
Postings fromn elements eachk such samples are called those that contain k elements each, selected from among the given n elements of the general population without repetition, and differ from each other either in the composition of the elements or in the order of their arrangement.
- number of placements from n by k.
Number of placements from n by k can be determined in the following way: the first selection object can be selected n ways, then the second object can be selected n -1 way, etc.
Transforming this formula, we have:
It should be remembered that 0!=1.
Examples:
1. There are 17 teams participating in the first class A group of the football championship. Medals are awarded: gold, silver and bronze. In how many ways can they be played?
Solution:The winning team combinations differ from each other in the composition and order of the elements, i.e. are placements from 17 to 3.
2. The scientific society consists of 25 people. It is necessary to elect a society president, vice-president, scientific secretary and treasurer. In how many ways can this be done?
Solution: Combinations of the company's management differ from each other in the composition and order of elements, i.e. are placements from 25 to 4.
Permutations without repetitions from nelementsare called placements without repetitions from n elements of n , i.e. placements differ from each other only in the order of the elements.
Number of permutations.
Examples:
1. How many different five-digit numbers can be made from the numbers 1, 2, 3, 4, 5, provided that they must consist of different numbers?
Solution:We have permutations of 5 elements.2. In how many ways can you assemble 6 multi-colored scraps into a colorful ribbon?Solution:We have permutations of 6 elements.
Combinations without repetitions from nelements byk such samples are called those that contain k elements each, selected from among the given n elements of the general population without repetition, and differ from each other only in the composition of the elements.
- number of combinations of n by k
Elements of eachcombinations can be arrangedways. ThenExamples:1. If 20 people participate in the semifinals of a chess championship, and only three make it to the finals, then in how many ways can these three be determined?
Solution:IN in this case The order in which this three is arranged is not significant. Therefore, the triplets that reached the finals are combinations of 20 by 3.
2. In how many ways can you select three delegates out of ten people for a conference?Solution:In this case, the order in which this triple is located is not significant. Therefore, triplets of delegates are combinations of 10 by 3.
Abstract:
4.Use of graphs (schemes) in solving combinatorial problems.
In the case where the number of possible choices at each step depends on which elements were selected earlier, the process of composing combinations can be depicted as a “tree”. First, as many segments are drawn from one point as there are different choices that can be made at the first step. From the end of each segment, draw as many segments as can be selected at the second step, if this element was selected at the first step, etc.
Task:
When composing teams spaceship The issue of psychological compatibility of travel participants is also taken into account. It is necessary to make up a spaceship crew of 3 people: a commander, an engineer and a doctor. There are 4 candidates for the commander's position: a 1 , a 2 , a 3 , a 4 .In place of engineer 3:b 1, b 2, b 3. For doctor's place - 3: c 1, c 2, c 3. The inspection showed that the commandera 1 is psychologically compatible with engineers b 1 and b 3 and doctors c 1 and c 3. Commander a 2 - with engineers b 1 and b 2. and all the doctors. Commandera 3 - with engineersb 1 and b 2 and doctorsc 1 and c 3. Commander a 4 - with all the engineers and the doctor c 2 . In addition, engineerb 1 not compatible with doctor c 3, b 2 - with a doctor c 1 and b 3 - with a doctor c 2. In how many ways can the ship's crew be composed under these conditions?
Solution:
Let’s create the corresponding “tree”.

Answer: 10 combinations.
Such a tree is a graph and is used to solve combinatorial problems.
Combinatorics is a branch of mathematics that studies questions about how many different combinations, subject to certain conditions, can be made from given objects. The basics of combinatorics are very important for estimating the probabilities of random events, because they allow us to calculate the fundamentally possible number various options developments of events.
Basic formula of combinatorics
Let there be k groups of elements, and i-th the group consists of n i elements. Let's select one element from each group. Then total number
Example 1. Let us explain this rule with a simple example. Let there be two groups of elements, and the first group consists of n 1 elements, and the second - of n 2 elements. How many different pairs of elements can be made from these two groups, such that the pair contains one element from each group? Let's say we took the first element from the first group and, without changing it, went through all possible pairs, changing only the elements from the second group. There can be n 2 such pairs for this element. Then we take the second element from the first group and also make all possible pairs for it. There will also be n 2 such pairs.
Example 2. Since there are only n 1 elements in the first group, the total possible options will be n 1 *n 2 .
Solution: How many three-digit even numbers can be made from the digits 0, 1, 2, 3, 4, 5, 6, if the digits can be repeated?
n 1 =6 (because you can take any number from 1, 2, 3, 4, 5, 6 as the first digit), n 2 =7 (because you can take any number from 0 as the second digit , 1, 2, 3, 4, 5, 6), n 3 =4 (since any number from 0, 2, 4, 6 can be taken as the third digit).
So, N=n 1 *n 2 *n 3 =6*7*4=168. In the case when all groups consist of the same number elements, i.e. n 1 =n 2 =...n k =n we can assume that each selection is made from the same group, and the element after selection is returned to the group. Then the number of all selection methods is n k . This method of selection in combinatorics is called
Example 3. samples with return.
Solution. How many four-digit numbers can be made from the digits 1, 5, 6, 7, 8?
For each digit of a four-digit number there are five possibilities, which means N=5*5*5*5=5 4 =625. Consider a set consisting of n elements. In combinatorics this set is called.
general population
Number of placements of n elements by m Definition 1. n Accommodation from elements by m in combinatorics any ordered set elements by from n various elements selected from the population in
Example 4. elements.
Different arrangements of three elements (1, 2, 3) by two will be the sets (1, 2), (2, 1), (1, 3), (3, 1), (2, 3), (3, 2 ). Placements may differ from each other both in elements and in their order.
The number of placements in combinatorics is denoted by A n m and is calculated by the formula: Comment:
n!=1*2*3*...*n (read: "en factorial"), in addition, it is assumed that 0!=1. Example 5
Solution: because If there are five odd digits, namely 1, 3, 5, 7, 9, then this task comes down to selecting and placing two of the five different digits in two different positions, i.e. specified numbers will:
Definition 2. Combination from n Accommodation from elements by in combinatorics any unordered set ordered set elements by various elements selected from the population in n elements.
Example 6. For the set (1, 2, 3), the combinations are (1, 2), (1, 3), (2, 3).
Number of combinations of n elements, m each
The number of combinations is denoted by C n m and is calculated by the formula:
Example 7. In how many ways can a reader choose two books out of six available?
Solution: The number of methods is equal to the number of combinations of six books of two, i.e. equals:
![]()
Permutations of n elements
Definition 3. Permutation from n elements are called any in combinatorics any these elements.
Example 7a. All possible permutations of a set consisting of three elements (1, 2, 3) are: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), ( 3, 2, 1), (3, 1, 2).
The number of different permutations of n elements is denoted by P n and is calculated by the formula P n =n!.
Example 8. In how many ways are seven books different authors Can you place it on a shelf in one row?
Solution: This problem is about the number of permutations of seven different books. There are P 7 =7!=1*2*3*4*5*6*7=5040 ways to arrange the books.
Discussion. We see that the number possible combinations can be calculated by different rules(permutations, combinations, placements) and the result will be different, because The calculation principle and the formulas themselves are different. Looking carefully at the definitions, you will notice that the result depends on several factors simultaneously.
Firstly, from how many elements we can combine their sets (how large population elements).
Secondly, the result depends on the size of the sets of elements we need.
Finally, it is important to know whether the order of the elements in the set is significant to us. Let us explain the last factor using the following example.
Example 9. On parent meeting 20 people are present. How many different options are there for the composition of the parent committee if it must include 5 people?
Solution: In this example, we are not interested in the order of names on the committee list. If, as a result, the same people turn out to be part of it, then in meaning for us this is the same option. Therefore, we can use the formula to calculate the number combinations of 20 elements 5 each.
Things will be different if each committee member is initially responsible for a specific area of work. Then, with the same list composition of the committee, there are possibly 5 within it! options permutations that matter. The number of different (both in composition and area of responsibility) options is determined in this case by the number placements of 20 elements 5 each.
Self-test tasks
1. How many three-digit even numbers can be made from the digits 0, 1, 2, 3, 4, 5, 6, if the digits can be repeated?
2. How many five-digit numbers are there that are read the same from left to right and from right to left?
3. There are ten subjects in the class and five lessons a day. In how many ways can you create a schedule for one day?
4. In how many ways can 4 delegates be selected for a conference if there are 20 people in the group?
5. In how many ways can eight different letters be placed in eight different envelopes, if only one letter is placed in each envelope?
6. A commission consisting of two mathematicians and six economists should be composed of three mathematicians and ten economists. In how many ways can this be done?
Purpose of the lesson: be able to apply basic combinatorics formulas and know the conditions for applying these formulas; know the properties of binomial coefficients and be able to determine the expansion of a binomial for specific values of n.
Lesson plan:
1. Number of placements.
2. Number of permutations.
3. Number of combinations.
4. Repetitions.
5. Newton's binomial. Pascal's triangle.
Guidelines on studying the topic
In many practical cases, it becomes necessary to count the number of possible combinations of objects that satisfy certain conditions. Such problems are called combinatorial. The variety of combinatorial problems cannot be described exhaustively, but among them there are whole line especially frequently occurring ones for which counting methods are known.
Combinatorics- a field of mathematics in which questions are studied about how many different combinations, subject to certain conditions, can be made from elements belonging to a given set. The term "combinatorics" comes from Latin word combina – combine, unite.
Let there be a set of n elements: x 1, x 2, x 3, ..., x n.
From this set one can form various subsets, that is, samples, each of which contains m elements (0 ≤ m ≤ n). There are ordered selections (placements), permutations and unordered selections (combinations).
Placements
Placements n various elements according to elements by elements that differ either in the composition of the elements or in their order.
Number of placements from n Accommodation from elements by elements are designated (A is the first letter French word arrangement, which means placing, putting in order) and is calculated using the formula:
The concept of factorial
Work n natural numbers from 1 to n indicated by the symbol n! (n factorial), that is
For example, 2!=
5!= ![]()
Note that it is convenient to calculate 0!, assuming, by definition, 0!=1.
Examples:

From the last two formulas it follows that
Example.
8 teams participate in a one-round football tournament. How many options for the top three are there?
Solution: Since the order of the teams in the top three is important, we are dealing with placements. Then
(options).
Example.
In how many ways can three persons be selected from ten candidates for three different positions?
Solution:
(ways).
Example.
How many can you make telephone numbers of 5 digits so that in each individual number all the digits are different?
(telephone numbers).
Rearrangements
Permutations are combinations consisting of the same n different elements and differing only in the order of their arrangement.
The number of all possible permutations of n elements is denoted by P n (P is the first letter of the French word permutation, which means permutation) and is calculated using the formula:
Example.
8 athletes compete in the 100 meter final. How many race protocol options are there?
Solution:
In this case we are talking about all permutations of 8 elements. Then (options)
Example.
In how many different ways can 10 people sit on a bench?
Solution:
(ways)
Example.
In how many ways can 7 people be seated at a table with 7 cutlery?
Solution:
(ways).
Combinations
Combinations are combinations made from n various elements according to elements by elements that differ in at least one element.
The number of combinations is calculated using the formula: ![]() (C is the first letter of the French word combinasion).
(C is the first letter of the French word combinasion).
Example.
In how many ways can three persons be selected for three identical positions out of ten candidates?
Solution:
 (ways).
(ways).
Example.
In how many ways can you select three parts from a box containing 15 parts?
Solution:
 (ways).
(ways).
Another type of formula for the number of placements and the number of combinations
;  , that is
, that is  .
.
Properties of the number of combinations:
5) ![]()
When solving combinatorics problems, the following rules are used:
Sum rule. If some object A can be selected from a set of objects in n ways, and another object B - in k ways, then the object “either A or B” can be selected in n + k ways.
Product rule. If a certain object A can be selected from a set of objects in n ways and after each such selection another object B in k ways, then a pair of objects (A, B) in the specified order can be selected in n × k ways.
If some elements are repeated, then in this case combinations with repetitions are calculated using other formulas.
Placements with repetitions
Number of placements by elements by elements with repetitions from n different elements are equal n m,that is ![]()
Example.
From the numbers 1,2,3,4,5 you can make 5 3 =125 three digit numbers, if the same number can contain the same digits.
Permutations with repetitions
If among n there are elements n 1 elements of the same type, n 2 elements of a different type, etc., then the number of permutations with repetitions
 Where
Where ![]()
Example.
How many different permutations of letters can be made in the word "mathematics"?
Solution:
Combinations with repetitions
Number of combinations with repetitions from n various elements according to elements by elements is equal to the number of combinations without repetitions from ( n+elements by-1) various elements according to elements by elements:
![]()
Example.
Find the number of combinations with repetitions of four elements a, b, c, d 3 elements each.
Solution:
The required number will be 
Binomial theorem
For an arbitrary positive integer n the following formula holds:
This is Newton's binomial. The coefficients are called binomial coefficients.
For n = 2 we get the formula;
For n = 3 we get the formula.
Example. Determine the expansion for n=4.
Solution:
Binomial coefficients have a number of properties:
2. ![]() ;
;
Consider the following triangle:
………………………….
Line numbered n contains binomial expansion coefficients. Taking advantage of the property ![]() , you can notice that every internal element triangle equal to the sum two elements located above it, and the lateral elements of the triangle are units:
, you can notice that every internal element triangle equal to the sum two elements located above it, and the lateral elements of the triangle are units:
……………………….
This is Pascal's triangle. It allows you to quickly find the values of binomial coefficients.
In Russian-language literature, permutations composed of n different elements by selecting m elements that differ either in the composition of the elements or in their order are usually called placements, and permutations are understood as the entire set of combinations consisting of the same n different elements and differing only in order their locations. In this sense, the number of all possible permutations for a set of n different elements is calculated using the factorial formula Pn = n! or in Excel “=FACT(N)” (see Fig. No. 1)



For example, if you enter “=PERST(3;2)”, we get 6. These are 6 combinations: (1,2), (2,1), (1,3), (3,1), (2,3) , (3.2).
But the built-in function “=NUMBERCOMB(N;K)” produces a combinatorial formula, which we call “Number of Combinations”. In Russian-language literature, this is the name for permutations made up of n different elements by choosing m elements each, which differ only in the composition of the elements, and the order of their selection is indifferent (see figure, No. 4)

When using built-in functions, use Help for this function. For example:

Tasks for independent decision
1. Calculate: 
2. Calculate:
3. Calculate: 
4. Find n, if 5С n 3 =
5. Find n, If
6. Find n, If
7. Find n, If 
8. Find n, If  ,kn
,kn
9. Solve the equation 
10. Solve the system
11. How many signals can you make from 6 flags of different colors, taken in groups of 2?
12. In how many ways can four persons be selected for four different positions from nine candidates?
13. How many telephone numbers can be composed of 6 digits so that in each individual number all the digits are different?
14. In class 10 educational subjects and 5 different lessons in a day. In how many ways can lessons be distributed on one day?
15. How many four-digit numbers can you write using all 10 digits without repeating?
16. A company selects from nine candidates for three different positions. How many ways are there to make this choice?
17. In the eighth grade, 15 subjects are studied. In how many ways can you create a schedule for Wednesday if you know that there should be 6 lessons on that day?
18. There are 16 teams in the top league of the national football championship. The fight is for gold, silver and bronze medals. In how many ways can medals be distributed between teams?
19. In how many ways can 9 people be placed at a table on which 9 cutlery is placed?
20. 6 speakers will speak at the meeting. In how many ways can their names be arranged in the list?
21. How many three-digit numbers can be made from the digits 1, 2, 3 if each digit appears in the image of the number only once?
22. In how many different ways can 10 different books be arranged on a shelf so that certain 4 books stand next to each other?
23. 8 teams participate in a one-round football tournament. How many matches will be played?
24. Out of 25 students, three delegates must be selected for the conference. In how many ways can this be done?
25. In how many ways can you select two parts from a box containing 10 parts?
26. There are 36 cards in the deck, 4 of which are aces. In how many ways can 6 cards be drawn so that there are 2 aces among them?
27. A complex team consists of two painters, three plasterers and one carpenter. How many different teams can be created from a work team consisting of 15 painters, 10 plasterers and 5 carpenters?
28. 10 teams participate in the qualifying tournament for 3 tickets to the World Championship. How many variations of the “lucky three” are there?
29. Out of 12 people, four are selected to be appointed to 4 identical positions. In how many ways can such a choice be made?
30. In how many different ways can a reconnaissance group of 3 soldiers and one commander be composed if there are 12 soldiers and 3 commanders?
31. Given on the plane n points of which no three lie on the same line. Find the number of straight lines that can be obtained by connecting points in pairs.
32. Morse code letters are formed as a sequence of dots and dashes. How many different letters can be formed using 5 symbols?
33. How many different seven-digit telephone numbers are there?
34. Let the letters of a certain alphabet be formed as a sequence of dots, dashes and spaces. How many different letters can be formed using 5 symbols?
35. When playing bridge, a deck of cards of 52 sheets is distributed among four players, with 13 cards for each player. How many different ways are there to deal cards?
36. B post office Five types of postcards are sold. Determine the number of ways to buy seven postcards.
37. Two collectors exchange stamps. Find the number of exchange methods if the first collector exchanges 3 stamps, and the second - 6 stamps. (The exchange takes place for one stamp).
38. One student has 6 books on mathematics, and the other has 5. In how many ways can they exchange 2 books of one for 2 books of another?
39. How many different permutations of letters can be made in the words: “lock”, “rotor”, “defensiveness”, “bell”, “seminar”?
40. In how many different ways can the following 9 letters be placed in 9 cells: a, a, a, b, b, b, c, c, c?
41. There are 6 seats in the car. In how many ways can 6 people get into this car if only two of them can take the driver's seat?
42. In how many ways can 6 cards containing an Ace and a King of the same suit be drawn from a deck of 52 cards?
43. Determine the expansion for n=5.
44. Determine the expansion for n=8.
45. Find a term in the expansion that does not contain x (that is, containing x to the zeroth power).
46. Find the sixth term of expansion  , If binomial coefficient the third term from the end is 45.
, If binomial coefficient the third term from the end is 45.
47. In decay  the coefficient of the third term is 44 greater than the coefficient of the second term. Find the free term, that is, the expansion term that does not depend on x (the term that does not depend on x will be the one that contains x to the zeroth power).
the coefficient of the third term is 44 greater than the coefficient of the second term. Find the free term, that is, the expansion term that does not depend on x (the term that does not depend on x will be the one that contains x to the zeroth power).
48. In the binomial expansion  find terms that do not contain irrationality.
find terms that do not contain irrationality.
49. Find the number of that expansion term  , which contains a and b to equal powers.
, which contains a and b to equal powers.
(interactive lesson in small groups)
Boolean functions
Purpose of the lesson: be able to construct various Boolean functions, check the equivalence of Boolean formulas (using the truth table), determine essential and fictitious variables.
Lesson plan:
1. Basic operations
2. Boolean functions of n variables
3. Basic equivalences
Number of placements without repetitions from n By k n k different coordinates.
The number of placements without repetitions is determined by the formula:
Example: In how many ways can you construct a 3-digit number with different digits that does not contain the digit 0?
Number of digits  , dimension of a vector with different coordinates
, dimension of a vector with different coordinates 

Number of placements with repetitions
Number of placements with repetitions from n By k is the number of ways in which one can n different elements build vectors with k coordinates, some of which may be identical.
The number of placements with repetitions is determined by the formula:
 .
.
Example: How many words of length 6 can be made from 26 letters of the Latin alphabet?
Number of letters  , vector dimension
, vector dimension 

Number of permutations without repetitions
Number of permutations without repetitions from n elements is the number of ways in which it can be placed in n different places n various elements.
The number of permutations without repetitions is found by the formula:
 .
.
The number of placements in combinatorics is denoted by A n m and is calculated by the formula: Power of the required set A It’s convenient to search using the formula:  , Where X– the number of ways to select the desired places; at– the number of ways to arrange the necessary elements on them; z– the number of ways to arrange the remaining elements in the remaining places.
, Where X– the number of ways to select the desired places; at– the number of ways to arrange the necessary elements on them; z– the number of ways to arrange the remaining elements in the remaining places.
Example. In how many ways can 5 different books be arranged on a bookshelf? In how many cases will two specific books A and B be next to each other?
The total number of ways to arrange 5 books in 5 places is equal to  = 5! = 120.
= 5! = 120.
In the problem X– the number of ways to choose two places nearby, X= 4;at– the number of ways to arrange two books in two places, at = 2! = 2;
z– the number of ways to place the remaining 3 books in the remaining 3 places, z= 3! = 6. So  =
48.
=
48.
Number of combinations without repetitions
Number of combinations without repetitions from n By k is the number of ways in which one can n different items to choose k pieces without regard to order.
The number of combinations without repetitions is found by the formula:
 .
.
Properties:
1)
 ;
2)
;
2) ;
3)
;
3) ;
;
4)
 ;
5)
;
5) ;
6)
;
6) .
.
Example. There are 7 balls in the urn. Of these, 3 are white. 3 balls are chosen at random. In how many ways can this be done? In how many cases will there be exactly one white person among them?
Total ways  . To get the number of ways choose 1 white ball(from 3 white) and 2 black balls (from 4 black), you need to multiply
. To get the number of ways choose 1 white ball(from 3 white) and 2 black balls (from 4 black), you need to multiply  And
And  Thus, the required number of ways
Thus, the required number of ways 
Exercises
1. Out of 35 students in the class at the end of the year, 14 people had “5” in mathematics; in physics – 15 people; in chemistry – 18 people; in mathematics and physics – 7 people; in mathematics and chemistry – 9 people; in physics and chemistry – 6 people; in all three subjects – 4 people. How many people have “5” in these subjects? How many people do not have an “A” in these subjects? Has an “A” only in mathematics? Has “A” in only two subjects?
2. In a group of 30 students, everyone knows at least one foreign language– English or German. 22 students speak English, 17 speak German. How many students know both languages? How many students know German but do not know English?
3. Students from Russia live in 20 rooms of the dormitory of the Institute of Peoples' Friendship; in 15 - from Africa; in 20 – from countries South America. Moreover, in 7 - Russians and Africans live, in 8 - Russians and South Americans; in 9 – Africans and South Americans; in 3 – Russians, South Americans, and Africans. How many rooms do students live in: 1) from only one continent; 2) only from two continents; 3) only Africans.
4. Each of the 500 students is required to attend at least one of three special courses: mathematics, physics and astronomy. Three special courses are attended by 10 students, in mathematics and physics - 30 students, in mathematics and astronomy - 25; special course in physics only – 80 students. It is also known that 345 students attend a special course in mathematics, 145 in physics, and 100 students in astronomy. How many students take a special course in astronomy only? How many students take two special courses?
5. The head of the course presented the following report on physical education work. Total – 45 students. Football section – 25 people, basketball section – 30 people, chess section – 28 people. At the same time, 16 people simultaneously attend the football and basketball sections, 18 – football and chess, 17 – basketball and chess, 15 people attend all three sections. Explain why the report was not accepted.
6. There are 11 fish in the aquarium. Of these, 4 are red, the rest are gold. 4 fish are chosen at random. In how many ways can this be done? Find the number of ways to do this so that among them there will be: 1) exactly one is red; 2) exactly 2 gold; 3) at least one is red.
7. There are 8 names on the list. Of these, 4 are female. In how many ways can they be divided into two equal groups so that each has a female surname?
8. From a deck of 36 cards, choose 4. How many ways can this be done so that: 1) all the cards are of different suits; 2) all cards were of the same suit; 3) 2 red and 2 black.
9. On the cut alphabet cards there are the letters K, K, K, U, U, A, E, R. How many ways can you put them in a row so that it turns out “crow”.
10. Cards of the cut alphabet with the letters O, T, O, L, O, R, I, N, G, O, L, O, G are given. How many ways can they be folded so that the word “otolaryngologist” is formed?
11. Given are cards of cut alphabet with the letters L, I, T, E, R, A, T, U, R, A. How many ways can you put them in a row so that you get the word “literature”.
12. 8 people stand in line. How many ways can this be done so that two specific people A and B are: 1) nearby; 2) at the edges of the queue;
13. 10 people sit down at round table for 10 seats. In how many ways can this be done so that the following are nearby: 1) two specific people A and B; 2) three specific people A, B and C.
14. 10 Arabic numerals make up a 5-digit code. In how many ways can this be done so that: 1) all the numbers are different; 2) in last place is an even number.
15. 26 letters of the Latin alphabet (including 6 vowels) form a six-letter word. In how many ways can this be done so that the word contains: 1) exactly one letter “a”; 2) exactly one vowel letter; exactly two letters “a”; c) exactly two vowels.
16. How many four-digit numbers are divisible by 5?
17. How many four-digit numbers with different digits are divisible by 25?
19. 3 dice are thrown. In how many cases did you get: 1) exactly 1 “six”; 2) at least one “six”.
20. 3 dice are thrown. In how many cases will it be: 1) everyone is different; 2) exactly two identical numbers of points.
21. How many words with different letters can be made from the alphabet a, b, c, d. List them all in lexicographical order: abcd, abcd….
 The problem of the teacher's influence on the student
The problem of the teacher's influence on the student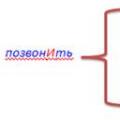 In which word is the letter denoting the stressed vowel sound correctly highlighted?
In which word is the letter denoting the stressed vowel sound correctly highlighted? The best historical novels What historical novels
The best historical novels What historical novels