Milleks on Euleri ringid? Euleri ring

Euleri ringid on geomeetriline diagramm. Selle abil saate kujutada visuaalse esituse jaoks alamhulkade (mõistete) vahelisi seoseid.

Mõistete kujutamise viis ringidena võimaldab teil arendada kujutlusvõimet ja loogilist mõtlemist mitte ainult lastel, vaid ka täiskasvanutel. Alates 4-5 eluaastast saavad lapsed lahendada lihtsaid ülesandeid Euleri ringidega, esmalt täiskasvanute selgitustega ja seejärel iseseisvalt. Euleri ringide abil ülesannete lahendamise meetodi valdamine arendab lapse võimet analüüsida, võrrelda, üldistada ja rühmitada oma teadmisi laiemaks rakendamiseks.

Näide

Pildil on erinevaid võimalikke mänguasju. Mõned mänguasjad on ehituskomplektid – need on eraldi ovaalina esile tõstetud. See on osa suurest "mänguasjade" komplektist ja samal ajal eraldi komplektist (ehituskomplekt võib ju olla "Lego" või primitiivsed klotsidest valmistatud ehituskomplektid lastele). Osa suurest valikust mänguasjadest võivad olla kokkukeritavad mänguasjad. Nad ei ole konstruktorid, seega joonistame neile eraldi ovaali. Kollane ovaalne „keeratav auto“ viitab nii komplektile „mänguasja“ kui ka osa väiksemast komplektist „kerimismänguasi“. Seetõttu on see kujutatud mõlema ovaali sees korraga.

Siin on mõned loogilise mõtlemise ülesanded väikelastele:

Määrake ringid, mis sobivad objekti kirjeldusega. Sel juhul on soovitatav pöörata tähelepanu nendele omadustele, mis objektil püsivalt ja ajutiselt on. Näiteks klaasklaas mahlaga jääb alati klaasiks, kuid selles pole alati mahla. Või on mingi lai definitsioon, mis sisaldab erinevaid mõisteid; sellist klassifikatsiooni saab kujutada ka Euleri ringide abil. Näiteks tšello on muusikainstrument, kuid mitte iga muusikariist pole tšello.

Vanematele lastele saate pakkuda arvutusprobleemide jaoks võimalusi - üsna lihtsast kuni väga keerukani. Veelgi enam, lastele nende ülesannete iseseisvalt väljamõtlemine annab vanematele vaimule väga hea treeningu.

1. 27 viiendast klassist õpivad kõik võõrkeeli – inglise ja saksa keelt. 12 õpivad saksa keelt ja 19 inglise keelt. Tuleb kindlaks teha, kui palju viienda klassi õpilasi õpib kahte võõrkeelt; kui palju inimesi ei õpi saksa keelt; kui palju inimesi ei õpi inglise keelt; Kui paljud õpivad ainult saksa keelt ja ainult inglise keelt?

Samas vihjab probleemi esimene küsimus üldjoontes selle probleemi lahendamise teele, andes teada, et osa õpilasi õpib mõlemat keelt, mille puhul diagrammi kasutamine hõlbustab ka lastel probleemi mõistmist.

Muide, kui te ei suuda otsustada, millist elukutset valida, proovige joonistada diagramm Euleri ringide kujul. Võib-olla aitab selline joonis teil valikut teha:

Need valikud, mis asuvad kõigi kolme ringi ristumiskohas, on elukutse, mis ei saa teid mitte ainult toita, vaid ka rõõmustada.

Ja veel üks märk...

Kui arvate, et te ei tea midagi sellisest kontseptsioonist nagu Euleri ringid, siis eksite sügavalt. Juba algklassidest on teada skemaatilised kujutised või ringid, mis võimaldavad visuaalselt mõista mõistete ja süsteemi elementide vahelisi seoseid.

Leonhard Euleri leiutatud meetodit kasutas teadlane keerukate matemaatiliste probleemide lahendamiseks. Ta kujutas komplekte ringidena ja tegi selle diagrammi sellise kontseptsiooni kui sümboolse aluseks. Meetod on loodud selleks, et võimalikult palju lihtsustada konkreetse probleemi lahendamisele suunatud arutluskäiku, mistõttu kasutatakse tehnikat aktiivselt nii algkoolis kui ka akadeemilises keskkonnas. Huvitaval kombel kasutas sarnast lähenemist varem saksa filosoof Leibniz ning hiljem võtsid selle kasutusele ja rakendasid mitmesugustes modifikatsioonides kuulsad matemaatika valdkonna mõistused. Näiteks tšehhi Bolzano, Schroederi, Venni ristkülikukujulised diagrammid, mis on kuulsad selle lihtsa, kuid üllatavalt tõhusa meetodi põhjal populaarse diagrammi loomise eest.

Ringid on nn visuaalsete Interneti-meemide aluseks, mis põhinevad üksikute komplektide omaduste sarnasusel. See on naljakas, visuaalne ja mis kõige tähtsam, arusaadav.

Mõtteringid

Ringid võimaldavad teil selgelt kirjeldada probleemi tingimusi ja teha koheselt õige otsuse või määrata õige vastuse suunas liikumise suuna. Tavaliselt kasutatakse Euleri ringe loogilis-matemaatika probleemide lahendamiseks, mis hõlmavad hulki, nende liite või osalisi superpositsioone. Ringide ristumiskoht hõlmab objekte, millel on iga ringis kujutatud hulga omadused. Komplekti mittekuuluvad objektid asuvad väljaspool üht või teist ringi. Kui mõisted on absoluutselt samaväärsed, tähistatakse neid ühe ringiga, mis on kahe võrdsete omaduste ja mahuga hulga liit.

Suhete loogika

Euleri ringide abil saate lahendada mitmeid igapäevaseid probleeme ja isegi otsustada tulevase elukutse valiku üle, peate lihtsalt analüüsima oma võimalusi ja soove ning valima nende maksimaalse ristumiskoha.

Nüüd saab selgeks, et Euleri ringid ei ole üldse abstraktne matemaatiline ja filosoofiline mõiste teoreetiliste teadmiste kategooriast, neil on väga rakenduslik ja praktiline tähendus, mis võimaldab teil tegeleda mitte ainult kõige lihtsamate matemaatiliste probleemidega, vaid ka lahendada olulisi matemaatilisi probleeme. elu dilemmasid visuaalselt ja kõigile arusaadavalt.

Igal objektil või nähtusel on teatud omadused (märgid).

Selgub, et eseme kohta mõiste kujundamine tähendab ennekõike oskust eristada seda teistest temaga sarnastest objektidest.

Võime öelda, et mõiste on sõna vaimne sisu.

Kontseptsioon - see on mõttevorm, mis kuvab objekte nende kõige üldisemates ja olulisemates omadustes.

Mõiste on mõttevorm, mitte sõna vorm, kuna sõna on ainult silt, millega me seda või teist mõtet tähistame.

Sõnad võivad olla erinevad, kuid tähendavad siiski sama mõistet. Vene keeles - "pliiats", inglise keeles - "pliiats", saksa keeles - bleistift. Samal mõttel on erinevates keeltes erinevad verbaalsed väljendused.

MÕISTETE VAHELISED SUHTED. EULERI RINGID.

Mõisteid, mille sisus on ühiseid jooni, nimetatakse VÕRDLAVAD("advokaat" ja "asetäitja"; "õpilane" ja "sportlane").

Vastasel juhul arvestatakse mõistetega VÕRRELMATU("krokodill" ja "märkmik"; "mees" ja "aurulaev").

Kui mõistetel on lisaks üldtunnustele ka ühiseid mahuelemente, siis neid nimetatakse ÜHTILAB.

Võrreldavate mõistete vahel on kuut tüüpi seoseid. Mõistete mahtude vahelisi seoseid on mugav tähistada Euleri ringide abil (ringdiagrammid, kus iga ring tähistab mõiste mahtu).

MÕISTETE VAHELINE SUHE	PILT EULERI RINGIDE KASUTAMISEGA
VÕRDVÄÄRSUS (IDENTITEET) Mõistete ulatused langevad täielikult kokku. Need. Need on mõisted, mis sisult erinevad, kuid neis mõeldakse samadele mahuelementidele.	1) A – Aristoteles B – loogika rajaja 2) A – ruut B – võrdkülgne ristkülik
ALLUMINE (ALLUMINE) Ühe mõiste ulatus on täielikult hõlmatud teise mõistega, kuid ei ammenda seda.	1) A - inimene B - õpilane 2) A - loom B - elevant
RISTIK (RIISTUMINE) Kahe mõiste mahud langevad osaliselt kokku. See tähendab, et mõisted sisaldavad ühiseid elemente, kuid hõlmavad ka elemente, mis kuuluvad ainult ühte neist.	1) A - jurist B - asetäitja 2) A - üliõpilane B - sportlane
KOORDINEERIMINE (KOORDINEERIMINE) Mõisted, millel pole ühiseid elemente, kuuluvad täielikult kolmanda, laiema mõiste ulatusse.	1) A - loom B - kass; C - koer; D - hiir 2) A - väärismetall B - kuld; C - hõbe; D - plaatina
VASTASED (KONTRAPARAARSUS) Mõisted A ja B ei kuulu lihtsalt kolmanda mõiste ulatusse, vaid näivad olevat selle vastandpoolustel. See tähendab, et kontseptsioonil A on oma sisus selline tunnus, mis mõistes B on asendatud vastupidise tunnusega.	1) A - valge kass; B - punane kass (kassid on nii mustad kui hallid) 2) A - kuum tee; jäätee (tee võib olla ka soe) st. mõisted A ja B ei ammenda kogu mõiste ulatust, millesse nad kuuluvad.
KONTRADITSIOON (KONTRADITSIOONIVSUS) Suhe mõistete vahel, millest üks väljendab mõne tunnuse olemasolu ja teine - nende puudumist, see tähendab, et see lihtsalt eitab neid omadusi, asendamata neid ühegi teisega.	1) A - kõrge maja B - madal maja 2) A - võidupilet B - mittevõidupilet S.t. mõisted A ja mitte-A ammendavad kogu selle mõiste ulatuse, millesse nad kuuluvad, kuna nende vahele ei saa paigutada täiendavaid mõisteid.

Harjutus: Määrake suhte tüüp allolevate mõistete ulatuse alusel. Joonistage need Euleri ringide abil.

1) A - kuum tee; B - jäätee; C - tee sidruniga

Kuum tee (B) ja jäätee (C) on vastandlikus suhtes.

Tee sidruniga (C) võib olla kas kuum,

nii külm, aga võib olla ka näiteks soe.

2)A- puit; IN- kivi; KOOS- struktuur; D- maja.

Kas iga hoone (C) on maja (D)? - Ei.

Kas iga maja (D) on hoone (C)? - Jah.

Midagi puidust (A), kas see on tingimata maja (D) või hoone (C) - Ei.

Kuid võite leida puitkonstruktsiooni (näiteks putka),

Võib leida ka puitmaja.

Miski kivist (B) ei pruugi olla maja (D) või hoone (C).

Kuid seal võib olla kivihoone või kivimaja.

3)A- Vene linn; IN- Venemaa pealinn;

KOOS- Moskva; D- linn Volga ääres; E- Uglich.

Venemaa (B) pealinn ja Moskva (C) on sama linn.

Uglich (E) on linn Volga (D) ääres.

Samal ajal Moskva, Uglich, nagu iga Volga linn,

on Venemaa linnad (A)

Krimmi Vabariigi Haridus-, Teadus- ja Noorsooministeerium Väike Teaduste Akadeemia “Iskatel”

Suund: matemaatika

G. Krasnoperekopsk– 2017

Töö lõpetatud:

Šumilina Maria Sergeevna,

vallaeelarve 7-A klassi õpilane Üldharidus asutused "Keskaarne Üldharidus Kool nr 5" omavalitsuse moodustamise linnaosa Krasnoperekopsk

Teadusnõustaja:

Sheina Jelena Nikolaevna, valla eelarve matemaatika õpetaja Üldharidus asutused "Keskaarne Üldharidus kool nr 5 » omavalitsuse moodustamise linnaosa Krasnoperekopsk

SISSEJUHATUS ………………………………………………………………… 3

1. PEATÜKK. Natuke ajalugu…………………………………. 5

PEATÜKK 2. Hulgateooriast……………………………………….7

2.1. Kogumi mõiste.………………………………………………………..8

2.2. Operatsioonid komplektidel.…………………………..9

3. PEATÜKK.Ülesannete lahendamine Euleri ringide abil………………..10

KOKKUVÕTE…………………………………………………………..22

KASUTATUD ALLIKATE LOETELU…………………….23

SISSEJUHATUS

Miski ei aita

vaimse kultuuri kujunemine,

loogikaülesannete lahendusena. Matemaatika-

mitte kuiv ja igav teadus, vaid täielik

ebatavalised ja huvitavad avastused

Loogikaülesannete lahendamine on väga põnev. On inimesi, kelle jaoks loogikaülesande lahendamine on põnev, kuid mitte raske ülesanne. Nende aju, nagu prožektor, valgustab kohe kõik geniaalsed konstruktsioonid ja õige vastuseni jõuavad nad ebatavaliselt kiiresti. Tore, et nad ei suuda selgitada, kuidas nad otsuseni jõudsid.

Loogilised probleemid moodustavad suure hulga mittestandardseid probleeme. See hõlmab ennekõike tekstülesandeid, milles on vaja objekte ära tunda või olemasolevate omaduste järgi teatud järjekorda järjestada.

Tekstiloogikaülesannete lahendamiseks kasutatakse palju tehnikaid. Väga sageli aitab lahendus leida joonist. Pildi kasutamine muudab probleemi lahendamise lihtsaks ja selgeks. Probleemi tingimuste kujutamine Euleri ringidena lihtsustab ja hõlbustab reeglina selle lahendamise teed.

Asjakohasus seisneb selles, et ülesanded on praktilist laadi, mis on tänapäeva elus oluline. Probleemid sunnivad sind mõtlema, lähenema probleemi lahendamisele teise nurga alt, suutma valida erinevate lahenduste hulgast, kõige lihtsama, lihtsaima viisi.

Töö eesmärk:

Tutvuge Euleri-Venni ringidega;

Õppige rakendama ülesannete lahendamise meetodit Euleri ringide abil;

Loo praktilise sisuga ülesandeid.

Peatükk 1. Natuke ajalugu

Leonhard Euler, suurim matemaatikXVIIIc., sündinud Šveitsis 1707. aastal.1727. aastal tuli ta Peterburi Teaduste Akadeemia kutsel Venemaale. Peterburis sattus Euler silmapaistvate teadlaste ringi: matemaatikud, füüsikud, astronoomid ning sai suurepärased võimalused oma tööde loomiseks ja avaldamiseks. Ta töötas kirega ja temast sai peagi oma kaasaegsete üksmeelse tunnustuse kohaselt esimene matemaatik maailmas. Euleri teaduslik pärand on silmatorkav oma mahu ja mitmekülgsuse poolest. Tema teoste nimekirjas on üle 800 nimetuse. Teadlase täielikud kogutud tööd hõlmavad 72 köidet. Tema tööde hulgas on esimesed diferentsiaal- ja integraalarvutuse õpikud. Arvuteoorias jätkas Euler prantsuse matemaatiku P. Fermat’ tööd.

Euler töötab palju matemaatilise analüüsi valdkonnas. Teadlane oli esimene, kes töötas välja üldise doktriini logaritmilisest funktsioonist. Geomeetrias pani Euler aluse täiesti uuele uurimisvaldkonnale, mis hiljem kasvas iseseisvaks teaduseks – topoloogiaks.

Euleri nimi on antud valemile, mis ühendab kumera hulktahuka tippude (B), servade (P) ja tahkude (G) arvu: B -P + G = 2. Isegi Euleri teadusliku töö põhitulemusi on raske saavutada. nimekirja. Siin on kõverate ja pindade geomeetria ning variatsioonide arvutuse esimene esitlus paljude uute konkreetsete tulemustega. Ta kirjutas töid hüdraulika, laevaehituse, suurtükiväe, geomeetrilise optika ja isegi muusikateooria kohta. Esimest korda esitab ta Newtoni geomeetrilise esituse asemel mehaanika analüütilise esitluse ja konstrueerib tahke keha, mitte ainult materiaalse punkti või tahke plaadi mehaanikat. Euleri üks tähelepanuväärsemaid saavutusi on seotud astronoomia ja taevamehaanikaga. Ta koostas Kuu liikumise täpse teooria, võttes arvesse mitte ainult Maa, vaid ka Päikese külgetõmbejõudu. See on näide väga keerulise probleemi lahendamisest.

Euleri viimased 17 eluaastat rikkus peaaegu täielik nägemise kaotus. Kuid ta jätkas loomist sama intensiivselt kui nooruses. Alles nüüd ei kirjutanud ta enam ise, vaid dikteeris oma õpilastele, kes tegid tema eest kõige tülikamad arvutused.

Aastatel 1761–1768 kirjutas ta kuulsa "Kirjad Saksa printsessile", kus Euler rääkis oma meetodist, komplektide kujutamisest ringidena. Seetõttu nimetatakse ringikujulisi jooniseid tavaliselt Euleri ringideks. Euler märkis, et hulkade kujutamine ringidena "on meie arutluskäigu hõlbustamiseks väga sobiv".

Pärast Eulerit töötas sama meetodi välja Tšehhi matemaatik Bernard Bolzano (1781 – 1848). Ainult et erinevalt Eulerist ei joonistanud ta mitte ringikujulisi, vaid ristkülikukujulisi diagramme. Euleri ringi meetodit kasutas ka saksa matemaatik Ernst Schroeder (1841 – 1902). Seda meetodit kasutatakse laialdaselt tema raamatus Algebra Logic. Kuid graafilised meetodid saavutasid suurima õitsengu inglise loogiku John Venni (1843–1923) töödes. Ta kirjeldas seda meetodit kõige põhjalikumalt oma raamatus "Symbolic Logic", mis avaldati Londonis 1881. aastal. Venni auks nimetatakse Euleri ringide asemel vastavaid jooniseid mõnikord Venni diagrammideks; mõnes raamatus nimetatakse neid ka Euleri–Venni diagrammideks (või ringideks).

Peatükk 2. Hulgateooriast

2.1. Komplekti mõiste.

Üks peamisi matemaatikas kasutatavaid mõisteid on hulga mõiste. Selle jaoks pole definitsiooni antud. Võib seletada, et hulk on suvaline objektide kogum ja objektid ise on antud hulga elemendid. Seega võime rääkida klassi õpilaste hulgast (elemendid on õpilased), nädalapäevade hulgast (elemendid on nädalapäevad), arvu 6 loomulike jagajate hulgast (elemendid on numbrid 1, 2, 3, 6) jne.

Algebras ja algebrakursustes võetakse analüüsi alguses kõige sagedamini arvesse hulki, mille elementideks on arvud, ja seetõttu nimetatakse neid arvuhulkadeks.

Reeglina tähistatakse komplekte ladina tähestiku suurtähtedega. Näiteks kui komplektMkoosneb numbritest 1; 2; 3, siis on see tähistatud järgmiselt:M= (1; 2; 3). Asjaolu, et number 2 sisaldub selles komplektis

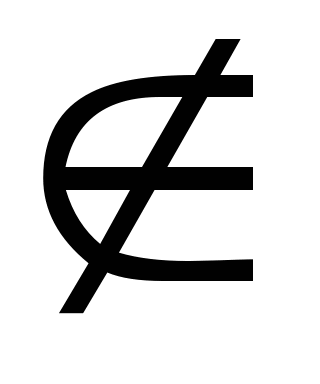(on selle komplekti elementM) salvestatakse spetsiaalse ikooni abil järgmiselt: 2M; ja asjaolu, et number 5 ei sisaldu selles komplektis (ei ole selle komplekti elementM), kirjutatud järgmiselt: 5 M.

Võime käsitleda ka hulka, mis ei sisalda ühtki elementi – tühja hulka. Näiteks: arvu 1 algtegurite hulk on tühi hulk.

Mõne komplekti jaoks on spetsiaalsed märgid. Seega on tühi komplekt tähistatud sümboliga , kõigi naturaalarvude hulk – tähtN, kõigi täisarvude hulk – tähtZ, kõigi ratsionaalarvude hulk – tähtK, ja kõigi reaalarvude hulk on tähtR. Kasutades Euleri-Venni ringe, saab seda kujutada järgmiselt:

Joonis 1

Kui komplekti iga elementAon komplekti elementB, siis öeldakse, et komplektAon hulga alamhulkB.

See on kirjutatud järgmiselt:A B.

Joonis 2

2.2. Operatsioonid komplektidel.

Saate komplektidega teatud toiminguid teha: leida nende ristumiskoht, liit. Defineerime need toimingud ja illustreerime neid ringide abil.

Hulkade ristumiskoht A Ja B nimetada nende ühisosa ehk komplektCkõik elemendid, mis kuuluvad mõlemasse komplektiA, ja paljudB

Hulkade ristumiskohta tähistatakse märgiga∩ ja kirjuta ülesA∩ B .

Joonis 3

Komplektide liit A Ja B kutsu komplektiC, mis koosneb kõigist elementidest, mis kuuluvad vähemalt ühte nendest komplektidest (AvõiB). Hulkade liitu tähistab märk
ja kirjuta üles A
B

3. peatükk. Probleemide lahendamine Euleri ringide abil

Ülesanne nr 1.

52 kooliõpilasest kogub märke 23, marke 35 ja nii märke kui ka marke 16.

Ülejäänud pole kollektsioneerimisest huvitatud. Kui palju on neid koolilapsi, kes ei ole kollektsioneerimisest huvitatud?

Lahendus.

Selle probleemi tingimusi pole nii lihtne mõista. Kui liita 23 ja 35, saab rohkem kui 52. Seda seletab asjaolu, et osa koolilapsi lugesime siin kaks korda, nimelt neid, kes koguvad nii märke kui ka marke.

Probleemi lahendamise hõlbustamiseks esitame selle andmed järgmisel diagrammil

Joonis 5

Sellel diagrammil tähistab suur ring kõiki kõnealuseid koolilapsi. RingZ kujutab koolinoori kogumas märke (kokku 23) ja ringiM - koolinoored marke kogumas (kokku 35). Ringide ristumiskohasZ Ja M Number 16 on väärt – need on need, kes koguvad nii märke kui ka marke. See tähendab, et 23 - 16 = 7 inimest koguvad ainult märke, 35 - 16 = 19 inimest koguvad ainult marke. Kokku kogub marke ja märke 19 + 7 + 16 = 42 inimest. Järele jääb 52–42 = 10 inimest, kes ei soovi koguda. Selle numbri saab sisestada ringi vabale väljale. Vastus: 10 inimest.

2. ülesanne.

Klassis on 15 poissi. Neist 10 inimest mängivad võrkpalli ja 9 korvpalli. Kui paljud poisid teevad mõlemat?

Lahendus.

Kujutagem tingimust Euleri ringide abil. See arv annab meile mõningaid põhjendusi. Analüüsime seda arutluskäiku ja sisestame igasse diagrammil moodustatud osasse vajalik arv.

Las x poiss tegeleb igasuguste spordialadega. Siis mängivad võrkpalli ainult (10.) poisid ja korvpalli ainult (9.) poisid. Koostame võrrandi: 10-d + x+ 9-d = 15, millest x = 4

10-ndad B

x 9

Joonis 6

Vastus: 4 inimest.

Ülesanne nr 3.

Mõnele poisile meie klassist meeldib kinos käia. Filmi “Hirmutist” vaatas teadaolevalt 15 last, filmi “Taeva kohal” 11 inimest, kellest 6 vaatas nii “Hirmutist” kui ka"Taeva kohal". Kui palju inimesi on vaadanud ainult filmi “Above the Sky”?

Lahendus:Joonistame kaks sellist komplekti: Asetame 6 inimest, kes vaatasid filme “Hirmutis” ja “Taeva kohal” võtteplatside ristumiskohta.

15 – 6 = 9 – inimesed, kes vaatasid ainult “Hirmutist”.
11 – 6 = 5 – inimesed, kes vaatasid ainult "Above the Sky".

Saame:

Joonis 7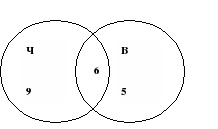

Vastus. 5 inimest vaatasid ainult filmi "Above the Sky".

Ülesanne nr 4.

Moskvasse ekskursioonile tulnud 80-liikmelises turistirühmas soovib 52 külastada Suurt Teatrit, 30 Kunstiteatrit, 12 mõlemat teatrit, ülejäänud ei taha teatrisse minna. Kui palju inimesi ei kavatse teatris käia?

Lahendus.

Ainult suurt teatrit külastavad: 52-12=40 turisti;

külastatakse ainult kunstiteatrit

30-12=18 turisti;

8
0-(40+18+12)=10 turisti ei kavatse teatris käia.

Joonis 8

Vastus: 10 inimest.

Ülesanne nr 5.

Riiulil oli 26 võluraamatut loitsu peal. Neist 4 lugesid nii Harry Potter kui ka Ron. Hermione luges 7 raamatut, mida Harry Potter ega Ron polnud lugenud, ja kaks raamatut, mida Harry Potter oli lugenud. Kokku luges Harry Potter 11 raamatut. Mitu raamatut on Ron lugenud?

Lahendus.

Arvestades probleemi tingimusi, on joonis järgmine:

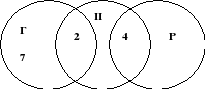
Joonis 9

Kuna Harry Potter luges kokku 11 raamatut, millest 4 raamatut luges Ron ja 2 raamatut Hermione, siis ainult Harry luges 11 - 4 - 2 = 5 - raamatut.

Seetõttu luges Ron 26 – 7 – 2 – 5 – 4 = 8 raamatut.Vastus. Ron luges 8 raamatut.

Ülesanne nr 6.

100-liikmelises turismigrupis oskab saksa keelt 75 inimest, inglise keelt 65 inimest ja 10 inimest ei oska saksa ega inglise keelt. Kui palju turiste räägib kahte keelt? Lahendus.

Kujutame probleemi tingimusi Euleri ringide kujul.

On lihtne näha, et 90 turisti (100-10) oskab vähemalt ühte keelt; Las x turistil oskab nii inglise kui saksa keelt. Siis oskavad (65.) turistid ainult inglise keelt ja (75.) inimesed ainult saksa keelt. Saame võrrandi 65 + 75 + x = 90, millest x = 50 - turistid oskavad mõlemat keelt. Vastus: 50 turisti.

Ülesanne nr 7.

Kui palju inimesi jalutuskäigul osaleb, kui on teada, et 16 neist võtsid võileiva singiga, 24 vorstiga, 15 juustuga, 11 nii singi kui vorstiga, 8 nii singi kui juustuga, 12 vorstiga ja juust, 6 - igasuguseid võileibu ja 5 - võttis pirukaid? Lahendus : Esitagem komplekte järgmiselt: Joonis 11

16+24+15-11-8-12+6=30 (in) - osalesid jalutuskäigul ja võtsid võileivad kaasa või 3+2+6+5+7+6+1=30 (in)

30+5=35 (isikut) - võtsid osa jalutuskäigust
Vastus. 35 inimest

Probleem nr 8

Meie kooli 5. klassis õpib 22, 6. klassis - 16, 7. klassis - 23 last. Teadaolevalt käib 4 inimest suusa-, male- ja spordiklubides. Igas kahes sektsioonis osaleb 9 inimest. Kui palju inimesi läheb igast klassist sektsioonidesse? Kui palju on õpilasi, kes ei käi üheski spordiklubis?

Lahendus. Kui kõigis kolmes klubis on 4 õpilast ja igas kahes 9 inimest, siis 5. ja 6. klassist, 6. ja 7. klassist ning 5. ja 7. klassist osaleb kahes sektsioonis 5.

Inimene.

Joonis 12

Meil käib klubis 5+5+4=14 viiendat klassi, 22-14=8 inimest ei käi üheski klubis. Põhjendus ka, et kuuenda klassi õpilastest ei käi kuskil 16-14=2 õpilast ja seitsmendast klassist 23-14=9 inimest.

Vastus: Igast klassist käib klubis 14 õpilast, 5. klassist 7, 6. 2 õpilast, 7. klassist 9 õpilast ei käi.

Ülesanne nr 9.

100 laste terviselaagrisse minevast lapsest saab lumelauaga sõita 30 last, rulaga 28, rulluiskudega 42. Rula ja lumelauaga 8 last, rulaga ja rulluisuga 10, lumelaua ja rulluisuga – 5 ning kõigil kolmel – 3. Kui paljud poisid ei tea, kuidas lumelaua, rula või rulluiskudega sõita?

Lahendus: IN Kasutame Euleri ringe.

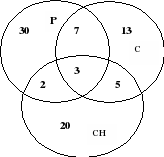
Joonis 13

Kõik kolm spordivarustust omavad kolmele inimesele, mis tähendab, et ringide üldosas sisestame numbriga 3. Rula- ja rulluisutamisega saab sõita 10 inimest ning neist 3 ka lumelauda. Järelikult saab 10-3=7 meest ainult rula ja rulluisuga sõita. Samamoodi leiame, et rula- ja lumelauaga saab sõita vaid 8-3=5 meest ning lume- ja rulluiskudega sõita vaid 5-3=2 inimest. Sisestame need andmed vastavatesse osadesse. Teeme nüüd kindlaks, kui palju inimesi saab sõita ainult ühe spordivarustusega. Lumelauda oskab 30 inimest, aga 5+3+2=10 neist oskab ka muud varustust, seega ainult lumelauaga sõitmist oskab 20 inimest. Samamoodi leiame, et 13 last oskavad ainult rulaga ja 30 last ainult rulluisutada. Probleemi tingimuste kohaselt on tüüpe ainult 100. 20+13+30+5+7+2+3=80 – poisid oskavad sõita vähemalt ühe spordivarustusega. Järelikult ei oska 20 inimest ühegi spordivarustusega sõita.
Vastus. 20 inimest ei oska ühegi spordivarustusega sõita.

Ülesanne nr 10 .

Kolmes seitsmendas klassis õpib 70 last. Neist 27 on seotud draamaklubiga, 32 laulab kooris, 22 armastab sporti. Draamaklubis on 10 kutti koorist, kooris 6 sportlast, draamaklubis 8 sportlast; Nii draamaklubis kui ka kooris käib 3 sportlast. Kui paljud lapsed ei laula kooris, ei tunne huvi spordi vastu ega tegele draamaklubiga? Kui paljud mehed tegelevad ainult spordiga?

Lahendus . D - draamaklubi; X - koor; S - sport. Ringis D - 27 last, ringis X - 32 inimest, ringis C - 22 õpilast.Need 10 draamaklubi kutti, kes laulavad kooris, saavad D ja X ringide ühisosa. Kolm neist on ka sportlased, nemad on kõigi kolme ringi ühisosas. Ülejäänud seitse pole spordist huvitatud. Samamoodi 8-3=5

sportlased, kes ei laula kooris ja 6-3=3, kes ei käi draamaringis. On hästi näha, et kooris või näiteringis käib 5+3+3=11 sportlast, 22-(5+3+3)=11 tegeleb ainult spordiga; 70-(11+12+19+7+3+3+5)=10 - ei laula kooris, ei osale draamaringis, ei ole spordist huvitatud.

Joonis 14 Vastus: 10 inimest.

Ülesanne nr 11 . Klassis on 30 inimest. Neist 20 kasutab iga päev metroo, 15 bussi, 23 trolli, 10 nii metroo kui trolli, 12 nii metroo kui bussi, 9 nii trolli kui bussi. Kui palju inimesi kasutab iga päev kõiki kolme transpordiliiki?

Lahendus.

Joonis 15

Las x inimene kasutab kõiki kolme transpordiviisi. Siis kasutavad nad ainult metrood ja trolli - (10 - x) inimest, ainult bussi ja trolli - (9 - x) inimest, ainult metroo ja bussi - (12 - x) inimest. Vaatame, kui palju inimesi üksi metrood kasutab:

20 - (12 - x) - (10 - x) - x = x - 2

Samamoodi saame: x − 6 - ainult bussiga ja x + 4 - ainult trollibussiga, kuna seal on ainult 30 inimest, loome võrrandi:

x + (12 - ×) + (9 - x) + (10 - x) + (x + 4) + (x - 2) + (x - 6) = 30.

seega x = 3.

Vastus: 3 inimest.

Ülesanne nr 12.

Ettevõtte töötajatest külastas Prantsusmaad 16, Itaaliat 10, Inglismaad 6; Inglismaal ja Itaalias - 5; Inglismaal ja Prantsusmaal -6; kõigis kolmes riigis - 5 töötajat. Kui palju inimesi külastas nii Itaaliat kui ka Prantsusmaad, kui ettevõttes töötab kokku 19 inimest ja igaüks neist külastas vähemalt ühte neist riikidest?

Lahendus:

Teame, et kõigis kolmes riigis oli 5 töötajat. Inglismaal ja Itaalias on ka 5, mis tähendab, et samad töötajad olid ka Prantsusmaal ja seetõttu panime ringide A ja I ristumiskohta 0. Prantsusmaal ja Itaalias me ei tea, seega kirjutame x-5 ringide A ja F ristumiskoht. Kuna Inglismaal oli 6 inimest, siis 6-5-1=0 kirjutame 0, Prantsusmaal on 16+5-6 ja Itaalias 10+5-5 ja kokku on firmas 19 töötajat, siis kõik see jääb üle luua ja lahendada võrrand: 1 +16x+5-6+5+x-5+10x+5-5=19, seega x=7, mis tähendab 7-5=2 Itaaliat külastanud ettevõtte töötajat ja Prantsusmaa.

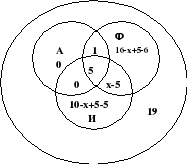
Joonis 16

Vastus: 2 töötajat.

Ülesanne nr 13.

Seal oli 10 meest, kes tahtsid erinevaid ajakirju vahetada. Nende hulgas tellib K 6 inimest, T 5 inimest, Yu 5 inimest, K ja T 3 inimest, T ja Yu 2 inimest, K ja Yu 3 inimest ning üks inimene ei telli ühtegi ajakirja. kuid loeb kõiki neid ajakirju raamatukogus. Peame välja selgitama, kui palju inimesi tellib kõiki kolme ajakirja, kui palju kahte ja kui palju ainult ühte ajakirja.

Lahendus. Olgu suur 10-liikmeline ring, kus kõik ajakirju vahetavad poisid. Suure ringi sisse joonistame kolm väiksemat ringi: K, T, Yu, millel on kujutatud tüübid, kes on tellinud vastavad ajakirjad.. Teatavasti ei telli üks inimene ühtki ajakirja.

Las x kutt tellib kõiki kolme ajakirja, siis (3) kutti tellib ainult K ja T, (2) ainult T ja Yu, (3) ainult K ja Yu. See tähendab, et ainult ajakiri K on tellitud 6 - (3-x+x+3-x)=x inimest, T ajakiri 5-(3-x+x+2-x)=x, Yu ajakiri 5-(3-x+x+2-x)= X .

Joonis 17

Teeme võrrandi: x+3-x+3-x+x+x+x+x+2-x=9, 8+x=9,x=1

Niisiis, 3 on meeste arv, kes tellisid ainult ühe ajakirja, 5 on meeste arv, kes tellisid kaks ajakirja, ja 1 on meeste arv, kes tellisid kõik kolm ajakirja.

KOKKUVÕTE

Matemaatika teema on nii tõsine

mida te ei saa kasutamata jätta

see on natuke meelelahutuslik.

B. Pascal

Matemaatiliste ülesannete hulgas on erilisel kohal loogikaülesanded, mille lahendamine aitab kaasa matemaatilise mõtlemise arendamisele. Need erinevad enamikust matemaatilistest probleemidest selle poolest, et nende lahendamine ei nõua sageli eriteadmisi, vaid reeglina intelligentsust. Iga loogika üks iseloomulikke tunnuseid on see, et see võimaldab pärast teatud teabe saamist selles sisalduvaid uusi teadmisi eraldada (identifitseerida).

Selgub, et tekstiloogikaülesannete lahendamiseks on mitu tehnikat. Need on mitmekesised ja igal neist on oma rakendusvaldkond.

Minu töö uurib probleeme, mis koosnevad paljudest andmetest.Leitud lahendused järgivad sama meetodit: tee joonis; sisestage algandmed ringidesse; analüüsides ja arutledes paneme tulemused kirja osade ringide kaupa; Otsime ja paneme vastuse kirja.Probleemi tingimuste kujutamine Euleri ringidena lihtsustab ja hõlbustab reeglina selle lahendamise teed. Lisaks saate nende abiga vastata paljudele probleemi ühe tingimuse kohta esitatud küsimustele.

See teema laiendas minu matemaatilist silmaringi ja rikastas erinevate ülesannete lahendamisel kasutatavate tööriistade arsenali.

Kasutatud allikate loetelu:

1. Gavrilova T.D.. Meelelahutuslik matemaatika. 5-11 klassid. Volgograd: Õpetaja, 2005.-96 lk.

2. Germanovitš P. Yu. "Matemaatika ülesannete kogumine intelligentsuse jaoks."

3. Getmanova A.D. Matemaatika loogilised alused, klass 10–11: õpik. – M.: Bustard, 2005.

4. Glazer G.I. . - M.: Haridus, 1964. - Lk 232.

5. Gusev V.A., Orlov A.I., Rosenthal A.L. "Kooliväline töö matemaatikas." M.: Haridus, 1984.

6. Nelin E.P., Dolgova O.E.. Algebra õpik ja analüüsi algus, 11. klass.

Abstraktid töö jaoks

Minu uurimistöö teemaks on “Probleemide lahendamine Euleri ringide abil”. Olümpiaadiks valmistudes seisin silmitsi ülesannetega, mis hõlmasid suurt hulka andmeid. Selgub, et selliste ülesannete lahendamist aitavad lihtsustada nn Euleri ringid, mille abil saab kujutada paljusid elemente, millel on teatud omadus. Käesoleva töö eesmärk on uurida seda meetodit ja osata seda probleemide lahendamisel rakendada.

Töös käsitletakse ülesandeid, mille lahendamine allub ühele algoritmile: joonise koostamine; Sisestame algandmed ringidena, alustades tingimusest, mis sisaldab rohkem omadusi; analüüsides ja arutledes paneme tulemused kirja ringi osade kaupa; kirjuta vastus üles.

Asjakohasus seisneb selles, et ülesanded on praktilist laadi, mis on tänapäeva elus oluline. Probleemid sunnivad sind mõtlema, lähenema probleemi lahendamisele teise nurga alt, suutma valida erinevate lahenduste hulgast, kõige lihtsama, lihtsaima viisi. Töös käsitletud meetodjuurdepääsetav ja hõlpsasti mõistetav, mis võimaldab teil selle rakendusala laiendada. Euleri ringe võib leida ajaloost, bioloogiast ja teiste ainete õppimisest.

Töös uuritud materjal, samuti praktiline osa,saab kasutada lisatundides matemaatikaolümpiaadideks valmistumisel.

Materjali ülevaade

Matemaatika on üks mu lemmikaineid keskkoolis. Mulle meeldib lahendada erinevaid matemaatilisi mõistatusi ja loogikaülesandeid. Matemaatikaklubis tutvume erinevate ülesannete lahendamise viisidega. Ühel päeval klubitunnis anti meile kodutöö järgmise ülesande lahendamiseks: „Klassis on 35 õpilast, 12 matemaatikaringis, 9 bioloogiaringis ja 16 last nendes klubides ei käi. . Kui paljud bioloogid on matemaatikast huvitatud? Mina lahendasin selle nii:

35 - 16=19 (lapsed) - käivad klubides

19-9 = 10 (lapsed) – matemaatikaklubis osalemine

12 - 10=2 (bioloogid) – meeldib matemaatikale.

Ja ta palus mul vaadata lahendust mu vanema venna probleemile. Ta ütles, et

Probleem lahendati õigesti, kuid selle lahendamiseks on mugavam ja kiirem viis. Selgub, et selle ülesande lahendamist aitavad lihtsustada nn Euleri ringid, mille abil saab kujutada paljusid elemente, millel on teatud omadus. Mind huvitas uudne viis probleemi lahendamiseks ja otsustasin kirjutada uurimistöö teemal: “Ülesannete lahendamine Euleri ringide abil”

Seadsin endale eesmärgi: õppida uut viisi ebastandardsete probleemide lahendamiseks Euleri ringide abil.

Minu uurimistöö teema paljastamiseks püstitati järgmised ülesanded:

Õppige kasutama teaduskirjandust.

Siit saate teada, mis on Euleri ringid.

Koostage ülesannete lahendamise algoritm.

Õppige Euleri ringide abil probleeme lahendama.

Koosta valik matemaatikaringi tundides kasutamiseks mõeldud ülesandeid.

Uurimismeetodid:

Teaduskirjanduse uurimine ja analüüs;

Induktiivse üldistuse meetod, täpsustamine.

Uurimisobjekt: Euleri ringid

Uurimisobjekt: hulga mõiste, peamised toimingud nendega, mis on vajalikud ülesannete lahendamisel Euleri ringide abil

Õppes osalejad: gümnaasiumi 5.-9.klassi õpilased

Uurimishüpotees: Euleri meetod lihtsustab teatud probleemide lahendamisel arutluskäiku ja hõlbustab teed selle lahenduseni.

Uuringu asjakohasus seisneb selles, et mittestandardsete loogikaülesannete lahendamiseks on palju tehnikaid ja viise. Sageli kasutatakse ülesande lahendamisel jooniseid, mis muudab ülesande lahendamise lihtsamaks ja visuaalsemaks. Üks selline visuaalne ja mugav viis ülesannete lahendamiseks on Euleri ringi meetod. See meetod võimaldab teil lahendada tülikate tingimuste ja paljude andmetega probleeme.

Matemaatikaolümpiaadidel pakutakse sageli Euleri ringide abil lahendatud ülesandeid. Sellised ülesanded on sageli praktilist laadi, mis on tänapäeva elus oluline. Need panevad mõtlema ja lähenema probleemi lahendamisele erinevate nurkade alt. Nad õpetavad teid erinevate meetodite hulgast valima kõige lihtsama ja lihtsaima.

Teoreetiline osa

Lühike ajalooline taust.

Leonhard Euler (1707-1783) – 18. sajandi Peterburi Akadeemia suur matemaatik. Sündis Šveitsi linnas Baselis. Ta avastas matemaatilised võimed varakult. 13-aastaselt sai temast Baseli ülikooli kunstiteaduskonna üliõpilane, kus õpetati nii matemaatikat kui ka astronoomiat. 17-aastaselt omistati talle magistrikraad. 20-aastaselt kutsuti Euler tööle Peterburi Teaduste Akadeemiasse ja 23-aastaselt oli ta juba füüsikaprofessor ning kolm aastat hiljem sai ta kõrgema matemaatika osakonna.

Oma pika eluea jooksul jättis Leonhard Euler olulisi töid matemaatika, mehaanika, füüsika, astronoomia ja mitmete rakendusteaduste erinevatest valdkondadest ning kirjutas üle 850 teadusartikli. Ühes neist tekkisid need ringid.

Mis on Euleri ringid?

Sellele küsimusele leidsin vastuse erinevat õppekirjandust lugedes. Leonhard Euler uskus, et "ringid on meie mõtlemise hõlbustamiseks väga sobivad." Mitmete ülesannete lahendamisel kasutas ta ideed kujutada hulgad ringide abil, mistõttu hakati neid nimetama "Euleri ringideks".

Matemaatikas on hulk kogum, mingite objektide (objektide) kogum. Objekte, mis moodustavad hulga, nimetatakse selle elementideks. Tavapäraselt aktsepteeritakse, et ring kujutab visuaalselt ühe kontseptsiooni mahtu. Näiteks meie 5. klass on komplekt ja õpilaste arv klassis on selle elemendid.

Matemaatikas tähistatakse hulki suurtähtedega ja nende elemente suurtähtedega. Sageli kirjutatakse kujul A = (a, b, c, ...), kus hulga A elemendid on märgitud lokkis sulgudes.

Kui hulga A iga element on samal ajal hulga B element, siis öeldakse, et A on hulga B alamhulk. Näiteks meie gümnaasiumi 5. klassi õpilaste hulk on kõigi gümnaasiumi õpilaste alamhulk. .

Komplektidega, nagu ka objektidega, saab sooritada teatud toiminguid (operatsioone). Komplektidega toimingute selgemaks ettekujutamiseks kasutatakse spetsiaalseid jooniseid - Euleri diagramme (ringe). Tutvume mõnega neist.

Ühiste elementide hulka A ja B nimetatakse hulkade A ja B ristumiskohaks ning seda tähistatakse märgiga ∩.

A∩B = (m), C ∩B = (e, u).

Hulkadel A ja C pole ühiseid elemente, seega on nende hulkade ristumiskohaks tühi hulk: A∩C =∅.

Kui luua hulk A ja B elementidest uus hulk, mis koosneb kõigist nende hulkade elementidest ja ei sisalda muid elemente, siis saadakse hulkade A ja B liit, mida tähistatakse märgiga ∪.

Vaatleme näidet: Olgu A = (t, o, h, k, a), B = (t, i, p, e), C = (d, e, f, u, s).

A∪B = (t, o, h, k, a, i, p, e), B∪ C = (t, i, p, e, d, f, s), A ∪ B ∪ C = (t , o, h, k, a, i, p, e, d, f, s).

Järeldused: Euleri ringid on geomeetriline diagramm, mis võimaldab muuta loogilised seosed nähtuste ja mõistete vahel selgemaks. Samuti aitab see kujutada komplekti ja selle osa vahelist suhet.

Saate seda kontrollida näidisülesande abil.

Kõik mu sõbrad kasvatavad oma korterites lilli. Neist kuus kasvatavad kaktusi ja viis kannikest. Ja ainult kahel on nii kaktused kui kannikesed. Mitu sõbrannat mul on?

Teeme kindlaks, mitu komplekti ülesandes on (st mitu ringi me ülesande lahendamisel joonistame).

Ülesandes kasvatavad sõbrad 2 tüüpi lilli: kaktused ja kannikesed.

See tähendab esimest komplekti (1 ring on sõbrad, kes kasvatavad kaktusi).

Teine komplekt (2. ring on sõbrad, kes kasvatavad kannikest).

Esimeses ringis määrame kaktuste ja teises ringis kannikeste omanikud.

Valime tingimuse, mis sisaldab ringide joonistamiseks rohkem omadusi. Mõnel sõbral on mõlemad lilled, nii et joonistame ringid, et neil oleks ühine osa.

Teeme joonistamise.

Üldosasse paneme numbri 2, kuna kahel sõbral on nii kaktused kui kannikesed.

Vastavalt probleemi tingimustele kasvatavad 6 sõpra kaktusi ja 2 on juba ühisosas, siis ülejäänud kaktuste ossa paneme numbri 4 (6-2 = 4).

5 sõpra kasvatavad kannikest ja 2 on juba ühisosas, siis ülejäänud osa kannikest paneme numbri 3 (5-2=3)

Pilt ise ütleb meile vastuse 4+2+3=9. Kirjutame vastuse üles.

Vastus: 9 sõbrannat

Praktiline osa

Ülesannete lahendamine Euleri ringide abil

Olles ülesande näite ja uuritud materjali põhjal välja mõelnud, millised on Euleri ringid, otsustasin liikuda selle meetodi abil ülesannete lahendamise algoritmi koostamise juurde.

2.1 Algoritm ülesannete lahendamiseks

Uurime hoolikalt ja kirjutame lühidalt üles probleemi tingimused.

Määrame komplektide arvu ja määrame need.

Teeme joonistamise. Konstrueerime hulkade ristumiskoha.

Algandmed kirjutame ringidesse.

Valige tingimus, mis sisaldab rohkem atribuute.

Puuduvad andmed kirjutame Euleri ringidesse (arutluskäik ja analüüs)

Kontrollime ülesande lahendust ja paneme vastuse kirja.

Olles loonud algoritmi probleemide lahendamiseks Euleri ringide abil, otsustasin sellega töötada veel mitme ülesande kallal.

Probleemid, mis on seotud kahe hulga ristumise ja liitumisega

Ülesanne 1.

Minu klassis on 15 õpilast. Neist 9 on seotud kergejõustiku sektsiooniga, 5 ujumise sektsiooniga ja 3 mõlema sektsiooniga. Kui palju õpilasi klassis sektsioonides ei käi?

Lahendus.

Probleemil on üks hulk ja kaks alamhulka. 1 ring – õpilased kokku. 2. ring – kergejõustikuga tegelevate õpilaste arv. 3 ring – ujumisega tegelevate õpilaste arv.

Esitagem kõiki õpilasi suurema ringi abil. Asetame sisse väiksemad ringid ja joonistame need nii, et neil oleks ühine osa (kuna mõlemas osas õpib kolm meest).

Kokku

Teeme joonistamise.

Suures ringis on 15 õpilast. Väiksemate ringide üldossa paneme arvu 3. Ülejäänud ringi ossa l/a paneme numbri 6 (9-3=6). Ringi ülejäänud osasse n - pane arv 2 (5-3=2).

5. Vastuse kirjutame üles pildilt: 15-(6+3+2) = 4 (õpilast) ei tegele üheski neist osadest.

Ülesanne 2. (mille lahendasin teistmoodi, kuid nüüd lahendan selle Euleri ringide abil)

Klassis on 35 õpilast, 12 õpib matemaatikaringis, 9 bioloogiaringis ja 16 last nendes klubides ei käi. Kui paljud bioloogid on matemaatikast huvitatud?

Lahendus:

Probleemil on üks hulk ja kaks alamhulka. 1 ring – õpilased kokku klassis. 2. ring matemaatikaringis õppivate õpilaste arv (tähistatakse tähega M). 3. ring - bioloogiaringis õppivate õpilaste arv (tähistatakse tähega B).

Kujutagem kogu õpilaste klassi suure ringi abil. Sisse asetame väiksemad ringid, millel on ühine osa, sest Matemaatika vastu tunnevad huvi mitmed bioloogid.

Teeme joonise:

Suures ringis on ainult 35 õpilast. 35-16 = 19 (õpilast) käivad nendes klubides. Ringi M sisemusse panime matemaatikaringi 12 õpilast. Ringi B sisemusse panime bioloogiaklubisse õppima 9 õpilast.

Kirjutame vastuse pildilt: (12 + 9) – 19 = 2 (õpilased) – neile meeldivad bioloogia ja matemaatika. Vastus: 2 õpilast.

2.3. Probleemid, mis on seotud kolme hulga ristumise ja liitumisega

3. ülesanne.

Klassis on 40 inimest. Neist 19 inimesel on vene keele hinne “C”, matemaatikas 17 inimesel ja ajaloos 22 inimesel. Ainult ühel ainel on hinded C: vene keeles - 4 inimest, matemaatikas - 4 inimest, ajaloos - 11 inimest. Seitse õpilast on nii matemaatikas kui ajaloos “C” ja 5 õpilasel kõigis ainetes “C”. Kui palju inimesi õpib ilma hinneteta? Kui paljudel inimestel on C-d kahes õppeaines kolmest?

Lahendus:

Probleemil on üks hulk ja kolm alamhulka. 1 suur ring – õpilaste koguarv klassis. 2. ring on matemaatika C-hinnetega õpilaste arv (tähistatakse tähega M), 3. ring on väiksem - vene keele C-hinnetega õpilaste arv (tähistatakse tähega P), 4. ring on väiksem - õpilaste arv ajaloos C hindega (tähistatakse tähega I)

Joonistame Euleri ringid. Suurema ringi sisse, mis kujutab kõiki klassi õpilasi, asetame kolm väiksemat ringi M, R, I, mis tähendavad vastavalt matemaatikat, vene keelt ja ajalugu ning kõik kolm ringi ristuvad, kuna kokku on 5 õpilast “C” hinded. teemasid.

Kirjutame andmed ringidesse, arutledes, analüüsides ja vajalikke arvutusi tehes. Kuna matemaatikas ja ajaloos on “C” hindega õpilasi 7, siis ainult kahe “C” hindega - matemaatikas ja ajaloos - on õpilaste arv 7-5 = 2. Siis on 17-4-5-2=6 õpilasel kaks C-hinnet - matemaatikas ja vene keeles ning 22-5-2-11=4 õpilasel ainult kaks "C" - ajaloos ja vene keeles. . Sel juhul õpib ilma C-ta 40-22-4-6-4 = 4 õpilast. Ja neil on “C” hinded kahes aines kolmest 6+2+4=12 inimest.

7-5=2 - õpilaste arv, kellel on ainult kaks C-hinnet - M, I.

17-4-5-2=6 - õpilaste arv, kellel on ainult kaks C-hinnet - M, R.

22-5-2-11=4 - õpilaste arv, kellel on ainult kaks C-hinnet - I, R.

40-22-4-6-4=4 - ilma C-ta õppivate õpilaste arv

6+2+4=12 - C-hindega õpilaste arv - kahes õppeaines kolmest

Vastus: 4 õpilast õpib ilma “C” hinneteta, 12 õpilasel on “C” hinded kahes aines kolmest.

4. ülesanne.

Klassis on 30 inimest. Neist 20 kasutab iga päev metroo, 15 bussi, 23 trolli, 10 nii metroo kui trolli, 12 nii metroo kui bussi, 9 nii trolli kui bussi. Kui palju inimesi kasutab iga päev kõiki kolme transpordiliiki?

Lahendus. 1 viis. Lahendamiseks kasutame taas Euleri ringe:

20 - (12 - x) - (10 - x) - x = x - 2

Sarnaselt saame: 15 –(12 − x) -(9 − x) - x = x − 6 - ainult bussiga ja

23 - (9 - x) - (10 - x) - x = x + 4 - ainult trollibussiga, kuna seal on ainult 30 inimest, loome võrrandi:

X + (12 - ×) + (9 - x) + (10 - x) + (x + 4) + (x - 2) + (x - 6) = 30. Seega x = 3.

2. meetod. Või saate selle probleemi lahendada muul viisil:

20+15+23-10-12-9+x=30, 27+x=30, x=3.

Vastus: Iga päev kasutab kõiki kolme transpordiliiki 3 inimest.

2.4. Praktilise tähtsusega probleemide ettevalmistamine

Ülesanne 1. 5A klassis on 15 inimest. Ringi “Erudiidid” läheb 5 inimest, ringi “Tee Sõna juurde” 13 inimest, spordisektsioonis 3 inimest. Lisaks käivad 2 inimest ringis “Erudiidid” ja “Tee sõna juurde”, “Eruditsioon” ja spordirubriigis, spordirubriigis ja “Tee sõna juurde”. Kui palju inimesi kõigis kolmes klubis käib?

Lahendus:

1. Las x inimest käivad siis kõigis kolmes klubis

2. 5+13+3-2-2-2+x=15, 13+x=15, x=2

Vastus: Kõigis kolmes klubis käib 2 inimest.

Probleem 2

On teada, et 6.B klassi õpilased on registreeritud sotsiaalvõrgustikes: “VK”, “Odnoklassniki”, “Dating Galaxy”. 2 õpilast ei ole registreeritud üheski suhtlusvõrgustikus, 7 õpilast on registreeritud nii Odnoklassnikis kui ka VK-s; 2 õpilast ainult Odnoklassnikis ja 1 ainult VK-s; ja 2 õpilast on registreeritud kõigis 3 suhtlusvõrgustikus. Kui palju inimesi klassis on igas suhtlusvõrgustikus registreeritud? Kui palju inimesi klassis küsitluses osales?

Lahendus:

Euleri ringide abil saame:

VK-s on registreeritud 1+5+2=8 inimest,

Odnoklassnikis on 2+5+2=9 inimest,

Kohtingugalaktikas on ainult 2 inimest.

Kokku osales küsitluses 1+5+2+2+2=12 inimest

2.5. Ülesanded kasutamiseks matemaatikaringi tundides

Ülesanne 1: "Harry Potter, Ron ja Hermione"

Riiulil oli 26 loitsuraamatut, kõik olid läbi loetud. Neist 4 lugesid nii Harry Potter kui ka Ron. Hermione luges 7 raamatut, mida Harry Potter ega Ron polnud lugenud, ja kaks raamatut, mida Harry Potter oli lugenud. Kokku luges Harry Potter 11 raamatut. Mitu raamatut on Ron üksi lugenud?

Ülesanne 2: "Pioneerilaager"

Ülesanne 3: "Äärmuslik"

Ülesanne 4: "Jalgpallimeeskond"

Spartaki jalgpallimeeskonnas on 30 mängijat, sealhulgas 18 ründajat, 11 poolkaitsjat, 17 kaitsjat ja väravavahti. Teadaolevalt kolm võivad olla ründajad ja kaitsjad, 10 kaitsjat ja poolkaitsjat, 6 ründajat ja kaitsjat ning 1 võib olla ründaja, kaitsja ja poolkaitsja. Väravavahid on asendamatud. Mitu väravavahti on Spartaki meeskonnas?

Ülesanne 5: "pood"

Kauplust külastas 65 inimest. Teadaolevalt osteti 35 külmkappi, 36 mikrolaineahju, 37 televiisorit. Neist 20 ostsid nii külmkapi kui ka mikrolaineahju, 19 ostsid nii mikrolaineahju kui televiisori, 15 ostsid külmiku ja teleri ning kõik kolm ostu sooritasid kolm inimest. Kas nende hulgas oli külaline, kes midagi ei ostnud?

Ülesanne 6: “Lasteaed”

Lasteaias käib 52 last. Igaüks neist armastab kas kooki või jäätist või mõlemat. Pooltele lastest maitseb kook ning 20 inimesele kook ja jäätis. Kui paljud lapsed armastavad jäätist?

Ülesanne 7: "Üliõpilasbrigaad"

Õpilasproduktsiooni meeskonnas on 86 gümnasisti. 8 neist ei oska juhtida ei traktorit ega kombaini. 54 õpilast õppis hästi traktorit, 62 kombaini. Kui palju inimesi sellest meeskonnast saab töötada nii traktori kui ka kombaini peal?

Uurimistöö osa

Eesmärk: Euleri meetodi kasutamine gümnasistide poolt mittestandardsete ülesannete lahendamisel.

Katse viidi läbi matemaatikahuviliste 5.-9. klassi õpilaste osavõtul. Neil paluti lahendada kaks järgmist probleemi:

Klassist kuus õpilast käib muusikakoolis, kümme on seotud jalgpallisektsiooniga ja veel kümme kunstistuudios. Kolm neist käivad nii jalgpalli- kui ka muusikakoolis. Mitu inimest on klassis?

Katses osalenud 10-st (igast paralleelklassist 2 inimest) lahendas esimest ülesannet vaid 4 inimest, teise ülesande vaid kaks (8. ja 9. klassi õpilased). Pärast seda, kui esitasin neile oma uurimistöö, milles rääkisin Euleri ringidest, analüüsisin selle meetodi abil mitmete lihtsate ja pakutud ülesande lahendusi, said õpilased ise lihtsamaid ülesandeid lahendada.

Katse lõpus anti lastele järgmine ülesanne:

Pioneerilaagris on 70 last. Neist 27 on seotud draamaklubiga, 32 laulab kooris, 22 armastab sporti. Draamaklubis on 10 kutti koorist, kooris 6 sportlast, draamaklubis 8 sportlast; Nii draamaklubis kui ka kooris käib 3 sportlast. Kui palju on lapsi, kes ei laula, ei ole spordist huvitatud, ei osale draamaringis? Kui paljud mehed tegelevad ainult spordiga?

Kümnest katses osalejast said kõik selle ülesandega hakkama.

Järeldus: Ülesannete lahendamine Euleri ringide abil arendab loogilist mõtlemist ja võimaldab lahendada ülesandeid, mida saab tavapärasel viisil lahendada vaid kolme tundmatuga kolme võrrandisüsteemi koostamisega. 5.-7. klassi õpilased ei oska võrrandisüsteeme lahendada, kuid nad saavad lahendada samu ülesandeid. See tähendab, et lapsed peavad teadma seda ülesannete lahendamise meetodit Euleri ringide abil.

Rakendused