Läbiva sirge võrrand 2. Sirge võrrand - sirge võrrandi tüübid: punkti läbiv, üldine, kanooniline, parameetriline jne.
Definitsioon. Descartes'i ristkülikukujulises koordinaatsüsteemis on vektor komponentidega (A, B) risti sirgega, mis on antud võrrandiga Ax + By + C = 0.
Näide. Leidke vektoriga (3, -1) risti punkti A(1, 2) läbiva sirge võrrand.
Lahendus. Kui A = 3 ja B = -1, koostame sirge võrrandi: 3x – y + C = 0. Koefitsiendi C leidmiseks asendame saadud avaldisega antud punkti A koordinaadid Saame: 3 – 2 + C = 0, seega C = -1. Kokku: nõutav võrrand: 3x – y – 1 = 0.
Kaht punkti läbiva sirge võrrand
Olgu ruumis antud kaks punkti M 1 (x 1, y 1, z 1) ja M 2 (x 2, y 2, z 2), siis neid punkte läbiva sirge võrrand on:

Kui mõni nimetajatest on võrdne nulliga, peaks vastav lugeja olema võrdne nulliga Tasapinnal on ülaltoodud sirge võrrand lihtsustatud:

kui x 1 ≠ x 2 ja x = x 1, kui x 1 = x 2.
Murd = k nimetatakse kalle sirge.
Näide. Leidke punkte A(1, 2) ja B(3, 4) läbiva sirge võrrand.
Lahendus. Rakendades ülaltoodud valemit, saame:

Punktist ja kaldest lähtuva sirge võrrand
Kui sirge Ax + By + C = 0 üldvõrrand taandatakse järgmisele kujule:

ja määrata  , siis nimetatakse saadud võrrandit kaldega sirge võrrandk.
, siis nimetatakse saadud võrrandit kaldega sirge võrrandk.
Punkti ja suunavektori sirge võrrand
Analoogiliselt punktiga, mis käsitleb sirge võrrandit läbi normaalvektori, saate sisestada läbi punkti sirge definitsiooni ja sirge suunavektori.
Definitsioon. Iga nullist erinevat vektorit (α 1, α 2), mille komponendid vastavad tingimusele A α 1 + B α 2 = 0, nimetatakse sirge suunavaks vektoriks
Ax + Wu + C = 0.
Näide. Leidke sirge võrrand suunavektoriga (1, -1) ja läbib punkti A(1, 2).
Lahendus. Otsime soovitud sirge võrrandit kujul: Ax + By + C = 0. Definitsiooni kohaselt peavad koefitsiendid vastama järgmistele tingimustele:
1 * A + (-1) * B = 0, st. A = B.
Siis on sirgjoone võrrand järgmine: Ax + Ay + C = 0 või x + y + C / A = 0. x = 1, y = 2 korral saame C/ A = -3, st. nõutav võrrand:
Sirge võrrand segmentides
Kui sirge üldvõrrandis Ах + Ву + С = 0 С≠0, siis –С-ga jagades saame:  või
või

Koefitsientide geomeetriline tähendus on see, et koefitsient A on sirge ja Ox-telje lõikepunkti koordinaat ja b – sirge ja Oy telje lõikepunkti koordinaat.
Näide. Antud on sirge x – y + 1 = 0 üldvõrrand.Leia selle sirge võrrand lõikudes.
C = 1, , a = -1, b = 1.
Sirge normaalvõrrand
Kui võrrandi Ax + By + C = 0 mõlemad pooled jagatakse arvuga  mida nimetatakse normaliseeriv tegur, siis saame
mida nimetatakse normaliseeriv tegur, siis saame
xcosφ + ysinφ - p = 0 –
sirge normaalvõrrand. Normaliseeriva teguri märk ± tuleb valida nii, et μ * C< 0. р – длина перпендикуляра, опущенного из начала координат на прямую, а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.
Näide. Antud on sirge üldvõrrand 12x – 5y – 65 = 0. Sellele reale on vaja kirjutada erinevat tüüpi võrrandeid.
selle sirge võrrand segmentides: 
selle sirge võrrand kaldega: (jagage 5-ga)

sirge tavavõrrand:
 ; cos φ = 12/13; sin φ= -5/13; p = 5.
; cos φ = 12/13; sin φ= -5/13; p = 5.
C Tuleb märkida, et iga sirget ei saa esitada võrrandiga lõikudes, näiteks sirged, mis on paralleelsed telgedega või läbivad alguspunkti.
Näide. Sirge lõikab koordinaattelgedel ära võrdsed positiivsed lõigud. Kirjutage sirge võrrand, kui nendest lõikudest moodustatud kolmnurga pindala on 8 cm 2.
Lahendus. Sirge võrrand on kujul: , ab /2 = 8; a = 4; -4. a = -4 ei sobi vastavalt ülesande tingimustele. Kokku: või x + y – 4 = 0.
Näide. Kirjutage võrrand sirge jaoks, mis läbib punkti A(-2, -3) ja alguspunkti.
Lahendus.
Sirge võrrand on järgmine:  , kus x 1 = y 1 = 0; x2 = -2; y 2 = -3.
, kus x 1 = y 1 = 0; x2 = -2; y 2 = -3.
Vaatame näidete abil, kuidas luua võrrandit kahte punkti läbivale sirgele.
Näide 1.
Kirjutage võrrand punkte A(-3; 9) ja B(2;-1) läbiva sirge jaoks.
1. meetod – loo nurgakoefitsiendiga sirgjoone võrrand.
Nurgakoefitsiendiga sirge võrrand on kujul . Asendades punktide A ja B koordinaadid sirge võrrandisse (x= -3 ja y=9 - esimesel juhul x=2 ja y= -1 - teisel), saame võrrandisüsteemi millest leiame k ja b väärtused:
Liites 1. ja 2. võrrandi liikme kaupa, saame: -10=5k, kust k= -2. Asendades teise võrrandi k= -2, leiame b: -1=2·(-2)+b, b=3.
Seega y= -2x+3 on nõutav võrrand.
2. meetod – loome sirgjoone üldvõrrandi.
Sirge üldvõrrandil on vorm . Asendades võrrandisse punktide A ja B koordinaadid, saame süsteemi:
Kuna tundmatute arv on suurem kui võrrandite arv, ei ole süsteem lahendatav. Kuid kõiki muutujaid saab väljendada ühe kaudu. Näiteks läbi b.
Korrutades süsteemi esimese võrrandi -1-ga ja liites termini kaupa teisega:
saame: 5a-10b=0. Seega a=2b.
Asendame saadud avaldise teise võrrandiga: 2·2b -b+c=0; 3b+c=0; c= -3b.
Asendage võrrandis ax+by+c=0 a=2b, c= -3b:
2bx+by-3b=0. Jääb jagada mõlemad pooled b-ga:
Sirge üldvõrrandi saab hõlpsasti taandada nurkkoefitsiendiga sirge võrrandiks:
3. meetod – loo võrrand 2 punkti läbivast sirgest.
Kaht punkti läbiva sirge võrrand on järgmine:
![]()
Asendame selles võrrandis punktide A(-3; 9) ja B(2;-1) koordinaadid
(st x 1 = -3, y 1 = 9, x 2 = 2, y 2 = -1):
![]()
ja lihtsustada:
kust 2x+y-3=0.
Koolikursustel kasutatakse kõige sagedamini sirge võrrandit nurga koefitsiendiga. Kuid kõige lihtsam on tuletada ja kasutada kahte punkti läbiva sirge võrrandi valemit.
Kommenteeri.
Kui antud punktide koordinaatide asendamisel üks võrrandi nimetajatest
![]()
osutub võrdseks nulliga, siis saadakse vajalik võrrand, võrdsustades vastava lugeja nulliga.
Näide 2.
Kirjutage võrrand sirge jaoks, mis läbib kahte punkti C(5; -2) ja D(7;-2).
Asendame punktide C ja D koordinaadid 2 punkti läbiva sirge võrrandisse.
See artikkel on osa tasapinna sirge teemavõrrandist. Siin vaatleme seda igast küljest: alustame joone üldvõrrandi kuju määrava teoreemi tõestusega, seejärel käsitleme sirge mittetäielikku üldvõrrandit, toome näiteid mittetäielikest võrranditest joonest koos graafiliste illustratsioonidega ja kokkuvõtteks peatume üleminekul sirge üldvõrrandilt selle sirge teist tüüpi võrranditele ning anname üksikasjalikud lahendused tüüpilistele probleemidele sirge üldvõrrandi koostamisel.
Leheküljel navigeerimine.
Sirge üldvõrrand – põhiteave.
Analüüsime seda algoritmi näite lahendamisel.
Näide.
Kirjutage sirge parameetrilised võrrandid, mis on antud sirge üldvõrrandiga ![]() .
.
Lahendus.
Esiteks taandame sirge algse üldvõrrandi joone kanooniliseks võrrandiks:
Nüüd võtame saadud võrrandi vasaku ja parema külje parameetriga võrdseks. Meil on 
Vastus:

Sirge üldvõrrandist on võimalik saada nurgakoefitsiendiga sirge võrrand ainult siis, kui . Mida peate ülemineku tegemiseks tegema? Esiteks jätke üldise sirge võrrandi vasakusse serva ainult termin , ülejäänud liikmed tuleb nihutada vastupidise märgiga paremale: ![]() . Teiseks jagage saadud võrdsuse mõlemad pooled arvuga B, mis ei ole null,
. Teiseks jagage saadud võrdsuse mõlemad pooled arvuga B, mis ei ole null, ![]() . See on kõik.
. See on kõik.
Näide.
Sirge ristkülikukujulises koordinaatsüsteemis Oxy on antud sirge üldvõrrandiga. Hankige selle sirge võrrand kaldega.
Lahendus.
Teeme vajalikud toimingud: .
Vastus:
Kui sirge on antud sirge täieliku üldvõrrandiga, on sirge võrrandit lihtne saada vormi segmentides. Selleks kanname arvu C vastasmärgiga võrrandi paremale poolele, jagame saadud võrrandi mõlemad pooled –C-ga ning lõpuks kanname muutujate x ja y koefitsiendid nimetajateks: 
Vaatleme punkti ja normaalvektorit läbiva sirge võrrandit. Olgu koordinaatsüsteemis antud punkt ja nullist erinev vektor (joon. 1).
Definitsioon
Nagu näeme, on üks sirgjoon, mis läbib punkti, mis on risti vektori suunaga (antud juhul nimetatakse seda normaalvektor otse).

Riis. 1
Tõestame, et lineaarvõrrand
see on sirge võrrand, see tähendab, et sirge iga punkti koordinaadid vastavad võrrandile (1), kuid punkti koordinaadid, millel ei asu, ei rahulda võrrandit (1).
Selle tõestamiseks paneme tähele, et vektorite ja = skalaarkorrutis koordinaadi kujul ühtib võrrandi (1) vasaku küljega.
Järgmiseks kasutame sirge ilmset omadust: vektorid ja on risti siis ja ainult siis, kui punkt asub . Ja eeldusel, et mõlemad vektorid on risti, muutub nende skalaarkorrutis (2) kõigi punktide jaoks, mis asuvad, ja ainult nende jaoks. See tähendab, et (1) on sirgjoone võrrand.
Definitsioon
Võrrandit (1) nimetatakse antud punkti läbiva sirge võrrandnormaalvektoriga = .
Teisendame võrrandi (1)
Tähistades = , saame
Seega vastab kuju (3) lineaarvõrrand sirgele. Vastupidi, kasutades antud võrrandit kujul (3), kus vähemalt üks koefitsient ei ole võrdne nulliga, saab konstrueerida sirge.
Tõepoolest, olgu arvude paaril võrrand (3) täidetud, see tähendab
Lahutades viimase punktist (3), saame seose, mis määrab vektori ja punkti taga oleva sirge.
Sirge üldvõrrandi uurimine
Rea paigutamise tunnuseid on kasulik teada teatud juhtudel, kui üks või kaks arvudest on võrdne nulliga.
1. Üldvõrrand näeb välja selline: . Punkt rahuldab seda, mis tähendab, et joon läbib alguspunkti. Selle võib kirjutada: = – x (vt joonis 2).

Riis. 2
Usume, et:
Kui paneme , siis , saame teise punkti (vt joonis 2).
2. , siis näeb võrrand välja selline, kus = –. Normaalvektor asub teljel, sirgel. Seega on sirgjoon punktis risti ehk teljega paralleelne (vt joonis 3). Eelkõige kui ja , siis ja võrrand on ordinaattelje võrrand.

Riis. 3
3. Samamoodi, kui võrrand on kirjutatud, kus . Vektor kuulub teljele. Sirge punktis (joonis 4).

Kui, siis telje võrrand on .
Uurimuse saab sõnastada sellisel kujul: sirge on paralleelne koordinaatteljega, mille muutus sirge üldvõrrandis puudub.
Näiteks:
Ehitame sirge, kasutades üldvõrrandit, eeldusel, et - ei ole võrdsed nulliga. Selleks piisab, kui leida kaks sellel joonel asuvat punkti. Selliseid punkte on mõnikord mugavam leida koordinaatide telgedel.
Olgu siis = –.
Millal , siis = –.
Tähistame – = , – = . Punkte ja leiti. Joonistame ja tõmbame telgedele ja nende kaudu sirge (vt joon. 5).

Riis. 5
Üldisest saate liikuda võrrandi juurde, mis sisaldab numbreid ja:
Ja siis selgub:
Või vastavalt tähistusele saame võrrandi
Mida nimetatakse sirgjoone võrrand segmentides. Arvud ja, märgi täpsusega, on võrdsed lõikudega, mis on koordinaatide telgedel sirgjoonega ära lõigatud.
Sirge ja kalde võrrand
Et teada saada, mis on kaldega sirge võrrand, kaaluge võrrandit (1):
Tähistades – = , saame
võrrand sirgest, mis läbib punkti antud suunas. Koefitsiendi geomeetriline sisu on selge jooniselt fig. 6.
B = = , kus on väikseim nurk, mille võrra tuleb telje positiivset suunda pöörata ümber ühispunkti, kuni see joondub sirgjoonega. Ilmselgelt, kui nurk on terav, siis title="Rendered by QuickLaTeX.com" height="17" width="97" style="vertical-align: -4px;">; если же – тупой угол, тогда .!}
Avame sulud punktis (5) ja lihtsustame seda:
Kus. Seos (6) – võrrand sirge kaldega. Kui , on segment, mis lõikab teljel sirge (vt joonis 6).
Märge!
Üldise sirgjoone võrrandilt kaldekoefitsiendiga võrrandile liikumiseks tuleb esmalt lahendada .

Riis. 6
= – x + – =
kus tähistatakse = –, = –. Kui, siis üldvõrrandi uurimisest on juba teada, et selline sirge on teljega risti.
Vaatame näite abil sirge kanoonilist võrrandit.
Olgu koordinaatsüsteemis määratud punkt ja nullist erinev vektor (joon. 7).

Riis. 7
On vaja luua võrrand sirge jaoks, mis läbib vektoriga paralleelset punkti, mida nimetatakse suunavektoriks. Suvaline punkt kuulub sellele reale siis ja ainult siis, kui . Kuna vektor on antud ja vektor on , siis vastavalt paralleelsuse tingimusele on nende vektorite koordinaadid võrdelised, see tähendab:
Definitsioon
Seost (7) nimetatakse sirge võrrandiks, mis läbib antud punkti antud suunas või sirge kanooniliseks võrrandiks.
Pangem tähele, et joonte pliiatsi võrrandist (4) saame liikuda näiteks võrrandile (7)
või punkti ja normaalvektorit läbiva sirge võrrandist (1):
Eespool eeldati, et suunavektor on nullist erinev, kuid võib juhtuda, et üks selle koordinaatidest on näiteks . Seejärel kirjutatakse avaldis (7) formaalselt:
millel pole üldse mõtet. Siiski aktsepteerime ja saame teljega risti oleva sirge võrrandi. Tõepoolest, võrrandist on selge, et sirge on defineeritud punkti ja suunavektoriga, mis on teljega risti. Kui eemaldame sellest võrrandist nimetaja, saame:
Või - teljega risti asetseva sirgjoone võrrand. Sarnane tulemus saadakse ka vektori puhul.
Sirge parameetriline võrrand
Et mõista, mis on sirge parameetriline võrrand, peate naasma võrrandi (7) juurde ja võrdsustama iga murdosa (7) parameetriga. Kuna vähemalt üks nimetajatest punktis (7) ei ole võrdne nulliga ja vastav lugeja võib omandada suvalisi väärtusi, siis on parameetri muutumise piirkond kogu numbritelg.
Definitsioon
Võrrandit (8) nimetatakse sirge parameetriliseks võrrandiks.
Näited sirgjoonelistest probleemidest
Muidugi on raske midagi ainult definitsioonide põhjal lahendada, sest peate iseseisvalt lahendama vähemalt mõned näited või probleemid, mis aitavad käsitletud materjali koondada. Seetõttu analüüsime põhiülesandeid sirgjooneliselt, kuna sarnaseid probleeme tuleb eksamitel ja testidel sageli ette.
Kanooniline ja parameetriline võrrand
Näide 1
Leidke võrrandiga antud sirgel punkt, mis asub selle sirge punktist 10 ühiku kaugusel.
Lahendus:
Lase otsitud sirge punkt, siis kauguse kohta kirjutame . Arvestades seda. Kuna punkt kuulub sirgele, millel on normaalvektor, siis võib sirge võrrandi kirjutada: = = ja siis selgub:
Siis vahemaa. Vastavalt , või . Parameetrilisest võrrandist:
Näide 2
Ülesanne
Punkt liigub ühtlaselt kiirusega alguspunktist vektori suunas. Leidke punkti koordinaadid liikumise algusest.
Lahendus
Kõigepealt peate leidma ühikuvektori. Selle koordinaadid on suunakoosinused:
Siis kiirusvektor:
X = x = .
Nüüd kirjutatakse sirge kanooniline võrrand:
= = , = – parameetriline võrrand. Pärast seda peate kasutama sirge parameetrilist võrrandit .
Lahendus:
Punkti läbiva sirge võrrand leitakse joonte pliiatsi valemi abil, kus kalle sirge jaoks ja = sirge jaoks.
Arvestades joonist, kus on näha, et sirgjoonte ja vahel on kaks nurka: üks on terav ja teine on nüri. Valemi (9) kohaselt on see nurk sirgjoonte vahel, mille võrra peate pöörama sirget nende ristumispunkti suhtes vastupäeva, kuni see joondub sirgjoonega .

Niisiis, me mäletasime valemit, mõtlesime välja nurgad ja nüüd saame naasta oma näite juurde. See tähendab, et võttes arvesse valemit (9), leiame kõigepealt jala võrrandid.

Kuna sirge pööramine punkti suhtes vastupäeva nurga võrra viib joonduseni sirgjoonega, siis valemis (9) , a . Võrrandist:
Kiirvalemi abil kirjutatakse sirgjoone võrrand:
Samamoodi leiame , ja
Joone võrrand:
Sirge võrrand – sirge võrrandi tüübid: punkti läbiv, üldine, kanooniline, parameetriline jne. värskendatud: 22. novembril 2019: Teaduslikud artiklid.Ru
Sirge omadused eukleidilises geomeetrias.
Läbi mis tahes punkti saab tõmmata lõpmatu arvu sirgeid.
Kahe mittekattuvad punkti kaudu saab tõmmata ühe sirge.
Tasapinna kaks lahknevat sirget kas lõikuvad ühes punktis või on
paralleelne (järgneb eelmisest).
Kolmemõõtmelises ruumis on kahe joone suhtelise asukoha jaoks kolm võimalust:
- jooned ristuvad;
- sirged on paralleelsed;
- sirgjooned ristuvad.
Otse rida— esimest järku algebraline kõver: sirgjoon Descartes'i koordinaatsüsteemis
on antud tasapinnal esimese astme võrrandiga (lineaarvõrrand).
Sirge üldvõrrand.
Definitsioon. Mis tahes tasapinna sirget saab määrata esimest järku võrrandiga
Ax + Wu + C = 0,
ja pidev A, B ei ole samal ajal võrdsed nulliga. Seda esimest järku võrrandit nimetatakse üldine
sirgjoone võrrand. Sõltuvalt konstantide väärtustest A, B Ja KOOS Võimalikud on järgmised erijuhud:
. C = 0, A ≠0, B ≠ 0- alguspunkti läbib sirgjoon
. A = 0, B ≠0, C ≠0 (+ C = 0)- teljega paralleelne sirgjoon Oh
. B = 0, A ≠0, C ≠ 0 (Ax + C = 0)- teljega paralleelne sirgjoon OU
. B = C = 0, A ≠0- sirgjoon ühtib teljega OU
. A = C = 0, B ≠0- sirgjoon ühtib teljega Oh
Sirge võrrandit saab esitada erineval kujul, olenevalt mis tahes etteantust
esialgsed tingimused.
Punkti ja normaalvektori sirge võrrand.
Definitsioon. Descartes'i ristkülikukujulises koordinaatsüsteemis vektor komponentidega (A, B)
võrrandiga antud sirgega risti
Ax + Wu + C = 0.
Näide. Leidke punkti läbiva sirge võrrand A(1, 2) vektoriga risti (3, -1).
Lahendus. Kui A = 3 ja B = -1, koostame sirgjoone võrrandi: 3x - y + C = 0. Koefitsiendi C leidmiseks
Asendame saadud avaldisesse antud punkti A koordinaadid. Saame: 3 - 2 + C = 0, seega
C = -1. Kokku: nõutav võrrand: 3x - y - 1 = 0.
Kaht punkti läbiva sirge võrrand.
Olgu ruumis antud kaks punkti M 1 (x 1, y 1, z 1) Ja M2 (x 2, y 2, z 2), Siis sirge võrrand,
läbides neid punkte:
Kui mõni nimetajatest on null, tuleb vastav lugeja määrata nulliga. Peal
tasapinnal on ülaltoodud sirgjoone võrrand lihtsustatud:

Kui x 1 ≠ x 2 Ja x = x 1, Kui x 1 = x 2 .
Murd = k helistas kalle otse.
Näide. Leidke punkte A(1, 2) ja B(3, 4) läbiva sirge võrrand.
Lahendus. Rakendades ülaltoodud valemit, saame:

Sirge võrrand punkti ja kalde abil.
Kui sirge üldvõrrand Ax + Wu + C = 0 viia selleni:

ja määrata  , siis nimetatakse saadud võrrandit
, siis nimetatakse saadud võrrandit
sirge võrrand kaldega k.
Punkti ja suunavektori sirge võrrand.
Analoogiliselt punktiga, mis võtab arvesse normaalvektorit läbiva sirge võrrandit, saate ülesande sisestada
punkti läbiv sirge ja sirge suunav vektor.
Definitsioon. Iga nullist erinev vektor (α 1 , α 2), mille komponendid vastavad tingimusele
Aα 1 + Bα 2 = 0 helistas sirge suunav vektor.
Ax + Wu + C = 0.
Näide. Leidke sirge võrrand suunavektoriga (1, -1) ja läbib punkti A(1, 2).
Lahendus. Otsime soovitud rea võrrandit kujul: Ax + By + C = 0. Definitsiooni järgi,
koefitsiendid peavad vastama järgmistele tingimustele:
1 * A + (-1) * B = 0, st. A = B.
Siis on sirgjoone võrrandil järgmine kuju: Ax + Ay + C = 0, või x + y + C / A = 0.
juures x = 1, y = 2 saame C/A = -3, st. nõutav võrrand:
x + y - 3 = 0
Segmentides sirgjoone võrrand.
Kui sirge Ах + Ву + С = 0 С≠0 üldvõrrandis, siis -С-ga jagades saame:
 või kus
või kus

Koefitsientide geomeetriline tähendus on see, et koefitsient a on lõikepunkti koordinaat
teljega sirge Oh, A b- sirge ja telje lõikepunkti koordinaat OU.
Näide. Sirge üldvõrrand on antud x - y + 1 = 0. Leidke selle sirge võrrand segmentides.
C = 1, , a = -1, b = 1.
Sirge normaalvõrrand.
Kui võrrandi mõlemad pooled Ax + Wu + C = 0 arvuga jagada  mida nimetatakse
mida nimetatakse
normaliseeriv tegur, siis saame
xcosφ + ysinφ - p = 0 -sirge normaalvõrrand.
Normaliseeriva teguri märk ± tuleb valida nii, et μ*C< 0.
R- risti pikkus, mis on langenud lähtepunktist sirgele,
A φ - nurk, mille see risti moodustab telje positiivse suunaga Oh.
Näide. Antud on sirge üldvõrrand 12x - 5a - 65 = 0. Nõutav erinevat tüüpi võrrandite kirjutamiseks
see sirgjoon.
Selle sirge võrrand segmentides:

Selle sirge võrrand kaldega: (jaga 5-ga)

Sirge võrrand:

cos φ = 12/13; sin φ= -5/13; p = 5.
Tuleb märkida, et mitte iga sirget ei saa esitada võrrandiga segmentides, näiteks sirged,
paralleelselt telgedega või läbides alguspunkti.
Tasapinna sirgjoonte vaheline nurk.
Definitsioon. Kui on antud kaks rida y = k 1 x + b 1, y = k 2 x + b 2, siis nende joonte vaheline teravnurk
määratletakse kui

Kaks sirget on paralleelsed, kui k 1 = k 2. Kaks joont on risti
Kui k 1 = -1/ k 2 .
Teoreem.
Otsene Ax + Wu + C = 0 Ja A 1 x + B 1 y + C 1 = 0 paralleelselt, kui koefitsiendid on proportsionaalsed
A1 = λA, B1 = λB. Kui ka С 1 = λС, siis jooned langevad kokku. Kahe sirge lõikepunkti koordinaadid
on leitud nende sirgete võrrandisüsteemi lahendusena.
Antud punkti läbiva sirge võrrand, mis on antud sirgega risti.
Definitsioon. Punkti läbiv sirge M 1 (x 1, y 1) ja joonega risti y = kx + b
mida esindab võrrand:

Kaugus punktist jooneni.
Teoreem. Kui punkt antakse M(x 0, y 0), siis kaugus sirgjooneni Ax + Wu + C = 0 defineeritud kui:

Tõestus. Olgu punkt M 1 (x 1, y 1)- punktist langenud risti alus M antud jaoks
otsene. Siis punktide vaheline kaugus M Ja M 1:
![]() (1)
(1)
Koordinaadid x 1 Ja kell 1 võib leida võrrandisüsteemi lahendusena:

Süsteemi teine võrrand on antud punkti M 0 risti läbiva sirge võrrand
antud sirge. Kui teisendame süsteemi esimese võrrandi vormiks:
A(x - x 0) + B(y - y 0) + Ax 0 + 0 järgi + C = 0,
siis lahendades saame:

Asendades need avaldised võrrandisse (1), leiame:

Teoreem on tõestatud.
 Nikolai Martõnov, kes tappis M duellis
Nikolai Martõnov, kes tappis M duellis Nihkevektori projektsioonid Keha nihke moodul ajas
Nihkevektori projektsioonid Keha nihke moodul ajas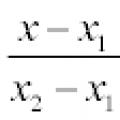 Sirge võrrand - sirge võrrandi tüübid: punkti läbiv, üldine, kanooniline, parameetriline jne.
Sirge võrrand - sirge võrrandi tüübid: punkti läbiv, üldine, kanooniline, parameetriline jne.