Y x leidke funktsiooni periood. Funktsioonide y = sin x, y = cos x perioodilisus - Teadmiste hüpermarket
Argument x, siis nimetatakse seda perioodiliseks, kui on olemas selline arv T, et mis tahes x korral F(x + T) = F(x). Seda arvu T nimetatakse funktsiooni perioodiks.
Perioode võib olla mitu. Näiteks funktsioon F = const võtab argumendi mis tahes väärtuse jaoks sama väärtuse ja seetõttu võib selle perioodiks pidada mis tahes arvu.
Tavaliselt huvitab teid funktsiooni väikseim nullist erinev periood. Lühiduse mõttes nimetatakse seda lihtsalt perioodiks.
Perioodiliste funktsioonide klassikaline näide on trigonomeetriline: siinus, koosinus ja puutuja. Nende periood on sama ja võrdne 2π-ga, st sin(x) = sin(x + 2π) = sin(x + 4π) ja nii edasi. Muidugi pole trigonomeetrilised funktsioonid ainsad perioodilised.
Lihtsate põhifunktsioonide puhul on ainus viis määrata, kas need on perioodilised või mitteperioodilised, arvutamise kaudu. Kuid keerukate funktsioonide jaoks on juba mitu lihtsat reeglit.
Kui F(x) on perioodiga T ja selle jaoks on defineeritud tuletis, siis see tuletis f(x) = F′(x) on samuti perioodiline funktsioon perioodiga T. Tuletise väärtus punktis ju x on võrdne tema antituletise graafiku puutuja nurga puutujaga selles punktis x-telje suhtes ja kuna antiderivaat kordub perioodiliselt, peab ka tuletis korduma. Näiteks funktsiooni sin(x) tuletis on võrdne cos(x) ja see on perioodiline. Võttes cos(x) tuletise, saad –sin(x). Sagedus jääb muutumatuks.
Kuid vastupidine pole alati tõsi. Seega funktsioon f(x) = const on perioodiline, kuid selle antiderivatiiv F(x) = const*x + C mitte.
Kui F(x) on perioodiline funktsioon perioodiga T, siis G(x) = a*F(kx + b), kus a, b ja k on konstandid ja k ei võrdu nulliga – on samuti perioodiline funktsioon , ja selle periood on T/k. Näiteks sin(2x) on perioodiline funktsioon ja selle periood on π. Seda saab visuaalselt kujutada järgmiselt: korrutades x mingi arvuga, tundub, et funktsiooni graafik tihendatakse horisontaalselt täpselt nii mitu korda
Kui F1(x) ja F2(x) on perioodilised funktsioonid ning nende perioodid on vastavalt T1 ja T2, siis võib ka nende funktsioonide summa olla perioodiline. Selle periood ei ole aga perioodide T1 ja T2 lihtne summa. Kui jaotuse T1/T2 tulemus on ratsionaalarv, siis funktsioonide summa on perioodiline ja selle periood võrdub perioodide T1 ja T2 vähima ühiskordsega (LCM). Näiteks kui esimese funktsiooni periood on 12 ja teise periood on 15, siis on nende summa periood võrdne LCM (12, 15) = 60.
Seda saab visuaalselt kujutada järgmiselt: funktsioonidel on erinevad “sammulaiused”, kuid kui nende laiuste suhe on ratsionaalne, siis varem või hiljem (õigemini, just astmete LCM-i kaudu) muutuvad need jälle võrdseks ja nende summa alustab uut perioodi.
Kui aga perioodide suhe on irratsionaalne, siis kogufunktsioon ei ole üldse perioodiline. Näiteks olgu F1(x) = x mod 2 (jääk, kui x jagatakse 2-ga) ja F2(x) = sin(x). T1 on siin võrdne 2-ga ja T2 on võrdne 2π-ga. Perioodide suhe on võrdne π - irratsionaalarvuga. Seetõttu ei ole funktsioon sin(x) + x mod 2 perioodiline.
Videotunnis “Funktsioonide perioodilisus y = sin x, y = cos x” paljastatakse funktsiooni perioodilisuse mõiste, käsitletakse ülesannete lahendamise näidete kirjeldust, milles kasutatakse funktsiooni perioodilisuse mõistet. See videotund on visuaalne abivahend teema selgitamiseks õpilastele. Samuti võib sellest juhendist saada tunni iseseisev osa, mis annab õpetajale vabaduse õpilastega individuaalse töö tegemiseks.
Nähtavus selle teema esitamisel on väga oluline. Funktsiooni käitumise kujutamiseks, selle joonistamiseks, tuleb see visualiseerida. Tahvli ja kriidi abil ei ole alati võimalik teha konstruktsioone nii, et need oleksid kõigile õpilastele arusaadavad. Videoõpetuses on võimalik konstrueerimisel joonise osi värviga esile tuua ning animatsiooni abil teisendusi teha. Nii muutuvad konstruktsioonid enamikule õpilastele arusaadavamaks. Samuti aitavad videotunni funktsioonid materjali paremini meelde jätta.
Demonstratsioon algab tunni teema tutvustamisega, samuti tuletatakse õpilastele meelde eelmistes tundides õpitud materjali. Eelkõige võetakse kokku loetelu omadustest, mis tuvastati funktsioonides y = sin x ja y = cos x. Vaadeldavate funktsioonide omaduste hulgas märgitakse ära määratluspiirkond, väärtuste vahemik, paarsus (veidrus), muud tunnused - piiritus, monotoonsus, järjepidevus, väikseima (suurima) väärtusega punktid. Õpilastele antakse teada, et selles tunnis uuritakse funktsiooni teist omadust – perioodilisust.
Perioodilise funktsiooni y=f(x) definitsioon, kus xϵX, milles esitatakse mingi Т≠0 tingimus f(x-Т)= f(x)= f(x+Т). Vastasel juhul nimetatakse arvu T funktsiooni perioodiks.
Vaadeldavate siinus- ja koosinusfunktsioonide puhul kontrollitakse tingimuse täitmist redutseerimisvalemite abil. On ilmne, et identiteedi kuju sin(x-2π)=sinx=sin(x+2π) vastab funktsiooni perioodilisuse tingimust määratleva avaldise vormile. Sama võrdsust võib märkida koosinus cos (x-2π)= cos x= cos (x+2π) puhul. See tähendab, et need trigonomeetrilised funktsioonid on perioodilised.
Lisaks märgitakse, kuidas perioodilisuse omadus aitab koostada perioodiliste funktsioonide graafikuid. Vaadeldakse funktsiooni y = sin x. Ekraanile konstrueeritakse koordinaattasand, millele on π sammuga märgitud abstsissid vahemikus -6π kuni 8π. Siinusgraafiku osa kantakse tasapinnale, mida kujutab üks laine segmendil. Joonisel on näidatud, kuidas funktsiooni graafik moodustatakse kogu definitsioonipiirkonna ulatuses, nihutades konstrueeritud fragmenti, mille tulemuseks on pikk sinusoid.
Funktsiooni y = cos x graafik koostatakse selle perioodilisuse omadust kasutades. Selleks konstrueeritakse joonisel koordinaattasand, millel on kujutatud graafiku fragment. Märgitakse, et selline fragment konstrueeritakse tavaliselt segmendile [-π/2;3π/2]. Sarnaselt siinusfunktsiooni graafikule toimub koosinusgraafiku konstrueerimine fragmendi nihutamise teel. Ehituse tulemusena moodustub pikk sinusoid.
Perioodilise funktsiooni graafikul on funktsioone, mida saab kasutada. Seetõttu on need esitatud üldistatud kujul. Märgitakse, et sellise funktsiooni graafiku koostamiseks konstrueeritakse esmalt graafiku haru teatud intervallile pikkusega T. Seejärel on vaja konstrueeritud haru nihutada T, 2T, 3T võrra paremale ja vasakule, jne. Samas tuuakse välja veel üks perioodi tunnus - iga täisarvu k≠0 korral on arv kT ühtlasi funktsiooni periood. T-d nimetatakse siiski põhiperioodiks, kuna see on kõigist väikseim. Trigonomeetriliste funktsioonide siinus ja koosinus puhul on põhiperioodiks 2π. Perioodid on aga ka 4π, 6π jne.
Järgmisena tehakse ettepanek kaaluda funktsiooni y = cos 5x põhiperioodi leidmist. Lahendus algab eeldusega, et T on funktsiooni periood. See tähendab, et tingimus f(x-T)= f(x)= f(x+T) peab olema täidetud. Selles identiteedis f(x)= cos 5x ja f(x+T)=cos 5(x+T)= cos (5x+5T). Sel juhul cos (5x+5T)= cos 5x, seega 5T=2πn. Nüüd leiate T=2π/5. Probleem on lahendatud.
Teises ülesandes tuleb leida funktsiooni y=sin(2x/7) põhiperiood. Eeldatakse, et funktsiooni T põhiperiood antud funktsiooni korral on f(x)= sin(2x/7) ja pärast perioodi f(x+T)=sin(2x/7)(x+T) = sin(2x/7 +(2/7)T). pärast redutseerimist saame (2/7)Т=2πn. Peame aga leidma põhiperioodi, seega võtame väikseima väärtuse (2/7)T=2π, millest leiame T=7π. Probleem on lahendatud.
Demonstratsiooni lõpus võetakse näidete tulemused kokku, et moodustada reegel funktsiooni põhiperioodi määramiseks. Tuleb märkida, et funktsioonide y=sinkx ja y=coskx puhul on põhiperioodid 2π/k.

Videotundi “Funktsioonide y = sin x, y = cos x perioodilisus” saab kasutada traditsioonilises matemaatikatunnis tunni tulemuslikkuse tõstmiseks. Seda materjali on soovitatav kasutada ka kaugõpet pakkuval õpetajal, et seletus oleks selgem. Videot võib soovitada raskustes olevale õpilasele teemast arusaamise süvendamiseks.
TEKSTI DEKOODE:
Funktsioonide y = cos x, y = sin x perioodilisus.
Funktsioonide y = sin x ja y = cos x graafikute koostamiseks kasutati funktsioonide omadusi:
1 määratluspiirkond,
2 väärtusega piirkond,
3 paaris või paaritu,
4 monotoonsus,
5 piirang,
6 järjepidevus,
7 kõrgeim ja madalaim väärtus.
Täna uurime teist omadust: funktsiooni perioodilisust.
MÄÄRATLUS. Funktsiooni y = f (x), kus x ϵ X (kreeka keel on võrdne x ef-ga, kus x kuulub hulka x), nimetatakse perioodiliseks, kui on olemas nullist erinev arv T, nii et iga x korral alates hulk X kehtib topeltvõrdsus: f (x - T)= f (x) = f (x + T) (eff x-st miinus te võrdub ef-ga x-st ja ef-ga x-st pluss te). Arvu T, mis seda topeltvõrdsust rahuldab, nimetatakse funktsiooni perioodiks

Ja kuna siinus ja koosinus on defineeritud tervel arvujoonel ja mis tahes x korral on võrdsused sin(x - 2π)= sin x= sin(x+ 2π) täidetud (siinus x miinus kaks pi on võrdne siinus x ja võrdne siinus x pluss kaks pi ) Ja
cos (x- 2π)= cos x = cos (x+ 2π) (koosinus x miinus kaks pi on võrdne x koosinusega ja võrdne koosinusega x pluss kaks pi), siis siinus ja koosinus on perioodilised funktsioonid periood 2π.
Perioodilisus võimaldab kiiresti koostada funktsiooni graafiku. Tõepoolest, funktsiooni y = sin x graafiku koostamiseks piisab, kui joonistada üks laine (kõige sagedamini segmendile (nullist kahe pi) ja seejärel graafiku konstrueeritud osa nihutamisest piki x -telg paremale ja vasakule 2π võrra, seejärel 4π võrra ja nii edasi, et saada siinuslaine.
(näita nihet paremale ja vasakule 2π, 4π võrra)
Samamoodi ka funktsiooni graafiku puhul
y = cos x, kuid me ehitame ühe laine kõige sagedamini segmendile [; ] (miinus pi üle kahe kuni kolm pi üle kahe).
Teeme eeltoodu kokkuvõtte ja teeme järelduse: perioodilise funktsiooni graafiku koostamiseks perioodiga T peate esmalt konstrueerima graafiku haru (või laine või osa) mis tahes pikkusega T intervallil (enamasti sellel on intervall, mille otsad on punktides 0 ja T või - ja (miinus te kahega ja te kahega), ning seejärel liigutage seda haru piki x(x) telge paremale ja vasakule T, 2T, 3T jne võrra.
Ilmselgelt, kui funktsioon on perioodiline perioodiga T, siis mis tahes täisarvu k0 (ka ei võrdu nulliga) korral on arv kujul kT (ka te) ka selle funktsiooni periood. Tavaliselt püüavad nad eraldada väikseima positiivse perioodi, mida nimetatakse põhiperioodiks.
Funktsioonide y = cos x, y = sin x perioodiks võiks võtta - 4π, 4π, - 6π, 6π jne (miinus neli pi, neli pi, miinus kuus pi, kuus pi jne) . Kuid arv 2π on mõlema funktsiooni põhiperiood.
Vaatame näiteid.
NÄIDE 1. Leidke funktsiooni y = cos5x põhiperiood (y võrdub viie x koosinusega).
Lahendus. Olgu T funktsiooni y = cos5x põhiperiood. Paneme
f (x) = cos5x, siis f (x + T) = cos5(x + T) = cos (5x + 5T) (eff x pluss te võrdub koosinusega viiega, mis on korrutatud x summaga ja te on võrdne viie x ja viie te summa koosinusega).
cos (5x + 5T) = cos5x. Seega 5T = 2πn (viis te võrdub kahe pi en), kuid tingimuse järgi tuleb leida põhiperiood, mis tähendab 5T = 2π. Saame T =
(selle funktsiooni periood on kaks pi jagatuna viiega).
Vastus: T=.

NÄIDE 2. Leia funktsiooni y = sin põhiperiood (y võrdub kahe x jagatise siinusega seitsmega).
Lahendus. Olgu T funktsiooni y = sin põhiperiood. Paneme
f (x) = sin, siis f (x + T) = sin (x + T) = sin (x + T) (x ef pluss te võrdub kahe seitsmendiku ja x summa korrutise siinusega ja te on võrdne kahe seitsmendiku x ja kahe seitsmendiku te summa siinusega).
Et arv T oleks funktsiooni periood, peab identsus olema täidetud
sin (x + T) = patt. Seega T= 2πn (kaks seitsmendikku te võrdub kahe pi en-iga), kuid tingimuse järgi tuleb leida põhiperiood, mis tähendab T= 2π. Saame T=7
(selle funktsiooni periood on seitse pi).
Vastus: T=7.
Võttes kokku näidetes saadud tulemused, võime järeldada: funktsioonide y = sin kx või y = cos kx põhiperiood (y võrdub siinus ka x või y võrdub koosinus ka x) on võrdne (kaks pi jagatud ka-ga).
Eesmärk: võtta kokku ja süstematiseerida õpilaste teadmisi teemal "Funktsioonide perioodilisus"; kujundab perioodilisuse funktsiooni omaduste rakendamise, funktsiooni väikseima positiivse perioodi leidmise, perioodiliste funktsioonide graafikute koostamise oskusi; tõsta huvi matemaatika õppimise vastu; kasvatada tähelepanelikkust ja täpsust.
Varustus: arvuti, multimeediaprojektor, töökaardid, slaidid, kellad, kaunistuslauad, rahvakunsti elemendid
"Matemaatika on see, mida inimesed kasutavad looduse ja enda kontrollimiseks."
A.N. Kolmogorov
Tundide ajal
I. Organisatsioonietapp.
Õpilaste tunniks valmisoleku kontrollimine. Teatage tunni teemast ja eesmärkidest.
II. Kodutööde kontrollimine.
Kontrollime kodutöid näidiste abil ja arutame läbi kõige keerulisemad punktid.
III. Teadmiste üldistamine ja süstematiseerimine.
1. Suuline frontaaltöö.
Teooriaprobleemid.
1) Moodustage funktsiooni perioodi määratlus
2) Nimetage funktsioonide y=sin(x), y=cos(x) väikseim positiivne periood
3). Mis on funktsioonide y=tg(x), y=ctg(x) väikseim positiivne periood
4) Tõesta ringi abil seoste õigsust:
y=sin(x) = sin(x+360º)
y=cos(x) = cos(x+360º)
y=tg(x) = tg(x+180º)
y=ctg(x) = ctg(x+180º)
tg(x+π n)=tgx, n € Z
ctg(x+π n)=ctgx, n € Z

sin(x+2π n)=sinx, n € Z
cos(x+2π n)=cosx, n € Z
5) Kuidas joonistada perioodilist funktsiooni?
Suulised harjutused.
1) Tõesta järgmised seosed
a) sin(740º) = sin(20º)
b) cos(54º) = cos(-1026º)
c) sin(-1000º) = sin(80º)
2. Tõesta, et nurk 540º on üks funktsiooni y= cos(2x) perioodidest.
3. Tõesta, et nurk 360º on üks funktsiooni y=tg(x) perioodidest.
4. Teisenda need avaldised nii, et neis sisalduvad nurgad ei ületaks absoluutväärtuses 90º.
a) tg375º
b)ctg530º
c) sin1268º
d)cos (-7363º)
5. Kust sa kohtasid sõnu PERIOOD, PERIOODSUS?
Õpilane vastab: Periood muusikas on struktuur, milles esitatakse enam-vähem terviklik muusikaline mõte. Geoloogiline periood on osa ajastust ja jaguneb ajajärkudeks ajavahemikuga 35–90 miljonit aastat.
Radioaktiivse aine poolestusaeg. Perioodiline murd. Perioodika on trükiväljaanded, mis ilmuvad rangelt kindlaksmääratud tähtaegadel. Mendelejevi perioodiline süsteem.
6. Joonistel on kujutatud perioodiliste funktsioonide graafikute osi. Määrake funktsiooni periood. Määrake funktsiooni periood.

Vastus: T=2; T = 2; T = 4; T=8.
7. Kus oma elus oled korduvate elementide konstrueerimisega kokku puutunud?
Õpilase vastus: Ornamendi elemendid, rahvakunst.

IV. Probleemide kollektiivne lahendamine.
(ülesannete lahendamine slaididel.)
Vaatleme ühte funktsiooni perioodilisuse uurimise viisidest.
See meetod väldib raskusi, mis on seotud tõestamisega, et konkreetne periood on väikseim, ning välistab ka vajaduse puudutada küsimusi perioodiliste funktsioonide aritmeetiliste toimingute ja keeruka funktsiooni perioodilisuse kohta. Põhjendus põhineb ainult perioodilise funktsiooni definitsioonil ja järgmisel faktil: kui T on funktsiooni periood, siis nT(n?0) on selle periood.
Ülesanne 1. Leia funktsiooni f(x)=1+3(x+q>5) väikseim positiivne periood
Lahendus: oletame, et selle funktsiooni T-periood. Siis f(x+T)=f(x) kõigi x € jaoks D(f), s.t.
1+3 (x+T+0,25)=1+3 (x+0,25)
(x+T+0,25)=(x+0,25)
Paneme x=-0,25 saame
(T)=0 T=n, n € Z
Saime, et kõik kõnealuse funktsiooni perioodid (kui need on olemas) on täisarvude hulgas. Valime nende arvude hulgast väikseima positiivse arvu. See on 1. Vaatame, kas see on tõesti 1. periood.
f(x+1) =3(x+1+0,25)+1
Kuna (T+1)=(T) mis tahes T korral, siis f(x+1)=3((x+0,25)+1)+1=3(x+0,25)+1=f(x ), st. 1 – periood f. Kuna 1 on kõigist positiivsetest täisarvudest väikseim, siis T=1.
Ülesanne 2. Näidake, et funktsioon f(x)=cos 2 (x) on perioodiline ja leidke selle põhiperiood.

Ülesanne 3. Leia funktsiooni põhiperiood
f(x)=sin(1,5x)+5cos (0,75x)
Oletame funktsiooni T-perioodi, siis suvalise x korral kehtib seos
sin1,5(x+T)+5cos0,75(x+T)=sin(1,5x)+5cos(0,75x)
Kui x = 0, siis
sin(1,5T)+5cos(0,75T)=sin0+5cos0
sin(1,5T)+5cos(0,75T)=5
Kui x=-T, siis
sin0+5cos0=sin(-1,5T)+5cos0,75(-T)
5= – sin(1,5T)+5cos(0,75T)
| sin(1,5T)+5cos(0,75T)=5 – sin(1,5T)+5cos(0,75T)=5 |
Selle liitmisel saame:
10cos(0,75T)=10
2π n, n € Z
Valime perioodi kõigist "kahtlastest" numbritest väikseima positiivse arvu ja kontrollime, kas see on periood f jaoks. See number
f(x+)=sin(1,5x+4π)+5cos(0,75x+2π)= sin(1,5x)+5cos(0,75x)=f(x)
See tähendab, et see on funktsiooni f põhiperiood.
Ülesanne 4. Kontrollime, kas funktsioon f(x)=sin(x) on perioodiline
Olgu T funktsiooni f periood. Siis mis tahes x jaoks
sin|x+Т|=sin|x|
Kui x=0, siis sin|Т|=sin0, sin|Т|=0 Т=π n, n € Z.
Oletame. Et mõne n puhul on arv π n periood
vaadeldav funktsioon π n>0. Siis sin|π n+x|=sin|x|

See tähendab, et n peab olema nii paaris kui ka paaritu arv, kuid see on võimatu. Seetõttu ei ole see funktsioon perioodiline.
Ülesanne 5. Kontrolli, kas funktsioon on perioodiline
f(x)= 
Olgu T siis f periood
 , seega sinT=0, Т=π n, n € Z. Oletame, et mõne n korral on arv π n tõepoolest selle funktsiooni periood. Siis on punkt 2π n
, seega sinT=0, Т=π n, n € Z. Oletame, et mõne n korral on arv π n tõepoolest selle funktsiooni periood. Siis on punkt 2π n

Kuna lugejad on võrdsed, on nende nimetajad seega võrdsed

See tähendab, et funktsioon f ei ole perioodiline.
Grupitöö.
Ülesanded 1. rühmale.
Ülesanded 2. rühmale.
Kontrollige, kas funktsioon f on perioodiline, ja leidke selle põhiperiood (kui see on olemas).
f(x)=cos(2x)+2sin(2x)
Ülesanded 3. rühmale.
Töö lõpus esitlevad rühmad oma lahendusi.
VI. Õppetunni kokkuvõte.
Peegeldus.
Õpetaja annab õpilastele joonistega kaardid ja palub neil värvida osa esimesest joonisest vastavalt sellele, mil määral nad arvavad, et nad on omandanud funktsiooni perioodilisuse uurimise meetodid, ja osa teisest joonisest vastavalt oma joonisele. panus tunnis tehtavasse töösse.
VII. Kodutöö
1). Kontrollige, kas funktsioon f on perioodiline ja leidke selle põhiperiood (kui see on olemas)
b). f(x)=x2 -2x+4
c). f(x)=2tg(3x+5)
2). Funktsioonil y=f(x) on periood T=2 ja f(x)=x 2 +2x x € jaoks [-2; 0]. Leidke avaldise -2f(-3)-4f(3,5) väärtus
Kirjandus/
2020. aasta juulis käivitab NASA ekspeditsiooni Marsile. Kosmoselaev toimetab Marsile elektroonilise andmekandja kõigi registreeritud ekspeditsioonil osalejate nimedega.
Osalejate registreerimine on avatud. Hankige pilet Marsile, kasutades seda linki.
Kui see postitus lahendas teie probleemi või teile see lihtsalt meeldis, jagage selle linki oma sõpradega sotsiaalvõrgustikes.
Üks neist koodivalikutest tuleb kopeerida ja kleepida oma veebilehe koodi, eelistatavalt siltide vahele ja või kohe pärast märgendit. Esimese variandi järgi laadib MathJax kiiremini ja aeglustab lehte vähem. Kuid teine valik jälgib ja laadib automaatselt MathJaxi uusimad versioonid. Kui sisestate esimese koodi, tuleb seda perioodiliselt värskendada. Kui sisestate teise koodi, laaditakse lehed aeglasemalt, kuid te ei pea pidevalt MathJaxi värskendusi jälgima.
Lihtsaim viis MathJaxi ühendamiseks on Bloggeris või WordPressis: lisage saidi juhtpaneelile vidin, mis on mõeldud kolmanda osapoole JavaScripti koodi sisestamiseks, kopeerige sellesse ülaltoodud allalaadimiskoodi esimene või teine versioon ja asetage vidin lähemale. malli algusesse (muide, see pole üldse vajalik, kuna MathJaxi skript laaditakse asünkroonselt). See on kõik. Nüüd õppige MathML-i, LaTeX-i ja ASCIIMathML-i märgistussüntaksit ning olete valmis oma saidi veebilehtedele matemaatilisi valemeid sisestama.
Järjekordne aastavahetus... pakaseline ilm ja lumehelbed aknaklaasil... See kõik ajendas mind uuesti kirjutama... fraktalidest ja sellest, mida Wolfram Alpha sellest teab. Sellel teemal on huvitav artikkel, mis sisaldab näiteid kahemõõtmeliste fraktaalstruktuuride kohta. Siin vaatleme keerukamaid näiteid kolmemõõtmelistest fraktaalidest.
Fraktaali saab visuaalselt kujutada (kirjeldada) geomeetrilise kujundi või kehana (see tähendab, et mõlemad on hulk, antud juhul punktide kogum), mille detailid on sama kujuga kui algkujund ise. See tähendab, et tegemist on isesarnase struktuuriga, mille detaile uurides näeme suurendatuna sama kuju kui ilma suurenduseta. Kui tavalise geomeetrilise kujundi (mitte fraktaali) puhul näeme suurendamisel detaile, mis on lihtsama kujuga kui algkuju ise. Näiteks piisavalt suure suurenduse korral näeb osa ellipsist välja sirgjoonelise lõiguna. Fraktalidega seda ei juhtu: nende suurenemise korral näeme jälle sama keerulist kuju, mis kordub iga suurenemisega ikka ja jälle.
Fraktaaliteaduse rajaja Benoit Mandelbrot kirjutas oma artiklis Fraktaalid ja kunst teaduse nimel: "Fraktalid on geomeetrilised kujundid, mis on oma detailides sama keerulised kui ka üldisel kujul. See tähendab, et kui osa fraktaalist Suurendatakse terviku suuruseni, siis näeb see välja tervikuna, kas täpselt või võib-olla väikese deformatsiooniga."
Trigonomeetrilised funktsioonid on perioodilised, st korduvad teatud perioodi järel. Selle tulemusena piisab funktsiooni uurimisest sellel intervallil ja avastatud omaduste laiendamisest kõigile teistele perioodidele.
Juhised1. Kui teile antakse primitiivne avaldis, milles on ainult üks trigonomeetriline funktsioon (sin, cos, tg, ctg, sec, cosec) ja funktsiooni sees olevat nurka ei korrutata ühegi arvuga ja seda ennast ei tõsteta igal määral – kasutage määratlust. Avaldiste puhul, mis sisaldavad sin, cos, sec, cosec, määrake periood julgelt 2P-ks ja kui võrrand sisaldab tg, ctg, siis P. Oletame, et funktsiooni y=2 sinx+5 puhul võrdub periood 2P-ga. .
2. Kui trigonomeetrilise funktsiooni märgi all olev nurk x korrutada mingi arvuga, siis selle funktsiooni perioodi leidmiseks jaga tüüpperiood selle arvuga. Oletame, et teile antakse funktsioon y = sin 5x. Siinuse tüüpiline periood on 2P; jagades selle 5-ga, saate 2P/5 - see on selle avaldise soovitud periood.
3. Et leida astmeni tõstetud trigonomeetrilise funktsiooni perioodi, hinnake astme paarsust. Ühtlase kraadi saamiseks vähendage tüüpilist perioodi poole võrra. Oletame, et kui teile antakse funktsioon y = 3 cos^2x, siis tüüpiline periood 2P väheneb 2 korda, nii et periood võrdub P-ga. Pange tähele, et funktsioonid tg, ctg on perioodilised P suhtes iga kraadi.
4. Kui teile antakse võrrand, mis sisaldab kahe trigonomeetrilise funktsiooni korrutist või jagatist, leidke kõigepealt nende kõigi jaoks eraldi periood. Pärast seda leidke minimaalne arv, mis sisaldaks mõlema perioodi täisarvu. Oletame, et funktsioon y=tgx*cos5x on antud. Tangensi korral on periood P, koosinuse 5x korral on periood 2P/5. Nende mõlema perioodi minimaalne arv on 2P, seega on soovitav periood 2P.
5. Kui teil on raske teha nii, nagu soovitatud, või kahtlete tulemuses, proovige seda teha nii, nagu on määratletud. Võtke funktsiooni perioodiks T, see on suurem kui null. Asendage võrrandis avaldis (x + T) x asemel ja lahendage saadud võrrand nii, nagu oleks T parameeter või arv. Selle tulemusena saate teada trigonomeetrilise funktsiooni väärtuse ja saate leida väikseima perioodi. Oletame, et leevenduse tulemusena saate identiteedi patu (T/2) = 0. T minimaalne väärtus, mille juures see sooritatakse, on 2P, see on ülesande tulemus.
Perioodiline funktsioon on funktsioon, mis kordab oma väärtusi pärast mõnda nullist erinevat perioodi. Funktsiooni periood on arv, mis funktsiooni argumendile lisatuna ei muuda funktsiooni väärtust.

Sa vajad
- Algmatemaatika tundmine ja põhiülevaade.
1. Tähistame funktsiooni f(x) perioodi arvuga K. Meie ülesandeks on leida see K väärtus. Selleks kujutame ette, et funktsioon f(x), kasutades perioodilise funktsiooni definitsiooni, võrdsustame f(x+K)=f(x).
2. Lahendame saadud võrrandi tundmatu K suhtes, nagu oleks x konstant. Sõltuvalt K väärtusest on mitu võimalust.
3. Kui K>0 – siis see on sinu funktsiooni periood Kui K=0 – siis funktsioon f(x) ei ole perioodiline Kui võrrandi f(x+K)=f(x) lahend on ei eksisteeri ühegi K puhul, mis ei ole võrdne nulliga, siis nimetatakse sellist funktsiooni aperioodiliseks ja sellel pole ka perioodi.
Video teemal
Märge!
Kõik trigonomeetrilised funktsioonid on perioodilised ja kõik polünoomfunktsioonid, mille aste on suurem kui 2, on aperioodilised.
Abistavad nõuanded
Kahest perioodilisest funktsioonist koosneva funktsiooni periood on nende funktsioonide perioodide vähim universaalne kordne.
Trigonomeetrilised võrrandid on võrrandid, mis sisaldavad tundmatu argumendi trigonomeetrilisi funktsioone (näiteks: 5sinx-3cosx =7). Nende lahendamise õppimiseks peate teadma mõningaid viise, kuidas seda teha.

1. Selliste võrrandite lahendamine koosneb kahest etapist, millest esimene on võrrandi reformimine, et saada selle kõige lihtsam kuju. Lihtsamad trigonomeetrilised võrrandid on: Sinx=a; Cosx=a jne.
2. Teine on kõige lihtsama saadud trigonomeetrilise võrrandi lahendus. Seda tüüpi võrrandite lahendamiseks on põhilised viisid: Algebraline lahendamine. See meetod on tuntud koolist, algebra kursusest. Muidu nimetatakse muutuja asendamise ja asendamise meetodiks. Reduktsioonivalemeid kasutades teisendame, teeme asendused ja seejärel leiame juured.
3. Võrrandi faktoriseerimine. Esiteks liigutame kõik terminid vasakule ja faktorime need.
4. Võrrandi taandamine homogeenseks. Võrratusi nimetatakse homogeenseteks võrranditeks, kui kõik liikmed on sama astmega ning siinus ja koosinus sama nurga all Selle lahendamiseks tuleks: esmalt kanda kõik selle liikmed paremalt küljelt vasakule poole; teisaldage kõik universaalsed tegurid sulgudest välja; võrdsusta tegurid ja sulud nulliga; võrdsustatud sulud annavad homogeense madalama astme võrrandi, mis tuleks jagada cos-iga (või siniga) kõrgeima astmeni; lahendage saadud algebraline võrrand tan kohta.
5. Järgmine meetod on liikuda poole nurga alla. Ütleme, lahendage võrrand: 3 sin x – 5 cos x = 7. Liigume edasi poolnurga juurde: 6 sin (x / 2) · cos (x / 2) – 5 cos? (x / 2) + 5 sin ? (x / 2) = 7 sin ? (x / 2) + 7 cos ? (x/ 2) , mille järel taandame kõik liikmed üheks osaks (soovitavalt parempoolseks) ja lahendame võrrandi.
6. Abinurga sisestamine. Kui asendame täisarvu väärtuse cos(a) või sin(a). Märk “a” on abinurk.
7. Toote summaks muutmise meetod. Siin peate rakendama sobivaid valemeid. Oletame antud: 2 sin x · sin 3x = cos 4x. Lahendage see, teisendades vasaku külje summaks, see tähendab: cos 4x – cos 8x = cos 4x ,cos 8x = 0 ,8x = p / 2 + pk , x = p / 16 + pk / 8.
8. Lõplikku meetodit nimetatakse multifunktsionaalseks asendamiseks. Teisendame avaldise ja teeme muudatuse, ütleme Cos(x/2)=u ja seejärel lahendame võrrandi parameetriga u. Kogusumma ostmisel teisendame väärtuse vastupidiseks.
Video teemal
Kui arvestada ringjoone punkte, siis punktid x, x + 2π, x + 4π jne. omavahel kokku langevad. Seega kordavad sirgjoonel olevad trigonomeetrilised funktsioonid perioodiliselt oma väärtust. Kui funktsiooni periood on teada, on võimalik funktsioon sellele perioodile konstrueerida ja seda teistel korrata.

1. Periood on arv T, mille puhul f(x) = f(x+T). Perioodi leidmiseks lahendage vastav võrrand, asendades argumendina x ja x+T. Sel juhul kasutavad nad funktsioonide jaoks juba tuntud perioode. Siinus- ja koosinusfunktsioonide puhul on periood 2π ning puutuja- ja kootangensfunktsioonide puhul π.
2. Olgu antud funktsioon f(x) = sin^2(10x). Vaatleme avaldist sin^2(10x) = sin^2(10(x+T)). Kasutage astme vähendamiseks valemit: sin^2(x) = (1 – cos 2x)/2. Siis saad 1 – cos 20x = 1 – cos 20(x+T) või cos 20x = cos (20x+20T). Teades, et koosinuse periood on 2π, 20T = 2π. See tähendab, et T = π/10. T on minimaalne õige periood ja funktsiooni korratakse pärast 2T ja pärast 3T ning teises suunas piki telge: -T, -2T jne.
Abistavad nõuanded
Funktsiooni astme vähendamiseks kasutage valemeid. Kui teate juba mõne funktsiooni perioode, proovige olemasolevat funktsiooni taandada teadaolevateks.
Funktsiooni tasasuse ja veidruse uurimine aitab koostada funktsiooni graafiku ja mõista selle käitumise olemust. Selle uurimistöö jaoks peate võrdlema seda funktsiooni, mis on kirjutatud argumendi "x" ja argumendi "-x" jaoks.
1. Kirjuta funktsioon, mida soovid uurida kujul y=y(x).
2. Asendage funktsiooni argument "-x"-ga. Asendage see argument funktsionaalse avaldisega.
3. Lihtsusta väljendit.
4. Seega on argumentide “x” ja “-x” jaoks kirjutatud sama funktsioon. Vaadake neid kahte kirjet. Kui y(-x)=y(x), siis on see paarisfunktsioon. Kui y(-x)=-y(x), siis on see paaritu funktsioon. Kui see on võimatu ütleme funktsiooni kohta, et y (-x)=y(x) või y(-x)=-y(x), siis pariteedi omaduse järgi on see universaalse vormi funktsioon. See tähendab, et see pole paaris ega paaritu.
5. Pane oma leiud kirja. Nüüd saate neid kasutada funktsiooni graafiku koostamisel või funktsiooni omaduste tulevases analüütilises uuringus.
6. Funktsiooni paarisusest ja paarisusest saab rääkida ka juhul, kui funktsiooni graafik on juba antud. Oletame, et graafik toimis füüsikalise katse tulemusena Kui funktsiooni graafik on ordinaattelje suhtes sümmeetriline, siis y(x) on paarisfunktsioon Kui funktsiooni graafik on sümmeetriline abstsisstelje suhtes, siis x(y) on paarisfunktsioon. x(y) on funktsiooniga y(x) pöördfunktsioon Kui funktsiooni graafik on sümmeetriline lähtepunkti (0,0) suhtes, siis y(x) on paaritu funktsioon. Pöördfunktsioon x(y) on samuti paaritu.
7. Oluline on meeles pidada, et funktsiooni ühtluse ja veidruse ideel on otsene seos funktsiooni määratlusvaldkonnaga. Kui näiteks paaris või paaritu funktsioon ei eksisteeri x=5, siis ei eksisteeri seda ka x=-5 juures, mida ei saa öelda universaalse vormi funktsiooni kohta. Paaris- ja paaritupariteedi määramisel pöörake tähelepanu funktsiooni domeenile.
8. Tasasuse ja paarituse funktsiooni leidmine korreleerub funktsiooni väärtuste hulga leidmisega. Paarisfunktsiooni väärtuste komplekti leidmiseks piisab, kui vaadata poolt funktsioonist, nullist paremale või vasakule. Kui x>0 korral võtab paarisfunktsioon y(x) väärtused A-st B-sse, siis võtab see samad väärtused ja x0 korral võtab paaritu funktsioon y(x) väärtuste vahemiku A-st B-sse, siis punktis x sin^2 ? + cos^2 ? = 1. Kolmas ja neljas identsus saadakse, jagades vastavalt b^2 ja a^2: a^2/b^2 + 1 = c^2/b^2 => tg^2 ? + 1 = 1/cos^2?;1 + b^2/a^2 = c^2/a^2 => 1 + 1/tg^2? = 1/sin^ ? või 1 + ctg^2? = 1/sin^2 ?. Viies ja kuues põhiidentsus tõestatakse täisnurkse kolmnurga teravnurkade summa määramisega, mis võrdub 90° või?/2. Keerulisemad trigonomeetrilised identiteedid: argumentide lisamise valemid, topelt- ja kolmiknurgad, astme vähendamine, funktsioonide summa või korrutiste reformimine, samuti trigonomeetrilise asendusvalemid, nimelt trigonomeetriliste põhifunktsioonide avaldised tan poolnurga järgi: sin ?= (2*tg ?/2)/ (1 + tan^2 ?/2);cos ? = (1 – tg^2 ?/2)/(1 = tg^2 ?/2);tg ? = (2*tg ?/2)/(1 – tg^2 ?/2).
Vajadus leida matemaatilise funktsiooni minimaalne väärtus pakub tegelikku huvi rakendusülesannete lahendamisel, näiteks majandusteaduses. Kahjude minimeerimine on äritegevuse jaoks väga oluline.

1. Funktsiooni minimaalse väärtuse leidmiseks on vaja kindlaks teha, millise argumendi x0 väärtuse korral täidetakse võrratus y(x0)? y(x), kus x? x0. Nagu tavaliselt, lahendatakse see probleem teatud intervalli või funktsiooni igas väärtusvahemikus, kui seda pole määratud. Lahenduse üks aspekt on fikseeritud punktide leidmine.
2. Statsionaarne punkt on argumendi väärtus, mille juures funktsiooni tuletis muutub nulliks. Fermat' teoreemi kohaselt, kui diferentseeruv funktsioon võtab mingil hetkel äärmusliku väärtuse (antud juhul lokaalse miinimumi), siis see punkt on statsionaarne.
3. Funktsioon võtab sageli oma minimaalse väärtuse just sellel hetkel, kuid seda ei saa alati määrata. Pealegi ei ole alati võimalik täpselt öelda, millega funktsiooni miinimum on võrdne või kas see võtab lõpmata väikese väärtuse. Siis, nagu tavaliselt, leiavad nad piiri, milleni see vähenedes kipub.
4. Funktsiooni minimaalse väärtuse määramiseks on vaja läbi viia toimingute jada, mis koosneb neljast etapist: funktsiooni määratluspiirkonna leidmine, fikseeritud punktide hankimine, funktsiooni väärtuste ülevaatamine nendel. punktid ja intervalli lõpus, leides miinimumi.
5. Selgub, et anda mingi funktsioon y(x) intervallile, mille piirid on punktides A ja B. Leia selle definitsioonipiirkond ja kas intervall on selle alamhulk.
6. Arvutage funktsiooni tuletis. Võrdsusta saadud avaldis nulliga ja leia võrrandi juured. Kontrollige, kas need paigalseisvad punktid jäävad tühimikusse. Kui ei, siis neid edasises etapis arvesse ei võeta.
7. Uurige lünka piiride tüübi järgi: avatud, suletud, liit või mõõtmatu. See määrab, kuidas te minimaalset väärtust otsite. Oletame, et lõik [A, B] on suletud intervall. Ühendage need funktsiooniga ja arvutage väärtused. Tehke sama statsionaarse punktiga. Valige madalaim summa.
8. Lahtiste ja mõõtmatute intervallidega on olukord mõnevõrra keerulisem. Siin peate otsima ühekülgseid piire, mis ei anna alati ühemõttelist tulemust. Ütleme, et ühe suletud ja ühe punkteeritud piiriga intervalli jaoks [A, B) tuleks leida funktsioon punktis x = A ja ühepoolne piir lim y punktis x? B-0.

 Kunstlik gravitatsioon pole enam ulme
Kunstlik gravitatsioon pole enam ulme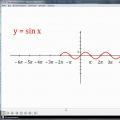 Funktsioonide y = sin x, y = cos x perioodilisus - Teadmiste hüpermarket
Funktsioonide y = sin x, y = cos x perioodilisus - Teadmiste hüpermarket DPR ja LPR teatab: võimsad lahingud Gorlovka lähedal, Donetski tulistamine suurtükiväelt, kokkupõrked kogu rindejoonel
DPR ja LPR teatab: võimsad lahingud Gorlovka lähedal, Donetski tulistamine suurtükiväelt, kokkupõrked kogu rindejoonel