Kako pronaći površinu trokuta ako je visina nepoznata. Kako možete pronaći površinu trokuta

Trokut je lik poznat svima. I to unatoč bogatoj raznolikosti njegovih oblika. Pravokutan, jednakostraničan, šiljast, jednakokračan, tup. Svaki od njih je drugačiji na neki način. Ali za svakoga morate saznati područje trokuta.

Formule zajedničke za sve trokute koje koriste duljine stranica ili visine

Oznake usvojene u njima: strane - a, b, c; visine na odgovarajućim stranama na a, n in, n sa.

1. Površina trokuta izračunava se kao umnožak ½, strane i visine oduzete od toga. S = ½ * a * n a. Formule za druge dvije strane treba napisati na sličan način.

2. Heronova formula, u kojoj se pojavljuje poluopseg (obično se označava malim slovom p, za razliku od punog oboda). Poluopseg se mora izračunati na sljedeći način: zbrojite sve stranice i podijelite ih s 2. Formula za poluopseg je: p = (a+b+c) / 2. Tada vrijedi jednakost za površinu ​​figura izgleda ovako: S = √ (p * (p - a) * ( r - v) * (r - s)).

3. Ako ne želite koristiti poluopseg, tada će formula koja sadrži samo duljine stranica biti korisna: S = ¼ * √ ((a + b + c) * (b + c - a ) * (a + c - c) * (a + b - c)). Nešto je duži od prethodnog, ali će vam pomoći ako ste zaboravili kako pronaći poluopseg.

Opće formule koje uključuju kutove trokuta

Oznake potrebne za čitanje formula: α, β, γ - kutovi. Leže nasuprot stranicama a, b, c.

1. Prema njemu, polovica proizvoda dviju strana i sinusa kuta između njih jednaka je površini trokuta. To je: S = ½ a * b * sin γ. Formule za druga dva slučaja treba napisati na sličan način.

2. Površina trokuta može se izračunati iz jedne strane i tri poznata kuta. S = (a 2 * sin β * sin γ) / (2 sin α).

3. Postoji i formula s jednim poznata stranka i dva susjedna kuta. To izgleda ovako: S = c 2 / (2 (ctg α + ctg β)).

Posljednje dvije formule nisu najjednostavnije. Prilično ih je teško zapamtiti.

Opće formule za situacije u kojima su poznati polumjeri upisanih ili opisanih kružnica

Dodatne oznake: r, R - radijusi. Prvi se koristi za radijus upisane kružnice. Drugi je za opisani.

1. Prva formula kojom se izračunava površina trokuta odnosi se na poluopseg. S = r * r. Drugi način za pisanje je: S = ½ r * (a + b + c).

2. U drugom slučaju, morat ćete pomnožiti sve stranice trokuta i podijeliti ih s četiri puta polumjerom opisane kružnice. U doslovnom izrazu to izgleda ovako: S = (a * b * c) / (4R).

3. Treća situacija vam omogućuje da ne znate strane, ali će vam trebati vrijednosti sva tri kuta. S = 2 R 2 * sin α * sin β * sin γ.

Poseban slučaj: pravokutni trokut

Ovo je najjednostavnija situacija, jer je potrebna samo duljina obje noge. Određeni su latiničnim slovima a i c. Kvadrat pravokutni trokut jednako polovici površine pravokutnika koja mu je dodana.

Matematički to izgleda ovako: S = ½ a * b. Najlakše ga je zapamtiti. Budući da izgleda kao formula za površinu pravokutnika, pojavljuje se samo razlomak koji označava polovicu.

Poseban slučaj: jednakokračni trokut

Budući da ima dvije jednake strane, neke formule za njegovu površinu izgledaju pomalo pojednostavljene. Na primjer, Heronova formula, koja izračunava površinu jednakokračan trokut, ima sljedeći oblik:

S = ½ in √((a + ½ in)*(a - ½ in)).

Ako ga transformirate, postat će kraći. U ovom slučaju, Heronova formula za jednakokračni trokut je napisana na sljedeći način:

S = ¼ u √(4 * a 2 - b 2).

Formula površine izgleda nešto jednostavnije nego za proizvoljni trokut ako su poznate stranice i kut između njih. S = ½ a 2 * sin β.

Poseban slučaj: jednakostranični trokut

Obično se u problemima strana o tome zna ili se može saznati na neki način. Tada je formula za pronalaženje područja takvog trokuta sljedeća:

S = (a 2 √3) / 4.

Problemi s pronalaženjem područja ako je trokut prikazan na kariranom papiru

Najjednostavnija situacija je kada je pravokutni trokut nacrtan tako da se njegove noge podudaraju s linijama papira. Zatim samo trebate prebrojati broj stanica koje stanu u noge. Zatim ih pomnožite i podijelite s dva.

Kada je trokut šiljasti ili tupokutni, potrebno ga je nacrtati u pravokutnik. Tada će rezultirajuća figura imati 3 trokuta. Jedan je onaj dan u zadatku. A druga dva su pomoćna i pravokutna. Područja zadnja dva potrebno je odrediti gore opisanom metodom. Zatim izračunajte površinu pravokutnika i od njega oduzmite one izračunate za pomoćne. Određuje se površina trokuta.

Situacija u kojoj se niti jedna stranica trokuta ne poklapa s linijama papira pokazuje se mnogo kompliciranijom. Zatim ga treba upisati u pravokutnik tako da vrhovi izvorne figure leže na njegovim stranama. U ovom slučaju bit će tri pomoćna pravokutna trokuta.

Primjer problema s Heronovom formulom

Stanje. Neki trokut ima poznate stranice. One su jednake 3, 5 i 6 cm. Trebate saznati njegovu površinu.

Sada možete izračunati površinu trokuta pomoću gornje formule. Pod kvadratnim korijenom nalazi se umnožak četiri broja: 7, 4, 2 i 1. To jest, površina je √(4 * 14) = 2 √(14).

Ako nije potrebna veća točnost, tada možete uzeti kvadratni korijen od 14. To je jednako 3,74. Tada će površina biti 7,48.

Odgovor. S = 2 √14 cm 2 ili 7,48 cm 2.

Primjer problema s pravokutnim trokutom

Stanje. Jedna kateta pravokutnog trokuta je 31 cm veća od druge. Trebate saznati njihove duljine ako je površina trokuta 180 cm 2.
Riješenje. Morat ćemo riješiti sustav dviju jednadžbi. Prvi se odnosi na područje. Drugi je s omjerom nogu, koji je dan u problemu.
180 = ½ a * b;

a = b + 31.
Prvo, vrijednost "a" mora se zamijeniti u prvoj jednadžbi. Ispada: 180 = ½ (in + 31) * in. Ima samo jednu nepoznatu količinu, pa ju je lako riješiti. Nakon otvaranja zagrada dobivamo kvadratna jednadžba: in 2 + 31 in - 360 = 0. Daje dvije vrijednosti za "in": 9 i - 40. Drugi broj nije prikladan kao odgovor, budući da duljina stranice trokuta ne može biti negativna vrijednost.

Ostaje izračunati drugu nogu: dobivenom broju dodajte 31. Ispada 40. To su količine koje se traže u problemu.

Odgovor. Kraci trokuta su 9 i 40 cm.

Problem određivanja stranice kroz površinu, stranicu i kut trokuta

Stanje. Površina određenog trokuta je 60 cm 2. Potrebno je izračunati jednu njegovu stranicu ako je druga stranica 15 cm, a kut između njih 30º.

Riješenje. Na temelju prihvaćene oznake, željena strana “a”, poznata strana “b”, navedeni kut"γ". Tada se formula površine može prepisati na sljedeći način:

60 = ½ a * 15 * sin 30º. Ovdje je sinus od 30 stupnjeva 0,5.

Nakon transformacija, "a" se ispostavlja da je jednako 60 / (0,5 * 0,5 * 15). To je 16.

Odgovor. Tražena stranica je 16 cm.

Zadatak o kvadratu upisanom u pravokutni trokut

Stanje. Vrh kvadrata sa stranicom 24 cm poklapa se s pravim kutom trokuta. Druga dva leže sa strane. Trećina pripada hipotenuzi. Duljina jednog od krakova je 42 cm. Kolika je površina pravokutnog trokuta?

Riješenje. Promotrimo dva pravokutna trokuta. Prva je ona navedena u zadatku. Drugi se temelji na poznata noga originalni trokut. Slični su jer imaju zajednički kut i tvore ih paralelni pravci.

Tada su im omjeri kateta jednaki. Kraci manjeg trokuta jednaki su 24 cm (stranica kvadrata) i 18 cm (od datog kraka 42 cm oduzmite stranicu kvadrata 24 cm). Odgovarajuće noge veliki trokut- 42 cm i x cm potreban je za izračunavanje površine trokuta.

18/42 = 24/x, odnosno x = 24 * 42 / 18 = 56 (cm).

Tada je površina jednaka umnošku 56 i 42 podijeljenom s dva, odnosno 1176 cm 2.

Odgovor. Tražena površina je 1176 cm 2.

Trokut je jedan od najčešćih geometrijskih oblika s kojim se već upoznajemo osnovna škola. Svaki se učenik suočava s pitanjem kako pronaći područje trokuta u nastavi geometrije. Dakle, koje se značajke pronalaženja područja određene figure mogu identificirati? U ovom ćemo članku pogledati osnovne formule potrebne za dovršenje takvog zadatka, a također ćemo analizirati vrste trokuta.

Vrste trokuta

Apsolutno možete pronaći površinu trokuta različiti putevi, jer u geometriji postoji više od jedne vrste likova koji sadrže tri kuta. Ove vrste uključuju:

• Tupi.
• Jednakostraničan (ispravan).
• Pravokutni trokut.
• Jednakokračan.

Pogledajmo pobliže svaki od njih postojeće vrste trokuta.

Ova se geometrijska figura smatra najčešćom prilikom rješavanja geometrijski problemi. Kada postane potrebno crtati proizvoljni trokut, ova opcija dolazi u pomoć.

U oštrokutnom trokutu, kao što naziv govori, svi kutovi su oštri i zbroj je 180°.

Ova vrsta trokuta također je vrlo česta, ali je nešto rjeđa od oštrokutnog trokuta. Na primjer, kada rješavate trokute (odnosno, poznato je nekoliko njegovih stranica i kutova i trebate pronaći preostale elemente), ponekad morate odrediti je li kut tup ili ne. Kosinus je negativan broj.

B, vrijednost jednog od kutova prelazi 90 °, tako da preostala dva kuta mogu imati male vrijednosti (na primjer, 15 ° ili čak 3 °).

Da biste pronašli površinu trokuta ove vrste, morate znati neke nijanse, o kojima ćemo dalje govoriti.

Pravilni i jednakokračni trokut

Pravilni poligon je lik koji ima n kutova i čije su stranice i kutovi jednaki. To je ono što je pravilan trokut. Kako je zbroj svih kutova trokuta 180°, svaki od triju kutova iznosi 60°.

Pravilni trokut, zbog svog svojstva, nazivamo i jednakostraničan lik.

Također je vrijedno napomenuti da se u pravilan trokut može upisati samo jedna kružnica, oko koje se može opisati samo jedna kružnica, a središta su im u istoj točki.

Osim jednakostraničnog tipa, može se razlikovati i jednakokračni trokut, koji se malo razlikuje od njega. U takvom su trokutu dvije stranice i dva kuta međusobno jednaki, a treća stranica (kojoj je susjedna jednaki kutovi) je baza.

Na slici je prikazan jednakokračni trokut DEF čiji su kutovi D i F jednaki, a DF je osnovica.

Pravokutni trokut

Pravokutni trokut nazvan je tako jer mu je jedan kut prav, odnosno jednak 90°. Zbroj druga dva kuta iznosi 90°.

Najveća stranica takvog trokuta, koja leži nasuprot kutu od 90°, je hipotenuza, dok su preostale dvije stranice katete. Za ovu vrstu trokuta vrijedi Pitagorina teorema:

Zbroj kvadrata duljina kateta jednak je kvadratu duljine hipotenuze.

Na slici je prikazan pravokutni trokut BAC s hipotenuzom AC i katetama AB i BC.

Da biste pronašli područje trokuta s pravim kutom, morate znati numeričke vrijednosti svoje noge.

Prijeđimo na formule za pronalaženje područja zadane figure.

Osnovne formule za određivanje površine

U geometriji postoje dvije formule koje su prikladne za pronalaženje površine većine vrsta trokuta, naime za šiljasti, tupi, pravilni i jednakokračni trokut. Pogledajmo svaki od njih.

Po strani i visini

Ova formula je univerzalan za pronalaženje područja figure koju razmatramo. Da biste to učinili, dovoljno je znati duljinu stranice i duljinu visine nacrtane na nju. Sama formula (polovica umnoška baze i visine) je sljedeća:

gdje je A stranica danog trokuta, a H je visina trokuta.

Na primjer, pronaći područje oštrokutni trokut ACB, trebate pomnožiti njegovu stranicu AB s visinom CD i dobivenu vrijednost podijeliti s dva.

Međutim, nije uvijek lako pronaći površinu trokuta na ovaj način. Na primjer, koristiti ovu formulu za tupokutni trokut, potrebno je nastaviti jednu njegovu stranu i tek nakon toga nacrtati visinu do nje.

U praksi se ova formula koristi češće od ostalih.

S obje strane i kut

Ova je formula, kao i prethodna, prikladna za većinu trokuta i po svom je značenju posljedica formule za određivanje površine stranice i visine trokuta. Odnosno, formula o kojoj je riječ može se lako izvesti iz prethodne. Njegova formulacija izgleda ovako:

S = ½*sinO*A*B,

gdje su A i B stranice trokuta, a O je kut između stranica A i B.

Podsjetimo se da se sinus kuta može vidjeti u posebnoj tablici, nazvanoj po istaknutom sovjetski matematičar V. M. Bradis.

Sada prijeđimo na druge formule koje su prikladne samo za iznimne vrste trokuta.

Površina pravokutnog trokuta

Osim univerzalne formule, koja uključuje potrebu za pronalaženjem nadmorske visine u trokutu, područje trokuta koji sadrži pravi kut može se pronaći iz njegovih nogu.

Dakle, površina trokuta koji sadrži pravi kut je pola umnoška njegovih krakova, ili:

gdje su a i b katete pravokutnog trokuta.

Pravilni trokut

Ovaj tip geometrijski likovi se razlikuju po tome što se njegovo područje može pronaći s naznačenom vrijednošću samo jedne njegove strane (jer sve strane pravilan trokut su jednaki). Dakle, kada se suočite sa zadatkom "pronalaženja površine trokuta kada su strane jednake", morate koristiti sljedeću formulu:

S = A 2 *√3 / 4,

gdje je A stranica jednakostraničnog trokuta.

Heronova formula

Zadnja opcija pronaći površinu trokuta je Heronova formula. Da biste ga koristili, morate znati duljine triju stranica figure. Heronova formula izgleda ovako:

S = √p·(p - a)·(p - b)·(p - c),

gdje su a, b i c stranice zadanog trokuta.

Ponekad se daje problem: "površina pravilnog trokuta je pronaći duljinu njegove strane." U u ovom slučaju moramo upotrijebiti već poznatu formulu za pronalaženje površine pravilnog trokuta i iz nje izvesti vrijednost stranice (ili njezinog kvadrata):

A 2 = 4S / √3.

Ispitni zadaci

Postoje mnoge formule u GIA problemima iz matematike. Osim toga, često je potrebno pronaći površinu trokuta na kariranom papiru.

U ovom slučaju, najprikladnije je nacrtati visinu na jednu od strana figure, odrediti njezinu duljinu iz ćelija i koristiti univerzalnu formulu za pronalaženje područja:

Dakle, nakon proučavanja formula predstavljenih u članku, nećete imati problema s pronalaženjem površine trokuta bilo koje vrste.

Da biste odredili površinu trokuta, možete koristiti različite formule. Od svih metoda, najjednostavnija i najčešće korištena je da se visina pomnoži s duljinom baze i zatim rezultat podijeli s dva. Međutim ovu metodu daleko od jedinog. U nastavku možete pročitati kako pronaći površinu trokuta pomoću različitih formula.

Zasebno ćemo pogledati načine izračuna površine specifične vrste trokut - pravokutni, jednakokračni i jednakostranični. Svaku formulu pratimo kratkim objašnjenjem koje će vam pomoći da shvatite njezinu bit.

Univerzalne metode za pronalaženje površine trokuta

Formule u nastavku koriste posebne oznake. Dešifrirat ćemo svaki od njih:

• a, b, c – duljine triju stranica figure koju razmatramo;
• r je polumjer kruga koji se može upisati u naš trokut;
• R je polumjer kruga koji se može opisati oko njega;
• α je veličina kuta koji čine stranice b i c;
• β je veličina kuta između a i c;
• γ je veličina kuta koji čine stranice a i b;
• h je visina našeg trokuta, spuštena od kuta α na stranu a;
• p – polovica zbroja stranica a, b i c.

Logično je jasno zašto možete pronaći područje trokuta na ovaj način. Trokut se lako može dovršiti u paralelogram, u kojem će jedna stranica trokuta djelovati kao dijagonala. Područje paralelograma nalazi se množenjem duljine jedne od njegovih stranica s vrijednošću visine nacrtane na nju. Dijagonala dijeli ovaj uvjetni paralelogram na 2 identična trokuta. Stoga je sasvim očito da površina našeg izvornog trokuta mora biti jednaka polovici površine ovog pomoćnog paralelograma.

S=½ a b sin γ

Prema ovoj formuli, površina trokuta nalazi se množenjem duljina njegovih dviju stranica, to jest a i b, sa sinusom kuta koji one čine. Ova formula je logično izvedena iz prethodne. Spustimo li visinu s kuta β na stranicu b, tada, prema svojstvima pravokutnog trokuta, kad pomnožimo duljinu stranice a sa sinusom kuta γ, dobivamo visinu trokuta, odnosno h .

Područje dotične figure nalazi se množenjem polovice polumjera kruga koji se u njega može upisati s njegovim opsegom. Drugim riječima, nalazimo umnožak polumjera i polumjera spomenute kružnice.

S= a b c/4R

Prema ovoj formuli, vrijednost koja nam je potrebna može se pronaći dijeljenjem umnoška stranica figure s 4 radijusa kruga opisanog oko njega.

Ove formule su univerzalne, jer omogućuju određivanje površine bilo kojeg trokuta (razmjerni, jednakokračni, jednakostranični, pravokutni). To se može učiniti pomoću složenijih izračuna, na kojima se nećemo detaljnije zadržavati.

Površine trokuta s određenim svojstvima

Kako pronaći područje pravokutnog trokuta? Osobitost ove figure je u tome što su njene dvije strane istovremeno i visine. Ako su a i b katete, a c postaje hipotenuza, tada područje nalazimo ovako:

Kako pronaći površinu jednakokračnog trokuta? Ima dvije stranice duljine a i jednu stranicu duljine b. Prema tome, njegova se površina može odrediti dijeljenjem s 2 umnoška kvadrata stranice a sa sinusom kuta γ.

Kako pronaći područje jednakostraničnog trokuta? U njemu je duljina svih stranica jednaka a, a veličina svih kutova α. Njegova visina jednaka je polovici umnoška duljine stranice a i kvadratnog korijena od 3. Da biste pronašli površinu pravilnog trokuta, morate kvadrat stranice a pomnožiti s kvadratnim korijenom od 3 i podijeliti s 4.

Na internetu možete pronaći više od 10 formula za izračunavanje površine trokuta. Mnoge od njih se koriste u problemima s poznatim stranicama i kutovima trokuta. Međutim, postoji niz složeni primjeri gdje su prema uvjetima zadatka poznati samo jedna stranica i kutovi trokuta ili polumjer opisane ili upisane kružnice i još jedna karakteristika. U takvim slučajevima jednostavna formula neće se moći prijaviti.

Dolje navedene formule omogućit će vam da riješite 95 posto problema u kojima trebate pronaći površinu trokuta.
Prijeđimo na razmatranje formula zajedničke površine.
Razmotrite trokut prikazan na donjoj slici

Na slici i dolje u formulama uvedene su klasične oznake svih njegovih karakteristika.
a,b,c – stranice trokuta,
R – polumjer opisane kružnice,
r – radijus upisane kružnice,
h[b],h[a],h[c] – visine nacrtane u skladu sa stranicama a,b,c.
alfa, beta, hamma – kutovi u blizini vrhova.

Osnovne formule za površinu trokuta

1. Površina je jednaka polovici umnoška stranice trokuta i visine spuštene na ovu stranicu. U jeziku formula ova se definicija može napisati na sljedeći način

Dakle, ako su poznata stranica i visina, tada će svaki učenik pronaći površinu.
Inače, iz ove formule može se izvesti jedan koristan odnos između visina

2. Ako uzmemo u obzir da se visina trokuta kroz susjednu stranicu izražava ovisnošću

Nakon prve formule površine slijede druge iste vrste

Pažljivo pogledajte formule - lako ih je zapamtiti, jer rad uključuje dvije strane i kut između njih. Ako ispravno označimo stranice i kutove trokuta (kao na gornjoj slici), dobit ćemo dva strane a,b a kut je povezan s trećim Sa (hamma).

3. Za kutove trokuta vrijedi relacija

Ovisnost vam omogućuje korištenje sljedećih formula za područje trokuta u izračunima:

Primjeri ove ovisnosti izuzetno su rijetki, ali morate zapamtiti da postoji takva formula.

4. Ako su poznata stranica i dva susjedna kuta, tada se površina nalazi prema formuli

5. Formula za površinu u smislu stranice i kotangensa susjednih kutova je sljedeća

Preuređivanjem indeksa možete dobiti ovisnosti za druge strane.

6. Donja formula površine koristi se u zadacima kada su vrhovi trokuta određeni na ravnini koordinatama. U ovom slučaju, površina je jednaka polovici determinante uzete modulo.

7. Heronova formula koristi se u primjerima s poznatim stranicama trokuta.
Najprije pronađite poluopseg trokuta

Zatim odredite područje pomoću formule

ili

Često se koristi u kodu programa kalkulatora.

8. Ako su poznate sve visine trokuta, tada se površina određuje formulom

Teško je izračunati na kalkulatoru, ali u paketima MathCad, Mathematica, Maple područje je "vrijeme dva".

9. Sljedeće formule koriste poznate polumjere upisane i opisane kružnice.

Konkretno, ako su poznati polumjer i stranice trokuta ili njegov opseg, tada se površina izračunava prema formuli

10. U primjerima gdje su dane stranice i polumjer ili promjer opisane kružnice, površina se nalazi pomoću formule

11. Sljedeća formula određuje površinu trokuta u smislu stranice i kutova trokuta.

I na kraju - posebni slučajevi:
Površina pravokutnog trokuta s katetama a i b jednakim polovici njihovog umnoška

Formula za površinu jednakostraničnog (pravilnog) trokuta=

= jedna četvrtina umnoška kvadrata stranice i korijena iz tri.

Pojam područja

Koncept područja bilo koje geometrijske figure, posebno trokuta, bit će povezan s figurom kao što je kvadrat. Za jedinicu površine bilo koje geometrijske figure uzet ćemo površinu kvadrata čija je stranica jednaka jedan. Radi potpunosti, prisjetimo se dva glavna svojstva za pojam površina geometrijskih likova.

Svojstvo 1: Ako geometrijske figure jednaki, onda su im površine također jednake.

Svojstvo 2: Svaka figura se može podijeliti na nekoliko figura. Štoviše, površina izvorne figure jednaka je zbroju površina svih njegovih sastavnih figura.

Pogledajmo primjer.

Primjer 1

Očito je da je jedna od stranica trokuta dijagonala pravokutnika čija je jedna stranica duljine $5$ (budući da ima $5$ ćelija), a druga je $6$ (budući da ima $6$ ćelija). Stoga će površina ovog trokuta biti jednaka polovici takvog pravokutnika. Površina pravokutnika je

Tada je površina trokuta jednaka

Odgovor: 15 dolara.

Zatim ćemo razmotriti nekoliko metoda za pronalaženje područja trokuta, naime pomoću visine i baze, pomoću Heronove formule i površine jednakostraničnog trokuta.

Kako pronaći površinu trokuta pomoću njegove visine i baze

Teorem 1

Površina trokuta može se pronaći kao polovica umnoška duljine stranice i visine te stranice.

Matematički to izgleda ovako

$S=\frac(1)(2)αh$

gdje je $a$ duljina stranice, $h$ je visina povučena na nju.

Dokaz.

Promotrimo trokut $ABC$ u kojem je $AC=α$. Ovoj stranici je povučena visina $BH$ koja je jednaka $h$. Izgradimo ga do kvadrata $AXYC$ kao na slici 2.

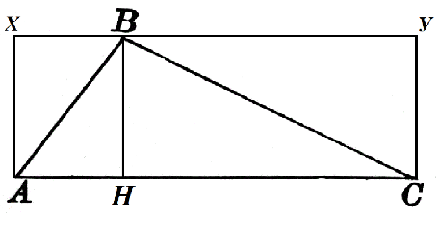
Površina pravokutnika $AXBH$ je $h\cdot AH$, a površina pravokutnika $HBYC$ je $h\cdot HC$. Zatim

$S_ABH=\frac(1)(2)h\cdot AH$, $S_CBH=\frac(1)(2)h\cdot HC$

Stoga je tražena površina trokuta, prema svojstvu 2, jednaka

$S=S_ABH+S_CBH=\frac(1)(2)h\cdot AH+\frac(1)(2)h\cdot HC=\frac(1)(2)h\cdot (AH+HC)=\ frac(1)(2)αh$

Teorem je dokazan.

Primjer 2

Pronađite površinu trokuta na donjoj slici ako ćelija ima površinu jednaku jedan

Osnovica ovog trokuta jednaka je $9$ (budući da je $9$ kvadrat od $9$). Visina je također $9$. Tada, prema teoremu 1, dobivamo

$S=\frac(1)(2)\cdot 9\cdot 9=40,5$

Odgovor: 40,5 dolara.

Heronova formula

Teorem 2

Ako su nam dane tri stranice trokuta $α$, $β$ i $γ$, tada se njegova površina može pronaći na sljedeći način

$S=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

ovdje $ρ$ znači poluopseg ovog trokuta.

Dokaz.

Razmotrite sljedeću sliku:

Po Pitagorinoj teoremi, iz trokuta $ABH$ dobivamo

Iz trokuta $CBH$, prema Pitagorinom teoremu, imamo

$h^2=α^2-(β-x)^2$

$h^2=α^2-β^2+2βx-x^2$

Iz ove dvije relacije dobivamo jednakost

$γ^2-x^2=α^2-β^2+2βx-x^2$

$x=\frac(γ^2-α^2+β^2)(2β)$

$h^2=γ^2-(\frac(γ^2-α^2+β^2)(2β))^2$

$h^2=\frac((α^2-(γ-β)^2)((γ+β)^2-α^2))(4β^2)$

$h^2=\frac((α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α))(4β^2)$

Budući da je $ρ=\frac(α+β+γ)(2)$, onda je $α+β+γ=2ρ$, što znači

$h^2=\frac(2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α))(4β^2)$

$h^2=\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2 )$

$h=\sqrt(\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2))$

$h=\frac(2)(β)\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

Prema teoremu 1, dobivamo

$S=\frac(1)(2) βh=\frac(β)(2)\cdot \frac(2)(β) \sqrt(ρ(ρ-α)(ρ-β)(ρ-γ) )=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$