Osnove teorije vjerojatnosti i matematičke statistike. Osnovni pojmovi teorije vjerojatnosti i matematičke statistike
Teorija vjerojatnosti i matematička statistika
- Agekyan T.A. Osnove teorije pogreške za astronome i fizičare (2. izdanje). M.: Nauka, 1972 (djvu, 2,44 M)
- Agekyan T.A. Teorija vjerojatnosti za astronome i fizičare. M.: Nauka, 1974 (djvu, 2,59 M)
- Anderson T. Statistička analiza vremenskih serija. M.: Mir, 1976 (djvu, 14 M)
- Bakelman I.Ya. Werner A.L. Kantor B.E. Uvod u diferencijalnu geometriju "općenito". M.: Nauka, 1973 (djvu, 5,71 M)
- Bernstein S.N. Teorija vjerojatnosti. M.-L.: GI, 1927 (djvu, 4,51 M)
- Billingsley P. Konvergencija mjera vjerojatnosti. M.: Nauka, 1977 (djvu, 3,96 M)
- Okvir J. Jenkins G. Analiza vremenskih serija: predviđanje i upravljanje. Izdanje 1. M.: Mir, 1974 (djvu, 3,38 M)
- Okvir J. Jenkins G. Analiza vremenskih serija: predviđanje i upravljanje. Izdanje 2. M.: Mir, 1974 (djvu, 1,72 M)
- Borel E. Vjerojatnost i pouzdanost. M.: Nauka, 1969 (djvu, 1,19 M)
- Van der Waerden B.L. Matematička statistika. M.: IL, 1960 (djvu, 6,90 M)
- Vapnik V.N. Oporavak ovisnosti na temelju empirijskih podataka. M.: Nauka, 1979 (djvu, 6,18M)
- Ventzel E.S. Uvod u operacijska istraživanja. M.: Sovjetski radio, 1964 (djvu, 8,43 M)
- Ventzel E.S. Elementi teorije igara (2. izdanje). Serija: Popularna predavanja iz matematike. Izdanje 32. M.: Nauka, 1961 (djvu, 648 K)
- Ventstel E.S. Teorija vjerojatnosti (4. izdanje). M.: Nauka, 1969 (djvu, 8,05 M)
- Ventstel E.S., Ovcharov L.A. Teorija vjerojatnosti. Zadaci i vježbe. M.: Nauka, 1969 (djvu, 7,71 M)
- Vilenkin N.Ya., Potapov V.G. Praktična bilježnica iz teorije vjerojatnosti s elementima kombinatorike i matematičke statistike. M.: Obrazovanje, 1979 (djvu, 1,12M)
- Gmurman V.E. Vodič za rješavanje problema iz teorije vjerojatnosti i matematičke statistike (3. izdanje). M.: Više. škola, 1979 (djvu, 4,24 M)
- Gmurman V.E. Teorija vjerojatnosti i matematička statistika (4. izdanje). M.: Viša škola, 1972 (djvu, 3,75 M)
- Gnedenko B.V., Kolmogorov A.N. Granične distribucije za sume nezavisnih slučajnih varijabli. M.-L.: GITTL, 1949 (djvu, 6,26 M)
- Gnedenko B.V., Khinchin A.Ya. Elementarni uvod u teoriju vjerojatnosti (7. izdanje). M.: Nauka, 1970 (djvu, 2,48 M)
- Hrast J.L. Probabilistički procesi. M.: IL, 1956 (djvu, 8,48 M)
- David G. Ordinalna statistika. M.: Nauka, 1979 (djvu, 2,87M)
- Ibragimov I.A., Linnik Yu.V. Neovisne i stacionarne povezane veličine. M.: Nauka, 1965 (djvu, 6,05M)
- Idier V., Dryard D., James F., Rus M., Sadoulet B. Statističke metode u eksperimentalnoj fizici. M.: Atomizdat, 1976 (djvu, 5,95M)
- Kamalov M.K. Distribucija kvadratnih oblika u uzorcima iz normalne populacije. Taškent: Akademija nauka UzSSR-a, 1958 (djvu, 6,29M)
- Kassandra O.N., Lebedev V.V. Obrada rezultata motrenja. M.: Nauka, 1970 (djvu, 867 K)
- Katz M. Vjerojatnost i srodna pitanja u fizici. M.: Mir, 1965 (djvu, 3,67 M)
- Katz M. Nekoliko probabilističkih problema fizike i matematike. M.: Nauka, 1967 (djvu, 1,50 M)
- Katz M. Statistička neovisnost u teoriji vjerojatnosti, analizi i teoriji brojeva. M.: IL, 1963 (djvu, 964 K)
- Kendall M., Moran P. Geometrijske vjerojatnosti. M.: Nauka, 1972 (djvu, 1,40 M)
- Kendall M., Stewart A. Svezak 2. Statističko zaključivanje i veze. M.: Nauka, 1973 (djvu, 10 M)
- Kendall M., Stewart A. Svezak 3. Multivarijatna statistička analiza i vremenske serije. M.: Nauka, 1976 (djvu, 7,96 M)
- Kendall M., Stewart A. sv. 1. Teorija distribucija. M.: Nauka, 1965 (djvu, 6,02 M)
- Kolmogorov A.N. Osnovni pojmovi teorije vjerojatnosti (2. izdanje) M.: Nauka, 1974. (djvu, 2,14M)
- Kolchin V.F., Sevastyanov B.A., Chistyakov V.P. Slučajni položaji. M.: Nauka, 1976 (djvu, 2,96 M)
- Kramer G. Matematičke metode statistike (2. izdanje). M.: Mir, 1976 (djvu, 9,63 M)
- Leman E. Testiranje statističkih hipoteza. M.: Znanost. 1979. godine (djvu, 5,18 M)
- Linnik Yu.V., Ostrovsky I.V. Dekompozicije slučajnih varijabli i vektora. M.: Nauka, 1972 (djvu, 4,86 M)
- Likholetov I.I., Matskevich I.P. Vodič za rješavanje problema iz više matematike, teorije vjerojatnosti i matematičke statistike (2. izdanje). Mn.: Vysh. škola, 1969 (djvu, 4,99 M)
- Loev M. Teorija vjerojatnosti. M.: IL, 1962 (djvu, 7,38 M)
- Malakhov A.N. Kumulantna analiza slučajnih ne-Gaussovih procesa i njihovih transformacija. M.: Sov. radio, 1978 (djvu, 6,72 M)
- Meshalkin L.D. Zbirka zadataka iz teorije vjerojatnosti. M.: MSU, 1963 (djvu, 1 004 K)
- Mitropolsky A.K. Teorija momenata. M.-L.: GIKSL, 1933 (djvu, 4,49 M)
- Mitropolsky A.K. Tehnike statističkog računanja (2. izdanje). M.: Nauka, 1971 (djvu, 8,35 M)
- Mosteller F., Rurke R., Thomas J. Vjerojatnost. M.: Mir, 1969 (djvu, 4,82 M)
- Nalimov V.V. Primjena matematičke statistike u analizi materije. M.: GIFML, 1960 (djvu, 4,11M)
- Neveu J. Matematičke osnove teorije vjerojatnosti. M.: Mir, 1969 (djvu, 3,62 M)
- Preston K. Matematika. Novo u stranoj znanosti br.7. Gibbsova stanja na prebrojivim skupovima. M.: Mir, 1977 (djvu, 2,15 M)
- Saveljev L.Ja. Elementarna teorija vjerojatnosti. Dio 1. Novosibirsk: NSU, 2005 (
Mnogi se, kada se suoče s konceptom “teorije vjerojatnosti”, uplaše, misleći da je to nešto neodoljivo, vrlo složeno. Ali zapravo sve nije tako tragično. Danas ćemo pogledati osnovni koncept teorije vjerojatnosti i naučiti kako rješavati probleme koristeći konkretne primjere.
Znanost
Što proučava takva grana matematike kao što je "teorija vjerojatnosti"? Bilježi uzorke i količine. Znanstvenici su se prvi put zainteresirali za ovo pitanje još u osamnaestom stoljeću, kada su proučavali kockanje. Osnovni pojam teorije vjerojatnosti je događaj. To je svaka činjenica koja je utvrđena iskustvom ili opažanjem. Ali što je iskustvo? Drugi temeljni koncept teorije vjerojatnosti. To znači da ovaj splet okolnosti nije stvoren slučajno, već s određenom svrhom. Što se tiče promatranja, ovdje sam istraživač ne sudjeluje u eksperimentu, već je samo svjedok tih događaja, on ni na koji način ne utječe na ono što se događa.
Događaji
Naučili smo da je osnovni koncept teorije vjerojatnosti događaj, ali nismo razmatrali klasifikaciju. Svi su podijeljeni u sljedeće kategorije:
- Pouzdan.
- Nemoguće.
- Slučajno.
Bez obzira na vrstu događaja, opaženih ili stvorenih tijekom iskustva, svi oni podliježu ovoj klasifikaciji. Pozivamo vas da se upoznate sa svakom vrstom zasebno.
Pouzdan događaj

To je okolnost za koju je poduzet potreban niz mjera. Da bismo bolje razumjeli suštinu, bolje je navesti nekoliko primjera. Ovom zakonu podliježu fizika, kemija, ekonomija i viša matematika. Teorija vjerojatnosti uključuje tako važan koncept kao pouzdani događaj. Evo nekoliko primjera:
- Radimo i primamo naknadu u vidu plaće.
- Dobro smo položili ispite, prošli na natjecanju i za to dobivamo nagradu u vidu upisa u obrazovnu ustanovu.
- Novac smo uložili u banku, a ako treba, vratit ćemo ga.
Takvi događaji su pouzdani. Ako smo ispunili sve potrebne uvjete, sigurno ćemo dobiti očekivani rezultat.
Nemogući događaji
Sada razmatramo elemente teorije vjerojatnosti. Predlažemo prijeći na objašnjenje sljedeće vrste događaja, naime nemogućeg. Prvo, odredimo najvažnije pravilo - vjerojatnost nemogućeg događaja je nula.
Od ove formulacije ne može se odstupiti pri rješavanju problema. Radi pojašnjenja, evo primjera takvih događaja:
- Voda se smrzavala na temperaturi od plus deset (to je nemoguće).
- Nedostatak električne energije ni na koji način ne utječe na proizvodnju (jednako nemoguće kao u prethodnom primjeru).
Ne vrijedi navoditi više primjera, budući da gore opisani vrlo jasno odražavaju bit ove kategorije. Nemoguć događaj se nikada neće dogoditi tijekom eksperimenta ni pod kojim okolnostima.
Slučajni događaji

Prilikom proučavanja elemenata posebnu pozornost treba obratiti na ovu vrstu događaja. To je ono što znanost proučava. Kao rezultat iskustva, nešto se može dogoditi, ali i ne mora. Osim toga, test se može provoditi neograničeni broj puta. Živopisni primjeri uključuju:
- Bacanje novčića je iskustvo ili test, pad glava je događaj.
- Izvlačenje lopte na slijepo iz vreće je test, dobivanje crvene lopte je događaj, i tako dalje.
Takvih primjera može biti neograničen broj, ali, općenito, suština bi trebala biti jasna. Kako bismo saželi i sistematizirali stečena znanja o događajima, donosimo tablicu. Teorija vjerojatnosti proučava samo posljednju vrstu od svih prikazanih.
Ime | definicija | |
Pouzdan | Događaji koji se odvijaju uz 100% jamstvo ako su zadovoljeni određeni uvjeti. | Upis u obrazovnu ustanovu nakon dobrog položenog prijemnog ispita. |
Nemoguće | Događaji koji se neće dogoditi ni pod kojim okolnostima. | Pada snijeg pri temperaturi zraka od plus trideset Celzijevih stupnjeva. |
Slučajno | Događaj koji se može ili ne mora dogoditi tijekom eksperimenta/testiranja. | Pogodak ili promašaj prilikom ubacivanja košarkaške lopte u obruč. |
Zakoni
Teorija vjerojatnosti je znanost koja proučava mogućnost događanja događaja. Kao i drugi, ima neka pravila. Postoje sljedeći zakoni teorije vjerojatnosti:
- Konvergencija nizova slučajnih varijabli.
- Zakon velikih brojeva.
Kada izračunavate mogućnost nečeg složenog, možete koristiti skup jednostavnih događaja kako biste na lakši i brži način postigli rezultat. Imajte na umu da se zakoni teorije vjerojatnosti lako dokazuju pomoću određenih teorema. Predlažemo da se najprije upoznate s prvim zakonom.
Konvergencija nizova slučajnih varijabli

Imajte na umu da postoji nekoliko vrsta konvergencije:
- Niz slučajnih varijabli konvergira u vjerojatnosti.
- Skoro nemoguće.
- Srednja kvadratna konvergencija.
- Konvergencija distribucije.
Dakle, odmah na početku, vrlo je teško shvatiti suštinu. Evo definicija koje će vam pomoći razumjeti ovu temu. Počnimo s prvim pogledom. Niz se zove konvergentan u vjerojatnosti, ako je ispunjen sljedeći uvjet: n teži beskonačnosti, broj kojem niz teži je veći od nule i blizak jedinici.
Prijeđimo na sljedeći prikaz, skoro sigurno. Za niz se kaže da konvergira skoro sigurno na slučajnu varijablu s n koja teži beskonačnosti i P koja teži vrijednosti blizu jedinici.
Sljedeća vrsta je konvergencija srednjeg kvadrata. Kada se koristi SC konvergencija, proučavanje vektorskih slučajnih procesa svodi se na proučavanje njihovih koordinatnih slučajnih procesa.
Ostaje posljednja vrsta, pogledajmo je ukratko kako bismo mogli izravno prijeći na rješavanje problema. Konvergencija u distribuciji ima još jedno ime - "slaba", a kasnije ćemo objasniti zašto. Slaba konvergencija je konvergencija funkcija distribucije u svim točkama kontinuiteta granične funkcije distribucije.
Obećanje ćemo svakako održati: slaba konvergencija se od svega navedenog razlikuje po tome što slučajna varijabla nije definirana u prostoru vjerojatnosti. To je moguće jer se uvjet formira isključivo pomoću distribucijskih funkcija.
Zakon velikih brojeva
Teoreme teorije vjerojatnosti, kao što su:
- Čebiševljeva nejednakost.
- Čebiševljev teorem.
- Generalizirani Čebiševljev teorem.
- Markovljev teorem.
Ako uzmemo u obzir sve te teoreme, onda se ovo pitanje može povući na nekoliko desetaka listova. Naš glavni zadatak je primijeniti teoriju vjerojatnosti u praksi. Predlažemo da to učinite odmah. Ali prije toga, pogledajmo aksiome teorije vjerojatnosti; oni će biti glavni pomoćnici u rješavanju problema.
Aksiomi

S prvim smo se već susreli kada smo govorili o nemogućem događaju. Podsjetimo: vjerojatnost nemogućeg događaja je nula. Dali smo vrlo živopisan i nezaboravan primjer: snijeg je pao na temperaturi zraka od trideset stupnjeva Celzijusa.
Drugi je sljedeći: pouzdani događaj događa se s vjerojatnošću jednakom jedan. Sada ćemo pokazati kako ovo napisati matematičkim jezikom: P(B)=1.
Treće: Slučajni događaj se može, ali i ne mora dogoditi, ali mogućnost se uvijek kreće od nula do jedan. Što je vrijednost bliža jedinici, veće su šanse; ako se vrijednost približava nuli, vjerojatnost je vrlo mala. Zapišimo ovo matematičkim jezikom: 0<Р(С)<1.
Razmotrimo posljednji, četvrti aksiom, koji zvuči ovako: vjerojatnost zbroja dva događaja jednaka je zbroju njihovih vjerojatnosti. Zapisujemo to matematičkim jezikom: P(A+B)=P(A)+P(B).
Aksiomi teorije vjerojatnosti su najjednostavnija pravila koja nije teško zapamtiti. Pokušajmo riješiti neke probleme na temelju već stečenog znanja.
Listić lutrije

Prvo, pogledajmo najjednostavniji primjer – lutriju. Zamislite da ste kupili jednu srećku za sreću. Koja je vjerojatnost da ćete osvojiti najmanje dvadeset rubalja? Ukupno u optjecaju sudjeluje tisuću ulaznica, od kojih jedna ima nagradu od petsto rubalja, deset ih ima po stotinu rubalja, pedeset ima nagradu od dvadeset rubalja, a sto ima nagradu od pet. Problemi vjerojatnosti temelje se na pronalaženju mogućnosti sreće. Sada ćemo zajedno analizirati rješenje gornjeg zadatka.
Ako koristimo slovo A za označavanje dobitka od pet stotina rubalja, tada će vjerojatnost dobivanja A biti jednaka 0,001. Kako smo ovo dobili? Samo trebate podijeliti broj "sretnih" listića s njihovim ukupnim brojem (u ovom slučaju: 1/1000).
B je dobitak od sto rubalja, vjerojatnost će biti 0,01. Sada smo postupili po istom principu kao u prethodnoj akciji (10/1000)
C - dobitak je dvadeset rubalja. Pronalazimo vjerojatnost, ona je jednaka 0,05.
Preostale ulaznice nas ne zanimaju jer je njihov nagradni fond manji od navedenog u uvjetu. Primijenimo četvrti aksiom: Vjerojatnost da dobijete najmanje dvadeset rubalja je P(A)+P(B)+P(C). Slovo P označava vjerojatnost pojave određenog događaja, već smo ih pronašli u prethodnim radnjama. Ostaje još samo zbrojiti potrebne podatke, a odgovor koji dobivamo je 0,061. Ovaj broj će biti odgovor na pitanje zadatka.
Špil karata
Problemi u teoriji vjerojatnosti mogu biti složeniji; na primjer, uzmimo sljedeći zadatak. Pred vama je špil od trideset i šest karata. Vaš zadatak je izvući dvije karte u nizu bez miješanja hrpe, prva i druga karta moraju biti asovi, boja nije bitna.
Prvo, pronađimo vjerojatnost da će prva karta biti as, za to dijelimo četiri sa trideset šest. Stavili su ga na stranu. Izvadimo drugu kartu, to će biti as s vjerojatnošću tri trideset petine. Vjerojatnost drugog događaja ovisi o tome koju smo kartu prvu izvukli, pitamo se je li to bio as ili ne. Iz ovoga slijedi da događaj B ovisi o događaju A.
Sljedeći korak je pronaći vjerojatnost istovremenog događanja, odnosno množimo A i B. Njihov umnožak nalazimo na sljedeći način: množimo vjerojatnost jednog događaja s uvjetnom vjerojatnošću drugog, koju izračunavamo, pretpostavljajući da je prvi dogodio se događaj, odnosno izvukli smo asa s prvom kartom.
Da bi sve bilo jasno, dajmo oznaku takvom elementu kao što su događaji. Izračunava se pod pretpostavkom da se dogodio događaj A. Izračunava se na sljedeći način: P(B/A).
Nastavimo rješavati naš problem: P(A * B) = P(A) * P(B/A) ili P(A * B) = P(B) * P(A/B). Vjerojatnost je jednaka (4/36) * ((3/35)/(4/36). Računamo zaokruživanjem na najbližu stotinku. Imamo: 0,11 * (0,09/0,11) = 0,11 * 0, 82 = 0,09.Vjerojatnost da ćemo izvući dva asa zaredom je devet stotinki.Vrijednost je vrlo mala, iz čega slijedi da je vjerojatnost da se događaj dogodi izuzetno mala.
Zaboravljeni broj
Predlažemo da analiziramo još nekoliko varijanti zadataka koje proučava teorija vjerojatnosti. Primjere rješavanja nekih od njih već ste vidjeli u ovom članku. Pokušajmo riješiti sljedeći problem: dječak je zaboravio zadnju znamenku telefonskog broja svog prijatelja, ali kako je poziv bio vrlo važan, počeo je birati sve redom . Moramo izračunati vjerojatnost da neće nazvati više od tri puta. Rješenje problema je najjednostavnije ako se poznaju pravila, zakoni i aksiomi teorije vjerojatnosti.
Prije nego pogledate rješenje, pokušajte ga sami riješiti. Znamo da posljednja znamenka može biti od nula do devet, odnosno deset vrijednosti ukupno. Vjerojatnost da dobijete pravu je 1/10.
Zatim, moramo razmotriti opcije za podrijetlo događaja, pretpostavimo da je dječak dobro pogodio i odmah upisao pravu, vjerojatnost takvog događaja je 1/10. Druga opcija: prvi poziv promašuje, a drugi je na meti. Izračunajmo vjerojatnost takvog događaja: pomnožimo 9/10 s 1/9, a kao rezultat također dobivamo 1/10. Treća opcija: prvi i drugi poziv pokazali su se na krivoj adresi, tek trećim je dječak stigao gdje je htio. Izračunavamo vjerojatnost takvog događaja: 9/10 pomnoženo s 8/9 i 1/8, što rezultira 1/10. Druge mogućnosti prema uvjetima problema nas ne zanimaju, pa samo trebamo zbrajati dobivene rezultate, na kraju imamo 3/10. Odgovor: vjerojatnost da se dječak neće javiti više od tri puta je 0,3.
Kartice s brojevima

Pred vama je devet karata, na svakoj je ispisan broj od jedan do devet, brojevi se ne ponavljaju. Stavili su ih u kutiju i temeljito izmiješali. Morate izračunati vjerojatnost da
- pojavit će se paran broj;
- dvoznamenkasti.
Prije nego prijeđemo na rješenje, uvjetujmo da je m broj uspješnih slučajeva, a n ukupan broj opcija. Nađimo vjerojatnost da će broj biti paran. Neće biti teško izračunati da postoje četiri parna broja, to će biti naše m, ukupno je devet mogućih opcija, odnosno m=9. Tada je vjerojatnost 0,44 ili 4/9.
Razmotrimo drugi slučaj: broj opcija je devet, a ne može uopće biti uspješnih ishoda, odnosno m je jednako nula. Vjerojatnost da će izvučena karta sadržavati dvoznamenkasti broj također je nula.
UVOD
Mnoge stvari su nam neshvatljive ne zato što su naši pojmovi slabi;
nego zato što te stvari nisu uključene u raspon naših pojmova.
Kozma Prutkov
Glavni cilj studija matematike u srednjim specijaliziranim obrazovnim ustanovama je dati učenicima skup matematičkih znanja i vještina potrebnih za proučavanje drugih programskih disciplina koje koriste matematiku u jednom ili drugom stupnju, za sposobnost izvođenja praktičnih izračuna, za formiranje i razvoj logičkog razmišljanja.
U ovom radu, svi osnovni koncepti dijela matematike „Osnove teorije vjerojatnosti i matematičke statistike“, predviđeni programom i Državnim obrazovnim standardima srednjeg strukovnog obrazovanja (Ministarstvo obrazovanja Ruske Federacije. M., 2002. ), dosljedno se uvode, formuliraju se glavni teoremi od kojih većina nije dokazana . Razmatraju se glavni problemi i metode za njihovo rješavanje te tehnologije za primjenu tih metoda u rješavanju praktičnih problema. Izlaganje je popraćeno detaljnim komentarima i brojnim primjerima.
Metodičke upute mogu poslužiti za početno upoznavanje s gradivom koje se uči, za pisanje bilježaka na predavanjima, za pripremu za praktičnu nastavu, za utvrđivanje stečenih znanja, vještina i sposobnosti. Osim toga, priručnik će biti koristan i studentima preddiplomskih studija kao referentni alat koji će im omogućiti da se brzo prisjete onoga što su prethodno proučavali.
Na kraju rada nalaze se primjeri i zadaci koje učenici mogu obaviti u načinu samokontrole.
Smjernice su namijenjene izvanrednim i redovitim studentima.
OSNOVNI KONCEPTI
Teorija vjerojatnosti proučava objektivne obrasce masovnih slučajnih događaja. To je teorijska osnova matematičke statistike koja se bavi razvojem metoda za prikupljanje, opisivanje i obradu rezultata promatranja. Promatranjima (testovima, pokusima), tj. iskustvo u širem smislu riječi, dolazi do spoznaje o pojavama stvarnog svijeta.
U svom praktičnom djelovanju često se susrećemo s pojavama čiji se ishod ne može predvidjeti, čiji ishod ovisi o slučaju.
Slučajni fenomen može se karakterizirati omjerom broja njegovih pojavljivanja prema broju pokušaja, u svakom od njih, pod istim uvjetima svih pokušaja, mogao bi se dogoditi ili ne dogoditi.
Teorija vjerojatnosti je grana matematike u kojoj se proučavaju slučajni fenomeni (događaji) i utvrđuju uzorci kada se masovno ponavljaju.
Matematička statistika je grana matematike koja se bavi proučavanjem metoda prikupljanja, sistematiziranja, obrade i korištenja statističkih podataka za dobivanje znanstveno utemeljenih zaključaka i donošenje odluka.
U ovom slučaju, statistički podaci se shvaćaju kao skup brojeva koji predstavljaju kvantitativne karakteristike karakteristika objekata koji se proučavaju koji nas zanimaju. Statistički podaci dobivaju se kao rezultat posebno osmišljenih pokusa i promatranja.
Statistički podaci po svojoj biti ovise o mnogim slučajnim čimbenicima, stoga je matematička statistika usko povezana s teorijom vjerojatnosti, koja je njezina teorijska osnova.
I. VJEROJATNOST. TEOREMI ZBRAJANJA I MNOŽENJA VJEROJATNOSTI
1.1. Osnovni pojmovi kombinatorike
U grani matematike, koja se naziva kombinatorika, rješavaju se neki problemi vezani uz razmatranje skupova i sastavljanje raznih kombinacija elemenata tih skupova. Na primjer, ako uzmemo 10 različitih brojeva 0, 1, 2, 3,: , 9 i napravimo kombinacije od njih, dobit ćemo različite brojeve, na primjer 143, 431, 5671, 1207, 43 itd.
Vidimo da se neke od ovih kombinacija razlikuju samo u redoslijedu znamenki (na primjer, 143 i 431), druge - u znamenkama koje su u njima uključene (na primjer, 5671 i 1207), a druge se također razlikuju u broju znamenki. (na primjer, 143 i 43).
Dakle, dobivene kombinacije zadovoljavaju različite uvjete.
Ovisno o pravilima sastava, mogu se razlikovati tri vrste kombinacija: permutacije, postavljanja, kombinacije.
Najprije se upoznajmo s pojmom faktorijel.
Umnožak svih prirodnih brojeva od 1 do uključivo n naziva se n-faktorijal i napiši.
Izračunaj: a) ; b) ; V) .
Riješenje. A) .
b) Budući da ![]() , onda ga možemo staviti izvan zagrada
, onda ga možemo staviti izvan zagrada
Onda dobivamo
V) ![]() .
.
Preuređivanja.
Kombinacija od n elemenata koji se međusobno razlikuju samo po redoslijedu elemenata naziva se permutacija.
Permutacije su označene simbolom P n , gdje je n broj elemenata uključenih u svaku permutaciju. ( R- prvo slovo francuske riječi permutacija- preuređenje).
Broj permutacija može se izračunati pomoću formule
ili koristeći faktorijel:
Zapamtimo to 0!=1 i 1!=1.
Primjer 2. Na koliko se načina na jednu policu može složiti šest različitih knjiga?
Riješenje. Traženi broj načina jednak je broju permutacija 6 elemenata, tj.
Plasmani.
Objave od m elementi u n u svakom se nazivaju takvi spojevi koji se međusobno razlikuju bilo po samim elementima (barem jednom), bilo po redu njihova rasporeda.
Položaji su označeni simbolom, gdje m- broj svih raspoloživih elemenata, n- broj elemenata u svakoj kombinaciji. ( A- prvo slovo francuske riječi uređenje, što znači “postavljanje, dovođenje u red”).
Pritom se vjeruje da nm.
Broj plasmana može se izračunati pomoću formule
![]() ,
,
oni. broj svih mogućih plasmana od m elementi po n jednako umnošku n uzastopnih cijelih brojeva, od kojih je najveći m.
Zapišimo ovu formulu u faktorijelnom obliku:
Primjer 3. Koliko se opcija za raspodjelu tri bona u lječilišta različitih profila može sastaviti za pet podnositelja zahtjeva?
Riješenje. Potreban broj opcija jednak je broju postavljanja 5 elemenata od 3 elementa, tj.
![]() .
.
Kombinacije.
Kombinacije su sve moguće kombinacije m elementi po n, koji se međusobno razlikuju barem po jednom elementu (ovdje m I n- prirodni brojevi, i n m).
Broj kombinacija od m elementi po n označeni su sa ( S- prvo slovo francuske riječi kombinacija- kombinacija).
Općenito, broj m elementi po n jednak broju plasmana iz m elementi po n, podijeljeno s brojem permutacija iz n elementi:
Koristeći faktorske formule za brojeve plasmana i permutacija, dobivamo:
![]()
Primjer 4. U timu od 25 ljudi trebate rasporediti četvero za rad na određenom području. Na koliko načina se to može učiniti?
Riješenje. Budući da redoslijed četiri odabrane osobe nije bitan, postoje načini da to učinite.
Nalazimo pomoću prve formule
![]() .
.
Osim toga, pri rješavanju problema koriste se sljedeće formule koje izražavaju osnovna svojstva kombinacija:
(po definiciji pretpostavljaju i);
![]() .
.
1.2. Rješavanje kombinatornih zadataka
Zadatak 1. Na fakultetu se izučava 16 predmeta. Morate staviti 3 predmeta na raspored za ponedjeljak. Na koliko načina se to može učiniti?
Riješenje. Postoji onoliko načina za raspoređivanje tri stavke od 16 koliko možete rasporediti 16 stavki po 3.
Zadatak 2. Od 15 objekata potrebno je odabrati 10 objekata. Na koliko načina se to može učiniti?

Zadatak 3. Na natjecanju su sudjelovale četiri ekipe. Koliko je opcija za raspodjelu mjesta između njih moguće?
![]() .
.
Zadatak 4. Na koliko se načina može formirati ophodnja od tri vojnika i jednog časnika ako ima 80 vojnika i 3 časnika?
Riješenje. Možete odabrati vojnika u patroli
načini, a službenici u načinima. Budući da svaki časnik može ići sa svakim timom vojnika, postoji toliko mnogo načina.
Zadatak 5. Nađi , ako je poznato da .
Od , dobivamo
![]() ,
,
![]() ,
,
![]()
Iz definicije kombinacije slijedi da je , . Da. .
1.3. Pojam slučajnog događaja. Vrste događaja. Vjerojatnost događaja
Svaka radnja, pojava, opažanje s nekoliko različitih ishoda, realiziranih pod danim skupom uvjeta, nazvat će se test.
Rezultat ove radnje ili promatranja naziva se događaj .
Ako se događaj u danim uvjetima može dogoditi ili ne dogoditi, tada se naziva slučajan . Kada je izvjesno da će se neki događaj dogoditi, on se poziva pouzdan , au slučaju kada se to očito ne može dogoditi, - nemoguće.
Događaji se zovu nekompatibilan , ako se svaki put može pojaviti samo jedan od njih.
Događaji se zovu spojnica , ako, pod danim uvjetima, pojava jednog od ovih događaja ne isključuje pojavu drugog tijekom istog ispitivanja.
Događaji se zovu suprotan , ako su pod uvjetima ispitivanja oni, kao jedini ishodi, nekompatibilni.
Događaji se obično označavaju velikim slovima latinične abecede: A, B, C, D, : .
Potpuni sustav događaja A 1 , A 2 , A 3 , : , A n je skup nekompatibilnih događaja od kojih je pojava barem jednog obavezna tijekom danog testa.
Ako se kompletan sustav sastoji od dva nekompatibilna događaja, tada se takvi događaji nazivaju suprotnim i označavaju se A i .
Primjer. Kutija sadrži 30 numeriranih kuglica. Odredite koji su od sljedećih događaja nemogući, pouzdani ili suprotni:
izvadio kuglicu s brojem (A);
dobio lopticu s parnim brojem (U);
dobio lopticu s neparnim brojem (S);
dobio loptu bez broja (D).
Koji od njih čine potpunu skupinu?
Riješenje . A- pouzdan događaj; D- nemoguć događaj;
U i S- suprotni događaji.
Kompletnu grupu događaja čine A I D, V I S.
Vjerojatnost događaja smatra se mjerom objektivne mogućnosti nastanka slučajnog događaja.
1.4. Klasična definicija vjerojatnosti
Naziva se broj koji izražava mjeru objektivne mogućnosti da se neki događaj dogodi vjerojatnost ovaj događaj i označen je simbolom R(A).
Definicija. Vjerojatnost događaja A je omjer broja ishoda m koji pogoduju pojavi danog događaja A, na broj n svi ishodi (nedosljedni, samo mogući i jednako mogući), tj. .
Stoga, da bismo pronašli vjerojatnost događaja, potrebno je, nakon razmatranja različitih ishoda testa, izračunati sve moguće nedosljedne ishode. n, odabrati broj ishoda m koji nas zanima i izračunati omjer m Do n.
Iz ove definicije proizlaze sljedeća svojstva:
Vjerojatnost bilo kojeg testa je nenegativan broj koji ne prelazi jedinicu.
Doista, broj m traženih događaja je unutar . Podijelivši oba dijela na n, dobivamo
2. Vjerojatnost pouzdanog događaja jednaka je jedinici jer .
3. Vjerojatnost nemogućeg događaja je nula, jer .
Zadatak 1. U lutriji od 1000 listića nalazi se 200 dobitnih. Slučajno se izvlači jedna karta. Koja je vjerojatnost da je ovaj listić dobitni?
Riješenje. Ukupan broj različitih ishoda je n=1000. Broj ishoda povoljnih za pobjedu je m=200. Prema formuli dobivamo
![]() .
.
Problem 2. U seriji od 18 dijelova nalaze se 4 neispravna. Nasumično se bira 5 dijelova. Nađite vjerojatnost da će dva od ovih 5 dijelova biti neispravna.
Riješenje. Broj svih jednako mogućih neovisnih ishoda n jednak broju kombinacija od 18 puta 5 tj.
Izbrojimo broj m koji ide u prilog događaju A. Među 5 nasumce uzetih dijelova trebala bi biti 3 dobra i 2 neispravna. Broj načina odabira dva neispravna dijela od 4 postojeća neispravna jednak je broju kombinacija 4 puta 2:
Broj načina odabira tri kvalitetna dijela od 14 dostupnih kvalitetnih dijelova jednak je
![]() .
.
Bilo koja skupina dobrih dijelova može se kombinirati s bilo kojom skupinom neispravnih dijelova, dakle ukupni broj kombinacija m iznosi
Tražena vjerojatnost događaja A jednaka je omjeru broja ishoda m povoljnih za taj događaj prema broju n svih jednako mogućih neovisnih ishoda:
![]() .
.
Zbroj konačnog broja događaja je događaj koji se sastoji od pojave barem jednog od njih.
Zbroj dva događaja označava se simbolom A+B, a zbroj n događaja sa simbolom A 1 +A 2 + : +A n.
Teorem zbrajanja vjerojatnosti.
Vjerojatnost zbroja dvaju nekompatibilnih događaja jednaka je zbroju vjerojatnosti tih događaja.
Korolar 1. Ako događaji A 1, A 2, :,A n čine potpuni sustav, tada je zbroj vjerojatnosti tih događaja jednak jedan.
Korolar 2. Zbroj vjerojatnosti suprotnih događaja i jednak je jedinici.
![]() .
.
Problem 1. Postoji 100 srećki. Poznato je da 5 ulaznica osvaja po 20.000 rubalja, 10 ulaznica osvaja 15.000 rubalja, 15 ulaznica osvaja 10.000 rubalja, 25 ulaznica osvaja 2.000 rubalja. a za ostalo ništa. Pronađite vjerojatnost da će kupljeni listić dobiti dobitak od najmanje 10 000 rubalja.
Riješenje. Neka su A, B i C događaji koji se sastoje u činjenici da kupljeni listić dobiva dobitak od 20 000, 15 000 odnosno 10 000 rubalja. budući da su događaji A, B i C nekompatibilni, onda
Zadatak 2. Dopisni odjel tehničke škole prima testove iz matematike iz gradova A, B I S. Vjerojatnost da dobijete test od grada A jednako 0,6, od grada U- 0,1. Nađite vjerojatnost da će sljedeći test doći iz grada S.
Mama je oprala okvir
Na kraju dugih ljetnih praznika, vrijeme je da se polako vratimo višoj matematici i svečano otvorimo praznu Verdov datoteku kako bismo počeli stvarati novu sekciju - . Priznajem, prvi redovi nisu laki, ali prvi korak je pola puta, stoga predlažem svima da pažljivo prouče uvodni članak, nakon čega će svladavanje teme biti 2 puta lakše! Uopće ne pretjerujem. …Uoči idućeg 1. rujna sjećam se prvog razreda i početnice…. Slova tvore slogove, slogovi tvore riječi, riječi tvore kratke rečenice - Mama je prala okvir. Savladavanje statistike prometa i matematike jednostavno je poput učenja čitanja! Međutim, za to morate znati ključne pojmove, koncepte i oznake, kao i neka specifična pravila, koji su predmet ove lekcije.
Ali prvo primite moje čestitke za početak (nastavak, završetak, označite prikladnim) školske godine i primite dar. Najbolji dar je knjiga, a za samostalan rad preporučujem sljedeću literaturu:
1) Gmurman V.E. Teorija vjerojatnosti i matematička statistika
Legendarni udžbenik koji je doživio više od deset ponovljenih izdanja. Odlikuje se razumljivošću i krajnje jednostavnom prezentacijom gradiva, a prva su poglavlja potpuno dostupna, mislim, već učenicima 6.-7.
2) Gmurman V.E. Vodič za rješavanje problema iz teorije vjerojatnosti i matematičke statistike
Knjiga rješenja istog Vladimira Efimoviča s detaljnim primjerima i problemima.
OBAVEZNO preuzmite obje knjige s interneta ili nabavite njihove papirnate originale! Radit će i verzija iz 60-ih i 70-ih, što je još bolje za glupane. Iako fraza "teorija vjerojatnosti za lutke" zvuči prilično smiješno, budući da je gotovo sve ograničeno na elementarne aritmetičke operacije. Preskaču, međutim, na mjestima izvedenice I integrali, ali to je samo mjestimično.
Pokušat ću postići istu jasnoću izlaganja, ali moram upozoriti da je moj tečaj usmjeren na rješavanje problema a teorijski proračuni svedeni su na minimum. Dakle, ako trebate detaljnu teoriju, dokaze teorema (teorema-teorema!), molimo pogledajte udžbenik. Pa tko hoće naučiti rješavati probleme u teoriji vjerojatnosti i matematičkoj statistici u najkraćem mogućem roku, prati me!
Dovoljno za pocetak =)
Dok čitate članke, preporučljivo je upoznati se (barem ukratko) s dodatnim zadacima razmatranih vrsta. Na stranici Gotova rješenja za višu matematiku Bit će objavljeni odgovarajući pdf-ovi s primjerima rješenja. Također će biti pružena značajna pomoć IDZ 18.1 Rjabuško(jednostavnije) i riješen IDZ prema Čudesenkovoj zbirci(teže).
1) Iznos dva događaja, a događaj se naziva da će se dogoditi ili događaj ili događaj ili oba događaja u isto vrijeme. U slučaju da događaji nekompatibilan, posljednja opcija nestaje, odnosno može se pojaviti ili događaj ili događaj .
Pravilo vrijedi i za veći broj pojmova, npr. događaj ![]() je ono što će se dogoditi najmanje jedan od događaja
je ono što će se dogoditi najmanje jedan od događaja ![]() , A ako su događaji nespojivi – onda jedno i samo jedno događaj od ovog iznosa: ili događaj, ili događaj, ili događaj, ili događaj, ili događaj .
, A ako su događaji nespojivi – onda jedno i samo jedno događaj od ovog iznosa: ili događaj, ili događaj, ili događaj, ili događaj, ili događaj .
Ima dosta primjera:
Događaji (kada bacate kocku, 5 bodova se neće pojaviti) su ono što će se pojaviti ili 1, ili 2, ili 3, ili 4, ili 6 bodova.
Događaj (će ispasti ne više dvije točke) je da će se pojaviti 1 ili 2bodova.
Događaj ![]() (bit će paran broj bodova) je ono što se pojavljuje ili 2 ili 4 ili 6 bodova.
(bit će paran broj bodova) je ono što se pojavljuje ili 2 ili 4 ili 6 bodova.
Događaj je da se iz špila izvuče crveni karton (srce). ili tambura), te priredbu ![]() – da će se “slika” izvući (jack ili dama ili kralj ili as).
– da će se “slika” izvući (jack ili dama ili kralj ili as).
Malo zanimljiviji je slučaj sa zajedničkim događanjima:
Događaj je da će se iz špila izvući tref ili sedam ili sedam klubova Prema gornjoj definiciji, barem nešto- ili bilo koji tref ili bilo koja sedmorka ili njihovo "presjecište" - tref sedmorka. Lako je izračunati da ovaj događaj odgovara 12 elementarnih ishoda (9 tref karata + 3 preostale sedmice).
Događaj je da će doći sutra u 12.00 BAREM JEDAN od skupnih zajedničkih događaja, naime:
– ili će biti samo kiša / samo grmljavina / samo sunce;
– ili će se dogoditi samo neki par događaja (kiša + grmljavina / kiša + sunce / grmljavina + sunce);
– ili će se sva tri događaja pojaviti istovremeno.
Odnosno, događaj uključuje 7 mogućih ishoda.
Drugi stup algebre događaja:
2) Posao dva događaja i nazvati događaj koji se sastoji od zajedničkog događanja tih događaja, drugim riječima, množenje znači da će pod nekim okolnostima biti I događaj, I događaj . Slična tvrdnja vrijedi i za veći broj događaja, npr. djelo implicira da će se pod određenim uvjetima dogoditi I događaj, I događaj, I događaj, …, I događaj .
Razmotrimo test u kojem se bacaju dva novčića i sljedeći događaji:
– glave će se pojaviti na 1. novčiću;
– 1. novčić će ispasti glave;
– glave će se pojaviti na 2. novčiću;
– 2. novčić će ispasti glave.
Zatim:
I na 2.) pojavit će se glave;
– događaj je da je na obje kovanice (1 I na 2.) to će biti glave;
– događaj je da će 1. novčić ispasti glave I 2. novčić je rep;
– događaj je da će 1. novčić ispasti glave I na 2. novčiću je orao.
Lako je vidjeti da događaji nekompatibilan (jer npr. ne mogu biti 2 glave i 2 repa u isto vrijeme) i oblik puna grupa (budući da je uzeto u obzir svi mogući ishodi bacanja dva novčića). Rezimirajmo ove događaje: . Kako protumačiti ovaj unos? Vrlo jednostavno – množenje znači logički veznik I, i dodatak – ILI. Dakle, iznos je lako pročitati razumljivim ljudskim jezikom: „pojavit će se dvije glave ili dvije glave ili 1. novčić će ispasti glave I na 2. repovima ili 1. novčić će ispasti glave I na 2. novčiću je orao"
Ovo je bio primjer kada u jednom testu radi se o nekoliko predmeta, u ovom slučaju o dva novčića. Još jedna uobičajena shema u praktičnim problemima je ponovno testiranje , kada se, na primjer, ista kocka baci 3 puta zaredom. Kao demonstraciju, razmotrite sljedeće događaje:
– u 1. bacanju dobit ćete 4 boda;
– u 2. bacanju dobit ćete 5 bodova;
– u 3. bacanju dobit ćete 6 bodova.
Zatim događaj ![]() je da ćete u 1. bacanju dobiti 4 boda I u 2. bacanju dobit ćete 5 bodova I na 3. bacanju ćete dobiti 6 bodova. Očito je da će u slučaju kocke biti znatno više kombinacija (ishoda) nego da bacamo novčić.
je da ćete u 1. bacanju dobiti 4 boda I u 2. bacanju dobit ćete 5 bodova I na 3. bacanju ćete dobiti 6 bodova. Očito je da će u slučaju kocke biti znatno više kombinacija (ishoda) nego da bacamo novčić.
...Razumijem da možda primjeri koji se analiziraju nisu previše zanimljivi, ali to su stvari koje se često susreću u problemima i od njih se ne može pobjeći. Osim novčića, kocke i špila karata očekuju vas urne s raznobojnim kuglicama, nekoliko anonimaca koji pucaju u metu i neumorni radnik koji neprestano brusi neke detalje =)
Vjerojatnost događaja
Vjerojatnost događaja je središnji koncept teorije vjerojatnosti. ...Ubitačno logično, ali negdje smo morali početi =) Postoji nekoliko pristupa njegovoj definiciji:
;
Geometrijska definicija vjerojatnosti
;
Statistička definicija vjerojatnosti
.
U ovom ću se članku usredotočiti na klasičnu definiciju vjerojatnosti, koja se najčešće koristi u obrazovnim zadacima.
Oznake. Vjerojatnost određenog događaja označena je velikim latiničnim slovom, a sam događaj uzet je u zagradu i služi kao svojevrsni argument. Na primjer:
Također, malo slovo se naširoko koristi za označavanje vjerojatnosti. Konkretno, možete napustiti glomazne oznake događaja i njihove vjerojatnosti ![]() u korist sljedećeg stila::
u korist sljedećeg stila::
– vjerojatnost da će bacanje novčića rezultirati glavama;
– vjerojatnost da će bacanje kocke rezultirati s 5 bodova;
– vjerojatnost da će iz špila biti izvučena karta tref boje.
Ova je opcija popularna pri rješavanju praktičnih problema jer vam omogućuje značajno smanjenje snimanja rješenja. Kao iu prvom slučaju, ovdje je prikladno koristiti indekse/superskripte koji govore.
Svi su odavno pogodili brojeve koje sam upravo zapisao gore, a sada ćemo saznati kako su ispali:
Klasična definicija vjerojatnosti:
Vjerojatnost da se događaj dogodi u određenom testu naziva se omjer, gdje je:
– ukupan broj svih jednako moguće, elementarni ishode ovog testa, koji oblikuju puna grupa događaja;
- količina elementarni ishodi, povoljan događaj.
Prilikom bacanja novčića mogu ispasti glave ili repići - ovi se događaji formiraju puna grupa, dakle, ukupan broj ishoda; u isto vrijeme, svaki od njih elementarni I jednako moguće. Događaj favorizira ishod (glave). Prema klasičnoj definiciji vjerojatnosti: ![]() .
.
Slično, kao rezultat bacanja kocke, mogu se pojaviti elementarni podjednako mogući ishodi, tvoreći potpunu grupu, a događaj je favoriziran jednim ishodom (bacanje petice). Zato: ![]() OVO SE NE PRIHVAĆA RADITI (iako nije zabranjeno procjenjivati postotke u glavi).
OVO SE NE PRIHVAĆA RADITI (iako nije zabranjeno procjenjivati postotke u glavi).
Uobičajeno je koristiti razlomke jedinice, i, očito, vjerojatnost može varirati unutar . Štoviše, ako je , tada je događaj nemoguće, ako - pouzdan, a ako , tada govorimo o slučajan događaj.
! Ako tijekom rješavanja bilo kojeg problema dobijete neku drugu vrijednost vjerojatnosti, potražite pogrešku!
U klasičnom pristupu određivanju vjerojatnosti, ekstremne vrijednosti (nula i jedan) dobivaju se potpuno istim razmišljanjem. Neka se nasumično izvuče 1 kuglica iz određene urne koja sadrži 10 crvenih kuglica. Razmotrite sljedeće događaje:
u jednom pokusu neće se dogoditi događaj male mogućnosti.
Zbog toga nećete osvojiti jackpot na lutriji ako je vjerojatnost tog događaja, recimo, 0,00000001. Da, da, to ste vi - s jedinom ulaznicom u određenoj tiraži. No, veći broj ulaznica i veći broj izvlačenja neće vam puno pomoći. ...Kad drugima pričam o tome, gotovo uvijek čujem kao odgovor: "ali netko pobjeđuje." U redu, onda napravimo sljedeći eksperiment: danas ili sutra kupite srećku za bilo koju lutriju (ne odgađajte!). A ako osvojite... pa, barem više od 10 kilorublja, svakako se prijavite - objasnit ću vam zašto se to dogodilo. Za postotak, naravno =) =)
Ali ne treba biti žalostan, jer postoji suprotno načelo: ako je vjerojatnost nekog događaja vrlo blizu jedinici, tada će u jednom pokušaju gotovo sigurno dogodit će se. Stoga, prije skoka s padobranom, nema potrebe za strahom, naprotiv, nasmijte se! Uostalom, moraju se dogoditi potpuno nezamislive i fantastične okolnosti da bi oba padobrana otkazala.
Iako je sve ovo lirika, jer ovisno o sadržaju događaja prvi princip može ispasti vedar, a drugi – tužni; ili su čak oba paralelna.
Možda je to dovoljno za sada, na nastavi Klasični problemi vjerojatnosti izvući ćemo maksimum iz formule. U završnom dijelu ovog članka razmotrit ćemo jedan važan teorem:
Zbroj vjerojatnosti događaja koji čine potpunu skupinu jednak je jedan. Grubo govoreći, ako događaji čine potpunu skupinu, tada će se sa 100% vjerojatnošću jedan od njih dogoditi. U najjednostavnijem slučaju, potpunu skupinu čine suprotni događaji, na primjer:
– kao rezultat bacanja novčića pojavit će se glave;
– rezultat bacanja novčića bit će glave.
Prema teoremu: ![]()
Potpuno je jasno da su ovi događaji jednako mogući i da su im vjerojatnosti iste ![]() .
.
Zbog jednakosti vjerojatnosti često se nazivaju jednako mogući događaji jednako vjerojatno . A evo i jezičke za određivanje stupnja alkoholiziranosti =)
Primjer s kockom: događaji su suprotni, dakle ![]() .
.
Teorem koji se razmatra prikladan je jer vam omogućuje brzo pronalaženje vjerojatnosti suprotnog događaja. Dakle, ako je poznata vjerojatnost da je petica bačena, lako je izračunati vjerojatnost da nije bačena:
![]()
Ovo je puno jednostavnije od zbrajanja vjerojatnosti pet osnovnih ishoda. Za elementarne ishode, usput, ovaj teorem je također istinit:
. Na primjer, ako je vjerojatnost da će strijelac pogoditi metu, onda je vjerojatnost da će promašiti.
! U teoriji vjerojatnosti nepoželjno je koristiti slova u bilo koje druge svrhe.
U čast Dana znanja, neću zadavati domaću zadaću =), ali je vrlo važno da možete odgovoriti na sljedeća pitanja:
– Koje vrste događaja postoje?
– Što je slučajnost i jednaka mogućnost događaja?
– Kako shvaćate pojmove kompatibilnost/nespojivost događaja?
– Što je potpuna skupina događaja, suprotnih događaja?
– Što znači zbrajanje i množenje događaja?
– Što je bit klasične definicije vjerojatnosti?
– Zašto je teorem za zbrajanje vjerojatnosti događaja koji tvore potpunu grupu koristan?
Ne, ne trebate ništa trpati, ovo su samo osnove teorije vjerojatnosti - neka vrsta početnice koja će vam brzo stati u glavu. A kako bi se to dogodilo što je prije moguće, predlažem da se upoznate s lekcijama
Teorija vjerojatnosti i matematička statistika
1. TEORIJSKI DIO
1. Konvergencija nizova slučajnih varijabli i distribucija vjerojatnosti
U teoriji vjerojatnosti imamo posla s različitim tipovima konvergencije slučajnih varijabli. Razmotrimo sljedeće glavne tipove konvergencije: po vjerojatnosti, s vjerojatnošću jedan, po redu p, po distribuciji.
Neka su,... slučajne varijable definirane na nekom prostoru vjerojatnosti (, F, P).
Definicija 1. Za niz slučajnih varijabli, ... kaže se da konvergira u vjerojatnosti prema slučajnoj varijabli (oznaka:), ako je za bilo koji > 0
Definicija 2. Za niz slučajnih varijabli, ... kaže se da konvergira s vjerojatnošću jedan (gotovo sigurno, gotovo posvuda) prema slučajnoj varijabli ako
oni. ako skup ishoda za koje () ne konvergiraju u () ima nultu vjerojatnost.
Ovaj tip konvergencije označava se na sljedeći način: , ili, ili.
Definicija 3. Niz slučajnih varijabli ... naziva se konvergent srednje vrijednosti reda p, 0< p < , если
Definicija 4. Za niz slučajnih varijabli... kaže se da konvergira u distribuciji prema slučajnoj varijabli (oznaka:) ako za bilo koju ograničenu kontinuiranu funkciju
Konvergencija u distribuciji slučajnih varijabli definirana je samo u smislu konvergencije njihovih funkcija distribucije. Stoga ima smisla govoriti o ovoj vrsti konvergencije čak i kada su slučajne varijable navedene u različitim prostorima vjerojatnosti.
Teorem 1.
a) Da bi bilo (P-a.s.), potrebno je i dovoljno da za bilo koje > 0
) Niz () je fundamentalan s vjerojatnošću jedan ako i samo ako za bilo koji > 0.
Dokaz.
a) Neka je A = (: |- | ), A = A. Tada
Stoga je iskaz a) rezultat sljedećeg lanca implikacija:
P(: )= 0 P() = 0 = 0 P(A) = 0, m 1 P(A) = 0, > 0 P() 0, n 0, > 0 P( ) 0,
n 0, > 0.) Označimo = (: ), = . Tada (: (()) nije fundamentalno ) = i na isti način kao u a) pokazuje se da (: (()) nije fundamentalno ) = 0 P( ) 0, n.
Teorem je dokazan
Teorem 2. (Cauchyjev kriterij za gotovo sigurnu konvergenciju)
Da bi niz slučajnih varijabli () bio konvergentan s vjerojatnošću jedan (nekoj slučajnoj varijabli), potrebno je i dovoljno da bude fundamentalan s vjerojatnošću jedan.
Dokaz.
Ako, onda +
iz čega slijedi nužnost uvjeta teorema.
Sada neka niz () bude fundamentalan s vjerojatnošću jedan. Označimo L = (: (()) nije fundamentalno). Tada je za sve niz brojeva () fundamentalan i, prema Cauchyjevom kriteriju za nizove brojeva, () postoji. Stavimo
Ova definirana funkcija je slučajna varijabla i.
Teorem je dokazan.
2 Metoda karakterističnih funkcija
Metoda karakterističnih funkcija jedan je od glavnih alata analitičkog aparata teorije vjerojatnosti. Uz slučajne varijable (uzimajući realne vrijednosti), teorija karakterističnih funkcija zahtijeva korištenje slučajnih varijabli složenih vrijednosti.
Mnoge definicije i svojstva koja se odnose na slučajne varijable lako se prenose na složeni slučaj. Dakle, matematičko očekivanje M ?slučajna varijabla kompleksne vrijednosti ?=?+?? smatra se sigurnim ako su određena matematička očekivanja M ?ih ?. U ovom slučaju, po definiciji pretpostavljamo M ?= M ? + ?M ?. Iz definicije neovisnosti slučajnih elemenata proizlazi da kompleksno vrijedne veličine ?1 =?1+??1 , ?2=?2+??2neovisni ako i samo ako su parovi slučajnih varijabli neovisni ( ?1 , ?1) i ( ?2 , ?2), ili, što je isto, neovisno ?-algebra F ?1, ?1 i F ?2, ?2.
Uz prostor L 2realne slučajne varijable s konačnim sekundnim momentom, možemo uvesti Hilbertov prostor slučajnih varijabli kompleksnih vrijednosti ?=?+?? s M | ?|2?|2= ?2+?2, i skalarni produkt ( ?1 , ?2)= M ?1?2¯ , Gdje ?2¯ - kompleksno konjugirana slučajna varijabla.
U algebarskim operacijama, vektori Rn se tretiraju kao algebarski stupci,
Kao vektori reda, a* - (a1,a2,…,an). Ako je Rn , tada će se njihov skalarni produkt (a,b) shvatiti kao veličina. Jasno je da
Ako su aRn i R=||rij|| je onda matrica reda nhn
Definicija 1. Neka je F = F(x1,....,xn) - n-dimenzionalna funkcija distribucije u (, ()). Njegova karakteristična funkcija naziva se funkcija
Definicija 2 . Ako? = (?1,…,?n) je slučajni vektor definiran na prostoru vjerojatnosti s vrijednostima u, tada se njegova karakteristična funkcija naziva funkcija
gdje je F? = F?(h1,….,hn) - funkcija vektorske distribucije?=(?1,…, ?n).
Ako funkcija distribucije F(x) ima gustoću f = f(x), tada
U ovom slučaju, karakteristična funkcija nije ništa drugo nego Fourierova transformacija funkcije f(x).
Iz (3) slijedi da se karakteristična funkcija ??(t) slučajnog vektora također može definirati jednakošću
Osnovna svojstva karakterističnih funkcija (u slučaju n=1).
Neka bude? = ?(?) - slučajna varijabla, F? =F? (x) je njegova distribucijska funkcija i karakteristična je funkcija.
Treba napomenuti da ako, onda.
Doista,
pri čemu smo iskoristili činjenicu da je matematičko očekivanje umnoška neovisnih (omeđenih) slučajnih varijabli jednako umnošku njihovih matematičkih očekivanja.
Svojstvo (6) je ključno pri dokazivanju graničnih teorema za sume nezavisnih slučajnih varijabli metodom karakterističnih funkcija. S tim u vezi, distribucijska funkcija se izražava kroz distribucijske funkcije pojedinih članova na mnogo složeniji način, naime, gdje znak * označava konvoluciju distribucija.
Svaka funkcija distribucije u može se pridružiti slučajnoj varijabli koja ima tu funkciju kao funkciju distribucije. Stoga se pri prikazu svojstava karakterističnih funkcija možemo ograničiti na razmatranje karakterističnih funkcija slučajnih varijabli.
Teorem 1. Neka bude? - slučajna varijabla s funkcijom raspodjele F=F(x) i - njezina karakteristična funkcija.
Događaju se sljedeća svojstva:
) je uniformno neprekidan u;
) je funkcija realne vrijednosti ako i samo ako je distribucija F simetrična
)ako za neki n? 1, onda za sve postoje izvodnice i
)Ako postoji i konačan je, tada
) Neka za sve n ? 1 i
onda za sve |t| Sljedeći teorem pokazuje da karakteristična funkcija jednoznačno određuje funkciju distribucije. Teorem 2 (jedinstvenost). Neka su F i G dvije funkcije distribucije s istom karakterističnom funkcijom, tj. za sve Teorem kaže da se funkcija distribucije F = F(x) može jedinstveno obnoviti iz svoje karakteristične funkcije. Sljedeći teorem daje eksplicitan prikaz funkcije F u smislu. Teorem 3 (formula generalizacije). Neka je F = F(x) funkcija distribucije i neka je njezina karakteristična funkcija. a) Za bilo koje dvije točke a, b (a< b), где функция F = F(х) непрерывна, ) Ako tada funkcija raspodjele F(x) ima gustoću f(x), Teorem 4. Da bi komponente slučajnog vektora bile neovisne, potrebno je i dovoljno da njegova karakteristična funkcija bude umnožak karakterističnih funkcija komponenti: Bochner-Khinchinov teorem .
Neka je kontinuirana funkcija. Da bi bila karakteristična potrebno je i dovoljno da bude nenegativno određena, odnosno za bilo koje realne t1, ... , tn i bilo koje kompleksne brojeve Teorem 5. Neka je karakteristična funkcija slučajne varijable. a) Ako je za neke, onda je slučajna varijabla rešetka sa korakom, tj ) Ako je za dvije različite točke, gdje je iracionalan broj, onda je to slučajna varijabla? je degeneriran: gdje je a neka konstanta. c) Ako, onda je to slučajna varijabla? degenerirati. 1.3 Središnji granični teorem za neovisne identično distribuirane slučajne varijable Neka je () niz neovisnih, identično raspoređenih slučajnih varijabli. Očekivanje M= a, varijanca D= , S = , a F(h) je funkcija distribucije normalnog zakona s parametrima (0,1). Uvedimo još jedan niz slučajnih varijabli Teorema. Ako je 0<<, то при n P(< x) Ф(х) равномерно относительно х (). U tom slučaju niz () se naziva asimptotski normalan. Iz činjenice da je M = 1 i iz teorema o kontinuitetu slijedi da, uz slabu konvergenciju, FM f() Mf() za bilo koje kontinuirano ograničeno f, postoji i konvergencija M f() Mf() za bilo koje kontinuirano f , tako da je |f(x)|< c(1+|x|) при каком-нибудь. Dokaz. Uniformna konvergencija ovdje je posljedica slabe konvergencije i kontinuiteta F(x). Nadalje, bez gubitka općenitosti, možemo pretpostaviti a = 0, jer bismo inače mogli uzeti u obzir niz (), a niz () se ne bi promijenio. Dakle, da bi se dokazala tražena konvergencija dovoljno je pokazati da je (t) e kada je a = 0. Imamo (t) = , gdje je =(t). Kako M postoji, onda dekompozicija postoji i vrijedi Prema tome, za n Teorem je dokazan. 1.4 Glavni zadaci matematičke statistike, njihov kratak opis Utvrđivanje obrazaca koji upravljaju masovnim slučajnim pojavama temelji se na proučavanju statističkih podataka – rezultata promatranja. Prvi zadatak matematičke statistike je ukazati na načine prikupljanja i grupiranja statističkih informacija. Drugi zadatak matematičke statistike je razviti metode za analizu statističkih podataka, ovisno o ciljevima proučavanja. Pri rješavanju bilo kojeg problema matematičke statistike postoje dva izvora informacija. Prvi i najodređeniji (eksplicitni) je rezultat opažanja (eksperiment) u obliku uzorka iz neke opće populacije skalarne ili vektorske slučajne varijable. U tom slučaju veličina uzorka n može biti fiksna ili se može povećavati tijekom eksperimenta (tj. mogu se koristiti tzv. postupci sekvencijalne statističke analize). Drugi izvor su sve apriorne informacije o svojstvima predmeta koji se proučava, akumulirane do sadašnjeg trenutka. Formalno, količina apriornih informacija ogleda se u početnom statističkom modelu koji se bira prilikom rješavanja problema. No, nema potrebe govoriti o približnom određivanju u uobičajenom smislu vjerojatnosti nekog događaja na temelju rezultata pokusa. Pod približnim određivanjem bilo koje količine obično se podrazumijeva da je moguće naznačiti granice pogreške unutar kojih se pogreška neće pojaviti. Učestalost događaja je slučajna za bilo koji broj eksperimenata zbog slučajnosti rezultata pojedinačnih eksperimenata. Zbog slučajnosti rezultata pojedinih eksperimenata, učestalost može značajno odstupati od vjerojatnosti događaja. Stoga, definiranjem nepoznate vjerojatnosti događaja kao učestalosti tog događaja tijekom velikog broja eksperimenata, ne možemo naznačiti granice pogreške i jamčiti da pogreška neće prijeći te granice. Stoga se u matematičkoj statistici obično ne govori o približnim vrijednostima nepoznatih veličina, već o njihovim prikladnim vrijednostima, procjenama. Problem procjene nepoznatih parametara javlja se u slučajevima kada je funkcija distribucije stanovništva poznata do parametra. U tom slučaju potrebno je pronaći statistiku čija bi se uzorkovana vrijednost za razmatranu implementaciju xn slučajnog uzorka mogla smatrati približnom vrijednošću parametra. Statistika čija je vrijednost uzorka za bilo koju realizaciju xn uzeta kao približna vrijednost nepoznatog parametra naziva se točkasta procjena ili jednostavno procjena, i vrijednost je točkaste procjene. Točkasta procjena mora zadovoljiti vrlo specifične zahtjeve kako bi njezina vrijednost uzorka odgovarala stvarnoj vrijednosti parametra. Moguć je i drugi pristup rješavanju problema koji se razmatra: pronaći takve statistike i, s vjerojatnošću? vrijedi sljedeća nejednakost: U ovom slučaju govorimo o intervalnoj procjeni za. Interval naziva se interval pouzdanosti za s koeficijentom pouzdanosti?. Nakon procjene jedne ili druge statističke karakteristike na temelju rezultata eksperimenata, postavlja se pitanje: koliko je konzistentna pretpostavka (hipoteza) da nepoznata karakteristika ima upravo onu vrijednost koja je dobivena kao rezultat njene procjene s eksperimentalnim podacima? Tako nastaje druga važna klasa problema matematičke statistike - problemi provjere hipoteza. U određenom smislu, problem testiranja statističke hipoteze je obrnut od problema procjene parametra. Kada procjenjujemo parametar, ne znamo ništa o njegovoj stvarnoj vrijednosti. Prilikom testiranja statističke hipoteze, iz nekog razloga se pretpostavlja da je njezina vrijednost poznata i potrebno je tu pretpostavku provjeriti na temelju rezultata eksperimenta. U mnogim problemima matematičke statistike razmatraju se nizovi slučajnih varijabli, koji u jednom ili drugom smislu konvergiraju do neke granice (slučajne varijable ili konstante), kada. Stoga su glavni zadaci matematičke statistike razvoj metoda za pronalaženje procjena i proučavanje točnosti njihove aproksimacije karakteristikama koje se procjenjuju te razvoj metoda za testiranje hipoteza. 5. Testiranje statističkih hipoteza: osnovni pojmovi Zadatak razvoja racionalnih metoda za provjeru statističkih hipoteza jedan je od glavnih zadataka matematičke statistike. Statistička hipoteza (ili jednostavno hipoteza) je svaka izjava o vrsti ili svojstvima distribucije slučajnih varijabli opaženih u eksperimentu. Neka postoji uzorak koji je realizacija slučajnog uzorka iz opće populacije čija gustoća distribucije ovisi o nepoznatom parametru. Statističke hipoteze o nepoznatoj stvarnoj vrijednosti parametra nazivaju se parametarske hipoteze. Štoviše, ako je skalar, tada govorimo o jednoparametarskim hipotezama, a ako je vektor, onda govorimo o višeparametarskim hipotezama. Statistička hipoteza se naziva jednostavnom ako ima oblik gdje je određena vrijednost parametra. Statistička hipoteza se naziva složenom ako ima oblik gdje je skup vrijednosti parametara koji se sastoji od više od jednog elementa. U slučaju testiranja dviju jednostavnih statističkih hipoteza oblika gdje su dvije zadane (različite) vrijednosti parametra, prva hipoteza se obično naziva glavna, a druga se naziva alternativna ili konkurentska hipoteza. Kriterij, odnosno statistički kriterij, za provjeru hipoteza je pravilo prema kojem se na temelju uzorka podataka donosi odluka o valjanosti prve ili druge hipoteze. Kriterij je određen pomoću kritičnog skupa, koji je podskup prostora uzorka slučajnog uzorka. Odluka se donosi na sljedeći način: ) ako uzorak pripada kritičnom skupu, odbaciti glavnu hipotezu i prihvatiti alternativnu hipotezu; ) ako uzorak ne pripada kritičnom skupu (tj. pripada komplementu skupa prostoru uzorka), tada se alternativna hipoteza odbacuje, a glavna hipoteza prihvaća. Pri korištenju bilo kojeg kriterija moguće su sljedeće vrste pogrešaka: 1) prihvatiti hipotezu kada je istinita - pogreška prve vrste; )prihvaćanje hipoteze kada je istinita je pogreška tipa II. Vjerojatnosti počinjenja pogrešaka prve i druge vrste označene su sa: gdje je vjerojatnost događaja pod uvjetom da je hipoteza istinita. Navedene vjerojatnosti izračunavaju se pomoću funkcije gustoće distribucije slučajnog uzorka: Vjerojatnost počinjenja pogreške tipa I naziva se i razina značajnosti kriterija. Vrijednost jednaka vjerojatnosti odbacivanja glavne hipoteze kada je istinita naziva se snaga testa. 1.6 Kriterij neovisnosti Postoji uzorak ((XY), ..., (XY)) iz dvodimenzionalne distribucije L s nepoznatom funkcijom distribucije za koju je potrebno provjeriti hipotezu H: , gdje su neke jednodimenzionalne funkcije distribucije. Jednostavan test prilagodbe za hipotezu H može se konstruirati na temelju metodologije. Ova tehnika se koristi za diskretne modele s konačnim brojem ishoda, pa se dogovorimo da slučajna varijabla uzima konačan broj s nekih vrijednosti koje ćemo označiti slovima, a druga komponenta - k vrijednosti. Ako izvorni model ima drugačiju strukturu, tada se moguće vrijednosti slučajnih varijabli preliminarno grupiraju zasebno u prvu i drugu komponentu. U ovom slučaju skup je podijeljen na s intervala, skup vrijednosti na k intervala, a sam skup vrijednosti na N=sk pravokutnika. Označimo s brojem opažanja para (broj elemenata uzorka koji pripadaju pravokutniku, ako su podaci grupirani), tako da. Pogodno je rezultate promatranja složiti u obliku tablice kontingencije dvaju predznaka (tablica 1.1). U primjenama i obično označava dva kriterija po kojima se klasificiraju rezultati promatranja. Neka je P, i=1,…,s, j=1,…,k. Tada hipoteza neovisnosti znači da postoje s+k konstante takve da i, tj. Tablica 1.1 Iznos . . .. . .. . . . . .. . .. . . . . . . . . . . . . . .Iznos . . .n Dakle, hipoteza H se svodi na tvrdnju da su frekvencije (njihov broj je N = sk) raspoređene prema polinomnom zakonu s vjerojatnostima ishoda zadane specifične strukture (vektor vjerojatnosti ishoda p određen je vrijednostima r = s + k-2 nepoznatih parametara. Kako bismo testirali ovu hipotezu, pronaći ćemo procjene najveće vjerojatnosti za nepoznate parametre koji određuju shemu koja se razmatra. Ako je nulta hipoteza točna, tada funkcija vjerojatnosti ima oblik L(p)= gdje množitelj c ne ovisi o nepoznatim parametrima. Odavde, korištenjem Lagrangeove metode neodređenih množitelja, dobivamo da tražene procjene imaju oblik Prema tome, statistika L() at, budući da je broj stupnjeva slobode u graničnoj distribuciji jednak N-1-r=sk-1-(s+k-2)=(s-1)(k-1). Dakle, za dovoljno veliki n, može se koristiti sljedeće pravilo testiranja hipoteze: hipoteza H se odbacuje ako i samo ako t statistička vrijednost izračunata iz stvarnih podataka zadovoljava nejednakost Ovaj kriterij ima asimptotski (na) zadanoj razini značajnosti i naziva se kriterij neovisnosti. 2. PRAKTIČNI DIO 1 Rješenja zadataka o vrstama konvergencije 1. Dokažite da konvergencija gotovo sigurno implicira konvergenciju u vjerojatnosti. Navedite testni primjer da pokažete da obrnuto nije točno. Riješenje. Neka niz slučajnih varijabli gotovo sigurno konvergira prema slučajnoj varijabli x. Dakle, za bilo koga? > 0 Od tad a iz konvergencije xn u x gotovo sigurno slijedi da xn konvergira u x po vjerojatnosti, jer u ovom slučaju Ali suprotna izjava nije istinita. Neka je niz neovisnih slučajnih varijabli s istom funkcijom distribucije F(x), jednak nuli na x? 0 i jednaki za x > 0. Promotrimo niz Ovaj niz konvergira prema nuli u vjerojatnosti, jer teži nuli za bilo koji fiksni? I. Međutim, gotovo sigurno se neće dogoditi konvergencija na nulu. Stvarno teži jedinici, odnosno s vjerojatnošću 1 za bilo koji i n postojat će realizacije u nizu koje prelaze ?. Imajte na umu da u prisutnosti nekih dodatnih uvjeta nametnutih veličinama xn, konvergencija u vjerojatnosti implicira konvergenciju gotovo sigurno. Neka je xn monoton niz. Dokažite da u ovom slučaju konvergencija xn prema x u vjerojatnosti povlači za sobom konvergenciju xn prema x s vjerojatnošću 1. Riješenje. Neka je xn monotono opadajući niz, tj. Da bismo pojednostavili svoje razmišljanje, pretpostavit ćemo da je x º 0, xn ³ 0 za sve n. Neka xn vjerojatno konvergira prema x, ali do konvergencije gotovo sigurno neće doći. Postoji li onda? > 0, tako da za sve n Ali ono što je rečeno također znači da za sve n što je u suprotnosti s konvergencijom xn prema x u vjerojatnosti. Dakle, za monotoni niz xn, koji po vjerojatnosti konvergira prema x, također konvergira s vjerojatnošću 1 (gotovo sigurno). Neka niz xn konvergira prema x po vjerojatnosti. Dokažite da je iz ovog niza moguće izolirati niz koji konvergira k x s vjerojatnošću 1 at. Riješenje. Dopustiti biti neki niz pozitivnih brojeva, i neka i biti pozitivni brojevi tako da niz. Konstruirajmo niz indeksa n1 Zatim serija Budući da niz konvergira, onda za bilo koji? > 0 ostatak niza teži nuli. Ali tada teži nuli i Dokažite da konvergencija u prosjeku bilo kojeg pozitivnog reda implicira konvergenciju u vjerojatnosti. Navedite primjer koji pokazuje da obrnuto nije točno. Riješenje. Neka niz xn konvergira do vrijednosti x u prosjeku reda p > 0, tj Upotrijebimo generaliziranu Chebyshevljevu nejednakost: za proizvoljne? > 0 i p > 0 Usmjeravajući i uzimajući u obzir to, dobivamo to to jest, xn konvergira prema x po vjerojatnosti. Međutim, konvergencija u vjerojatnosti ne povlači za sobom konvergenciju u prosjeku reda p > 0. To je ilustrirano sljedećim primjerom. Razmotrimo prostor vjerojatnosti áW, F, Rñ, gdje je F = B Borelova s-algebra, R Lebesgueova mjera. Definirajmo niz slučajnih varijabli na sljedeći način: Niz xn konvergira prema 0 po vjerojatnosti, jer ali za svaki p > 0 odnosno neće konvergirati u prosjeku. Neka, što za sve n . Dokažite da u tom slučaju xn konvergira k x u srednjem kvadratu. Riješenje. Imajte na umu da... Uzmimo procjenu za. Razmotrimo slučajnu varijablu. Neka bude? - proizvoljan pozitivan broj. Zatim na i na. Ako, onda i. Stoga, . A zato? proizvoljno mali i tada na, to jest, u srednjem kvadratu. Dokažite da ako xn konvergira prema x po vjerojatnosti, tada dolazi do slabe konvergencije. Navedite testni primjer da pokažete da obrnuto nije točno. Riješenje. Dokažimo da ako, onda je u svakoj točki x, koja je točka kontinuiteta (ovo je nužan i dovoljan uvjet za slabu konvergenciju), funkcija raspodjele vrijednosti xn, i - vrijednosti x. Neka je x točka kontinuiteta funkcije F. Ako, tada je barem jedna od nejednakosti ili istinita. Zatim Slično, za barem jednu od nejednakosti ili i Ako, onda za onoliko malo koliko želite? > 0 postoji N takav da za sve n > N S druge strane, ako je x točka kontinuiteta, je li moguće pronaći ovako nešto? > 0, što za proizvoljno male Dakle, koliko god želite? i postoji N takav da je za n >N ili, što je isto, To znači da se konvergencija odvija u svim točkama kontinuiteta. Prema tome, slaba konvergencija slijedi iz konvergencije u vjerojatnosti. Obratna tvrdnja, općenito govoreći, ne vrijedi. Da bismo to provjerili, uzmimo niz slučajnih varijabli koje nisu jednake konstantama s vjerojatnošću 1 i imaju istu funkciju distribucije F(x). Pretpostavljamo da su za svih n količine i neovisne. Očito dolazi do slabe konvergencije, budući da svi članovi niza imaju istu funkciju distribucije. Smatrati: |Iz neovisnosti i identične distribucije vrijednosti proizlazi da Odaberimo između svih funkcija distribucije nedegeneriranih slučajnih varijabli takvu F(x) koja će biti različita od nule za sve dovoljno male ?. Tada ne teži nuli s neograničenim rastom n i neće doći do konvergencije u vjerojatnosti. 7. Neka postoji slaba konvergencija, gdje uz vjerojatnost 1 postoji konstanta. Dokažite da će u tom slučaju konvergirati prema in vjerojatnosti. Riješenje. Neka je vjerojatnost 1 jednaka a. Tada slaba konvergencija znači konvergenciju za bilo koji. Pošto, zatim na i na. Odnosno, na i na. Slijedi da za bilo koga? > 0 vjerojatnosti teže nuli pri. To znači da teži nuli pri, odnosno konvergira prema vjerojatnosti. 2.2 Rješavanje problema na centralnom grijanju Vrijednost gama funkcije G(x) pri x= izračunava se Monte Carlo metodom. Nađimo minimalni broj potrebnih testova da s vjerojatnošću od 0,95 možemo očekivati da će relativna pogreška izračuna biti manja od jedan posto. Za točnost koju imamo Poznato je da Izmjenom (1) dolazimo do integrala po konačnom intervalu: Kod nas, dakle Kao što se može vidjeti, može se predstaviti u obliku gdje, i ravnomjerno je raspoređen na. Neka se provedu statistički testovi. Tada je statistički analog kvantitet gdje su neovisne slučajne varijable s uniformnom distribucijom. pri čemu Iz CLT-a slijedi da je asimptotski normalan s parametrima. To znači da minimalni broj testova koji s vjerojatnošću osigurava relativnu pogrešku izračuna nije veći od jednakog. Razmatramo niz od 2000 neovisnih identično distribuiranih slučajnih varijabli s matematičkim očekivanjem od 4 i varijancom od 1,8. Aritmetička sredina ovih veličina je slučajna varijabla. Odredite vjerojatnost da će slučajna varijabla poprimiti vrijednost u intervalu (3,94; 4,12). Neka je …,… niz neovisnih slučajnih varijabli koje imaju istu distribuciju s M=a=4 i D==1,8. Tada je CLT primjenjiv na niz (). Slučajna vrijednost Vjerojatnost da će uzeti vrijednost u intervalu (): Za n=2000, 3,94 i 4,12 dobivamo 3. Testiranje hipoteza pomoću kriterija neovisnosti Kao rezultat istraživanja utvrđeno je da 782 svijetlookih očeva imaju i svijetlooke sinove, a 89 svijetlookih očeva ima tamnooke sinove. 50 tamnookih očeva također ima tamnooke sinove, a 79 tamnookih očeva ima svijetlooke sinove. Postoji li veza između boje očiju očeva i boje očiju njihovih sinova? Uzmite da je razina pouzdanosti 0,99. Tablica 2.1 Djeca Očevi SumaSvijetlookiTamnookiSvijetlooki78279861Tamnooki8950139Zbroj8711291000 H: Nema veze između boje očiju djece i očeva. H: Postoji veza između boje očiju djece i očeva. s=k=2 =90.6052 sa 1 stupnjem slobode Izračuni su napravljeni u Mathematici 6. Kako je > , onda hipotezu H o nepostojanju veze između boje očiju očeva i djece na razini značajnosti treba odbaciti i prihvatiti alternativnu hipotezu H. Navedeno je da učinak lijeka ovisi o načinu primjene. Provjerite ovu tvrdnju pomoću podataka prikazanih u tablici. 2.2 Uzmite razinu pouzdanosti 0,95. Tablica 2.2 Rezultat Metoda primjene ABC Nepovoljno 111716 Povoljno 202319 Riješenje. Da bismo riješili ovaj problem, koristit ćemo tablicu kontingencije od dvije karakteristike. Tablica 2.3 Rezultat Način prijave Iznos ABC Nepovoljno 11171644 Povoljno 20231962 Iznos 314035106 H: učinak lijekova ne ovisi o načinu primjene H: učinak lijekova ovisi o načinu primjene Statistika se izračunava pomoću sljedeće formule s=2, k=3, =0,734626 sa 2 stupnja slobode. Izračuni napravljeni u Mathematici 6 Iz distribucijskih tablica nalazimo da. Jer< , то гипотезу H, про отсутствия зависимости действия лекарств от способа применения, при уровне значимости, следует принять. Zaključak U ovom radu prikazani su teorijski izračuni iz odjeljka “Kriterij neovisnosti”, kao i “Granični teoremi teorije vjerojatnosti”, kolegija “Teorija vjerojatnosti i matematička statistika”. Tijekom rada u praksi je ispitan kriterij neovisnosti; Također, za zadane nizove nezavisnih slučajnih varijabli provjerena je ispunjenost središnjeg graničnog teorema. Ovaj rad mi je pomogao poboljšati poznavanje ovih dijelova teorije vjerojatnosti, rad s literarnim izvorima i čvrsto ovladati tehnikom provjere kriterija neovisnosti. probabilistic statistička hipoteza teorem Popis poveznica 1. Zbirka zadataka iz teorije vjerojatnosti s rješenjima. uč. dodatak / Ed. V.V. Semenets. - Kharkov: KhTURE, 2000. - 320 str. Gikhman I.I., Skorokhod A.V., Yadrenko M.I. Teorija vjerojatnosti i matematička statistika. - K.: Vishcha škola, 1979. - 408 str. Ivchenko G.I., Medvedev Yu.I., Matematička statistika: Udžbenik. dodatak za fakultete. - M.: Viši. škola, 1984. - 248 str., . Matematička statistika: Udžbenik. za sveučilišta / V.B. Gorjainov, I.V. Pavlov, G.M. Tsvetkova i drugi; ur. V.S. Zarubina, A.P. Kriščenko. - M.: Izdavačka kuća MSTU im. N.E. Bauman, 2001. - 424 str. Trebate pomoć u proučavanju teme?
Naši stručnjaci savjetovat će vam ili pružiti usluge podučavanja o temama koje vas zanimaju. Podučavanje
Pošaljite svoju prijavu naznačite temu upravo sada kako biste saznali o mogućnosti dobivanja konzultacija.
 Zbirka ruskih čudaka i modifikatora tijela
Zbirka ruskih čudaka i modifikatora tijela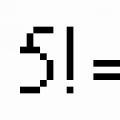 Teorija vjerojatnosti i matematička statistika
Teorija vjerojatnosti i matematička statistika Osnovni pojmovi teorije vjerojatnosti i matematičke statistike
Osnovni pojmovi teorije vjerojatnosti i matematičke statistike