Niz distribucije diskretnih c u x. Primjeri rješavanja problema na temu "Slučajne varijable"
Poglavlje 1. Diskretna slučajna varijabla
§ 1. Pojmovi slučajne varijable.
Zakon distribucije diskretne slučajne varijable.
Definicija : Slučajna je veličina koja, kao rezultat testiranja, uzima samo jednu vrijednost iz mogućeg skupa svojih vrijednosti, unaprijed nepoznatih i ovisno o slučajnim razlozima.
Postoje dvije vrste slučajnih varijabli: diskretne i kontinuirane.
Definicija : Poziva se slučajna varijabla X diskretna (diskontinuiran) ako je skup njegovih vrijednosti konačan ili beskonačan, ali prebrojiv.
Drugim riječima, moguće vrijednosti diskretne slučajne varijable mogu se prenumerirati.
Slučajna varijabla može se opisati korištenjem zakona distribucije.
Definicija : Zakon distribucije diskretne slučajne varijable nazvati korespondenciju između mogućih vrijednosti slučajne varijable i njihove vjerojatnosti.
Zakon raspodjele diskretne slučajne varijable X može se specificirati u obliku tablice, u čijem su prvom retku sve moguće vrijednosti slučajne varijable naznačene uzlaznim redoslijedom, au drugom redu odgovarajuće vjerojatnosti tih vrijednosti, tj.
gdje je r1+ r2+…+ rn=1
Takva se tablica naziva serija distribucije diskretne slučajne varijable.
Ako je skup mogućih vrijednosti slučajne varijable beskonačan, tada niz p1+ p2+…+ pn+… konvergira i njegov zbroj je jednak 1.
Zakon raspodjele diskretne slučajne varijable X može se prikazati grafički, za što se u pravokutnom koordinatnom sustavu konstruira isprekidana linija koja povezuje sekvencijalne točke s koordinatama (xi; pi), i=1,2,…n. Rezultirajući pravac naziva se distribucijski poligon (Sl. 1).
Organska kemija" href="/text/category/organicheskaya_hiimya/" rel="bookmark">organska kemija su 0,7 odnosno 0,8. Napravite zakon raspodjele za slučajnu varijablu X - broj ispita koje će student položiti.
Riješenje. Razmatrana slučajna varijabla X kao rezultat ispita može poprimiti jednu od sljedećih vrijednosti: x1=0, x2=1, x3=2.
Nađimo vjerojatnost ovih vrijednosti Označimo događaje:
https://pandia.ru/text/78/455/images/image004_81.jpg" width="259" height="66 src=">
 |
Dakle, zakon raspodjele slučajne varijable X dan je tablicom:
Kontrola: 0,6+0,38+0,56=1.
§ 2. Funkcija distribucije
Potpuni opis slučajne varijable također daje funkcija distribucije.
Definicija: Funkcija distribucije diskretne slučajne varijable X naziva se funkcija F(x), koja za svaku vrijednost x određuje vjerojatnost da će slučajna varijabla X poprimiti vrijednost manju od x:
F(x)=P(X<х)
Geometrijski, funkcija distribucije tumači se kao vjerojatnost da će slučajna varijabla X poprimiti vrijednost koja je na brojevnom pravcu predstavljena točkom koja leži lijevo od točke x.
1)0≤ F(x) ≤1;
2) F(x) je neopadajuća funkcija na (-∞;+∞);
3) F(x) - kontinuirano lijevo u točkama x= xi (i=1,2,...n) i kontinuirano u svim ostalim točkama;
4) F(-∞)=P (X<-∞)=0 как вероятность невозможного события Х<-∞,
F(+∞)=P(X<+∞)=1 как вероятность достоверного события Х<-∞.
Ako je zakon raspodjele diskretne slučajne varijable X dan u obliku tablice:
tada je funkcija distribucije F(x) određena formulom:
https://pandia.ru/text/78/455/images/image007_76.gif" height="110">
0 za x≤ x1,
r1 na x1< х≤ x2,
F(x)= r1 + r2 u x2< х≤ х3
1 za x> xn.
Njegov graf je prikazan na sl. 2:
§ 3. Numeričke karakteristike diskretne slučajne varijable.
Jedna od važnih numeričkih karakteristika je matematičko očekivanje.
Definicija: Matematičko očekivanje M(X) diskretna slučajna varijabla X je zbroj umnožaka svih njezinih vrijednosti i njihovih odgovarajućih vjerojatnosti:
M(X) = ∑ xiri= x1r1 + x2r2+…+ xnrn
Matematičko očekivanje služi kao karakteristika prosječne vrijednosti slučajne varijable.
Svojstva matematičkog očekivanja:
1)M(C)=C, gdje je C konstantna vrijednost;
2)M(C X)=C M(X),
3)M(X±Y)=M(X)±M(Y);
4)M(X Y)=M(X) M(Y), gdje su X, Y nezavisne slučajne varijable;
5)M(X±C)=M(X)±C, gdje je C konstantna vrijednost;
Za karakterizaciju stupnja disperzije mogućih vrijednosti diskretne slučajne varijable oko njezine srednje vrijednosti koristi se disperzija.
Definicija: Varijanca D ( x ) slučajna varijabla X je matematičko očekivanje kvadrata odstupanja slučajne varijable od njenog matematičkog očekivanja:
Disperzijska svojstva:
1)D(C)=0, gdje je C konstantna vrijednost;
2)D(X)>0, gdje je X slučajna varijabla;
3)D(C X)=C2 D(X), gdje je C konstantna vrijednost;
4)D(X+Y)=D(X)+D(Y), gdje su X, Y nezavisne slučajne varijable;
Za izračun varijance često je zgodno koristiti formulu:
D(X)=M(X2)-(M(X))2,
gdje je M(X)=∑ xi2ri= x12r1 + x22r2+…+ xn2rn
Varijanca D(X) ima dimenziju kvadrata slučajne varijable, što nije uvijek zgodno. Stoga se vrijednost √D(X) također koristi kao pokazatelj disperzije mogućih vrijednosti slučajne varijable.
Definicija: Standardna devijacija σ(X) slučajna varijabla X naziva se kvadratni korijen varijance:
Zadatak br. 2. Diskretna slučajna varijabla X određena je zakonom distribucije:
Nađite P2, funkciju distribucije F(x) i nacrtajte njen graf, kao i M(X), D(X), σ(X).
Riješenje: Budući da je zbroj vjerojatnosti mogućih vrijednosti slučajne varijable X jednak 1, tada
R2=1- (0,1+0,3+0,2+0,3)=0,1
Nađimo funkciju distribucije F(x)=P(X Geometrijski, ova se jednakost može protumačiti na sljedeći način: F(x) je vjerojatnost da će slučajna varijabla poprimiti vrijednost koja je na brojčanoj osi predstavljena točkom koja leži lijevo od točke x. Ako je x≤-1, tada je F(x)=0, jer ne postoji niti jedna vrijednost ove slučajne varijable na (-∞;x); Ako je -1<х≤0, то F(х)=Р(Х=-1)=0,1, т. к. в промежуток (-∞;х) попадает только одно значение x1=-1; Ako je 0<х≤1, то F(х)=Р(Х=-1)+ Р(Х=0)=0,1+0,1=0,2, т. к. в промежуток (-∞;x) postoje dvije vrijednosti x1=-1 i x2=0; Ako 1<х≤2, то F(х)=Р(Х=-1) + Р(Х=0)+ Р(Х=1)= 0,1+0,1+0,3=0,5, т. к. в промежуток (-∞;х) попадают три значения x1=-1, x2=0 и x3=1; Ako 2<х≤3, то F(х)=Р(Х=-1) + Р(Х=0)+ Р(Х=1)+ Р(Х=2)= 0,1+0,1+0,3+0,2=0,7, т. к. в промежуток (-∞;х) попадают четыре значения x1=-1, x2=0,x3=1 и х4=2; Ako je x>3, tada je F(x)=P(X=-1) + P(X=0)+ P(X=1)+ P(X=2)+P(X=3)= 0,1 +0,1 +0,3+0,2+0,3=1, jer četiri vrijednosti x1=-1, x2=0, x3=1, x4=2 spadaju u interval (-∞;x) i x5=3. https://pandia.ru/text/78/455/images/image006_89.gif" width="14 height=2" height="2"> 0 pri x≤-1, 0,1 na -1<х≤0, 0,2 na 0<х≤1, F(x)= 0,5 na 1<х≤2, 0,7 na 2<х≤3, 1 na x>3 Predstavimo funkciju F(x) grafički (slika 3): https://pandia.ru/text/78/455/images/image014_24.jpg" width="158 height=29" height="29">≈1,2845. §
4. Binomni zakon raspodjele diskretna slučajna varijabla, Poissonov zakon. Definicija: Binomni
naziva se zakon distribucije diskretne slučajne varijable X - broj pojavljivanja događaja A u n neovisnih ponovljenih pokušaja, u svakom od kojih se događaj A može dogoditi s vjerojatnošću p ili ne dogoditi s vjerojatnošću q = 1-p. Zatim se P(X=m) - vjerojatnost pojavljivanja događaja A točno m puta u n pokušaja izračunava pomoću Bernoullijeve formule: R(H=m)=Smnpmqn-m Matematičko očekivanje, disperzija i standardna devijacija slučajne varijable X raspoređene prema binarnom zakonu nalaze se pomoću formula: https://pandia.ru/text/78/455/images/image016_31.gif" width="26"> Vjerojatnost događaja A - "ispadanje petice" u svakom pokušaju je ista i jednaka 1/6 , tj. P(A)=p=1/6, tada P(A)=1-p=q=5/6, gdje je - "nedobivanje A." Slučajna varijabla X može poprimiti sljedeće vrijednosti: 0;1;2;3. Pronalazimo vjerojatnost svake od mogućih vrijednosti X pomoću Bernoullijeve formule: R(H=0)=R3(0)=S03r0q3=1 (1/6)0 (5/6)3=125/216; R(H=1)=R3(1)=S13r1q2=3 (1/6)1 (5/6)2=75/216; R(H=2)=R3(2)=S23r2q =3 (1/6)2 (5/6)1=15/216; R(H=3)=R3(3)=S33r3q0=1 (1/6)3 (5/6)0=1/216. Da. zakon distribucije slučajne varijable X ima oblik: Kontrola: 125/216+75/216+15/216+1/216=1. Nađimo numeričke karakteristike slučajne varijable X: M(X)=np=3 (1/6)=1/2, D(X)=npq=3 (1/6) (5/6)=5/12, Zadatak br. 4. Automatski stroj štanca dijelove. Vjerojatnost da će proizvedeni dio biti neispravan je 0,002. Odredite vjerojatnost da će među 1000 odabranih dijelova biti: a) 5 neispravnih; b) najmanje jedan je neispravan. Riješenje:
Broj n=1000 je velik, vjerojatnost proizvodnje neispravnog dijela p=0,002 je mala, a događaji koji se razmatraju (pokazuje se da je dio neispravan) su neovisni, stoga vrijedi Poissonova formula: Rn(m)= e-
λ
λm Nađimo λ=np=1000 0,002=2. a) Odredite vjerojatnost da će biti 5 neispravnih dijelova (m=5): R1000(5)= e-2
25
= 32 0,13534
= 0,0361 b) Odredite vjerojatnost da će biti barem jedan neispravan dio. Događaj A - "barem jedan od odabranih dijelova je neispravan" suprotan je događaju - "svi odabrani dijelovi nisu neispravni." Prema tome, P(A) = 1-P(). Stoga je željena vjerojatnost jednaka: P(A)=1-P1000(0)=1- e-2
20
= 1- e-2=1-0,13534≈0,865. Zadaci za samostalan rad.
1.1
1.2.
Raspršena slučajna varijabla X određena je zakonom distribucije: Nađite p4, funkciju distribucije F(X) i nacrtajte njen graf, kao i M(X), D(X), σ(X). 1.3.
U kutiji je 9 markera, od kojih 2 više ne pišu. Nasumično uzmite 3 markera. Slučajna varijabla X je broj markera za pisanje među uzetima. Nacrtati zakon raspodjele slučajne varijable. 1.4.
Na polici knjižnice nalazi se 6 udžbenika nasumično poredanih, od kojih su 4 uvezana. Knjižničar nasumce uzima 4 udžbenika. Slučajna varijabla X je broj ukoričenih udžbenika među uzetima. Nacrtati zakon raspodjele slučajne varijable. 1.5.
Na listiću su dva zadatka. Vjerojatnost ispravnog rješavanja prvog problema je 0,9, drugog 0,7. Slučajna varijabla X je broj točno riješenih zadataka na listiću. Nacrtajte zakon distribucije, izračunajte matematičko očekivanje i varijancu ove slučajne varijable, a također pronađite funkciju distribucije F(x) i izgradite njezin grafikon. 1.6.
Tri strijelca gađaju metu. Vjerojatnost pogotka mete jednim hicem je 0,5 za prvog strijelca, 0,8 za drugog i 0,7 za trećeg. Slučajna varijabla X je broj pogodaka u metu ako strijelci pucaju jedan po jedan. Pronađite zakon raspodjele, M(X),D(X). 1.7.
Košarkaš ubacuje loptu u koš s vjerojatnošću da će pogoditi svaki šut od 0,8. Za svaki pogodak dobiva 10 bodova, a ako promaši ne dobiva bodove. Nacrtajte zakon raspodjele za slučajnu varijablu X - broj poena koje je košarkaš primio u 3 udarca. Nađite M(X),D(X), kao i vjerojatnost da dobije više od 10 bodova. 1.8.
Na karticama su ispisana slova, ukupno 5 samoglasnika i 3 suglasnika. Nasumično se biraju 3 karte i svaki put se uzeta karta vraća natrag. Slučajna varijabla X je broj samoglasnika među uzetima. Nacrtajte zakon raspodjele i pronađite M(X),D(X),σ(X). 1.9.
U prosjeku ispod 60% ugovora osiguravajuće društvo isplaćuje iznose osiguranja u vezi s nastupom osiguranog slučaja. Napravite zakon raspodjele za slučajnu varijablu X - broj ugovora za koje je isplaćen iznos osiguranja među četiri slučajno odabrana ugovora. Odredite brojčane karakteristike te veličine. 1.10.
Radio postaja šalje pozivne znakove (ne više od četiri) u određenim intervalima dok se ne uspostavi dvosmjerna komunikacija. Vjerojatnost primanja odgovora na pozivni znak je 0,3. Slučajna varijabla X je broj poslanih pozivnih znakova. Nacrtajte zakon raspodjele i pronađite F(x). 1.11.
Ima 3 ključa od kojih samo jedan odgovara bravi. Napravite zakon raspodjele slučajne varijable X-broj pokušaja otvaranja brave, ako isprobani ključ ne sudjeluje u sljedećim pokušajima. Pronađite M(X),D(X). 1.12.
Provedena su uzastopna neovisna testiranja pouzdanosti tri uređaja. Svaki sljedeći uređaj testira se samo ako se prethodni pokazao pouzdanim. Vjerojatnost prolaska testa za svaki uređaj je 0,9. Nacrtajte zakon raspodjele za slučajnu varijablu X-broj testiranih uređaja. 1.13
.Diskretna slučajna varijabla X ima tri moguće vrijednosti: x1=1, x2, x3 i x1<х2<х3. Вероятность того, что Х примет значения х1 и х2, соответственно равны 0,3 и 0,2. Известно, что М(Х)=2,2, D(X)=0,76. Составить закон распределения случайной величины. 1.14.
Blok elektroničkog uređaja sadrži 100 identičnih elemenata. Vjerojatnost kvara svakog elementa tijekom vremena T je 0,002. Elementi rade neovisno. Odredite vjerojatnost da tijekom vremena T neće otkazati više od dva elementa. 1.15.
Udžbenik je objavljen u nakladi od 50.000 primjeraka. Vjerojatnost da je udžbenik krivo uvezan je 0,0002. Odredite vjerojatnost da cirkulacija sadrži: a) četiri neispravne knjige, b) manje od dvije neispravne knjige. 1
.16.
Broj poziva koji pristignu na PBX svake minute raspoređuje se prema Poissonovom zakonu s parametrom λ=1,5. Nađite vjerojatnost da će za minutu stići sljedeće: a) dva poziva; b) najmanje jedan poziv. 1.17.
Nađite M(Z),D(Z) ako je Z=3X+Y. 1.18.
Dati su zakoni raspodjele dviju neovisnih slučajnih varijabli: Nađite M(Z),D(Z) ako je Z=X+2Y. odgovori:
https://pandia.ru/text/78/455/images/image007_76.gif" height="110"> 1.1.
p3=0,4; 0 pri x≤-2, 0,3 na -2<х≤0, F(x)= 0,5 na 0<х≤2, 0,9 u 2<х≤5, 1 na x>5 0,3 na -1<х≤0, 0,4 na 0<х≤1, F(x)= 0,6 na 1<х≤2, 0,7 na 2<х≤3, 1 na x>3 M(X)=1; D(X)=2,6; σ(X) ≈1,612. https://pandia.ru/text/78/455/images/image025_24.gif" width="2 height=98" height="98"> 0 na x≤0, 0,03 na 0<х≤1, F(x)= 0,37 na 1<х≤2, 1 za x>2 M(X)=2; D(X)=0,62 M(X)=2,4; D(X)=0,48, P(X>10)=0,896 1.
8
.
M(X)=15/8; D(X)=45/64; σ(X) ≈ M(X)=2,4; D(X)=0,96 https://pandia.ru/text/78/455/images/image008_71.gif" width="14"> 1.11.
M(X)=2; D(X)=2/3 1.14.
1,22 e-0,2≈0,999 1.15.
a) 0,0189; b) 0,00049 1.16.
a) 0,0702; b) 0,77687 1.17.
3,8; 14,2 1.18.
11,2; 4. 2. Poglavlje. Kontinuirana slučajna varijabla
Definicija: Stalan
Veličinom se nazivaju sve moguće vrijednosti od kojih u potpunosti ispunjavaju konačni ili beskonačni raspon brojevnog pravca. Očito je da je broj mogućih vrijednosti kontinuirane slučajne varijable beskonačan. Kontinuirana slučajna varijabla može se specificirati pomoću funkcije distribucije. Definicija: F distribucijska funkcija
kontinuirana slučajna varijabla X naziva se funkcija F(x), koja za svaku vrijednost određuje xhttps://pandia.ru/text/78/455/images/image028_11.jpg" width="14" height="13"> R Funkcija distribucije se ponekad naziva i kumulativna funkcija distribucije. Svojstva funkcije distribucije:
1)1≤ F(x) ≤1 2) Za kontinuiranu slučajnu varijablu, funkcija distribucije je kontinuirana u bilo kojoj točki i diferencijabilna posvuda, osim, možda, u pojedinačnim točkama. 3) Vjerojatnost da slučajna varijabla X padne u jedan od intervala (a;b), [a;b], [a;b], jednaka je razlici između vrijednosti funkcije F(x) u točkama a i b, tj. R(a)<Х 4) Vjerojatnost da će kontinuirana slučajna varijabla X poprimiti jednu zasebnu vrijednost je 0. 5) F(-∞)=0, F(+∞)=1 Određivanje kontinuirane slučajne varijable pomoću funkcije distribucije nije jedini način. Uvedimo pojam gustoće distribucije vjerojatnosti (gustoće distribucije). Definicija
:
Gustoća distribucije vjerojatnosti
f
(
x
)
kontinuirane slučajne varijable X je derivacija njene distribucijske funkcije, tj.: Funkcija gustoće vjerojatnosti ponekad se naziva funkcija diferencijalne distribucije ili zakon diferencijalne distribucije. Graf distribucije gustoće vjerojatnosti f(x) naziva se krivulja distribucije vjerojatnosti
.
Svojstva distribucije gustoće vjerojatnosti:
1) f(x) ≥0, na xhttps://pandia.ru/text/78/455/images/image029_10.jpg" width="285" height="141">DIV_ADBLOCK13"> https://pandia.ru/text/78/455/images/image032_23.gif" height="38 src="> +∞ 2 6 +∞ 6 6 ∫ f(x)dx=∫ 0dx+ ∫ c(x-2)dx +∫ 0dx= c∫ (x-2)dx=c(x2/2-2x) =c(36/2-12-(4/ 2-4))=8s; b) Poznato je da je F(x)= ∫ f(x)dx Stoga, x ako je x≤2, tada je F(x)= ∫ 0dx=0; https://pandia.ru/text/78/455/images/image032_23.gif" height="38 src="> 2 6 x 6 6 ako je x>6, tada je F(x)= ∫ 0dx+∫ 1/8(x-2)dx+∫ 0dx=1/8∫(x-2)dx=1/8(x2/2-2x) = 1/8(36/2-12-(4/2+4))=1/8 8=1. Tako, 0 pri x≤2, F(x)= (x-2)2/16 na 2<х≤6, 1 za x>6. Graf funkcije F(x) prikazan je na slici 3 https://pandia.ru/text/78/455/images/image034_23.gif" width="14" height="62 src="> 0 na x≤0, F(x)= (3 arctan x)/π na 0<х≤√3, 1 za x>√3. Pronađite funkciju diferencijalne distribucije f(x) Riješenje:
Budući da je f(x)= F’(x), tada DIV_ADBLOCK14"> · Matematičko očekivanje M (X)
kontinuirana slučajna varijabla X određena je jednakošću: M(X)= ∫ x f(x)dx, uz uvjet da taj integral apsolutno konvergira. · Disperzija
D
(
x
)
kontinuirana slučajna varijabla X određena je jednakošću: D(X)= ∫ (x-M(x)2) f(x)dx, ili D(X)= ∫ x2 f(x)dx - (M(x))2 · Standardna devijacija σ(H)
kontinuirana slučajna varijabla određena je jednakošću: Sva svojstva matematičkog očekivanja i disperzije, o kojima smo ranije govorili za disperzirane slučajne varijable, vrijede i za one kontinuirane. Zadatak br. 3. Slučajna varijabla X određena je diferencijalnom funkcijom f(x): https://pandia.ru/text/78/455/images/image036_19.gif" height="38"> -∞ 2 X3/9 + x2/6 = 8/9-0+9/6-4/6=31/18, https://pandia.ru/text/78/455/images/image032_23.gif" height="38"> +∞ D(X)= ∫ x2 f(x)dx-(M(x))2=∫ x2 x/3 dx+∫1/3x2 dx=(31/18)2=x4/12 + x3/9 - - (31/18)2=16/12-0+27/9-8/9-(31/18)2=31/9- (31/18)2==31/9(1-31/36)=155/324, https://pandia.ru/text/78/455/images/image032_23.gif" height="38"> P(1<х<5)= ∫ f(x)dx=∫ х/3 dx+∫ 1/3 dx+∫ 0 dx= х2/6 +1/3х = 4/6-1/6+1-2/3=5/6. Problemi za samostalno rješavanje.
2.1.
Kontinuirana slučajna varijabla X određena je funkcijom distribucije: 0 pri x≤0, F(x)= https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86"> 0 za x≤ π/6, F(x)= - cos 3x pri π/6<х≤ π/3, 1 za x> π/3. Nađite funkciju diferencijalne distribucije f(x), a također R(2π /9<Х< π /2). 2.3.
0 pri x≤2, f(x)= c x na 2<х≤4, 0 za x>4. 2.4.
Kontinuirana slučajna varijabla X određena je gustoćom distribucije: 0 pri x≤0, f(x)= c √x na 0<х≤1, 0 za x>1. Nađi: a) broj c; b) M(X), D(X). 2.5.
https://pandia.ru/text/78/455/images/image041_3.jpg" width="36" height="39"> na x, 0 na x. Nađite: a) F(x) i konstruirajte njegov graf; b) M(X),D(X), σ(X); c) vjerojatnost da će u četiri neovisna pokusa vrijednost X poprimiti točno 2 puta vrijednost koja pripada intervalu (1;4). 2.6.
Gustoća distribucije vjerojatnosti kontinuirane slučajne varijable X dana je: f(x)= 2(x-2) na x, 0 na x. Nađite: a) F(x) i konstruirajte njegov graf; b) M(X),D(X), σ (X); c) vjerojatnost da će u tri neovisna pokušaja vrijednost X poprimiti točno 2 puta vrijednost koja pripada segmentu . 2.7.
Funkcija f(x) dana je kao: https://pandia.ru/text/78/455/images/image045_4.jpg" width="43" height="38 src=">.jpg" width="16" height="15">[-√ 3/2; √3/2]. 2.8.
Funkcija f(x) dana je kao: https://pandia.ru/text/78/455/images/image046_5.jpg" width="45" height="36 src="> .jpg" width="16" height="15">[- π /4 ; π /4]. Odredite: a) vrijednost konstante c pri kojoj će funkcija biti gustoća vjerojatnosti neke slučajne varijable X; b) funkcija raspodjele F(x). 2.9.
Slučajna varijabla X, koncentrirana na interval (3;7), određena je funkcijom distribucije F(x)= . Nađite vjerojatnost da slučajna varijabla X poprimit će vrijednost: a) manju od 5, b) ne manju od 7. 2.10.
Slučajna varijabla X, koncentrirana na interval (-1;4), dana je funkcijom raspodjele F(x)= . Nađite vjerojatnost da slučajna varijabla X poprimit će vrijednost: a) manju od 2, b) ne manju od 4. 2.11.
https://pandia.ru/text/78/455/images/image049_6.jpg" width="43" height="44 src="> .jpg" width="16" height="15">. Nađi: a) broj c; b) M(X); c) vjerojatnost P(X> M(X)). 2.12.
Slučajna varijabla određena je funkcijom diferencijalne distribucije: https://pandia.ru/text/78/455/images/image050_3.jpg" width="60" height="38 src=">.jpg" width="16 height=15" height="15"> . Nađi: a) M(X); b) vjerojatnost P(X≤M(X)) 2.13.
Rem distribucija dana je gustoćom vjerojatnosti: https://pandia.ru/text/78/455/images/image052_5.jpg" width="46" height="37"> za x ≥0. Dokažite da je f(x) doista funkcija gustoće vjerojatnosti. 2.14.
Gustoća distribucije vjerojatnosti kontinuirane slučajne varijable X dana je: DIV_ADBLOCK17"> https://pandia.ru/text/78/455/images/image055_3.jpg" width="187 height=136" height="136">(Sl. 5) 2.16.
Slučajna varijabla X raspoređena je prema zakonu “pravokutnog trokuta” u intervalu (0;4) (slika 5). Nađite analitički izraz za gustoću vjerojatnosti f(x) na cijelom brojevnom pravcu. Odgovori
0 pri x≤0, f(x)= https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86"> 0 za x≤ π/6, F(x)= 3sin 3x pri π/6<х≤ π/3,
Непрерывная случайная величина Х имеет равномерный закон распределения на некотором интервале (а;b), которому принадлежат все возможные значения Х, если плотность распределения вероятностей f(x) постоянная на этом интервале и равна 0 вне его, т. е. 0 za x≤a, f(x)= za a<х 0 za x≥b. Graf funkcije f(x) prikazan je na sl. 1 F(x)= https://pandia.ru/text/78/455/images/image077_3.jpg" width="30" height="37">, D(X)=, σ(X)=. Zadatak br. 1. Slučajna varijabla X jednoliko je raspoređena na segmentu. Pronaći: a) gustoću distribucije vjerojatnosti f(x) i nacrtajte je; b) funkciju distribucije F(x) i nacrtajte je; c) M(X),D(X), σ(X). Riješenje:
Koristeći formule o kojima smo raspravljali gore, s a=3, b=7, nalazimo: https://pandia.ru/text/78/455/images/image081_2.jpg" width="22" height="39"> na 3≤h≤7, 0 za x>7 Izgradimo njegov grafikon (Sl. 3): https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86 src="> 0 na x≤3, F(x)= https://pandia.ru/text/78/455/images/image084_3.jpg" width="203" height="119 src=">Sl. 4 D(X) = ==https://pandia.ru/text/78/455/images/image089_1.jpg" width="37" height="43">==https://pandia.ru/text/ 78/455/images/image092_10.gif" width="14" height="49 src="> 0 na x<0, f(x)= λe-λh za x≥0. Funkcija distribucije slučajne varijable X, raspodijeljena prema eksponencijalnom zakonu, dana je formulom: DIV_ADBLOCK19"> https://pandia.ru/text/78/455/images/image095_4.jpg" width="161" height="119 src="> Sl. 6 Matematičko očekivanje, varijanca i standardna devijacija eksponencijalne distribucije jednaki su: M(X)= , D(X)=, σ (H)= Stoga su matematičko očekivanje i standardna devijacija eksponencijalne distribucije međusobno jednaki. Vjerojatnost da X padne u interval (a;b) izračunava se po formuli: Godišnje<Х Zadatak br. 2. Prosječno vrijeme rada uređaja bez kvara je 100 sati. Uz pretpostavku da vrijeme rada uređaja bez kvara ima eksponencijalni zakon raspodjele, nađite: a) gustoća distribucije vjerojatnosti; b) distribucijska funkcija; c) vjerojatnost da će vrijeme rada uređaja bez greške prijeći 120 sati. Riješenje:
Prema uvjetu, matematička distribucija M(X)=https://pandia.ru/text/78/455/images/image098_10.gif" height="43 src="> 0 na x<0, a) f(x)= 0,01e -0,01x za x≥0. b) F(x)= 0 na x<0, 1-e -0,01x pri x≥0. c) Željenu vjerojatnost nalazimo pomoću funkcije distribucije: P(X>120)=1-F(120)=1-(1- e -1,2)= e -1,2≈0,3. §
3. Zakon normalne distribucije Definicija:
Kontinuirana slučajna varijabla X ima zakon normalne distribucije (Gaussov zakon),
ako njegova gustoća distribucije ima oblik: gdje je m=M(X), σ2=D(X), σ>0. Krivulja normalne distribucije naziva se normalna ili Gaussova krivulja
(Sl.7) Funkcija distribucije slučajne varijable X, distribuirana prema normalnom zakonu, izražava se preko Laplaceove funkcije F (x) prema formuli: gdje je Laplaceova funkcija. Komentar:
Funkcija F(x) je neparna (F(-h)=-F(h)), osim toga, za x>5 možemo pretpostaviti da je F(h) ≈1/2. Graf funkcije distribucije F(x) prikazan je na sl. 8 https://pandia.ru/text/78/455/images/image106_4.jpg" width="218" height="33"> Vjerojatnost da je apsolutna vrijednost odstupanja manja od pozitivnog broja δ izračunava se formulom: Konkretno, za m=0 vrijedi jednakost: "Pravilo tri sigme"
Ako slučajna varijabla X ima normalan zakon raspodjele s parametrima m i σ, tada je gotovo sigurno da njezina vrijednost leži u intervalu (a-3σ; a+3σ), jer https://pandia.ru/text/78/455/images/image110_2.jpg" width="157" height="57 src=">a) b) Upotrijebimo formulu: https://pandia.ru/text/78/455/images/image112_2.jpg" width="369" height="38 src="> Iz tablice vrijednosti funkcije F(h) nalazimo F(1,5)=0,4332, F(1)=0,3413. Dakle, željena vjerojatnost: P(28 Zadaci za samostalan rad
3.1.
Slučajna varijabla X jednoliko je raspoređena u intervalu (-3;5). Pronaći: b) funkcija raspodjele F(x); c) numeričke karakteristike; d) vjerojatnost P(4<х<6). 3.2.
Slučajna varijabla X jednoliko je raspoređena na segmentu. Pronaći: a) gustoća raspodjele f(x); b) funkcija raspodjele F(x); c) numeričke karakteristike; d) vjerojatnost P(3≤h≤6). 3.3.
Na autocesti postoji automatski semafor na kojem zeleno svijetli 2 minute, žuto 3 sekunde, crveno 30 sekundi itd. Automobil se vozi autocestom u slučajnom trenutku. Nađite vjerojatnost da će automobil proći pored semafora bez zaustavljanja. 3.4.
Vlakovi podzemne voze redovito u intervalima od 2 minute. Putnik ulazi na peron u nasumično određeno vrijeme. Kolika je vjerojatnost da će putnik morati čekati vlak više od 50 sekundi? Nađite matematičko očekivanje slučajne varijable X - vrijeme čekanja vlaka. 3.5.
Nađite varijancu i standardnu devijaciju eksponencijalne distribucije dane funkcijom distribucije: F(x)= 0 na x<0, 1.-8x za x≥0. 3.6.
Kontinuirana slučajna varijabla X određena je gustoćom distribucije vjerojatnosti: f(x)= 0 na x<0, 0,7 e-0,7x pri x≥0. a) Navedite zakon raspodjele slučajne varijable o kojoj se radi. b) Pronađite funkciju distribucije F(X) i numeričke karakteristike slučajne varijable X. 3.7.
Slučajna varijabla X distribuira se prema eksponencijalnom zakonu određenom gustoćom distribucije vjerojatnosti: f(x)= 0 na x<0, 0,4 e-0,4 x pri x≥0. Odredite vjerojatnost da će kao rezultat testa X uzeti vrijednost iz intervala (2,5;5). 3.8.
Kontinuirana slučajna varijabla X raspoređena je prema eksponencijalnom zakonu određenom funkcijom distribucije: F(x)= 0 na x<0, 1.-0,6x pri x≥0 Odredite vjerojatnost da će, kao rezultat testa, X uzeti vrijednost iz segmenta. 3.9.
Očekivana vrijednost i standardna devijacija normalno distribuirane slučajne varijable su 8 odnosno 2. Pronađite: a) gustoća raspodjele f(x); b) vjerojatnost da će kao rezultat testa X uzeti vrijednost iz intervala (10;14). 3.10.
Slučajna varijabla X normalno je raspodijeljena s matematičkim očekivanjem od 3,5 i varijancom od 0,04. Pronaći: a) gustoća raspodjele f(x); b) vjerojatnost da će kao rezultat testa X uzeti vrijednost iz segmenta . 3.11.
Slučajna varijabla X je normalno distribuirana s M(X)=0 i D(X)=1. Koji je od događaja: |X|≤0,6 ili |X|≥0,6 vjerojatniji? 3.12.
Slučajna varijabla X raspodijeljena je normalno s M(X)=0 i D(X)=1. Iz kojeg je intervala (-0,5;-0,1) ili (1;2) veća vjerojatnost da će uzeti vrijednost tijekom jednog testa? 3.13.
Trenutna cijena po dionici može se modelirati korištenjem normalnog zakona distribucije s M(X)=10 den. jedinice i σ (X)=0,3 den. jedinice Pronaći: a) vjerojatnost da će trenutna cijena dionice biti od 9,8 den. jedinice do 10,4 dana jedinice; b) pomoću „pravila tri sigme“ pronađite granice unutar kojih će se nalaziti trenutna cijena dionice. 3.14.
Tvar se važe bez sustavnih grešaka. Slučajne pogreške vaganja podliježu normalnom zakonu sa srednjim kvadratnim omjerom σ=5g. Odredite vjerojatnost da se u četiri neovisna pokusa neće pojaviti pogreška u tri vaganja u apsolutnoj vrijednosti 3r. 3.15.
Slučajna varijabla X normalno je raspodijeljena s M(X)=12,6. Vjerojatnost da slučajna varijabla padne u interval (11,4;13,8) je 0,6826. Nađite standardnu devijaciju σ. 3.16.
Slučajna varijabla X raspodijeljena je normalno s M(X)=12 i D(X)=36. Pronađite interval u koji će slučajna varijabla X pasti kao rezultat testa s vjerojatnošću 0,9973. 3.17.
Dio proizveden automatskim strojem smatra se neispravnim ako odstupanje X njegovog kontroliranog parametra od nazivne vrijednosti prelazi modulo 2 mjerne jedinice. Pretpostavlja se da je slučajna varijabla X normalno distribuirana s M(X)=0 i σ(X)=0,7. Koliki postotak neispravnih dijelova proizvodi stroj? 3.18.
Parametar X dijela distribuira se normalno s matematičkim očekivanjem 2 jednakim nominalnoj vrijednosti i standardnom devijacijom od 0,014. Odredite vjerojatnost da odstupanje X od nominalne vrijednosti neće prijeći 1% od nominalne vrijednosti. Odgovori
https://pandia.ru/text/78/455/images/image116_9.gif" width="14" height="110 src="> b) 0 za x≤-3, F(x)= lijevo"> 3.10.
a)f(x)= , b) R(3,1≤H≤3,7) ≈0,8185. 3.11.
|x|≥0,6. 3.12.
(-0,5;-0,1). 3.13.
a) P(9,8≤H≤10,4) ≈0,6562. 3.14.
0,111. 3.15.
σ=1,2. 3.16.
(-6;30). 3.17.
0,4%. Primjeri rješavanja zadataka na temu "Slučajne varijable".
Zadatak 1
. Za lutriju je izdano 100 listića. Izvučen je jedan dobitak od 50 USD. i deset dobitaka po 10 USD. Nađite zakon raspodjele vrijednosti X - cijene mogućih dobitaka. Riješenje. Moguće vrijednosti za X: x 1
= 0; x 2
= 10 i x 3
= 50. Budući da ima 89 “praznih” listića, str 1
= 0,89, vjerojatnost dobitka 10 USD. (10 ulaznica) – str 2
= 0,10 i osvojiti 50 USD -str 3
= 0,01. Tako: 0,89
0,10
0,01
Jednostavan za upravljanje: . Zadatak 2.
Vjerojatnost da je kupac unaprijed pročitao reklamu proizvoda je 0,6 (p=0,6). Selektivna kontrola kvalitete oglašavanja provodi se anketiranjem kupaca prije prvog koji je prethodno proučio oglašavanje. Napravite niz distribucije za broj anketiranih kupaca. Riješenje. Prema uvjetima zadatka p = 0,6. Od: q=1 -p = 0,4. Zamjenom ovih vrijednosti dobivamo: i konstruirajte distribucijski niz: p i 0,24
Zadatak 3.
Računalo se sastoji od tri neovisna radna elementa: sistemske jedinice, monitora i tipkovnice. S jednim oštrim povećanjem napona, vjerojatnost kvara svakog elementa je 0,1. Na temelju Bernoullijeve distribucije izraditi zakon raspodjele broja otkazanih elemenata tijekom strujnog udara u mreži. Riješenje. Razmotrimo Bernoullijeva distribucija(ili binom): vjerojatnost da n testova, događaj A će se pojaviti točno k jednom: q n str n U Vratimo se zadatku. Moguće vrijednosti za X (broj kvarova): x 0 =0 – niti jedan element nije otkazao; x 1 =1 – kvar jednog elementa; x 2 =2 – kvar dva elementa; x 3 =3 – otkaz svih elemenata. Kako je prema uvjetu p = 0,1, onda je q = 1 – p = 0,9. Koristeći Bernoullijevu formulu, dobivamo , ,
, .
Kontrolirati: . Prema tome, traženi zakon raspodjele: 0,729
0,243
0,027
0,001
Problem 4. Proizvedeno 5000 metaka. Vjerojatnost da je jedan uložak neispravan Riješenje. Primjenjivo Poissonova distribucija: Ova distribucija se koristi za određivanje vjerojatnosti da, za vrlo velike broj testova (masovnih testova), u svakom od kojih je vjerojatnost događaja A vrlo mala, događaj A će se dogoditi k puta: Ovdje je n = 5000, p = 0,0002, k = 3. Nalazimo , zatim željenu vjerojatnost: Problem 5. Pri pucanju do prvog pogotka s vjerojatnošću pogotka p
= 0,6 kod pucanja treba pronaći vjerojatnost da će do pogotka doći pri trećem hicu. Riješenje. Primijenimo geometrijsku distribuciju: neka se provode neovisni pokusi, u svakom od kojih događaj A ima vjerojatnost pojavljivanja p (i nepojavljivanja q = 1 – p). Test završava čim se dogodi događaj A. Pod takvim uvjetima, vjerojatnost da će se događaj A dogoditi u k-tom pokušaju određena je formulom: . Ovdje je p = 0,6; q = 1 – 0,6 = 0,4; k = 3. Prema tome, . Problem 6. Neka je dan zakon raspodjele slučajne varijable X: Nađite matematičko očekivanje. Riješenje. . Imajte na umu da je vjerojatnosno značenje matematičkog očekivanja prosječna vrijednost slučajne varijable. Problem 7. Pronađite varijancu slučajne varijable X sa sljedećim zakonom distribucije: Riješenje. Ovdje
.
Zakon distribucije za kvadrat vrijednosti X 2
:
x 2
Zahtijevana varijanca: . Disperzija karakterizira mjeru odstupanja (disperzije) slučajne varijable od njenog matematičkog očekivanja. Problem 8. Neka je slučajna varijabla dana distribucijom: 10m Pronađite njegove numeričke karakteristike. Rješenje: m, m 2
,
M 2
, m. Za slučajnu varijablu X možemo reći jedno: njezino matematičko očekivanje je 6,4 m s varijancom od 13,04 m 2
, ili – njegovo matematičko očekivanje je 6,4 m s odstupanjem od m. Druga je formulacija očito jasnija. Zadatak 9.
Slučajna vrijednost x dana distribucijskom funkcijom: Nađite vjerojatnost da će kao rezultat testa vrijednost X poprimiti vrijednost sadržanu u intervalu Riješenje. Vjerojatnost da će X uzeti vrijednost iz zadanog intervala jednaka je prirastu integralne funkcije u tom intervalu, tj. . U našem slučaju i, dakle Zadatak 10.
Diskretna slučajna varijabla x daje zakon raspodjele: Pronađite funkciju distribucije F(x ) i iscrtajte ga. Riješenje. Budući da funkcija distribucije, u ; u ; u ; u ; Relevantni grafikon: Problem 11. Kontinuirana slučajna varijabla x dana funkcijom diferencijalne distribucije: Pronađite vjerojatnost pogotka X po intervalu Riješenje. Imajte na umu da je ovo poseban slučaj zakona eksponencijalne distribucije. Upotrijebimo formulu: Zadatak 12.
Pronađite numeričke karakteristike diskretne slučajne varijable X određene zakonom distribucije: –5
X2: X 2 .
,
Gdje Vrijednosti ove funkcije nalaze se pomoću tablice. U našem slučaju: . Iz tablice nalazimo: , dakle: Definicija 1 Slučajna varijabla $X$ naziva se diskretnom (diskontinuiranom) ako je skup njezinih vrijednosti beskonačan ili konačan, ali prebrojiv. Drugim riječima, veličina se naziva diskretnom ako se njezine vrijednosti mogu numerirati. Slučajna varijabla može se opisati pomoću zakona distribucije. Zakon distribucije diskretne slučajne varijable $X$ može se zadati u obliku tablice u kojoj su u prvom retku sve moguće vrijednosti slučajne varijable u rastućem redoslijedu, a u drugom retku su odgovarajuće vjerojatnosti tih vrijednosti: Slika 1. gdje je $r1+ r2+ ... + rn = 1$. Ova tablica je blizu distribucije diskretne slučajne varijable. Ako je skup mogućih vrijednosti slučajne varijable beskonačan, tada niz $r1+ r2+ ... + rn+ ...$ konvergira i njegova suma će biti jednaka $1$. Zakon distribucije diskretne slučajne varijable $X$ može se prikazati grafički, za što se u koordinatnom sustavu konstruira izlomljena linija (pravokutnik), koja sekvencijalno povezuje točke s koordinatama $(xi;pi), i=1,2, ... n$. Linija koju smo dobili zove se distribucijski poligon. Slika 2. Zakon distribucije diskretne slučajne varijable $X$ može se prikazati i analitički (pomoću formule): $P(X=xi)= \varphi (xi),i =1,2,3 ... n$. Pri rješavanju mnogih problema u teoriji vjerojatnosti potrebno je izvesti operacije množenja diskretne slučajne varijable s konstantom, zbrajanja dviju slučajnih varijabli, njihovog množenja, zamjene na potenciju. U tim slučajevima potrebno je pridržavati se sljedećih pravila za slučajne diskretne veličine: Definicija 3 Množenje diskretne slučajne varijable $X$ konstantom $K$ je diskretna slučajna varijabla $Y=KX,$ koja je određena jednakostima: $y_i=Kx_i,\ \ p\left(y_i\right)=p\ lijevo(x_i\desno)= p_i,\ \ i=\overline(1,\ n).$ Definicija 4 Pozivaju se dvije slučajne varijable $x$ i $y$ nezavisna, ako zakon raspodjele jedne od njih ne ovisi o tome koje je moguće vrijednosti stekla druga količina. Definicija 5 Iznos dvije neovisne diskretne slučajne varijable $X$ i $Y$ nazivaju se slučajna varijabla $Z=X+Y,$ određena je jednakostima: $z_(ij)=x_i+y_j$, $P\left(z_(ij )\desno)= P\lijevo(x_i\desno)P\lijevo(y_j\desno)=p_ip"_j$, $i=\overline(1,n)$, $j=\overline(1,m)$ , $P\lijevo (x_i\desno)=p_i$, $P\lijevo(y_j\desno)=p"_j$. Definicija 6 Množenje dvije neovisne diskretne slučajne varijable $X$ i $Y$ nazivaju se slučajna varijabla $Z=XY,$ određena je jednakostima: $z_(ij)=x_iy_j$, $P\lijevo(z_(ij)\desno) =P\lijevo( x_i\desno)P\lijevo(y_j\desno)=p_ip"_j$, $i=\overline(1,n)$, $j=\overline(1,m)$, $P\ lijevo(x_i\desno )=p_i$, $P\lijevo(y_j\desno)=p"_j$. Uzmimo u obzir da neki umnošci $x_(i\ \ \ \ \ )y_j$ mogu biti međusobno jednaki. U tom je slučaju vjerojatnost zbrajanja umnoška jednaka zbroju odgovarajućih vjerojatnosti. Na primjer, ako je $x_2\ \ y_3=x_5\ \ y_7,\ $tada će vjerojatnost $x_2y_3$ (ili istog $x_5y_7$) biti jednaka $p_2\cdot p"_3+p_5\cdot p"_7 .$ Gore navedeno vrijedi i za iznos. Ako je $x_1+\ y_2=x_4+\ \ y_6,$ tada će vjerojatnost $x_1+\ y_2$ (ili istog $x_4+\ y_6$) biti jednaka $p_1\cdot p"_2+p_4\cdot p"_6. $ Slučajne varijable $X$ i $Y$ određene su zakonima distribucije: Slika 3. Gdje je $p_1+p_2+p_3=1,\ \ \ p"_1+p"_2=1.$ Tada će zakon raspodjele zbroja $X+Y$ imati oblik Slika 4. I zakon distribucije proizvoda $XY$ će imati oblik Slika 5. Potpuni opis slučajne varijable također daje funkcija distribucije. Geometrijski, funkcija distribucije se objašnjava kao vjerojatnost da slučajna varijabla $X$ poprimi vrijednost koja je na brojevnom pravcu predstavljena točkom koja leži lijevo od točke $x$. Možemo istaknuti najčešće zakone raspodjele diskretnih slučajnih varijabli: Za zadane distribucije diskretnih slučajnih varijabli izračun vjerojatnosti njihovih vrijednosti, kao i numeričkih karakteristika (matematičko očekivanje, varijanca, itd.) provodi se pomoću određenih "formula". Stoga je vrlo važno poznavati ove vrste distribucija i njihova osnovna svojstva. Diskretna slučajna varijabla $X$ podliježe binomnom zakonu distribucije vjerojatnosti ako uzima vrijednosti $0,\ 1,\ 2,\ \dots ,\ n$ s vjerojatnostima $P\left(X=k\right)= C^k_n\cdot p^k\cdot (\lijevo(1-p\desno))^(n-k)$. Zapravo, slučajna varijabla $X$ je broj pojavljivanja događaja $A$ u $n$ neovisnih pokušaja. Zakon distribucije vjerojatnosti slučajne varijable $X$: $\begin(niz)(|c|c|) Za takvu slučajnu varijablu matematičko očekivanje je $M\left(X\right)=np$, varijanca je $D\left(X\right)=np\left(1-p\right)$. Primjer
. Obitelj ima dvoje djece. Pretpostavljajući da su vjerojatnosti rođenja dječaka i djevojčice jednake 0,5$, pronađite zakon distribucije slučajne varijable $\xi$ - broja dječaka u obitelji. Neka je slučajna varijabla $\xi $ broj dječaka u obitelji. Vrijednosti koje $\xi može poprimiti:\ 0,\ 1,\ 2$. Vjerojatnosti ovih vrijednosti mogu se pronaći pomoću formule $P\lijevo(\xi =k\desno)=C^k_n\cdot p^k\cdot (\lijevo(1-p\desno))^(n-k )$, gdje je $n =2$ broj neovisnih pokušaja, $p=0,5$ je vjerojatnost da će se događaj dogoditi u nizu od $n$ pokušaja. Dobivamo: $P\lijevo(\xi =0\desno)=C^0_2\cdot (0,5)^0\cdot (\lijevo(1-0,5\desno))^(2-0)=(0, 5)^2=0,25;$ $P\lijevo(\xi =1\desno)=C^1_2\cdot 0,5\cdot (\lijevo(1-0,5\desno))^(2-1)=2\cdot 0,5\ cdot 0,5=0,5;$ $P\lijevo(\xi =2\desno)=C^2_2\cdot (0,5)^2\cdot (\lijevo(1-0,5\desno))^(2-2)=(0, 5)^2 =0,25 $ Tada je zakon raspodjele slučajne varijable $\xi $ korespondencija između vrijednosti $0,\ 1,\ 2$ i njihovih vjerojatnosti, to jest: $\begin(niz)(|c|c|) Zbroj vjerojatnosti u zakonu distribucije trebao bi biti jednak $1$, odnosno $\sum _(i=1)^(n)P(\xi _((\rm i)))=0,25+0,5+ 0, 25=1 dolar. Očekivanje $M\lijevo(\xi \desno)=np=2\cdot 0,5=1$, varijanca $D\lijevo(\xi \desno)=np\lijevo(1-p\desno)=2\ cdot 0,5\ cdot 0,5=0,5$, standardna devijacija $\sigma \lijevo(\xi \desno)=\sqrt(D\lijevo(\xi \desno))=\sqrt(0,5 )\približno 0,707 $. Ako diskretna slučajna varijabla $X$ može poprimiti samo nenegativne cjelobrojne vrijednosti $0,\ 1,\ 2,\ \dots ,\ n$ s vjerojatnostima $P\left(X=k\right)=((( \lambda )^k )\preko (k}\cdot e^{-\lambda }$, то говорят, что она подчинена закону распределения Пуассона с параметром $\lambda $. Для такой случайной величины математическое ожидание и дисперсия равны между собой и равны параметру $\lambda $, то есть $M\left(X\right)=D\left(X\right)=\lambda $.!} Komentar. Posebnost ove distribucije je da, na temelju eksperimentalnih podataka, nalazimo procjene $M\lijevo(X\desno),\ D\lijevo(X\desno)$, ako su dobivene procjene bliske jedna drugoj, tada imamo razloga za tvrdnju da slučajna varijabla podliježe Poissonovom zakonu distribucije. Primjer
. Primjeri slučajnih varijabli koje podliježu Poissonovom zakonu distribucije mogu biti: broj automobila koje će benzinska postaja opsluživati sutra; broj neispravnih artikala u proizvedenim proizvodima. Primjer
. Tvornica je poslala 500$ proizvoda u bazu. Vjerojatnost oštećenja proizvoda u transportu je 0,002$. Naći zakon raspodjele slučajne varijable $X$ jednak broju oštećenih proizvoda; što je $M\lijevo(X\desno),\ D\lijevo(X\desno)$. Neka diskretna slučajna varijabla $X$ bude broj oštećenih proizvoda. Takva slučajna varijabla podliježe Poissonovom zakonu distribucije s parametrom $\lambda =np=500\cdot 0,002=1$. Vjerojatnosti vrijednosti jednake su $P\lijevo(X=k\desno)=(((\lambda )^k)\preko (k}\cdot e^{-\lambda }$. Очевидно, что все вероятности всех значений $X=0,\ 1,\ \dots ,\ 500$ перечислить невозможно, поэтому мы ограничимся лишь первыми несколькими значениями.!} $P\lijevo(X=0\desno)=((1^0)\preko (0}\cdot e^{-1}=0,368;$!} $P\lijevo(X=1\desno)=((1^1)\preko (1}\cdot e^{-1}=0,368;$!} $P\lijevo(X=2\desno)=((1^2)\preko (2}\cdot e^{-1}=0,184;$!} $P\lijevo(X=3\desno)=((1^3)\preko (3}\cdot e^{-1}=0,061;$!} $P\lijevo(X=4\desno)=((1^4)\preko (4}\cdot e^{-1}=0,015;$!} $P\lijevo(X=5\desno)=((1^5)\preko (5}\cdot e^{-1}=0,003;$!} $P\lijevo(X=6\desno)=((1^6)\preko (6}\cdot e^{-1}=0,001;$!} $P\lijevo(X=k\desno)=(((\lambda )^k)\preko (k}\cdot e^{-\lambda }$!} Zakon distribucije slučajne varijable $X$: $\begin(niz)(|c|c|) Za takvu slučajnu varijablu, matematičko očekivanje i varijanca su međusobno jednaki i jednaki parametru $\lambda $, to jest, $M\left(X\right)=D\left(X\right)=\lambda =1$. Ako diskretna slučajna varijabla $X$ može poprimiti samo prirodne vrijednosti $1,\ 2,\ \dots ,\ n$ s vjerojatnostima $P\left(X=k\right)=p(\left(1-p\ desno)) ^(k-1),\ k=1,\ 2,\ 3,\ \točkice $, onda kažu da takva slučajna varijabla $X$ podliježe geometrijskom zakonu distribucije vjerojatnosti. Zapravo, geometrijska distribucija je Bernoullijev test do prvog uspjeha. Primjer
. Primjeri slučajnih varijabli koje imaju geometrijsku raspodjelu mogu biti: broj hitaca prije prvog pogotka u metu; broj testiranja uređaja do prvog kvara; broj bacanja novčića dok se ne pojavi prva glava, itd. Matematičko očekivanje i varijanca slučajne varijable podložne geometrijskoj distribuciji jednaki su $M\left(X\right)=1/p$, $D\left(X\right)=\left(1-p\right )/p^ $2. Primjer
. Na putu kretanja ribe do mrijestilišta nalazi se prevodnica od 4$. Vjerojatnost da riba prođe kroz svaku bravu je $p=3/5$. Konstruirajte niz distribucije slučajne varijable $X$ - broja prevoja koje je riba prošla prije prvog zadržavanja u preklopu. Pronađite $M\lijevo(X\desno),\ D\lijevo(X\desno),\ \sigma \lijevo(X\desno)$. Neka slučajna varijabla $X$ bude broj lokacija koje je riba prošla prije prvog zaustavljanja u kopči. Takva slučajna varijabla podliježe geometrijskom zakonu distribucije vjerojatnosti. Vrijednosti koje slučajna varijabla $X može poprimiti: $ 1, 2, 3, 4. Vjerojatnosti ovih vrijednosti izračunavaju se pomoću formule: $P\lijevo(X=k\desno)=pq^(k -1)$, gdje je: $ p=2/5$ - vjerojatnost da riba bude zadržana kroz prevodnicu, $q=1-p=3/5$ - vjerojatnost da riba prođe kroz prevodnicu, $k=1,\ 2,\ 3,\ 4$. $P\lijevo(X=1\desno)=((2)\preko (5))\cdot (\lijevo(((3)\preko (5))\desno))^0=((2)\ preko (5))=0,4;$ $P\lijevo(X=2\desno)=((2)\preko (5))\cdot ((3)\preko (5))=((6)\preko (25))=0,24; $ $P\lijevo(X=3\desno)=((2)\preko (5))\cdot (\lijevo(((3)\preko (5))\desno))^2=((2)\ preko (5))\cdot ((9)\preko (25))=((18)\preko (125))=0,144;$ $P\lijevo(X=4\desno)=((2)\preko (5))\cdot (\lijevo(((3)\preko (5))\desno))^3+(\lijevo(( (3)\preko (5))\desno))^4=((27)\preko (125))=0,216.$ $\begin(niz)(|c|c|) Očekivana vrijednost: $M\lijevo(X\desno)=\sum^n_(i=1)(x_ip_i)=1\cdot 0,4+2\cdot 0,24+3\cdot 0,144+4\cdot 0,216=2,176.$ Disperzija: $D\lijevo(X\desno)=\sum^n_(i=1)(p_i(\lijevo(x_i-M\lijevo(X\desno)\desno))^2=)0,4\cdot (\ lijevo( 1-2,176\desno))^2+0,24\cdot (\lijevo(2-2,176\desno))^2+0,144\cdot (\lijevo(3-2,176\desno))^2+$ $+\0,216\cdot (\lijevo(4-2,176\desno))^2\približno 1,377.$ Standardna devijacija: $\sigma \lijevo(X\desno)=\sqrt(D\lijevo(X\desno))=\sqrt(1377)\približno 1173.$ Ako $N$ objekata, među kojima $m$ objekata ima zadano svojstvo. $n$ objekata se nasumično dohvaća bez vraćanja, među kojima je bilo $k$ objekata koji imaju zadano svojstvo. Hipergeometrijska distribucija omogućuje procjenu vjerojatnosti da točno $k$ objekata u uzorku ima zadano svojstvo. Neka je slučajna varijabla $X$ broj objekata u uzorku koji imaju određeno svojstvo. Tada su vjerojatnosti vrijednosti slučajne varijable $X$: $P\lijevo(X=k\desno)=((C^k_mC^(n-k)_(N-m))\preko (C^n_N))$ Komentar. Statistička funkcija HYPERGEOMET čarobnjaka za $f_x$ funkciju programa Excel omogućuje određivanje vjerojatnosti da će određeni broj testova biti uspješan. $f_x\to$ statistički$\do$ HIPERGEOMET$\do$ u redu. Pojavit će se dijaloški okvir koji trebate ispuniti. U kolumni Broj_uspjeha_u_uzorku označiti vrijednost $k$. veličina uzorka jednako $n$. U kolumni Broj_uspjeha_zajedno označite vrijednost $m$. veličina_populacije jednako $N$. Matematičko očekivanje i varijanca diskretne slučajne varijable $X$, podložne geometrijskom zakonu raspodjele, redom su jednake $M\lijevo(X\desno)=nm/N$, $D\lijevo(X\desno)= ((nm\lijevo(1 -((m)\preko (N))\desno)\lijevo(1-((n)\preko (N))\desno))\preko (N-1))$. Primjer
. U kreditnom odjelu banke zaposleno je 5 stručnjaka s višom financijskom spremom i 3 stručnjaka s višom pravnom spremom. Uprava banke odlučila je poslati 3 stručnjaka da poboljšaju svoje kvalifikacije, odabirući ih slučajnim redoslijedom. a) Napraviti seriju raspodjele za broj stručnjaka s višim financijskim obrazovanjem koji se mogu poslati na usavršavanje svojih vještina; b) Odredite numeričke karakteristike ove distribucije. Neka je slučajna varijabla $X$ broj stručnjaka s visokim financijskim obrazovanjem među tri odabrana. Vrijednosti koje $X može primiti: 0,\ 1,\ 2,\ 3$. Ova slučajna varijabla $X$ raspoređena je prema hipergeometrijskoj distribuciji sa sljedećim parametrima: $N=8$ - veličina populacije, $m=5$ - broj uspjeha u populaciji, $n=3$ - veličina uzorka, $ k=0,\ 1, \2,\3$ - broj uspjeha u uzorku. Tada se vjerojatnosti $P\lijevo(X=k\desno)$ mogu izračunati pomoću formule: $P(X=k)=(C_(m)^(k) \cdot C_(N-m)^(n-k) \ preko C_( N)^(n) ) $. Imamo: $P\lijevo(X=0\desno)=((C^0_5\cdot C^3_3)\preko (C^3_8))=((1)\preko (56))\približno 0,018;$ $P\lijevo(X=1\desno)=((C^1_5\cdot C^2_3)\preko (C^3_8))=((15)\preko (56))\približno 0,268;$ $P\lijevo(X=2\desno)=((C^2_5\cdot C^1_3)\preko (C^3_8))=((15)\preko (28))\približno 0,536;$ $P\lijevo(X=3\desno)=((C^3_5\cdot C^0_3)\preko (C^3_8))=((5)\preko (28))\približno 0,179.$ Tada niz distribucije slučajne varijable $X$: $\begin(niz)(|c|c|) Izračunajmo numeričke karakteristike slučajne varijable $X$ pomoću općih formula hipergeometrijske distribucije. $M\lijevo(X\desno)=((nm)\preko (N))=((3\cdot 5)\preko (8))=((15)\preko (8))=1,875.$ $D\lijevo(X\desno)=((nm\lijevo(1-((m)\preko (N))\desno)\lijevo(1-((n)\preko (N))\desno)) \preko (N-1))=((3\cdot 5\cdot \lijevo(1-((5)\preko (8))\desno)\cdot \lijevo(1-((3)\preko (8) ))\desno))\preko (8-1))=((225)\preko (448))\približno 0,502.$ $\sigma \lijevo(X\desno)=\sqrt(D\lijevo(X\desno))=\sqrt(0,502)\približno 0,7085.$ x; značenje F(5); vjerojatnost da slučajna varijabla xće uzeti vrijednosti iz segmenta. Konstruirajte poligon distribucije. Postaviti zakon raspodjele slučajne varijable x u obliku tablice. Pronađite funkciju distribucije slučajne varijable x. Konstruirajte grafove funkcija i . Izračunajte matematičko očekivanje, varijancu, mod i medijan slučajne varijable x. Uzorak A: 6 9 7 6 4 4 Uzorak B: 55 72 54 53 64 53 59 48 42 46 50 63 71 56 54 59 54 44 50 43 51 52 60 43 50 70 68 59 53 58 62 49 59 51 52 47 57 71 60 46 55 58 72 47 60 65 63 63 58 56 55 51 64 54 54 63 56 44 73 41 68 54 48 52 52 50 55 49 71 67 58 46 50 51 72 63 64 48 47 55 Opcija 17. Izračunajte njegovo matematičko očekivanje i varijancu. Pronađite funkciju distribucije slučajne varijable x. Konstruirajte grafove funkcija i . Izračunajte matematičko očekivanje, varijancu, modus i medijan slučajne varijable X. · prosjek uzorka; · varijanca uzorka; Mod i medijan; Uzorak A: 0 0 2 2 1 4 · prosjek uzorka; · varijanca uzorka; standardna devijacija uzorka; · mod i medijan; Uzorak B: 166 154 168 169 178 182 169 159 161 150 149 173 173 156 164 169 157 148 169 149 157 171 154 152 164 157 177 155 167 169 175 166 167 150 156 162 170 167 161 158 168 164 170 172 173 157 157 162 156 150 154 163 143 170 170 168 151 174 155 163 166 173 162 182 166 163 170 173 159 149 172 176 Opcija 18. Izračunajte njegovo matematičko očekivanje i varijancu. Nađite funkciju distribucije slučajne varijable X. Nacrtajte grafove funkcija i . Izračunajte matematičko očekivanje, varijancu, mod i medijan slučajne varijable X. · prosjek uzorka; · varijanca uzorka; standardna devijacija uzorka; · mod i medijan; Uzorak A: 4 7 6 3 3 4 · prosjek uzorka; · varijanca uzorka; standardna devijacija uzorka; · mod i medijan; Uzorak B: 152 161 141 155 171 160 150 157 154 164 138 172 155 152 177 160 168 157 115 128 154 149 150 141 172 154 144 177 151 128 150 147 143 164 156 145 156 170 171 142 148 153 152 170 142 153 162 128 150 146 155 154 163 142 171 138 128 158 140 160 144 150 162 151 163 157 177 127 141 160 160 142 159 147 142 122 155 144 170 177 Opcija 19. 1. Na gradilištu radi 16 žena i 5 muškaraca. 3 osobe su odabrane nasumično pomoću njihovih osobnih brojeva. Nađite vjerojatnost da će svi odabrani ljudi biti muškarci. 2. Bacaju se četiri novčića. Nađite vjerojatnost da će samo dva novčića imati "grb". 3. Riječ “PSIHOLOGIJA” sastoji se od kartica od kojih svaka ima jedno slovo napisano na sebi. Karte se miješaju i vade jedna po jedna bez vraćanja. Odredite vjerojatnost da izvađena slova tvore riječ: a) PSIHOLOGIJA; b) OSOBLJE. 4. Urna sadrži 6 crnih i 7 bijelih kuglica. Nasumično se izvlači 5 kuglica. Odredite vjerojatnost da među njima ima: a. 3 bijele kuglice; b. manje od 3 bijele kuglice; c. barem jednu bijelu kuglu. 5. Vjerojatnost događanja događaja A u jednom pokusu jednak je 0,5. Odredite vjerojatnosti sljedećih događaja: a. događaj A pojavljuje se 3 puta u nizu od 5 neovisnih ispitivanja; b. događaj A pojavit će se najmanje 30 i ne više od 40 puta u seriji od 50 suđenja. 6. Postoji 100 strojeva iste snage, koji rade neovisno jedan o drugom u istom režimu, pri čemu im je pogon uključen 0,8 radnih sati. Kolika je vjerojatnost da će u bilo kojem trenutku biti uključeno od 70 do 86 strojeva? 7. Prva urna sadrži 4 bijele i 7 crnih kuglica, a druga urna sadrži 8 bijelih i 3 crne kuglice. Iz prve urne nasumično se izvlače 4 kuglice, a iz druge 1 kuglica. Odredite vjerojatnost da među izvučenim kuglicama budu samo 4 crne kuglice. 8. Autosalon dnevno prima automobile tri marke u količinama: “Moskvich” – 40%; "Oka" - 20%; "Volga" - 40% svih uvezenih automobila. Među automobilima Moskvich, 0,5% ima protuprovalni uređaj, Oka – 0,01%, Volga – 0,1%. Nađite vjerojatnost da automobil odveden na pregled ima protuprovalni uređaj. 9. Na segmentu se slučajno biraju brojevi i . Odredite vjerojatnost da ti brojevi zadovoljavaju nejednadžbe. 10. Zadan je zakon raspodjele slučajne varijable x: Pronađite funkciju distribucije slučajne varijable x; značenje F(2); vjerojatnost da slučajna varijabla xće uzeti vrijednosti iz intervala. Konstruirajte poligon distribucije.
1.2.
p4=0,1; 0 pri x≤-1,
https://pandia.ru/text/78/455/images/image038_17.gif" width="14" height="86"> 0 za x≤a,
,
Normalna krivulja je simetrična u odnosu na ravnu liniju x=m, ima maksimum pri x=a, jednak .
,
, ili:
. Koja je vjerojatnost da će u cijeloj seriji biti točno 3 neispravna patrona?
, Gdje .
.
.
.
.
Za 
, To
.
.
– Laplaceova funkcija.
Operacije na diskretnim vjerojatnostima
Funkcija distribucije
1. Binomni zakon raspodjele.
\hline
X_i & 0 & 1 & \točke & n \\
\hline
p_i & P_n\lijevo(0\desno) & P_n\lijevo(1\desno) & \točke & P_n\lijevo(n\desno) \\
\hline
\end(niz)$
\hline
\xi & 0 & 1 & 2 \\
\hline
P(\xi) & 0,25 & 0,5 & 0,25 \\
\hline
\end(niz)$2. Poissonov zakon distribucije.
\hline
X_i & 0 & 1 & 2 & 3 & 4 & 5 & 6 & ... & k \\
\hline
P_i & 0,368; & 0,368 & 0,184 & 0,061 & 0,015 & 0,003 & 0,001 & ... & (((\lambda )^k)\preko (k}\cdot e^{-\lambda } \\!}
\hline
\end(niz)$3. Geometrijski zakon raspodjele.
\hline
X_i & 1 & 2 & 3 & 4 \\
\hline
P\lijevo(X_i\desno) & 0,4 & 0,24 & 0,144 & 0,216 \\
\hline
\end(niz)$4. Hipergeometrijski zakon raspodjele.
\hline
X_i & 0 & 1 & 2 & 3 \\
\hline
p_i & 0,018 & 0,268 & 0,536 & 0,179 \\
\hline
\end(niz)$ x
–28
–20
–12
–4
str
0,22
0,44
0,17
0,1
0,07
x
str
0,1
0,2
0,3
0,4
Pogledajte što je "Legija (broj)" u drugim rječnicima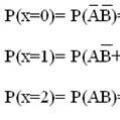
Primjeri rješavanja problema na temu "Slučajne varijable"
Čitam pjesmu Nekrasova "Mraz, crveni nos".