Лінійні різницеві рівняння із постійними коефіцієнтами. Диференціальні рівняння для "чайників"

Часто лише згадка диференціальних рівнянь викликає у студентів неприємне почуття. Чому так відбувається? Найчастіше тому, що при вивченні основ матеріалу виникає пробіл у знаннях, через яке подальше вивчення дифурів ставати просто тортурами. Нічого не зрозуміло, що робити, як вирішувати, з чого почати?

Однак ми намагатимемося вам показати, що дифури – це не так складно, як здається.

Основні поняття теорії диференціальних рівнянь

Зі школи нам відомі найпростіші рівняння, в яких потрібно знайти невідому x. По суті диференційне рівняннялише трішки відрізняються від них – замість змінної х у них потрібно знайти функцію y(х) , яка оберне рівняння в тотожність.

Диференціальні рівняння мають велике прикладне значення. Це не абстрактна математика, яка не має відношення до навколишнього світу. За допомогою диференціальних рівнянь описуються багато реальних природних процесів. Наприклад, коливання струни, рух гармонійного осцилятора, за допомогою диференціальних рівнянь у завданнях механіки знаходять швидкість та прискорення тіла. Також ДКзнаходять широке застосування у біології, хімії, економіці та багатьох інших науках.

Диференціальне рівняння (ДК) – це рівняння, що містить похідні функції y(х), саму функцію, незалежні змінні та інші параметри у різних комбінаціях.

Існує безліч видів диференціальних рівнянь: звичайні диференціальні рівняння, лінійні та нелінійні, однорідні та неоднорідні, диференціальні рівняння першого та вищих порядків, дифури у приватних похідних тощо.

Рішенням диференціального рівняння є функція, яка перетворює його на тотожність. Існують загальні та приватні рішення ДК.

Загальним рішенням ДК є загальна кількість рішень, що обертають рівняння у тотожність. Приватним рішенням диференціального рівняння називається рішення, що задовольняє додатковим умовам, заданим спочатку.

Порядок диференціального рівняння визначається найвищим порядком похідних, що входять до нього.

Звичайні диференціальні рівняння

Звичайні диференціальні рівняння- Це рівняння, що містять одну незалежну змінну.

Розглянемо найпростіше звичайне диференціальне рівняння першого ладу. Воно має вигляд:

Вирішити таке рівняння можна, просто проінтегрувавши його праву частину.

Приклади таких рівнянь:

Рівняння з змінними, що розділяються

Загалом цей тип рівнянь виглядає так:

Наведемо приклад:

Вирішуючи таке рівняння, потрібно розділити змінні, привівши його до вигляду:

Після цього залишиться проінтегрувати обидві частини та отримати рішення.

Лінійні диференціальні рівняння першого порядку

Такі рівняння мають вигляд:

Тут p(x) і q(x) – деякі функції незалежної змінної, а y=y(x) – потрібна функція. Наведемо приклад такого рівняння:

Вирішуючи таке рівняння, найчастіше використовують метод варіації довільної постійної чи представляють потрібну функцію як твори двох інших функцій y(x)=u(x)v(x).

Для вирішення таких рівнянь необхідна певна підготовка і взяти їх з наскоку буде досить складно.

Приклад рішення ДК з змінними, що розділяються.

Ось ми й розглянули найпростіші типи дистанційного керування. Тепер розберемо рішення одного з них. Нехай це буде рівняння з змінними, що розділяються.

Спочатку перепишемо похідну у більш звичному вигляді:

Потім розділимо змінні, тобто в одній частині рівняння зберемо всі "ігреки", а в іншій - "ікси":

Тепер залишилося проінтегрувати обидві частини:

Інтегруємо та отримуємо загальне рішення даного рівняння:

Звісно, розв'язання диференціальних рівнянь – свого роду мистецтво. Потрібно вміти розуміти, якого типу належить рівняння, і навіть навчитися бачити, які перетворення треба з ним зробити, щоб призвести до того чи іншого виду, не кажучи вже просто про вміння диференціювати та інтегрувати. І щоб досягти успіху у вирішенні ДК, потрібна практика (як і у всьому). А якщо у Вас в даний момент немає часу розбиратися з тим, як вирішуються диференціальні рівняння або завдання Коші стала як кістка в горлі або ви не знаєте, як правильно оформити презентацію, зверніться до наших авторів. У стислий термін ми надамо Вам готове та докладне рішення, розібратися в подробицях якого Ви зможете у будь-який зручний для Вас час. А поки що пропонуємо подивитися відео на тему "Як вирішувати диференціальні рівняння":

Розглянемо різницеве рівняння n-го порядку

y(k) = F(k) (92)

Як і для диференціальних рівнянь, рішення завжди визначається рівнянь першого порядку й у випадку може бути знайдено для рівнянь вищого порядку.

Допоміжне рішення.

Розглянемо однорідне рівняння першого порядку

a 1 (k) y (k + 1) + a 0 (k) y (k) = 0, (93)

де a 0 (k)≠0 та a 1 (k)≠0. Його можна переписати у вигляді

y(k+1) = a(k)y(k). (94)

при k=0,1,2...

у(1)=а(0)у(0),

у(2)=а(1)а(0)у(0)

у(3)=а(2)а(1)а(0)у(0)

або, у загальному випадку,

так що загальне рішення рівняння (94) одно

Нижня межа твору довільна, тому що будь-яке фіксоване число множників а(0), а(1), і а(2), ... можна об'єднати з довільною постійною С.

Рішення однорідного рівняння вище за перший порядок у загальному випадку не виражається у вигляді елементарних функцій, оскільки процедура, заснована на рівняннях (81) і (82), при залежних від k коефіцієнтах перестає бути справедливою. Якщо відомі всі, крім одного, незалежні рішення рівняння, то можна визначити і рішення, що залишилося. Як і для диференціальних рівнянь, у деяких випадках вдається отримати рішення в явному вигляді. Рівняння виду

a n f (k + n) y (k + n) + ... + a 1 f (k + 1) y (k + 1) + a n f (k) y (k) = 0,

де коефіцієнти а i - постійні величини шляхом підстановки z(k)=f(k)y(k) зводиться до різницевого рівняння з постійними коефіцієнтами. Процедура частково подібна до використовуваної для диференціального рівняння Ейлера, але заміні в цьому випадку підлягає залежна (а не незалежна) змінна. Цей метод широко використовується під час вирішення рівнянь зі змінними коефіцієнтами.

Диференціальні рівняння систем автоматичного регулювання. Методика складання диференціальних рівнянь систем автоматичного регулирования.

Загальні зауваження.

Системи автоматичного регулювання різноманітні за своїм призначенням та конструктивним виконанням. Поведінка САР може описуватися звичайними диференціальними рівняннями у приватних похідних, різницевими рівняннями тощо.

Будь-яка САР представляє сукупність окремих елементів, що взаємодіють один з одним, з'єднаних між собою зв'язками. Першим етапом при складанні диференціальних рівнянь САР є розподіл системи на окремі елементи та складання диференціальних рівнянь цих елементів. Рівняння елементів і рівняння зв'язків між окремими елементами описують процес у системі регулювання, тобто. зміна часу всіх координат системи. Знаючи рівняння елементів та рівняння зв'язків, можна скласти структурну схему САР.

Структурна схема САР характеризує геометрію системи, тобто. показує, із яких елементів складається САР і як ці елементи пов'язані між собою. Стан САР, а також кожного елемента, що входить до неї, характеризується деяким числом незалежних змінних. Цими змінними може бути як електричні величини (струм, напруга, тощо.), і механічні (швидкість, кут повороту, переміщення тощо.). Зазвичай, щоб характеризувати стан системи чи її елемента, вибирають одну узагальнену координату на вході системи чи елемента (g(t)) і одну – виході (x(t)). У ряді випадків таке уявлення неможливе, оскільки система або її елемент можуть мати кілька вхідних та вихідних величин. У багатовимірних системах можна розглядати векторні вхідну та вихідну величини з розмірностями, що збігаються відповідно до числа вхідних та вихідних величин САР.

Складання та лінеаризація диференціальних рівнянь елементів систем.

p align="justify"> При складанні диференціальних рівнянь САР основним завданням є складання диференціальних рівнянь окремих елементів системи. Рівняння окремих елементів складаються з урахуванням тих фізичних законів, які характеризують поведінка елемента.

При складанні диференціальних рівнянь елементів САР слід прагнути якомога точніше описати поведінку цього елемента. Проте складність отриманих у своїй рівнянь ускладнює дослідження властивостей їх рішень. Тому при складанні диференціальних рівнянь необхідно прагнути розумного компромісу між можливо більш повним описом поведінки елемента і можливістю огляду та дослідження отриманих рівнянь.

Якщо динаміка елемента описується лінійним диференціальним рівнянням, цей елемент називається лінійнимякщо диференціальне рівняння не лінійне, то елемент називається нелінійним.

Для спрощення аналізу, коли це можливо, приблизно замінюють нелінійні диференціальні рівняння такими лінійними рівняннями, рішення яких з достатнім ступенем точності збігаються з рішеннями нелінійних рівнянь. Цей процес заміни нелінійного диференціального рівняння лінійним називається лінеаризацією.

Якщо диференціальне рівняння елемента нелінійно через нелінійність його статичної характеристики, лінеаризація рівняння зводиться до заміни нелінійної характеристики елемента x=φ(g) деякою лінійною функцією x= ag+ b. Аналітично ця заміна проводиться за допомогою розкладання в ряд Тейлора функції x=φ(g) в околиці точки, що відповідає встановленому стану і відкидання всіх членів, що містять відхилення ∆g вхідної величини елемента в ступені вище першої. Геометрично це означає заміну кривої x=φ(g) дотичної, проведеної до кривої в точці (x 0 , g 0), що відповідає стану роботи елемента, що встановився (рис. 29). В інших випадках лінеаризація проводиться шляхом проведення січної, що мало відхиляється від функції x=φ(g) у необхідному діапазоні зміни вхідної величини елемента.

Поряд з лінеаризується характеристиками є такі характеристики, які не піддаються такої лінеаризації. До них відносяться, наприклад, характеристики, що не розкладаються в ряд Тейлора в околиці точки стану, що встановився. Такі характеристики називатимемо суттєво нелінійними.

Розглянемо процес лінеаризації нелінійного рівняння елемента з допомогою низки Тейлора. Нехай поведінка елемента описується нелінійним диференціальним рівнянням

F(x n , x ', x, g) = 0 (1). Тоді стан елемента характеризується рівнянням F(0, 0, x, g) = 0 (2). нехай g 0 і х 0 - значення стану, що встановився. Тоді координати g і х можна записати у вигляді x = x 0 + ∆x, g = g 0 + ∆g, де ∆g і ∆x - відхилення координат g і х від стану, що встановився. Рівняння (1) у відхиленнях має вигляд:

F(∆x '' , ∆x ' , x 0 + ∆x, g 0 + ∆g) = 0 (3).

Розкладемо ліву частину рівняння (3) в ряд Тейлора щодо точки стану (0, 0, x 0 , g 0):

Приватні похідні в лівій частині рівняння (4) є деякими числами, величини яких залежать від виду функції F(x '' , x ' , x, g) і значень координат x 0 і g 0 .

Вважаючи відхилення ∆g, ∆x від стану, а також їх похідні за часом малими і пологуючи, що функція F(x '' , x ' , x, g) досить гладка за всіма аргументами в околиці точки, що відповідає стану, що залишився, відкинемо у рівнянні (4) всі члени, які містять відхилення ∆g і ∆x, а також їх похідні ступеня вище першої. Отримане рівняння (5) є лінійним диференціальним рівнянням із постійними коефіцієнтами ,,,і є результатом лінеаризації рівняння (1).

Очевидно, що необхідною умовою лінеаризації є можливість розкладання в ряд Тейлора функції F(x '' , x ' , x, g) в околиці точки, що відповідає стану, що встановився.

Процес лінеаризації рівняння (1) може бути геометрично інтерпретований в такий спосіб. У просторі змінних x '' , x ' , x, g рівняння (1) задає деяку поверхню. Перехід від рівняння (1) до лінійного рівняння (5) означає заміну поверхні деякою дотичної площиною, проведеної до поверхні в точці, що відповідає стану, що встановився. Природно, що помилка при такій заміні тим менша, чим менше відрізняються один від одного точки поверхні та точки площини. Це справедливо лише в деякій малій околиці стану, що встановився.

Поняття керованості та спостережуваності.

Процес або об'єкт прийнято називати повністю керованим, якщо він може бути переведений з деякого стану х(t 0) бажаний стан рівноваги х(t 1) за кінцевий інтервал часу t 1 - t 0 . Іншими словами, процес є повністю керованим, якщо існує керуючий вплив m(t), визначений на кінцевому інтервалі часу t 0 t t 1 , яке переводить процес з початкового стану х (t 0) в бажаний стан рівноваги х (t 1) за час t1 - t0.

Необхідні та достатні умови повної керованості для випадку дискретних систем можна сформулювати в такий спосіб.

Лінійний дискретний процес n-го порядку є повністю керованим тоді і лише тоді, коли вектори

s 1 = φ(-T)h(T),

s 2 = φ(-T)h(T),

s n = φ(-T)h(T)

лінійно незалежні.

Ці вектори виникають у зв'язку із такими перетвореннями.

(t) = Ax(t) + d m(t),

в якому m(t) - єдиний вплив, що управляє. Випадок єдиного керуючого впливу розглядається задля спрощення інтерпретації одержуваних виразів. Рівняння перехідних станів процесу має вигляд

де φ(Т) – матриця переходу процесу та
.

Поняття керованості можна дати ще й інше тлумачення, що сприяє кращому його розумінню. Нехай лінійний багатовимірний процес описується векторним диференціальним рівнянням (t) = Ax(t) + D m(t), де х - n-мірний вектор стану;

m - r-вимірний вектор, що представляє керуючі дії;

А – квадратична матриця коефіцієнтів n-го порядку;

D – матриця керування розміру n×r.

Матриця А може бути наведена до діагональної форми

де λ i – власні значення матриці А лінійного процесу, які передбачаються всі різними.

Застосовуючи підстановку x=Tz, рівняння запишемо в канонічній формі

(t) = Λz(t) + m(t),

де
. Векторz називатимемо канонічним вектором стану.

Процес, що описується рівнянням (t) = Ax(t) + D m(t), є керованим, якщо матриця ∆ не містить рядків, всі елементи яких дорівнюють нулю; координати, що відповідають ненульовим рядкам ∆, вважаються керованими.

Приклад:

Вивести диференціальне рівняння відцентрового маятника, який застосовується як чутливий елемент у деяких САР. Схема маятника зображено малюнку. Вхідною величиною є кутова швидкість ω, а вихідною величиною – переміщення x платформи. При збільшенні швидкості обертання кулі під дією відцентрової сили розходяться та переміщують платформу. На платформу впливає сила пружності пружини, сили демпфування і сили інерції.

Введемо позначення: с – коефіцієнт жорсткості пружини; k – коефіцієнт в'язкого тертя; m – маса кулі; М – маса елементів, що у поступальному русі вздовж осі ОХ; ω – кутова швидкість валу; f 0 – сила попереднього підібгання пружини.

Для складання диференціального рівняння відцентрового маятника використовуємо рівняння Лагранжа другого роду:
(I = 1, 2, ..., n) (*). Як узагальнену координату x i виберемо вихідну координату – переміщення платформи х. Знайдемо вираз для кінетичної енергії Т, потенційної енергії П та дисипативної функції R відцентрового маятника. З малюнка видно, що

ρ = r + l sin α, x = 2a(1 – cos α).

Кінетична енергія системи Т = Т 1 + Т 2 + Т 3 де Т 1 - кінетична енергія в обертальному русі навколо осі ОХ; Т 2 – кінетична енергія куль у обертальному русі навколо точок А та А'; Т 3 – кінетична енергія мас у поступальному русі вздовж осі ОХ. Маємо:

,
. (*1)

Потенційна енергія маятника П = П 1 + П 2 + П 3 де П 1 - потенційна енергія мас, що рухаються паралельно осі ОХ; П 2 – потенційна енергія; П 3 - Потенційна енергія пружини. Для даного випадку маємо:

,
,
. (*2)

Знайдемо узагальнену дисипативну силу QR. Завдяки наявності демпфера сила сухого тертя мала в порівнянні з силою в'язкого тертя і нею можна знехтувати. Згідно з формулою
будемо мати

. (*3)

Обчислимо значення окремих доданків, що входять до рівняння Лагранжа (*):

Підставимо отримані вирази рівняння Лагранжа другого роду (*), тоді

Введемо наступне позначення:

,
,

; (*5)

. (*6)

З урахуванням прийнятих позначень рівняння відцентрового маятника запишеться як

Рівняння (*7) є нелінійне диференціальне рівняння. Стан рівноваги (х 0 ω 0) є рішенням рівняння

Розглянемо малі коливання маятника щодо стану рівноваги

х = х 0 + ∆х, ω = ω 0 + ∆ω. (*9)

Розкладемо функції f 1 (x), f 2 (x), f 3 (x, ω) у ряд Тейлора в околиці стану рівноваги (х 0, ω 0).

де функції F 1 (∆x), F 2 (∆x), F 3 (∆x, ∆ω) мають більш високий порядок трошки порівняно з ∆x і ∆ω. Враховуючи, що x' = ∆x' та x” = ∆x”, і зважаючи на вирази (*8), (*9), (*10), рівняння (*7) можна переписати у вигляді

де функція

має більш високий порядок дещиці порівняно з
. Відкидаючи функцію
отримаємо лінеаризоване рівняння коливань маятника щодо стану рівноваги (х 0 , ω 0)

, (*11)

(*12)

Системи, у яких вхідна та вихідна послідовності та пов'язані лінійним різницевим рівнянням з постійними коефіцієнтами, утворюють підмножину класу лінійних систем із постійними параметрами. Опис ЛПП-систем різнісними рівняннями дуже важливе, оскільки часто дозволяє знайти ефективні способи побудови таких систем. Понад те, по різницевому рівнянню можна визначити багато характеристик аналізованої системи, включаючи власні частоти та його кратність, порядок системи, частоти, відповідні нульовому коефіцієнту передачі, тощо.

У загальному випадку лінійне різницеве рівняння -го порядку з постійними коефіцієнтами, що відноситься до системи, що фізично реалізується, має вигляд

(2.18)

де коефіцієнти та описують конкретну систему, причому . Яким чином порядок системи характеризує математичні властивості різницевого рівняння, буде показано нижче. Рівняння (2.18) записано у вигляді, зручному для вирішення методом прямої підстановки. Маючи набір початкових умов [наприклад, , ] і вхідну послідовність за формулою (2.18) можна безпосередньо обчислити вихідну послідовність для . Наприклад, різницеве рівняння

(2.19)

з початковою умовою і можна вирішити підстановкою, що дає

Хоча розв'язання різницевих рівнянь прямою підстановкою і доцільно в деяких випадках, значно корисніше отримати розв'язування рівняння у явному вигляді. Методи знаходження таких рішень докладно висвітлені в літературі з різницевих рівнянь, і тут буде дано лише короткий огляд. Основна ідея зводиться до двох рішень різницевого рівняння: однорідного і приватного. Однорідне рішення виходить шляхом підстановки нулів замість всіх членів, що містять елементи вхідної послідовності і визначення відгуку при нульовій вхідній послідовності. Саме цей клас рішень описує основні властивості заданої системи. Приватне рішення отримують, підбираючи вигляд послідовності на виході при заданій послідовності вхідної . Для визначення довільних постійних однорідних рішень використовуються початкові умови. Як приклад розв'яжемо цим методом рівняння (2.19). Однорідне рівняння має вигляд

(2.20)

Відомо, що характеристичними рішеннями однорідних рівнянь, що відповідають лінійним різницевим рівнянням з постійними коефіцієнтами, є рішення виду. Тому, підставивши в рівняння (2.20) замість

(2.21)

Приватне рішення, що відповідає вхідній послідовності, спробуємо знайти у вигляді

(2.22)

З рівняння (2.19) отримуємо

Оскільки коефіцієнти при рівних ступенях повинні збігатися, B, СиD повинні бути рівні

(2.24)

Таким чином, загальне рішення має вигляд

(2.25)

Коефіцієнт визначається з початкової умови , звідки і

(2.26)

Вибіркова перевірка рішення (2.26) показує повний його збіг з наведеним вище прямим рішенням. Очевидна перевага рішення (2.26) полягає в тому, що воно дозволяє дуже просто визначити для будь-якого конкретного.

Фіг. 2.7. Схема реалізації простого різницевого рівняння першого ладу.

Важливе значення різницевих рівнянь у тому, що вони безпосередньо визначають спосіб побудови цифрової системи. Так, різницеве рівняння першого порядку найзагальнішого виду

можна реалізувати за допомогою схеми, зображеної на фіг. 2.7. Блок «затримка» здійснює затримку однією відлік. Розглянута форма побудови системи, в якій для вхідної та вихідної послідовностей використовуються роздільні елементи затримки, називається прямою формою 1. Нижче обговоримо різні методи побудови цієї та інших цифрових систем.

Різнинне рівняння другого порядку найзагальнішого виду

Фіг. 2.8. Схема реалізації різницевого рівняння другого порядку.

може бути реалізовано за допомогою схеми, наведеної на фіг. 2.8. У цій схемі для вхідної та вихідної послідовностей також використовуються роздільні елементи затримки.

З наступного викладу матеріалів цього розділу стане ясно, що системи першого і другого порядку можуть бути використані при реалізації систем вищого порядку, оскільки останні можуть бути представлені у вигляді послідовно або паралельно з'єднаних систем першого та другого порядку.

Розпізнання м урівняння зв. рівняння виду

де - шукана та F -задана функція. Заміна в (2) кінцевих різниць їх виразами через значення шуканої функції згідно з (1) призводить до рівняння виду

Якщо , Т. е. рівняння (3) дійсно містить як , так і , то рівняння (3) зв. р о д о с т н і м у р а в н е н н е м m-го по рядку, або д і ф ф е р ен ц і а ль н о р а знанням урівняння.

(6)

де – довільні постійні.

3) Загальне рішення неоднорідного Р. в. (4) подається у вигляді суми будь-якого приватного його рішення та загального рішення однорідного Р. у. (5).

Приватне рішення неоднорідного рівняння (5) можна побудувати, виходячи із загального рішення (6) однорідного рівняння шляхом застосування методу варіації довільних постійних (див., напр., ). У разі Р. в. з постійними коефіцієнтами

можна безпосередньо знайти тлінійно незалежні приватні рішення. Для цього розглядається характер-теристич. рівняння

і шукається його коріння. Якщо все коріння просте, то функції

утворюють лінійно незалежну систему розв'язків рівняння (7). У разі, коли - корінь кратності r,лінійно незалежними є рішення

Якщо коефіцієнти а 0 , a 1 , . . ., а тдійсні та рівняння (8) має комплексний корінь, напр. простий корінь, то замість комплексних рішень виділяють два лінійно незалежні дійсні рішення

Нехай є Р. в. 2-го порядку з постійними дійсними коефіцієнтами

(9) Характеристич. рівняння

має коріння

Загальне рішення рівняння (9) у разі зручно записувати у вигляді

(10)

де з 1 і з 2 – довільні постійні. Якщо і - комплексно пов'язане коріння:

то інше подання загального рішення має вигляд

У разі кратного кореня загальне рішення може бути отримане граничним переходом (10) або (11). Воно має вигляд

Як і у разі рівнянь довільного порядку, для Р. в. 2-го порядку можна розглядати завдання Коші чи різні крайові завдання. Напр., для завдання Коші

Вирішення звичайних лінійних різницевих рівнянь

з постійними коефіцієнтами

Зв'язок виходу та входу лінійної дискретної системи може бути описаний звичайним лінійним різницевим рівнянням з постійними коефіцієнтами

де y[n]- Вихідний сигнал в момент n,

x[n]- вхідний сигнал у момент n,

a i ,b k- Постійні коефіцієнти.

Для вирішення таких рівнянь можуть використовуватись два методи

Прямий метод,
Метод Z – перетворення.

Спочатку розглянемо рішення лінійного різницевого рівняння за допомогою прямого методу.

Загальне рішення неоднорідного (з відмінною від нуля правою частиною) лінійного різницевого рівняння дорівнює сумі вищого рішеннялінійного однорідного різницевого рівняння та приватного рішеннянеоднорідного рівняння

Загальне рішення однорідного різницевого рівняння ( zero-inputresponse) y h [n]

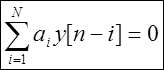
визначається у вигляді

Підставляючи це рішення в однорідне рівняння, отримуємо

Такий поліном називають характеристичний поліномсистеми. Він має Nкоріння . Коріння може бути дійсним або комплексним і деякі коріння - збігаються (кратними).

Якщо коріння є дійсними та різними, то рішення однорідного рівняння має вигляд

де коефіцієнти

Якщо деякий корінь, наприклад, λ 1має кратність m, то відповідний йому член рішення набуває форми

Якщо всі коефіцієнти однорідного рівняння і відповідно характеристичного багаточлена дійсні, то два члени рішення, що відповідають простим комплексно пов'язаним корінням можна уявити (записати) у вигляді , при цьому коефіцієнти A,Bвизначаються за початковими умовами.

Вигляд приватного рішення y p [n]рівняння залежить від правої частини (вхідного сигналу) і визначається згідно з наведеною нижче таблицею

Таблиця 1. Вид приватного рішення для різного характеру правої частини

Вхідний сигналx[n]

Приватне рішенняy p [n]

A(Константа)

Рішення лінійного різницевого рівняння методом Z – перетворення полягає у застосуванні Z- Перетворення до рівняння з використанням властивостей лінійності та тимчасового зсуву. В результаті виходить лінійне рівняння алгебри щодо Z- Зображення шуканої функції. Назад Z- Перетворення дає шукане рішення в тимчасовій області. Для отримання зворотного Z - перетворення найчастіше використовується розкладання раціонального виразу на прості (елементарні) дроби, оскільки зворотне перетворення від окремого елементарного дробу має простий вигляд.

Зауважимо, що з переходу у тимчасову область можуть використовуватися інші методи обчислення зворотного Z – перетворення.

приклад. Визначимо відгук (вихідний сигнал) системи, що описується лінійним різницевим рівнянням на вхідний сигнал