Намерете собствените вектори на матрицата. Система от еднородни линейни уравнения

Собствен вектор на квадратна матрица е този, който, когато се умножи по дадена матрица, води до колинеарен вектор. С прости думи, когато една матрица се умножи по собствен вектор, последният остава същият, но умножен по някакво число.

Определение

Собственият вектор е ненулев вектор V, който, когато се умножи по квадратна матрица M, става себе си, увеличен с някакво число λ. В алгебрична нотация това изглежда така:

M × V = λ × V,

където λ е собствена стойност на матрицата M.

Обмисли числен пример. За удобство на писане числата в матрицата ще бъдат разделени с точка и запетая. Да кажем, че имаме матрица:

М = 0; четири;
6; 10.

Нека го умножим по колонен вектор:

V = -2;

Когато умножаваме матрица по вектор колона, също получаваме вектор колона. Строг математически езикформулата за умножаване на матрица 2 × 2 по колонен вектор ще изглежда така:

M × V = M11 × V11 + M12 × V21;
M21 x V11 + M22 x V21.

M11 означава елемента от матрицата M, стоящ в първия ред и първа колона, а M22 е елементът, разположен във втория ред и втора колона. За нашата матрица тези елементи са M11 = 0, M12 = 4, M21 = 6, M22 10. За колонен вектор тези стойности са V11 = –2, V21 = 1. Според тази формула получаваме следното резултат от произведението на квадратна матрица с вектор:

M × V = 0 × (-2) + (4) × (1) = 4;
6 × (-2) + 10 × (1) = -2.

За удобство записваме вектора на колоната в ред. И така, ние умножихме квадратната матрица по вектора (-2; 1), което води до вектора (4; -2). Очевидно това е същият вектор, умножен по λ = -2. ламбда в този случайобозначава собствена стойност на матрицата.

Собственият вектор на матрицата е колинеарен вектор, тоест обект, който не променя позицията си в пространството, когато се умножи по матрица. Концепцията за колинеарност в векторна алгебраподобно на термина паралелизъм в геометрията. В геометрична интерпретация колинеарни вектори- Това са успоредни насочени отсечки с различна дължина. От времето на Евклид знаем, че една права има безкраен брой успоредни линии, така че е логично да приемем, че всяка матрица има безкраен брой собствени вектори.

От предишния пример може да се види, че както (-8; 4), така и (16; -8), и (32, -16) могат да бъдат собствени вектори. Всички те са колинеарни вектори, съответстващи на собствената стойност λ = -2. Когато умножим оригиналната матрица по тези вектори, пак ще получим вектор като резултат, който се различава от оригинала 2 пъти. Ето защо при решаване на задачи за намиране на собствен вектор се изисква да се намират само линейно независими векторни обекти. Най-често за n × n матрица има n-ти брой собствени вектори. Нашият калкулатор е предназначен за анализ на квадратни матрици от втори ред, така че почти винаги ще бъдат намерени два собствени вектора като резултат, освен когато съвпадат.

В примера по-горе знаехме предварително собствения вектор на оригиналната матрица и визуално определихме ламбда числото. На практика обаче всичко се случва обратното: в началото има собствени стойности и едва след това собствени вектори.

Алгоритъм за решение

Нека погледнем оригиналната матрица M отново и се опитаме да намерим и двата й собствени вектора. Така че матрицата изглежда така:

М = 0; четири;
6; 10.

Като начало трябва да определим собствената стойност λ, за която трябва да изчислим детерминантата на следната матрица:

(0 − λ); четири;
6; (10 − λ).

Тази матрицаполучено чрез изваждане на неизвестното λ от елементите на главния диагонал. Детерминантата се определя по стандартната формула:

detA = M11 × M21 − M12 × M22
detA = (0 − λ) × (10 − λ) − 24

Тъй като нашият вектор не трябва да е нула, приемаме полученото уравнение като линейно зависимо и приравняваме нашата детерминанта detA към нула.

(0 − λ) × (10 − λ) − 24 = 0

Нека разгънем скобите и да получим характеристично уравнениематрици:

λ 2 − 10λ − 24 = 0

Това е стандартно квадратно уравнение, което трябва да се реши по отношение на дискриминанта.

D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 = 100 + 96 = 196

Коренът на дискриминанта е sqrt(D) = 14, така че λ1 = -2, λ2 = 12. Сега за всяка ламбда стойност трябва да намерим собствен вектор. Нека изразим коефициентите на системата за λ = -2.

M − λ × E = 2; четири;
6; 12.

В тази формула E е матрица на идентичността. Въз основа на получената матрица ще съставим системата линейни уравнения:

2x + 4y = 6x + 12y

където x и y са елементи на собствения вектор.

Нека съберем всички X отляво и всички Y отдясно. Очевидно - 4x = 8y. Разделете израза на - 4 и получете x = -2y. Сега можем да определим първия собствен вектор на матрицата, като вземем всякакви стойности на неизвестните (помнете за безкрайността на линейно зависимите собствени вектори). Да вземем y = 1, тогава x = -2. Следователно първият собствен вектор изглежда като V1 = (–2; 1). Върнете се в началото на статията. Това беше този векторен обект, по който умножихме матрицата, за да демонстрираме концепцията за собствен вектор.

Сега нека намерим собствения вектор за λ = 12.

M - λ × E = -12; четири
6; -2.

Нека съставим същата система от линейни уравнения;

-12x + 4y = 6x − 2y
-18x = -6y
3x=y.

Сега нека вземем x = 1, следователно y = 3. Така вторият собствен вектор изглежда като V2 = (1; 3). При умножаване на оригиналната матрица по даден вектор, резултатът винаги ще бъде един и същ вектор, умножен по 12. Това завършва алгоритъма за решение. Вече знаете как ръчно да дефинирате собствен вектор на матрица.

определител;
следа, тоест сумата от елементите на главния диагонал;
ранг, т.е максимална сумалинейно независими редове/колони.

Програмата работи съгласно горния алгоритъм, минимизирайки процеса на решаване. Важно е да се отбележи, че в програмата ламбда се обозначава с буквата "c". Нека да разгледаме числен пример.

Примерна програма

Нека се опитаме да дефинираме собствени вектори за следната матрица:

М=5; 13;
4; 14.

Нека въведем тези стойности в клетките на калкулатора и да получим отговора в следната форма:

Ранг на матрицата: 2;
Матрична детерминанта: 18;
Следа на матрицата: 19;
Изчисление на собствения вектор: c 2 − 19.00c + 18.00 (характерно уравнение);
Изчисление на собствения вектор: 18 (първа ламбда стойност);
Изчисление на собствения вектор: 1 (втора ламбда стойност);
Система от уравнения на вектор 1: -13x1 + 13y1 = 4x1 − 4y1;
Система от уравнения на вектор 2: 4x1 + 13y1 = 4x1 + 13y1;
Собствен вектор 1: (1; 1);
Собствен вектор 2: (-3,25; 1).

Така получихме два линейно независими собствени вектора.

Заключение

Линейната алгебра и аналитичната геометрия са стандартни предмети за всеки първокурсник техническа специалност. Голям бройвектори и матрици е ужасяващо и е лесно да се направи грешка в такива тромави изчисления. Нашата програма ще позволи на учениците да проверят своите изчисления или автоматично да решат задачата за намиране на собствен вектор. В нашия каталог има и други калкулатори за линейна алгебра, използвайте ги в ученето или работата си.

Как да залепите математически формуликъм уебсайта?

Ако някога трябва да добавите една или две математически формули към уеб страница, тогава най-лесният начин да направите това е както е описано в статията: математическите формули лесно се вмъкват в сайта под формата на снимки, които Wolfram Alpha автоматично генерира. В допълнение към простотата, това универсален начинще помогне за подобряване на видимостта на сайта в търсачки. Работи отдавна (и мисля, че ще работи завинаги), но е морално остарял.

Ако постоянно използвате математически формули на вашия сайт, препоръчвам ви да използвате MathJax, специална JavaScript библиотека, която показва математическа нотацияв уеб браузъри, използващи MathML, LaTeX или ASCIIMathML маркиране.

Има два начина да започнете да използвате MathJax: (1) като използвате прост код, можете бързо да свържете скрипт MathJax към вашия сайт, който ще бъде в точният моментавтоматично изтегляне от отдалечен сървър (списък със сървъри); (2) качете скрипта MathJax от отдалечен сървър на вашия сървър и го свържете към всички страници на вашия сайт. Вторият метод е по-сложен и отнема много време и ще ви позволи да ускорите зареждането на страниците на вашия сайт, а ако родителският MathJax сървър стане временно недостъпен по някаква причина, това няма да засегне собствения ви сайт по никакъв начин. Въпреки тези предимства избрах първия метод, тъй като е по-прост, по-бърз и не изисква технически умения. Следвайте примера ми и след 5 минути ще можете да използвате всички функции на MathJax на вашия уебсайт.

Можете да свържете скрипта на библиотеката MathJax от отдалечен сървър, като използвате две опции за код, взети от основния уебсайт на MathJax или от страницата с документация:

Една от тези опции за код трябва да бъде копирана и поставена в кода на вашата уеб страница, за предпочитане между таговете иили веднага след етикета . Според първата опция MathJax се зарежда по-бързо и забавя страницата по-малко. Но втората опция автоматично проследява и зарежда най-новите версии на MathJax. Ако поставите първия код, той ще трябва да се актуализира периодично. Ако поставите втория код, тогава страниците ще се зареждат по-бавно, но няма да е необходимо постоянно да наблюдавате актуализациите на MathJax.

Най-лесният начин да свържете MathJax е в Blogger или WordPress: в контролния панел на сайта добавете изпълним модул, предназначен да вмъква JavaScript код на трета страна, копирайте първата или втората версия на кода за зареждане по-горе в него и поставете изпълнимия модул по-близо до началото на шаблона (между другото, това изобщо не е необходимо, тъй като скриптът MathJax се зарежда асинхронно). Това е всичко. Сега научете синтаксиса за маркиране на MathML, LaTeX и ASCIIMathML и сте готови да вграждате математически формули във вашите уеб страници.

Всеки фрактал се изгражда според определено правило, което се прилага последователно неограничен брой пъти. Всяко такова време се нарича итерация.

Итеративният алгоритъм за конструиране на гъба на Менгер е доста прост: оригиналният куб със страна 1 е разделен от равнини, успоредни на лицата му, на 27 равни куба. От него се отстраняват един централен куб и 6 куба, съседни на него по стените. Получава се комплект, състоящ се от 20 останали по-малки кубчета. Като направим същото с всяко от тези кубчета, получаваме комплект, състоящ се от 400 по-малки кубчета. Продължавайки този процес за неопределено време, получаваме гъбата Menger.

www.сайтви позволява да намерите. Сайтът прави изчисленията. След няколко секунди сървърът ще издаде правилното решение. Характеристичното уравнение за матрицатаще бъде алгебричен израз, намираща се по правилото за изчисляване на детерминантата матрици матрици, докато на главния диагонал ще има разлики в стойностите на диагоналните елементи и променливата. При изчисляване характеристично уравнение за матрица онлайн, всеки елемент матрицище бъдат умножени със съответните други елементи матрици. Намерете в режим онлайнвъзможно само за квадрат матрици. Намерете операция характеристично уравнение за матрица онлайнсе свежда до пресмятане алгебрична сумапродукти от елементи матрицив резултат на намиране на детерминантата матрици, само с цел определяне характеристично уравнение за матрица онлайн. Тази операция отнема специално мястона теория матрици, ви позволява да намирате собствени стойности и вектори с помощта на корени. Задача за намиране характеристично уравнение за матрица онлайне да се умножават елементи матрицис последващо сумиране на тези продукти по определено правило. www.сайтнамира характеристично уравнение за матрицададено измерение в режима онлайн. изчисление характеристично уравнение за матрица онлайнза дадено измерение, това е намиране на полином с числени или символни коефициенти, намерени по правилото за изчисляване на детерминантата матрици- като сбор от произведенията на съответните елементи матрици, само с цел определяне характеристично уравнение за матрица онлайн. Намиране на полином по променлива за квадрат матрици, като определение характеристично уравнение за матрицата, често срещано на теория матрици. Стойността на корените на полинома характеристично уравнение за матрица онлайнизползвани за дефиниране на собствени вектори и собствени стойностиза матрици. Ако обаче детерминантата матрицитогава ще бъде нула матрично характеристично уравнениевсе още ще съществува, за разлика от обратното матрици. За да се изчисли характеристично уравнение за матрицаили потърсете няколко наведнъж матрици характеристични уравнения, трябва да отделите много време и усилия, докато нашият сървър ще намери характеристично уравнение за онлайн матрица. В този случай отговорът чрез намиране характеристично уравнение за матрица онлайнще бъде правилен и с достатъчна точност, дори ако числата при намиране характеристично уравнение за матрица онлайнще бъде ирационално. На сайта www.сайтвписванията на символи са разрешени в елементи матрици, това е характеристично уравнение за онлайн матрицамогат да бъдат представени в обща символна форма при изчисляване матрица на характеристично уравнение онлайн. Полезно е да проверите получения отговор при решаване на задачата за намиране характеристично уравнение за матрица онлайнизползване на сайта www.сайт. При извършване на операцията за изчисляване на полином - характеристично уравнение на матрицата, е необходимо да бъдете внимателни и изключително концентрирани при решаването на този проблем. От своя страна нашият сайт ще ви помогне да проверите решението си по темата матрица на характеристично уравнение онлайн. Ако нямате време за дълги проверки на решени проблеми, тогава www.сайтсъс сигурност ще бъде удобен инструмент за проверка при намиране и пресмятане характеристично уравнение за матрица онлайн.

". Първата част очертава разпоредбите, които са минимално необходими за разбиране на химиометрията, а втората част съдържа фактите, които трябва да знаете за по-задълбочено разбиране на методите многовариантен анализ. Презентацията е илюстрирана с примери, направени в работна книга на Excel. Matrix.xlsкойто придружава този документ.

Връзките към примери се поставят в текста като Excel обекти. Тези примери са абстрактни по природа, те не са обвързани със задачи по никакъв начин. аналитична химия. Реални примериизползването на матрична алгебра в хемометрията се обсъжда в други текстове, посветени на различни хемометрични приложения.

Повечето от измерванията, извършвани в аналитичната химия, не са директни, а непряк. Това означава, че в експеримента вместо стойността на желания аналит С (концентрация) се получава друга стойност х(сигнал), свързан с, но не равен на C, т.е. х(C) ≠ C. Като правило видът на зависимостта х(C) не е известно, но за щастие в аналитичната химия повечето измервания са пропорционални. Това означава, че тъй като концентрацията на C в апъти, сигналът X ще се увеличи със същото количество., т.е. х(аВ) = a x(° С). В допълнение, сигналите също са адитивни, така че сигналът от проба, съдържаща две вещества с концентрации C1 и C2, ще бъде е равно на суматасигнали от всеки компонент, т.е. х(C1 + C2) = х(C1)+ х(C2). Пропорционалността и адитивността заедно дават линейност. Могат да се дадат много примери за илюстриране на принципа на линейността, но е достатъчно да споменем двата най-големи ясни примери- хроматография и спектроскопия. Втората особеност, присъща на експеримента в аналитичната химия е многоканален. Модерното аналитично оборудване измерва едновременно сигнали за много канали. Например, интензитетът на светлинното предаване се измерва за няколко дължини на вълната наведнъж, т.е. спектър. Следователно в експеримента имаме работа с различни сигнали х 1 , х 2 ,...., х n характеризираща набора от концентрации C 1 ,C 2 , ..., C m на веществата, присъстващи в изследваната система.

Ориз. 1 Спектри

И така, аналитичният експеримент се характеризира с линейност и многоизмерност. Следователно е удобно експерименталните данни да се разглеждат като вектори и матрици и да се манипулират с помощта на апарата на матричната алгебра. Плодотворността на този подход е илюстрирана от примера, показан в , който показва три спектъра, взети за 200 дължини на вълните от 4000 до 4796 cm–1. Първият ( х 1) и второ ( х 2) спектрите са получени за стандартни проби, в които са известни концентрациите на две вещества A и B: в първата проба [A] = 0,5, [B] = 0,1, а във втората проба [A] = 0,2, [ B] = 0,6. Какво може да се каже за нова, неизвестна проба, чийто спектър е посочен х 3 ?

Разгледайте три експериментални спектъра х 1 , х 2 и х 3 като три вектора с размерност 200. Използвайки линейна алгебра, човек може лесно да покаже това х 3 = 0.1 х 1 +0.3 х 2, така че третата проба очевидно съдържа само вещества А и В в концентрации [A] = 0,5×0,1 + 0,2×0,3 = 0,11 и [B] = 0,1×0,1 + 0,6×0,3 = 0,19.

1. Основна информация

1.1 Матрици

Матрицанаречена например правоъгълна таблица с числа

Ориз. 2 Матрица

Матриците се означават с главни удебелени букви ( А), а техните елементи - съответни малки буквис индекси, т.е. а ij . Първият индекс номерира редовете, а вторият номерира колоните. В хемометрията е обичайно да се обозначава максимална стойностиндекс със същата буква като самия индекс, но с главна буква. Следователно матрицата Аможе да се запише и като ( а ij , аз = 1,..., аз; й = 1,..., Дж). За примерната матрица аз = 4, Дж= 3 и а 23 = −7.5.

Двойка числа ази Джсе нарича размерност на матрицата и се означава като аз× Дж. Пример за матрица в хемометрията е набор от спектри, получени за азпроби на Дждължини на вълните.

1.2. Най-простите операции с матрици

Матриците могат умножете по числа. В този случай всеки елемент се умножава по това число. Например -

Ориз. 3 Умножение на матрица по число

Две матрици с едно и също измерение могат да бъдат елементарни гънкаи изваждам. Например,

Ориз. 4 Събиране на матрици

В резултат на умножение с число и събиране се получава матрица със същата размерност.

Нулевата матрица е матрица, състояща се от нули. Обозначава се О. Очевидно е, че А+О = А, А−А = Ои 0 А = О.

Матрицата може транспонирам. По време на тази операция матрицата се обръща, т.е. редовете и колоните се разменят. Транспонирането се обозначава с тире, А“ или индекс А T . По този начин, ако А = {а ij , аз = 1,..., аз; й = 1,...,Дж), тогава А t = ( а джи , й = 1,...,Дж; i = 1,..., аз). Например

Ориз. 5 Транспониране на матрица

Очевидно е, че ( А t) t = А, (А+б) T = А t+ б T .

1.3. Матрично умножение

Матриците могат умножават се, но само ако имат съответните размери. Защо това е така ще стане ясно от определението. Матричен продукт А, измерение аз× К, и матрици б, измерение К× Дж, се нарича матрица ° С, измерение аз× Дж, чиито елементи са числа

Така за продукта ABнеобходимо е броят на колоните в лявата матрица Абеше равен на броя на редовете в дясната матрица б. Пример за продукт Matrix -

Фиг.6 Произведение на матрици

Правилото за умножение на матрицата може да се формулира по следния начин. Да се намери елемент от матрица ° Сстои на кръстовището аз-ти ред и й-та колона ( ° С ij) трябва да се умножава елемент по елемент аз-ти ред на първата матрица Ана й-та колона на втората матрица би съберете всички резултати. Така че в показания пример елементът от третия ред и втората колона се получава като сбор от продуктите по елементи на третия ред Аи втора колона б

Фиг.7 Елемент от произведението на матрици

Продуктът на матриците зависи от реда, т.е. AB ≠ BA, поне поради размери. Казват, че е некомутативно. Продуктът на матриците обаче е асоциативен. Означава, че ABC = (AB)° С = А(пр.н.е). Освен това той е и разпределителен, т.е. А(б+° С) = AB+AC. Очевидно е, че AO = О.

1.4. Квадратни матрици

Ако броят на колоните на една матрица е равен на броя на нейните редове ( аз = J=N), тогава такава матрица се нарича квадратна. В този раздел ще разгледаме само такива матрици. Сред тези матрици могат да се отделят матрици със специални свойства.

Самотникматрица (обозначена ази понякога д) е матрица, в която всички елементи са равни на нула, с изключение на диагоналните, които са равни на 1, т.е.

очевидно AI = IA = А.

Матрицата се нарича диагонал, ако всички негови елементи, с изключение на диагоналните ( а ii) са равни на нула. Например

Ориз. 8 Диагонална матрица

Матрица Анаречен върхът триъгълна, ако всички негови елементи, лежащи под диагонала, са равни на нула, т.е. а ij= 0, при аз>й. Например

Ориз. 9 Горна триъгълна матрица

Долната триъгълна матрица се дефинира по подобен начин.

Матрица АНаречен симетричен, ако А t = А. С други думи а ij = а джи. Например

Ориз. 10 Симетрична матрица

Матрица АНаречен ортогонален, ако

А T А = АА t = аз.

Матрицата се нарича нормалноако

1.5. Следа и определител

Следванеквадратна матрица А(означен като Tr( А) или Sp( А)) е сумата от неговите диагонални елементи,

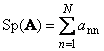
Например,

Ориз. 11 Матрична следа

Очевидно е, че

Sp(α А) = α Sp( А) и

Sp( А+б) = Sp( А)+ Sp( б).

Може да се покаже, че

Sp( А) = Sp( А t), Sp( аз) = н,

а също и това

Sp( AB) = Sp( BA).

Друг важна характеристикаквадратната матрица е неговата детерминант(означено с det( А)). Дефиницията на детерминантата в общ случайдоста сложно, така че ще започнем с най-простия вариант - матрицата Аразмер (2×2). Тогава

За матрица (3 × 3) детерминантата ще бъде равна на

В случай на матрица ( н× н) детерминантата се изчислява като сумата 1 2 3 ... н= н! членове, всеки от които е равен на

Индекси к 1 , к 2 ,..., к Нсе дефинират като всички възможни подредени пермутации rчислата в множеството (1, 2, ... , н). Изчисляването на матричната детерминанта е сложна процедура, която на практика се извършва с помощта на специални програми. Например,

Ориз. 12 Матрична детерминанта

Отбелязваме само очевидните свойства:

det( аз) = 1, det( А) = det( А T),

det( AB) = det( А)дет( б).

1.6. Вектори

Ако матрицата има само една колона ( Дж= 1), тогава се извиква такъв обект вектор. По-точно вектор колона. Например

Могат да се разглеждат например и матрици, състоящи се от един ред

Този обект също е вектор, но редов вектор. Когато анализираме данни, е важно да разберем с кои вектори имаме работа - колони или редове. Така че спектърът, взет за една проба, може да се разглежда като ред вектор. Тогава наборът от спектрални интензитети при някаква дължина на вълната за всички проби трябва да се третира като колонен вектор.

Размерността на вектора е броят на неговите елементи.

Ясно е, че всеки колонен вектор може да се трансформира във вектор на ред чрез транспониране, т.е.

В тези случаи, когато формата на вектора не е конкретно посочена, а просто се казва вектор, тогава те означават колонен вектор. Ние също ще се придържаме към това правило. Векторът се обозначава с малка директна удебелена буква. Нулев вектор е вектор, чийто всички елементи са равни на нула. Обозначава се 0 .

1.7. Най-простите операции с вектори

Векторите могат да се добавят и умножават по числа по същия начин като матриците. Например,

Ориз. 13 Операции с вектори

Два вектора хи гНаречен колинеарен, ако има число α такова, че

1.8. Продукти от вектори

Два вектора с едно и също измерение нможе да се умножи. Нека има два вектора х = (х 1 , х 2 ,...,х N) t и г = (г 1 , г 2 ,...,г N) t . Ръководейки се от правилото за умножение "ред по колона", можем да направим два продукта от тях: х T ги xy T . Първа работа

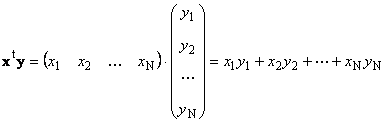
Наречен скаларенили вътрешни. Резултатът му е число. Той също така използва нотацията ( х,г)= х T г. Например,

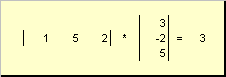
Ориз. 14 Вътрешно (скаларно) произведение

Втора работа

Наречен външен. Неговият резултат е размерна матрица ( н× н). Например,

Ориз. 15 Външен продукт

вектори, скаларно произведениекоето е равно на нула се наричат ортогонален.

1.9. Векторна норма

Скаларното произведение на вектор със себе си се нарича скаларен квадрат. Тази стойност

определя квадрат дължинавектор х. За обозначаване на дължина (наричана още норматавектор) се използва обозначението

Например,

Ориз. 16 Векторна норма

Вектор на единична дължина (|| х|| = 1) се нарича нормализиран. Ненулев вектор ( х ≠ 0 ) може да се нормализира, като се раздели на дължината, т.е. х = ||х|| (х/||х||) = ||х|| д. Тук д = х/||х|| е нормализиран вектор.

Векторите се наричат ортонормални, ако всички те са нормализирани и ортогонални по двойки.

1.10. Ъгъл между векторите

Скаларното произведение определя и ъгълφ между два вектора хи г

Ако векторите са ортогонални, тогава cosφ = 0 и φ = π/2, а ако са колинеарни, тогава cosφ = 1 и φ = 0.

1.11. Векторно представяне на матрица

Всяка матрица Аразмер аз× Джможе да се представи като набор от вектори

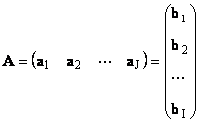
Тук всеки вектор а йе й-та колона и вектор на ред b азе аз-ти ред на матрицата А

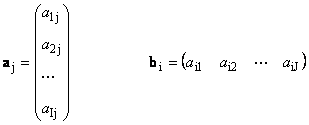
1.12. Линейно зависими вектори

Вектори с едно и също измерение ( н) могат да се добавят и умножават по число, точно като матриците. Резултатът е вектор със същото измерение. Нека има няколко вектора с еднаква размерност х 1 , х 2 ,...,х K и същия брой числа α α 1 , α 2 ,...,α К. вектор

г= α 1 х 1 + α 2 х 2 +...+α К х К

Наречен линейна комбинациявектори х к .

Ако има такива ненулеви числа α к ≠ 0, к = 1,..., К, Какво г = 0 , тогава такъв набор от вектори х кНаречен линейно зависими. В противен случай векторите се наричат линейно независими. Например вектори х 1 = (2, 2) t и х 2 = (−1, −1) t са линейно зависими, тъй като х 1 +2х 2 = 0

1.13. Ранг на матрицата

Помислете за набор от Квектори х 1 , х 2 ,...,х Кразмери н. Рангът на тази система от вектори е максималният брой линейно независими вектори. Например в комплекта

има само два линейно независими вектора, например х 1 и х 2, така че неговият ранг е 2.

Очевидно, ако има повече вектори в набора от тяхното измерение ( К>н), тогава те задължително са линейно зависими.

Ранг на матрицата(означено с ранг( А)) е рангът на системата от вектори, от които се състои. Въпреки че всяка матрица може да бъде представена по два начина (вектори на колони или вектори на редове), това не влияе на стойността на ранга, тъй като

1.14. обратна матрица

квадратна матрица Асе нарича неизроден, ако има уникален обратенматрица А-1 , определени от условията

АА −1 = А −1 А = аз.

Обратната матрица не съществува за всички матрици. Необходимо и достатъчно условие за неизроденост е

det( А) ≠ 0 или ранг( А) = н.

Обръщането на матрицата е сложна процедура, за която има специални програми. Например,

Ориз. 17 Инверсия на матрицата

Даваме формули за най-простия случай - матрици 2 × 2

Ако матрици Аи бтогава са неизродени

(AB) −1 = б −1 А −1 .

1.15. Псевдообратна матрица

Ако матрицата Ае изродена и обратната матрица не съществува, тогава в някои случаи може да се използва псевдообратноматрица, която се определя като такава матрица А+ това

АА + А = А.

Псевдообратната матрица не е единствената и нейната форма зависи от метода на конструиране. Например за правоъгълна матрицаможе да се използва методът на Мур-Пенроуз.

Ако броят на колоните по-малко от числолинии, тогава

А + =(А T А) −1 А T

Например,

Ориз. 17a Псевдоматрична инверсия

Ако броят на колоните повече бройлинии, тогава

А + =А T ( АА T) −1

1.16. Умножение на вектор по матрица

вектор хможе да се умножи по матрица Аподходящ размер. В този случай векторът на колоната се умножава отдясно брадва, а векторният низ е отляво х T А. Ако размерността на вектора Дж, и размерът на матрицата аз× Джтогава резултатът е вектор на измерение аз. Например,

Ориз. 18 Векторно-матрично умножение

Ако матрицата А- квадрат ( аз× аз), след това векторът г = брадваима същите размери като х. Очевидно е, че

А(α 1 х 1 + α 2 х 2) = α 1 брадва 1 + α 2 брадва 2 .

Следователно матриците могат да се разглеждат като линейни трансформации на вектори. По-специално х = х, вол = 0 .

2. Допълнителна информация

2.1. Системи линейни уравнения

Позволявам А- размер на матрицата аз× Дж, а b- размерен вектор Дж. Помислете за уравнението

брадва = b

по отношение на вектора х, размери аз. По същество това е система от азлинейни уравнения с Джнеизвестен х 1 ,...,х Дж. Решение съществува тогава и само ако

ранг ( А) = ранг ( б) = Р,

където бе увеличената матрица на размерите аз×( J+1), състоящ се от матрицата А, подплатени с колона b, б = (А b). В противен случай уравненията са непоследователни.

Ако Р = аз = Дж, тогава решението е уникално

х = А −1 b.

Ако Р < аз, тогава има много различни решения, което може да бъде изразено чрез линейна комбинация Дж−Рвектори. Система хомогенни уравнения брадва = 0 с квадратна матрица А (н× н) не тривиално решение (х ≠ 0 ) ако и само ако det( А) = 0. Ако Р= ранг( А)<н, тогава има н−Рлинейно независими решения.

2.2. Билинейни и квадратични форми

Ако А- това е квадратна матрица, а хи г- вектори със съответната размерност, след това скаларното произведение на формата х T даНаречен билинеенформата, определена от матрицата А. При х = гизразяване х T брадваНаречен квадратнаформа.

2.3. Положително определени матрици

квадратна матрица АНаречен положително определено, ако за всеки ненулев вектор х ≠ 0 ,

х T брадва > 0.

The отрицателен (х T брадва < 0), неотрицателни (х T брадва≥ 0) и неположителен (х T брадва≤ 0) определени матрици.

2.4. Разлагане на Холецки

Ако симетричната матрица Ае положително определена, тогава има уникална триъгълна матрица Uс положителни елементи, за които

А = U T U.

Например,

Ориз. 19 Разлагане на Холецки

2.5. полярно разлагане

Позволявам Ае неизродена квадратна матрица с размерност н× н. След това има уникален поляренпроизводителност

А = SR,

където Се неотрицателна симетрична матрица и Ре ортогонална матрица. матрици Си Рможе да се дефинира изрично:

С 2 = АА t или С = (АА t) ½ и Р = С −1 А = (АА t) −½ А.

Например,

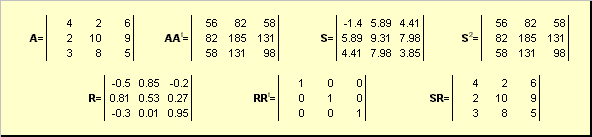
Ориз. 20 Полярно разлагане

Ако матрицата Ае изродено, тогава разлагането не е уникално - а именно: Свсе още сама, но Рможе да има много. Полярното разлагане представлява матрица Акато комбинация от компресия/разтягане Си обръщане Р.

2.6. Собствени вектори и собствени стойности

Позволявам Ае квадратна матрица. вектор vНаречен собствен векторматрици А, ако

Av = λ v,

където се нарича числото λ собствена стойностматрици А. По този начин трансформацията, която матрицата извършва Анад вектор v, се свежда до просто разтягане или компресия с фактор λ. Собственият вектор се определя с точност до умножение по константата α ≠ 0, т.е. ако vе собствен вектор, тогава α vсъщо е собствен вектор.

2.7. Собствени стойности

В матрицата А, измерение ( н× н) не може да бъде по-голямо от н собствени стойности. Те задоволяват характеристично уравнение

det( А − λ аз) = 0,

същество алгебрично уравнение н-та поръчка. По-специално, за матрица 2 × 2, характеристичното уравнение има формата

Например,

Ориз. 21 собствени стойности

Набор от собствени стойности λ 1 ,..., λ нматрици АНаречен спектър А.

Спектърът има различни свойства. По-специално

det( А) = λ 1×...×λ н, Sp( А) = λ 1 +...+λ н.

Собствените стойности на произволна матрица могат да бъдат комплексни числа, но ако матрицата е симетрична ( А t = А), тогава неговите собствени стойности са реални.

2.8. Собствени вектори

В матрицата А, измерение ( н× н) не може да бъде по-голямо от нсобствени вектори, всеки от които съответства на собствената си стойност. За определяне на собствения вектор v нтрябва да решите система от еднородни уравнения

(А − λ н аз)v н = 0 .

Има нетривиално решение, защото det( а-λ н аз) = 0.

Например,

Ориз. 22 Собствени вектора

Собствените вектори на симетрична матрица са ортогонални.

Собствени стойности (числа) и собствени вектори.
Примери за решения

Бъди себе си

От двете уравнения следва, че .

Да поставим тогава: .

Като резултат: е вторият собствен вектор.

Да повторим важни точкирешения:

– получената система със сигурност има общо решение(уравненията са линейно зависими);

- "Y" е избрано по такъв начин, че да е цяло число и първата координата "x" да е цяло число, положителна и възможно най-малка.

– проверяваме дали конкретното решение удовлетворява всяко уравнение на системата.

Отговор .

Междинните "контролни точки" бяха напълно достатъчни, така че проверката на равенствата по принцип е излишна.

В различни източници на информация координатите на собствените вектори често се записват не в колони, а в редове, например: (и, честно казано, аз самият ги писах на редове). Този вариант е приемлив, но в светлината на темата линейни трансформациитехнически по-удобен за използване колонни вектори.

Може би решението ви се стори много дълго, но това е само защото коментирах първия пример много подробно.

Пример 2

матрици

Тренираме сами! Приблизителна проба на окончателния дизайн на задачата в края на урока.

Понякога трябва да направите допълнителна задача, а именно:

напишете каноничното разлагане на матрицата

Какво е?

Ако матричните собствени вектори образуват база, то може да се представи като:

Където е матрица, съставена от координатите на собствените вектори, – диагоналматрица със съответните собствени стойности.

Това матрично разлагане се нарича канониченили диагонал.

Помислете за матрицата от първия пример. Нейните собствени вектори линейно независими(неколинеарни) и образуват основа. Нека направим матрица от техните координати:

На главен диагоналматрици по надлежния редсобствените стойности са разположени, а останалите елементи са равни на нула:
- още веднъж подчертавам важността на реда: "две" съответства на 1-ви вектор и следователно се намира в 1-ва колона, "три" - на 2-ри вектор.

По обичайния алгоритъм за намиране обратна матрицаили Метод на Гаус-Джорданнамирам . Не, това не е печатна грешка! - пред вас е рядко, като слънчево затъмнениесъбитие, когато обратната съответства на оригиналната матрица.

Остава да напишем каноничното разлагане на матрицата:

Системата може да бъде решена с елементарни трансформациии в следващите примери ще прибегнем този метод. Но тук „училищният“ метод работи много по-бързо. От 3-то уравнение изразяваме: - заместваме във второто уравнение:

Тъй като първата координата е нула, получаваме система , от всяко уравнение на която следва, че .

И отново обърнете внимание на задължителното наличие на линейна зависимост. Ако се получи само тривиално решение , тогава или собствената стойност е намерена неправилно, или системата е компилирана/решена с грешка.

Компактните координати дават стойност

Собствен вектор:

И още веднъж проверяваме дали намереното решение удовлетворява всяко уравнение на системата. В следващите параграфи и в следващите задачи препоръчвам това желание да се приеме като задължително правило.

2) За собствената стойност, следвайки същия принцип, получаваме следваща система:

От второто уравнение на системата изразяваме: - заместваме в третото уравнение:

Тъй като координатата "дзета" е равна на нула, получаваме система , от всяко уравнение на която следва линейна зависимост.

Позволявам

Проверяваме дали решението удовлетворява всяко уравнение на системата.

Така собственият вектор: .

3) И накрая, системата съответства на собствената си стойност:

Второто уравнение изглежда най-просто, така че го изразяваме от него и го заместваме в 1-во и 3-то уравнения:

Всичко е наред - разкри се линейна зависимост, която заместваме в израза:

В резултат на това "X" и "Y" бяха изразени чрез "Z": . На практика не е необходимо да се постигат точно такива отношения, в някои случаи е по-удобно да се изразят и двете чрез или и чрез . Или дори „влак“ - например „X“ до „Y“ и „Y“ до „Z“

Да поставим тогава:

Проверяваме дали намереното решение удовлетворява всяко уравнение на системата и напишете третия собствен вектор

Отговор: собствени вектори:

Геометрично тези вектори определят три различни пространствени посоки ("До там и обратно"), според която линейна трансформациятрансформира ненулеви вектори (собствени вектори) във вектори, колинеарни на тях.

Ако по условие се изискваше да се намери канонично разширение на , тогава това е възможно тук, защото различни собствени стойности съответстват на различни линейно независими собствени вектори. Ние правим матрица от техните координати, диагоналната матрица от релевантнисобствени стойности и намерете обратна матрица .

Ако според условието е необходимо да се пише матрица линейна трансформацияв основата на собствените вектори, тогава даваме отговора във формата . Разлика има и то съществена!За тази матрица е матрицата "de".

Предизвикайте с повече прости изчисленияза независимо решение:

Пример 5

Намерете собствени вектори на линейна трансформация, дадена от матрица

Когато намирате свои собствени числа, опитайте се да не доведете случая до полином от 3-та степен. Освен това вашите системни решения може да се различават от моите решения – тук няма еднозначност; и векторите, които намирате, може да се различават от примерните вектори до пропорционалност на съответните им координати. Например и . По-естетично е да представите отговора под формата на , но е добре, ако се спрете на втория вариант. Всичко обаче има разумни граници, версията не изглежда много добре.

Приблизителна окончателна извадка на заданието в края на урока.

Как да решим проблема в случай на множество собствени стойности?

Общ алгоритъмостава същият, но има свои собствени особености и е препоръчително да запазите някои раздели от решението в по-строг академичен стил:

Пример 6

Намерете собствени стойности и собствени вектори

Решение

Разбира се, нека изписваме страхотната първа колона с главни букви:

И след разграждане квадратен тричленза множители:

В резултат на това се получават собствени стойности, две от които са кратни.

Да намерим нашитевектори:

1) Ще се справим със самотен войник по „опростена“ схема:

От последните две уравнения ясно се вижда равенството, което очевидно трябва да бъде заменено в 1-вото уравнение на системата:

Няма по-добра комбинация:
Собствен вектор:

2-3) Сега премахваме няколко часови. В този случай може да бъде или две или еднасобствен вектор. Независимо от множествеността на корените, ние заместваме стойността в детерминанта , което ни носи следното хомогенна система от линейни уравнения:

Собствените вектори са точно векторите
фундаментална система за вземане на решения

Всъщност през целия урок бяхме ангажирани само с намирането на векторите на фундаменталната система. Само за момента този срокне беше особено необходимо. Между другото, онези сръчни ученици, които в камуфлаж хомогенни уравнения, ще бъде принуден да го изпуши сега.

Единственото действие беше премахването на допълнителни линии. Резултатът е матрица "едно към три" с формална "стъпка" в средата.
– основна променлива, – свободни променливи. Има две безплатни променливи, така че има и два вектора на фундаменталната система.

Нека изразим основната променлива чрез свободни променливи: . Нулевият фактор пред "x" му позволява да приема абсолютно всякакви стойности (което също се вижда ясно от системата от уравнения).

В контекста на този проблем е по-удобно да напишете общото решение не в ред, а в колона:

Двойката съответства на собствен вектор:
Двойката съответства на собствен вектор:

Забележка : опитните читатели могат да разберат тези вектори устно - просто като анализират системата , но тук са необходими известни знания: има три променливи, ранг на системната матрица- единица средства фундаментална система за вземане на решениясе състои от 3 – 1 = 2 вектора. Намерените вектори обаче са идеално видими дори и без това знание, чисто на интуитивно ниво. В този случай третият вектор ще бъде написан още „по-красиво“: . Въпреки това, едно предупреждение в друг пример прост изборможе и да не е, поради което резервацията е предназначена за хора с опит. Освен това, защо не вземем като трети вектор, да речем, ? В края на краищата неговите координати също удовлетворяват всяко уравнение на системата и векторите са линейно независими. Тази опция по принцип е подходяща, но "крива", тъй като "другият" вектор е линейна комбинация от вектори на основната система.

Отговор: собствени стойности: , собствени вектори:

Подобен пример за решение „направи си сам“:

Пример 7

Намерете собствени стойности и собствени вектори

Приблизителна проба за завършване в края на урока.

Трябва да се отбележи, че както в 6-ия, така и в 7-ия пример се получава тройка от линейно независими собствени вектори и следователно оригиналната матрица може да бъде представена в канонично разлагане. Но такива малини не се случват във всички случаи:

Пример 8