Τύπος μέσης διακύμανσης. Δείκτες διακύμανσης: έννοια, τύποι, τύποι για υπολογισμούς

Οι κύριοι γενικευτικοί δείκτες διακύμανσης των στατιστικών είναι οι διακυμάνσεις και ο μέσος όρος τυπική απόκλιση.

Διασπορά αυτό αριθμητικός μέσος όρος τετράγωνες αποκλίσεις κάθε τιμής χαρακτηριστικού από τον συνολικό μέσο όρο. Η διακύμανση συνήθως ονομάζεται μέσο τετράγωνο των αποκλίσεων και συμβολίζεται με  2 . Ανάλογα με τα αρχικά δεδομένα, η απόκλιση μπορεί να υπολογιστεί από τον αριθμητικό μέσο όρο, απλό ή σταθμισμένο:

 μη ζυγισμένη (απλή) διασπορά.

 σταθμισμένη διακύμανση.

Τυπική απόκλιση είναι γενικευτικό χαρακτηριστικό των απόλυτων διαστάσεων παραλλαγές χαρακτηριστικό στο σύνολο. Εκφράζεται στις ίδιες μονάδες με το πρόσημο (σε μέτρα, τόνους, τοις εκατό, εκτάρια κ.λπ.).

Η τυπική απόκλιση είναι η τετραγωνική ρίζα της διακύμανσης και συμβολίζεται με :

 μη σταθμισμένη τυπική απόκλιση.

 σταθμισμένη τυπική απόκλιση.

Η τυπική απόκλιση είναι ένα μέτρο της αξιοπιστίας του μέσου όρου. Όσο μικρότερη είναι η τυπική απόκλιση, τόσο καλύτερα ο αριθμητικός μέσος όρος αντικατοπτρίζει ολόκληρο τον αντιπροσωπευόμενο πληθυσμό.

Προηγείται ο υπολογισμός της τυπικής απόκλισης από τον υπολογισμό της διακύμανσης.

Η διαδικασία για τον υπολογισμό της σταθμισμένης διακύμανσης έχει ως εξής:

1) προσδιορίστε τον αριθμητικό σταθμισμένο μέσο όρο:

2) Υπολογίστε τις αποκλίσεις των επιλογών από τον μέσο όρο:

3) τετράγωνο της απόκλισης κάθε επιλογής από το μέσο όρο:

4) πολλαπλασιάστε τις αποκλίσεις στο τετράγωνο με τα βάρη (συχνότητες):

5) συνοψίστε τις ληφθείσες εργασίες:

6) το ποσό που προκύπτει διαιρείται με το άθροισμα των βαρών:

Παράδειγμα 2.1

Υπολογίστε τον αριθμητικό σταθμισμένο μέσο όρο:

Οι τιμές των αποκλίσεων από τον μέσο όρο και τα τετράγωνά τους παρουσιάζονται στον πίνακα. Ας ορίσουμε τη διακύμανση:

Η τυπική απόκλιση θα είναι ίση με:

Εάν τα δεδομένα πηγής παρουσιάζονται ως ένα διάστημα σειρά διανομής , τότε πρέπει πρώτα να προσδιορίσετε τη διακριτή τιμή της δυνατότητας και, στη συνέχεια, να εφαρμόσετε τη μέθοδο που περιγράφεται.

Παράδειγμα 2.2

Ας δείξουμε τον υπολογισμό της διακύμανσης για τις σειρές διαστήματος στα δεδομένα σχετικά με την κατανομή της σπαρμένης έκτασης του συλλογικού αγροκτήματος ανά απόδοση σιταριού.

Ο αριθμητικός μέσος όρος είναι:

Ας υπολογίσουμε τη διακύμανση:

6.3. Υπολογισμός της διασποράς σύμφωνα με τον τύπο για μεμονωμένα δεδομένα

Τεχνική υπολογισμού διασπορά περίπλοκο, και μεγάλες αξίεςΟι επιλογές και οι συχνότητες μπορεί να είναι δυσκίνητες. Οι υπολογισμοί μπορούν να απλοποιηθούν χρησιμοποιώντας τις ιδιότητες διασποράς.

Η διασπορά έχει τις ακόλουθες ιδιότητες.

1. Μια μείωση ή αύξηση των βαρών (συχνοτήτων) ενός μεταβλητού χαρακτηριστικού κατά συγκεκριμένο αριθμό φορών δεν αλλάζει τη διασπορά.

2. Μείωση ή αύξηση κάθε τιμής χαρακτηριστικού κατά την ίδια σταθερή τιμή ΑΛΛΑη διασπορά δεν αλλάζει.

3. Μείωση ή αύξηση κάθε τιμής χαρακτηριστικού κατά συγκεκριμένο αριθμό φορές καντίστοιχα μειώνει ή αυξάνει τη διακύμανση σε κ 2 φορές τυπική απόκλιση  σε κμια φορά.

4. Η διακύμανση ενός χαρακτηριστικού σε σχέση με μια αυθαίρετη τιμή είναι πάντα μεγαλύτερη από τη διακύμανση σε σχέση με τον αριθμητικό μέσο όρο κατά το τετράγωνο της διαφοράς μεταξύ του μέσου όρου και των αυθαίρετων τιμών:

Αν ένα ΑΛΛΑ 0, τότε καταλήγουμε στην ακόλουθη ισότητα:

δηλ. η διακύμανση ενός χαρακτηριστικού είναι ίση με τη διαφορά μεταξύ του μέσου τετραγώνου των τιμών των χαρακτηριστικών και του τετραγώνου του μέσου όρου.

Κάθε ιδιότητα μπορεί να χρησιμοποιηθεί μόνη της ή σε συνδυασμό με άλλες κατά τον υπολογισμό της διακύμανσης.

Η διαδικασία για τον υπολογισμό της διακύμανσης είναι απλή:

1) καθορίζει αριθμητικός μέσος όρος :

2) τετράγωνο του αριθμητικού μέσου όρου:

3) τετράγωνο της απόκλισης κάθε παραλλαγής της σειράς:

Χ Εγώ 2 .

4) βρείτε το άθροισμα των τετραγώνων των επιλογών:

5) διαιρέστε το άθροισμα των τετραγώνων των επιλογών με τον αριθμό τους, δηλ. καθορίστε μεσαίο τετράγωνο:

6) προσδιορίστε τη διαφορά μεταξύ του μέσου τετραγώνου του χαρακτηριστικού και του τετραγώνου του μέσου όρου:

Παράδειγμα 3.1Έχουμε τα ακόλουθα στοιχεία για την παραγωγικότητα των εργαζομένων:

Ας κάνουμε τους παρακάτω υπολογισμούς:

Αυτή η σελίδα περιγράφει τυπικό παράδειγμαβρίσκοντας τη διακύμανση, μπορείτε επίσης να δείτε άλλες εργασίες για να την βρείτε

Παράδειγμα 1. Προσδιορισμός ομάδας, μέσος όρος ομάδας, μεταξύ ομάδων και συνολικής διακύμανσης

Παράδειγμα 2. Εύρεση της διακύμανσης και του συντελεστή διακύμανσης σε έναν πίνακα ομαδοποίησης

Παράδειγμα 3. Εύρεση της διακύμανσης σε διακριτές σειρές

Παράδειγμα 4. Έχουμε τα παρακάτω στοιχεία για μια ομάδα 20 μαθητών τμήμα αλληλογραφίας. Ανάγκη κατασκευής σειρές μεσοδιαστημάτωνκατανομή του χαρακτηριστικού, υπολογίστε τη μέση τιμή του χαρακτηριστικού και μελετήστε τη διακύμανσή του

Ας χτίσουμε ομαδοποίηση διαστημάτων. Ας προσδιορίσουμε το εύρος του διαστήματος με τον τύπο:

όπου X max– μέγιστη αξίαομαδοποίηση σημάδι?
Το X min είναι η ελάχιστη τιμή του χαρακτηριστικού ομαδοποίησης.
n είναι ο αριθμός των διαστημάτων:

Δεχόμαστε n=5. Το βήμα είναι: h \u003d (192 - 159) / 5 \u003d 6,6

Ας κάνουμε μια ομαδοποίηση διαστημάτων

Για περαιτέρω υπολογισμούς, θα φτιάξουμε έναν βοηθητικό πίνακα:

X "i - το μέσο του διαστήματος. (για παράδειγμα, το μέσο του διαστήματος 159 - 165,6 \u003d 162,3)

μέση αξίαη ανάπτυξη των μαθητών καθορίζεται από τον τύπο του αριθμητικού σταθμισμένου μέσου όρου:

Καθορίζουμε τη διασπορά με τον τύπο:

Ο τύπος μπορεί να μετατραπεί ως εξής:

Από αυτόν τον τύπο προκύπτει ότι η διακύμανση είναι τη διαφορά μεταξύ του μέσου όρου των τετραγώνων των επιλογών και του τετραγώνου και του μέσου όρου.

Διακύμανση στη σειρά παραλλαγήςΜε σε ίσα διαστήματαμε τη μέθοδο των ροπών μπορεί να υπολογιστεί με τον εξής τρόποόταν χρησιμοποιείται η δεύτερη ιδιότητα της διακύμανσης (διαιρώντας όλες τις επιλογές με την τιμή του διαστήματος). Ορισμός διακύμανσης, που υπολογίζεται με τη μέθοδο των ροπών, σύμφωνα με τον ακόλουθο τύπο είναι λιγότερο χρονοβόρα:

όπου i είναι η τιμή του διαστήματος.
Το Α είναι ένα μηδενικό υπό όρους, για το οποίο είναι βολικό να χρησιμοποιείται το μέσο ενός διαστήματος που έχει υψηλότερη συχνότητα;
m1 είναι το τετράγωνο της στιγμής της πρώτης τάξης.
m2 - στιγμή της δεύτερης παραγγελίας

Διακύμανση χαρακτηριστικών (εάν στον στατιστικό πληθυσμό το χαρακτηριστικό αλλάζει με τέτοιο τρόπο ώστε να υπάρχουν μόνο δύο αμοιβαία αποκλειστικές επιλογές, τότε αυτή η μεταβλητότητα ονομάζεται εναλλακτική) μπορεί να υπολογιστεί με τον τύπο:

Αντικατάσταση σε αυτή τη φόρμουλαδιασπορά q \u003d 1- p, παίρνουμε:

Τύποι διασποράς

Συνολική διακύμανσημετρά τη διακύμανση ενός χαρακτηριστικού σε ολόκληρο τον πληθυσμό ως σύνολο υπό την επίδραση όλων των παραγόντων που προκαλούν αυτή τη διακύμανση. Είναι ίσο με το μέσο τετράγωνο των αποκλίσεων ατομικές αξίεςχαρακτηριστικό x της συνολικής μέσης τιμής του x και μπορεί να οριστεί ως απλή διακύμανση ή σταθμισμένη διακύμανση.

Διακύμανση εντός ομάδας χαρακτηρίζει την τυχαία παραλλαγή, δηλ. μέρος της διακύμανσης, το οποίο οφείλεται στην επιρροή μη λογιστικών παραγόντων και δεν εξαρτάται από τον παράγοντα πρόσημο που βρίσκεται κάτω από την ομαδοποίηση. Αυτή η απόκλιση είναι ίση με το μέσο τετράγωνο των αποκλίσεων των επιμέρους τιμών του χαρακτηριστικού εντός της ομάδας Χ από τον αριθμητικό μέσο όρο της ομάδας και μπορεί να υπολογιστεί ως απλή διακύμανση ή ως σταθμισμένη διακύμανση.

Με αυτόν τον τρόπο, μέτρα διακύμανσης εντός της ομάδαςπαραλλαγή ενός χαρακτηριστικού μέσα σε μια ομάδα και καθορίζεται από τον τύπο:

όπου xi - μέσος όρος ομάδας.
ni είναι ο αριθμός των μονάδων στην ομάδα.

Για παράδειγμα, οι διακυμάνσεις εντός του ομίλου που πρέπει να καθοριστούν στο έργο της μελέτης της επίδρασης των προσόντων των εργαζομένων στο επίπεδο παραγωγικότητας της εργασίας σε ένα κατάστημα δείχνουν διακυμάνσεις στην παραγωγή σε κάθε ομάδα που προκαλούνται από όλους τους πιθανούς παράγοντες (τεχνική κατάσταση του εξοπλισμού, διαθεσιμότητα εργαλείων και υλικών, ηλικία εργαζομένων, ένταση εργασίας κ.λπ. .), εκτός από τις διαφορές στην κατηγορία προσόντων (μέσα στην ομάδα, όλοι οι εργαζόμενοι έχουν τα ίδια προσόντα).

Ας υπολογίσουμε μέσαΚυρίαΠΡΟΕΧΩδιασπορά και τυπική απόκλισηδείγματα. Υπολογίζουμε επίσης τη διακύμανση μιας τυχαίας μεταβλητής εάν η κατανομή της είναι γνωστή.

Πρώτα σκεφτείτε διασπορά, έπειτα τυπική απόκλιση.

Διακύμανση δείγματος

Διακύμανση δείγματος (διακύμανση δείγματος,δείγμαδιαφορά) χαρακτηρίζει την εξάπλωση των τιμών στον πίνακα σε σχέση με το .

Και οι 3 τύποι είναι μαθηματικά ισοδύναμοι.

Από τον πρώτο τύπο φαίνεται ότι διακύμανση δείγματοςείναι το άθροισμα των τετραγωνικών αποκλίσεων κάθε τιμής στον πίνακα από το μέσο όροδιαιρούμενο με το μέγεθος του δείγματος μείον 1.

διασπορά δείγματαχρησιμοποιείται η συνάρτηση DISP(), eng. το όνομα του VAR, δηλ. Διαφορά. Από το MS EXCEL 2010, συνιστάται η χρήση του αναλογικού του DISP.V() , eng. το όνομα VARS, δηλ. Δείγμα Διακύμανσης. Επιπλέον, ξεκινώντας από την έκδοση του MS EXCEL 2010, υπάρχει μια λειτουργία DISP.G (), eng. Το όνομα VARP, δηλ. Μεταβλητή πληθυσμού που υπολογίζει διασποράΓια πληθυσμός . Η όλη διαφορά έγκειται στον παρονομαστή: αντί για n-1 όπως το DISP.V() , το DISP.G() έχει μόλις n στον παρονομαστή. Πριν από το MS EXCEL 2010, η συνάρτηση VARP() χρησιμοποιήθηκε για τον υπολογισμό της διακύμανσης του πληθυσμού.

Διακύμανση δείγματος
=SQUARE(Sample)/(COUNT(Sample)-1)
=(SUMSQ(Δείγμα)-COUNT(Δείγμα)*AVERAGE(Δείγμα)^2)/ (COUNT(Δείγμα)-1)- η συνήθης φόρμουλα
=SUM((Δείγμα -AVERAGE(Δείγμα))^2)/ (COUNT(Δείγμα)-1) –

Διακύμανση δείγματοςείναι ίσο με 0 μόνο εάν όλες οι τιμές είναι ίσες μεταξύ τους και, κατά συνέπεια, είναι ίσες μέση τιμή. Συνήθως, όσο μεγαλύτερη είναι η τιμή διασπορά, τόσο μεγαλύτερη είναι η εξάπλωση των τιμών στον πίνακα.

Διακύμανση δείγματοςείναι βαθμολογική εκτίμηση διασποράκατανομή της τυχαίας μεταβλητής από την οποία η δείγμα. Περί κατασκευής διαστήματα εμπιστοσύνης κατά την αξιολόγηση διασποράμπορεί να διαβαστεί στο άρθρο.

Διακύμανση τυχαίας μεταβλητής

Να υπολογίσω διασποράτυχαία μεταβλητή, πρέπει να τη γνωρίζετε.

Για διασποράΗ τυχαία μεταβλητή X χρησιμοποιεί συχνά τον συμβολισμό Var(X). Διασποράισούται με το τετράγωνο της απόκλισης από τη μέση E(X): Var(X)=E[(X-E(X)) 2 ]

διασποράυπολογίζεται με τον τύπο:

όπου x i είναι η τιμή που μπορεί να πάρει η τυχαία μεταβλητή και μ είναι η μέση τιμή (), p(x) είναι η πιθανότητα η τυχαία μεταβλητή να πάρει την τιμή x.

Εάν η τυχαία μεταβλητή έχει , τότε διασποράυπολογίζεται με τον τύπο:

Διάσταση διασποράαντιστοιχεί στο τετράγωνο της μονάδας μέτρησης των αρχικών τιμών. Για παράδειγμα, εάν οι τιμές στο δείγμα είναι μετρήσεις του βάρους του εξαρτήματος (σε kg), τότε η διάσταση της διακύμανσης θα είναι kg 2. Αυτό μπορεί να είναι δύσκολο να ερμηνευτεί, επομένως, να χαρακτηριστεί η εξάπλωση των αξιών, μια τιμή ίση με τετραγωνική ρίζααπό διασπορά – τυπική απόκλιση.

Μερικές ιδιότητες διασπορά:

Var(X+a)=Var(X), όπου το X είναι μια τυχαία μεταβλητή και η a είναι μια σταθερά.

Var(aΧ)=a 2 Var(X)

Var(X)=E[(X-E(X)) 2 ]=E=E(X 2)-E(2*X*E(X))+(E(X)) 2=E(X 2)- 2*E(X)*E(X)+(E(X)) 2 =E(X 2)-(E(X)) 2

Αυτή η ιδιότητα διασποράς χρησιμοποιείται σε άρθρο για τη γραμμική παλινδρόμηση.

Var(X+Y)=Var(X) + Var(Y) + 2*Cov(X;Y), όπου τα X και Y είναι τυχαίες μεταβλητές, Cov(Х;Y) - συνδιακύμανση αυτών των τυχαίων μεταβλητών.

Αν οι τυχαίες μεταβλητές είναι ανεξάρτητες, τότε τους συνδιακύμανσηείναι 0, και επομένως Var(X+Y)=Var(X)+Var(Y). Αυτή η ιδιότητα της διακύμανσης χρησιμοποιείται στην έξοδο.

Ας το δείξουμε για ανεξάρτητες ποσότητες Var(X-Y)=Var(X+Y). Πράγματι, Var(X-Y)= Var(X-Y)= Var(X+(-Y))= Var(X)+Var(-Y)= Var(X)+Var(-Y)= Var(X)+(- 1) 2 Var(Y)= Var(X)+Var(Y)= Var(X+Y). Αυτή η ιδιότητα της διακύμανσης χρησιμοποιείται για την γραφική παράσταση .

Δείγμα τυπικής απόκλισης

Δείγμα τυπικής απόκλισηςείναι ένα μέτρο του πόσο ευρέως διασκορπισμένες είναι οι τιμές στο δείγμα σε σχέση με τις τιμές τους.

Εξ ορισμού, τυπική απόκλισηισούται με την τετραγωνική ρίζα του διασπορά:

Τυπική απόκλισηδεν λαμβάνει υπόψη το μέγεθος των τιμών σε δειγματοληψία, αλλά μόνο ο βαθμός διασποράς των αξιών γύρω τους Μέσης. Ας πάρουμε ένα παράδειγμα για να το διευκρινίσουμε αυτό.

Ας υπολογίσουμε την τυπική απόκλιση για 2 δείγματα: (1; 5; 9) και (1001; 1005; 1009). Και στις δύο περιπτώσεις, s=4. Είναι προφανές ότι ο λόγος της τυπικής απόκλισης προς τις τιμές του πίνακα είναι σημαντικά διαφορετικός για τα δείγματα. Για τέτοιες περιπτώσεις, χρησιμοποιήστε Ο συντελεστής διακύμανσης(Συντελεστής Διακύμανσης, CV) - αναλογία τυπική απόκλισηστο μέσο όρο αριθμητική, εκφρασμένο ως ποσοστό.

Σε MS EXCEL 2007 και άνω πρώιμες εκδόσειςνα υπολογίσω Δείγμα τυπικής απόκλισηςχρησιμοποιείται η συνάρτηση =STDEV(), eng. το όνομα STDEV, δηλ. τυπική απόκλιση. Από το MS EXCEL 2010, συνιστάται η χρήση του αναλόγου του = STDEV.B () , eng. όνομα STDEV.S, δηλ. Δείγμα Τυπικής απόκλισης.

Επιπλέον, ξεκινώντας από την έκδοση του MS EXCEL 2010, υπάρχει μια συνάρτηση STDEV.G () , eng. όνομα STDEV.P, δηλ. Πληθυσμός Τυπική απόκλιση που υπολογίζει τυπική απόκλισηΓια πληθυσμός. Η όλη διαφορά καταλήγει στον παρονομαστή: αντί για n-1 όπως το STDEV.V() , το STDEV.G() έχει μόλις n στον παρονομαστή.

Τυπική απόκλισημπορεί επίσης να υπολογιστεί απευθείας από τους παρακάτω τύπους (δείτε παράδειγμα αρχείου)
=SQRT(SQUADROTIV(Δείγμα)/(COUNT(Δείγμα)-1))
=SQRT((SUMSQ(Δείγμα)-COUNT(Δείγμα)*AVERAGE(Δείγμα)^2)/(COUNT(Δείγμα)-1))

Άλλα μέτρα διασποράς

Η συνάρτηση SQUADRIVE() υπολογίζει με umm τετραγωνικών αποκλίσεων των τιμών από τους Μέσης. Αυτή η συνάρτηση θα επιστρέψει το ίδιο αποτέλεσμα με τον τύπο =VAR.G( Δείγμα)*ΕΛΕΓΧΟΣ( Δείγμα) , όπου Δείγμα- μια αναφορά σε μια περιοχή που περιέχει μια σειρά από τιμές δείγματος (). Οι υπολογισμοί στη συνάρτηση QUADROTIV() γίνονται σύμφωνα με τον τύπο:

Η συνάρτηση SROOT() είναι επίσης ένα μέτρο της διασποράς ενός συνόλου δεδομένων. Η συνάρτηση AVERAGE() υπολογίζει τον μέσο όρο απόλυτες τιμέςαποκλίσεις από Μέσης. Αυτή η συνάρτηση θα επιστρέψει το ίδιο αποτέλεσμα με τον τύπο =SUMPRODUCT(ABS(Sample-AVERAGE(Sample)))/COUNT(Sample), όπου Δείγμα- μια αναφορά σε μια περιοχή που περιέχει μια σειρά από τιμές δείγματος.

Οι υπολογισμοί στη συνάρτηση SROOTKL () γίνονται σύμφωνα με τον τύπο:

Για ομαδοποιημένα δεδομένα υπολειμματική διασπορά - μέσος όρος διακυμάνσεις εντός της ομάδας:

Όπου σ 2 j είναι η διακύμανση εντός της ομάδας της j -ης ομάδας.

Για μη ομαδοποιημένα δεδομένα υπολειμματική διασποράείναι ένα μέτρο της ακρίβειας προσέγγισης, δηλ. προσέγγιση της γραμμής παλινδρόμησης στα αρχικά δεδομένα:
όπου y(t) είναι η πρόβλεψη σύμφωνα με την εξίσωση τάσης. y t – αρχική σειρά δυναμικών. n είναι ο αριθμός των σημείων. p είναι ο αριθμός των συντελεστών της εξίσωσης παλινδρόμησης (ο αριθμός των επεξηγηματικών μεταβλητών).
Σε αυτό το παράδειγμα ονομάζεται αμερόληπτη εκτίμηση της διακύμανσης.

Παράδειγμα #1. Η κατανομή των εργαζομένων τριών επιχειρήσεων μιας ένωσης ανά δασμολογικές κατηγορίες χαρακτηρίζεται από τα ακόλουθα δεδομένα:

Κατηγορία μισθού εργαζομένου	Αριθμός εργαζομένων στην επιχείρηση
	επιχείρηση 1	επιχείρηση 2	επιχείρηση 3
1	50	20	40
2	100	80	60
3	150	150	200
4	350	300	400
5	200	150	250
6	150	100	150

Καθορίζω:
1. Διασπορά για κάθε επιχείρηση (ενδοομιλική διασπορά).
2. Μέσος όρος διασπορών εντός της ομάδας.
3. Διασπορά μεταξύ ομάδων.
4. συνολική διακύμανση.

Λύση.
Πριν προχωρήσετε στην επίλυση του προβλήματος, είναι απαραίτητο να μάθετε ποιο χαρακτηριστικό είναι αποτελεσματικό και ποιο είναι παραγοντικό. Στο υπό εξέταση παράδειγμα, το αποτελεσματικό χαρακτηριστικό είναι "Κατηγορία δασμών" και το χαρακτηριστικό παράγοντα είναι "Αριθμός (όνομα) της επιχείρησης".
Στη συνέχεια, έχουμε τρεις ομάδες (επιχειρήσεις) για τις οποίες είναι απαραίτητο να υπολογιστεί ο μέσος όρος της ομάδας και οι διακυμάνσεις εντός της ομάδας:

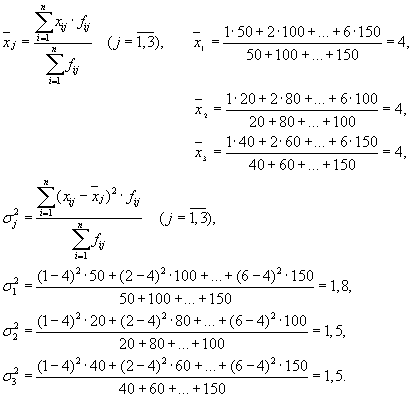
Εταιρία	μέσος όρος ομάδας,	διακύμανση εντός ομάδας,
1	4	1,8

Ο μέσος όρος των διακυμάνσεων εντός ομάδας ( υπολειμματική διασπορά) υπολογίζεται με τον τύπο:

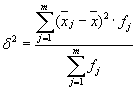
όπου μπορείτε να υπολογίσετε:
ή:

έπειτα:
Η συνολική διασπορά θα είναι ίση με: s 2 \u003d 1,6 + 0 \u003d 1,6.
Η συνολική διακύμανση μπορεί επίσης να υπολογιστεί χρησιμοποιώντας έναν από τους παρακάτω δύο τύπους:

Όταν λύνει κανείς πρακτικά προβλήματα, συχνά πρέπει να αντιμετωπίσει ένα ζώδιο που παίρνει μόνο δύο εναλλακτικές αξίες. Σε αυτήν την περίπτωση, δεν μιλούν για το βάρος μιας συγκεκριμένης αξίας ενός χαρακτηριστικού, αλλά για το μερίδιό του στο σύνολο. Εάν το ποσοστό των πληθυσμιακών μονάδων που έχουν το υπό μελέτη χαρακτηριστικό συμβολίζεται με " R", και όχι κατοχή - μέσω" q”, τότε η διασπορά μπορεί να υπολογιστεί με τον τύπο:
s 2 = p×q

Παράδειγμα #2. Σύμφωνα με τα δεδομένα για την ανάπτυξη έξι εργαζομένων της ταξιαρχίας, προσδιορίστε τη διασπορά μεταξύ ομάδων και αξιολογήστε την επίδραση της βάρδιας εργασίας στην παραγωγικότητα της εργασίας τους εάν η συνολική διακύμανση είναι 12,2.

Αρ. της εργατικής ταξιαρχίας	Έξοδος εργασίας, τεμ.
	στην πρώτη βάρδια	στη 2η βάρδια
1	18	13
2	19	14
3	22	15
4	20	17
5	24	16
6	23	15

Λύση. Αρχικά στοιχεία

Χ	στ1	στ2	στ 3	f4	f5	στ6	Σύνολο
1	18	19	22	20	24	23	126
2	13	14	15	17	16	15	90
Σύνολο	31	33	37	37	40	38

Έπειτα έχουμε 6 ομάδες για τις οποίες είναι απαραίτητος ο υπολογισμός του μέσου όρου της ομάδας και των ενδοομαδικών διακυμάνσεων.
1. Βρείτε τις μέσες τιμές κάθε ομάδας.







2. Βρείτε το μέσο τετράγωνο κάθε ομάδας.







Συνοψίζουμε τα αποτελέσματα του υπολογισμού σε έναν πίνακα:

Αριθμός ομάδας	Μέσος όρος ομάδας	Διακύμανση εντός ομάδας
1	1.42	0.24
2	1.42	0.24
3	1.41	0.24
4	1.46	0.25
5	1.4	0.24
6	1.39	0.24

3. Διακύμανση εντός ομάδαςχαρακτηρίζει την αλλαγή (παραλλαγή) του υπό μελέτη (προκύπτοντος) χαρακτηριστικού εντός της ομάδας υπό την επίδραση όλων των παραγόντων, εκτός από τον παράγοντα που βρίσκεται κάτω από την ομαδοποίηση:
Υπολογίζουμε τον μέσο όρο των ενδοομαδικών διασπορών χρησιμοποιώντας τον τύπο:


4. Διαομαδική διακύμανσηχαρακτηρίζει την αλλαγή (παραλλαγή) του υπό μελέτη (προκύπτοντος) χαρακτηριστικού υπό την επίδραση ενός παράγοντα (παραγοντικό γνώρισμα) που βρίσκεται κάτω από την ομαδοποίηση.
Η διασπορά μεταξύ ομάδων ορίζεται ως:

όπου


Επειτα

Συνολική διακύμανσηχαρακτηρίζει την αλλαγή (παραλλαγή) του υπό μελέτη (προκύπτοντος) χαρακτηριστικού υπό την επίδραση όλων των παραγόντων (παραγοντικά χαρακτηριστικά) ανεξαιρέτως. Με την προϋπόθεση του προβλήματος, είναι ίσο με 12,2.
Εμπειρική σχέση συσχέτισηςμετρά πόσο από τη συνολική διακύμανση του προκύπτοντος χαρακτηριστικού προκαλείται από τον παράγοντα που μελετήθηκε. Αυτός είναι ο λόγος της παραγοντικής διακύμανσης προς τη συνολική διακύμανση:

Καθορίζουμε την εμπειρική σχέση συσχέτισης:

Οι σχέσεις μεταξύ των χαρακτηριστικών μπορεί να είναι αδύναμες ή ισχυρές (στενές). Τα κριτήριά τους αξιολογούνται στην κλίμακα Chaddock:
0,1 0,3 0,5 0,7 0,9 Στο παράδειγμά μας, η σχέση μεταξύ του χαρακτηριστικού Υ παράγοντα X είναι ασθενής
Συντελεστής προσδιορισμού.

Ας ορίσουμε τον συντελεστή προσδιορισμού:

Έτσι, το 0,67% της διακύμανσης οφείλεται σε διαφορές μεταξύ των χαρακτηριστικών και το 99,37% οφείλεται σε άλλους παράγοντες.
συμπέρασμα: σε αυτή η υπόθεσηη ανάπτυξη των εργαζομένων δεν εξαρτάται από την εργασία σε μια συγκεκριμένη βάρδια, δηλ. η επίδραση της βάρδιας εργασίας στην παραγωγικότητα της εργασίας τους δεν είναι σημαντική και οφείλεται σε άλλους παράγοντες.

Παράδειγμα #3. Με βάση τον μέσο όρο μισθοίκαι στο τετράγωνο των αποκλίσεων από την τιμή του για δύο ομάδες εργαζομένων, βρείτε τη συνολική διακύμανση εφαρμόζοντας τον κανόνα για την προσθήκη διακυμάνσεων:

Λύση:
Μέσος όρος διακυμάνσεων εντός της ομάδας

Η διασπορά μεταξύ ομάδων ορίζεται ως:


Η συνολική διακύμανση θα είναι: 480 + 13824 = 14304

Μεταξύ των πολλών δεικτών που χρησιμοποιούνται στις στατιστικές, είναι απαραίτητο να επισημανθεί ο υπολογισμός της διακύμανσης. Θα πρέπει να σημειωθεί ότι η μη αυτόματη εκτέλεση αυτού του υπολογισμού είναι μια μάλλον κουραστική εργασία. Ευτυχώς, υπάρχουν λειτουργίες στο Excel που σας επιτρέπουν να αυτοματοποιήσετε τη διαδικασία υπολογισμού. Ας μάθουμε τον αλγόριθμο για την εργασία με αυτά τα εργαλεία.

Η διακύμανση είναι ένα μέτρο διακύμανσης, το οποίο είναι το μέσο τετράγωνο των αποκλίσεων από μαθηματική προσδοκία. Έτσι, εκφράζει την εξάπλωση των αριθμών σχετικά με τον μέσο όρο. Ο υπολογισμός της διασποράς μπορεί να πραγματοποιηθεί τόσο για τον γενικό πληθυσμό όσο και για το δείγμα.

Μέθοδος 1: υπολογισμός στο γενικό πληθυσμό

Για τον υπολογισμό αυτού του δείκτη στο Excel για τον γενικό πληθυσμό, χρησιμοποιείται η συνάρτηση ΔΙΣΠ.Γ. Η σύνταξη αυτής της έκφρασης είναι η εξής:

DISP.G (Αριθμός 1; Αριθμός 2;…)

Συνολικά, μπορούν να εφαρμοστούν από 1 έως 255 ορίσματα. Επιχειρήματα μπορεί να είναι αριθμητικές τιμές, καθώς και αναφορές στα κελιά στα οποία περιέχονται.

Ας δούμε πώς να υπολογίσουμε αυτήν την τιμή για ένα εύρος αριθμητικών δεδομένων.

Μέθοδος 2: υπολογισμός δείγματος

Σε αντίθεση με τον υπολογισμό της τιμής για το γενικό πληθυσμό, στον υπολογισμό για το δείγμα, δεν αναφέρεται ο παρονομαστής σύνολοαριθμούς, αλλά ένα λιγότερο. Αυτό γίνεται για να διορθωθεί το σφάλμα. Το Excel λαμβάνει υπόψη αυτήν την απόχρωση σε μια ειδική συνάρτηση που έχει σχεδιαστεί για αυτόν τον τύπο υπολογισμού - DISP.V. Η σύνταξή του αντιπροσωπεύεται από τον ακόλουθο τύπο:

VAR.B(Αριθμός1;Αριθμός2;…)

Ο αριθμός των ορισμάτων, όπως και στην προηγούμενη συνάρτηση, μπορεί επίσης να κυμαίνεται από 1 έως 255.

Όπως μπορείτε να δείτε, το πρόγραμμα Excel μπορεί να διευκολύνει σημαντικά τον υπολογισμό της διακύμανσης. Αυτό στατιστικόςμπορεί να υπολογιστεί από την εφαρμογή, τόσο για τον γενικό πληθυσμό όσο και για το δείγμα. Σε αυτήν την περίπτωση, όλες οι ενέργειες χρήστη περιορίζονται στην πραγματικότητα μόνο στον καθορισμό του εύρους των προς επεξεργασία αριθμών και το Excel κάνει το ίδιο το κύριο έργο. Φυσικά, αυτό θα εξοικονομήσει σημαντικό χρόνο για τους χρήστες.