Βασικά θεωρήματα δυναμικής. Γενικά θεωρήματα δυναμικής

Διάλεξη 3 Γενικά θεωρήματα δυναμικής

Δυναμική του συστήματος των υλικών σημείωναποτελεί σημαντικό κλάδο της θεωρητικής μηχανικής. Εδώ, εξετάζουμε κυρίως τα προβλήματα της κίνησης των μηχανικών συστημάτων (συστήματα υλικών σημείων) με πεπερασμένος αριθμόςβαθμοί ελευθερίας - ο μέγιστος αριθμός ανεξάρτητων παραμέτρων που καθορίζουν τη θέση του συστήματος. το κύριο καθήκονδυναμική συστήματος - η μελέτη των νόμων κίνησης ενός άκαμπτου σώματος και των μηχανικών συστημάτων.

Η απλούστερη προσέγγιση για τη μελέτη της κίνησης ενός συστήματος, που αποτελείται από Νυλικά σημεία, ανάγεται στην εξέταση των κινήσεων κάθε επιμέρους σημείου του συστήματος. Σε αυτή την περίπτωση, πρέπει να προσδιοριστούν όλες οι δυνάμεις που δρουν σε κάθε σημείο του συστήματος, συμπεριλαμβανομένων των δυνάμεων αλληλεπίδρασης μεταξύ σημείων.

Καθορίζοντας την επιτάχυνση κάθε σημείου σύμφωνα με τον δεύτερο νόμο του Νεύτωνα (1.2), λαμβάνουμε για κάθε σημείο τρεις βαθμωτούς διαφορικούς νόμους κίνησης δεύτερης τάξης, δηλ. 3 Ν διαφορικός νόμος κίνησης για ολόκληρο το σύστημα.

Να βρούμε τις εξισώσεις κίνησης μηχανικό σύστημαλαμβανόμενες δυνάμεις και αρχικές συνθήκες για κάθε σημείο του συστήματος διαφορικούς νόμουςπρέπει να ενσωματωθεί. Αυτό το πρόβλημα είναι δύσκολο ακόμη και στην περίπτωση δύο υλικών σημείων που κινούνται μόνο υπό τη δράση των δυνάμεων αλληλεπίδρασης σύμφωνα με τον νόμο της παγκόσμιας έλξης (το πρόβλημα των δύο σωμάτων) και είναι εξαιρετικά δύσκολο στην περίπτωση τριών σημείων αλληλεπίδρασης (το πρόβλημα τριών σωμάτων).

Επομένως, είναι απαραίτητο να βρεθούν τέτοιες μέθοδοι για την επίλυση προβλημάτων που θα οδηγούσαν σε επιλύσιμες εξισώσεις και θα έδιναν μια ιδέα για την κίνηση ενός μηχανικού συστήματος. Τα γενικά θεωρήματα της δυναμικής, ως συνέπεια των διαφορικών νόμων της κίνησης, καθιστούν δυνατή την αποφυγή της πολυπλοκότητας που προκύπτει κατά την ολοκλήρωση και τη λήψη των απαραίτητων αποτελεσμάτων.

3.1 Γενικές παρατηρήσεις

Τα σημεία του μηχανικού συστήματος θα αριθμούνται με δείκτες Εγώ, ι, κκ.λπ. που διατρέχουν όλες τις αξίες 1, 2, 3… Ν, που Ν είναι ο αριθμός των σημείων του συστήματος. Φυσικές ποσότητες που σχετίζονται με κτο σημείο συμβολίζεται με τον ίδιο δείκτη με το σημείο. Για παράδειγμα, εκφράζουν αντίστοιχα το διάνυσμα ακτίνας και την ταχύτητα κ-ο σημείο.

Δυνάμεις δύο προέλευσης δρουν σε καθένα από τα σημεία του συστήματος: πρώτον, δυνάμεις των οποίων οι πηγές βρίσκονται εκτός του συστήματος, που ονομάζονται εξωτερικόςδυνάμεις και συμβολίζεται με ; δεύτερον, δυνάμεις από άλλα σημεία αυτού του συστήματος, που καλούνται εσωτερικόςδυνάμεις και συμβολίζεται με . Οι εσωτερικές δυνάμεις ικανοποιούν τον τρίτο νόμο του Νεύτωνα. Εξετάστε τις απλούστερες ιδιότητες των εσωτερικών δυνάμεων που δρουν σε ολόκληρο το μηχανικό σύστημα σε οποιαδήποτε από τις καταστάσεις του.

Πρώτη ιδιοκτησία. Το γεωμετρικό άθροισμα όλων των εσωτερικών δυνάμεων του συστήματος (το κύριο διάνυσμα των εσωτερικών δυνάμεων) είναι ίσο με μηδέν.

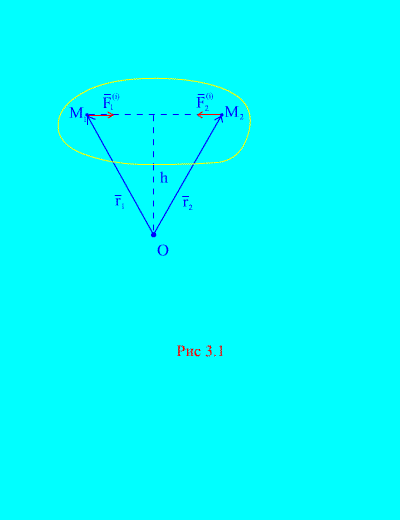
Πράγματι, αν λάβουμε υπόψη οποιαδήποτε δύο αυθαίρετα σημεία του συστήματος, για παράδειγμα, και (Εικ. 3.1), τότε για αυτούς , επειδή οι δυνάμεις της δράσης και της αντίδρασης είναι πάντα ίσες σε απόλυτη τιμή, ενεργούν κατά μήκος μιας γραμμής δράσης προς την αντίθετη κατεύθυνση, η οποία συνδέει τα σημεία αλληλεπίδρασης. Επομένως, το κύριο διάνυσμα των εσωτερικών δυνάμεων αποτελείται από ζεύγη δυνάμεων αλληλεπιδρώντων σημείων

(3.1)

Δεύτερη ιδιοκτησία. Το γεωμετρικό άθροισμα των ροπών όλων των εσωτερικών δυνάμεων σε σχέση με ένα αυθαίρετο σημείο του χώρου είναι μηδέν.

Εξετάστε το σύστημα των ροπών των δυνάμεων και σε σχέση με το σημείο Ο(Εικ. 3.1). Από (Εικ. 3.1). είναι ξεκάθαρο ότι

επειδή και οι δύο δυνάμεις έχουν τους ίδιους βραχίονες και αντίθετες κατευθύνσεις διανυσματικών ροπών. Η κύρια στιγμή των εσωτερικών δυνάμεων για το σημείο Οαποτελείται από το διανυσματικό άθροισμα τέτοιων παραστάσεων και ισούται με μηδέν. Ως εκ τούτου,

Αφήστε εξωτερικά και εσωτερικές δυνάμειςπου ενεργεί σε ένα μηχανικό σύστημα που αποτελείται από Νσημεία (Εικ. 3.2). Εάν το αποτέλεσμα των εξωτερικών δυνάμεων και το αποτέλεσμα όλων των εσωτερικών δυνάμεων εφαρμόζονται σε κάθε σημείο του συστήματος, τότε για οποιοδήποτε κΣτο σημείο του συστήματος, μπορεί κανείς να συνθέσει διαφορικές εξισώσεις κίνησης. Συνολικά τέτοιες εξισώσεις θα είναι Ν:

και σε προβολές σε σταθερούς άξονες συντεταγμένων 3 Ν:

(3.4)

Οι διανυσματικές εξισώσεις (3.3) ή οι ισοδύναμες βαθμωτές εξισώσεις (3.4) αντιπροσωπεύουν τους διαφορικούς νόμους κίνησης των υλικών σημείων ολόκληρου του συστήματος. Εάν όλα τα σημεία κινούνται παράλληλα σε ένα επίπεδο ή μια ευθεία γραμμή, τότε ο αριθμός των εξισώσεων (3.4) στην πρώτη περίπτωση θα είναι 2 Ν, στο δεύτερο Ν.

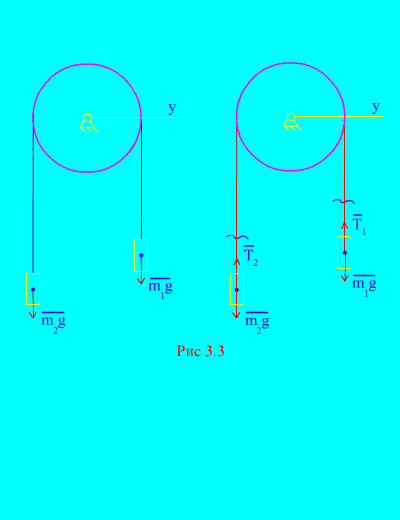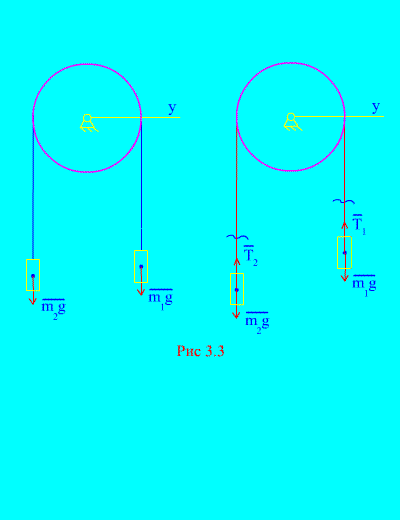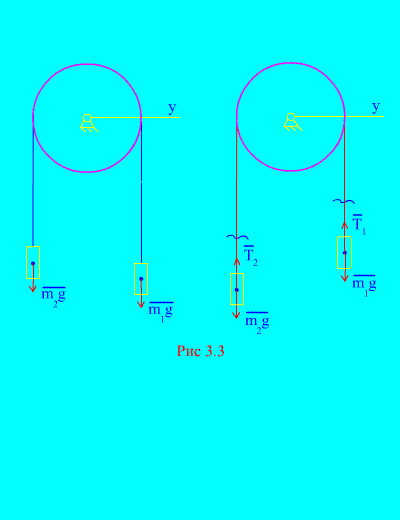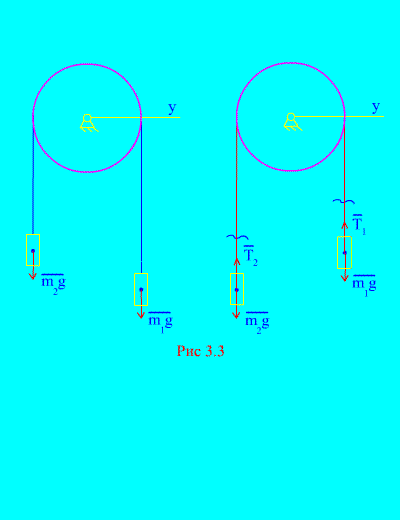
Παράδειγμα 1Δύο φορτία μάζας και συνδέονται μεταξύ τους με ένα μη εκτάσιμο καλώδιο που ρίχνεται πάνω από ένα μπλοκ (Εικ. 3.3). Παραβλέποντας τις δυνάμεις της τριβής, καθώς και τη μάζα του μπλοκ και του καλωδίου, καθορίζουν το νόμο της κίνησης των εμπορευμάτων και την τάση του καλωδίου.

Απόφαση. Το σύστημα αποτελείται από δύο υλικά σώματα (που συνδέονται με ένα μη εκτατό καλώδιο) που κινούνται παράλληλα σε έναν άξονα Χ.Ας γράψουμε τους διαφορικούς νόμους της κίνησης σε προβολές στον άξονα Χγια όλους.

Αφήστε το δεξί βάρος να κατεβαίνει με την επιτάχυνση, τότε το αριστερό βάρος θα αυξηθεί με την επιτάχυνση. Απελευθερωνόμαστε ψυχικά από τη σύνδεση (καλώδιο) και την αντικαθιστούμε με αντιδράσεις και (Εικ. 3.3). Υποθέτοντας ότι τα σώματα είναι ελεύθερα, θα συνθέσουμε τους διαφορικούς νόμους κίνησης στην προβολή στον άξονα Χ(που σημαίνει ότι οι τάσεις του νήματος είναι εσωτερικές δυνάμεις και το βάρος των φορτίων είναι εξωτερικά):

Δεδομένου ότι και (τα σώματα συνδέονται με ένα μη εκτατό καλώδιο), λαμβάνουμε

Επίλυση αυτών των εξισώσεων για την επιτάχυνση και την τάση του σχοινιού Τ, παίρνουμε

Σημειώστε ότι η τάση του καλωδίου στο δεν είναι ίση με τη βαρύτητα του αντίστοιχου φορτίου.

3. 2. Το θεώρημα για την κίνηση του κέντρου μάζας

Είναι γνωστό ότι ένα άκαμπτο σώμα και ένα μηχανικό σύστημα σε ένα αεροπλάνο μπορεί να κινούνται αρκετά δύσκολα. Το πρώτο θεώρημα για την κίνηση ενός σώματος και ενός μηχανικού συστήματος μπορεί να επιτευχθεί με τον εξής τρόπο: ρίξτε το c.-l. ένα αντικείμενο που αποτελείται από πολλά στερεά σώματα στερεωμένα μεταξύ τους. Είναι ξεκάθαρο ότι θα πετάξει σε παραβολή. Αυτό αποκαλύφθηκε κατά τη μελέτη της κίνησης ενός σημείου. Ωστόσο, τώρα το αντικείμενο δεν είναι ένα σημείο. Γυρίζει, ταλαντεύεται στη διαδικασία του να πετάει γύρω από κάποιο αποτελεσματικό κέντρο, το οποίο κινείται κατά μήκος μιας παραβολής. Πρώτο θεώρημα κίνησης δύσκολα θέματαλέει ότι ένα συγκεκριμένο ενεργό κέντρο είναι το κέντρο μάζας ενός κινούμενου αντικειμένου. Το κέντρο μάζας δεν βρίσκεται απαραίτητα στο ίδιο το σώμα, μπορεί να βρίσκεται κάπου έξω από αυτό.

Θεώρημα. Το κέντρο μάζας ενός μηχανικού συστήματος κινείται ως υλικό σημείο με μάζα ίσο με τη μάζαολόκληρο το σύστημα στο οποίο εφαρμόζονται όλες οι εξωτερικές δυνάμεις που δρουν στο σύστημα.

Για να αποδείξουμε το θεώρημα, ξαναγράφουμε τους διαφορικούς νόμους της κίνησης (3.3) στο παρακάτω φόρμα:

(3.5)

που Ν είναι ο αριθμός των σημείων του συστήματος.

Ας προσθέσουμε τις εξισώσεις μαζί ανά όρο:

(ένα)

Η θέση του κέντρου μάζας του μηχανικού συστήματος σε σχέση με το επιλεγμένο σύστημα συντεταγμένων προσδιορίζεται από τον τύπο (2.1): που Μείναι η μάζα του συστήματος. Τότε γράφεται η αριστερή πλευρά της ισότητας (α).

Το πρώτο άθροισμα, που βρίσκεται στη δεξιά πλευρά της ισότητας (α), είναι ίσο με το κύριο διάνυσμα των εξωτερικών δυνάμεων και το τελευταίο, με την ιδιότητα των εσωτερικών δυνάμεων, είναι ίσο με μηδέν. Στη συνέχεια, η ισότητα (α), λαμβάνοντας υπόψη το (β), θα ξαναγραφεί

, (3.6)

εκείνοι. το γινόμενο της μάζας του συστήματος και της επιτάχυνσης του κέντρου μάζας του είναι ίσο με γεωμετρικό άθροισμαόλες οι εξωτερικές δυνάμεις που δρουν στο σύστημα.

Από την εξίσωση (3.6) προκύπτει ότι οι εσωτερικές δυνάμεις δεν επηρεάζουν άμεσα την κίνηση του κέντρου μάζας. Ωστόσο, σε ορισμένες περιπτώσεις είναι η αιτία της εμφάνισης εξωτερικών δυνάμεων που εφαρμόζονται στο σύστημα. Έτσι, οι εσωτερικές δυνάμεις που περιστρέφουν τους κινητήριους τροχούς του αυτοκινήτου προκαλούν την επίδραση σε αυτό μιας εξωτερικής δύναμης πρόσφυσης που ασκείται στο χείλος του τροχού.

Παράδειγμα 2Ο μηχανισμός, που βρίσκεται σε κατακόρυφο επίπεδο, είναι εγκατεστημένος σε οριζόντιο λείο επίπεδο και προσαρτάται σε αυτό με ράβδους στερεωμένες άκαμπτα στην επιφάνεια. Προς τηνκαι μεγάλο (Εικ. 3.4).

Δίσκος 1 ακτίνας Rακίνητος. Δίσκος 2 μάζας Μκαι ακτίνα r στερεώνεται με μανιβέλα, μήκους R+ rστο σημείο Από 2. Ο στρόφαλος περιστρέφεται σταθερά

γωνιακή ταχύτητα. ΣΤΟ αρχική στιγμήο στρόφαλος κατέλαβε τη δεξιά οριζόντια θέση. Παραβλέποντας τη μάζα του στρόφαλου, προσδιορίστε τις μέγιστες οριζόντιες και κάθετες δυνάμεις που ασκούνται στις ράβδους, αν συνολικό βάροςκρεβάτι και τροχός 1 ισούται με Μ.Εξετάστε επίσης τη συμπεριφορά του μηχανισμού απουσία ράβδων.

Απόφαση. Το σύστημα αποτελείται από δύο μάζες ( Ν=2 ): ένας σταθερός δίσκος 1 με πλαίσιο και ένας κινητός δίσκος 2. Ας κατευθύνουμε τον άξονα στομέσω του κέντρου βάρους του σταθερού δίσκου κατακόρυφα προς τα πάνω, ο άξονας Χ- κατά μήκος οριζόντιο επίπεδο.

Γράφουμε το θεώρημα για την κίνηση του κέντρου μάζας (3.6) στη μορφή συντεταγμένων

Οι εξωτερικές δυνάμεις αυτού του συστήματος είναι: το βάρος του πλαισίου και του σταθερού δίσκου - mg, βάρος κινητού δίσκου mg, - η συνολική οριζόντια αντίδραση των μπουλονιών, - η κανονική ολική αντίδραση του επιπέδου. Ως εκ τούτου,

Στη συνέχεια οι νόμοι της κίνησης (β) ξαναγράφονται

Ας υπολογίσουμε τις συντεταγμένες του κέντρου μάζας του μηχανικού συστήματος:

; (ΣΟΛ)

όπως φαίνεται από (Εικ. 3.4), , , (γωνία περιστροφής του στρόφαλου), . Αντικατάσταση αυτών των παραστάσεων στο (r) και υπολογισμός των δεύτερων παραγώγων ως προς το χρόνο tαπό , , καταλαβαίνουμε ότι

(μι)

Αντικαθιστώντας τα (γ) και (ε) στο (β), βρίσκουμε

Η οριζόντια πίεση που ενεργεί στις ράβδους έχει τη μεγαλύτερη και μικρότερη τιμή, πότε συν = 1 αντίστοιχα, δηλ.

Η πίεση του μηχανισμού στο οριζόντιο επίπεδο έχει τις υψηλότερες και τις χαμηλότερες τιμές όταν αμαρτία αντίστοιχα, δηλ.

Στην πραγματικότητα, το πρώτο πρόβλημα της δυναμικής έχει λυθεί: σύμφωνα με τις γνωστές εξισώσεις κίνησης του κέντρου μάζας του συστήματος (e), οι δυνάμεις που εμπλέκονται στην κίνηση αποκαθίστανται.

Ελλείψει ράβδων κκαι μεγάλο (Εικ. 3.4), ο μηχανισμός μπορεί να αρχίσει να αναπηδά πάνω από το οριζόντιο επίπεδο. Αυτό θα γίνει όταν , δηλ. όταν , προκύπτει ότι η γωνιακή ταχύτητα περιστροφής του στρόφαλου, στην οποία αναπηδά ο μηχανισμός, πρέπει να ικανοποιεί την ισότητα

3. 3. Νόμος διατήρησης της κίνησης του κέντρου μάζας

Αν το κύριο διάνυσμα των εξωτερικών δυνάμεων που δρουν στο σύστημα είναι ίσο με μηδέν, δηλ. , μετά από(3.6)συνεπάγεται ότι η επιτάχυνση του κέντρου μάζας είναι μηδέν, επομένως, η ταχύτητα του κέντρου μάζας είναι σταθερή ως προς το μέγεθος και την κατεύθυνση. Εάν, ειδικότερα, την αρχική στιγμή το κέντρο μάζας βρίσκεται σε ηρεμία, τότε είναι σε ηρεμία καθ' όλη τη διάρκεια του χρόνου έως ότου το κύριο διάνυσμα των εξωτερικών δυνάμεων είναι ίσο με μηδέν.

Από αυτό το θεώρημα προκύπτουν αρκετά συμπεράσματα.

· Οι εσωτερικές δυνάμεις από μόνες τους δεν μπορούν να αλλάξουν τη φύση της κίνησης του κέντρου μάζας του συστήματος.

· Εάν το κύριο διάνυσμα των εξωτερικών δυνάμεων που δρουν στο σύστημα είναι ίσο με μηδέν, τότε το κέντρο μάζας βρίσκεται σε ηρεμία ή κινείται ομοιόμορφα και ευθύγραμμα.

· Αν η προβολή του κύριου διανύσματος των εξωτερικών δυνάμεων του συστήματος σε κάποιο σταθερό άξονα είναι ίση με μηδέν, τότε η προβολή της ταχύτητας του κέντρου μάζας του συστήματος σε αυτόν τον άξονα δεν αλλάζει.

· Μερικές δυνάμεις που ασκούνται σε ένα άκαμπτο σώμα δεν μπορούν να αλλάξουν την κίνηση του κέντρου μάζας του (μπορεί μόνο να προκαλέσει την περιστροφή του σώματος γύρω από το κέντρο μάζας).

Ας εξετάσουμε ένα παράδειγμα που απεικονίζει τον νόμο της διατήρησης της κίνησης του κέντρου μάζας.

Παράδειγμα 3Δύο βαρίδια με μάζες και συνδέονται με μια μη εκτάσιμη κλωστή που ρίχνεται πάνω από ένα μπλοκ (Εικ. 3.5), στερεωμένο σε σφήνα με μάζα Μ.Η σφήνα στηρίζεται σε λείο οριζόντιο επίπεδο. Αρχικά, το σύστημα ήταν σε ηρεμία. Βρείτε τη μετατόπιση της σφήνας κατά μήκος του επιπέδου όταν το πρώτο φορτίο χαμηλώσει σε ύψος Ν.Αγνοήστε τη μάζα του μπλοκ και του νήματος.

Απόφαση.Οι εξωτερικές δυνάμεις που δρουν στη σφήνα μαζί με τα βάρη είναι οι δυνάμεις της βαρύτητας και mg, καθώς φυσιολογική αντίδρασηλεία οριζόντια επιφάνεια Β. Επομένως,

Δεδομένου ότι το σύστημα ήταν σε ηρεμία την αρχική στιγμή, έχουμε .

Ας υπολογίσουμε τη συντεταγμένη του κέντρου μάζας του συστήματος τη στιγμή και τη στιγμή t 1 όταν το βάρος του φορτίου σολκατεβείτε σε ύψος H.

Για μια στιγμή:

που , , Χ- αντίστοιχα, οι συντεταγμένες του κέντρου μάζας φορτίων βάρους g, g και ζύγισης σφήνας Μσολ.

Ας υποθέσουμε ότι η σφήνα τη στιγμή του χρόνου κινείται προς τη θετική κατεύθυνση του άξονα Βόδικατά το ποσό μεγάλοαν το βάρος του φορτίου πέσει σε ύψος Ν.Μετά, για μια στιγμή

επειδή τα φορτία μαζί με τη σφήνα θα μετακινηθούν προς μεγάλοπρος τα δεξιά, το βάρος θα μετακινηθεί κατά μια απόσταση επάνω στη σφήνα. Αφού , μετά από υπολογισμούς παίρνουμε

3.4. Σύστημα ποσότητας κίνησης

3.4.1. Υπολογισμός της ορμής ενός συστήματος

Η ορμή ενός υλικού σημείου είναι ένα διανυσματικό μέγεθος, ίσο με το γινόμενομάζα ενός σημείου στο διάνυσμα της ταχύτητάς του

Μονάδα μέτρησης της ποσότητας κίνησης -

Η ορμή ενός μηχανικού συστήματος ονομάζεται διανυσματικό άθροισμα της ορμής των επιμέρους σημείων του συστήματος, δηλ.

που Ν είναι ο αριθμός των σημείων του συστήματος.

Η ορμή ενός μηχανικού συστήματος μπορεί να εκφραστεί ως προς τη μάζα του συστήματος Μκαι την ταχύτητα του κέντρου μάζας. Πραγματικά,

εκείνοι. η ορμή του συστήματος είναι ίση με το γινόμενο της μάζας ολόκληρου του συστήματος και της ταχύτητας του κέντρου μάζας του.Η κατεύθυνση είναι ίδια με την κατεύθυνση (Εικ. 3.6)

Σε προβολές σε ορθογώνιους άξονες, έχουμε

όπου , , - προβολές της ταχύτητας του κέντρου μάζας του συστήματος.

Εδώ Μείναι η μάζα του μηχανικού συστήματος. δεν αλλάζει καθώς το σύστημα κινείται.

Είναι ιδιαίτερα βολικό να χρησιμοποιείτε αυτά τα αποτελέσματα κατά τον υπολογισμό της ροπής των άκαμπτων σωμάτων.

Από τον τύπο (3.7) φαίνεται ότι εάν ένα μηχανικό σύστημα κινείται με τέτοιο τρόπο ώστε το κέντρο μάζας του να παραμένει ακίνητο, τότε η ορμή του συστήματος παραμένει ίση με μηδέν.

3.4.2. Στοιχειακή και πλήρης ισχύς ώθηση

Η δράση μιας δύναμης σε ένα υλικό σημείο με την πάροδο του χρόνου dtμπορεί να χαρακτηριστεί από μια στοιχειώδη παρόρμηση. Ολική ώθηση δύναμης στο χρόνο t, ή ώθηση δύναμης , καθορίζεται από τον τύπο

ή σε προβολές στις συντεταγμένες του άξονα

(3.8a)

Η μονάδα ώθησης δύναμης είναι .

3.4.3. Θεώρημα για τη μεταβολή της ορμής του συστήματος

Αφήστε τις εξωτερικές και εσωτερικές δυνάμεις να εφαρμοστούν στα σημεία του συστήματος. Στη συνέχεια, για κάθε σημείο του συστήματος, μπορούμε να εφαρμόσουμε τους διαφορικούς νόμους της κίνησης (3.3), έχοντας υπόψη ότι :

Αθροίζοντας όλα τα σημεία του συστήματος, παίρνουμε

Από την ιδιότητα των εσωτερικών δυνάμεων και εξ ορισμού έχουμε

(3.9)

Πολλαπλασιάζοντας και τις δύο πλευρές αυτής της εξίσωσης με dt, λαμβάνουμε ένα θεώρημα για τη μεταβολή της ορμής στο διαφορική μορφή:

, (3.10)

εκείνοι. το διαφορικό της ορμής ενός μηχανικού συστήματος είναι ίσο με το διανυσματικό άθροισμα των στοιχειωδών παλμών όλων των εξωτερικών δυνάμεων που δρουν στα σημεία του μηχανικού συστήματος.

Υπολογισμός του ολοκληρώματος και των δύο μερών του (3.10) σε βάθος χρόνου από 0 έως t, παίρνουμε το θεώρημα σε πεπερασμένη ή ολοκληρωμένη μορφή

(3.11)

Σε προβολές στους άξονες συντεταγμένων, θα έχουμε

Αλλαγή της ορμής ενός μηχανικού συστήματος με την πάροδο του χρόνουt, ισούται με το διανυσματικό άθροισμα όλων των παλμών των εξωτερικών δυνάμεων που δρουν στα σημεία του μηχανικού συστήματος ταυτόχρονα.

Παράδειγμα 4Φορτίο μάζας Μ κατεβαίνοντας το κεκλιμένο επίπεδοαπό την ανάπαυση υπό τη δράση μιας δύναμης φά, ανάλογη του χρόνου: , όπου (Εικ. 3.7). Ποια είναι η ταχύτητα του σώματος μετά t δευτερόλεπτα μετά την έναρξη της κίνησης, εάν ο συντελεστής τριβής ολίσθησης του φορτίου στο κεκλιμένο επίπεδο είναι ίσος με φά.

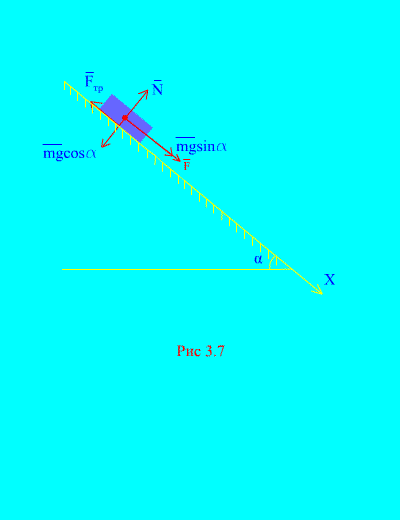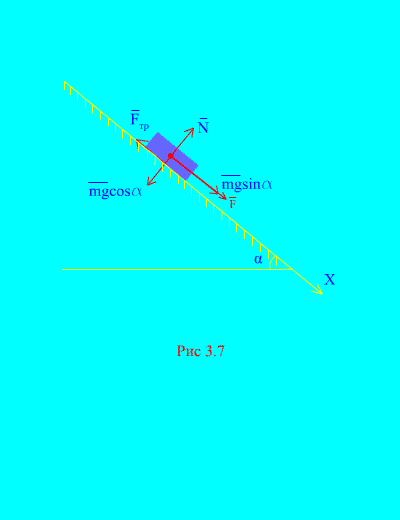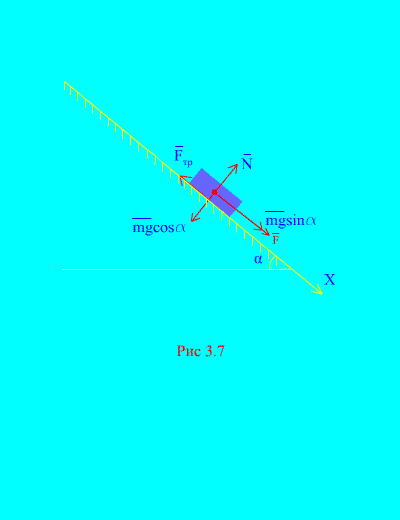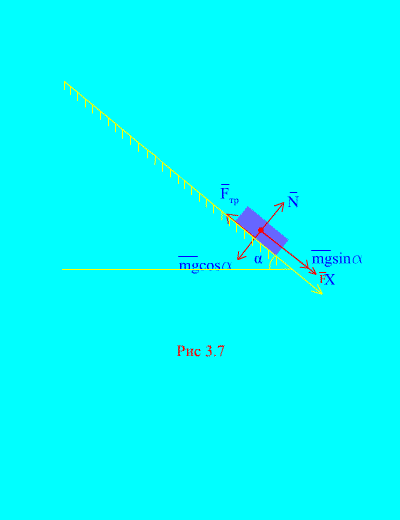
Απόφαση.Ας απεικονίσουμε τις δυνάμεις που ασκούνται στο φορτίο: mg - η βαρύτητα του φορτίου, Νείναι η κανονική αντίδραση του επιπέδου, είναι η δύναμη τριβής ολίσθησης του φορτίου στο επίπεδο, και . Η κατεύθυνση όλων των δυνάμεων φαίνεται στο (Εικ. 3.7).

Ας κατευθύνουμε τον άξονα Χκάτω από ένα κεκλιμένο επίπεδο. Ας γράψουμε το θεώρημα για τη μεταβολή της ορμής (3.11) στην προβολή στον άξονα Χ:

(ένα)

Κατά συνθήκη, επειδή την αρχική χρονική στιγμή, το φορτίο ήταν σε ηρεμία. Το άθροισμα των προβολών των παλμών όλων των δυνάμεων στον άξονα x είναι

Ως εκ τούτου,

3.4.4. Νόμοι διατήρησης της ορμής

Οι νόμοι διατήρησης λαμβάνονται ως ειδικές περιπτώσεις του θεωρήματος μεταβολής της ορμής. Δύο ειδικές περιπτώσεις είναι δυνατές.

· Αν το διανυσματικό άθροισμα όλων των εξωτερικών δυνάμεων που ασκούνται στο σύστημα είναι ίσο με μηδέν, δηλ. , τότε προκύπτει από το θεώρημα (3.9) , τι ,

εκείνοι. αν το κύριο διάνυσμα των εξωτερικών δυνάμεων του συστήματος είναι ίσο με μηδέν, τότε η ορμή του συστήματος είναι σταθερή σε μέγεθος και κατεύθυνση.

· Αν η προβολή του κύριου διανύσματος εξωτερικών δυνάμεων σε οποιαδήποτε άξονα συντεταγμένωνισούται με μηδέν, για παράδειγμα Oh, δηλ. , τότε η προβολή της ποσότητας κίνησης σε αυτόν τον άξονα είναι σταθερή.

Εξετάστε ένα παράδειγμα εφαρμογής του νόμου της διατήρησης της ορμής.

Παράδειγμα 5Ένα βαλλιστικό εκκρεμές είναι ένα σώμα μάζας, που αιωρείται σε μια μακριά χορδή (Εικ. 3.8).

Μια σφαίρα μάζας που κινείται με ταχύτητα Vκαι πέφτοντας σε ένα ακίνητο σώμα, κολλάει σε αυτό, και το σώμα εκτρέπεται. Ποια ήταν η ταχύτητα της σφαίρας αν το σώμα ανέβαινε σε ύψος η ?

Απόφαση.Αφήστε το σώμα με την κολλημένη σφαίρα να αποκτήσει ταχύτητα . Στη συνέχεια, χρησιμοποιώντας το νόμο της διατήρησης της ορμής στην αλληλεπίδραση δύο σωμάτων, μπορούμε να γράψουμε .

Η ταχύτητα μπορεί να υπολογιστεί χρησιμοποιώντας το νόμο διατήρησης μηχανική ενέργεια . Τότε . Ως αποτέλεσμα, βρίσκουμε

Παράδειγμα 6. Το νερό εισέρχεται σε ένα σταθερό κανάλι (Εικ. 3.9)μεταβλητό τμήμα με ταχύτητα υπό γωνία ως προς τον ορίζοντα. τετράγωνο διατομήκανάλι στην είσοδο? την ταχύτητα του νερού στην έξοδο του καναλιού και κάνει γωνία με τον ορίζοντα.

Προσδιορίστε την οριζόντια συνιστώσα της αντίδρασης που ασκεί το νερό στα τοιχώματα του καναλιού. Πυκνότητα νερού .

Απόφαση.Θα προσδιορίσουμε την οριζόντια συνιστώσα της αντίδρασης που ασκείται από τα τοιχώματα του καναλιού στο νερό. Αυτή η δύναμη είναι ίση σε απόλυτη τιμή και αντίθετη σε πρόσημο με την επιθυμητή δύναμη. Έχουμε, σύμφωνα με (3.11a),

. (ένα)

Υπολογίζουμε τη μάζα του όγκου του υγρού που εισέρχεται στο κανάλι κατά το χρόνο t:

Η τιμή του rAV 0 ονομάζεται δεύτερη μάζα - η μάζα του υγρού που ρέει μέσα από οποιοδήποτε τμήμα του σωλήνα ανά μονάδα χρόνου.

Η ίδια ποσότητα νερού φεύγει από το κανάλι ταυτόχρονα. Οι αρχικές και τελικές ταχύτητες δίνονται στη συνθήκη.

Υπολογίζω σωστη πλευραισότητα (α) που καθορίζει το άθροισμα των προβολών στον οριζόντιο άξονα των εξωτερικών δυνάμεων που ασκούνται στο σύστημα (νερό). Η μόνη οριζόντια δύναμη είναι η οριζόντια συνιστώσα της προκύπτουσας αντίδρασης των τοίχων Rx. Αυτή η δύναμη είναι σταθερή κατά τη σταθερή κίνηση του νερού. Έτσι

. (σε)

Αντικαθιστώντας τα (β) και (γ) στο (α), παίρνουμε

3.5. Κινητική ροπή του συστήματος

3.5.1. Κύρια ροπή ορμής του συστήματος

Έστω το διάνυσμα ακτίνας ενός σημείου με τη μάζα του συστήματος σε σχέση με κάποιο σημείο Α, που ονομάζεται κέντρο (Εικ. 3.10).

Ροπή ορμής (κινητική ροπή) σημείου σε σχέση με το κέντρο Απου ονομάζεται διάνυσμα , καθορίζεται από τον τύπο

. (3.12)

Στην περίπτωση αυτή, το διάνυσμα κατευθύνεται κάθετα στο επίπεδο που διέρχεται από το κέντρο ΑΛΛΑκαι διάνυσμα .

Ροπή ορμής (κινητική ροπή) σημείου γύρω από άξοναονομάζεται προβολή σε αυτόν τον άξονα της γωνιακής ορμής του σημείου σε σχέση με οποιοδήποτε κέντρο που επιλέγεται σε αυτόν τον άξονα.

Η κύρια ροπή ορμής (κινητική ροπή) του συστήματος σε σχέση με το κέντρο Αονομάζεται ποσότητα

(3.13)

Η κύρια ροπή ορμής (κινητική ροπή) του συστήματος ως προς τον άξοναονομάζεται προβολή σε αυτόν τον άξονα της κύριας ροπής της ορμής του συστήματος σε σχέση με οποιαδήποτε επιλεγμένη στο δεδομένο κεντρικός άξονας.

3.5.2. Ορμή ενός περιστρεφόμενου άκαμπτου σώματος γύρω από τον άξονα περιστροφής

Συμβατό σταθερό σημείο Οσώμα που βρίσκεται στον άξονα περιστροφής Οz, με την προέλευση του συστήματος συντεταγμένων Ωχz, του οποίου οι άξονες θα περιστρέφονται μαζί με το σώμα (Εικ. 3.11). Έστω η ακτίνα-διάνυσμα του σημείου του σώματος σε σχέση με την αρχή των συντεταγμένων, οι προβολές του στους άξονες θα συμβολίζονται με , , . Διανυσματικές προβολές γωνιακή ταχύτητασώματα στους ίδιους άξονες θα συμβολίζονται με 0, 0, ().

Αρκετά συχνά είναι δυνατή η διάκριση σημαντικά χαρακτηριστικάκίνηση ενός μηχανικού συστήματος χωρίς να καταφύγουμε σε ολοκλήρωση του συστήματος των διαφορικών εξισώσεων κίνησης. Αυτό επιτυγχάνεται με την εφαρμογή γενικών θεωρημάτων δυναμικής.

5.1. Βασικές έννοιες και ορισμοί

Εξωτερικές και εσωτερικές δυνάμεις.Οποιαδήποτε δύναμη ασκείται σε ένα σημείο ενός μηχανικού συστήματος είναι απαραίτητα είτε ενεργητική δύναμη, ή μια αντίδραση δεσμού. Ολόκληρο το σύνολο των δυνάμεων που δρουν στα σημεία του συστήματος μπορεί να χωριστεί σε δύο κατηγορίες με διαφορετικό τρόπο: σε εξωτερικές δυνάμεις και σε εσωτερικές δυνάμεις (παράγραφοι e και i - από Λατινικές λέξεις externus - εξωτερικό και internus - εσωτερικό). Εξωτερικές δυνάμεις ονομάζονται δυνάμεις που δρουν σε σημεία του συστήματος από σημεία και σώματα που δεν αποτελούν μέρος του υπό εξέταση συστήματος. Οι δυνάμεις αλληλεπίδρασης μεταξύ σημείων και σωμάτων του υπό εξέταση συστήματος ονομάζονται εσωτερικές.

Αυτή η διαίρεση εξαρτάται από το ποια υλικά σημεία και σώματα περιλαμβάνονται από τον ερευνητή στο εξεταζόμενο μηχανικό σύστημα. Εάν η σύνθεση του συστήματος επεκταθεί για να συμπεριλάβει επιπλέον σημεία και σώματα, τότε ορισμένες δυνάμεις που ήταν εξωτερικές για το προηγούμενο σύστημα μπορεί να γίνουν εσωτερικές για το διευρυμένο σύστημα.

Ιδιότητες εσωτερικών δυνάμεων.Δεδομένου ότι αυτές οι δυνάμεις είναι δυνάμεις αλληλεπίδρασης μεταξύ τμημάτων του συστήματος, περιλαμβάνονται στο πλήρες σύστημα εσωτερικών δυνάμεων σε «δύο» οργανωμένα σύμφωνα με το αξίωμα δράσης-αντίδρασης. Κάθε ένα τέτοιο «δύο» δυνάμεων

κύριο διάνυσμα και κύριο σημείοσε σχέση με ένα αυθαίρετο κέντρο ισούνται με μηδέν. Αφού το πλήρες σύστημα των εσωτερικών δυνάμεων αποτελείται μόνο από «δύο», τότε

1) το κύριο διάνυσμα του συστήματος εσωτερικών δυνάμεων είναι ίσο με μηδέν,

2) η κύρια ροπή του συστήματος εσωτερικών δυνάμεων σε σχέση με ένα αυθαίρετο σημείο είναι ίση με μηδέν.

Η μάζα του συστήματος είναι αριθμητικό άθροισμαμάζα mk όλων των σημείων και σωμάτων που αποτελούν το σύστημα:

κέντρο βαρύτητας(κέντρο αδράνειας) ενός μηχανικού συστήματος ονομάζεται γεωμετρικό σημείο C, το διάνυσμα ακτίνας και οι συντεταγμένες του οποίου καθορίζονται από τους τύπους

όπου είναι τα διανύσματα ακτίνας και οι συντεταγμένες των σημείων που σχηματίζουν το σύστημα.

Για ένα άκαμπτο σώμα σε ομοιόμορφο βαρυτικό πεδίο, οι θέσεις του κέντρου μάζας και του κέντρου βάρους συμπίπτουν· σε άλλες περιπτώσεις, πρόκειται για διαφορετικά γεωμετρικά σημεία.

Μαζί με το αδρανειακό πλαίσιο αναφοράς, κανείς συχνά θεωρεί ταυτόχρονα ένα μη αδρανειακό πλαίσιο αναφοράς που κινείται προς τα εμπρός. Οι άξονες συντεταγμένων του (άξονες Koenig) επιλέγονται έτσι ώστε το σημείο αναφοράς C να συμπίπτει πάντα με το κέντρο μάζας του μηχανικού συστήματος. Σύμφωνα με τον ορισμό, το κέντρο μάζας είναι σταθερό στους άξονες Koenig και βρίσκεται στην αρχή των συντεταγμένων.

Η ροπή αδράνειας του συστήματοςγύρω από τον άξονα ονομάζεται βαθμωτό μέγεθος ίσο με το άθροισματα γινόμενα των μαζών mk όλων των σημείων του συστήματος με τα τετράγωνα των αποστάσεων τους προς τον άξονα:

Εάν το μηχανικό σύστημα είναι ένα άκαμπτο σώμα, για να βρείτε το 12, μπορείτε να χρησιμοποιήσετε τον τύπο

πού είναι η πυκνότητα, ο όγκος που καταλαμβάνει το σώμα.

Εξετάστε την κίνηση ενός συγκεκριμένου συστήματος όγκων υλικού σε σχέση με ένα σταθερό σύστημα συντεταγμένων Όταν το σύστημα δεν είναι ελεύθερο, τότε μπορεί να θεωρηθεί ελεύθερο, εάν απορρίψουμε τους περιορισμούς που επιβάλλονται στο σύστημα και αντικαταστήσουμε τη δράση τους με τις αντίστοιχες αντιδράσεις.

Ας διαιρέσουμε όλες τις δυνάμεις που εφαρμόζονται στο σύστημα σε εξωτερικές και εσωτερικές. και τα δύο μπορεί να περιλαμβάνουν αντιδράσεις απορριφθέντων

συνδέσεις. Δηλώστε με και το κύριο διάνυσμα και την κύρια ροπή των εξωτερικών δυνάμεων σε σχέση με το σημείο Α.

1. Θεώρημα για τη μεταβολή της ορμής.Αν είναι η ορμή του συστήματος, τότε (βλ.

δηλ. ισχύει το θεώρημα: η χρονική παράγωγος της ορμής του συστήματος είναι ίση με το κύριο διάνυσμα όλων των εξωτερικών δυνάμεων.

Αντικαθιστώντας το διάνυσμα μέσω της έκφρασής του όπου είναι η μάζα του συστήματος, είναι η ταχύτητα του κέντρου μάζας, στην εξίσωση (4.1) μπορεί να δοθεί διαφορετική μορφή:

Αυτή η ισότητα σημαίνει ότι το κέντρο μάζας του συστήματος κινείται ως υλικό σημείο του οποίου η μάζα είναι ίση με τη μάζα του συστήματος και στο οποίο εφαρμόζεται μια δύναμη που είναι γεωμετρικά ίση με το κύριο διάνυσμα όλων των εξωτερικών δυνάμεων του συστήματος. Η τελευταία πρόταση ονομάζεται θεώρημα για την κίνηση του κέντρου μάζας (κέντρο αδράνειας) του συστήματος.

Αν τότε από το (4.1) προκύπτει ότι το διάνυσμα της ορμής είναι σταθερό σε μέγεθος και κατεύθυνση. Προβάλλοντάς το στον άξονα συντεταγμένων, λαμβάνουμε τρία βαθμωτά πρώτα ολοκληρώματα των διαφορικών εξισώσεων της διπλής αλυσίδας του συστήματος:

Αυτά τα ολοκληρώματα ονομάζονται ολοκληρώματα ορμής. Όταν η ταχύτητα του κέντρου μάζας είναι σταθερή, δηλ. κινείται ομοιόμορφα και ευθύγραμμα.

Εάν η προβολή του κύριου διανύσματος των εξωτερικών δυνάμεων σε οποιονδήποτε άξονα, για παράδειγμα, στον άξονα, είναι ίση με μηδέν, τότε έχουμε ένα πρώτο ολοκλήρωμα ή εάν δύο προβολές του κύριου διανύσματος είναι ίσες με μηδέν, τότε υπάρχουν δύο ολοκληρώματα της ορμής.

2. Θεώρημα για τη μεταβολή της κινητικής ροπής.Έστω Α κάποιο αυθαίρετο σημείο στο χώρο (κινούμενο ή ακίνητο), το οποίο δεν συμπίπτει απαραίτητα με κάποιο συγκεκριμένο υλικό σημείο του συστήματος καθ' όλη τη διάρκεια της κίνησης. Η ταχύτητά του σε ένα σταθερό σύστημα συντεταγμένων θα συμβολίζεται με το θεώρημα της μεταβολής της γωνιακής ορμής σύστημα υλικούως προς το σημείο Α έχει τη μορφή

Εάν το σημείο Α είναι σταθερό, τότε η ισότητα (4.3) παίρνει απλούστερη μορφή:

Αυτή η ισότητα εκφράζει το θεώρημα για τη μεταβολή της γωνιακής ορμής του συστήματος σε σχέση με σταθερό σημείο: η χρονική παράγωγος της γωνιακής ορμής του συστήματος, υπολογισμένη ως προς κάποιο σταθερό σημείο, είναι ίση με την κύρια ροπή όλων των εξωτερικών δυνάμεων ως προς αυτό το σημείο.

Αν τότε, σύμφωνα με το (4.4), το διάνυσμα της γωνιακής ορμής είναι σταθερό σε μέγεθος και κατεύθυνση. Προβάλλοντάς το στον άξονα συντεταγμένων, λαμβάνουμε τα βαθμωτά πρώτα ολοκληρώματα των διαφορικών εξισώσεων της κίνησης του συστήματος:

Αυτά τα ολοκληρώματα ονομάζονται ολοκληρώματα της γωνιακής ορμής ή ολοκληρώματα των εμβαδών.

Αν το σημείο Α συμπίπτει με το κέντρο μάζας του συστήματος, τότε ο πρώτος όρος στη δεξιά πλευρά της ισότητας (4.3) εξαφανίζεται και το θεώρημα για τη μεταβολή της γωνιακής ορμής έχει την ίδια μορφή (4.4) όπως στην περίπτωση ενός σταθερού σημείο Α. Σημειώστε (βλ. 4 § 3) ότι στην υπό εξέταση περίπτωση η απόλυτη γωνιακή ορμή του συστήματος στην αριστερή πλευρά της ισότητας (4.4) μπορεί να αντικατασταθεί από την ίση γωνιακή ορμή του συστήματος στην κίνησή του ως προς το κέντρο της μάζας.

Έστω κάποιος σταθερός άξονας ή ένας άξονας σταθερής κατεύθυνσης που διέρχεται από το κέντρο μάζας του συστήματος και έστω η γωνιακή ορμή του συστήματος σε σχέση με αυτόν τον άξονα. Από την (4.4) προκύπτει ότι

όπου είναι η ροπή των εξωτερικών δυνάμεων γύρω από τον άξονα. Αν σε όλο το χρόνο της κίνησης τότε έχουμε το πρώτο ολοκλήρωμα

Στα έργα του S. A. Chaplygin, προέκυψαν αρκετές γενικεύσεις του θεωρήματος σχετικά με την αλλαγή της γωνιακής ορμής, οι οποίες στη συνέχεια εφαρμόστηκαν στην επίλυση ορισμένων προβλημάτων σχετικά με την κύλιση των σφαιρών. Περαιτέρω γενικεύσεις του θεωρήματος για την αλλαγή της κπνητολογικής ροπής και τις εφαρμογές τους σε προβλήματα δυναμικής ενός άκαμπτου σώματος περιέχονται στα έργα. Τα κύρια αποτελέσματα αυτών των εργασιών σχετίζονται με το θεώρημα για τη μεταβολή της κινητικής ροπής σε σχέση με την κινούμενη, περνώντας συνεχώς από κάποιο κινούμενο σημείο Α. μονάδα διάνυσμακατευθύνεται κατά μήκος αυτού του άξονα. Πολλαπλασιάζοντας κλιμακωτά και με τις δύο πλευρές της ισότητας (4.3) και προσθέτοντας τον όρο και στα δύο μέρη του, παίρνουμε

Όταν πληρούται η κινηματική συνθήκη

Η εξίσωση (4.5) προκύπτει από την (4.7). Και αν η συνθήκη (4.8) ικανοποιείται καθ' όλη τη διάρκεια της κίνησης, τότε υπάρχει το πρώτο ολοκλήρωμα (4.6).

Εάν οι συνδέσεις του συστήματος είναι ιδανικές και επιτρέπουν την περιστροφή του συστήματος ως άκαμπτο σώμα γύρω από τον άξονα και στον αριθμό των εικονικών μετατοπίσεων, τότε η κύρια στιγμή των αντιδράσεων γύρω από τον άξονα και είναι ίση με μηδέν, και στη συνέχεια η τιμή στο η δεξιά πλευρά της εξίσωσης (4.5) είναι η κύρια ροπή όλων των εξωτερικών ενεργών δυνάμεων γύρω από τον άξονα και . Η ισότητα προς το μηδέν αυτής της στιγμής και η ικανοποίηση της σχέσης (4.8) θα είναι στην υπό εξέταση περίπτωση επαρκείς προϋποθέσειςγια την ύπαρξη του ολοκληρώματος (4.6).

Εάν η κατεύθυνση του άξονα και είναι αμετάβλητη, τότε η συνθήκη (4.8) μπορεί να γραφτεί ως

Αυτή η ισότητα σημαίνει ότι οι προβολές της ταχύτητας του κέντρου μάζας και της ταχύτητας του σημείου Α στον άξονα και στο επίπεδο που είναι κάθετο σε αυτόν είναι παράλληλες. Στο έργο του S. A. Chaplygin, αντί του (4.9), απαιτείται ότι λιγότερο από γενική κατάστασηόπου το Χ είναι αυθαίρετη σταθερά.

Σημειώστε ότι η συνθήκη (4.8) δεν εξαρτάται από την επιλογή ενός σημείου στο . Πράγματι, έστω P ένα αυθαίρετο σημείο στον άξονα. Τότε

και ως εκ τούτου

Συμπερασματικά, σημειώνουμε τη γεωμετρική ερμηνεία του Resal των εξισώσεων (4.1) και (4.4): τα διανύσματα απόλυτες ταχύτητεςτα άκρα των διανυσμάτων και είναι ίσα αντίστοιχα με το κύριο διάνυσμα και την κύρια ροπή όλων των εξωτερικών δυνάμεων σε σχέση με το σημείο Α.

ΥΠΟΥΡΓΕΙΟ ΓΕΩΡΓΙΑΣ ΚΑΙ ΤΡΟΦΙΜΩΝ ΤΗΣ ΔΗΜΟΚΡΑΤΙΑΣ ΤΗΣ ΛΕΥΚΟΡΩΣΙΑΣ

Εκπαιδευτικό Ίδρυμα «ΛΕΥΚΑΡΩΣΙΑΣ ΚΡΑΤΙΚΟΣ ΑΓΡΟ

ΠΟΛΥΤΕΧΝΕΙΟ"

Τμήμα Θεωρητικής Μηχανικής και Θεωρίας Μηχανισμών και Μηχανών

ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ

μεθοδολογικό συγκρότημα για μαθητές της ομάδας ειδικοτήτων

74 06 Γεωργική μηχανική

Σε 2 μέρη Μέρος 1

UDC 531.3(07) LBC 22.213ya7 T 33

Συντάχθηκε από:

Υποψήφιος Φυσικομαθηματικών Επιστημών, Αναπληρωτής Καθηγητής Yu. Σ. Μπίζα, υποψήφιος τεχνικές επιστήμες, Αναπληρωτής Καθηγητής Ν. L. Rakova, Senior LecturerI. Α. Ταράσεβιτς

Αξιολογητές:

Τμήμα Θεωρητικής Μηχανικής του Εκπαιδευτικού Ιδρύματος «Εθνικό Λευκορωσίας Πολυτεχνείο» (κεφάλι

Τμήμα Θεωρητικής Μηχανικής BNTU Διδάκτωρ Φυσικών και Μαθηματικών Επιστημών, Καθηγητής Α. V. Chigarev);

Κορυφαίος Ερευνητής του Εργαστηρίου «Δονητική προστασία Μηχανικών Συστημάτων» Κρατικό Επιστημονικό Ίδρυμα «Κοινό Ινστιτούτο Μηχανολόγων Μηχανικών

Εθνική Ακαδημία Επιστημών της Λευκορωσίας», Υποψήφιος Τεχνικών Επιστημών, Αναπληρωτής Καθηγητής A. M. Goman

Θεωρητική μηχανική. Ενότητα «Δυναμική»: εκπαιδευτική

Μέθοδος T33. συγκρότημα. Σε 2 μέρη Μέρος 1 / σύντ.: Yu. S. Biza, N. L. Rakova, I. A. Tarasevich. - Μινσκ: BGATU, 2013. - 120 σελ.

ISBN 978-985-519-616-8.

ΣΤΟ εκπαιδευτικό και μεθοδικό συγκρότημαπαρουσιάζει υλικά για τη μελέτη της ενότητας «Δυναμική», μέρος 1, που εντάσσεται στο γνωστικό αντικείμενο «Θεωρητική Μηχανική». Περιλαμβάνει μάθημα διαλέξεων, βασικά υλικά για την υλοποίηση πρακτικές ασκήσεις, εργασίες και δείγματα εργασιών για ανεξάρτητη εργασία και έλεγχο μαθησιακές δραστηριότητεςπλήρους απασχόλησης και έντυπα αλληλογραφίαςμάθηση.

UDC 531.3(07) LBC 22.213ya7


ΕΙΣΑΓΩΓΗ ..................................................... ..........................................
1. ΕΠΙΣΤΗΜΟΝΙΚΟ ΚΑΙ ΘΕΩΡΗΤΙΚΟ ΠΕΡΙΕΧΟΜΕΝΟ ΕΚΠΑΙΔΕΥΤΙΚΟΥ
ΤΟΥ ΜΕΘΟΔΟΛΟΓΙΚΟΥ ΣΥΓΚΡΟΤΗΜΑΤΟΣ .............................................. ..
1.1. Γλωσσάριο................................................. ................................
1.2. Θέματα διαλέξεων και το περιεχόμενό τους .............................................. ...
Κεφάλαιο 1. Εισαγωγή στη δυναμική. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ
κλασική μηχανική ..................................................... .................................................
Θέμα 1. Δυναμική υλικού σημείου.......................................... ....
1.1. Νόμοι της δυναμικής του υλικού σημείου
(νόμοι Γαλιλαίου - Νεύτωνα) .......................................... .............
1.2. Διαφορικές εξισώσειςκινήσεις

1.3. Δύο βασικά καθήκοντα της δυναμικής .............................................. .............


Θέμα 2. Δυναμική σχετικής κίνησης
υλικό σημείο ................................................ ......................................
Επιθεώρηση των ερωτήσεων ................................................ ......................................
Θέμα 3. Δυναμική ενός μηχανικού συστήματος .......................................... ....
3.1. Γεωμετρία μάζας. Κέντρο μάζας ενός μηχανικού συστήματος......
3.2. Εσωτερικές Δυνάμεις ................................................ .................................
Επιθεώρηση των ερωτήσεων ................................................ ......................................
Θέμα 4. Ροπές αδράνειας άκαμπτου σώματος ..........................................
4.1. Ροπές αδράνειας άκαμπτου σώματος
σε σχέση με τον άξονα και τον πόλο ................................................... ......................................
4.2. Θεώρημα για τις ροπές αδράνειας ενός άκαμπτου σώματος
για παράλληλους άξονες
(θεώρημα Huygens-Steiner) .............................................. .. ....
4.3. Φυγόκεντρες ροπές αδράνειας .............................................. .
Επιθεώρηση των ερωτήσεων ................................................ .................................
Κεφάλαιο 2

Θέμα 5. Το θεώρημα για την κίνηση του κέντρου μάζας του συστήματος ..............................
Επιθεώρηση των ερωτήσεων ................................................ ......................................
Εργασίες για αυτοδιδασκαλία ................................................... .......
Θέμα 6. Το μέγεθος της κίνησης ενός υλικού σημείου
και μηχανικό σύστημα ..................................................... ................................................
6.1. Ποσότητα κίνησης υλικού σημείου 43
6.2. Παρόρμηση δύναμης ..................................................... ...................................
6.3. Θεώρημα για την αλλαγή της ορμής
υλικό σημείο ................................................ ................................................
6.4. Θεώρημα αλλαγής του κύριου διανύσματος
ορμή ενός μηχανικού συστήματος ..........................................
Επιθεώρηση των ερωτήσεων ................................................ ......................................
Εργασίες για αυτοδιδασκαλία ................................................... .......
Θέμα 7. Ροπή ορμής υλικού σημείου
και μηχανικό σύστημα σε σχέση με το κέντρο και τον άξονα ................................
7.1. Ροπή ορμής υλικού σημείου
σε σχέση με το κέντρο και τον άξονα .............................................. .................................
7.2. Θεώρημα για τη μεταβολή της γωνιακής ορμής
υλικό σημείο σε σχέση με το κέντρο και τον άξονα ......................
7.3. Θεώρημα για τη μεταβολή της κινητικής ροπής
μηχανικό σύστημα σε σχέση με το κέντρο και τον άξονα ...................................
Επιθεώρηση των ερωτήσεων ................................................ ......................................
Εργασίες για αυτοδιδασκαλία ................................................... .......
Θέμα 8. Έργο και ισχύς δυνάμεων ...................................... .........
Επιθεώρηση των ερωτήσεων ................................................ ......................................
Εργασίες για αυτοδιδασκαλία ................................................... .......
Θέμα 9. Κινητική ενέργεια υλικού σημείου
και μηχανικό σύστημα ..................................................... ................................................
9.1. Κινητική ενέργεια υλικού σημείου
και μηχανικό σύστημα. Θεώρημα Koenig ..............................
9.2. Κινητική ενέργεια άκαμπτου σώματος
με διαφορετικές κινήσεις ..................................................... ......................................
9.3. Θεώρημα αλλαγής κινητική ενέργεια
υλικό σημείο ................................................ ................................................

9.4. Θεώρημα μεταβολής κινητικής ενέργειας
μηχανικό σύστημα ...................................................... .................................
Επιθεώρηση των ερωτήσεων ................................................ ......................................
Εργασίες για αυτοδιδασκαλία ................................................... .......
Θέμα 10. Δυνητικό πεδίο δύναμης
και δυναμική ενέργεια ..................................................... ................ ................................
Επιθεώρηση των ερωτήσεων ................................................ ......................................
Θέμα 11. Δυναμική άκαμπτου σώματος.......................................... .............
Επιθεώρηση των ερωτήσεων ................................................ ......................................
2. ΥΛΙΚΑ ΓΙΑ ΕΛΕΓΧΟ
ΚΑΤΑ ΜΟΝΑΔΑ................................................ ...................................

ΑΝΕΞΑΡΤΗΤΗ ΕΡΓΑΣΙΑ ΜΑΘΗΤΩΝ ..............................
4. ΑΠΑΙΤΗΣΕΙΣ ΓΙΑ ΤΟΝ ΣΧΕΔΙΑΣΜΟ ΤΟΥ ΕΛΕΓΧΟΥ
ΕΡΓΑΣΙΕΣ ΓΙΑ ΜΑΘΗΤΕΣ ΠΛΗΡΗΣ ΑΠΑΣΧΟΛΗΣΗΣ ΚΑΙ ΑΠΟΣΤΟΛΗΣ
ΜΟΡΦΕΣ ΕΚΠΑΙΔΕΥΣΗΣ ................................................... ......................................................
5. ΚΑΤΑΛΟΓΟΣ ΕΡΩΤΗΣΕΩΝ ΠΡΟΕΤΟΙΜΑΣΙΑΣ
ΣΤΙΣ ΕΞΕΤΑΣΕΙΣ (ΜΕΛΕΤΗ) ΤΩΝ ΜΑΘΗΤΩΝ
ΕΚΠΑΙΔΕΥΣΗ ΠΛΗΡΗΣ ΑΠΑΣΧΟΛΗΣΗΣ ΚΑΙ ΑΝΤΑΠΟΚΡΙΣΗΣ .............................................. ......
6. ΚΑΤΑΛΟΓΟΣ ΑΝΑΦΟΡΩΝ ................................................... ..................

ΕΙΣΑΓΩΓΗ

Θεωρητική μηχανική - η επιστήμη των γενικών νόμων μηχανική κίνηση, ισορροπία και αλληλεπίδραση υλικών σωμάτων.

Αυτός είναι ένας από τους θεμελιώδεις γενικούς επιστημονικούς φυσικούς και μαθηματικούς κλάδους. Είναι η θεωρητική βάση της σύγχρονης τεχνολογίας.

Η μελέτη της θεωρητικής μηχανικής, μαζί με άλλους φυσικούς και μαθηματικούς κλάδους, συμβάλλει στη διεύρυνση των επιστημονικών οριζόντων, διαμορφώνει την ικανότητα συγκεκριμένων και αφηρημένη σκέψηκαι συμβάλλει στη βελτίωση της γενικής τεχνικής κουλτούρας του μελλοντικού ειδικού.

Η θεωρητική μηχανική, που αποτελεί την επιστημονική βάση όλων τεχνικούς κλάδους, συμβάλλει στην ανάπτυξη δεξιοτήτων ορθολογικές αποφάσεις εργασίες μηχανικήςπου σχετίζονται με τη λειτουργία, επισκευή και σχεδιασμό γεωργικών μηχανημάτων και εξοπλισμού αποκατάστασης.

Ανάλογα με τη φύση των εργασιών που εξετάζουμε, η μηχανική χωρίζεται σε στατική, κινηματική και δυναμική. Η δυναμική είναι ένα τμήμα της θεωρητικής μηχανικής που μελετά την κίνηση των υλικών σωμάτων υπό τη δράση εφαρμοζόμενων δυνάμεων.

ΣΤΟ εκπαιδευτικό και μεθοδικόσυγκρότημα (UMK) παρουσιάζει υλικά για τη μελέτη της ενότητας "Δυναμική", η οποία περιλαμβάνει ένα μάθημα διαλέξεων, βασικά υλικά για τη διεξαγωγή πρακτική δουλειά, εργασίες και δείγματα εκτέλεσης για ανεξάρτητη εργασίακαι έλεγχος των εκπαιδευτικών δραστηριοτήτων των μερικών φοιτητών πλήρους φοίτησης.

ΣΤΟ ως αποτέλεσμα της μελέτης της ενότητας «Δυναμική», ο μαθητής πρέπει να μάθει θεωρητική βάσηδυναμική και να κατέχει τις βασικές μεθόδους για την επίλυση προβλημάτων δυναμικής:

Να γνωρίζει μεθόδους επίλυσης προβλημάτων δυναμικής, γενικά θεωρήματα δυναμικής, αρχές μηχανικής.

Να μπορεί να προσδιορίζει τους νόμους της κίνησης ενός σώματος ανάλογα με τις δυνάμεις που ασκούνται σε αυτό. εφαρμόζει τους νόμους και τα θεωρήματα της μηχανικής για την επίλυση προβλημάτων. προσδιορίζουν τις στατικές και δυναμικές αντιδράσεις των δεσμών που περιορίζουν την κίνηση των σωμάτων.

Το πρόγραμμα σπουδών του κλάδου "Θεωρητική Μηχανική" προβλέπει συνολικό αριθμό ωρών τάξης - 136, συμπεριλαμβανομένων 36 ωρών για τη μελέτη της ενότητας "Δυναμική".

1. ΕΠΙΣΤΗΜΟΝΙΚΟ ΚΑΙ ΘΕΩΡΗΤΙΚΟ ΠΕΡΙΕΧΟΜΕΝΟ ΤΟΥ ΕΚΠΑΙΔΕΥΤΙΚΟΥ ΚΑΙ ΜΕΘΟΔΟΛΟΓΙΚΟΥ ΣΥΓΚΡΟΤΗΜΑΤΟΣ

1.1. Γλωσσάριο

Η στατική είναι ένα τμήμα της μηχανικής που σκιαγραφεί το γενικό δόγμα των δυνάμεων, η αναγωγή μελετάται πολύπλοκα συστήματαοι δυνάμεις προς την απλούστερη μορφή και οι συνθήκες ισορροπίας καθορίζονται διάφορα συστήματαδυνάμεις.

Η κινηματική είναι ένα τμήμα της θεωρητικής μηχανικής στο οποίο μελετάται η κίνηση των υλικών αντικειμένων, ανεξάρτητα από τα αίτια που προκαλούν αυτή την κίνηση, δηλαδή ανεξάρτητα από τις δυνάμεις που ασκούν αυτά τα αντικείμενα.

Η δυναμική είναι ένα τμήμα της θεωρητικής μηχανικής που μελετά την κίνηση των υλικών σωμάτων (σημείων) υπό τη δράση εφαρμοζόμενων δυνάμεων.

Υλικό σημείο- ένα υλικό σώμα, η διαφορά στην κίνηση των σημείων του οποίου είναι ασήμαντη.

Η μάζα ενός σώματος είναι μια κλιμακωτή θετική τιμή που εξαρτάται από την ποσότητα της ύλης που περιέχεται σε ένα δεδομένο σώμα και καθορίζει το μέτρο της αδράνειάς του σε κίνηση προς τα εμπρός.

Σύστημα αναφοράς - ένα σύστημα συντεταγμένων που σχετίζεται με το σώμα, σε σχέση με το οποίο μελετάται η κίνηση ενός άλλου σώματος.

αδρανειακό σύστημα- ένα σύστημα στο οποίο πληρούνται ο πρώτος και ο δεύτερος νόμος της δυναμικής.

Η ορμή μιας δύναμης είναι ένα διανυσματικό μέτρο της δράσης μιας δύναμης για κάποιο χρονικό διάστημα.

Ποσότητα κίνησης υλικού σημείου είναι το διανυσματικό μέτρο της κίνησής του, το οποίο ισούται με το γινόμενο της μάζας του σημείου και του διανύσματος της ταχύτητάς του.

Κινητική ενέργειαείναι ένα βαθμωτό μέτρο της μηχανικής κίνησης.

Στοιχειώδες έργο δύναμηςείναι μια απειροελάχιστη κλιμακωτή τιμή ίση με προϊόν με κουκκίδεςδιάνυσμα δύναμης στο διάνυσμα απειροελάχιστης μετατόπισης του σημείου εφαρμογής της δύναμης.

Κινητική ενέργειαείναι ένα βαθμωτό μέτρο της μηχανικής κίνησης.

Η κινητική ενέργεια ενός υλικού σημείου είναι βαθμωτή

θετική τιμή ίση με το μισό γινόμενο της μάζας ενός σημείου και του τετραγώνου της ταχύτητάς του.

Η κινητική ενέργεια ενός μηχανικού συστήματος είναι μια αριθμητική

το κινητικό άθροισμα των κινητικών ενεργειών όλων των υλικών σημείων αυτού του συστήματος.

Η δύναμη είναι ένα μέτρο της μηχανικής αλληλεπίδρασης των σωμάτων, που χαρακτηρίζει την ένταση και την κατεύθυνσή της.

1.2. Τα θέματα των διαλέξεων και το περιεχόμενό τους

Ενότητα 1. Εισαγωγή στη δυναμική. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ

κλασική μηχανική

Θέμα 1. Δυναμική υλικού σημείου

Οι νόμοι της δυναμικής ενός υλικού σημείου (οι νόμοι του Γαλιλαίου - Νεύτωνα). Διαφορικές εξισώσεις κίνησης υλικού σημείου. Δύο βασικά καθήκοντα δυναμικής για ένα υλικό σημείο. Λύση του δεύτερου προβλήματος της δυναμικής. σταθερές ολοκλήρωσης και ο προσδιορισμός τους από τις αρχικές συνθήκες.

Παραπομπές:, σσ. 180-196, , σσ. 12-26.

Θέμα 2. Δυναμική της σχετικής κίνησης του υλικού

Σχετική κίνηση υλικού σημείου. Διαφορικές εξισώσεις σχετικής κίνησης σημείου. φορητές και δυνάμεις αδράνειας Coriolis. Η αρχή της σχετικότητας στην κλασική μηχανική. Περίπτωση σχετικής ανάπαυσης.

Παραπομπές: , σσ. 180-196, , σσ. 127-155.

Θέμα 3. Γεωμετρία μαζών. Κέντρο μάζας ενός μηχανικού συστήματος

Μάζα του συστήματος. Το κέντρο μάζας του συστήματος και οι συντεταγμένες του.

Λογοτεχνία:, σσ. 86-93, σσ. 264-265

Θέμα 4. Ροπές αδράνειας άκαμπτου σώματος

Ροπές αδράνειας ενός άκαμπτου σώματος ως προς τον άξονα και τον πόλο. Ακτίνα αδράνειας. Θεώρημα για ροπές αδράνειας για παράλληλους άξονες. Αξονικές ροπές αδράνειας ορισμένων σωμάτων.

Οι φυγόκεντρες ροπές αδράνειας ως χαρακτηριστικό της ασυμμετρίας του σώματος.

Παραπομπές: , σσ. 265-271, , σσ. 155-173.

Ενότητα 2. Γενικά θεωρήματα της δυναμικής ενός υλικού σημείου

και μηχανικό σύστημα

Θέμα 5. Το θεώρημα για την κίνηση του κέντρου μάζας του συστήματος

Το θεώρημα για την κίνηση του κέντρου μάζας του συστήματος. Συνέπειες από το θεώρημα για την κίνηση του κέντρου μάζας του συστήματος.

Παραπομπές: , σσ. 274-277, , σσ. 175-192.

Θέμα 6. Το μέγεθος της κίνησης ενός υλικού σημείου

και μηχανικό σύστημα

Ποσότητα κίνησης υλικού σημείου και μηχανικού συστήματος. Στοιχειώδης ώθηση και ώθηση δύναμης για πεπερασμένο χρονικό διάστημα. Θεώρημα για τη μεταβολή της ορμής ενός σημείου και ενός συστήματος σε διαφορικές και ολοκληρωτικές μορφές. Νόμος διατήρησης της ορμής.

Λογοτεχνία: , σσ. 280-284, , σσ. 192-207.

Θέμα 7. Ροπή ορμής υλικού σημείου

και μηχανικό σύστημα σε σχέση με το κέντρο και τον άξονα

Η ροπή της ορμής ενός σημείου γύρω από το κέντρο και τον άξονα. Το θεώρημα για τη μεταβολή της γωνιακής ορμής ενός σημείου. Κινητική ροπή ενός μηχανικού συστήματος γύρω από το κέντρο και τον άξονα.

Η γωνιακή ορμή ενός περιστρεφόμενου άκαμπτου σώματος γύρω από τον άξονα περιστροφής. Θεώρημα για τη μεταβολή της κινητικής ροπής του συστήματος. Νόμος διατήρησης της ορμής.

Παραπομπές: , σσ. 292-298, , σσ. 207-258.

Θέμα 8. Έργο και δύναμη δυνάμεων

Στοιχειώδες έργο δύναμης, η αναλυτική του έκφραση. Το έργο της δύναμης για τελικό μονοπάτι. Το έργο της βαρύτητας, ελαστική δύναμη. Ισότητα στο μηδέν του αθροίσματος του έργου των εσωτερικών δυνάμεων που δρουν σε ένα στερεό. Το έργο των δυνάμεων που ασκούνται σε ένα άκαμπτο σώμα που περιστρέφεται γύρω από έναν σταθερό άξονα. Εξουσία. Αποδοτικότητα.

Παραπομπές: , σσ. 208-213, , σσ. 280-290.

Θέμα 9. Κινητική ενέργεια υλικού σημείου

και μηχανικό σύστημα

Κινητική ενέργεια υλικού σημείου και μηχανικού συστήματος. Υπολογισμός της κινητικής ενέργειας ενός άκαμπτου σώματος σε διάφορες περιπτώσεις της κίνησής του. Θεώρημα Koenig. Θεώρημα για τη μεταβολή της κινητικής ενέργειας ενός σημείου σε διαφορικές και ολοκληρωτικές μορφές. Θεώρημα για τη μεταβολή της κινητικής ενέργειας ενός μηχανικού συστήματος σε διαφορικές και ολοκληρωτικές μορφές.

Παραπομπές: , σσ. 301-310, , σσ. 290-344.

Θέμα 10. Δυναμικό πεδίο και δυναμικό

Η έννοια του πεδίου δύναμης. Πεδίο δυνητικής δύναμης και συνάρτηση δύναμης. Το έργο μιας δύναμης στην τελική μετατόπιση ενός σημείου σε ένα δυναμικό πεδίο. Δυναμική ενέργεια.

Παραπομπές: , σσ. 317-320, , σσ. 344-347.

Θέμα 11. Δυναμική άκαμπτου σώματος

Διαφορικές εξισώσεις μεταφορικής κίνησης άκαμπτου σώματος. Διαφορική εξίσωση περιστροφική κίνησηάκαμπτο σώμα γύρω από σταθερό άξονα. φυσικό εκκρεμές. Διαφορικές εξισώσεις επίπεδης κίνησης άκαμπτου σώματος.

Παραπομπές: , σσ. 323-334, , σσ. 157-173.

Ενότητα 1. Εισαγωγή στη δυναμική. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ

κλασική μηχανική

υλικό σώμα- ένα σώμα που έχει μάζα.

Υλικό σημείο- ένα υλικό σώμα, η διαφορά στην κίνηση των σημείων του οποίου είναι ασήμαντη. Αυτό μπορεί να είναι είτε ένα σώμα, οι διαστάσεις του οποίου μπορούν να αγνοηθούν κατά την κίνησή του, είτε ένα σώμα πεπερασμένων διαστάσεων, εάν κινείται προς τα εμπρός.

Τα σωματίδια ονομάζονται επίσης υλικά σημεία, στα οποία διαιρείται διανοητικά ένα στερεό σώμα κατά τον προσδιορισμό ορισμένων από τα δυναμικά χαρακτηριστικά του. Παραδείγματα υλικών σημείων (Εικ. 1): α - η κίνηση της Γης γύρω από τον Ήλιο. Η γη είναι ένα υλικό σημείο· b είναι η μεταφορική κίνηση ενός άκαμπτου σώματος. Στερεός- μητέρα-

al σημείο, αφού V B \u003d V A; a B = a A ; γ - περιστροφή του σώματος γύρω από τον άξονα.

Ένα σωματίδιο σώματος είναι ένα υλικό σημείο.

Η αδράνεια είναι η ιδιότητα των υλικών σωμάτων να αλλάζουν την ταχύτητα της κίνησής τους πιο γρήγορα ή πιο αργά υπό τη δράση ασκούμενων δυνάμεων.

Η μάζα ενός σώματος είναι μια κλιμακωτή θετική τιμή που εξαρτάται από την ποσότητα της ύλης που περιέχεται σε ένα δεδομένο σώμα και καθορίζει το μέτρο αδράνειας του κατά τη μεταφορική κίνηση. Στην κλασική μηχανική, η μάζα είναι μια σταθερά.

δύναμη - ποσοτικό μέτρομηχανική αλληλεπίδραση μεταξύ σωμάτων ή μεταξύ σώματος (σημείου) και πεδίου (ηλεκτρικό, μαγνητικό κ.λπ.).

Η δύναμη είναι ένα διανυσματικό μέγεθος που χαρακτηρίζεται από το μέγεθος, το σημείο εφαρμογής και την κατεύθυνση (γραμμή δράσης) (Εικ. 2: Α - σημείο εφαρμογής, ΑΒ - γραμμή δράσης της δύναμης).

Ρύζι. 2

Στη δυναμική, μαζί με σταθερές δυνάμεις, υπάρχουν επίσης μεταβλητές δυνάμεις που μπορούν να εξαρτώνται από το χρόνο t, την ταχύτητα ϑ, την απόσταση r ή από έναν συνδυασμό αυτών των μεγεθών, δηλ.

F = const;

F = F(t);

F = F(ϑ ) ;

F = F(r) ;

F = F(t, r, ϑ ) .


Παραδείγματα τέτοιων δυνάμεων φαίνονται στα Σχ. 3: α			- σωματικό βάρος;
	(ϑ) – δύναμη αντίστασης αέρα;b −	Τ =	- ελκτική δύναμη

ηλεκτρική ατμομηχανή? c − F = F (r) είναι η δύναμη απώθησης από το κέντρο O ή έλξης προς αυτό.

Ένα αδρανειακό σύστημα είναι ένα σύστημα στο οποίο πληρούνται ο πρώτος και ο δεύτερος νόμος της δυναμικής. Αυτό είναι ένα σταθερό σύστημα συντεταγμένων ή ένα σύστημα που κινείται ομοιόμορφα και ευθύγραμμα.

Η κίνηση στη μηχανική είναι μια αλλαγή στη θέση ενός σώματος στο χώρο και στο χρόνο σε σχέση με άλλα σώματα.

Ο χώρος στην κλασική μηχανική είναι τρισδιάστατος, υπακούοντας στην Ευκλείδεια γεωμετρία.

Ο χρόνος είναι ένα βαθμωτό μέγεθος που ρέει με τον ίδιο τρόπο σε οποιοδήποτε σύστημα αναφοράς.

Ένα σύστημα μονάδων είναι ένα σύνολο μονάδων μέτρησης φυσικές ποσότητες. Για να μετρηθούν όλα τα μηχανικά μεγέθη, αρκούν τρεις βασικές μονάδες: μονάδες μήκους, χρόνου, μάζας ή δύναμης.




Μηχανικός	Διάσταση	Σημειογραφία	Διάσταση	Σημειογραφία
μέγεθος
			εκατοστόμετρο



	χιλιόγραμμο-

Όλες οι άλλες μονάδες μέτρησης των μηχανικών μεγεθών είναι παράγωγα αυτών. Χρησιμοποιούνται δύο τύποι συστημάτων μονάδων: διεθνές σύστημαΜονάδες SI (ή μικρότερες - CGS) και το τεχνικό σύστημα μονάδων - MKGSS.

Θέμα 1. Δυναμική υλικών σημείων

1.1. Οι νόμοι της δυναμικής ενός υλικού σημείου (οι νόμοι του Γαλιλαίου - Νεύτωνα)

Ο πρώτος νόμος (της αδράνειας).

απομονωμένη από εξωτερικές επιρροέςένα υλικό σημείο διατηρεί την κατάσταση ηρεμίας ή κινείται ομοιόμορφα και ευθύγραμμα έως ότου οι ασκούμενες δυνάμεις το αναγκάσουν να αλλάξει αυτή την κατάσταση.

Η κίνηση που γίνεται από ένα σημείο απουσία δυνάμεων ή υπό τη δράση ενός ισορροπημένου συστήματος δυνάμεων ονομάζεται κίνηση αδράνειας.

Για παράδειγμα, η κίνηση ενός σώματος κατά μήκος μιας ομαλής (η δύναμη τριβής είναι μηδέν) προ

οριζόντια επιφάνεια (Εικ. 4: G - σωματικό βάρος, N - κανονική αντίδραση του επιπέδου).

Αφού G = − N , τότε G + N = 0.

Όταν ϑ 0 ≠ 0 το σώμα κινείται με την ίδια ταχύτητα. σε ϑ 0 = 0 το σώμα βρίσκεται σε ηρεμία (ϑ 0 είναι η αρχική ταχύτητα).

Ο δεύτερος νόμος (βασικός νόμος της δυναμικής).

Το γινόμενο της μάζας ενός σημείου και της επιτάχυνσης που δέχεται υπό την επίδραση μιας δεδομένης δύναμης είναι ίσο σε απόλυτη τιμή με αυτή τη δύναμη και η διεύθυνση του συμπίπτει με την κατεύθυνση της επιτάχυνσης.

α β

Μαθηματικά, αυτός ο νόμος εκφράζεται με τη διανυσματική ισότητα

Για F = const,

a = const - η κίνηση του σημείου είναι ομοιόμορφη. ΕΕ-

αν a ≠ const, α

- αργή κίνηση (Εικ. 5, αλλά).

α ≠ συνθήκη,

ένα -

– επιταχυνόμενη κίνηση (Εικ. 5, β), m – σημειακή μάζα.

διάνυσμα επιτάχυνσης;

– διανυσματική δύναμη; ϑ 0 είναι το διάνυσμα της ταχύτητας).

Στο F = 0,a 0 = 0 = ϑ 0 = const - το σημείο κινείται ομοιόμορφα και ευθύγραμμα, ή στο ϑ 0 = 0 - βρίσκεται σε ηρεμία (ο νόμος της αδράνειας). Δεύτερος

ο νόμος σας επιτρέπει να δημιουργήσετε μια σχέση μεταξύ της μάζας m ενός σώματος που βρίσκεται κοντά η επιφάνεια της γης, και το βάρος του G .G = mg , όπου g είναι

επιτάχυνση βαρύτητος.

Ο τρίτος νόμος (ο νόμος της ισότητας δράσης και αντίδρασης). Δύο υλικά σημεία δρουν μεταξύ τους με δυνάμεις ίσες σε μέγεθος και κατευθυνόμενες κατά μήκος της ευθείας γραμμής που συνδέει

αυτά τα σημεία, σε αντίθετες κατευθύνσεις.

Εφόσον εφαρμόζονται οι δυνάμεις F 1 = − F 2 διαφορετικά σημεία, τότε το σύστημα δυνάμεων (F 1 , F 2 ) δεν είναι ισορροπημένο, δηλ. (F 1 , F 2 )≈ 0 (Εικ. 6).

Με τη σειρά του

m a = m a

- στάση

οι μάζες των σημείων που αλληλεπιδρούν είναι αντιστρόφως ανάλογες με τις επιταχύνσεις τους.

Ο τέταρτος νόμος (ο νόμος της ανεξαρτησίας της δράσης των δυνάμεων). Η επιτάχυνση που λαμβάνεται από ένα σημείο υπό τη δράση ενός ταυτόχρονου

αλλά πολλών δυνάμεων, ισούται με το γεωμετρικό άθροισμα εκείνων των επιταχύνσεων που θα λάμβανε ένα σημείο υπό την επίδραση κάθε δύναμης χωριστά πάνω του.

Επεξήγηση (Εικ. 7).

t a n

a 1 a kF n

Οι δυνάμεις R που προκύπτουν (F 1 ,...F k ,...F n ) .

Αφού ma = R ,F 1 = ma 1 , ...,F k = ma k , ...,F n = ma n , τότε

a = a 1 + ...+ a k + ...+ a n = ∑ a k , δηλαδή ο τέταρτος νόμος είναι ισοδύναμος με

k = 1

ο κανόνας της πρόσθεσης δυνάμεων.

1.2. Διαφορικές εξισώσεις κίνησης υλικού σημείου

Αφήστε πολλές δυνάμεις να δρουν ταυτόχρονα σε ένα υλικό σημείο, μεταξύ των οποίων υπάρχουν και σταθερές και μεταβλητές.

Γράφουμε τον δεύτερο νόμο της δυναμικής στη μορφή

= ∑

(t ,

k = 1

, ϑ=

r είναι το διάνυσμα ακτίνας της κίνησης

σημεία, τότε το (1.2) περιέχει παραγώγους του r και είναι μια διαφορική εξίσωση κίνησης ενός υλικού σημείου σε διανυσματική μορφή ή η βασική εξίσωση της δυναμικής ενός υλικού σημείου.

Προβολές ισότητας διανυσμάτων (1.2): - στον άξονα των καρτεσιανών συντεταγμένων (Εικ. 8, αλλά)

μέγ.=μδ
μέγ.=μδ	= ∑Fkx;
	k = 1
μπορεί=μδ
μπορεί=μδ	= ∑Fky;	(1.3)
	k = 1

μαζ=μ	= ∑Fkz;
μαζ=μ	= ∑Fkz;
	k = 1

Στον φυσικό άξονα (Εικ. 8, β)


χαλάκι				= ∑ Fk τ ,
χαλάκι				= ∑ Fk τ ,
				k = 1

				= ∑ F k n ;
				k = 1

mab = m0 = ∑ Fk β

k = 1

M t oM oa

β στο ο

Οι εξισώσεις (1.3) και (1.4) είναι διαφορικές εξισώσεις κίνησης ενός υλικού σημείου στους καρτεσιανούς άξονες συντεταγμένων και στους φυσικούς άξονες, αντίστοιχα, δηλ. φυσικές διαφορικές εξισώσεις που χρησιμοποιούνται συνήθως για την καμπυλόγραμμη κίνηση ενός σημείου εάν η τροχιά του σημείου και η ακτίνα καμπυλότητάς του είναι γνωστή.

1.3. Δύο βασικά προβλήματα δυναμικής για ένα υλικό σημείο και η επίλυσή τους

Η πρώτη (άμεση) εργασία.

Γνωρίζοντας το νόμο της κίνησης και τη μάζα του σημείου, προσδιορίστε τη δύναμη που ασκεί στο σημείο.

Για να λύσετε αυτό το πρόβλημα, πρέπει να γνωρίζετε την επιτάχυνση του σημείου. Σε προβλήματα αυτού του τύπου, μπορεί να προσδιοριστεί άμεσα ή να προσδιοριστεί ο νόμος κίνησης ενός σημείου, σύμφωνα με τον οποίο μπορεί να προσδιοριστεί.

1. Έτσι, αν η κίνηση ενός σημείου δίνεται σε καρτεσιανές συντεταγμένες

x \u003d f 1 (t) , y \u003d f 2 (t) και z \u003d f 3 (t) τότε προσδιορίζονται οι προβολές της επιτάχυνσης

στον άξονα συντεταγμένων x =

d2x

d2y

d2z

Και μετά - έργο-

Δυνάμεις F x , F y και F z σε αυτούς τους άξονες:

,k ) = F F z . (1.6)

2. Εάν το σημείο δεσμεύει καμπυλόγραμμη κίνησηκαι ο νόμος της κίνησης είναι γνωστός s = f (t), η τροχιά του σημείου και η ακτίνα καμπυλότητάς του ρ, τότε

είναι βολικό να χρησιμοποιείτε φυσικούς άξονες και οι προβολές επιτάχυνσης σε αυτούς τους άξονες καθορίζονται από τους γνωστούς τύπους:

Εφαπτομενικός άξονας

a τ = d ϑ = d 2 2 s – εφαπτομενική επιτάχυνση;dt dt

Αρχική Κανονική

ds 2

a n = ϑ 2 = dt είναι κανονική επιτάχυνση.

Η προβολή της επιτάχυνσης στο δικανονικό είναι μηδέν. Στη συνέχεια οι προβολές της δύναμης στους φυσικούς άξονες

F=m			F=m

Το μέτρο και η κατεύθυνση της δύναμης καθορίζονται από τους τύπους:

F \u003d F τ 2 + F n 2; cos (

; cos(

Η δεύτερη (αντίστροφη) εργασία.

Γνωρίζοντας τις δυνάμεις που δρουν στο σημείο, τη μάζα του και αρχικές συνθήκεςκίνηση, προσδιορίστε το νόμο της κίνησης ενός σημείου ή οποιοδήποτε άλλο κινηματικό του χαρακτηριστικό.

Οι αρχικές συνθήκες για την κίνηση ενός σημείου στους καρτεσιανούς άξονες είναι οι συντεταγμένες του σημείου x 0, y 0, z 0 και η προβολή της αρχικής ταχύτητας ϑ 0 σε αυτούς

άξονες ϑ 0 x \u003d x 0, ϑ 0 y \u003d y 0 και ϑ 0 z \u003d z 0 τη στιγμή που αντιστοιχεί σε

δίνοντας την αρχή της σημειακής κίνησης και λαμβάνεται ίση με το μηδέν. Η επίλυση προβλημάτων αυτού του τύπου περιορίζεται στη σύνταξη ενός διαφορικού

διαφορικές εξισώσεις (ή μία εξίσωση) κίνησης ενός υλικού σημείου και η επακόλουθη επίλυσή τους κατά άμεση ενσωμάτωσηή χρησιμοποιώντας τη θεωρία των διαφορικών εξισώσεων.

Επιθεώρηση των ερωτήσεων

1. Τι μελετά η δυναμική;

2. Τι είδους κίνηση ονομάζεται αδρανειακή κίνηση;

3. Κάτω από ποιες συνθήκες ένα υλικό σημείο θα βρίσκεται σε ηρεμία ή θα κινείται ομοιόμορφα και ευθύγραμμα;

4. Ποια είναι η ουσία του πρώτου κύριου προβλήματος της δυναμικής ενός υλικού σημείου; Δεύτερη εργασία;

5. Να γράψετε τις φυσικές διαφορικές εξισώσεις κίνησης ενός υλικού σημείου.

Εργασίες για αυτοδιδασκαλία

1. Σημείο μάζας m = 4 kg κινείται κατά μήκος μιας οριζόντιας ευθείας με επιτάχυνση a = 0,3 t. Προσδιορίστε το δομοστοιχείο της δύναμης που ασκεί το σημείο προς την κατεύθυνση της κίνησής του τη χρονική στιγμή t = 3 s.

2. Ένα μέρος μάζας m = 0,5 kg γλιστράει στο δίσκο. Σε ποια γωνία ως προς το οριζόντιο επίπεδο πρέπει να βρίσκεται ο δίσκος έτσι ώστε το τμήμα να κινείται με επιτάχυνση a = 2 m / s 2; Angle express

σε βαθμούς.

3. Σημείο με μάζα m = 14 kg κινείται κατά μήκος του άξονα Ox με επιτάχυνση a x = 2 t . Προσδιορίστε το μέτρο της δύναμης που ασκεί το σημείο προς την κατεύθυνση της κίνησης τη χρονική στιγμή t = 5 s.

(ΜΗΧΑΝΙΚΑ ΣΥΣΤΗΜΑΤΑ) - IV επιλογή

1. Η βασική εξίσωση της δυναμικής ενός υλικού σημείου, όπως είναι γνωστό, εκφράζεται με την εξίσωση . Διαφορικές εξισώσεις κίνησης αυθαίρετα σημείαενός μη ελεύθερου μηχανικού συστήματος σύμφωνα με δύο τρόπους διαίρεσης των δυνάμεων μπορεί να γραφτεί με δύο μορφές:

(1) , όπου k=1, 2, 3, … , n είναι ο αριθμός των σημείων του υλικού συστήματος.

(2)

πού είναι η μάζα του κ-ου σημείου; - διάνυσμα ακτίνας του k-ου σημείου, - δεδομένης (ενεργητικής) δύναμης που ασκεί το k-ο σημείο ή το αποτέλεσμα όλων των ενεργών δυνάμεων που δρουν στο k-ο σημείο. - το αποτέλεσμα των δυνάμεων αντίδρασης των δεσμών που δρουν στο k-ο σημείο. - αποτέλεσμα των εσωτερικών δυνάμεων που δρουν στο k-ο σημείο. - το αποτέλεσμα των εξωτερικών δυνάμεων που δρουν στο k-ο σημείο.

Οι εξισώσεις (1) και (2) μπορούν να χρησιμοποιηθούν για την επίλυση τόσο του πρώτου όσο και του δεύτερου προβλημάτων της δυναμικής. Ωστόσο, η λύση του δεύτερου προβλήματος της δυναμικής για το σύστημα γίνεται πολύ περίπλοκη όχι μόνο με μαθηματικό σημείοόραμα, αλλά και γιατί αντιμετωπίζουμε θεμελιώδεις δυσκολίες. Βρίσκονται στο γεγονός ότι τόσο για το σύστημα (1) όσο και για το σύστημα (2) ο αριθμός των εξισώσεων είναι σημαντικά μικρότερο από τον αριθμόάγνωστος.

Έτσι, αν χρησιμοποιήσουμε το (1), τότε το γνωστό για το δεύτερο (αντίστροφο) πρόβλημα της δυναμικής θα είναι και , και οι άγνωστοι θα είναι και . Οι διανυσματικές εξισώσεις θα είναι " n", και άγνωστο - "2n".

Αν προχωρήσουμε από το σύστημα των εξισώσεων (2), τότε η γνωστή και μέρος των εξωτερικών δυνάμεων . Γιατί ένα μέρος; Το γεγονός είναι ότι ο αριθμός των εξωτερικών δυνάμεων περιλαμβάνει εξωτερικές αντιδράσειςσυνδέσεις που είναι άγνωστες. Επιπλέον, θα υπάρχουν και άγνωστα.

Έτσι, τόσο το σύστημα (1) όσο και το σύστημα (2) είναι ΑΝΟΙΧΤΑ. Πρέπει να προσθέσουμε εξισώσεις, λαμβάνοντας υπόψη τις εξισώσεις των σχέσεων, και ίσως πρέπει ακόμα να επιβάλουμε κάποιους περιορισμούς στις ίδιες τις σχέσεις. Τι να κάνω?

Αν προχωρήσουμε από το (1), τότε μπορούμε να ακολουθήσουμε το μονοπάτι της σύνταξης των εξισώσεων Lagrange του πρώτου είδους. Όμως αυτός ο τρόπος δεν είναι λογικός γιατί ευκολότερο έργο(λιγότεροι βαθμοί ελευθερίας), τόσο πιο δύσκολο είναι να λυθεί από τη σκοπιά των μαθηματικών.

Τότε ας δώσουμε προσοχή στο σύστημα (2), όπου - είναι πάντα άγνωστα. Το πρώτο βήμα για την επίλυση του συστήματος είναι η εξάλειψη αυτών των αγνώστων. Θα πρέπει να ληφθεί υπόψη ότι, κατά κανόνα, δεν μας ενδιαφέρουν οι εσωτερικές δυνάμεις κατά την κίνηση του συστήματος, δηλαδή όταν το σύστημα κινείται, δεν είναι απαραίτητο να γνωρίζουμε πώς κινείται κάθε σημείο του συστήματος, αλλά είναι αρκετό για να γνωρίζουμε πώς κινείται το σύστημα στο σύνολό του.

Έτσι, εάν διαφορετικοί τρόποιεξαίρεση από το σύστημα (2) άγνωστες δυνάμεις, τότε λαμβάνουμε κάποιες σχέσεις, δηλ. κάποιες Γενικά χαρακτηριστικάγια το σύστημα, η γνώση του οποίου καθιστά δυνατό να κρίνουμε πώς κινείται το σύστημα γενικά. Αυτά τα χαρακτηριστικά εισάγονται χρησιμοποιώντας το λεγόμενο γενικά θεωρήματα δυναμικής. Υπάρχουν τέσσερα τέτοια θεωρήματα:

1. Θεώρημα για κίνηση του κέντρου μάζας του μηχανικού συστήματος;

2. Θεώρημα περί αλλαγή στην ορμή ενός μηχανικού συστήματος;

3. Θεώρημα περί αλλαγή στη γωνιακή ορμή ενός μηχανικού συστήματος;

4. Θεώρημα περί αλλαγή της κινητικής ενέργειας ενός μηχανικού συστήματος.