Find the indefinite integral: beginnings of beginnings, examples of solutions. Calculator online. Calculate the indefinite integral (antiderivative)

Finding an indefinite integral (a set of antiderivatives or "anti-derivatives") means restoring a function from the known derivative of this function. Restored set of antiderivatives F(x) + With for function f(x) takes into account the integration constant C. According to the speed of movement of a material point (derivative), the law of motion of this point (original) can be restored; according to the acceleration of the movement of a point - its speed and the law of motion. As you can see, integration is a wide field for the activity of Sherlock Holmes from physics. Yes, and in the economy, many concepts are represented through functions and their derivatives, and therefore, for example, it is possible to restore the volume of output produced at the appropriate time by labor productivity at a certain point in time (derivative).

To find the indefinite integral, a fairly small number of basic integration formulas are required. But the process of finding it is much more difficult than the mere application of these formulas. All the complexity does not relate to integration, but to bringing the integrable expression to such a form that makes it possible to find the indefinite integral using the basic formulas mentioned above. This means that to start the practice of integration, you need to activate the results obtained in high school expression transformation skills.

We will learn to find integrals using properties and the table of indefinite integrals from the lesson about the basic concepts of this topic (opens in a new window).

There are several methods for finding the integral, of which variable replacement method and method of integration by parts- a mandatory gentleman's set for everyone who has successfully passed higher mathematics. However, it is more useful and pleasant to start learning integration using the expansion method based on the following two theorems on the properties of the indefinite integral, which we will repeat here for convenience.

Theorem 3. The constant factor in the integrand can be taken out of the sign of the indefinite integral, i.e.

Theorem 4. Indefinite integral of an algebraic sum finite number functions is algebraic sum indefinite integrals of these functions, i.e.

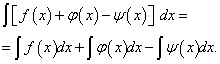(2)

In addition, the following rule may be useful in integration: if the expression of the integrand contains a constant factor, then the expression of the antiderivative is multiplied by the reciprocal of the constant factor, that is

(3)

Since this lesson is an introduction to solving integration problems, it is important to note two things that are either already initial stage, or a little later may surprise you. Surprise is due to the fact that integration is the inverse operation of differentiation and the indefinite integral can rightly be called "anti-derivative".

The first thing that should not be surprised when integrating. In the table of integrals there are formulas that have no analogues among the formulas of the derivative table . These are the following formulas:

However, one can verify that the derivatives of the expressions on the right-hand side of these formulas coincide with the corresponding integrands.

The second thing not to be surprised when integrating. Although the derivative of any elementary function is also an elementary function, indefinite integrals of some elementary functions are no longer elementary functions . Examples of such integrals are:

The following skills will be useful to develop an integration technique: reducing fractions, dividing a polynomial in the numerator of a fraction by a monomial in the denominator (to obtain the sum of indefinite integrals), converting roots to a power, multiplying a monomial by a polynomial, raising to a power. These skills are needed to transform the integrand, which should result in the sum of the integrals present in the table of integrals.

Finding indefinite integrals together

Example 1 Find the indefinite integral

Decision. We see in the denominator of the integrand a polynomial in which x is squared. This is almost a sure sign that the table integral 21 (with the arc tangent of the result) can be applied. We take out the factor-two from the denominator (there is such a property of the integral - a constant factor can be taken out of the integral sign, it was mentioned above as Theorem 3). The result of all this:

Now the denominator is the sum of squares, which means that we can apply the mentioned table integral. Finally we get the answer:

Example 2 Find the indefinite integral

Decision. We again apply Theorem 3 - the property of the integral, on the basis of which the constant factor can be taken out of the integral sign:

We apply formula 7 from the table of integrals (variable in degree) to the integrand:

We reduce the resulting fractions and we have the final answer:

Example 3 Find the indefinite integral

Decision. Applying first Theorem 4 and then Theorem 3 on properties, we find this integral as the sum of three integrals:

All three integrals obtained are tabular. We use formula (7) from the table of integrals for n = 1/2, n= 2 and n= 1/5, and then

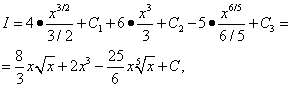
combines all three arbitrary constants that were introduced when finding three integrals. Therefore, in similar situations, only one arbitrary constant (constant) of integration should be introduced.

Example 4 Find the indefinite integral

Decision. When there is a monomial in the denominator of the integrand, we can divide the numerator by the denominator term by term. The original integral turned into the sum of two integrals:

To apply the table integral, we convert the roots to powers and here is the final answer:

We continue to find indefinite integrals together

Example 7 Find the indefinite integral

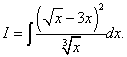
Decision. If we transform the integrand by squaring the binomial and dividing the numerator by the denominator term by term, then the original integral becomes the sum of three integrals.

The function F(x) is called antiderivative for the function f(x) on the interval (a; b) if f(x) for all x (a; b) satisfies the equality F (x) = f(x). 2

Theorem 1. If F(x) is an antiderivative for f(x) on (a; b), then F(x) + C, where C is a number, is also an antiderivative for f(x) on (a; b). Proof: (F + C) = F + C = f + 0 = f 3

Let us prove two auxiliary theorems: If the function g(x) is constant on (a; b), then g (x) = 0. If g (x) = 0 for all x (a; b), then g(x) = C on (a; b). 4

Theorem 2. If F(x) is an antiderivative for f(x) on the interval (a; b), and G(x) is another antiderivative for f(x) on (a; b), then G = F + C, where C is a number. 5

The set of all antiderivatives for the function f(x) on the interval (a; b) is called the indefinite integral and is denoted by the integral f(x)dx. dx Calculation not definite integral from given function is called integration 6

If the function f(x) is continuous and the function (t) has a continuous derivative (t), then the following formula holds: f((t)) (t) dt = f(x) dx, where x = (t). eight

Let u(x) and v(x) be functions differentiable on some interval. Then (uv) = u v + v u This implies (uv) dx = (u v + v u)dx = u v dx + v u dx or uv dx = uv – u v dx. ten

This implies a formula called the integration-by-parts formula: integration-by-parts u(x)dv(x) = u(x) v(x) – v(x)du(x) 11

The definite integral of a function over an interval is the limit to which the integral sum tends in this process, if the limit exists: 13

The number a is called the lower limit of integration, and the number b is called the upper limit of integration. In Figure 2 curvilinear trapezoid marked with a dash. The area S of this trapezoid is determined by the formula 14

Let the function f(t) be defined and continuous on some interval containing the point a. Then each number x from this interval can be associated with a number, thereby defining the function I(x) on the interval, which is called a definite integral with a variable upper limit 17

Derivative of a definite integral with respect to upper limit at the point x is equal to the value of the integrand at the point x. eighteen

Let the function y = f(x) be defined and continuous on a semi-infinite interval (t) dt

which, taking into account the introduced notation, is the initial assumption. The theorem has been proven.

Example. To find indefinite integral
.

Let's make a replacement t = sinx, dt = cosxdt.

Example.

Replacement
We get:

Below we will consider other examples of using the substitution method for various types of functions.

Integration by parts.

The method is based on the well-known formula for the derivative of a product:

(uv)=uv+vu

where u and v are some functions of x.

In differential form: d(uv) =udv+vdu

After integrating, we get:
, and in accordance with the above properties of the indefinite integral:

or
;

We have obtained an integration-by-parts formula that allows us to find the integrals of many elementary functions.

Example.

As you can see, the consistent application of the integration-by-parts formula allows you to gradually simplify the function and bring the integral to a tabular one.

Example.

It can be seen that as a result of the repeated application of integration by parts, the function could not be simplified to a tabular form. However, the last integral obtained is no different from the original one. Therefore, we transfer it to the left side of the equality.

Thus, the integral was found without the use of tables of integrals at all.

Before considering in detail the methods of integrating various classes of functions, we give a few more examples of finding indefinite integrals by reducing them to tabular ones.

Example.

Integration of elementary fractions.

Definition: Elementary fractions of the following four types are called:

I.
III.

II.
IV.

m,n– integers(m2,n2) and b 2 – 4ac<0.

The first two types of integrals of elementary fractions are quite simply reduced to tabular substitutions t=ax+b.

Consider a method for integrating elementary fractions of the form III.

The integral of a fraction of type III can be represented as:

Here, in general view the reduction of the integral of a fraction of the form III to two tabular integrals is shown.

Consider the application of the above formula with examples.

Example.

Generally speaking, if the trinomial ax 2 +bx+cexpressionb 2 - 4ac>0, then the fraction is by definition not elementary, however, nevertheless it can be integrated in the above way.

Example.

Let us now consider methods for integrating the simplest fractions of type IV.

First, consider a special case with M = 0, N = 1.

Then the integral of the form
can be represented by highlighting the full square in the denominator as
. Let's do the following transformation:

The second integral included in this equality will be taken by parts.

Denote:

For the original integral we get:

The resulting formula is called recurrent. If you apply it n-1 times, you get a table integral
.

Let us now return to the integral of an elementary fraction of the form IV in the general case.

In the resulting equality, the first integral using the substitution t = u 2 + s is reduced to tabular , and the recurrent formula considered above is applied to the second integral.

Despite the apparent complexity of integrating an elementary fraction of type IV, in practice it is quite easy to apply for fractions with a small degree n, and the universality and generality of the approach makes it possible to implement this method very simply on a computer.

Example:

Integration of rational functions.

Integration of rational fractions.

In order to integrate a rational fraction, it is necessary to decompose it into elementary fractions.

Theorem: If a
is a proper rational fraction whose denominator P(x) is represented as a product of linear and quadratic factors (note that any polynomial with real coefficients can be represented as follows: P(x) = (x - a)  …(x - b)  (x 2 + px + q)  …(x 2 + rx + s)  ), then this fraction can be decomposed into elementary ones according to the following scheme:

where A i ,B i ,M i ,N i ,R i ,S i are some constant values.

When integrating rational fractions, one resorts to decomposing the original fraction into elementary ones. To find the value A i ,B i ,M i ,N i ,R i ,S i use the so-called method of indeterminate coefficients, the essence of which is that in order for two polynomials to be identically equal, it is necessary and sufficient that the coefficients at the same powers of x be equal.

We will consider the application of this method on a specific example.

Example.

Reducing to a common denominator and equating the corresponding numerators, we get:

Example.

Because If the fraction is not correct, then you should first select the integer part from it:

6x 5 – 8x 4 – 25x 3 + 20x 2 – 76x– 7 3x 3 – 4x 2 – 17x+ 6

6x 5 – 8x 4 – 34x 3 + 12x 2 2x 2 + 3

9x3 + 8x2 - 76x - 7

9x 3 - 12x 2 - 51x +18

20x2-25x-25

We decompose the denominator of the resulting fraction into factors. It can be seen that at x = 3 the denominator of the fraction becomes zero. Then:

3x 3 – 4x 2 – 17x+ 6x- 3

3x 3 – 9x 2 3x 2 + 5x- 2

Thus 3x 3 – 4x 2 – 17x+ 6 = (x– 3)(3x 2 + 5x– 2) = (x– 3)(x+ 2)(3x– 1). Then:

In order to avoid when finding uncertain coefficients of opening brackets, grouping and solving a system of equations (which in some cases may turn out to be quite large), the so-called arbitrary value method. The essence of the method is that several (according to the number of uncertain coefficients) arbitrary values of x are substituted into the expression obtained above. To simplify the calculations, it is customary to take as arbitrary values the points at which the denominator of the fraction is equal to zero, i.e. in our case - 3, -2, 1/3. We get:

Finally we get:

Example.

Let's find indefinite coefficients:

Then the value of the given integral:

Integration of some trigonometric

functions.

Integrals from trigonometric functions there may be an infinite number. Most of these integrals cannot be calculated analytically at all, so consider some main types functions that can always be integrated.

Integral of the form
.

Here R is the designation of some rational function of the variables sinx and cosx.

Integrals of this type are calculated using the substitution
. This substitution allows you to convert a trigonometric function into a rational one.

Then

Thus:

The transformation described above is called universal trigonometric substitution.

Example.

The undoubted advantage of this substitution is that with its help it is always possible to transform a trigonometric function into a rational one and calculate the corresponding integral. The disadvantages include the fact that the transformation can result in a rather complex rational function, the integration of which will take a lot of time and effort.

However, if it is impossible to apply a more rational change of variable, this method is the only effective one.

Example.

Integral of the form
if

functionRcosx.

Despite the possibility of calculating such an integral using the universal trigonometric substitution, it is more rational to apply the substitution t = sinx.

Function
can contain cosx only to even powers, and therefore can be converted to a rational function with respect to sinx.

Example.

Generally speaking, to apply this method, only the oddness of the function with respect to the cosine is necessary, and the degree of the sine included in the function can be any, both integer and fractional.

Integral of the form
if

functionRis odd with respect tosinx.

By analogy with the case considered above, the substitution t = cosx.

Example.

Integral of the form

functionReven relativelysinxandcosx.

To transform the function R into a rational one, the substitution is used

t = tgx.

Example.

Integral of the product of sines and cosines

various arguments.

Depending on the type of work, one of three formulas will be applied:

Example.

Sometimes, when integrating trigonometric functions, it is convenient to use well-known trigonometric formulas to reduce the order of functions.

Example.

Sometimes some non-standard tricks are used.

Example.

Integration of some irrational functions.

Far from every irrational function may have an integral expressed by elementary functions. To find the integral of an irrational function, one should apply a substitution that will allow one to transform the function into a rational one, the integral of which can always be found, as is known.

Consider some techniques for integrating various types of irrational functions.

Integral of the form
wheren- natural number.

With the help of substitution
the function is rationalized.

Example.

If the irrational function includes roots of different degrees, then it is rational to take the root of the degree equal to the least common multiple of the powers of the roots included in the expression as a new variable.

Let's illustrate this with an example.

Example.

Integration of binomial differentials.

Definition: Binomial differential called expression

x m (a + bx n ) p dx

where m, n, and p are rational numbers.

As was proved by Academician Chebyshev P.L. (1821-1894), the integral of the binomial differential can be expressed in terms of elementary functions only in the following three cases:

If a R is an integer, then the integral is rationalized using the substitution

, where  is the common denominator m and n.

Previously, for a given function, guided by various formulas and rules, we found its derivative. The derivative has numerous applications: it is the speed of movement (or, more generally, the speed of any process); slope tangent to the graph of the function; using the derivative, you can investigate the function for monotonicity and extrema; It helps to solve optimization problems.

But along with the problem of finding the speed according to the known law of motion, there is also inverse problem- the problem of restoring the law of motion from a known speed. Let's consider one of these problems.

Example 1 Moves in a straight line material point, the speed of its movement at time t is given by the formula v=gt. Find the law of motion.
Decision. Let s = s(t) be the desired law of motion. It is known that s "(t) = v(t). So, to solve the problem, you need to choose a function s = s(t), whose derivative is equal to gt. It is easy to guess that $s(t) = \frac(gt^ 2)(2) $ Indeed
$s"(t) = \left(\frac(gt^2)(2) \right)" = \frac(g)(2)(t^2)" = \frac(g)(2) \ cdot 2t=gt$
Answer: $s(t) = \frac(gt^2)(2) $

We note right away that the example is solved correctly, but incompletely. We got $s(t) = \frac(gt^2)(2) $. In fact, the problem has infinitely many solutions: any function of the form $s(t) = \frac(gt^2)(2) + C $, where C is an arbitrary constant, can serve as a law of motion, since $\left (\frac(gt^2)(2) +C \right)" = gt $

To make the problem more specific, we had to fix the initial situation: indicate the coordinate of the moving point at some point in time, for example, at t = 0. If, say, s(0) = s 0 , then from the equality s(t) = (gt 2)/2 + C we get: s(0) = 0 + C, i.e. C = s 0 . Now the law of motion is uniquely defined: s(t) = (gt 2)/2 + s 0 .

In mathematics, reciprocal operations are assigned different names, come up with special notation, for example: squaring (x 2) and extracting square root($\sqrt(x) $), sine (sin x) and arcsine (arcsin x), etc. The process of finding the derivative with respect to a given function is called differentiation, and the inverse operation, i.e. the process of finding a function by a given derivative, - integration.

The term "derivative" itself can be justified "in a worldly way": the function y \u003d f (x) "produces into the world" new feature y" = f"(x). The function y \u003d f (x) acts as if as a “parent”, but mathematicians, of course, do not call it a “parent” or “producer”, they say that this is, in relation to the function y "= f" (x) , the primary image, or antiderivative.

Definition. A function y = F(x) is called an antiderivative for a function y = f(x) on an interval X if $x \in X $ satisfies the equality F"(x) = f(x)

In practice, the interval X is usually not specified, but implied (as the natural domain of the function).

Let's give examples.
1) The function y \u003d x 2 is an antiderivative for the function y \u003d 2x, since for any x the equality (x 2) "\u003d 2x is true
2) The function y \u003d x 3 is an antiderivative for the function y \u003d 3x 2, since for any x the equality (x 3)" \u003d 3x 2 is true
3) The function y \u003d sin (x) is an antiderivative for the function y \u003d cos (x), since for any x the equality (sin (x)) "= cos (x) is true

When finding antiderivatives, as well as derivatives, not only formulas are used, but also some rules. They are directly related to the corresponding rules for computing derivatives.

We know that the derivative of a sum is equal to the sum of the derivatives. This rule generates the corresponding rule for finding antiderivatives.

Rule 1 The antiderivative of a sum is equal to the sum of antiderivatives.

We know that the constant factor can be taken out of the sign of the derivative. This rule generates the corresponding rule for finding antiderivatives.

Rule 2 If F(x) is an antiderivative for f(x), then kF(x) is an antiderivative for kf(x).

Theorem 1. If y = F(x) is the antiderivative for the function y = f(x), then the antiderivative for the function y = f(kx + m) is the function $y=\frac(1)(k)F(kx+m) $

Theorem 2. If y = F(x) is an antiderivative for a function y = f(x) on an interval X, then the function y = f(x) has infinitely many antiderivatives, and they all have the form y = F(x) + C.

Integration methods

Variable replacement method (substitution method)

The substitution integration method consists in introducing a new integration variable (that is, a substitution). In this case, the given integral is reduced to a new integral, which is tabular or reducible to it. General Methods substitution selection does not exist. The ability to correctly determine the substitution is acquired by practice.
Let it be required to calculate the integral $\textstyle \int F(x)dx $. Let's make a substitution $x= \varphi(t) $ where $\varphi(t) $ is a function that has a continuous derivative.
Then $dx = \varphi " (t) \cdot dt $ and based on the invariance property of the indefinite integral integration formula, we obtain the substitution integration formula:
$\int F(x) dx = \int F(\varphi(t)) \cdot \varphi " (t) dt $

Integration of expressions like $\textstyle \int \sin^n x \cos^m x dx $

If m is odd, m > 0, then it is more convenient to make the substitution sin x = t.
If n is odd, n > 0, then it is more convenient to make the substitution cos x = t.
If n and m are even, then it is more convenient to make the substitution tg x = t.

Integration by parts

Integration by parts - applying the following formula for integration:
$\textstyle \int u \cdot dv = u \cdot v - \int v \cdot du $
or:
$\textstyle \int u \cdot v" \cdot dx = u \cdot v - \int v \cdot u" \cdot dx $

Table of indefinite integrals (antiderivatives) of some functions

$$ \int 0 \cdot dx = C $$ $$ \int 1 \cdot dx = x+C $$ $$ \int x^n dx = \frac(x^(n+1))(n+1 ) +C \;\; (n \neq -1) $$ $$ \int \frac(1)(x) dx = \ln |x| +C $$ $$ \int e^x dx = e^x +C $$ $$ \int a^x dx = \frac(a^x)(\ln a) +C \;\; (a>0, \;\; a \neq 1) $$ $$ \int \cos x dx = \sin x +C $$ $$ \int \sin x dx = -\cos x +C $$ $ $ \int \frac(dx)(\cos^2 x) = \text(tg) x +C $$ $$ \int \frac(dx)(\sin^2 x) = -\text(ctg) x +C $$ $$ \int \frac(dx)(\sqrt(1-x^2)) = \text(arcsin) x +C $$ $$ \int \frac(dx)(1+x^2 ) = \text(arctg) x +C $$ $$ \int \text(ch) x dx = \text(sh) x +C $$ $$ \int \text(sh) x dx = \text(ch )x+C $$

Is it possible to bring a non-linear function under the differential sign? Yes, if the integrand is a product of two factors: one factor is a complex function of some non-linear function, and the other factor is the derivative of this non-linear function. Let's look at the examples.

Find indefinite integrals.

Example 1. ∫(2x + 1)(x 2 + x + 2) 5 dx = ∫(x 2 + x + 2) 5 d (x 2 + x + 2) =(x²+x+2) 6 : 6+C.

What is this integrand? Work power function from (x 2 + x + 2) and the factor (2x + 1), which is equal to the derivative of the base of the degree: (x 2 + x + 2) "= 2x + 1.

This allowed us to bring (2x + 1) under the differential sign:

∫u 5 du=u 6 : 6+ C. (Formula 1). )

Examination. (F (x) + C)" = ((x² + x + 2) 6 : 6 + C)′=1/6 6 (x 2 + x + 2) 5 (x 2 + x + 2)" =

\u003d (x 2 + x + 2) 5 (2x + 1) \u003d (2x + 1) (x 2 + x + 2) 5 \u003d f (x).

Example 2∫(3x 2 - 2x + 3)(x 3 - x 2 + 3x + 1) 5 dx = ∫(x 3 - x 2 + 3x + 1) 5 d (x 3 - x 2 + 3x + 1) =

=(x³- x²+3x+1) 6 : 6+C

How is this example different from example 1? Nothing! The same fifth degree with the base (x 3 - x 2 + 3x + 1) is multiplied by the trinomial (3x 2 - 2x + 3), which is the derivative of the base of the degree: (x 3 - x 2 + 3x + 1) "= 3x 2 - 2x + 3. We brought this base of the degree under the differential sign, from which the value of the integrand did not change, and then applied the same formula 1).( Integrals)

Example 3

Here the derivative of (2x 3 - 3x) will give (6x 2 - 3), and we have

there is (12x 2 - 6), that is, the expression in 2 times greater, then let's sum (2x 3 - 3x) under the sign of the differential, and put the factor before the integral 2 . Let's apply the formula 2) ( sheet ).

Here's what happens:

Let's check, considering that:

Examples. Find indefinite integrals.

1. ∫(6x+5) 3 dx. How will we decide? Look at the sheet and we argue something like this: the integrand is a degree, and we have a formula for the degree integral (the formula 1) ), but in it the base of the degree u and integration variable too u.

And we have an integration variable X, and the base of the degree (6x+5). Let's make a change of the integration variable: instead of dx we write d (6x+5). What changed? Since, what comes after the differential sign d, by default, is differentiated,

then d (6x+5)=6dx, i.e. when the variable x is replaced by the variable (6x + 5), the integrand has increased by 6 times, so we put the factor 1/6 in front of the integral sign. You can write these arguments like this:

So, we solved this example by introducing a new variable (the variable x was replaced by the variable 6x+5). And where did you write the new variable (6x + 5)? Under the sign of the differential. So, this method introducing a new variable is often called method ( or way ) summing up(new variable ) under the differential sign.

In the second example, we first obtained a degree with negative indicator, and then brought under the sign of the differential (7x-2) and used the formula of the degree integral 1) (Integrals ).

Let's take an example solution 3.

The integral is preceded by the coefficient 1/5. Why? Since d (5x-2)=5dx, then, substituting the function u=5x-2 under the differential sign, we increased the integrand by 5 times, therefore, in order for the value of this expression not to change, it was necessary to divide by 5, i.e. . multiply by 1/5. Next, the formula was used 2) (integrals) .

All the simplest integral formulas will look like:

∫f (x) dx=F (x)+C, and the following equality must hold:

(F(x)+C)"=f(x).

Integration formulas can be obtained by inverting the corresponding differentiation formulas.

Really,

Exponent n may be fractional. Often you have to find the indefinite integral of the function y=√x. Calculate the integral of the function f (x)=√x using the formula 1) .

Let's write this example as a formula 2) .

Since (x+C)"=1, then ∫dx=x+C.

3) ∫dx=x+C.

Replacing 1 / x² by x -2, we calculate the integral of 1 / x².

And you could get this answer by appealing known formula differentiation:

We write our reasoning in the form of a formula 4).

Multiplying both sides of the resulting equality by 2, we obtain the formula 5).

Let's find the integrals of the main trigonometric functions, knowing their derivatives: (sinx)"=cosx; (cosx)"=-sinx; (tgx)"=1/cos²x; (ctgx)"=-1/sin²x. We get integration formulas 6) — 9).

6) ∫cosxdx=sinx+C;

7) ∫sinxdx=-cosx+C;

After studying the demonstration and logarithmic functions Let's add some more formulas.

Basic properties of the indefinite integral.

I. The derivative of the indefinite integral is equal to the integrand .

(∫f(x)dx)"=f(x).

II. The differential of the indefinite integral is equal to the integrand.

d∫f (x) dx=f (x) dx.

III. Indefinite integral of differential (derivative) of some function is equal to the sum this function and an arbitrary constant C.

∫dF(x)=F(x)+C or ∫F"(x) dx=F(x)+C.

Pay attention: in I, II and III properties, the signs of the differential and integral (integral and differential) "eat" each other!

IV. The constant factor of the integrand can be taken out of the integral sign.

∫kf (x) dx=k ∫f (x) dx, where k - constant, not equal to zero.

v. The integral of the algebraic sum of functions is equal to the algebraic sum of the integrals of these functions.

∫(f (x)±g (x)) dx=∫f (x) dx±∫g (x) dx.

VI. If F(x) is an antiderivative for f(x) and k and b are constant values, and, k≠0, then (1/k) F (kx+b) is the antiderivative for f (kx+b). Indeed, according to the rule for calculating the derivative complex function we have:

You can write:

For every mathematical action there is an inverse action. For the action of differentiation (finding derivatives of functions), there is also an inverse action - integration. By means of integration, a function is found (restored) by its given derivative or differential. The found function is called primitive.

Definition. Differentiable function F(x) is called antiderivative for the function f(x) on a given interval, if for all X from this interval the equality is true: F′(x)=f (x).

Examples. Find antiderivatives for functions: 1) f (x)=2x; 2) f(x)=3cos3x.

1) Since (x²)′=2x, then, by definition, the function F (x)=x² will be the antiderivative for the function f (x)=2x.

2) (sin3x)′=3cos3x. If we denote f (x)=3cos3x and F (x)=sin3x, then, by the definition of antiderivative, we have: F′(x)=f (x), and, therefore, F (x)=sin3x is an antiderivative for f ( x)=3cos3x.

Note that and (sin3x +5 )′= 3cos3x, and (sin3x -8,2 )′= 3cos3x, ... in general form, we can write: (sin3x +C)′= 3cos3x, where With is some constant value. These examples speak of the ambiguity of the action of integration, in contrast to the action of differentiation, when any differentiable function has a single derivative.

Definition. If the function F(x) is the antiderivative for the function f(x) on some interval, then the set of all antiderivatives of this function has the form:

F(x)+C where C is any real number.

The set of all antiderivatives F (x) + C of the function f (x) on the interval under consideration is called the indefinite integral and is denoted by the symbol ∫ (integral sign). Write down: ∫f (x) dx=F (x)+C.

Expression ∫f(x)dx read: "the integral ef from x to de x".

f(x)dx is the integrand,

f(x) is the integrand,

X is the integration variable.

F(x) is the antiderivative for the function f(x),

With is some constant value.

Now the considered examples can be written as follows:

1) ∫ 2хdx=x²+C. 2) ∫ 3cos3xdx=sin3x+C.

What does the sign d mean?

d- differential sign - has a dual purpose: firstly, this sign separates the integrand from the integration variable; secondly, everything after this sign is differentiated by default and multiplied by the integrand.

Examples. Find integrals: 3) ∫ 2pxdx; 4) ∫ 2pxdp.

3) After differential icon d costs XX, a R

∫ 2хрdx=px²+С. Compare with example 1).

Let's do a check. F′(x)=(px²+C)′=p (x²)′+C′=p 2x=2px=f (x).

4) After differential icon d costs R. So the integration variable R, and the multiplier X should be considered as a constant value.

∫ 2хрdр=р²х+С. Compare with examples 1) and 3).

Let's do a check. F′(p)=(p²x+C)′=x (p²)′+C′=x 2p=2px=f (p).

Page 1 of 1 1