Find the probability of the specified event using the Bernoulli formula. Bernoulli scheme

Let's not think about the lofty for a long time - let's start right away with a definition.

is when n independent experiments of the same type are performed, in each of which an event A of interest to us may appear, and the probability of this event P(A) = p is known. It is required to determine the probability that event A will occur exactly k times during n trials.

The tasks that are solved according to the Bernoulli scheme are extremely diverse: from simple ones (such as “find the probability that the shooter hits 1 time out of 10”) to very severe ones (for example, tasks for percentages or playing cards). In reality, this scheme is often used to solve problems related to product quality control and the reliability of various mechanisms, all the characteristics of which must be known before starting work.

Let's go back to the definition. Since we are talking about independent trials, and in each trial the probability of the event A is the same, only two outcomes are possible:

A is the occurrence of event A with probability p;
"not A" - event A did not appear, which happens with probability q = 1 − p.

The most important condition without which the Bernoulli scheme loses its meaning is constancy. No matter how many experiments we conduct, we are interested in the same event A, which occurs with the same probability p.

Incidentally, not all problems in probability theory can be reduced to constant conditions. Any competent tutor in higher mathematics will tell you about this. Even something as simple as picking colored balls out of a box is not an experiment with constant conditions. They took out another ball - the ratio of colors in the box changed. Therefore, the probabilities have also changed.

If the conditions are constant, one can accurately determine the probability that event A will occur exactly k times out of n possible. We formulate this fact in the form of a theorem:

Let the probability of occurrence of event A in each experiment be constant and equal to p. Then the probability that in n independent trials event A will appear exactly k times is calculated by the formula:

where C n k is the number of combinations, q = 1 − p.

This formula is called: It is interesting to note that the problems below are completely solved without using this formula. For example, you can apply probability addition formulas. However, the amount of computation will be simply unrealistic.

Task. The probability of producing a defective product on the machine is 0.2. Determine the probability that in a batch of ten parts produced on a given machine exactly k will be without defects. Solve the problem for k = 0, 1, 10.

By assumption, we are interested in the event A of the release of products without defects, which happens each time with a probability p = 1 − 0.2 = 0.8. We need to determine the probability that this event will occur k times. Event A is opposed to the event "not A", i.e. production of a defective product.

Thus, we have: n = 10; p=0.8; q = 0.2.

So, we find the probability that all parts in the batch are defective (k = 0), that only one part is defective (k = 1), and that there are no defective parts at all (k = 10):

Task. The coin is tossed 6 times. The loss of the coat of arms and tails is equally probable. Find the probability that:

the coat of arms will drop three times;

the coat of arms will drop once;

the coat of arms will appear at least twice.

So, we are interested in the event A, when the coat of arms falls out. The probability of this event is p = 0.5. The event A is countered by the event “not A”, when it comes up tails, which happens with the probability q = 1 − 0.5 = 0.5. It is necessary to determine the probability that the coat of arms will fall out k times.

Thus, we have: n = 6; p = 0.5; q = 0.5.

Let us determine the probability that the coat of arms fell out three times, i.e. k = 3:

Now let's determine the probability that the coat of arms fell out only once, i.e. k = 1:

It remains to determine with what probability the coat of arms will fall out at least twice. The main snag is in the phrase “no less”. It turns out that any k, except for 0 and 1, will suit us, i.e. you need to find the value of the sum X \u003d P 6 (2) + P 6 (3) + ... + P 6 (6).

Note that this sum is also equal to (1 − P 6 (0) − P 6 (1)), i.e. out of all possible options, it is enough to “cut out” those when the coat of arms fell out 1 time (k = 1) or did not fall out at all (k = 0). Since P 6 (1) we already know, it remains to find P 6 (0):

Task. The probability that a TV has hidden defects is 0.2. The warehouse received 20 TVs. Which event is more likely: that there are two TVs with hidden defects in this batch or three?

Event of interest A is the presence of a latent defect. Total TVs n = 20, the probability of a hidden defect p = 0.2. Accordingly, the probability of getting a TV set without a hidden defect is q = 1 − 0.2 = 0.8.

We get the starting conditions for the Bernoulli scheme: n = 20; p = 0.2; q = 0.8.

Let's find the probability of getting two "defective" TVs (k = 2) and three (k = 3):

\[\begin(array)(l)(P_(20))\left(2 \right) = C_(20)^2(p^2)(q^(18)) = \frac((20}{{2!18!}} \cdot {0,2^2} \cdot {0,8^{18}} \approx 0,137\\{P_{20}}\left(3 \right) = C_{20}^3{p^3}{q^{17}} = \frac{{20!}}{{3!17!}} \cdot {0,2^3} \cdot {0,8^{17}} \approx 0,41\end{array}\]!}

Obviously, P 20 (3) > P 20 (2), i.e. the probability of getting three TVs with hidden defects is more likely to get only two such TVs. Moreover, the difference is not weak.

A small note about factorials. Many people experience a vague feeling of discomfort when they see the entry "0!" (read "zero factorial"). So, 0! = 1 by definition.

P.S. And the biggest probability in the last task is to get four TVs with hidden defects. Do the math and see for yourself.

Online calculators for the Bernoulli formula

Some of the most popular types of problems that use the Bernoulli formula are analyzed in articles and provided with an online calculator, you can go to them using the links:

Examples of solutions to problems on the Bernoulli formula

Example. An urn contains 20 white and 10 black balls. 4 balls are taken out, and each ball taken out is returned to the urn before the next one is drawn and the balls in the urn are mixed.

Bernoulli formula. Problem solving

Find the probability that 2 of the 4 balls drawn are white.

Decision. Event BUT- got a white ball. Then the probabilities
, .
According to the Bernoulli formula, the required probability is
.

Example. Determine the probability that a family with 5 children will have no more than 3 girls. The probabilities of having a boy and a girl are assumed to be the same.

Decision. The probability of having a girl
, then .

Let's find the probabilities that there are no girls in the family, one, two or three girls were born:

, ,

, .

Therefore, the desired probability

Example. Among the parts processed by the worker, there are on average 4% non-standard. Find the probability that two of the 30 parts taken for testing will be non-standard.

Decision. Here the experience lies in checking each of the 30 parts for quality.

Event A is “the appearance of a non-standard part”, its probability is , then . From here, by the Bernoulli formula, we find
.

Example. For each individual shot from the gun, the probability of hitting the target is 0.9. Find the probability that out of 20 shots the number of successful shots will be at least 16 and at most 19.

Decision. We calculate by the Bernoulli formula:

Example. Independent trials continue until the event BUT will not happen k once. Find the probability that it will take n trials (n ³ k), if in each of them .

Decision. Event AT- exactly n tests before k-th occurrence of the event BUT is the product of the following two events:

D-in n th test BUT happened;

C - first (n–1) th test BUT appeared (k-1) once.

The multiplication theorem and Bernoulli's formula give the required probability:

It should be noted that the use of the binomial law is often associated with computational difficulties. Therefore, with increasing values n and m it becomes expedient to use approximate formulas (Poisson, Moivre-Laplace), which will be discussed in the following sections.

Video tutorial Bernoulli's formula

For those who are more visual in a sequential video explanation, a 15-minute video:

Total Probability Formula: Theory and Examples of Problem Solving

Total probability formula and conditional probabilities of events

Total Probability Formula is a consequence of the basic rules of probability theory - the rule of addition and the rule of multiplication.

The total probability formula allows you to find the probability of an event A, which can occur only with each of n mutually exclusive events that form a complete system if their probabilities are known, and conditional probabilities events A with respect to each of the events of the system are equal to .

Events are also called hypotheses, they are mutually exclusive. Therefore, in the literature you can also find their designation not by the letter B, but with a letter H(hypothesis).

To solve problems with such conditions, it is necessary to consider 3, 4, 5, or in the general case n the possibility of an event A with every event.

Using the theorems of addition and multiplication of probabilities, we obtain the sum of the products of the probability of each of the events of the system by conditional probability events A for each event in the system.

21 Trials of Bernoulli. Bernoulli formula

That is, the probability of an event A can be calculated by the formula

or in general

which is called total probability formula .

Total probability formula: examples of problem solving

Example 1 There are three identical-looking urns: in the first one there are 2 white balls and 3 black ones, in the second one there are 4 white ones and one black one, in the third one there are three white balls. Someone randomly approaches one of the urns and takes one ball out of it. Taking advantage total probability formula, find the probability that the ball is white.

Decision. Event A- the appearance of a white ball. We put forward three hypotheses:

— the first urn is selected;

— the second urn is chosen;

— the third urn is chosen.

Conditional event probabilities A for each of the hypotheses:

, , .

We apply the total probability formula, as a result - the required probability:

Example 2 At the first plant, out of every 100 light bulbs, an average of 90 standard ones are produced, at the second - 95, at the third - 85, and the products of these factories account for 50%, 30% and 20%, respectively, of all electric bulbs supplied to the shops of a certain area. Find the probability of purchasing a standard light bulb.

Decision. Let us denote the probability of acquiring a standard light bulb as A, and the events that the purchased light bulb was manufactured at the first, second and third factories, respectively, through . By condition, the probabilities of these events are known: , , and the conditional probabilities of the event A regarding each of them: , , . These are the probabilities of acquiring a standard light bulb, provided that it is manufactured at the first, second, and third factories, respectively.

Event A will occur if an event occurs or K– the light bulb is made at the first factory and is standard, or an event L- the light bulb is made at the second factory and is standard, or an event M- the light bulb is manufactured at the third factory and is standard.

Other possibilities for the occurrence of the event A no. Therefore, the event A is the sum of events K, L and M that are incompatible. Applying the probability addition theorem, we represent the probability of an event A as

and by the probability multiplication theorem we get

i.e, a special case of the total probability formula.

Substituting the probabilities into the left side of the formula, we obtain the probability of the event A:

Don't have time to delve into the solution? You can order a job!

Example 3 The aircraft is landing at the airport. If the weather allows, the pilot lands the plane, using, in addition to instruments, also visual observation. In this case, the probability of a successful landing is . If the airfield is overcast with low clouds, then the pilot lands the plane, orienting himself only on instruments. In this case, the probability of a successful landing is ; .

Devices that provide blind landing have reliability (probability of failure-free operation) P. In the presence of low cloudiness and failed blind landing instruments, the probability of a successful landing is ; . Statistics show that in k% of landings, the airfield is covered with low clouds. To find full probability of the eventA- safe landing of the aircraft.

Decision. Hypotheses:

— no low clouds;

- There is low cloud cover.

The probabilities of these hypotheses (events):

;

Conditional Probability.

The conditional probability is again found by the formula for the total probability with hypotheses

- blind landing devices are working;

- blind landing devices failed.

The probabilities of these hypotheses are:

According to the total probability formula

Example 4 The device can operate in two modes: normal and abnormal. Normal mode is observed in 80% of all cases of operation of the device, and abnormal - in 20% of cases. Probability of device failure in a certain time t equal to 0.1; in the abnormal 0.7. To find full probability device failure in time t.

Decision. We again denote the probability of device failure as A. So, regarding the operation of the device in each mode (events), the probabilities are known by condition: for the normal mode it is 80% (), for the abnormal mode - 20% (). Event Probability A(that is, the failure of the device) depending on the first event (normal mode) is 0.1 (); depending on the second event (abnormal mode) - 0.7 ( ). We substitute these values into the total probability formula (that is, the sum of the products of the probability of each of the events of the system and the conditional probability of the event A with respect to each of the events of the system) and we have the required result.

Let's not think about the lofty for a long time - let's start right away with a definition.

The Bernoulli scheme is when n independent experiments of the same type are performed, in each of which an event of interest to us A may appear, and the probability of this event is known P (A) \u003d p. It is required to determine the probability that event A will occur exactly k times during n trials.

Let's go back to the definition. Since we are talking about independent trials, and in each trial the probability of the event A is the same, only two outcomes are possible:

A is the occurrence of event A with probability p;
"not A" - event A did not appear, which happens with probability q = 1 − p.

The most important condition without which the Bernoulli scheme loses its meaning is constancy. No matter how many experiments we conduct, we are interested in the same event A that occurs with the same probability p.

If the conditions are constant, one can accurately determine the probability that event A will occur exactly k times out of n possible. We formulate this fact in the form of a theorem:

Bernoulli's theorem. Let the probability of occurrence of event A in each experiment be constant and equal to p. Then the probability that in n independent trials event A will appear exactly k times is calculated by the formula:

where C n k is the number of combinations, q = 1 − p.

This formula is called the Bernoulli formula. It is interesting to note that the problems below are completely solved without using this formula. For example, you can apply probability addition formulas. However, the amount of computation will be simply unrealistic.

Task. The probability of producing a defective product on the machine is 0.2. Determine the probability that in a batch of ten parts produced on a given machine exactly k will be without defects. Solve the problem for k = 0, 1, 10.

Thus, we have: n = 10; p=0.8; q = 0.2.

So, we find the probability that all parts in the batch are defective (k = 0), that only one part is defective (k = 1), and that there are no defective parts at all (k = 10):

Task. The coin is tossed 6 times. The loss of the coat of arms and tails is equally probable. Find the probability that:

the coat of arms will drop three times;

the coat of arms will drop once;

the coat of arms will appear at least twice.

So, we are interested in the event A when the coat of arms falls. The probability of this event is p = 0.5. The event A is countered by the event “not A”, when it comes up tails, which happens with the probability q = 1 − 0.5 = 0.5. It is necessary to determine the probability that the coat of arms will fall out k times.

Thus, we have: n = 6; p = 0.5; q = 0.5.

Let us determine the probability that the coat of arms fell out three times, i.e. k = 3:

Now let's determine the probability that the coat of arms fell out only once, i.e. k = 1:

It remains to determine with what probability the coat of arms will fall out at least twice. The main snag is in the phrase “no less”. It turns out that any k will suit us, except for 0 and 1, i.e. you need to find the value of the sum X \u003d P 6 (2) + P 6 (3) + ... + P 6 (6).

Task. The probability that a TV has hidden defects is 0.2. The warehouse received 20 TVs. Which event is more likely: that there are two TVs with hidden defects in this batch or three?

We get the starting conditions for the Bernoulli scheme: n = 20; p = 0.2; q = 0.8.

Let's find the probability of getting two "defective" TVs (k = 2) and three (k = 3):

Obviously, P 20 (3) > P 20 (2), i.e. the probability of getting three TVs with hidden defects is more likely to get only two such TVs. Moreover, the difference is not weak.

A small note about factorials. Many people experience a vague feeling of discomfort when they see the entry "0!" (read "zero factorial"). So, 0! = 1 by definition.

P. S. And the biggest probability in the last task is to get four TVs with hidden defects. Do the math and see for yourself.

Before presenting the third question of the lecture, the teacher indicates the problem that necessitates the consideration of the theorem on the repetition of experiments, while noting that in the course of probability theory being studied, only a particular theorem will be considered related to the repetition of independent experiments, in each of which the event A appears with a constant probability.

Then the teacher shows the proof of this theorem (the derivation of the Bernoulli formula).

To explain the physical essence of the theorem under consideration, the teacher uses an overhead projector and prepared slides.

At the end of the lecture, the teacher explains why the probability distribution of the occurrence of event A in a series of n trials, when they are incompatible and form a complete group of events, is called binomial and draws attention to the importance of knowing this distribution for solving applied problems.

So far, we have considered combinations of a relatively small number of events, when the direct application of the rules of addition and multiplication of probabilities did not cause great computational difficulties. However, with an increase in the number of events or the number of trials in which the event of interest to us may appear, the studied method of calculation becomes very cumbersome.

In this case, the problem was solved quite simply only if the experiments were independent.

Several experiments are called independent, if the probability of one or another outcome of each of the experiments does not depend on what outcomes the other experiments had.

In practice, there are cases when the probability of an event occurring BUT in all independent experiments can be either the same or change from experience to experience. For example, when adjusting the fire after each shot, the probability of hitting the target with each shot will change.

In the case when in independent experiments the probability of the occurrence of an event from experience to experience changes, the general theorem on the repetition of experiments is used, and when in independent experiments the probability of the occurrence of an event from experience to experience does not change, the particular theorem on the repetition of experiments is used.

In the course of probability theory we are studying, we will consider only a particular term about the repetition of experiments, when it is necessary to determine the probability of an event occurring BUT in a series of n independent experiments, in each of which event A occurs with the same probability.

For example, it is necessary to calculate the probability that with five shots from a gun at constant settings, exactly two hits will be received on the target, if the shots are independent and for each shot the probability of hitting the target is known and does not change.

If we make possible combinations of the occurrence of the event of interest to us A 1, then we get:

There will be 10 possible combinations in which the event A = (get 2 hits with five shots) will occur.

Applying the theorem on the sum and product of independent events, we will have:

An increase in the number of events of interest to us or the number of tests will lead to an even greater increase in the volume of computational operations, so the problem arises of finding less time-consuming methods of calculation.

Formulation of the problem:

Let it be assumed under the same conditions to carry out n independent tests, the result of each of which may be the onset or events BUT, or its opposite .

Denote by BUT 1 occurrence of an event BUT on the first test, BUT 2 - at the second test, BUT n- at the last test.

Due to the constancy of the test conditions:

P(A 1 ) = P(A 2 ) = … P(A n ) = p

We are interested in the probability that event A will occur exactly once during n trials, and will not occur in the remaining n-trials (i.e., the event opposite to event A will occur - ).

Let us assume that the event of interest to us BUT occurs in a row m times, starting from the first, i.e. an event takes place E.

E=A 1 BUT 2 … BUT m -1 BUT m 
(1)

m n- m

According to the test repetition condition, the events included in this combination are independent, while the probabilities of occurrence of events A 1 , BUT 2 ,… BUT m -1 , BUT m the same and equal p: P(A 1 ) = P(A 2 ) =…= P(A m ) = p, and the probabilities of not the occurrence of events
are the same and equal q=1-p:.

Applying the rule of multiplication of probabilities for independent events to expression 1, we get:

P(E) = P(A 1 ) P(A 2 ) … P(A m -1 ) P(A m ) R(
= p m (1-r) n  - m = p m q n - m

Due to the constancy of the test conditions, we assumed that the event of interest to us BUT occurs consecutively m times, starting from the first. But the event BUT in n trials can come exactly m times in various sequences or combinations. At the same time, we do not care in what particular sequence the event A appears exactly m once.

The number of such combinations is equal to the number of combinations from n elements by m.

Since these combinations of events (like combinations E) are incompatible and we are not interested in the sequence of occurrence of the event BUT exactly in the test m times, then denoting the probability of interest to us through R m, we get:

R m =
R m (1-r) n - m =
=

where
- number of combinations of n elements by m.

This formula is named after Bernoulli's formula.

The Bernoulli formula allows you to get an answer to the question: what is the probability that, when repeating n independent trials, some event BUT comes exactly m times if in each of these trials the probability of the event occurring is BUT constant and equal P(A) = p.

The above Bernoulli formula is of exceptional importance in the theory of probability for the reason that it is associated with the repetition of tests under the same conditions, i.e. with such conditions in which the laws of probability theory manifest themselves.

Lecture conclusion:

In the lecture, we considered the fundamental issues of probability theory in relation to random variables, introduced the basic conceptual apparatus necessary for further study of the discipline: the definition of a random variable, their classification; concepts of distribution law and its form for various types of random variable.

In preparation for subsequent lectures and practical exercises, you must independently supplement your lecture notes with an in-depth study of the recommended literature and solving the proposed problems.

In addition, in subsequent lessons we will study theorems and dependencies that allow us to determine the probability of a random variable occurring the required number of times or at a certain interval, for example, the probability of hitting a target.

Explore:

Wentzel E.S. Probability Theory. Textbook. Eighth edition, stereotypical. - M .: Higher School, 2002 - 575 p. – pp. 67-78, 80-84

Venttsel E.S., Ovcharov L.A. Probability theory and its engineering applications. Tutorial. Third edition, revised and enlarged. - M .: "Academy", 2003 - 464 p. – pp. 73-93

Gmurman V.E. Theory of Probability and Mathematical Statistics. Tutorial. Tenth edition, stereotypical.-M.: Higher school, 2004 - 480 p. pp 64-73

In this lesson, we will find the probability of an event occurring in independent trials when the trials are repeated. . Trials are called independent if the probability of one or another outcome of each trial does not depend on what outcomes other trials had. . Independent tests can be carried out both under the same conditions and under different conditions. In the first case, the probability of an event occurring in all trials is the same; in the second case, it varies from trial to trial.

Examples of Independent Retests :

one of the device nodes or two or three nodes will fail, and the failure of each node does not depend on the other node, and the probability of failure of one node is constant in all tests;
a part produced under certain constant technological conditions, or three, four, five parts, will turn out to be non-standard, and one part may turn out to be non-standard regardless of any other part, and the probability that the part will turn out to be non-standard is constant in all tests;
out of several shots on the target, one, three or four shots hit the target regardless of the outcome of other shots and the probability of hitting the target is constant in all trials;
when the coin is inserted, the machine will operate correctly one, two, or another number of times, regardless of what the other coin insertions have had, and the probability that the machine will operate correctly is constant in all trials.

These events can be described by one scheme. Each event occurs in each trial with the same probability, which does not change if the results of previous trials become known. Such tests are called independent, and the scheme is called Bernoulli scheme . It is assumed that such tests can be repeated as many times as desired.

If the probability p event A is constant in each trial, then the probability that in n independent test event A will come m times, located on Bernoulli formula :

(where q= 1 – p- the probability that the event will not occur)

Let's set the task - to find the probability that an event of this type in n independent trials will come m once.

Bernoulli formula: examples of problem solving

Example 1 Find the probability that among five randomly selected parts two are standard, if the probability that each part is standard is 0.9.

Decision. Event Probability BUT, consisting in the fact that a part taken at random is standard, is p=0.9 , and the probability that it is non-standard is q=1–p=0.1 . The event indicated in the condition of the problem (we denote it by AT) occurs if, for example, the first two parts are standard, and the next three are non-standard. But the event AT also occurs if the first and third parts are standard and the rest are non-standard, or if the second and fifth parts are standard and the rest are non-standard. There are other possibilities for the event to occur. AT. Any of them is characterized by the fact that out of five parts taken, two, occupying any places out of five, will turn out to be standard. Therefore, the total number of different possibilities for the occurrence of an event AT is equal to the number of possibilities for placing two standard parts in five places, i.e. is equal to the number of combinations of five elements by two, and .

The probability of each possibility, according to the probability multiplication theorem, is equal to the product of five factors, of which two, corresponding to the appearance of standard parts, are equal to 0.9, and the remaining three, corresponding to the appearance of non-standard parts, are equal to 0.1, i.e. this probability is . Since these ten possibilities are incompatible events, by the addition theorem, the probability of an event AT, which we denote

Example 2 The probability that the machine will require the attention of a worker within an hour is 0.6. Assuming that the failures on the machines are independent, find the probability that during an hour the attention of the worker will be required by any one of the four machines serviced by him.

Decision. Using Bernoulli's formula at n=4 , m=1 , p=0.6 and q=1–p=0.4 , we get

Example 3 For the normal operation of the car depot, there must be at least eight cars on the line, and there are ten of them. The probability of non-exit of each car to the line is equal to 0.1. Find the probability of normal operation of the depot in the next day.

Decision. Autobase will work fine (event F) if either or eight will enter the line (the event BUT), or nine (event AT), or all ten cars event (event C). According to the probability addition theorem,

We find each term according to the Bernoulli formula. Here n=10 , m=8; 10 and p\u003d 1-0.1 \u003d 0.9, since p should mean the probability of a car entering the line; then q=0.1 . As a result, we get

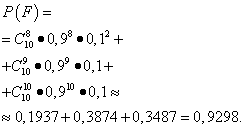
Example 4 Let the probability that a customer needs a size 41 men's shoe be 0.25. Find the probability that out of six buyers at least two need shoes of size 41.

Let n trials be carried out with respect to the event A. Let's introduce the following events: Аk -- event А was realized during the k-th test, $ k=1,2,\dots , n$. Then $\bar(A)_(k) $ is the opposite event (event A did not occur during the k-th trial, $k=1,2,\dots , n$).

What are peer and independent trials

Definition

Tests are called of the same type with respect to event A if the probabilities of the events $A1, A2, \dots , An$ are the same: $P(A1)=P(A2)= \dots =P(An)$ (i.e., the probability of occurrence event A in one trial is constant in all trials).

Obviously, in this case, the probabilities of opposite events also coincide: $P(\bar(A)_(1))=P(\bar(A)_(2))=...=P(\bar(A) _(n))$.

Definition

Trials are called independent with respect to event A if the events $A1, A2, \dots , An$ are independent.

In this case

In this case, equality is preserved when any event Ak is replaced by $\bar(A)_(k) $.

Let a series of n similar independent trials be conducted with respect to event A. We carry the notation: p - the probability of the event A in one test; q is the probability of the opposite event. Thus P(Ak)=p, $P(\bar(A)_(k))=q$ for any k and p+q=1.

The probability that in a series of n trials event A will occur exactly k times (0 ≤ k ≤ n) is calculated by the formula:

$P_(n) (k)=C_(n)^(k) p^(k) q^(n-k) $ (1)

Equality (1) is called the Bernoulli formula.

The probability that in a series of n independent trials of the same type event A will occur at least k1 times and at most k2 times is calculated by the formula:

$P_(n) (k_(1) \le k\le k_(2))=\sum \limits _(k=k_(1) )^(k_(2) )C_(n)^(k) p ^(k) q^(n-k) $ (2)

Application of the Bernoulli formula for large values of n leads to cumbersome calculations, so in these cases it is better to use other formulas - asymptotic ones.

Generalization of the Bernoulli scheme

Consider a generalization of the Bernoulli scheme. If in a series of n independent trials, each of which has m pairwise incompatible and possible results Ak with corresponding probabilities Рk= рk(Аk). Then the polynomial distribution formula is valid:

Example 1

The probability of getting the flu during an epidemic is 0.4. Find the probability that out of 6 employees of the company will fall ill

exactly 4 employees;
no more than 4 employees.

Decision. 1) Obviously, to solve this problem, the Bernoulli formula is applicable, where n=6; k=4; p=0.4; q=1-p=0.6. Applying formula (1), we get: $P_(6) (4)=C_(6)^(4) \cdot 0.4^(4) \cdot 0.6^(2) \approx 0.138$.

To solve this problem, formula (2) is applicable, where k1=0 and k2=4. We have:

\[\begin(array)(l) (P_(6) (0\le k\le 4)=\sum \limits _(k=0)^(4)C_(6)^(k) p^( k) q^(6-k) =C_(6)^(0) \cdot 0.4^(0) \cdot 0.6^(6) +C_(6)^(1) \cdot 0.4 ^(1) \cdot 0.6^(5) +C_(6)^(2) \cdot 0.4^(2) \cdot 0.6^(4) +) \\ (+C_(6) ^(3) \cdot 0.4^(3) \cdot 0.6^(3) +C_(6)^(4) \cdot 0.4^(4) \cdot 0.6^(2) \ approx 0.959.) \end(array)\]

It should be noted that this task is easier to solve using the opposite event - more than 4 employees fell ill. Then, taking into account formula (7) on the probabilities of opposite events, we obtain:

Answer: $\ $0.959.

Example 2

An urn contains 20 white and 10 black balls. 4 balls are taken out, and each ball taken out is returned to the urn before the next one is drawn and the balls in the urn are mixed. Find the probability that out of the four balls drawn there will be 2 white balls in Figure 1.

Picture 1.

Decision. Let the event A be that -- a white ball is drawn. Then the probabilities $D (A)=\frac(2)(3) ,\, \, D (\overline(A))=1-\frac(2)(3) =\frac(1)(3) $ .

According to the Bernoulli formula, the required probability is $D_(4) (2)=N_(4)^(2) \left(\frac(2)(3) \right)^(2) \left(\frac(1)( 3) \right)^(2) =\frac(8)(27) $.

Answer: $\frac(8)(27) $.

Example 3

Determine the probability that a family with 5 children will have no more than 3 girls. The probabilities of having a boy and a girl are assumed to be the same.

Decision. Probability of having a girl $\partial =\frac(1)(2) ,\, q=\frac(1)(2) $-probability of having a boy. There are no more than three girls in a family, which means that either one, or two, or three girls were born, or all boys in the family.

Find the probabilities that there are no girls in the family, one, two or three girls were born: $D_(5) (0)=q^(5) =\frac(1)(32) $,

\ \ \

Therefore, the required probability is $D =D_(5) (0)+D_(5) (1)+D_(5) (2)+D_(5) (3)=\frac(13)(16) $.

Answer: $\frac(13)(16)$.

Example 4

The first shooter with one shot can hit the top ten with a probability of 0.6, the nine with a probability of 0.3, and the eight with a probability of 0.1. What is the probability that, with 10 shots, he will hit ten six times, nine three times, and eight eight times?