Event 2 action. Theorems of addition and multiplication of probabilities: main tasks

transcript

1 Answers = A 5 12 = A3 7 = 7 3 = a) 126; b) P(4, 5, 6) = a) P 4 = 24; b) P(2, 2) = C22 4 C2 8 = , 30, 60, Insufficient, 9, Actions on events An event is called random or possible if the outcome of the test leads to the occurrence or non-occurrence of this event. For example, the loss of a coat of arms when tossing a coin; dropping a face with a number of points equal to 3 when throwing a dice. An event is called certain if, under the test conditions, it will definitely occur. For example, extracting a white ball from an urn containing only white balls; dropping no more than 6 points when throwing a dice. An event is said to be impossible if, under the conditions of the test, it is known not to occur. For example, the loss of seven points when throwing one dice; drawing more than four aces from a regular deck of cards. Random events are denoted by Latin letters of the alphabet A, B, C and so on. Events are joint and incompatible. Events are called incompatible if, under the test conditions, the occurrence of one of them excludes the occurrence of the others. For example, the loss of a coat of arms and tails with one toss of a coin; hit and miss with one shot. Events are called joint if, under the test conditions, the occurrence of one of them does not exclude the occurrence of the others. For example, hitting a target and missing when firing two rifles at the same time; the loss of two coats of arms when throwing two coins. Events are called equally likely if, under the conditions of a given test, the probability of each of these events occurring is the same. Examples of equally probable events: the loss of a coat of arms and the loss of tails in one toss of a coin; thirteen

2 dropping a number of points from 1 to 6 when throwing one dice. The event C, which consists in the occurrence of at least one of the events A or B, is called the sum (union) of events and is denoted C = A + B (C = A B). The event C, which consists in the joint occurrence of events A and B, is called the product (intersection) of these events and is denoted C = A B (C = A B). The event C, which consists in the fact that the event a does not occur, is called the opposite event and is denoted by A. The sum of the opposite events is a certain event Ω, that is, A + A = Ω. The product of opposite events is an impossible event (V), that is, A A = V. The set of possible events forms a complete group if at least one of these events appears as a result of testing: n A i = Ω. i=1 For example, when throwing a die, dropouts from one to six points make up a complete group of events Event A of four tested light bulbs, all defective; event B all bulbs are good. What do the events mean: 1) A + B; 2) A B; 3) A; 4) B? Decision. 1) Event A is that all light bulbs are defective, and event B is that all light bulbs are good. The sum of events A + B means that all bulbs must be either defective or good. 2) Event A B bulbs must be both defective and good, so event A B is impossible. 3) A all bulbs are defective, therefore A at least one bulb is good. 4) B all bulbs are good, therefore B at least one bulb is defective. fourteen

3 2.2. One number is taken at random from a table of random numbers. Event A the selected number is divisible by 2, event B the selected number is divisible by 3. What do the events mean: 1) A+B; 2) A B; 3) A B? Decision. 1) The sum of events a + B is an event consisting in the occurrence of at least one of the events A or B, that is, a randomly chosen number must be divisible by either 2, or 3, or 6. 2) The product of events A B means that events A and B occur at the same time. Therefore, the selected number must be divisible by 6. 3) A B the selected number is not divisible by Two shooters fire one shot at the same target. Event A the first shooter hits the target; event B the second shooter hits the target. What do the events mean: a) A + B; b) A B; c) A + B; d) A B? Decision. a) Event A+B means: at least one of the shooters hits the target; b) event A B means: both arrows hit the target; c) event A+B means: at least one misses; d) events A B means: both make mistakes Two chess players play one game. Event A will be won by the first player, event B by the second player. What event should be added to the specified set to get a complete group of events? Decision. Event C draw Given two duplicate blocks a 1 and a 2. Write down the event that the system is closed. Decision. Let's introduce the following notation: A 1 event, consisting in the fact that block a 1 is serviceable; a1 a A 2 2 event that block a 2 is healthy; S is an event that the system is closed. The blocks are redundant, so the system will be closed if at least one of the blocks is working, that is, S \u003d A 1 + A A system of three blocks a 1, a 2, b is given. Write down events - 15

4 tie, consisting in the fact that the system is closed. Decision. Let's introduce the notation: A 1 a a 1 2 b the following event, consisting in the fact that block a 1 is serviceable; A 2 event that block a 2 is healthy; B an event consisting in the fact that block b is healthy; S is an event that the system is closed. Let's break the system into two parts. The closure of a system consisting of duplicate blocks, as we see, can be written as an event A 1 + A 2. For the closure of the entire system, the serviceability of block B is always required, therefore S = (A 1 + A 2) B. Problems for independent solution 2.7 . One number is taken at random from a table of random numbers. Event A selected number is divisible by 5, event B this number ends in zero. What do the events mean: 1) A+B; 2) A B; 3) A B; 4) A B? 2.8. Three shooters shoot at a target. Events: A 1 hit on the target by the first shooter; A 2 hit by the second shooter; A 3 hit by the third shooter. Make a complete group of events There are several balls of the same size but different colors in the box: white, red, blue. Event K i a red ball taken at random; event B i is white; event C i is blue. Two balls are taken out in a row (i = 1, 2 is the serial number of the balls taken out). Write down the following events: a) event A, the second ball taken at random turned out to be blue; b) event A; c) event B are both balls red? Make up a complete group of events Three shots are fired at the target. Given the events A i (i = 1, 2, 3) hitting the target during the i-th shot. Express through A i and A i the following events: 1) not a single hit in 16

5 goal; 2) one hit on the target; 3) two hits on the target; 4) three hits on the target; 5) at least one hit on the target; 6) at least one miss Are the following events incompatible: a) the experience of tossing a coin; events: A the appearance of the coat of arms, B the appearance of numbers; b) experience two shots at the target; events: And at least one hit, At least one miss Are the following events equally possible: a) the experience of tossing a coin; events: A the appearance of the coat of arms, B the appearance of numbers; b) the experience of tossing a bent coin; events: A the appearance of the coat of arms, B the appearance of numbers; c) experience: shot at a target; events: A hit, B miss Do the following events form a complete group of events: a) coin toss experience; events: A coat of arms, B figure; b) the experience of tossing two coins; events: A two coats of arms, B two numbers Throw a dice. Let's designate the events: A loss of 6 points, B loss of 3 points, C loss of an even number of points; D dropping a number of points that is a multiple of three. What are the relationships between these events? Let A, B, C be arbitrary events. What do the following events mean: ABC; ABC; A+BC; ABC+ABC+ +ABC; ABC + ABC + ABC + ABC? Through arbitrary events A, B, C, find expressions for the following events: a) only event A occurred; b) A and B happened, C did not happen; c) all three events have occurred; d) at least one of these events has occurred; e) at least two events have occurred; e) one and only one event has occurred; g) two and only two events have occurred; 17

ELEMENTS OF PROBABILITY THEORY. Probability theory is a branch of mathematics that studies patterns that arise in random trials. The outcome of the test is random in relation to the test, if during this

1 Basic concepts of combinatorics 1 Application Definition The product of all natural numbers from 1 to n inclusive is called the n-factorial and is written Example Compute 4! 3! n! 1 3 n 4!-3!= 1 3 4 1 3 4 18

Reliable event. An event is called certain if it will necessarily occur under a certain set of conditions. Symbol: Ω (true). Impossible event. The event that

TOPIC 1. BASIC CONCEPTS OF PROBABILITY THEORY. CLASSICAL AND GEOMETRIC PROBABILITIES A subject of probability theory. The concept of a random event. Space of elementary events. classical and geometric

1.1. Classical definition of probability The basic concept of probability theory is the concept of a random event. A random event is an event that, under certain conditions, can

The main provisions of the theory of probability An event is called random with respect to certain conditions, which, under the implementation of these conditions, can either occur or not occur. Probability theory has

( σ-algebra - field of random events - first group of Kolmogorov's axioms - second group of Kolmogorov's axioms - basic formulas of probability theory - probability addition theorem - conditional probability

The subject of probability theory In various branches of science and technology, situations often arise when the result of each of the many experiments carried out cannot be predicted in advance, but it is possible to investigate

CONTENTS THEME III. INTRODUCTION TO PROBABILITY THEORY... 2 1. REFERENCE MATERIALS... 2 1.1. BASIC CONCEPTS AND DEFINITIONS... 2 1.2. ACTIONS ON RANDOM EVENTS... 4 1.3. CLASSICAL DEFINITION

LESSON 3 INTRODUCTION TO PROBABILITY THEORY METHODOLOGICAL RECOMMENDATIONS MISIS 2013 APPROVED: D.E. Kaputkin Chairman of the Educational and Methodological Commission for the implementation of the Agreement with the Department of Education of the mountains.

1.6. Independent tests. Bernoulli formula When solving probabilistic problems, one often has to deal with situations in which the same test is repeated many times and the outcome of each test

Probability. What is it? Probability theory, as the name suggests, deals with probabilities. We are surrounded by many things and phenomena about which, no matter how advanced science is, it is impossible to make accurate predictions.

Practical exercise 1. Determination of probability Properties of random events 1. [Wentzel E.S., 1.1.] Do the following groups of events form a complete group: a) The experience of throwing a coin; events: b) Throwing experience

SUBJECT. THEOREMS OF ADDITION AND MULTIPLICATION OF PROBABILITIES Operations on random events. Algebra of events. The concept of the compatibility of events. Complete group of events. Dependence and independence of random events. Conditional

Lecture 2. Theorems of addition and multiplication of probabilities The sum and product of an event

Mathematics (BkPl-100) M.P. Kharlamov 2011/2012 academic year, 1st semester Lecture 5. Topic: Combinatorics, introduction to probability theory 1 Topic: Combinatorics Combinatorics is a branch of mathematics that studies

Lesson topic: "The simplest probabilistic problems." Grade 11 Mathematics teacher Pereverzeva N.S. MOU Lyceum 6 It is remarkable that the science, which began with the consideration of gambling, promises to become the most important

Elements of the theory of probability. Plan. 1. Events, types of events. 2. Probability of an event a) Classical probability of an event. b) Statistical probability of an event. 3. Algebra of events a) Sum of events. Probability

Topic 33 “Probability of Events” We all often say “this is incredible”, “more likely”, “this is unlikely”, etc., when we are trying to predict the occurrence of an event. Wherein

Federal Agency for Education Tomsk State University of Control Systems and Radioelectronics NE Lugina WORKSHOP ON PROBABILITY THEORY Textbook Tomsk 2006 Reviewers: Cand.

TTÜ VIRUMAA KOLLEDŽ RAR0530 Tõenäosusteooria ja matemaatiline statistika Lecture 1 Random events Actions on events Õppejõud: I. Gusseva PROBABILITY THEORY Introduction Probability theory deals with

PROBABILITY OF A RANDOM EVENT Kolmogorov's Axioms In 1933, AN Kolmogorov in his book "Basic Concepts of Probability Theory" gave an axiomatic substantiation of the theory of probability. "This means that after

Homework 1 "Probability Theory" Task 1. 1.1. There are five tickets worth one ruble, three tickets for three rubles and two tickets for five rubles. Three tickets are drawn at random. Determine Probability

Examination in applied mathematics for students of the 2nd year of correspondence education of the Higher School of Economics, direction of preparation 08.03.01 construction Option 1 1) A natural number not exceeding

Practical work 3 Algebra of events. Addition and multiplication of probabilities The purpose of the work: to master the calculation of the probabilities of joint events, the definition of probability using the sum and product formulas. Equipment

MINISTRY OF EDUCATION OF THE RUSSIAN FEDERATION VOLGOGRAD STATE TECHNICAL UNIVERSITY VOLGA POLYTECHNICAL INSTITUTE DEPARTMENT OF MATHEMATICS Probability theory (introduction) Part 1 Methodical

Department of Mathematics and Informatics Mathematics Educational and methodological complex for students of secondary vocational education studying using distance technologies Module 6 Elements of probability theory and mathematical statistics

BASIC CONCEPTS OF PROBABILITY THEORY. 3.1. Random events. Each science, when studying the phenomena of the material world, operates with certain concepts, among which there are necessarily fundamental ones;

Practical work 2 Topic 2 Total probability formula and Bayes formula Repetition of experiments (Bernoulli scheme). We will say that the events H 1, H 2, H n form a complete group, if as a result of the experiment:

13 Addition and multiplication of probabilities An event A is called a special case of an event B if, when A occurs, B occurs and B is recorded: Events A and B are called equal if each of them is a special case

COMBINATORIAL PROBABILITY Topic 5 Lecture content 1 Introduction 2 3 4 Next paragraph 1 Introduction 2 3 4 Problem... Problem... Problem... ... and solution: Girl

Lecture Topic: ALGEBRA OF EVENTS BASIC THEOREMS ON PROBABILITY Algebra of events The sum of events is called the event S = +, which consists in the occurrence of at least one of them The product of events and is called

Lecture 9

CONTROL TASKS Examination 1 Option 1 1. Among the 0 ceramic products received by the store, there are 4 defective ones. To check the quality, the merchandiser randomly selects two products. Find Probability

(definitions - random event - operations on events probability on a discrete space of elementary outcomes classical definition of probability example hypergeometric distribution example

PRCTICUM Basic formulas of combinatorics Types of events Actions on events Classical probability Geometric probability Basic formulas of combinatorics Combinatorics studies the number of combinations,

LECTURE 1 PROBABILITY THEORY Probability theory is a science that studies regularities in random phenomena. A random phenomenon is such a phenomenon that, with repeated reproduction of the same

1 Probability Experimental data are processed using various methods. Usually, the researcher, having received experimental data on one or several groups of subjects and determining from them

Fundamentals of probability theory Lecture 2 Contents 1. Conditional probability 2. Probability of the product of events 3. Probability of the sum of events 4. Total probability formula Dependent and independent events Definition

Topic: Probability theory Discipline: Mathematics Authors: Nefedova G.A. Date: 9.0.0. The probability of a random event can be equal. 0.5. 3. 0. 0.7 5..5 6. - 7. 0.3. The probability of a certain event is equal.

Probability Theory Lecture Plan P On Probability as a Science P Basic Definitions of Probability P Frequency of a Random Event Definition of Probability P 4 Applying Combinatorics to Counting

Chiv through S the event, consisting in the fact that the system is not closed, can be written: S = A 1 A 2 + B = (A 1 + A 2) + B. 2.18. Similarly to the solution of Problems 2.5, 2.6, we obtain S = A(B 1 +B 2) C D; S = A + B 1 B 2 + C

Topic 8 Discrete random variables. Often the result of a random experiment is a number. For example, you can roll a die and get one of the numbers:,3,4,5,6. You can drive to the gas station

Conditional Probability. Probability multiplication theorem Number:..B Problem: The probability of the joint occurrence of independent events A and B is determined by the formula Answers:). P(A)PA(B)). P(A) + P(B)).

Lecture 10 TOPIC Fundamentals of probability theory (part 2). Author: Maksim Igorevich Pisarevsky, Lecturer at the Center for Pre-University Training, National Research Nuclear University MEPhI. Moscow, 2017 Definitions and properties Basic definitions of the theory

Task Solving problems in probability theory Topic: "Probability of a random event." Task. The coin is tossed three times in a row. By the outcome of the experiment we mean the sequence X X X. where each

Test 01 1. Random events and their classification. 2. Mathematical expectation of a random variable. 3. There are 15 red, 9 blue and 6 green balls in a box. 6 balls are drawn at random. What is the probability

LESSON 1 RANDOM EVENTS The main concept of natural science is the concept of experiment, regardless of it, nature or the researcher carries out this experiment.

Solving problems from the collection of Chudesenko Probability Theory Tasks -0. Option 6 Task. Two dice are thrown. Determine the probability that: a) the sum of the number of points does not exceed N; b) work

TOMSK STATE UNIVERSITY Faculty of Economics WORKSHOP ON PROBABILITY THEORY AND MATHEMATICAL STATISTICS FOR ECONOMISTS PART Tomsk 06 APPROVED by the Department of Mathematical Methods and Information

1 PART I. PROBABILITY THEORY CHAPTER 1. 1. Elements of combinatorics Definition 1. Examples: Definition. -factorial is the number denoted by !, while! = 1** * for all natural numbers 1, ; besides,

Paragraph: General concepts Probability theory Random events Definition: Probability theory is a mathematical science that studies quantitative patterns in random phenomena Probability theory is not

Evaluation tools for current monitoring of progress, intermediate certification based on the results of mastering the discipline and educational and methodological support for independent work of students 1 Variants of control work

Vorobyov V.V. "Lyceum" of Kalachinsk, Omsk region Workshop on solving problems in probability theory and mathematical statistics

A.V. Clubless Probability Theory Textbook Nizhny Novgorod 06 Ministry of Education and Science of the Russian Federation Federal State Budgetary Educational Institution of Higher Professional Education

Problem book Chudesenko, probability theory, variant Two dice are thrown. Determine the probability that: a the sum of the number of points does not exceed N ; b the product of the number of points does not exceed N; in

Compiled by: Associate Professor of the Department of Medical and Biological Physics Romanova N.Yu. Probability theory 1 lecture Introduction. Probability theory is a mathematical science that studies the patterns of random phenomena.

MVDubatovskaya Theory of Probability and Mathematical Statistics Lecture 3 Methods for determining probabilities 0 Classical definition of probabilities We call any of the possible results of an experiment elementary

1. The train consists of 12 cars. Each of the 7 passengers randomly chooses any car. Find the probabilities of the following events: A = (all passengers boarded the first three cars); B = (all passengers got into different

Elements of the theory of probability Random events Deterministic processes In science and technology, processes are considered, the outcome of which can be predicted with certainty: If a difference is applied to the ends of the conductor

Federal Agency for Education State Educational Institution of Higher Professional Education "NATIONAL RESEARCH TOMSK POLYTECHNICAL UNIVERSITY" LECTURE ON THEORY

1 Classic definition of probability 1 A deck of 3 cards is carefully shuffled Find the probability that all four aces are in the deck one after the other without interspersing other cards Solution Number

Lecture 3 CONDITIONAL PROBABILITY AND INDEPENDENCE OF EVENTS TOTAL PROBABILITY FORMULA AND THE BAYES THEOREM PURPOSE OF THE LECTURE: to define the concepts of conditional probability and independence of events; construct a multiplication rule

CONTROL TASKS Task. It is necessary to solve the problem corresponding to the number of your option. The box contains coils of four colors: white 5 red green blue 0. What is the probability that at random

1. There are 14 apples in a basket, 4 of them are red. At random (without returning) they got 4 apples. Find the probability that exactly 3 reds are caught. 2. A list of 20 business calls is made randomly.

1. The numbers 1,..., n are in random order. Find the probability that the numbers 1, 2 and 3 are next to each other in the given order. 2. Out of ten teams, four go to the final. Assuming that each

FEDERAL STATE BUDGETARY EDUCATIONAL INSTITUTION OF HIGHER PROFESSIONAL EDUCATION "Chelyabinsk State Academy of Culture and Art" Department of Informatics PROBABILITY THEORY

TOPIC 1 Combinatorics Calculation of probabilities Problem 1B 17 teams take part in the national football cup. How many ways are there to distribute gold, silver and bronze medals? Insofar as

We introduce the concept random events. Since in the future we will consider only random events, then, starting from this moment, we will, as a rule, call them simply events.

Any set elementary outcomes, or, in other words, an arbitrary subset spaces of elementary outcomes, called event .

Elementary outcomes that are elements of the considered subset (events) are called elementary outcomes, favorable given event , or generating This event .

Events will be denoted by capital Latin letters, supplying them with indices if necessary, for example: BUT, AT 1 ,With 3 etc.

They say that the event BUT happened (or happened) if any of the elementary outcomes appeared as a result of the experiment.

Remark 1. For the convenience of presenting the material, the term “event” as a subset of the space of elementary events Ω is identified with the term “an event occurred as a result of experience”, or “an event consists in the appearance of some elementary outcomes”.

So in example 2, where
, event BUT is a subset
. But we will also say that the event BUT is the occurrence of any of the elementary outcomes

Example 1.5. In example 2, it was shown that with a single throw of a dice

where - an elementary outcome, consisting in the loss i points. Consider the following events: BUT- loss of an even number of points; AT- loss of an odd number of points; With- loss of a number of points that is a multiple of three. It's obvious that

,
,

An event consisting of all elementary outcomes, i.e. an event that necessarily occurs in a given experience is called a certain event.

A certain event is denoted by the letter Ω .

Event , opposite to a certain event Ω, is called impossible. Obviously an impossible event cannot appear as a result of experience. For example, dropping more than six points when throwing a dice. An impossible event will be denoted by Ø.

An impossible event does not contain any elementary event. It corresponds to the so-called "empty set", which does not contain a single point.

Geometrically, random events are represented by sets of points in the domain Ω, i.e. regions lying inside Ω (Fig. 1.1). A reliable event corresponds to the entire region Ω.

In probability theory, various operations are performed on events, the totality of which forms the so-called event algebra, closely related to the algebra of logic, widely used in modern computers.

Rice. 1.1 Fig. 1.2

To consider the problems of the algebra of events, we introduce the main definitions.

The two events are called equivalent (equivalent) if they consist of the same elementary events. The equivalence of events is indicated by the equals sign:

BUT=AT.

Event B is called the consequence of the event BUT:

BUTAT,

If from the appearance BUT followed by the appearance AT. Obviously if BUTAT and ATBUT, then BUT=AT, if BUTAT and ATWith, then BUTWith(Fig. 1.2).

sum or association two events BUT and AT such an event is called With, which consists or in the realization of the event BUT, or events AT, or events BUT and AT together. Conditionally written like this:

With=BUT+AT or With=BUT
AT.

The sum of any number events BUT 1 ,BUT 2 , … , BUT n is called an event With, which consists in the occurrence of at least one of these events and is written as

work or overlap (intersection) two events BUT and AT called an event With, which also consists in the realization of the event BUT, and events AT. Conditionally written like this:

With=AB or With=BUTAT.

The product of any number of events is defined similarly. Event With, equivalent to the product n events BUT 1 ,BUT 2 , … , BUT n is written as

or
.

The sum and product of events have the following properties.

BUT+AT=AT+BUT.

(BUT+AT)+With=BUT+(AT+With)=BUT+AT+With.

AB=VA.

(AB)With=BUT(sun)=ABC.

BUT(AT+With)=AB+AC.

Most of them are easy to check on your own. We recommend using a geometric model for this.

We present the proof of the 5th property.

Event BUT(AT+With) consists of elementary events that belong to and BUT and AT+With, i.e. event BUT and at least one of the events AT,With. In other words, BUT(AT+With) is the set of elementary events belonging either to the event AB, or an event AC, i.e. event AB+AC. Geometric event BUT(AT+With) is the common part of the regions BUT and AT+With(Fig. 1.3.a), and the event AB+AC- merging areas AB and AC(Fig. 1.3.b), i.e. the same area BUT(AT+With).

Rice. 1.3.a Fig. 1.3.b

Event With, which means that the event BUT happens and the event AT does not happen, is called difference events BUT and AT. Conditionally written like this:

With=BUT-AT.

Events BUT and AT called joint if they can appear in the same trial. This means that there are such elementary events that are part of and BUT and AT at the same time (Fig. 1.4).

Events BUT and AT called incompatible , if the appearance of one of them excludes the appearance of the other, i.e. if AB= Ø. In other words, there is not a single elementary event that would be part of and BUT and AT at the same time (Fig. 1.5). In particular, opposite events and always incompatible.

Rice. 1.4 Fig. 1.5

Events
called pairwise incompatible if any two of them are incompatible.

Events
form full group , if they are pairwise incompatible and together give a reliable event, i.e. if for any i, k

Ø;
.

Obviously, each elementary event must be part of one and only one event of the full group
. Geometrically, this means that the entire region Ω of the region
divide by n parts that do not have common points among themselves (Fig. 1.6).

Opposite events and represent the simplest case of a complete group.

You can perform various actions on events while receiving other events. Let us define these actions.

Definition 2.13.

If for every trial in which an event occurs BUT, occurs and the event AT, then the event BUT called special case events B.

They also say that a entails B, and write: ( BUT invested in AT) or (Fig. 2.1).

For example, let the event BUT consists in the appearance of two points when throwing a dice, and the event AT consists in the appearance of an even number of points when throwing a dice B = (2; 4; 6). Then the event BUT there is a special case of the event AT because two is an even number. We can write down.

Rice. 2.1 . Event BUT- a special case of an event AT

Definition 2.14.

If a BUT entails AT, a AT entails BUT, then these events are tantamount to , since they attack together or do not attack together.

From what and (follows) A = B.

For example, BUT- an event consisting in the fact that an even number less than three fell out on a dice. This event is equivalent to the event AT, consisting in the fact that the number 2 fell on the die.

Definition 2.15.

An event consisting in the joint occurrence of both events and BUT, and AT, is called intersection these events A∩B, or work these events AB(Fig. 2.2).

Rice. 2.2. Intersection of events

For example, let the event BUT consists in the loss of an even number of points when throwing a dice, then its offensive is favored by elementary events consisting in the loss of 2, 4 and 6 points. BUT -(2; 4; 6). Event AT consists in the loss of a number of points more than three when throwing a dice, then its onset is favored by elementary events consisting in the loss of 4, 5 and 6 points. AT= (4; 5; 6). Then by the intersection or product of events BUT and AT there will be an event consisting in the loss of an even number of points greater than three (the event BUT, and event AT):

A∩B =AB={4; 6}.

The intersection of events, one of which BUT- the loss of a lady from a deck of cards, and another AT- loss of clubs, there will be a queen of clubs.

Note. If two events BUT and AT are incompatible, then their joint offensive is impossible AB = 0.

Definition 2.16.

An event consisting of an occurrence or an event BUT, or events AT(at least one of the events, at least one of these events), is called their union BUT and AT, or the sum of events BUT and AT and is denoted by A + B (Fig. 2.3).

Rice. 2.3. Merging events

For example, event BUT consists in the loss of an even number of points when throwing a dice, then its occurrence is favored by elementary events consisting in the loss of 2, 4 and 6 points, or BUT -(2; 4; 6). event AT consists in the loss of a number of points more than three when throwing a dice, then its onset is favored by elementary events consisting in the loss of 4, 5 and 6 points, or B \u003d (4; 5; 6). Then the union, or the sum of events BUT and AT there will be an event consisting in the loss of at least one of them - either an even number of points, or a number of points greater than three (performed or the event BUT, or event AT):

A ∩ B = A + B ={2; 4; 5; 6}.

Definition 2.17.

An event consisting in the fact that the event BUT does not occur, is called the opposite of the event BUT and is denoted by Ā (Fig. 2.4).

Rice. 2.4. Opposite events

For example, let the event BUT consists in the loss of an even number of points when throwing a dice, then its occurrence is favored by elementary events consisting in the loss of 2, -4 and 6 points, or A =(2; 4; 6). Then the event Ā consists in the loss of an odd number of points, and its occurrence is favored by elementary events consisting in the loss of 1st, 3rd and 5th points. Ā ={1;3;5}.

Definition 2.18.

Event (A and B), consisting in the fact that BUT happens, but does not happen, is called the difference of events BUT and AT and is denoted by A-B. However, this notation can be dispensed with, since it follows from the definition that A - B -(Fig. 2.5).

Rice. 2.5. Event Difference BUT and AT

For example, let the event BUT consists in the loss of an even number of points when throwing a dice, then A =(2; 4; 6). Event AT consists in the loss of a number of points more than three. AT= {4; 5; 6}.

Then - an event consisting in the loss of a number of points not more than three, and its occurrence is favored by elementary events consisting in the loss of the 1st, 2nd and 3rd points. = {1; 2; 3}.

difference of events BUT and AT there will be an event consisting in that the event is executed BUT and the event is not executed AT. Its offensive is favored by an elementary event consisting in the loss of 2 points:

A-B= A∩= {2}.

Definitions sums and products events apply to more events:

A + B + ... + N =(BUT or AT, or or N) (2.1)

there is an event consisting in the occurrence at least one from events A, B, ... N;

AB ... N =(BUT and AT and... and N), (2.2)

there is an event that joint offensive all events A, B, ... N.

The sum and product of an infinite number of events are defined similarly A 1, A 2, ... A p, ...

Note that, nevertheless, some rules of algebra are preserved for actions on events. For example, there is a commutative law (communicativity):

A + B \u003d B + A, AB \u003d BA,(2.3)

the distributive law (distributivity) holds:

(A + B) C \u003d AC + BC,(2.4)

since the left and right sides represent the event that event C and at least one of the events BUT and AT. The association law (associativity) is also valid:

A + (B + C) \u003d (A + B) + C \u003d A + B + C;

A(BC) = (AB)C = ABC.(2.5)

In addition, there are such equalities that would seem absurd in ordinary algebra. For example, for any A, B, C:

AA=A(2.6)

A+A= BUT(2.7)

A+AB= BUT(2.8)

AB + C \u003d (A + C) (B + C)(2.9)

Opposite events are related:

The law of double negation:

= A;(2.10)

the law of the excluded middle

BUT + = Ω. (their sum is a certain event); (2.11)

The law of contradiction:

A =Ø(the product of their impossible event). (2.12)

Equalities (2.6)-(2.12) are proved for propositions in the course of discrete mathematics. We invite the reader to check this for himself, using the definitions of the sum and the product of events.

If a B \u003d A 1 + A 2 + ... + A p and events BUT are pairwise incompatible, i.e. each is incompatible with the others: A j A k= Ø at i≠k say that the event B is subdivided into special cases A 1, A 2 , ..., A p. For example, event AT, consisting in the loss of an odd number of points, is divided into special cases E 1, E 3, E 5, consisting respectively in the loss of 1, 3 and 5 points.

Based on the definition of actions on events, we can define a complete group of events more clearly.

Definition 2.19.

If a A 1 + A 2 + ... + A p = Ω , i.e. if at least one of the events A 1 + A 2 + ... + A p must certainly come true, and if at the same time A j pairwise incompatible (i.e. certain event Ω subdivided into special cases A 1 + A 2 + ... + A p), then we say that the events A 1 + A 2 + ... + A p form a complete group of events. Thus, if A 1 + A 2 + ... + A p- a complete group of events, then at each test one and only one of the events necessarily occurs A 1 + A 2 + ... + A p.

For example, when throwing a dice, the complete group of events also includes the events E 1, E 2, E 3, E 4, E 5 and E 6, consisting respectively in the loss of 1, 2, 3.4, 5 and 6 points.

General statement of the problem: the probabilities of some events are known, but the probabilities of other events that are associated with these events need to be calculated. In these problems, there is a need for such operations on probabilities as addition and multiplication of probabilities.

For example, two shots were fired while hunting. Event A- hitting a duck from the first shot, event B- hit from the second shot. Then the sum of events A and B- hit from the first or second shot or from two shots.

Tasks of a different type. Several events are given, for example, a coin is tossed three times. It is required to find the probability that either all three times the coat of arms will fall out, or that the coat of arms will fall out at least once. This is a multiplication problem.

Addition of probabilities of incompatible events

Probability addition is used when it is necessary to calculate the probability of a combination or a logical sum of random events.

Sum of events A and B designate A + B or A ∪ B. The sum of two events is an event that occurs if and only if at least one of the events occurs. It means that A + B- an event that occurs if and only if an event occurs during the observation A or event B, or at the same time A and B.

If events A and B are mutually inconsistent and their probabilities are given, then the probability that one of these events will occur as a result of one trial is calculated using the addition of probabilities.

The theorem of addition of probabilities. The probability that one of two mutually incompatible events will occur is equal to the sum of the probabilities of these events:

For example, two shots were fired while hunting. Event BUT– hitting a duck from the first shot, event AT– hit from the second shot, event ( BUT+ AT) - hit from the first or second shot or from two shots. So if two events BUT and AT are incompatible events, then BUT+ AT- the occurrence of at least one of these events or two events.

Example 1 A box contains 30 balls of the same size: 10 red, 5 blue and 15 white. Calculate the probability that a colored (not white) ball is taken without looking.

Decision. Let's assume that the event BUT– “the red ball is taken”, and the event AT- "The blue ball is taken." Then the event is “a colored (not white) ball is taken”. Find the probability of an event BUT:

and events AT:

Events BUT and AT- mutually incompatible, since if one ball is taken, then balls of different colors cannot be taken. Therefore, we use the addition of probabilities:

The theorem of addition of probabilities for several incompatible events. If the events make up the complete set of events, then the sum of their probabilities is equal to 1:

The sum of the probabilities of opposite events is also equal to 1:

Opposite events form a complete set of events, and the probability of a complete set of events is 1.

The probabilities of opposite events are usually denoted in small letters. p and q. In particular,

from which the following formulas for the probability of opposite events follow:

Example 2 The target in the dash is divided into 3 zones. The probability that a certain shooter will shoot at a target in the first zone is 0.15, in the second zone - 0.23, in the third zone - 0.17. Find the probability that the shooter hits the target and the probability that the shooter misses the target.

Solution: Find the probability that the shooter will hit the target:

Find the probability that the shooter misses the target:

More difficult tasks in which you need to apply both addition and multiplication of probabilities - on the page "Various tasks for addition and multiplication of probabilities" .

Addition of probabilities of mutually joint events

Two random events are said to be joint if the occurrence of one event does not preclude the occurrence of a second event in the same observation. For example, when throwing a dice, the event BUT is considered to be the occurrence of the number 4, and the event AT- dropping an even number. Since the number 4 is an even number, the two events are compatible. In practice, there are tasks for calculating the probabilities of the occurrence of one of the mutually joint events.

The theorem of addition of probabilities for joint events. The probability that one of the joint events will occur is equal to the sum of the probabilities of these events, from which the probability of the common occurrence of both events is subtracted, that is, the product of the probabilities. The formula for the probabilities of joint events is as follows:

Because the events BUT and AT compatible, event BUT+ AT occurs if one of three possible events occurs: or AB. According to the theorem of addition of incompatible events, we calculate as follows:

Event BUT occurs if one of two incompatible events occurs: or AB. However, the probability of occurrence of one event from several incompatible events is equal to the sum of the probabilities of all these events:

Similarly:

Substituting expressions (6) and (7) into expression (5), we obtain the probability formula for joint events:

When using formula (8), it should be taken into account that the events BUT and AT can be:

mutually independent;
mutually dependent.

Probability formula for mutually independent events:

Probability formula for mutually dependent events:

If events BUT and AT are inconsistent, then their coincidence is an impossible case and, thus, P(AB) = 0. The fourth probability formula for incompatible events is as follows:

Example 3 In auto racing, when driving in the first car, the probability of winning, when driving in the second car. To find:

the probability that both cars will win;
the probability that at least one car will win;

1) The probability that the first car will win does not depend on the result of the second car, so the events BUT(first car wins) and AT(second car wins) - independent events. Find the probability that both cars win:

2) Find the probability that one of the two cars will win:

More difficult tasks in which you need to apply both addition and multiplication of probabilities - on the page "Various tasks for addition and multiplication of probabilities" .

Solve the problem of addition of probabilities yourself, and then look at the solution

Example 4 Two coins are thrown. Event A- loss of coat of arms on the first coin. Event B- loss of coat of arms on the second coin. Find the probability of an event C = A + B .

Probability multiplication

Multiplication of probabilities is used when the probability of a logical product of events is to be calculated.

In this case, random events must be independent. Two events are said to be mutually independent if the occurrence of one event does not affect the probability of the occurrence of the second event.

Probability multiplication theorem for independent events. The probability of the simultaneous occurrence of two independent events BUT and AT is equal to the product of the probabilities of these events and is calculated by the formula:

Example 5 The coin is tossed three times in a row. Find the probability that the coat of arms will fall out all three times.

Decision. The probability that the coat of arms will fall on the first toss of a coin, the second time, and the third time. Find the probability that the coat of arms will fall out all three times:

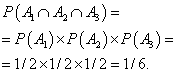
Solve problems for multiplying probabilities yourself, and then look at the solution

Example 6 There is a box with nine new tennis balls. Three balls are taken for the game, after the game they are put back. When choosing balls, they do not distinguish between played and unplayed balls. What is the probability that after three games there will be no unplayed balls in the box?

Example 7 32 letters of the Russian alphabet are written on cut alphabet cards. Five cards are drawn at random, one after the other, and placed on the table in the order in which they appear. Find the probability that the letters will form the word "end".

Example 8 From a full deck of cards (52 sheets), four cards are taken out at once. Find the probability that all four of these cards are of the same suit.

Example 9 The same problem as in example 8, but each card is returned to the deck after being drawn.

More complex tasks, in which you need to apply both addition and multiplication of probabilities, as well as calculate the product of several events, on the page "Various tasks for addition and multiplication of probabilities" .

The probability that at least one of the mutually independent events will occur can be calculated by subtracting the product of the probabilities of opposite events from 1, that is, by the formula.