Expressions, Equations, and Systems of Equations
with complex numbers

Today in the lesson we will work out typical actions with complex numbers, as well as master the technique of solving expressions, equations and systems of equations that these numbers contain. This workshop is a continuation of the lesson, and therefore if you are unfamiliar with the topic, then please follow the link above. Well, I suggest that more prepared readers immediately warm up:

Example 1

Simplify Expression , if . Present the result in trigonometric form and depict it on the complex plane.

Decision: so, you need to substitute in the "terrible" fraction, carry out simplifications, and translate the resulting complex number in trigonometric form. Plus damn.

What is the best way to make a decision? It is more profitable to deal with a “fancy” algebraic expression in stages. Firstly, attention is less scattered, and, secondly, if the task is not credited, it will be much easier to find an error.

1) Let's simplify the numerator first. Substitute the value into it, open the brackets and fix the hairstyle:

... Yes, such a Quasimodo from complex numbers turned out ...

I remind you that in the course of transformations, completely ingenuous things are used - the rule of multiplication of polynomials and the equality that has already become banal. The main thing is to be careful and not get confused in the signs.

2) Now the denominator is next. If , then:

Note in what an unusual interpretation is used sum square formula. Alternatively, you can change here subformula . The results will, of course, match.

3) And finally, the whole expression. If , then:

To get rid of the fraction, we multiply the numerator and denominator by the expression conjugate to the denominator. However, for the purposes of applying difference of squares formulas should be preliminarily (and for sure!) put the negative real part in the 2nd place:

And now the key rule:

IN NO EVENT WE DO NOT HURRY! Better to play it safe and prescribe an extra step.
In expressions, equations and systems with complex numbers presumptuous oral calculations fraught as ever!

There was a nice contraction in the final step and that's just a great sign.

Note : strictly speaking, the division of the complex number by the complex number 50 took place here (recall that ). I have kept silent about this nuance until now and we will talk about it a little later.

Let's denote our achievement with the letter

Let's represent the result in trigonometric form. Generally speaking, here you can do without a drawing, but as soon as it is required, it is somewhat more rational to complete it right now:

Calculate the modulus of a complex number:

If you perform a drawing on a scale of 1 unit. \u003d 1 cm (2 tetrad cells), then the resulting value is easy to check using a regular ruler.

Let's find an argument. Since the number is located in the 2nd coordinate quarter, then:

The angle is simply checked by a protractor. This is the undoubted plus of the drawing.

Thus: - the desired number in trigonometric form.

Let's check:
, which was to be verified.

It is convenient to find unfamiliar values ​​of sine and cosine by trigonometric table.

Answer:

A similar example for a do-it-yourself solution:

Example 2

Simplify Expression , where . Draw the resulting number on the complex plane and write it in exponential form.

Try not to skip the tutorials. They may seem simple, but without training, “getting into a puddle” is not just easy, but very easy. So let's get our hands on it.

Often the problem allows more than one solution:

Example 3

Calculate if ,

Decision: first of all, let's pay attention to the original condition - one number is presented in algebraic form, and the other in trigonometric form, and even with degrees. Let's immediately rewrite it in a more familiar form: .

In what form should the calculations be carried out? The expression , obviously, involves the first multiplication and further raising to the 10th power in De Moivre formula, which is formulated for the trigonometric form of a complex number. Thus, it seems more logical to convert the first number. Find its module and argument:

We use the rule of multiplication of complex numbers in trigonometric form:
if , then

Making the fraction correct, we come to the conclusion that it is possible to “twist” 4 turns ( glad.):

The second way to solve is to translate the 2nd number into the algebraic form , perform the multiplication in algebraic form, translate the result into trigonometric form and use the De Moivre formula.

As you can see, one "extra" action. Those who wish can follow the solution to the end and make sure that the results match.

The condition says nothing about the form of the resulting complex number, so:

Answer:

But “for beauty” or on demand, the result can be easily represented in algebraic form:

On one's own:

Example 4

Simplify Expression

Here it is necessary to remember actions with powers, although there is no one useful rule in the training manual, here it is:.

And one more important note: the example can be solved in two styles. The first option is to work with two numbers and put up with fractions. The second option is to represent each number in the form quotient of two numbers: and get rid of the four-story. From a formal point of view, it makes no difference how to decide, but there is a meaningful difference! Please consider well:
is a complex number;
is the quotient of two complex numbers ( and ), however, depending on the context, one can also say this: a number represented as a quotient of two complex numbers.

Short solution and answer at the end of the lesson.

Expressions are good, but equations are better:

Equations with complex coefficients

How do they differ from "ordinary" equations? Coefficients =)

In light of the above remark, let's start with this example:

Example 5

solve the equation

And an immediate preamble in hot pursuit: initially the right side of the equation is positioned as a quotient of two complex numbers ( and 13), and therefore it would be bad form to rewrite the condition with the number (even though it won't cause an error). By the way, this difference is more clearly seen in fractions - if, relatively speaking, , then this value is primarily understood as "full" complex root of the equation, and not as a divisor of the number , and even more so - not as part of the number !

Decision, in principle, it can also be arranged step by step, but in this case the game is not worth the candle. The initial task is to simplify everything that does not contain an unknown "Z", as a result of which the equation will be reduced to the form:

Confidently simplify the average fraction:

We transfer the result to the right side and find the difference:

Note : and again I draw your attention to the meaningful point - here we did not subtract the number from the number, but summed the fractions to a common denominator! It should be noted that already in the course of the solution it is not forbidden to work with numbers: , however, in the example under consideration, such a style is more harmful than useful =)

According to the rule of proportion, we express "z":

Now you can again divide and multiply by the adjoint expression, but the suspiciously similar numbers of the numerator and denominator suggest the following move:

Answer:

For verification purposes, we substitute the resulting value into the left side of the original equation and perform simplifications:

- the right side of the original equation is obtained, so the root is found correctly.

…Now-now…I’ll pick something more interesting for you…hold on:

Example 6

solve the equation

This equation reduces to the form , and therefore is linear. The hint, I think, is clear - go for it!

Of course ... how can you live without it:

Quadratic equation with complex coefficients

On the lesson Complex numbers for dummies we learned that a quadratic equation with real coefficients can have conjugate complex roots, after which a logical question arises: why, in fact, the coefficients themselves cannot be complex? I will formulate the general case:

Quadratic equation with arbitrary complex coefficients (1 or 2 of which or all three may in particular be valid) It has two and only two complex roots (possibly one of which or both are valid). While the roots (both real and with a non-zero imaginary part) may coincide (be multiple).

A quadratic equation with complex coefficients is solved in the same way as "school" equation, with some differences in computational technique:

Example 7

Find the roots of a quadratic equation

Decision: the imaginary unit is in the first place, and, in principle, you can get rid of it (multiplying both sides by ), however, there is no particular need for this.

For convenience, we write the coefficients:

We do not lose the "minus" of the free member! ... It may not be clear to everyone - I will rewrite the equation in standard form :

Let's calculate the discriminant:

Here is the main hurdle:

Application of the general formula for extracting the root (see the last paragraph of the article Complex numbers for dummies) is complicated by serious difficulties associated with the argument of the radical complex number (see for yourself). But there is another, "algebraic" way! We will look for the root in the form:

Let's square both sides:

Two complex numbers are equal if their real and imaginary parts are equal. Thus, we get the following system:

The system is easier to solve by choosing (a more thorough way is to express from the 2nd equation - substitute in the 1st, get and solve the biquadratic equation). Assuming that the author of the problem is not a monster, we hypothesize that and are integers. From the 1st equation it follows that "x" modulo more than "y". In addition, the positive product tells us that the unknowns are of the same sign. Based on the foregoing, and focusing on the 2nd equation, we write down all the pairs that match it:

Obviously, the last two pairs satisfy the 1st equation of the system, thus:

An intermediate check will not hurt:

which was to be checked.

As a "working" root, you can choose any meaning. It is clear that it is better to take the version without the "cons":

We find the roots, not forgetting, by the way, that:

Answer:

Let's check whether the found roots satisfy the equation :

1) Substitute:

correct equality.

2) Substitute:

correct equality.

Thus, the solution is found correctly.

Inspired by the problem just discussed:

Example 8

Find the roots of the equation

Note that the square root of purely complex numbers are perfectly extracted and using the general formula , where , so both methods are shown in the sample. The second useful remark concerns the fact that preliminary extraction of the root from the constant does not simplify the solution at all.

And now you can relax - in this example, you will get off with a slight fright :)

Example 9

Solve the equation and check

Solutions and answers at the end of the lesson.

The final paragraph of the article is devoted to

system of equations with complex numbers

We relaxed and… we don’t strain =) Let’s consider the simplest case – a system of two linear equations with two unknowns:

Example 10

Solve the system of equations. Present the answer in algebraic and exponential forms, depict the roots in the drawing.

Decision: the condition itself suggests that the system has a unique solution, that is, we need to find two numbers that satisfy to each system equation.

The system can really be solved in a “childish” way (express one variable in terms of another) , but it is much more convenient to use Cramer's formulas. Compute main determinant systems:

, so the system has a unique solution.

I repeat that it is better not to rush and prescribe the steps as detailed as possible:

We multiply the numerator and denominator by an imaginary unit and get the 1st root:

Similarly:

The corresponding right-hand sides, p.t.p.

Let's execute the drawing:

We represent the roots in exponential form. To do this, you need to find their modules and arguments:

1) - the arc tangent of the "two" is calculated "poorly", so we leave it like this:

To solve problems with complex numbers, you need to understand the basic definitions. The main objective of this review article is to explain what complex numbers are and present methods for solving basic problems with complex numbers. Thus, a complex number is a number of the form z = a + bi, where a, b- real numbers, which are called the real and imaginary parts of the complex number, respectively, and denote a = Re(z), b=Im(z).
i is called the imaginary unit. i 2 \u003d -1. In particular, any real number can be considered complex: a = a + 0i, where a is real. If a = 0 and b ≠ 0, then the number is called purely imaginary.

We now introduce operations on complex numbers.
Consider two complex numbers z 1 = a 1 + b 1 i and z 2 = a 2 + b 2 i.

Consider z = a + bi.

The set of complex numbers extends the set of real numbers, which in turn extends the set of rational numbers, and so on. This chain of embeddings can be seen in the figure: N - natural numbers, Z - integers, Q - rational, R - real, C - complex.

Representation of complex numbers

Algebraic notation.

Consider a complex number z = a + bi, this form of writing a complex number is called algebraic. We have already discussed this form of writing in detail in the previous section. Quite often use the following illustrative drawing

trigonometric form.

It can be seen from the figure that the number z = a + bi can be written differently. It's obvious that a = rcos(φ), b = rsin(φ), r=|z|, hence z = rcos(φ) + rsin(φ)i, φ ∈ (-π; π) is called the argument of a complex number. This representation of a complex number is called trigonometric form. The trigonometric form of notation is sometimes very convenient. For example, it is convenient to use it for raising a complex number to an integer power, namely, if z = rcos(φ) + rsin(φ)i, then z n = r n cos(nφ) + r n sin(nφ)i, this formula is called De Moivre's formula.

Demonstrative form.

Consider z = rcos(φ) + rsin(φ)i is a complex number in trigonometric form, we write it in a different form z = r(cos(φ) + sin(φ)i) = re iφ, the last equality follows from the Euler formula, so we got a new form of writing a complex number: z = re iφ, which is called demonstrative. This form of notation is also very convenient for raising a complex number to a power: z n = r n e inφ, here n not necessarily an integer, but can be an arbitrary real number. This form of writing is quite often used to solve problems.

Fundamental theorem of higher algebra

Imagine that we have a quadratic equation x 2 + x + 1 = 0 . It is obvious that the discriminant of this equation is negative and it has no real roots, but it turns out that this equation has two different complex roots. So, the main theorem of higher algebra states that any polynomial of degree n has at least one complex root. It follows from this that any polynomial of degree n has exactly n complex roots, taking into account their multiplicity. This theorem is a very important result in mathematics and is widely applied. A simple corollary of this theorem is that there are exactly n distinct n-degree roots of unity.

Main types of tasks

In this section, the main types of simple complex number problems will be considered. Conventionally, problems on complex numbers can be divided into the following categories.

• Performing simple arithmetic operations on complex numbers.
• Finding the roots of polynomials in complex numbers.
• Raising complex numbers to a power.
• Extraction of roots from complex numbers.
• Application of complex numbers to solve other problems.

Now consider the general methods for solving these problems.

The simplest arithmetic operations with complex numbers are performed according to the rules described in the first section, but if complex numbers are presented in trigonometric or exponential forms, then in this case they can be converted into algebraic form and perform operations according to known rules.

Finding the roots of polynomials usually comes down to finding the roots of a quadratic equation. Suppose we have a quadratic equation, if its discriminant is non-negative, then its roots will be real and are found according to a well-known formula. If the discriminant is negative, then D = -1∙a 2, where a is a certain number, then we can represent the discriminant in the form D = (ia) 2, hence √D = i|a|, and then you can use the already known formula for the roots of the quadratic equation.

Example. Let's return to the quadratic equation mentioned above x 2 + x + 1 = 0.
Discriminant - D \u003d 1 - 4 ∙ 1 \u003d -3 \u003d -1 (√3) 2 \u003d (i√3) 2.
Now we can easily find the roots:

Raising complex numbers to a power can be done in several ways. If you want to raise a complex number in algebraic form to a small power (2 or 3), then you can do this by direct multiplication, but if the degree is larger (in problems it is often much larger), then you need to write this number in trigonometric or exponential forms and use already known methods.

Example. Consider z = 1 + i and raise to the tenth power.
We write z in exponential form: z = √2 e iπ/4 .
Then z 10 = (√2 e iπ/4) 10 = 32 e 10iπ/4.
Let's return to the algebraic form: z 10 = -32i.

Extracting roots from complex numbers is the inverse operation of exponentiation, so it is done in a similar way. To extract the roots, the exponential form of writing a number is often used.

Example. Find all roots of degree 3 of unity. To do this, we find all the roots of the equation z 3 = 1, we will look for the roots in exponential form.
Substitute in the equation: r 3 e 3iφ = 1 or r 3 e 3iφ = e 0 .
Hence: r = 1, 3φ = 0 + 2πk, hence φ = 2πk/3.
Various roots are obtained at φ = 0, 2π/3, 4π/3.
Hence 1 , e i2π/3 , e i4π/3 are roots.
Or in algebraic form: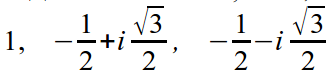

The last type of problems includes a huge variety of problems and there are no general methods for solving them. Here is a simple example of such a task:

Find the amount sin(x) + sin(2x) + sin(2x) + … + sin(nx).

Although the formulation of this problem does not refer to complex numbers, but with their help it can be easily solved. To solve it, the following representations are used:


If we now substitute this representation into the sum, then the problem is reduced to the summation of the usual geometric progression.

Conclusion

Complex numbers are widely used in mathematics, this review article discussed the basic operations on complex numbers, described several types of standard problems and briefly described general methods for solving them, for a more detailed study of the possibilities of complex numbers, it is recommended to use specialized literature.

Literature

Service for solving equations online will help you solve any equation. Using our site, you will not only get the answer to the equation, but also see a detailed solution, that is, a step-by-step display of the process of obtaining the result. Our service will be useful for high school students and their parents. Students will be able to prepare for tests, exams, test their knowledge, and parents will be able to control the solution of mathematical equations by their children. The ability to solve equations is a mandatory requirement for students. The service will help you self-learn and improve your knowledge in the field of mathematical equations. With it, you can solve any equation: quadratic, cubic, irrational, trigonometric, etc. The benefit of the online service is invaluable, because in addition to the correct answer, you get a detailed solution to each equation. Benefits of solving equations online. You can solve any equation online on our website absolutely free of charge. The service is fully automatic, you do not have to install anything on your computer, you just need to enter the data and the program will issue a solution. Any calculation errors or typographical errors are excluded. It is very easy to solve any equation online with us, so be sure to use our site to solve any kind of equations. You only need to enter the data and the calculation will be completed in seconds. The program works independently, without human intervention, and you get an accurate and detailed answer. Solution of the equation in general form. In such an equation, the variable coefficients and the desired roots are interconnected. The highest power of a variable determines the order of such an equation. Based on this, various methods and theorems are used for equations to find solutions. Solving equations of this type means finding the desired roots in a general form. Our service allows you to solve even the most complex algebraic equation online. You can get both the general solution of the equation and the private one for the numerical values ​​of the coefficients you specified. To solve an algebraic equation on the site, it is enough to correctly fill in only two fields: the left and right parts of the given equation. Algebraic equations with variable coefficients have an infinite number of solutions, and by setting certain conditions, particular ones are selected from the set of solutions. Quadratic equation. The quadratic equation has the form ax^2+bx+c=0 for a>0. The solution of equations of a square form implies finding the values ​​of x, at which the equality ax ^ 2 + bx + c \u003d 0 is satisfied. To do this, the value of the discriminant is found by the formula D=b^2-4ac. If the discriminant is less than zero, then the equation has no real roots (the roots are from the field of complex numbers), if it is zero, then the equation has one real root, and if the discriminant is greater than zero, then the equation has two real roots, which are found by the formula: D \u003d -b + -sqrt / 2a. To solve a quadratic equation online, you just need to enter the coefficients of such an equation (whole numbers, fractions or decimal values). If there are subtraction signs in the equation, you must put a minus in front of the corresponding terms of the equation. You can also solve a quadratic equation online depending on the parameter, that is, the variables in the coefficients of the equation. Our online service for finding common solutions perfectly copes with this task. Linear equations. To solve linear equations (or systems of equations), four main methods are used in practice. Let's describe each method in detail. Substitution method. Solving equations using the substitution method requires expressing one variable in terms of the others. After that, the expression is substituted into other equations of the system. Hence the name of the solution method, that is, instead of a variable, its expression through the rest of the variables is substituted. In practice, the method requires complex calculations, although it is easy to understand, so solving such an equation online will save time and make calculations easier. You just need to specify the number of unknowns in the equation and fill in the data from linear equations, then the service will make the calculation. Gauss method. The method is based on the simplest transformations of the system in order to arrive at an equivalent triangular system. The unknowns are determined one by one from it. In practice, you need to solve such an equation online with a detailed description, thanks to which you will learn the Gauss method well for solving systems of linear equations. Write down the system of linear equations in the correct format and take into account the number of unknowns in order to correctly solve the system. Cramer's method. This method solves systems of equations in cases where the system has a unique solution. The main mathematical operation here is the calculation of matrix determinants. The solution of equations by the Cramer method is carried out online, you get the result instantly with a complete and detailed description. It is enough just to fill the system with coefficients and choose the number of unknown variables. matrix method. This method consists in collecting the coefficients of the unknowns in matrix A, the unknowns in column X, and the free terms in column B. Thus, the system of linear equations is reduced to a matrix equation of the form AxX=B. This equation has a unique solution only if the determinant of the matrix A is non-zero, otherwise the system has no solutions, or an infinite number of solutions. The solution of equations by the matrix method is to find the inverse matrix A.

The use of equations is widespread in our lives. They are used in many calculations, construction of structures and even sports. Equations have been used by man since ancient times and since then their use has only increased. For clarity, let's solve the following problem:

Compute \[ (z_1\cdot z_2)^(10),\] if \

First of all, let's pay attention to the fact that one number is represented in algebraic form, the other - in trigonometric form. It needs to be simplified and brought to the following form

\[ z_2 = \frac(1)(4) (\cos\frac(\pi)(6)+i\sin\frac(\pi)(6)).\]

The expression \ says that, first of all, we do multiplication and raising to the 10th power according to the Moivre formula. This formula was formulated for the trigonometric form of a complex number. We get:

\[\begin(vmatrix) z_1 \end(vmatrix)=\sqrt ((-1)^2+(\sqrt 3)^2)=\sqrt 4=2\]

\[\varphi_1=\pi+\arctan\frac(\sqrt 3)(-1)=\pi\arctan\sqrt 3=\pi-\frac(\pi)(3)=\frac(2\pi)( 3)\]

Adhering to the rules for multiplying complex numbers in trigonometric form, we will do the following:

In our case:

\[(z_1+z_2)^(10)=(\frac(1)(2))^(10)\cdot(\cos (10\cdot\frac(5\pi)(6))+i\sin \cdot\frac(5\pi)(6)))=\frac(1)(2^(10))\cdot\cos \frac(25\pi)(3)+i\sin\frac(25\ pi)(3).\]

Making the fraction \[\frac(25)(3)=8\frac(1)(3)\] correct, we conclude that it is possible to "twist" 4 turns \[(8\pi rad.):\]

\[ (z_1+z_2)^(10)=\frac(1)(2^(10))\cdot(\cos \frac(\pi)(3)+i\sin\frac(\pi)(3 ))\]

Answer: \[(z_1+z_2)^(10)=\frac(1)(2^(10))\cdot(\cos \frac(\pi)(3)+i\sin\frac(\pi) (3))\]

This equation can be solved in another way, which boils down to bringing the 2nd number into algebraic form, then performing multiplication in algebraic form, translating the result into trigonometric form and applying the Moivre formula:

Where can I solve a system of equations with complex numbers online?

You can solve the system of equations on our website https: // site. Free online solver will allow you to solve an online equation of any complexity in seconds. All you have to do is just enter your data into the solver. You can also watch the video instruction and learn how to solve the equation on our website. And if you have any questions, you can ask them in our Vkontakte group http://vk.com/pocketteacher. Join our group, we are always happy to help you.