Središte mase sustava točaka. Određivanje težišta velikih
upute
Pokušajte pronaći središte gravitacija ravan figure empirijski. Uzmite novu, nenašiljenu olovku i postavite je okomito. Stavite ravnu figuru na vrh. Označite točku na slici gdje je stabilna na olovci. Ovo će biti centar gravitacija tvoje figure. Umjesto olovke, jednostavno koristite kažiprst ispružen prema gore. Ali to je zato što morate osigurati da prst stoji ravno, da se ne klati ili drhti.
Kako biste pokazali da je rezultirajuća točka središte mase, iglom napravite rupu u njoj. Kroz rupu provucite konac i na jednom kraju zavežite čvor kako konac ne bi iskočio. Držeći drugi kraj konca, objesite svoje tijelo na njega. Ako centar gravitacija Tako je, figura će biti postavljena točno, paralelno s podom. Bokovi joj se neće ljuljati.
Pronađite centar gravitacija figure geometrijski. Ako vam je dan trokut, konstruirajte . Ovi segmenti povezuju vrhove trokuta sa sredinom suprotna strana. Točka će postati centar mase trokuta. Da biste pronašli središte stranice, možete čak presavinuti lik na pola, ali imajte na umu da će to poremetiti jednolikost figure.
Usporedite dobivene rezultate geometrijski i eksperimentalno. Izvijestite o tijeku eksperimenta. Male greške se smatraju normalnim. Objašnjavaju se nesavršenošću figure, netočnost instrumenata, ljudski faktor (manji nedostaci u radu, nesavršenost ljudskog oka itd.).
Izvori:
- Izračunavanje koordinata težišta ravnog lika
Središte figure može se pronaći na više načina, ovisno o tome koji su podaci o njoj već poznati. Vrijedno je razmisliti o pronalaženju središta kruga, koji je skup točaka koje se nalaze na jednakoj udaljenosti od središta, budući da je ova figura jedna od najčešćih.
Trebat će vam
- - kvadrat;
- - vladar.
upute
Najjednostavniji način pronađite središte kruga - savijte komad papira na kojem je nacrtan, pazeći, gledajući u razmak, da je presavijen točno na pola. Zatim presavijte list okomito na prvi nabor. Tako ćete dobiti promjere čija je sjecišna točka središte figure.
P1= m1*g, P2= m2*g;
Težište je između dviju masa. A ako se cijelo tijelo objesi u t.O, nastupit će ravnoteža, to jest, ovi će prestati prevladavati jedan nad drugim.
Raznolik geometrijske figure imati fizičke i proračune u vezi s težištem. Svaki ima svoj pristup i svoju metodu.
S obzirom na disk, pojašnjavamo da se unutar njega nalazi težište, točnije promjeri (kao što je prikazano na slici u t.C - točka sjecišta promjera). Na isti način se nalaze središta paralelopipeda ili homogene kugle.
Predstavljeni disk i dva tijela masa m1 i m2 su homogene mase i ispravan oblik. Ovdje se može primijetiti da je centar gravitacije koji tražimo unutar ovih objekata. Međutim, u tijelima s nejednolikom masom i nepravilnog oblika središte može biti iza . I sami osjećate da zadatak postaje sve teži.
Moda za “žene koje izgledaju kao dječaci” je odavno prošla, ali mnoge pripadnice ljepšeg spola i dalje žele imati ravnu zadnjicu. Iako je danas "u modi" pokazati svu rascvjetanu seksualnost, skladno, lijepo i utrenirano tijelo. Dapače, upravo je u ovom slučaju lijepa zadnjica neizostavna komponenta ne samo ženske, već i muške ljepote.
upute
Da bi dupe ravni, morate učiniti sljedeće. Vježba 1: “Podizanje nogu.” Ovu vježbu možete izvoditi u nekoliko varijanti.Stanite na sve četiri – u početni položaj, a potom podižite svaku nogu redom tako da bedro bude paralelno s podom. Popravite nogu u pritisnutom položaju i napravite opružne pokrete prema gore. Istodobno obratite pozornost na fiksaciju noge u zglobovima gležnja i koljena, pokušajte ne mijenjati ovaj položaj.
Vježba 2: “Podizanje zdjelice.” Lezite, postavite ruke paralelno uz tijelo, a noge savijte u koljenima. Nakon toga podignite zdjelicu od poda, snažno naprežući stražnjicu. pri čemu gornji dio a ruke se ne smiju odvajati od poda.U istom položaju radite opružne pokrete prema gore.
Vježba 3: “Podizanje” Stanite sa stopalima u širini ramena. Naizmjenično podižite i spuštajte jedno po jedno koljeno što je više moguće. Kada podižete koljeno, pokušajte što duže ostati na jednoj nozi bez pomicanja.Ova vježba jako dobro djeluje na područje koje se nalazi odmah iznad stražnjice.
Vježba 4: “Čučnjevi s abdukcijom zdjelice.” Stanite tako da su vam noge šire od ramena, a stopala paralelna s njima. U ovom slučaju, lijeva noga bi trebala biti malo iza desne. Zatim čučnite, oslanjajući se na lijevu nogu i pomičući zdjelicu prema natrag. Istodobno ispružite ruke ispred lijevog stopala, leđa držite ravno. Nakon toga ustanite, svu težinu prenesite na desnu nogu, lijevu nogu vratite unatrag i podignite ruke iznad glave.Ovu vježbu ponovite 10 puta, a zatim promijenite nogu.
Vježba 5: "Iskoraci s kotačem". Iskorak naprijed, počevši s lijevom nogom, lagano okrenite stopalo u smjeru kazaljke na satu. Zatim se iz kuka nagnite naprijed. Istodobno raširite ruke, kao da želite napraviti kolo. Zadržite se u ovom položaju nekoliko sekundi, zatim ustanite, zadržavajući položaj desne noge. Lijevicom napravite korak ulijevo i okrenite nožni prst prema van. Čučnite i nagnite se ulijevo.
Video na temu
Izvori:
- ravne guze u 2019
U uobičajenom smislu, težište se shvaća kao točka na koju se može primijeniti rezultanta svih sila koje djeluju na tijelo. Najjednostavniji primjer je dječja ljuljačka u obliku obične daske. Bez ikakvih kalkulacija, svako će dijete odabrati oslonac daske na takav način da uravnoteži (a možda čak i nadmaši) teškog čovjeka na ljuljački. Kod složenih tijela i presjeka neophodni su precizni proračuni i odgovarajuće formule. Čak i ako dobijete glomazne izraze, glavna stvar je ne bojati ih se, već zapamtiti da u početku govorimo o o gotovo elementarnom zadatku.
upute
Smatrati jednostavna poluga(vidi sliku 1), koji se nalazi u ravnotežnom položaju. Postavite x₁₂ na vodoravnu os s apscisom i postavite materijalne točke masa m₁ i m₂ na rubove. Razmotrite njihove koordinate duž osi 0x kao poznate i jednake x₁ i x₂. Poluga je u ravnotežnom položaju ako su momenti sila težine R₁=m₁g i P₂=m₂g jednaki. Trenutak jednak umnošku sila na njezino rame, koja se može pronaći kao duljina okomice spuštene s točke primjene sile na okomicu x=x₁₂. Stoga, u skladu sa slikom 1, m₁gℓ₁= m₂gℓ₂, ℓ₁=h₁₂-h₁, ℓ₂=h₂-h₁₂. Tada je m₁(h₁₂-h₁)=m₂(h₂-h₁₂). Riješite ovu jednadžbu i dobijete x₁₂=(m₁x₁+m₂x₂)/(m₁+m₂).
Da biste saznali ordinatu y₁₂, primijenite isto razmišljanje i izračune kao u koraku 1. I dalje slijedite ilustraciju prikazanu na slici 1, gdje je m₁gh₁= m₂gh₂, h₁=y₁₂-y₁, h₂=y₂-y₁₂. Tada je m₁(y₁₂-y₁)=m₂(y₂-y₁₂). Rezultat je y₁₂=(m₁u₁+m₂u₂)/(m₁+m₂). Zatim, uzmite u obzir da umjesto sustava dviju točaka postoji jedna točka M₁₂(x12,u12) ukupna masa(m1+m2).
Sustavu dviju točaka dodajte još jednu masu (m₃) s koordinatama (x₃, y₃). Kada računate, i dalje biste trebali pretpostaviti da imate posla s dvije točke, pri čemu druga od njih ima masu (m₁+m₂) i koordinate (x12,y12). Ponavljajući sve radnje koraka 1 i 2 za ove dvije točke, doći ćete do središta triju točaka x₁x₁+m₂x₂+m3x₃)/(m₁+m₂+m3), y₁₂₃=(m₁u₁+m₂u₂+m₃y₃)/( m ₁+m₂ +m3). Zatim dodajte četvrtu, petu i tako dalje točke. Nakon ponavljanja istog postupka mnogo puta, provjerite jesu li za sustav od n točaka koordinate težišta izračunate pomoću formule (vidi sliku 2). Imajte na umu činjenicu da tijekom rada ubrzanje slobodan pad g je smanjen. Stoga se koordinate središta mase i gravitacije podudaraju.
Zamislimo da u dijelu koji se razmatra postoji određeno područje D, površinska gustoća koji je ρ=1. Odozgo i odozdo slika je ograničena grafovima krivulja y=φ(x) i y=ψ(x), x ê [a,b]. Podijelite područje D s vertikalama x=x₍i-1₎, x=x₍i₎ (i=1,2,…,n) na tanke trake, tako da se mogu približno smatrati pravokutnicima s bazama ∆hi (vidi sliku .3). U ovom slučaju smatrajte da se sredina segmenta ∆hi poklapa s apscisom središta mase ξi=(1/2). Smatrajte da je visina pravokutnika približno jednaka [φ(ξi)-ψ(ξi)]. Tada je ordinata središta mase elementarne površine ηi=(1/2)[φ(ξi)+ψ(ξi)].
Zbog jednolike raspodjele gustoće, smatrajte da će se središte mase trake podudarati s njezinim geometrijskim središtem. Odgovarajuća elementarna masa ∆mi=ρ[φ(ξi)-ψ(ξi)]∆hi=[φ(ξi)-ψ(ξi)]∆hi koncentrirana je u točki (ξi,ηi). Došao je trenutak za obrnuti prijelaz iz mase prikazane u diskretnom obliku u kontinuiranu. U skladu s formulama za izračunavanje koordinata (vidi sl. 2) težišta, formiraju se integralni zbrojevi, prikazani na sl. 4a. Pri prelasku na limit kao ∆xi→0 (ξi→xi) od zbrojeva do određeni integrali, dobiti konačni odgovor (slika 4b). U odgovoru nema mase. Jednakost S=M treba shvatiti samo kao kvantitativnu. Dimenzije se ovdje razlikuju jedna od druge.
U inženjerskoj praksi se događa da postoji potreba za izračunavanjem koordinata težišta složene ravne figure koja se sastoji od jednostavnih elemenata za koje je poznato mjesto težišta. Ovaj zadatak je dio zadatka određivanja...
Geometrijske karakteristike kompozita presjeci grede i šipke. Inženjeri dizajna reznih matrica često se moraju suočiti sa sličnim pitanjima pri određivanju koordinata središta pritiska, razvijači shema opterećenja za različita vozila pri postavljanju tereta, projektanti građevinskih metalnih konstrukcija pri odabiru presjeka elemenata i, naravno, studenti pri proučavanju discipline” Teorijska mehanika" i "Čvrstoća materijala".
Biblioteka elementarnih figura.
Za simetrične plošne figure težište se poklapa sa središtem simetrije. Simetrična skupina elementarnih objekata uključuje: krug, pravokutnik (uključujući kvadrat), paralelogram (uključujući romb), pravilan mnogokut.
Od deset figura prikazanih na gornjoj slici, samo su dvije osnovne. Odnosno, koristeći trokute i sektore krugova, možete kombinirati gotovo sve figure od praktičnog interesa. Sve proizvoljne krivulje mogu se podijeliti u dijelove i zamijeniti kružnim lukovima.
Preostalih osam figura su najčešće, pa su zato i uvrštene u ovu jedinstvenu biblioteku. U našoj klasifikaciji ti elementi nisu osnovni. Od dva trokuta mogu se oblikovati pravokutnik, paralelogram i trapez. Šesterokut je zbroj četiriju trokuta. Isječak kruga je razlika između isječka kruga i trokuta. Prstenasti isječak kruga je razlika između dva isječka. Kružnica je isječak kružnice s kutom α=2*π=360˚. Polukrug je, prema tome, isječak kruga s kutom α=π=180˚.
Izračunavanje u Excelu koordinata težišta složene figure.
Uvijek je lakše prenijeti i percipirati informacije uzimajući u obzir primjer nego proučavati problem koristeći čisto teoretske izračune. Razmotrimo rješenje problema "Kako pronaći centar gravitacije?" na primjeru kompozitne figure prikazane na slici ispod ovog teksta.
Kompozitni presjek je pravokutnik (s dimenzijama a1 =80 mm, b1 =40 mm), koji je dodan gore lijevo jednakokračan trokut(s osnovnom veličinom a2 =24 mm i vis h2 =42 mm) i iz kojeg je gore desno izrezan polukrug (sa središtem u točki s koordinatama x03 =50 mm i g03 =40 mm, polumjer r3 =26 mm).
Koristit ćemo program koji će vam pomoći u izračunima MS Excel ili programa OOo Izračun . Bilo koji od njih lako će se nositi s našim zadatkom!
U stanicama sa žuta boja napunit ćemo ga pomoćni preliminaran kalkulacije .
Rezultate izračunavamo u ćelijama sa svijetlo žutom bojom.
Plava font je početni podaci .
Crno font je srednji rezultati proračuna .
Crvena font je konačni rezultati proračuna .
Počinjemo rješavati problem - počinjemo tražiti koordinate težišta presjeka.
Početni podaci:
1. U skladu s tim ćemo napisati nazive elementarnih figura koje čine kompozitni presjek
u ćeliju D3: Pravokutnik
u ćeliju E3: Trokut
u ćeliju F3: Polukrug
2. Koristeći "Biblioteku elementarnih slika" predstavljenu u ovom članku, odredit ćemo koordinate težišta elemenata kompozitnog presjeka xci I yci u mm u odnosu na proizvoljno odabrane osi 0x i 0y i upiši
u ćeliju D4: =80/2 = 40,000
xc 1 = a 1 /2
u ćeliju D5: =40/2 =20,000
yc 1 = b 1 /2
u ćeliju E4: =24/2 =12,000
xc 2 = a 2 /2
do ćelije E5: =40+42/3 =54,000
yc 2 = b 1 + h 2 /3
u ćeliju F4: =50 =50,000
xc 3 = x03
u ćeliju F5: =40-4*26/3/PI() =28,965
yc 3 = g 03 -4* r3 /3/ π
3. Izračunajmo površine elemenata F 1 , F 2 , F3 u mm2, ponovno koristeći formule iz odjeljka "Biblioteka elementarnih brojki"
u ćeliji D6: =40*80 =3200
F1 = a 1 * b1
u ćeliji E6: =24*42/2 =504
F2 = a2 *h2 /2
u ćeliji F6: =-PI()/2*26^2 =-1062
F3 =-π/2*r3 ^2
Površina trećeg elementa - polukruga - je negativna jer je izrez - prazan prostor!
Izračun koordinata težišta:
4. Odredite ukupnu površinu konačne figure F0 u mm2
u spojenoj ćeliji D8E8F8: =D6+E6+F6 =2642
F0 = F 1 + F 2 + F3
5. Izračunajmo statičke momente složenog lika Sx I Sy u mm3 u odnosu na odabrane osi 0x i 0y
u spojenoj ćeliji D9E9F9: =D5*D6+E5*E6+F5*F6 =60459
Sx = yc1 * F1 + yc2 *F2 + yc3 *F3
u spojenoj ćeliji D10E10F10: =D4*D6+E4*E6+F4*F6 =80955
Sy = xc1 * F1 + xc2 *F2 + xc3 *F3
6. I na kraju, izračunajmo koordinate težišta kompozitnog presjeka Xc I Yc u mm u odabranom koordinatnom sustavu 0x - 0y
u spojenoj ćeliji D11E11F11: =D10/D8 =30,640
Xc = Sy / F0
u spojenoj ćeliji D12E12F12: =D9/D8 =22,883
Yc =Sx /F0
Problem je riješen, izračun u Excelu je završen - pronađene su koordinate težišta presjeka, sastavljene pomoću tri jednostavna elementa!
Zaključak.
Primjer u članku odabran je kao vrlo jednostavan kako bi se lakše razumjela metodologija izračuna težišta složenog presjeka. Metoda je da bilo koja složena figura treba podijeliti na jednostavni elementi S poznata mjesta položaj težišta i napraviti konačne proračune za cijelu dionicu.
Ako je profil sastavljen od valjanih profila - kutnika i kanala, tada ih nije potrebno dijeliti na pravokutnike i kvadrate s izrezanim kružnim "π/2" sektorima. Koordinate težišta ovih profila dane su u GOST tablicama, odnosno, i kut i kanal bit će osnovni elementarni elementi u vašim izračunima kompozitnih presjeka (nema smisla govoriti o I-gredama, cijevi, šipke i šesterokuti - to su središnje simetrični presjeci).
Položaj koordinatnih osi, naravno, ne utječe na položaj težišta figure! Stoga odaberite koordinatni sustav koji pojednostavljuje vaše izračune. Ako bih, na primjer, u našem primjeru rotirao koordinatni sustav za 45˚ u smjeru kazaljke na satu, tada bi se izračunavanje koordinata težišta pravokutnika, trokuta i polukruga pretvorilo u još jednu zasebnu i glomaznu fazu izračuna koja se ne može izvesti “ u glavi".
Excel datoteka za izračun prikazana je u nastavku u ovom slučaju nije program. Umjesto toga, to je skica kalkulatora, algoritam, predložak koji slijedi u svakom konkretnom slučaju izradite vlastiti slijed formula za ćelije sa jarko žutom ispunom.
Dakle, sada znate kako pronaći težište bilo kojeg odjeljka! Potpuni izračun svih geometrijskih karakteristika proizvoljnih složenih kompozitnih presjeka bit će razmotren u jednom od nadolazećih članaka u odjeljku "". Pratite novosti na blogu.
Za primanje informacije o izdavanju novih članaka i za preuzimanje radnih programskih datoteka Molim vas da se pretplatite na obavijesti u prozoru koji se nalazi na kraju članka ili u prozoru na vrhu stranice.
Nakon unosa vaše adrese E-mail i klikom na gumb "Primaj najave članaka". NE ZABORAVI POTVRDI SVOJU PRETPLATU klikom na poveznicu u pismu koje će vam odmah stići na navedenu e-mail adresu (ponekad u mapi « Spam » )!
Nekoliko riječi o čaši, novčiću i dvjema vilicama, koji su prikazani u “ikoni ilustracije” na samom početku članka. Mnogima od vas sigurno je poznat ovaj “trik” koji izaziva zadivljene poglede djece i neupućenih odraslih. Tema ovog članka je težište. Upravo on i uporište, igrajući se s našom sviješću i iskustvom, jednostavno nam zavaravaju um!
Težište sustava “vilica+kovanica” uvijek se nalazi na fiksni udaljenost okomito prema dolje od ruba novčića, koji je pak uporište. Ovo je položaj stabilne ravnoteže! Ako protresete vilice, odmah postaje očito da sustav nastoji zauzeti prijašnji stabilan položaj! Zamislimo visak - točku učvršćenja (= točku oslonca novčića na rub čaše), šipku - os njihala (= u našem slučaju os je virtualna, budući da je masa dviju vilica je odvojen od različite strane prostor) i opterećenje na dnu osovine (=težište cijelog sustava “vilica + novčić”). Ako visak počnete skrenuti s okomice u bilo kojem smjeru (naprijed, natrag, lijevo, desno), tada će se ono neizbježno vratiti u svoj prvobitni položaj pod utjecajem gravitacije. stacionarno stanje ravnoteže(isto se događa s našim vilicama i novčićem)!
Ako ne razumijete, ali želite razumjeti, shvatite sami. Vrlo je zanimljivo "doći tamo" sam! Dodat ću da je isti princip korištenja stabilne ravnoteže također implementiran u igračku Vanka-stand-up. Samo se težište ove igračke nalazi iznad uporišne točke, ali ispod središta hemisfere nosive površine.
Uvijek mi je drago vidjeti vaše komentare, dragi čitatelji!!!
pitaj, POŠTUJUĆI autorski rad, download file NAKON PRETPLATE za najave članaka.
Centar gravitacije(ili centar mase) određenog tijela je točka koja ima svojstvo da će tijelo, ako se okači o tu točku, zadržati svoj položaj.
U nastavku razmatramo dvodimenzionalne i trodimenzionalne probleme povezane s traženjem različitih centara mase - uglavnom sa stajališta računalne geometrije.
U rješenjima koja se razmatraju u nastavku, mogu se razlikovati dva glavna: činjenica. Prvi je da je središte mase sustava materijalnih točaka jednako prosjeku njihovih koordinata, uzeto s koeficijentima proporcionalnim njihovim masama. Druga činjenica je da ako znamo središta mase dvaju figura koje se ne sijeku, tada će središte mase njihovog spoja ležati na segmentu koji povezuje ta dva središta i dijelit će ga u istom omjeru kao masa druga brojka odnosi se na masu prve.
Dvodimenzionalni slučaj: poligoni
Zapravo, kada se govori o centru mase dvodimenzionalne figure, može se misliti na jedan od sljedeća tri zadaci:
- Središte mase sustava točaka – t.j. sva je masa koncentrirana samo na vrhovima poligona.
- Središte mase okvira - tj. Masa poligona je koncentrirana na njegovom obodu.
- Središte mase čvrste figure - tj. Masa poligona raspoređena je po cijeloj njegovoj površini.
Svaki od ovih zadataka ima neovisna odluka, a o njima će se zasebno raspravljati u nastavku.
Središte mase točkastog sustava
Ovo je najjednostavniji od tri problema, a njegovo rješenje je dobro poznata fizikalna formula za središte mase sustava materijalnih točaka:
gdje su mase točaka, su njihovi radijus vektori (specificirajući njihov položaj u odnosu na ishodište), a je željeni radijus vektor centra mase.
Konkretno, ako sve točke imaju istu masu, tada su koordinate središta mase prosjek koordinate točaka. Za trokut ova točka se zove težište i poklapa se sa sjecištem medijana:
Za dokaz Ove formule su dovoljne za zapamtiti da se ravnoteža postiže u točki u kojoj je zbroj momenata svih sila jednak nuli. U ovom slučaju to se pretvara u uvjet da je zbroj radijus vektora svih točaka u odnosu na točku, pomnožen s masama odgovarajućih točaka, jednak nuli:
i, izražavajući odavde, dobivamo traženu formulu.
Središte mase okvira
Ali tada se svaka strana poligona može zamijeniti jednom točkom - sredinom ovog segmenta (budući da je središte mase homogenog segmenta sredina ovog segmenta), s masom jednakom duljini tog segmenta.
Sada imamo problem o sustavu materijalnih točaka, a primjenjujući na njega rješenje iz prethodnog paragrafa, nalazimo:
gdje je središte i-te stranice mnogokuta, duljina i-te stranice, opseg, tj. zbroj duljina stranica.
Za trokut može se pokazati sljedeća izjava: ova točka je sjecište simetrale trokut formiran središtima stranica izvornog trokuta. (da biste to pokazali, trebate upotrijebiti gornju formulu, a zatim uočite da simetrale dijele stranice dobivenog trokuta u istim omjerima kao i središta mase tih stranica).
Središte mase čvrste figure
Vjerujemo da je masa ravnomjerno raspoređena po liku, tj. gustoća u svakoj točki figure jednaka je istom broju.
Slučaj trokut
Tvrdi se da će za trokut odgovor biti isti težište, tj. točka koju čini aritmetička sredina koordinata vrhova:
Slučaj trokuta: dokaz
Dajmo ga ovdje elementarni dokaz, koji ne koristi integralnu teoriju.
Arhimed je bio prvi koji je dao takav čisto geometrijski dokaz, ali je bio vrlo kompliciran, s veliki broj geometrijske konstrukcije. Ovdje naveden dokaz preuzet je iz članka "Pronalaženje centroida na jednostavan način" autora Apostola, Mnatsakaniana.
Dokaz se svodi na pokazivanje da središte mase trokuta leži na jednoj od središnjica; Ponavljajući ovaj proces još dva puta, pokazat ćemo da središte mase leži u točki presjeka medijana, koja je težište.
Podijelimo ovaj trokut na četiri, povezujući središta strana, kao što je prikazano na slici:
Četiri dobivena trokuta slična su trokutu s koeficijentom .
Trokuti br. 1 i br. 2 zajedno tvore paralelogram čije središte mase leži u sjecištu njegovih dijagonala (budući da se radi o liku koji je simetričan s obzirom na obje dijagonale, pa je stoga njegovo središte masa mora ležati na svakoj od dvije dijagonale). Poanta je u sredini zajednička strana trokuta br. 1 i br. 2, a također leži na središnjici trokuta:
Neka sada vektor bude vektor povučen iz vrha u središte mase trokuta br. 1, a vektor neka bude vektor povučen iz točke (koja je, podsjetimo, sredina stranice na kojoj leži) :
Naš cilj je pokazati da su vektori i kolinearni.
Označimo s i točke koje su središta mase trokuta br. 3 i br. 4. Tada će, očito, središte mase skupa ova dva trokuta biti točka koja je sredina segmenta. Štoviše, vektor od točke do točke podudara se s vektorom.
Željeno središte mase trokuta nalazi se u sredini segmenta koji povezuje točke i (budući da smo trokut podijelili na dva dijela jednakih površina: br. 1-br. 2 i br. 3-br. 4):
Dakle, vektor od vrha do težišta je . S druge strane, jer trokut br. 1 sličan je trokutu s koeficijentom, tada je isti vektor jednak . Odavde dobivamo jednadžbu:
gdje nalazimo:
Dakle, dokazali smo da su vektori i kolinearni, što znači da željeno težište leži na središnjici koja izlazi iz vrha.
Štoviše, usput smo dokazali da centroid dijeli svaki medijan u omjeru, računajući od vrha.
Slučaj poligona
Prijeđimo sada na opći slučaj- tj. prigodi poligon. Za njega takvo zaključivanje više nije primjenjivo, pa problem svodimo na trokutasti: naime, mnogokut podijelimo na trokute (tj. trianguliramo ga), svakom trokutu nađemo središte mase, a zatim središte trokuta. masa nastalih centara mase trokuta.
Konačna formula je sljedeća:
gdje je težište th trokuta u triangulaciji danog poligona, je površina th trokuta triangulacije, je površina cijelog poligona.
Triangulacija konveksni poligon- trivijalan zadatak: za ovo, na primjer, možete uzeti trokute, gdje .
Slučaj poligona: alternativni način
S druge strane, uporaba gornje formule nije baš prikladna za nekonveksni poligoni, budući da njihova triangulacija sama po sebi nije lak zadatak. Ali za takve poligone možete smisliti jednostavniji pristup. Naime, povucimo analogiju s tim kako možete tražiti područje proizvoljnog poligona: odaberite proizvoljna točka, a zatim se zbroje predznačne površine trokuta koje čine ta točka i točke mnogokuta: . Slična se tehnika može upotrijebiti za pronalaženje središta mase: samo sada ćemo zbrojiti središta mase trokuta uzeta s koeficijentima proporcionalnima njihovim površinama, tj. Konačna formula za centar mase je:
gdje je proizvoljna točka, su točke poligona, je težište trokuta, je označeno područje ovog trokuta, je označeno područje cijelog poligona (tj.
Trodimenzionalni slučaj: poliedri
Slično dvodimenzionalnom slučaju, u 3D možemo odmah govoriti o četiri moguće formulacije problema:
- Središte mase sustava točaka – vrhova poliedra.
- Središte mase okvira su rubovi poliedra.
- Središte mase površine – tj. masa se raspoređuje po površini poliedra.
- Središte mase čvrstog poliedra – tj. masa je raspoređena po poliedru.
Središte mase točkastog sustava
Kao i u dvodimenzionalnom slučaju, možemo primijeniti fizička formula i dobiti isti rezultat:
koji u slučaju jednake mase pretvara u aritmetičku sredinu koordinata svih točaka.
Središte mase okvira poliedra
Slično dvodimenzionalnom slučaju, svaki brid poliedra jednostavno zamijenimo materijalnom točkom koja se nalazi u sredini tog brida i masom jednakom duljini tog brida. Dobivši problem materijalnih točaka, lako nalazimo njegovo rješenje kao težinski zbroj koordinata tih točaka.
Središte mase plohe poliedra
Svaka strana plohe poliedra je dvodimenzionalni lik čije središte mase možemo tražiti. Nakon što smo pronašli te centre mase i zamijenili svako lice svojim centrom mase, dobili smo problem sa materijalne bodove, što je već lako riješiti.
Središte mase čvrstog poliedra
Slučaj tetraedra
Kao u dvodimenzionalnom slučaju, prvo riješimo najjednostavniji zadatak- problem za tetraedar.
Tvrdi se da se središte mase tetraedra poklapa s točkom presjeka njegovih medijana (središte tetraedra je segment povučen od njegova vrha do središta mase suprotne strane; dakle, središte tetraedra prolazi kroz vrh i kroz točku presjeka središnjica trokutaste plohe).
Zašto je to tako? Ovdje je rezoniranje slično dvodimenzionalnom slučaju ispravno: ako tetraedar presiječemo na dva tetraedra pomoću ravnine koja prolazi kroz vrh tetraedra i neku sredinu suprotne strane, tada će oba rezultirajuća tetraedra imati isti volumen (jer trokutasto lice bit će podijeljeno središnjom u dva trokuta jednaka površina, a visina dva tetraedra se neće promijeniti). Ponavljajući ove argumente nekoliko puta, nalazimo da središte mase leži u točki presjeka medijana tetraedra.
Ova točka - točka presjeka medijana tetraedra - naziva se njegova težište. Može se pokazati da zapravo ima koordinate jednake aritmetičkoj sredini koordinata vrhova tetraedra:
(ovo se može zaključiti iz činjenice da centroid dijeli medijane u omjeru)
Dakle, nema temeljne razlike između slučajeva tetraedra i trokuta: točka jednaka aritmetičkoj sredini vrhova je središte mase u dvije formulacije problema: obje kada su mase smještene samo na vrhovima, a kada su mase raspoređene po cijeloj površini/volumenu. Zapravo, ovaj se rezultat generalizira na proizvoljnu dimenziju: središte mase proizvoljne jednostavan(simpleks) je aritmetička sredina koordinata njegovih vrhova.
Slučaj proizvoljnog poliedra
Prijeđimo sada na opći slučaj - slučaj proizvoljnog poliedra.
Opet, kao u dvodimenzionalnom slučaju, ovaj problem reduciramo na već riješen: poliedar podijelimo na tetraedre (tj. tetraedroniziramo), pronađemo središte mase svakog od njih i dobijemo konačni odgovor na problem u obliku ponderirane sume pronađenih središta težinski.
Pojam gravitacijskog centra nastao je već u antici; Arhimed je dao veliki doprinos razvoju teorije o težištima. Unatoč činjenici da se koncept centra gravitacije danas više proučava u nastavi fizike nego u matematici, on igra važnu ulogu u geometriji. Konkretno, već za Arhimeda, koncept težišta olakšao je pronalaženje područja nekih figura (na primjer, segmenta parabole), kao i volumena različitih prostornih tijela (osobito lopte). ).
U traktatu “O ravnoteži” ravna tijela, ili o težištima ravnih likova” Arhimed izlaže teoriju težišta aksiomatski, kao što Euklid izlaže geometriju u svojoj knjizi “Principia”. Prvo se daje određeni broj “pretpostavki”, odnosno aksioma.
Ovdje, "jednak" opet znači jednak u veličini, u ovom slučaju - imati istu težinu. Smisao prijedloga je da ako su određene figure, obješene, u ravnoteži, tada se ravnoteža neće poremetiti kada se bilo koja od njih zamijeni figurom jednake težine.
 |
|
Riža. 2. Dvije figure jednake težine trećoj su jednake |
Na temelju ovih pretpostavki Arhimed dokazuje niz posljedica.
Dokazi u knjizi “O ravnoteži...” uglavnom se provode metodom “kontradikcije”. Razmotrimo, na primjer, korolar 1. Neka su dani utezi, uravnoteženi na istoj duljini, nejednaki. Zatim, nakon što se nešto oduzme većem i doda manjem, ravnoteža bi se trebala poremetiti (prema aksiomima 2 i 3), a to je u suprotnosti s činjenicom da jednaka tijela na jednake duljine su uravnoteženi (prema aksiomu 1).
|
Da bi to dokazao, Arhimed odvojeno razmatra dva slučaja: dane težine su sumjerljive ili nesamjerljive. U prvom slučaju, težine obaju tijela višekratnici su određene težine P 0: P 1 = n 1 P 0, P 2 = n 2 P 0. Arhimed tijelo težine P 1 zamjenjuje s n 1 tijela težine P 0 svako, a tijelo težine P 2 s n 2 tijela težine P 0 svako, i sva ta (n 1 + n 2) tijela postavlja na jednu ravnu liniju. tako da su središta utega susjednih bila smještena na jednakoj udaljenosti jedna od druge.
Štoviše, prema pretpostavci 6, ovakva zamjena ne utječe na položaj težišta. A kako, prema korolariji 3, ova (n 1 + n 2) tijela imaju težište u sredini, onda je ono na istom mjestu za izvorna dva tijela. Iz toga slijedi da je l 1 /l 2 = P 2 /P 1 .
U slučaju nesamjerljivih utega, Arhimed ponovno argumentira kontradikcijom: on pretpostavlja da tijela s utezima i ovješena na segmentima koji zadovoljavaju uvjet neće biti uravnotežena. To znači da će težina biti veća ili manja od potrebne za ravnotežu. Ako je veća, tada ćemo od nje oduzeti nešto težine tako da preostala težina bude, s jedne strane, još uvijek veća od potrebne za ravnotežu, a s druge strane, tako da bude razmjerna s Tada, s jedne strane, (budući da je veći nego što je potrebno za ravnotežu), a s druge strane, (jer se ispostavlja da je kontradikcija, što znači da ne može biti više nego što je potrebno za ravnotežu. Ako je manji od onoga što je potrebno za ravnotežu, znači više, a isto se zaključivanje može izvesti relativno. Dakle, zakon poluge je dokazan.
(Poznato je da je poluga zauzimala veliko mjesto u aktivnostima Arhimeda - ne samo teorijskog mehaničara, već i dizajnera stvarno korištenih mehaničkih naprava; Arhimedove riječi "Dajte mi točku oslonca i pomaknut ću Zemlju" često citiran).
|
Medijan trokuta je promjer koji raspolavlja tetive paralelne s osnovicom, stoga na njemu leži težište (br. 217) područja trokuta. Posljedično, tri medijana trokuta, sijekući se, određuju težište područja trokuta.
Elementarna razmatranja pokazuju da se središnje strane trokuta sijeku u točki dvije trećine duljine svake od njih od odgovarajućeg vrha. Prema tome, težište područja trokuta leži na bilo kojem od njegovih medijana na udaljenosti od dvije trećine njegove duljine od vrha.
219. Četverokut.
Težište područja četverokuta određeno je sjecištem dviju ravnih linija koje dobivamo primjenom svojstva raspodjele težišta (točka 213).
Prvo podijelite četverokut dijagonalno na dva trokuta. Težište četverokuta leži na pravcu koji spaja težišta ovih trokuta. Ova ravna linija je prva od dvije tražene prave.
Na isti način dobivamo drugu ravnu liniju, dijeleći četverokut na dva trokuta (različita od prethodnih) pomoću druge dijagonale.
220. Poligon.
Znamo pronaći težišta površine trokuta i četverokuta. Da bismo odredili težište područja mnogokuta s proizvoljnim brojem stranica, pretpostavimo da znamo pronaći težište područja mnogokuta s manje strane
Zatim možete učiniti isto kao u slučaju četverokuta. Područje zadanog poligona podijeljeno je na dva dijela s dva različiti putevi crtanje dijagonala. U svakom od dva slučaja, težišta pojedinih dijelova su izravno povezana. Ove dvije linije sijeku se u željenom težištu.
221. Kružni luk.
Neka je potrebno odrediti težište kružnog luka AB duljine s. Povežimo kružnicu s dva međusobno okomita promjera OX i OY, od kojih prvi prolazi središtem C luka AB. Težište leži na osi OX, koja je os simetrije. Stoga je dovoljno odrediti 5. Za to imamo formulu:
Neka budu: a - polumjer kruga, c - duljina akorda AB, - kut između osi OX i polumjera nacrtanog na vrijednosti elementa, koji odgovaraju krajevima luka AB. Imamo:
Zatim, uzimajući B biti integracijska varijabla i izvodeći integraciju duž luka AB, dobivamo:
Prema tome, težište kružnog luka leži na polumjeru povučenom kroz sredinu luka, u točki čija je udaljenost od središta kružnice četvrtina proporcionalna duljini luka, polumjeru i tetivi.
222. Kružni sektor.
Sektor koji se nalazi između kružnog luka i dva radijusa OA i OB može se rastaviti međuradijusima na infinitezimalne sektore koji su međusobno jednaki. Ovi se elementarni sektori mogu smatrati beskonačno uskim trokutima; težište svakog od njih, prema prethodnom, leži na polumjeru povučenom kroz sredinu elementarnog luka ovog sektora, na udaljenosti od dvije trećine duljine polumjera od središta kruga . Jednake mase svih elementarnih trokuta, koncentrirane u njihovim težištima, tvore jedinstveni luk kružnice, čiji je polumjer jednak dvije trećine polumjera luka sektora. Slučaj koji razmatramo stoga se svodi na traženje težišta tog homogenog luka, tj. na problem riješen u prethodnom paragrafu.
223. Tetraedar.
Odredimo težište volumena tetraedra. Ravnina koja prolazi kroz jedan od bridova i kroz sredinu suprotnog brida je dijametralna ravnina koja raspolavlja tetive paralelne ovom posljednjem bridu: ona stoga sadrži težište volumena tetraedra. Prema tome, šest ravnina tetraedra, od kojih svaka prolazi kroz jedan od bridova i kroz sredinu suprotnog brida, sijeku se u jednoj točki, koja predstavlja težište volumena tetraedra.
Promotrimo tetraedar ABCD (slika 37); spojiti vrh A s težištem I baze BCD; pravac AI je sjecište dijametralnih ravnina koje prolaze
kroz bridove AB i zato sadrži željeno težište. Točka se nalazi na udaljenosti od dvije trećine medijane BH od vrha B. Na isti način uzmimo točku K na medijani AH koja je udaljena od vrha dvije trećine njezine duljine. Pravac B K presijecat će pravac A u težištu tetraedra. Izvucimo iz sličnosti trokuta ABN i JN, jasno je da je IK treći dio od AB), pa iz sličnosti trokuta i BGA zaključujemo da postoji treći dio.
Prema tome, težište volumena tetraedra leži na segmentu koji povezuje bilo koji vrh tetraedra sa težištem suprotne strane, na udaljenosti od tri četvrtine duljine tog segmenta od vrha.
Napomenimo također da je ravna crta koja spaja središnje točke R i L dvaju suprotnih bridova (slika 38) sjecište dijametralnih ravnina koje prolaze kroz te bridove, a također prolazi i kroz težište tetraedra. Dakle, tri ravne crte koje spajaju središta suprotnih rubova tetraedra sijeku se u njegovom težištu.
Neka su H i polovišta jednog para suprotnih bridova (slika 38), a M, N polovišta dva druga suprotna brida. Lik HNLM je paralelogram čije su stranice međusobno paralelne
dva rebra. Pravci HL i MN, koji spajaju središta dvaju suprotnih bridova, dijagonale su ovog paralelograma, što znači da se u točki sjecišta dijele na pola. Dakle, težište tetraedra leži u sredini segmenta koji povezuje središta dva suprotna ruba tetraedra.
224. Piramida s poligonalnom bazom.
Težište piramide leži na segmentu koji povezuje vrh piramide sa težištem baze na udaljenosti od tri četvrtine duljine tog segmenta od vrha.
Da bismo dokazali ovaj teorem, rastavljamo piramidu na tetraedre pomoću ravnina povučenih kroz vrh piramide i kroz dijagonale baze ABCD (na primjer, BD na slici 39).
Nacrtajmo ravninu koja siječe rubove na udaljenosti od tri četvrtine njihove duljine od vrha. Ova ravnina sadrži težišta tetraedra, a time i piramida. Mase tetraedra, za koje pretpostavljamo da su koncentrirani u njihovim težištima, proporcionalne su njihovim volumenima, a time i površinama baza (sl. 39) ili također površinama trokuta bad, bed,... , slične prethodnima i nalaze se u sekansnoj ravnini abcd... Dakle, dakle, željeno težište se poklapa s težištem mnogokuta abcd. Potonji leži na ravnoj crti koja spaja vrh S piramide sa težištem (slično smještenim) osnovnog poligona.
225. Prizma. Cilindar. Konus.
Na temelju simetrije, težišta prizme i cilindra leže u sredini segmenta koji povezuje težišta baza.
Uzimajući u obzir stožac kao granicu piramide upisane u njega s istim vrhom, uvjereni smo da težište stošca leži na segmentu koji povezuje vrh stošca s težištem baze, na udaljenosti od tri četvrtine duljine ovog segmenta od vrha. Također možemo reći da se težište stošca poklapa s težištem presjeka stošca ravninom koja je paralelna s osnovicom i povučena na udaljenosti jedne četvrtine visine stošca od baze.
Albert Einstein kratka biografija
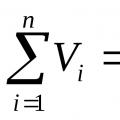Daltonov zakon za smjesu plinova: primjeri rješavanja problema
Disanje Boyle-Mariotteov zakon Boyle-Mariotteov zakon odvija se pri konstantnoj