Số so sánh modulo 7. So sánh modulo một số tự nhiên
So sánh với một cái chưa biết x giống như
Ở đâu . Nếu như Một N không chia hết cho tôi, đó là cái gọi là bằng cấp so sánh.
Theo quyết định so sánh là bất kỳ số nguyên nào x 0 , mà
Nếu như X 0 thỏa mãn phép so sánh thì theo tính chất của 9 phép so sánh, mọi số nguyên so sánh được với x 0 modulo tôi. Do đó, tất cả các nghiệm so sánh thuộc cùng một lớp dư theo modulo T, chúng tôi sẽ coi đó là một giải pháp. Như vậy, phép so sánh có nhiều nghiệm cũng như có nhiều phần tử của hệ thống dư lượng hoàn chỉnh thỏa mãn nó.
Những phép so sánh có tập nghiệm trùng nhau được gọi là tương đương.
2.2.1 So sánh bậc một
So sánh mức độ đầu tiên với một ẩn số X giống như
![]() (2.2)
(2.2)
Định lý 2.4. Để so sánh có ít nhất một nghiệm thì điều cần và đủ là số b chia cho GCD( Một, tôi).
Bằng chứng.Đầu tiên ta chứng minh sự cần thiết. Cho phép d
=
GCD( Một,
tôi)
Và X 0
- Giải pháp so sánh Sau đó ![]() , tức là sự khác biệt Ồ 0
−
b
chia T. Vậy có một số nguyên như vậy q,
Cái gì Ồ 0
−
b
=
qm.
Từ đây b= à 0
−
qm.
Và kể từ khi d,
làm ước số chung, chia các số MỘT Và T, thì số trừ và số trừ được chia cho d,
và do đó b
chia d.
, tức là sự khác biệt Ồ 0
−
b
chia T. Vậy có một số nguyên như vậy q,
Cái gì Ồ 0
−
b
=
qm.
Từ đây b= à 0
−
qm.
Và kể từ khi d,
làm ước số chung, chia các số MỘT Và T, thì số trừ và số trừ được chia cho d,
và do đó b
chia d.
Bây giờ hãy chứng minh tính đủ. Cho phép d- ước chung lớn nhất của các số MỘT Và T, Và b chia d. Khi đó, theo định nghĩa tính chia hết, tồn tại các số nguyên sau Một 1 , b 1 ,T 1 , Cái gì .
Sử dụng thuật toán Euclide mở rộng, chúng ta tìm thấy biểu diễn tuyến tính của số 1 = gcd( Một 1 , tôi 1 ):
![]()
đối với một số người x 0 , y 0 . Hãy nhân cả hai vế của đẳng thức cuối cùng với b 1 d:
hoặc, cái gì giống nhau,
,
nghĩa là, và là giải pháp cho sự so sánh. □
Ví dụ 2.10. So sánh 9 X= 6 (mod 12) có nghiệm vì gcd(9, 12) = 3 và 6 chia hết cho 3. □
Ví dụ 2.11. So sánh 6x= 9 (mod 12) không có nghiệm, vì gcd(6, 12) = 6, và 9 không chia hết cho 6. □
Định lý 2.5. Giả sử so sánh (2.2) có thể giải được và d = GCD( Một, tôi). Khi đó tập nghiệm so sánh (2.2) gồm d lớp dư lượng modulo T, cụ thể là, nếu X 0 - một trong các giải pháp, sau đó tất cả các giải pháp khác là
Bằng chứng. Cho phép X 0
- nghiệm so sánh (2.2), tức là ![]() Và ,
.
Vậy là có chuyện như vậy q, Cái gì Ồ 0
−
b
=
qm.
Bây giờ thay thế vào đẳng thức cuối cùng thay vì X 0
một giải pháp tùy ý có dạng, trong đó, chúng ta thu được biểu thức
Và ,
.
Vậy là có chuyện như vậy q, Cái gì Ồ 0
−
b
=
qm.
Bây giờ thay thế vào đẳng thức cuối cùng thay vì X 0
một giải pháp tùy ý có dạng, trong đó, chúng ta thu được biểu thức
, chia hết cho tôi. □
Ví dụ 2.12. So sánh 9 X=6 (mod 12) có đúng ba nghiệm, vì gcd(9, 12)=3. Những giải pháp này: X 0 = 2, x 0 + 4 = 6, X 0 + 2∙4=10.□
Ví dụ 2.13. So sánh 11 X=2 (mod 15) có một giải pháp duy nhất X 0 = 7, vì GCD(11,15)=1.□
Chúng tôi sẽ chỉ cho bạn cách giải các so sánh cấp độ một. Không mất tính tổng quát, ta giả sử GCD( Một, t) = 1. Khi đó có thể tìm nghiệm của phép so sánh (2.2), chẳng hạn bằng cách sử dụng thuật toán Euclide. Thật vậy, bằng cách sử dụng thuật toán Euclide mở rộng, chúng tôi biểu diễn số 1 dưới dạng tổ hợp tuyến tính của các số Một Và T:
Hãy nhân cả hai vế của đẳng thức này với b, chúng tôi nhận được: b = bụng + ông bà, Ở đâu bụng - b = - ông bà, đó là Một ∙ (bq) = b(mod tôi) Và bq- Giải pháp so sánh (2.2).
Một giải pháp khác là sử dụng định lý Euler. Một lần nữa chúng ta tin rằng GCD(a, T)= 1. Chúng ta áp dụng định lý Euler: ![]() . Nhân cả hai vế so sánh với b:
. Nhân cả hai vế so sánh với b:
![]() .
Viết lại biểu thức cuối cùng dưới dạng
.
Viết lại biểu thức cuối cùng dưới dạng  , ta thu được nghiệm so sánh (2.2).
, ta thu được nghiệm so sánh (2.2).
Bây giờ hãy để GCD( Một, tôi) = d>1. Sau đó Một = Mộttd, tôi = tôitd, trong đó GCD( MỘT 1 , tôi 1) = 1. Ngoài ra, cần b = b 1 d, để việc so sánh có thể giải quyết được. Nếu như X 0 - Giải pháp so sánh MỘT 1 x = b 1 (mod tôi 1), và là duy nhất, vì GCD( MỘT 1 , tôi 1) = 1 thì X 0 sẽ là giải pháp và so sánh MỘT 1 xd = db 1 (mod tôi 1), tức là so sánh ban đầu (2.2). Nghỉ ngơi d- Tìm được 1 nghiệm theo Định lý 2.5.
Dự án toán học theo chủ đề
"So sánh modulo"
Zaripova Aisylu
Quận Sovetsky của Kazan
MBU "Trường trung học số 166", lớp 7a
Người hướng dẫn khoa học: Antonova N.A.
Mục lục
Giới thiệu__________________________________________________________3
So sánh là gì______________________________________________4
Khái niệm so sánh modulo__________________________4
Lịch sử ra đời của khái niệm so sánh modulo_____4
Tính chất của so sánh__________________________________________4
Cách sử dụng so sánh modulo đơn giản nhất là để xác định tính chia hết của các số__________________________6
Một nhiệm vụ so sánh______________________________8
Việc sử dụng so sánh modulo trong hoạt động nghề nghiệp________________________________________________9
Áp dụng so sánh để giải quyết vấn đề______________________________6
Kết luận________________________________________________10
Danh sách tài liệu đã sử dụng______________________________________11
Giới thiệu.
Chủ đề: So sánh Modulo.
Bài toán: Nhiều học sinh gặp phải các bài toán khi chuẩn bị cho kỳ thi Olympic, giải bài toán này dựa trên kiến thức về số dư khi chia số nguyên cho số tự nhiên. Chúng tôi quan tâm đến những loại vấn đề này và các phương pháp khả thi để giải quyết chúng. Hóa ra chúng có thể được giải bằng cách sử dụng so sánh modulo.
Mục tiêu: Tìm hiểu bản chất của so sánh modulo, các phương pháp chính để làm việc với so sánh modulo.
Mục tiêu: tìm tài liệu lý thuyết về chủ đề này, xem xét các vấn đề được giải bằng so sánh modulo, chỉ ra các phương pháp phổ biến nhất để giải các vấn đề đó, rút ra kết luận.
Đối tượng nghiên cứu: lý thuyết số.
Đối tượng nghiên cứu: lý thuyết so sánh modulo.
Công trình liên quan đến nghiên cứu lý thuyết và có thể được sử dụng để chuẩn bị cho các kỳ thi Olympic toán học. Nội dung của nó tiết lộ các khái niệm cơ bản về so sánh modulo và các tính chất chính của chúng, đồng thời cung cấp các ví dụ về cách giải các bài toán về chủ đề này.
TÔI . So sánh là gì?
Khái niệm so sánh modulo
Các số và được gọi là có thể so sánh được về mô đun nếu chúng chia hết cho, nói cách khác, a và b có cùng số dư khi chia cho.
chỉ định
Ví dụ:
12 và 32 tương đương với modulo 5, vì 12 chia cho 5 dư 2 và 32 chia cho 2 dư 2. Nó được viết12 ;
101 và 17 tương đương với modulo 21;
Lịch sử xuất hiện của khái niệm so sánh modulo.
Lý thuyết chia hết phần lớn được tạo ra bởi Euler. Định nghĩa về so sánh được đưa ra trong cuốn sách “Nghiên cứu số học” của K.F. Gauss. Tác phẩm này viết bằng tiếng Latin bắt đầu được in từ năm 1797, nhưng cuốn sách chỉ được xuất bản vào năm 1801 do quá trình in ấn vào thời điểm đó cực kỳ tốn nhiều công sức và thời gian. Phần đầu tiên trong cuốn sách của Gauss có tên: “Về việc so sánh các con số”. Chính Gauss là người đã đề xuất biểu tượng của phép so sánh modulo đã được thiết lập trong toán học.
Tính chất của so sánh.
Nếu như
Bằng chứng:
Nếu chúng ta thêm đẳng thức thứ hai vào đẳng thức thứ nhất, chúng ta sẽ nhận được
là tổng của hai số nguyên, do đó là một số nguyên.
Nếu chúng ta trừ đi số thứ hai từ đẳng thức thứ nhất, chúng ta sẽ nhận được
đây là hiệu của hai số nguyên, do đó có nghĩa nó là một số nguyên.
Hãy xem xét biểu thức:
Đây là sự khác biệt của tích của các số nguyên, do đó có nghĩa là nó là một số nguyên.
Đây là hệ quả của tính chất so sánh thứ ba.
Q.E.D.
5) Nếu như.
Bằng chứng: Hãy tìm tổng của hai biểu thức sau:
là tổng của hai số nguyên nên nó là số nguyên, do đó .
Q.E.D.
6) Nếu là số nguyên thì
Chứng minh: , ở đâuP– một số nguyên, nhân đẳng thức này với, ta được: . Vì là tích của các số nguyên nên điều cần chứng minh là
7) Nếu như
Bằng chứng: cách lập luận tương tự như cách chứng minh tính chất 6.
8) Nếu như - các số nguyên tố cùng nhau thì
Bằng chứng: , chia biểu thức này cho, ta được: - các số nguyên tố cùng nhau, có nghĩa là chúng chia hết cho một số nguyên, tức là =. Và điều này có nghĩa là điều cần phải chứng minh.
II . Vận dụng so sánh để giải quyết vấn đề
2.1. Cách sử dụng so sánh modulo đơn giản nhất là xác định tính chia hết của các số.
Ví dụ. Tìm số dư của 2 2009 vào lúc 7 giờ.
Giải: Xét lũy thừa của 2:
nâng so sánh lên lũy thừa 668 và nhân với, ta được: .
Trả lời: 4.
Ví dụ. Chứng minh rằng 7+7 2 +7 3 +…+7 4 N chia hết cho 100 với mọiNtừ một tập hợp số nguyên.
Giải pháp: Xét sự so sánh
vân vân. Tính chất chu kỳ của số dư được giải thích bằng quy tắc nhân các số trong một cột. Cộng bốn so sánh đầu tiên, chúng tôi nhận được:
Điều này có nghĩa là số tiền này được chia cho 100 mà không có phần dư. Tương tự, bằng cách cộng các phép so sánh sau đây về 4, chúng ta nhận được rằng mỗi tổng như vậy chia hết cho 100 mà không có số dư. Điều này có nghĩa là toàn bộ số tiền bao gồm 4Nsố hạng chia hết cho 100 không có số dư. Q.E.D.
Ví dụ. Xác định ở giá trị nàoNbiểu thức chia hết cho 19 mà không có phần dư.
Giải pháp: .
Hãy nhân sự so sánh này với 20. Chúng ta nhận được.
Vậy hãy cộng các so sánh lại. . Như vậy vế phải của phép so sánh luôn chia hết cho 19 đối với mọi số tự nhiênN, có nghĩa là biểu thức ban đầu chia hết cho 19 với tự nhiênN.
Trả lời N - số tự nhiên bất kỳ
Ví dụ. Số đó kết thúc bằng chữ số nào?
Giải pháp. Để giải quyết vấn đề này, chúng ta sẽ chỉ theo dõi chữ số cuối cùng. Xét lũy thừa của số 14:
Bạn có thể nhận thấy rằng nếu số mũ là số lẻ thì giá trị của bậc kết thúc bằng 4 và nếu số mũ là số chẵn thì nó kết thúc bằng 6. Sau đó, nó kết thúc bằng 6, tức là. là một số chẵn Vì vậy, nó sẽ kết thúc sau 6.
Trả lời 6.
2.2. Một nhiệm vụ so sánh
Bài viết của N. Vilenkin “So sánh và các loại dư lượng” trình bày một vấn đề đã được nhà vật lý nổi tiếng người Anh Dirac giải quyết trong những năm sinh viên của ông.
Ngoài ra còn có một giải pháp ngắn gọn cho vấn đề này bằng cách sử dụng so sánh modulo. Nhưng chúng tôi đã gặp phải một số vấn đề tương tự. Ví dụ.
Một người qua đường tìm thấy một đống táo gần gốc cây có một con khỉ đang ngồi. Sau khi đếm chúng, anh nhận ra rằng nếu đưa 1 quả táo cho khỉ thì số táo còn lại sẽ được chia thành N Không một dâu vêt. Sau khi đưa quả táo thừa cho khỉ, nó lấy 1/ N những quả táo còn lại và bỏ đi. Sau đó, người qua đường tiếp theo đến gần đống đổ nát, rồi người tiếp theo, v.v. Mỗi người qua đường sau khi đếm số táo đều nhận thấy rằng số của chúng khi chia cho N đưa phần còn lại 1 và sau khi đưa quả táo thừa cho con khỉ, nó lấy cho mình 1 quả. N những quả táo còn lại và đi tiếp. Sau khi người cuối cùng rời đi, N người qua đường, số táo còn lại trong đống được chia cho N Không một dâu vêt. Hỏi lúc đầu trong đống táo có bao nhiêu quả táo?
Thực hiện lập luận tương tự như Dirac, chúng ta thu được một công thức tổng quát để giải một lớp các bài toán tương tự: , trong đóN- số tự nhiên.
2.3. Ứng dụng so sánh module trong hoạt động chuyên môn.
Lý thuyết so sánh được áp dụng vào lý thuyết mã hóa nên tất cả những người chọn nghề liên quan đến máy tính đều sẽ nghiên cứu và có thể áp dụng so sánh vào hoạt động nghề nghiệp của mình. Ví dụ, một số khái niệm lý thuyết số, bao gồm so sánh modulo, được sử dụng để phát triển các thuật toán mã hóa khóa công khai.
Phần kết luận.
Tác phẩm phác thảo các khái niệm và tính chất cơ bản của so sánh modulo và minh họa việc sử dụng so sánh modulo bằng các ví dụ. Tài liệu này có thể được sử dụng để chuẩn bị cho các kỳ thi Olympic toán học và Kỳ thi Thống nhất cấp Bang.
Danh sách tài liệu tham khảo đã cho cho phép, nếu cần, xem xét một số khía cạnh phức tạp hơn của lý thuyết so sánh modulo và các ứng dụng của nó.
Danh sách tài liệu được sử dụng
Alfutova N.B. Đại số và lý thuyết số./N.B.Alfutova, A.V.Ustinov. M.:MCNMO, 2002, 466 tr.
Bukhshtab A.A. Lý thuyết số. /A.A.Bukhshtab. M.: Giáo dục, 1960.
Vilenkin N. So sánh và phân loại dư lượng./N.Vilenkin.//Quantum. – 1978.- 10.
Fedorova N.E. Nghiên cứu đại số và phân tích toán học. Lớp 10.http:// www. thuận lợi. ru/ sách điện tử/ Fedorova_ Đại số học_10 kl/1/ xht
ru. wikipedia. tổ chức/ wiki/So sánh_modulo.
Sự định nghĩa 1. Nếu hai số là 1) Một Và b khi chia cho Pđưa ra số dư tương tự r, thì những con số như vậy được gọi là cân bằng hoặc so sánh trong mô-đun P.
Tuyên bố 1. Cho phép P một số dương nào đó. Khi đó mỗi số Một luôn luôn và hơn nữa, theo cách duy nhất có thể được biểu diễn dưới dạng
Nhưng những con số này có thể đạt được bằng cách thiết lập r bằng 0, 1, 2,..., P−1. Kể từ đây sp+r=a sẽ nhận được tất cả các giá trị số nguyên có thể.
Hãy chứng minh rằng biểu diễn này là duy nhất. Hãy giả vờ như vậy P có thể được biểu diễn theo hai cách a=sp+r Và a=s 1 P+r 1 . Sau đó
| (2) |
Bởi vì r 1 chấp nhận một trong các số 0,1, ..., P−1 thì giá trị tuyệt đối r 1 −rít hơn P. Nhưng từ (2) suy ra rằng r 1 −r nhiều P. Kể từ đây r 1 =r Và S 1 =S.
Con số r gọi điện dấu trừ con số Một modulo P(nói cách khác là số r gọi là phần còn lại của một số Một TRÊN P).
Tuyên bố 2. Nếu hai số Một Và b so sánh trong mô-đun P, Cái đó a−b chia P.
Thật sự. Nếu hai số Một Và b so sánh trong mô-đun P, thì khi chia cho P có cùng số dư P. Sau đó
chia P, bởi vì vế phải của phương trình (3) được chia cho P.
Tuyên bố 3. Nếu hiệu của hai số chia hết cho P, thì những con số này có thể so sánh được về mô đun P.
Bằng chứng. Hãy ký hiệu bằng r Và r dư 1 phép chia Một Và b TRÊN P. Sau đó
Ví dụ 25≡39 (mod 7), −18≡14 (mod 4).
Từ ví dụ đầu tiên, 25 khi chia cho 7 sẽ có cùng số dư là 39. Thật vậy, 25 = 3·7+4 (dư lượng 4). 39=3·7+4 (dư lượng 4). Khi xem xét ví dụ thứ hai, bạn cần tính đến số dư phải là số không âm nhỏ hơn mô đun (tức là 4). Khi đó chúng ta có thể viết: −18=−5·4+2 (dư lượng 2), 14=3·4+2 (dư lượng 2). Do đó, −18 khi chia cho 4 thì dư 2, và 14 khi chia cho 4 thì dư 2.
Thuộc tính của so sánh modulo
Tài sản 1. Cho bât ki ai Một Và P Luôn luôn
không phải lúc nào cũng có sự so sánh
Ở đâu λ là ước chung lớn nhất của các số tôi Và P.
Bằng chứng. Cho phép λ ước chung lớn nhất của các số tôi Và P. Sau đó
Bởi vì m(a−b) chia k, Cái đó
Kể từ đây
Và tôi là một trong các ước của số P, Cái đó
Ở đâu h=pqs.
Lưu ý rằng chúng tôi có thể cho phép so sánh dựa trên các mô-đun phủ định, tức là so sánh a≡b mod( P) có nghĩa là trong trường hợp này sự khác biệt a−b chia P. Tất cả các thuộc tính so sánh vẫn có hiệu lực đối với các mô-đun phủ định.
So sánh bậc một với ẩn số có dạng:
f(x) 0 (chế độ tôi); f(X) = Ồ + và N. (1)
Giải quyết so sánh- nghĩa là tìm tất cả các giá trị của x thỏa mãn nó. Hai phép so sánh thỏa mãn cùng giá trị của x gọi là tương đương.
Nếu so sánh (1) được thỏa mãn bởi bất kỳ x = x 1 thì (theo 49) tất cả các số có thể so sánh được với x 1, mô-đun tôi: x x 1 (chế độ tôi). Toàn bộ lớp số này được coi là một cách giải quyết. Với sự thỏa thuận như vậy, kết luận sau đây có thể được rút ra.
66.C căn chỉnh (1) sẽ có số nghiệm bằng số dư của hệ thống hoàn chỉnh thỏa mãn nó.
Ví dụ. So sánh
6x– 4 0 (mod 8)
Trong các số 0, 1,2, 3, 4, 5, 6, 7 có hai số thỏa mãn hệ dư lượng đầy đủ modulo 8: X= 2 và X= 6. Do đó phép so sánh này có hai nghiệm:
x 2 (mod 8), X 6 (mod 8).
So sánh bậc một bằng cách di chuyển số hạng tự do (có dấu ngược lại) sang vế phải có thể rút gọn về dạng
cây rìu b(mod tôi). (2)
Hãy xem xét một so sánh thỏa mãn điều kiện ( MỘT, tôi) = 1.
Theo 66, sự so sánh của chúng tôi có nhiều giải pháp cũng như số dư của hệ thống hoàn chỉnh thỏa mãn nó. Nhưng khi x chạy qua hệ thống dư lượng modulo hoàn chỉnh T, Cái đó Ồ chạy qua hệ thống khấu trừ hoàn chỉnh (trong số 60). Vì vậy, với một và chỉ một giá trị X, lấy từ hệ thống hoàn chỉnh, Ồ sẽ sánh ngang với b. Vì thế,
67. Khi (a, m) = 1 trục so sánh b(mod tôi)có một giải pháp.
Hãy để bây giờ ( Một, tôi) = d> 1. Khi đó, để so sánh (2) có nghiệm thì cần thiết (trong số 55) rằng b chia d, mặt khác không thể so sánh (2) với bất kỳ số nguyên x nào . Do đó giả sử b bội số d, chúng ta hãy đặt Một = Một 1 d, b = b 1 d, tôi = tôi 1 d. Khi đó so sánh (2) sẽ tương đương với điều này (viết tắt là d): Một 1 x b 1 (chế độ tôi), trong đó đã có ( MỘT 1 , tôi 1) = 1, và do đó nó sẽ có một nghiệm modulo tôi 1 . Cho phép X 1 – phần dư không âm nhỏ nhất của nghiệm này modulo m 1 , thì mọi số đều là x , tạo thành dung dịch này được tìm thấy ở dạng
x x 1 (chế độ tôi 1). (3)
Modulo m, các số (3) không phải tạo thành một nghiệm mà còn nhiều hơn, chính xác bằng nhiều nghiệm như các số (3) trong dãy 0, 1, 2, ..., tôi – 1 dư lượng modulo không âm nhỏ nhất m. Nhưng những con số sau (3) sẽ rơi vào đây:
x 1 , x 1 + tôi 1 , x 1 + 2tôi 1 , ..., x 1 + (d – 1) tôi 1 ,
những thứ kia. Tổng cộng d số (3); do đó so sánh (2) có d các quyết định.
Ta thu được định lý:
68. Đặt (a, m) = d. So sánh ax b ( mod m) không thể xảy ra nếu b không chia hết cho d. Khi b là bội số của d thì phép so sánh có d nghiệm.
69. Phương pháp giải so sánh bậc một dựa trên lý thuyết phân số liên tục:
Khai triển thành một phân số liên tục quan hệ tôi: một,

và nhìn vào hai phân số phù hợp cuối cùng:

theo tính chất của phân số liên tục (theo 30 ) chúng ta có

Vậy phép so sánh có nghiệm
để tìm, đủ để tính toán Pn- 1 theo phương pháp quy định ở 30.
Ví dụ. Hãy giải quyết sự so sánh
111x= 75 (mod 321). (4)
Ở đây (111, 321) = 3 và 75 là bội số của 3. Do đó, phép so sánh có ba nghiệm.
Chia cả hai vế so sánh và mô đun cho 3, ta được so sánh
37x= 25 (mod 107), (5)
mà trước tiên chúng ta phải giải quyết. Chúng ta có
| q | |||||
| P 3 |

Vì vậy, trong trường hợp này N = 4, P n – 1 = 26, b= 25, ta có nghiệm so sánh (5) ở dạng
x–26 ∙ 25 99 (mod 107).
Do đó nghiệm so sánh (4) được trình bày như sau:
X 99; 99 + 107; 99 + 2 ∙ 107 (mod 321),
X°99; 206; 313 (mod 321).
Tính phần tử nghịch đảo theo modulo đã cho
70.Nếu số là số nguyên Một Và N là nguyên tố cùng nhau thì có một số Một', thỏa mãn sự so sánh a ∙ a′ ≡ 1(chế độ N). Con số Một' gọi điện nghịch đảo nhân của modulo n và ký hiệu được sử dụng cho nó là Một- 1 (chế độ N).
Việc tính các đại lượng nghịch đảo modulo một giá trị nhất định có thể được thực hiện bằng cách giải một phép so sánh bậc một với một ẩn số, trong đó x số được chấp nhận Một'.
Tìm giải pháp so sánh
a∙x≡ 1(mod tôi),
Ở đâu ( là)= 1,
bạn có thể sử dụng thuật toán Euclid (69) hoặc định lý Fermat-Euler, trong đó phát biểu rằng nếu ( là) = 1 thì
Một φ( tôi) ≡ 1(mod tôi).
x ≡ Một φ( tôi)–1 (mod tôi).
Các nhóm và thuộc tính của chúng
Nhóm là một trong những lớp phân loại được sử dụng trong việc phân loại các cấu trúc toán học có đặc tính chung. Các nhóm có hai thành phần: một loạt (G) Và hoạt động() được xác định trên tập hợp này.
Các khái niệm về tập hợp, phần tử và thành viên là những khái niệm cơ bản chưa được xác định của toán học hiện đại. Bất kỳ tập hợp nào cũng được xác định bởi các phần tử có trong nó (do đó, các phần tử này cũng có thể là tập hợp). Vì vậy, chúng ta nói rằng một tập hợp được xác định hoặc cho trước nếu với bất kỳ phần tử nào, chúng ta có thể biết liệu nó có thuộc tập hợp này hay không.
Đối với hai bộ A, B Hồ sơ B MỘT, B MỘT, B∩ MỘT, B MỘT, B \ MỘT, MỘT × B tương ứng có nghĩa là B là tập con của tập hợp MỘT(tức là bất kỳ phần tử nào từ B cũng có trong MỘT, chẳng hạn tập hợp số tự nhiên chứa trong tập hợp số thực; ngoài ra, luôn luôn MỘT MỘT), B là tập con đúng của tập hợp MỘT(những thứ kia. B MỘT Và B ≠ MỘT), giao điểm của nhiều B Và MỘT(tức là tất cả các phần tử nằm đồng thời trong MỘT, và trong B, ví dụ giao của số nguyên và số thực dương là tập hợp các số tự nhiên), hợp của các tập hợp B Và MỘT(tức là một tập hợp bao gồm các phần tử nằm trong MỘT, hoặc trong B), đặt chênh lệch B Và MỘT(tức là tập hợp các phần tử nằm trong B, nhưng đừng nói dối MỘT), tích Descartes của tập hợp MỘT Và B(tức là một tập hợp các cặp có dạng ( Một, b), Ở đâu Một MỘT, b B). Qua | MỘT| sức mạnh của tập hợp luôn được biểu thị MỘT, I E. số phần tử trong tập hợp MỘT.
Một phép toán là một quy tắc theo đó hai phần tử bất kỳ của một tập hợp G(Một Và b) được so khớp với phần tử thứ ba từ G: một b.
Rất nhiều yếu tố G với một thao tác được gọi là nhóm, nếu các điều kiện sau được thỏa mãn.
Tại n họ cho số dư như nhau.
Công thức tương đương: a và b so sánh trong mô-đun n nếu sự khác biệt của họ Một - b chia hết cho n, hoặc nếu a có thể được biểu diễn dưới dạng Một = b + kN , Ở đâu k- một số nguyên. Ví dụ: 32 và −10 tương đương với modulo 7, vì
Câu “a và b so sánh được theo modulo n” được viết như sau:
Thuộc tính đẳng thức Modulo
Mối quan hệ so sánh modulo có các tính chất
Hai số nguyên bất kỳ Một Và b so sánh modulo 1.
Để có những con số Một Và b có thể so sánh được về mô-đun N, điều cần và đủ là hiệu của chúng chia hết cho N.
Nếu các số và có thể so sánh theo cặp theo mô đun N, sau đó là tổng và , cũng như tích của chúng và cũng có thể so sánh được về mô đun N.
Nếu những con số Một Và b so sánh trong mô-đun N, thì bằng cấp của họ Một k Và b k cũng có thể so sánh được về mô-đun N dưới bất kỳ điều kiện tự nhiên nào k.
Nếu những con số Một Và b so sánh trong mô-đun N, Và N chia tôi, Cái đó Một Và b so sánh trong mô-đun tôi.
Để có những con số Một Và b có thể so sánh được về mô-đun N, được trình bày dưới dạng phân tích kinh điển của nó thành các thừa số đơn giản P Tôi
cần thiết và đủ để
Quan hệ so sánh là quan hệ tương đương và có nhiều tính chất của quan hệ bình đẳng thông thường. Ví dụ: chúng có thể được cộng và nhân: nếu
Tuy nhiên, nói chung, những so sánh không thể được chia cho nhau hoặc cho những con số khác. Ví dụ: tuy nhiên, giảm đi 2 thì ta có một so sánh sai: . Các quy tắc viết tắt để so sánh như sau.
Bạn cũng không thể thực hiện các thao tác so sánh nếu mô đun của chúng không khớp.
Các tài sản khác:
Các định nghĩa liên quan
Các lớp khấu trừ
Tập hợp tất cả các số có thể so sánh được với Một modulo N gọi điện lớp khấu trừ Một modulo N , và thường được ký hiệu là [ Một] N hoặc . Như vậy, việc so sánh tương đương với sự bình đẳng của các lớp dư lượng [Một] N = [b] N .
Vì so sánh modulo N là một quan hệ tương đương trên tập hợp các số nguyên thì các lớp dư lượng theo modulo Nđại diện cho các lớp tương đương; số của chúng bằng nhau N. Tập hợp tất cả các lớp dư lượng modulo N ký hiệu là hoặc.
Các phép tính cộng, nhân bằng các phép toán cảm ứng tương ứng trên tập hợp:
[Một] N + [b] N = [Một + b] NĐối với các phép toán này thì tập hợp là một vành hữu hạn và nếu N trường đơn giản - hữu hạn.
Hệ thống khấu trừ
Hệ thống dư lượng cho phép bạn thực hiện các phép tính số học trên một tập hợp số hữu hạn mà không vượt quá giới hạn của nó. Hệ thống khấu trừ đầy đủ modulo n là tập hợp n số nguyên không thể so sánh được modulo n. Thông thường, các số dư không âm nhỏ nhất được coi là một hệ dư lượng hoàn chỉnh theo modulo n
0,1,...,N − 1hoặc các khoản khấu trừ nhỏ nhất tuyệt đối bao gồm các số
,trong trường hợp kỳ lạ N và những con số
trong trường hợp thậm chí N .
Giải quyết so sánh
So sánh cấp độ đầu tiên
Trong lý thuyết số, mật mã học và các lĩnh vực khoa học khác, vấn đề tìm lời giải cho phép so sánh cấp một về dạng thường nảy sinh:
Việc giải một so sánh như vậy bắt đầu bằng việc tính gcd (a, m)=d. Trong trường hợp này có thể xảy ra 2 trường hợp:
- Nếu như b không phải là bội số d, thì phép so sánh không có nghiệm.
- Nếu như b nhiều d, thì phép so sánh có nghiệm duy nhất modulo tôi / d, hoặc, cái gì giống nhau, d giải pháp modulo tôi. Trong trường hợp này, do giảm so sánh ban đầu bằng d sự so sánh là:
Ở đâu Một 1 = Một / d , b 1 = b / d Và tôi 1 = tôi / d là các số nguyên và Một 1 và tôi 1 là tương đối nguyên tố. Do đó số Một 1 có thể đảo ngược modulo tôi 1, tức là tìm số như vậy c, đó (nói cách khác, ). Bây giờ nghiệm được tìm thấy bằng cách nhân kết quả so sánh với c:
Tính toán thực tế giá trị c có thể được thực hiện theo nhiều cách khác nhau: sử dụng định lý Euler, thuật toán Euclid, lý thuyết phân số liên tục (xem thuật toán), v.v. Đặc biệt, định lý Euler cho phép viết giá trị c BẰNG:
Ví dụ
Để so sánh chúng ta có d= 2, vậy modulo 22 phép so sánh có hai nghiệm. Hãy thay 26 bằng 4, tương đương với modulo 22, rồi giảm cả 3 số đi 2:
Vì 2 nguyên tố cùng nhau với modulo 11 nên ta có thể giảm vế trái và vế phải đi 2. Kết quả là ta thu được một nghiệm modulo 11: , tương đương với hai nghiệm modulo 22: .
So sánh bậc hai
Việc giải các phép so sánh bậc hai bắt nguồn từ việc tìm hiểu xem một số đã cho có phải là thặng dư bậc hai hay không (sử dụng luật nghịch đảo bậc hai) và sau đó tính modulo căn bậc hai.
Câu chuyện
Định lý phần dư của Trung Quốc, được biết đến trong nhiều thế kỷ, phát biểu (bằng ngôn ngữ toán học hiện đại) rằng vành thặng dư modulo tích của một số số nguyên tố cùng nhau là
 Đạo hàm riêng của hàm ba biến
Đạo hàm riêng của hàm ba biến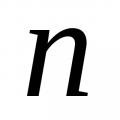 Hàm phân phối theo kinh nghiệm Sử dụng mẫu này, xây dựng hàm phân phối theo kinh nghiệm
Hàm phân phối theo kinh nghiệm Sử dụng mẫu này, xây dựng hàm phân phối theo kinh nghiệm Không có tiền nhưng bạn vẫn giữ
Không có tiền nhưng bạn vẫn giữ