ο μεθοδικό υλικόείναι για λόγους αναφοράς και καλύπτει ένα ευρύ φάσμα θεμάτων. Το άρθρο παρέχει μια επισκόπηση των γραφημάτων των κύριων στοιχειωδών συναρτήσεων και εξετάζει το πιο σημαντικό ερώτημα – πώς να φτιάξετε σωστά και ΓΡΗΓΟΡΑ ένα γράφημα. Κατά τη διάρκεια της μελέτης ανώτερα μαθηματικάχωρίς γνώση βασικών διαγραμμάτων στοιχειώδεις λειτουργίεςθα είναι δύσκολο, επομένως είναι πολύ σημαντικό να θυμάστε πώς μοιάζουν τα γραφήματα μιας παραβολής, υπερβολής, ημιτόνου, συνημιτόνου κ.λπ., θυμηθείτε κάποιες τιμές συναρτήσεων. Επίσης θα μιλήσουμεσε ορισμένες ιδιότητες βασικών συναρτήσεων.

Δεν προσποιούμαι την πληρότητα και την επιστημονική πληρότητα των υλικών, η έμφαση θα δοθεί, πρώτα απ 'όλα, στην πράξη - εκείνα τα πράγματα με τα οποία πρέπει να αντιμετωπίσει κανείς κυριολεκτικά σε κάθε βήμα, σε οποιοδήποτε θέμα ανώτερων μαθηματικών. Διαγράμματα για ανδρείκελα; Μπορείς να το πεις.

Με λαϊκή απαίτηση των αναγνωστών πίνακα περιεχομένων με δυνατότητα κλικ:

Επιπλέον, υπάρχει μια εξαιρετικά σύντομη περίληψη για το θέμα
– κατακτήστε 16 τύπους γραφημάτων μελετώντας ΕΞΙ σελίδες!

Σοβαρά, έξι, ακόμα κι εγώ ο ίδιος εξεπλάγην. Αυτή η περίληψη περιέχει βελτιωμένα γραφικά και είναι διαθέσιμη με ονομαστική χρέωση, μπορείτε να δείτε μια έκδοση επίδειξης. Είναι βολικό να εκτυπώσετε το αρχείο έτσι ώστε τα γραφήματα να είναι πάντα διαθέσιμα. Ευχαριστούμε για την υποστήριξη του έργου!

Και ξεκινάμε αμέσως:

Πώς να δημιουργήσετε σωστά τους άξονες συντεταγμένων;

Στην πράξη, τα τεστ συντάσσονται σχεδόν πάντα από τους μαθητές σε ξεχωριστά τετράδια, γραμμωμένα σε κλουβί. Γιατί χρειάζεστε καρό σημάδια; Μετά από όλα, η εργασία, κατ 'αρχήν, μπορεί να γίνει σε φύλλα Α4. Και το κλουβί είναι απαραίτητο μόνο για τον υψηλής ποιότητας και ακριβή σχεδιασμό των σχεδίων.

Οποιοδήποτε σχέδιο ενός γραφήματος συνάρτησης ξεκινά με άξονες συντεταγμένων.

Τα σχέδια είναι δισδιάστατα και τρισδιάστατα.

Ας εξετάσουμε πρώτα τη δισδιάστατη περίπτωση Καρτεσιανή ορθογώνιο σύστημασυντεταγμένες:

1) Ζωγραφίζουμε άξονες συντεταγμένων. Ο άξονας ονομάζεται άξονας x , και τον άξονα άξονας y . Προσπαθούμε πάντα να τα σχεδιάζουμε προσεγμένο και όχι στραβό. Τα βέλη δεν πρέπει επίσης να μοιάζουν με τα γένια του Papa Carlo.

2) Υπογράφουμε τους άξονες με κεφαλαία γράμματα «x» και «y». Μην ξεχάσετε να υπογράψετε τα τσεκούρια.

3) Ρυθμίστε την κλίμακα κατά μήκος των αξόνων: σχεδιάστε μηδέν και δύο ένα. Όταν κάνετε ένα σχέδιο, η πιο βολική και κοινή κλίμακα είναι: 1 μονάδα = 2 κελιά (σχέδιο στα αριστερά) - επιμείνετε σε αυτήν αν είναι δυνατόν. Ωστόσο, κατά καιρούς συμβαίνει ότι το σχέδιο δεν χωράει σε ένα φύλλο σημειωματάριου - τότε μειώνουμε την κλίμακα: 1 μονάδα = 1 κελί (σχέδιο στα δεξιά). Σπάνια, αλλά συμβαίνει ότι η κλίμακα του σχεδίου πρέπει να μειωθεί (ή να αυξηθεί) ακόμη περισσότερο

ΜΗΝ γράφετε από πολυβόλο ... -5, -4, -3, -1, 0, 1, 2, 3, 4, 5, ....Για επίπεδο συντεταγμένωνδεν είναι μνημείο του Ντεκάρτ και ο μαθητής δεν είναι περιστέρι. Βάζουμε μηδένκαι δύο μονάδες κατά μήκος των αξόνων. Ωρες ωρες αντίμονάδες, είναι βολικό να "ανιχνεύσετε" άλλες τιμές, για παράδειγμα, "δύο" στον άξονα της τετμημένης και "τρία" στον άξονα τεταγμένων - και αυτό το σύστημα (0, 2 και 3) θα ορίσει επίσης μοναδικά το πλέγμα συντεταγμένων.

Είναι καλύτερο να εκτιμήσετε τις εκτιμώμενες διαστάσεις του σχεδίου ΠΡΙΝ σχεδιαστεί το σχέδιο.. Έτσι, για παράδειγμα, εάν η εργασία απαιτεί τη σχεδίαση ενός τριγώνου με κορυφές , , , τότε είναι ξεκάθαρο ότι η δημοφιλής κλίμακα 1 μονάδα = 2 κελιά δεν θα λειτουργήσει. Γιατί; Ας δούμε το σημείο - εδώ πρέπει να μετρήσετε δεκαπέντε εκατοστά προς τα κάτω και, προφανώς, το σχέδιο δεν χωράει (ή μόλις χωράει) σε ένα φύλλο σημειωματάριου. Επομένως, επιλέγουμε αμέσως μια μικρότερη κλίμακα 1 μονάδα = 1 κελί.

Παρεμπιπτόντως, περίπου εκατοστά και κελιά σημειωματάριου. Είναι αλήθεια ότι υπάρχουν 15 εκατοστά σε 30 κελιά σημειωματάριων; Μετρήστε σε τετράδιο για τόκο 15 εκατοστά με χάρακα. Στην ΕΣΣΔ, ίσως αυτό ήταν αλήθεια... Είναι ενδιαφέρον να σημειωθεί ότι αν μετρήσετε αυτά τα ίδια εκατοστά οριζόντια και κάθετα, τότε τα αποτελέσματα (σε κελιά) θα είναι διαφορετικά! Αυστηρά μιλώντας, τα μοντέρνα σημειωματάρια δεν είναι καρό, αλλά ορθογώνια. Μπορεί να φαίνεται σαν ανοησία, αλλά το να σχεδιάσεις, για παράδειγμα, έναν κύκλο με πυξίδα σε τέτοιες καταστάσεις είναι πολύ άβολο. Για να είμαι ειλικρινής, σε τέτοιες στιγμές αρχίζεις να σκέφτεσαι την ορθότητα του συντρόφου Στάλιν, ο οποίος στάλθηκε σε στρατόπεδα για χάκερ στην παραγωγή, για να μην αναφέρουμε την εγχώρια αυτοκινητοβιομηχανία, την πτώση αεροπλάνων ή την έκρηξη σταθμών παραγωγής ενέργειας.

Μιλώντας για ποιότητα, ή μια σύντομη σύσταση για χαρτικά. Μέχρι σήμερα, τα περισσότερα σημειωματάρια που πωλούνται, χωρίς να λέμε άσχημα λόγια, είναι εντελώς καλικάντζαροι. Για τον λόγο ότι βρέχονται και όχι μόνο από στυλό gel, αλλά και από στυλό! Αποθήκευση σε χαρτί. Για εκκαθάριση εργασίες ελέγχουΣυνιστώ να χρησιμοποιήσετε τα σημειωματάρια του Arkhangelsk Pulp and Paper Mill (18 φύλλα, κλουβί) ή Pyaterochka, αν και είναι πιο ακριβό. Συνιστάται να επιλέξετε ένα στυλό gel, ακόμα και το φθηνότερο κινέζικο ξαναγέμισμα gel είναι πολύ καλύτερο από ένα στυλό, το οποίο είτε λερώνει είτε σκίζει χαρτί. Το μόνο «ανταγωνιστικό» στυλό στη μνήμη μου είναι το Erich Krause. Γράφει καθαρά, όμορφα και σταθερά - είτε με γεμάτο στέλεχος, είτε με σχεδόν άδειο.

Επιπροσθέτως: το όραμα ενός ορθογώνιου συστήματος συντεταγμένων μέσα από τα μάτια της αναλυτικής γεωμετρίας καλύπτεται στο άρθρο Γραμμική (μη) εξάρτηση διανυσμάτων. Διανυσματική βάση, λεπτομερείς πληροφορίεςσχετικά με συντεταγμένα τέταρταμπορείτε να βρείτε στη δεύτερη παράγραφο του μαθήματος Γραμμικές ανισότητες.

τρισδιάστατη θήκη

Είναι σχεδόν το ίδιο εδώ.

1) Σχεδιάζουμε άξονες συντεταγμένων. Πρότυπο: άξονας εφαρμογής – κατευθυνόμενος προς τα πάνω, άξονας – κατευθυνόμενος προς τα δεξιά, άξονας – προς τα κάτω προς τα αριστερά αυστηράσε γωνία 45 μοιρών.

2) Υπογράφουμε τα τσεκούρια.

3) Ρυθμίστε την κλίμακα κατά μήκος των αξόνων. Κλίμακα κατά μήκος του άξονα - δύο φορές μικρότερη από την κλίμακα κατά μήκος των άλλων αξόνων. Σημειώστε επίσης ότι στο σωστό σχέδιο, χρησιμοποίησα ένα μη τυπικό "serif" κατά μήκος του άξονα (Αυτή η δυνατότητα έχει ήδη αναφερθεί παραπάνω). Από την άποψή μου, είναι πιο ακριβές, πιο γρήγορο και πιο ευχάριστο αισθητικά - δεν χρειάζεται να αναζητήσετε τη μέση του κυττάρου κάτω από ένα μικροσκόπιο και να «σμιλεύσετε» τη μονάδα μέχρι την αρχή.

Όταν κάνετε ξανά ένα τρισδιάστατο σχέδιο - δώστε προτεραιότητα στην κλίμακα
1 μονάδα = 2 κελιά (σχέδιο στα αριστερά).

Σε τι χρησιμεύουν όλοι αυτοί οι κανόνες; Οι κανόνες υπάρχουν για να παραβιάζονται. Τι θα κάνω τώρα. Το γεγονός είναι ότι τα επόμενα σχέδια του άρθρου θα γίνουν από εμένα στο Excel και οι άξονες συντεταγμένων θα φαίνονται λανθασμένοι από την άποψη της σωστής σχεδίασης. Θα μπορούσα να σχεδιάσω όλα τα γραφήματα με το χέρι, αλλά είναι πραγματικά τρομακτικό να τα σχεδιάζω, καθώς το Excel είναι απρόθυμο να τα σχεδιάσει με μεγαλύτερη ακρίβεια.

Γραφήματα και βασικές ιδιότητες στοιχειωδών συναρτήσεων

Γραμμική συνάρτησηδίνεται από την εξίσωση. Το γράφημα της γραμμικής συνάρτησης είναι απευθείας. Για να κατασκευάσουμε μια ευθεία γραμμή, αρκεί να γνωρίζουμε δύο σημεία.

Παράδειγμα 1

Σχεδιάστε τη συνάρτηση. Ας βρούμε δύο σημεία. Συμφέρει να επιλέξετε το μηδέν ως ένα από τα σημεία.

Αν τότε

Παίρνουμε κάποιο άλλο σημείο, για παράδειγμα, 1.

Αν τότε

Κατά την προετοιμασία των εργασιών, οι συντεταγμένες των σημείων συνήθως συνοψίζονται σε έναν πίνακα:

Και οι ίδιες οι τιμές υπολογίζονται προφορικά ή σε προσχέδιο, αριθμομηχανή.

Βρίσκονται δύο σημεία, ας σχεδιάσουμε:

Κατά την κατάρτιση ενός σχεδίου, υπογράφουμε πάντα τα γραφικά.

Δεν θα είναι περιττό να ανακαλέσουμε ειδικές περιπτώσεις μιας γραμμικής συνάρτησης:

Προσέξτε πώς τοποθέτησα τις λεζάντες, Οι υπογραφές δεν πρέπει να είναι διφορούμενες κατά τη μελέτη του σχεδίου. ΣΤΟ αυτή η υπόθεσηΉταν εξαιρετικά ανεπιθύμητο να βάλετε μια υπογραφή δίπλα στο σημείο τομής των γραμμών ή κάτω δεξιά μεταξύ των γραφημάτων.

1) Μια γραμμική συνάρτηση της μορφής () ονομάζεται ευθεία αναλογικότητα. Για παράδειγμα, . Το γράφημα της ευθείας αναλογικότητας διέρχεται πάντα από την αρχή. Έτσι, η κατασκευή μιας ευθείας γραμμής απλοποιείται - αρκεί να βρείτε μόνο ένα σημείο.

2) Μια εξίσωση της μορφής ορίζει μια ευθεία παράλληλη προς τον άξονα, συγκεκριμένα, ο ίδιος ο άξονας δίνεται από την εξίσωση. Η γραφική παράσταση της συνάρτησης κατασκευάζεται αμέσως, χωρίς να βρεθούν σημεία. Δηλαδή, η καταχώρηση θα πρέπει να γίνει κατανοητή ως εξής: "y είναι πάντα ίσο με -4, για οποιαδήποτε τιμή του x."

3) Μια εξίσωση της μορφής ορίζει μια ευθεία παράλληλη προς τον άξονα, συγκεκριμένα, ο ίδιος ο άξονας δίνεται από την εξίσωση. Το γράφημα της συνάρτησης δημιουργείται επίσης αμέσως. Η καταχώρηση θα πρέπει να γίνει κατανοητή ως εξής: "το x είναι πάντα, για οποιαδήποτε τιμή του y, ίση με 1."

Κάποιοι θα ρωτήσουν, καλά, γιατί να θυμάστε την 6η δημοτικού;! Έτσι είναι, ίσως έτσι, μόνο κατά τη διάρκεια των ετών πρακτικής συνάντησα μια καλή ντουζίνα μαθητές που είχαν μπερδευτεί με το έργο της κατασκευής ενός γραφήματος όπως ή .

Η σχεδίαση μιας ευθείας γραμμής είναι η πιο κοινή ενέργεια κατά τη δημιουργία σχεδίων.

Η ευθεία γραμμή συζητείται αναλυτικά στο μάθημα της αναλυτικής γεωμετρίας και όσοι επιθυμούν μπορούν να ανατρέξουν στο άρθρο Εξίσωση ευθείας γραμμής σε επίπεδο.

Γράφημα τετραγωνικής συνάρτησης, γράφημα κυβικής συνάρτησης, πολυωνυμικό γράφημα

Παραβολή. Πρόγραμμα τετραγωνική λειτουργία () είναι μια παραβολή. Σκεφτείτε διάσημη υπόθεση:

Ας θυμηθούμε μερικές ιδιότητες της συνάρτησης.

Άρα, η λύση της εξίσωσής μας: - σε αυτό το σημείο βρίσκεται η κορυφή της παραβολής. Γιατί συμβαίνει αυτό, μπορούμε να μάθουμε από το θεωρητικό άρθρο για την παράγωγο και το μάθημα για τα άκρα της συνάρτησης. Στο μεταξύ, υπολογίζουμε την αντίστοιχη τιμή του "y":

Άρα η κορυφή βρίσκεται στο σημείο

Τώρα βρίσκουμε άλλα σημεία, ενώ χρησιμοποιούμε ευθαρσώς τη συμμετρία της παραβολής. Πρέπει να σημειωθεί ότι η συνάρτηση – δεν είναι καν, αλλά, παρόλα αυτά, κανείς δεν ακύρωσε τη συμμετρία της παραβολής.

Με ποια σειρά θα βρεθούν οι υπόλοιποι βαθμοί, νομίζω ότι θα φανεί από τον τελικό πίνακα:

Αυτός ο αλγόριθμοςΗ κατασκευή μπορεί μεταφορικά να ονομαστεί «σαΐτα» ή η αρχή του «μπρος-πίσω» με την Ανφίσα Τσέχοβα.

Ας κάνουμε ένα σχέδιο:

Από τα εξεταζόμενα γραφήματα, ένα άλλο χρήσιμο χαρακτηριστικό έρχεται στο μυαλό:

Για μια τετραγωνική συνάρτηση () ισχύει το εξής:

Αν , τότε οι κλάδοι της παραβολής κατευθύνονται προς τα πάνω.

Αν , τότε οι κλάδοι της παραβολής κατευθύνονται προς τα κάτω.

Η εις βάθος γνώση της καμπύλης μπορεί να αποκτηθεί στο μάθημα Υπερβολή και παραβολή.

Η κυβική παραβολή δίνεται από τη συνάρτηση . Εδώ είναι ένα οικείο σχέδιο από το σχολείο:

Ας παραθέσουμε βασικές ιδιότητεςλειτουργίες

Γράφημα συνάρτησης

Αντιπροσωπεύει έναν από τους κλάδους της παραβολής. Ας κάνουμε ένα σχέδιο:

Οι κύριες ιδιότητες της συνάρτησης:

Σε αυτή την περίπτωση, ο άξονας είναι κάθετη ασύμπτωτη για το γράφημα υπερβολής στο .

Θα είναι ΚΑΚΟ λάθος, εάν, όταν κάνουμε ένα σχέδιο, από αμέλεια, αφήσουμε το γράφημα να τέμνεται με την ασύμπτωτη .

Επίσης μονόπλευρα όρια, πείτε μας ότι μια υπερβολή δεν περιορίζεται από πάνωκαι δεν περιορίζεται από κάτω.

Ας εξερευνήσουμε τη συνάρτηση στο άπειρο: , δηλαδή, αν αρχίσουμε να κινούμαστε κατά μήκος του άξονα προς τα αριστερά (ή δεξιά) στο άπειρο, τότε τα «παιχνίδια» θα είναι ένα λεπτό βήμα απείρως κοντάπλησιάζει το μηδέν και, κατά συνέπεια, τους κλάδους της υπερβολής απείρως κοντάπλησιάζει τον άξονα.

Άρα ο άξονας είναι οριζόντια ασύμπτωτη για τη γραφική παράσταση της συνάρτησης, αν το "x" τείνει στο συν ή πλην άπειρο.

Η συνάρτηση είναι Περιττός, που σημαίνει ότι η υπερβολή είναι συμμετρική ως προς την αρχή. Αυτό το γεγονόςείναι προφανές από το σχέδιο, επιπλέον, μπορεί εύκολα να επαληθευτεί αναλυτικά: .

Η γραφική παράσταση μιας συνάρτησης της μορφής () αναπαριστά δύο κλάδους μιας υπερβολής.

Αν , τότε η υπερβολή βρίσκεται στο πρώτο και το τρίτο τεταρτημόριο συντεταγμένων(βλ. εικόνα παραπάνω).

Αν , τότε η υπερβολή βρίσκεται στο δεύτερο και τέταρτο τεταρτημόριο συντεταγμένων.

Δεν είναι δύσκολο να αναλυθεί η καθορισμένη κανονικότητα του τόπου διαμονής της υπερβολής από την άποψη των γεωμετρικών μετασχηματισμών των γραφημάτων.

Παράδειγμα 3

Κατασκευάστε τον δεξιό κλάδο της υπερβολής

Χρησιμοποιούμε τη μέθοδο κατασκευής κατά σημείο, ενώ συμφέρει να επιλέγουμε τις τιμές ώστε να διαιρούνται πλήρως:

Ας κάνουμε ένα σχέδιο:

Δεν θα είναι δύσκολο να κατασκευάσετε τον αριστερό κλάδο της υπερβολής, εδώ απλά θα βοηθήσει η παραδοξότητα της συνάρτησης. Σε γενικές γραμμές, στον πίνακα κατά σημείο κατασκευής, προσθέστε νοερά ένα μείον σε κάθε αριθμό, βάλτε τις αντίστοιχες τελείες και σχεδιάστε το δεύτερο κλάδο.

Λεπτομερείς γεωμετρικές πληροφορίες σχετικά με την εξεταζόμενη γραμμή μπορείτε να βρείτε στο άρθρο Υπερβολή και παραβολή.

Γράφημα εκθετικής συνάρτησης

Σε αυτή την παράγραφο, θα εξετάσω αμέσως την εκθετική συνάρτηση, αφού σε προβλήματα ανώτερων μαθηματικών στο 95% των περιπτώσεων είναι ο εκθέτης που εμφανίζεται.

Σας θυμίζω ότι αυτό είναι παράλογος αριθμός: , αυτό θα απαιτηθεί κατά την κατασκευή ενός γραφήματος, το οποίο, στην πραγματικότητα, θα κατασκευάσω χωρίς τελετή. Τρεις βαθμοίμάλλον αρκετά:

Ας αφήσουμε το γράφημα της συνάρτησης μόνο προς το παρόν, σχετικά αργότερα.

Οι κύριες ιδιότητες της συνάρτησης:

Βασικά, τα γραφήματα των συναρτήσεων φαίνονται ίδια, κ.λπ.

Πρέπει να πω ότι η δεύτερη περίπτωση είναι λιγότερο συχνή στην πράξη, αλλά συμβαίνει, γι' αυτό θεώρησα απαραίτητο να τη συμπεριλάβω σε αυτό το άρθρο.

Γράφημα λογαριθμικής συνάρτησης

Σκεφτείτε μια συνάρτηση με φυσικός λογάριθμος.
Ας κάνουμε ένα γραμμικό σχέδιο:

Αν ξεχάσατε τι είναι ο λογάριθμος, ανατρέξτε στα σχολικά εγχειρίδια.

Οι κύριες ιδιότητες της συνάρτησης:

Τομέα:

Εύρος τιμών: .

Η λειτουργία δεν περιορίζεται από πάνω: , αν και αργά, αλλά ο κλάδος του λογαρίθμου ανεβαίνει στο άπειρο.
Ας εξετάσουμε τη συμπεριφορά της συνάρτησης κοντά στο μηδέν στα δεξιά: . Άρα ο άξονας είναι κάθετη ασύμπτωτη για τη γραφική παράσταση της συνάρτησης με το "x" να τείνει προς το μηδέν στα δεξιά.

Φροντίστε να γνωρίζετε και να θυμάστε την τυπική τιμή του λογαρίθμου: .

Βασικά, η γραφική παράσταση του λογαρίθμου στη βάση μοιάζει με την ίδια: , , ( δεκαδικός λογάριθμοςστη βάση 10) κ.λπ. Ταυτόχρονα, όσο μεγαλύτερη είναι η βάση, τόσο πιο επίπεδο θα είναι το γράφημα.

Δεν θα εξετάσουμε την περίπτωση, κάτι που δεν θυμάμαι πότε την τελευταία φορά έφτιαξα ένα γράφημα με τέτοια βάση. Ναι, και ο λογάριθμος φαίνεται να είναι ένας πολύ σπάνιος επισκέπτης σε προβλήματα ανώτερων μαθηματικών.

Κλείνοντας την παράγραφο, θα πω ένα ακόμη γεγονός: Εκθετική συνάρτηση και λογαριθμική συνάρτηση είναι δύο αμοιβαία αντίστροφες συναρτήσεις . Αν κοιτάξετε προσεκτικά το γράφημα του λογάριθμου, μπορείτε να δείτε ότι αυτός είναι ο ίδιος εκθέτης, απλώς βρίσκεται λίγο διαφορετικά.

Γραφήματα τριγωνομετρικών συναρτήσεων

Πώς αρχίζει το τριγωνομετρικό μαρτύριο στο σχολείο; Σωστά. Από το ημίτονο

Ας σχεδιάσουμε τη συνάρτηση

Αυτή η γραμμή ονομάζεται ημιτονοειδής.

Σας θυμίζω ότι το «πι» είναι ένας παράλογος αριθμός: και στην τριγωνομετρία θαμπώνει στα μάτια.

Οι κύριες ιδιότητες της συνάρτησης:

Αυτή η λειτουργίαείναι περιοδικόςμε περίοδο. Τι σημαίνει? Ας δούμε την περικοπή. Στα αριστερά και στα δεξιά του, το ίδιο ακριβώς κομμάτι του γραφήματος επαναλαμβάνεται ατελείωτα.

Τομέα: , δηλαδή για οποιαδήποτε τιμή του "x" υπάρχει ημιτονική τιμή.

Εύρος τιμών: . Η συνάρτηση είναι περιορισμένος: , δηλαδή, όλα τα «παιχνίδια» βρίσκονται αυστηρά στο τμήμα .
Αυτό δεν συμβαίνει: ή, ακριβέστερα, συμβαίνει, αλλά τις εν λόγω εξισώσειςδεν έχω λύση.

Το εύρος και το εύρος της λειτουργίας.Στα δημοτικά μαθηματικά, οι συναρτήσεις μελετώνται μόνο στο σύνολο πραγματικούς αριθμούς R.Αυτό σημαίνει ότι το όρισμα συνάρτησης μπορεί να λάβει μόνο εκείνες τις πραγματικές τιμές για τις οποίες έχει οριστεί η συνάρτηση, π.χ. δέχεται επίσης μόνο πραγματικές αξίες. Πολλά Χόλες οι έγκυρες έγκυρες τιμές του ορίσματος Χ, για την οποία η συνάρτηση y= φά(Χ) ορίζεται, ονομάζεται εύρος λειτουργίας. Πολλά Υόλες τις πραγματικές αξίες yπου δέχεται η συνάρτηση καλείται εύρος λειτουργίας. Τώρα μπορείτε να δώσετε περισσότερα ακριβής ορισμόςχαρακτηριστικά: κανόνας(νόμος) της αντιστοιχίας μεταξύ των συνόλων X και Y, με την οποία για κάθε στοιχείο από το σύνολοΤο X μπορεί να βρει ένα και μόνο ένα στοιχείο από το σύνολο Y, ονομάζεται συνάρτηση.

Από αυτόν τον ορισμό προκύπτει ότι μια συνάρτηση θεωρείται δεδομένη εάν:

Το εύρος της λειτουργίας έχει οριστεί Χ ;

Το εύρος της λειτουργίας έχει οριστεί Υ ;

Ο κανόνας (νόμος) της αντιστοιχίας είναι γνωστός, και τέτοιος ώστε για καθένα

Μόνο μία τιμή συνάρτησης μπορεί να βρεθεί για μια τιμή ορίσματος.

Αυτή η απαίτηση μοναδικότητας της λειτουργίας είναι υποχρεωτική.

μονοτονική λειτουργία.Εάν για οποιεσδήποτε δύο τιμές του ορίσματος Χ 1 και Χ 2 της συνθήκης Χ 2 > Χ 1 ακολουθεί φά(Χ 2) > φά(Χ 1), μετά η συνάρτηση φά(Χ) λέγεται αυξανόμενη; αν για κανένα Χ 1 και Χ 2 της συνθήκης Χ 2 > Χ 1 ακολουθεί φά(Χ 2) < φά(Χ 1), μετά η συνάρτηση φά(Χ) λέγεται φθίνουσα. Μια συνάρτηση που μόνο αυξάνεται ή μόνο μειώνεται ονομάζεται μονότονος.

Περιορισμένες και απεριόριστες λειτουργίες.Η συνάρτηση καλείται περιορισμένοςαν υπάρχει τέτοιο θετικός αριθμός Μτι | φά(Χ) | Μγια όλες τις αξίες Χ .Εάν δεν υπάρχει τέτοιος αριθμός, τότε η συνάρτηση είναι απεριόριστος.

ΠΑΡΑΔΕΙΓΜΑΤΑ.

Η συνάρτηση που απεικονίζεται στο Σχ. 3 είναι οριοθετημένη, αλλά όχι μονότονη. Η συνάρτηση στο Σχήμα 4 είναι ακριβώς η αντίθετη, μονότονη, αλλά απεριόριστη. (Εξηγήστε το παρακαλώ!)

Συνεχείς και ασυνεχείς λειτουργίες.Λειτουργία y = φά (Χ) λέγεται συνεχής στο σημείοΧ = ένα, αν:

1) η συνάρτηση έχει οριστεί για Χ = ένα, δηλ. φά (ένα) υπάρχει;

2) υπάρχει πεπερασμένοςόριο lim φά (Χ) ;

Χ→ένα

(Βλ. "Όρια λειτουργιών")

3) φά (ένα) = λιμ φά (Χ) .

Χ→ένα

Εάν δεν πληρούται τουλάχιστον μία από αυτές τις προϋποθέσεις, τότε καλείται η συνάρτηση διακεκομμένοςστο σημείο Χ = ένα.

Αν η συνάρτηση είναι συνεχής μέσα όλα σημεία του τομέα ορισμού του, τότε λέγεται συνεχής λειτουργία.

Ζυγές και περιττές συναρτήσεις.Αν για όποιος Χ φά(- Χ) = φά (Χ), τότε καλείται η συνάρτηση ακόμη και; εάν συμβαίνει: φά(- Χ) = - φά (Χ), τότε καλείται η συνάρτηση Περιττός. Πρόγραμμα ομοιόμορφη λειτουργίασυμμετρικά ως προς τον άξονα Υ(Εικ.5), ένα γράφημα περιττή συνάρτηση Simμετρική για την προέλευση(Εικ. 6).

Περιοδική συνάρτηση.Λειτουργία φά (Χ) - περιοδικόςαν υπάρχει τέτοιο μη μηδενικόαριθμός Τγια ποιο λόγο όποιος Χαπό το πεδίο του ορισμού συνάρτησης λαμβάνει χώρα: φά (Χ + Τ) = φά (Χ). Τέτοιος ελάχιστακαλείται ο αριθμός περίοδο λειτουργίας. Ολα τριγωνομετρικές συναρτήσειςείναι περιοδικές.

ΠΑΡΑΔΕΙΓΜΑ 1. Απόδειξε αυτή την αμαρτία Χέχει περίοδο 2.

ΛΥΣΗ Γνωρίζουμε ότι η αμαρτία ( x+ 2n) = αμαρτία Χ, όπου n= 0, ± 1, ± 2, …

Επομένως, προσθέτοντας 2 nστο ημιτονικό επιχείρημα

Αλλάζει την αξία του. Υπάρχει άλλος αριθμός με αυτό

Ίδιο ακίνητο;

Ας το προσποιηθούμε Π- ένας τέτοιος αριθμός, δηλ. ισότητα:

Αμαρτία ( x+P) = αμαρτία Χ,

Ισχύει για οποιαδήποτε τιμή Χ. Αλλά μετά έχει

Τοποθεσία και Χ= / 2, δηλ.

αμαρτία(/2 + Π) = αμαρτία / 2 = 1.

Αλλά σύμφωνα με τον τύπο μείωσης sin ( / 2 + Π) = κοσ Π. Επειτα

Από τις δύο τελευταίες ισότητες προκύπτει ότι κο Π= 1, αλλά εμείς

Γνωρίζουμε ότι αυτό ισχύει μόνο όταν Π = 2n. Από το μικρότερο

Ένας μη μηδενικός αριθμός από το 2 nείναι 2, τότε αυτός ο αριθμός

Και υπάρχει μια περίοδος αμαρτίας Χ. Ομοίως αποδεικνύεται ότι 2από nείναι , άρα αυτή είναι η περίοδος αμαρτία 2 Χ.

Η συνάρτηση είναι μηδενική.Καλείται η τιμή του ορίσματος για το οποίο η συνάρτηση είναι ίση με 0 μηδέν (ρίζα) συναρτήσεις. Μια συνάρτηση μπορεί να έχει πολλαπλά μηδενικά.Για παράδειγμα, η συνάρτηση y = Χ (Χ + 1) (Χ-3) έχει τρία μηδενικά: Χ= 0, Χ= -1, Χ= 3. Γεωμετρικά μηδενική συνάρτηση - είναι η τετμημένη του σημείου τομής της γραφικής παράστασης της συνάρτησης με τον άξονα Χ .

Το σχήμα 7 δείχνει τη γραφική παράσταση της συνάρτησης με μηδενικά: Χ= ένα, Χ = σικαι Χ= ντο.

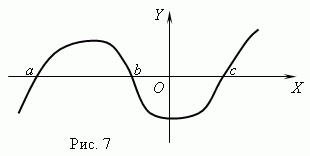
Ασύμπτωτο.Εάν η γραφική παράσταση μιας συνάρτησης προσεγγίζει μια ορισμένη ευθεία γραμμή επ' αόριστον καθώς απομακρύνεται από την αρχή, τότε αυτή η ευθεία γραμμή ονομάζεται ασύμπτωτο.

Προστασία της ιδιωτικής ζωής σας είναι σημαντική για εμάς. Για το λόγο αυτό, έχουμε αναπτύξει μια Πολιτική Απορρήτου που περιγράφει τον τρόπο με τον οποίο χρησιμοποιούμε και αποθηκεύουμε τις πληροφορίες σας. Διαβάστε την πολιτική απορρήτου μας και ενημερώστε μας εάν έχετε ερωτήσεις.

Συλλογή και χρήση προσωπικών πληροφοριών

Οι προσωπικές πληροφορίες αναφέρονται σε δεδομένα που μπορούν να χρησιμοποιηθούν για την αναγνώριση ή επικοινωνία με ένα συγκεκριμένο άτομο.

Ενδέχεται να σας ζητηθεί να δώσετε τα προσωπικά σας στοιχεία ανά πάσα στιγμή όταν επικοινωνήσετε μαζί μας.

Τα παρακάτω είναι μερικά παραδείγματα των τύπων προσωπικών πληροφοριών που ενδέχεται να συλλέγουμε και πώς μπορούμε να χρησιμοποιήσουμε αυτές τις πληροφορίες.

Ποιες προσωπικές πληροφορίες συλλέγουμε:

• Όταν υποβάλλετε μια αίτηση στον ιστότοπο, ενδέχεται να συλλέξουμε διάφορες πληροφορίες, όπως το όνομά σας, τον αριθμό τηλεφώνου, τη διεύθυνσή σας ΗΛΕΚΤΡΟΝΙΚΗ ΔΙΕΥΘΥΝΣΗκαι τα λοιπά.

Πώς χρησιμοποιούμε τα προσωπικά σας στοιχεία:

• Συλλέγεται από εμάς προσωπικές πληροφορίεςμας επιτρέπει να επικοινωνήσουμε μαζί σας και να σας ενημερώσουμε για μοναδικές προσφορές, προσφορές και άλλες εκδηλώσεις και επερχόμενες εκδηλώσεις.
• Από καιρό σε καιρό, ενδέχεται να χρησιμοποιήσουμε τα προσωπικά σας στοιχεία για να σας στείλουμε σημαντικές ειδοποιήσεις και επικοινωνίες.
• Ενδέχεται επίσης να χρησιμοποιήσουμε προσωπικές πληροφορίες για εσωτερικούς σκοπούς, όπως διεξαγωγή ελέγχων, ανάλυση δεδομένων και διάφορες έρευνες, προκειμένου να βελτιώσουμε τις υπηρεσίες που παρέχουμε και να σας παρέχουμε συστάσεις σχετικά με τις υπηρεσίες μας.
• Εάν συμμετάσχετε σε κλήρωση, διαγωνισμό ή παρόμοιο κίνητρο, ενδέχεται να χρησιμοποιήσουμε τις πληροφορίες που παρέχετε για τη διαχείριση τέτοιων προγραμμάτων.

Αποκάλυψη σε τρίτους

Δεν αποκαλύπτουμε πληροφορίες που λαμβάνουμε από εσάς σε τρίτους.

Εξαιρέσεις:

• Εάν είναι απαραίτητο - σύμφωνα με το νόμο, δικαστική εντολή, σε νομικές διαδικασίες και/ή βάσει δημόσιων αιτημάτων ή αιτημάτων από κυβερνητικές υπηρεσίεςστο έδαφος της Ρωσικής Ομοσπονδίας - αποκαλύψτε τα προσωπικά σας στοιχεία. Ενδέχεται επίσης να αποκαλύψουμε πληροφορίες σχετικά με εσάς εάν κρίνουμε ότι αυτή η αποκάλυψη είναι απαραίτητη ή κατάλληλη για λόγους ασφάλειας, επιβολής του νόμου ή άλλους σκοπούς δημοσίου συμφέροντος.
• Σε περίπτωση αναδιοργάνωσης, συγχώνευσης ή πώλησης, ενδέχεται να μεταφέρουμε τα προσωπικά στοιχεία που συλλέγουμε στον αντίστοιχο τρίτο διάδοχο.

Προστασία προσωπικών πληροφοριών

Λαμβάνουμε προφυλάξεις - συμπεριλαμβανομένων διοικητικών, τεχνικών και φυσικών - για την προστασία των προσωπικών σας δεδομένων από απώλεια, κλοπή και κακή χρήση, καθώς και από μη εξουσιοδοτημένη πρόσβαση, αποκάλυψη, τροποποίηση και καταστροφή.

Διατήρηση του απορρήτου σας σε εταιρικό επίπεδο

Για να διασφαλίσουμε ότι τα προσωπικά σας στοιχεία είναι ασφαλή, κοινοποιούμε πρακτικές απορρήτου και ασφάλειας στους υπαλλήλους μας και εφαρμόζουμε αυστηρά τις πρακτικές απορρήτου.

Ρωσικό γυμνάσιο

ΑΦΗΡΗΜΕΝΗ

Εκπληρωμένος

μαθητής 10"F" τάξης Burmistrov Sergey

Επόπτης

καθηγητής μαθηματικών

Yulina O.A.

Νίζνι Νόβγκοροντ

Η συνάρτηση και οι ιδιότητές της

Λειτουργία-μεταβλητή εξάρτηση στοαπό μια μεταβλητή Χ , αν κάθε τιμή Χταιριάζει με μία μόνο τιμή στο .

Μεταβλητή x-ανεξάρτητη μεταβλητή ή όρισμα.

Μεταβλητή y-εξαρτημένη μεταβλητή

τιμή συνάρτησης-έννοια στοαντίστοιχος καθορισμένη τιμή Χ .

Πεδίο λειτουργίας-όλες τις τιμές που παίρνει η ανεξάρτητη μεταβλητή.

Εύρος συναρτήσεων (σύνολο τιμών) -όλες τις τιμές που παίρνει η συνάρτηση.

Η συνάρτηση είναι άρτια-αν για κανένα Χ f(x)=f(-x)

Η συνάρτηση είναι περίεργη-αν για κανένα Χαπό το εύρος της συνάρτησης, η ισότητα f(-x)=-f(x)

Αύξηση λειτουργίας-αν για κανένα x 1και x 2,τέτοια που x 1 < x 2, η ανισότητα φά( x 1 ) x 2 )

Μειωτική λειτουργία-αν για κανένα x 1και x 2,τέτοια που x 1 < x 2, η ανισότητα φά( x 1 )> στ( x 2 )

Τρόποι για να ορίσετε μια λειτουργία

¨ Για να ορίσετε μια συνάρτηση, πρέπει να καθορίσετε τον τρόπο με τον οποίο για κάθε τιμή ορίσματος μπορείτε να βρείτε την αντίστοιχη τιμή συνάρτησης. Ο πιο συνηθισμένος είναι ο τρόπος ορισμού μιας συνάρτησης χρησιμοποιώντας τον τύπο στο =f(x), όπου f(x)-κάποια έκφραση με μια μεταβλητή Χ. Σε αυτή την περίπτωση, λέμε ότι η συνάρτηση δίνεται από έναν τύπο ή ότι η συνάρτηση δίνεται από αναλυτικά.

¨ Στην πράξη, χρησιμοποιείται συχνά πινακοειδήςτον τρόπο που ορίζεται η συνάρτηση. Με αυτή τη μέθοδο, παρέχεται ένας πίνακας που υποδεικνύει τις τιμές της συνάρτησης για τις τιμές του ορίσματος που υπάρχουν στον πίνακα. Παραδείγματα ορισμού συνάρτησης με πίνακα είναι ένας πίνακας τετραγώνων, ένας πίνακας με κύβους.

Τύποι συναρτήσεων και οι ιδιότητές τους

1) Μόνιμη λειτουργία-λειτουργία, δίνεται από τον τύπο y= σι , όπου σι-κάποιο νούμερο. πρόγραμμα μόνιμη λειτουργία y \u003d b είναι μια ευθεία παράλληλη προς τον άξονα x και που διέρχεται από το σημείο (0; b) στον άξονα y

2) Άμεση αναλογικότητα-συνάρτηση που δίνεται από τον τύπο y= kx , όπου k¹0. Αριθμός κπου ονομάζεται συντελεστή αναλογικότητας .

Ιδιότητες λειτουργίας y=kx :

1. Τομέας ορισμού λειτουργίες - σύνολοόλους τους πραγματικούς αριθμούς

2. y=kx- περιττή συνάρτηση

3. Για k>0, η συνάρτηση αυξάνεται, και για k<0 убывает на всей числовой прямой

3)Γραμμική συνάρτηση-η συνάρτηση που δίνεται από τον τύπο y=kx+b, όπου κκαι σι - πραγματικούς αριθμούς. Εάν, ειδικότερα, k=0, τότε παίρνουμε μια σταθερή συνάρτηση y=b; αν b=0, τότε παίρνουμε μια ευθεία αναλογικότητα y=kx .

Ιδιότητες συνάρτησης y=kx+b :

1. Τομέας ορισμού - το σύνολο όλων των πραγματικών αριθμών

2. Λειτουργία y=kx+bγενική άποψη, δηλ. ούτε ζυγός ούτε περιττός.

3. Για k>0, η συνάρτηση αυξάνεται, και για k<0 убывает на всей числовой прямой

Η γραφική παράσταση της συνάρτησης είναι ευθεία .

4)αντίστροφη αναλογικότητα-συνάρτηση που δίνεται από τον τύπο y=k /Χ,όπου k¹0 Αριθμός κπου ονομάζεται αντιστρόφως αναλογικό παράγοντα.

Ιδιότητες συνάρτησης y=k / Χ:

1. Τομέας ορισμού - το σύνολο όλων των πραγματικών αριθμών εκτός από το μηδέν

2. y=k / Χ - περιττή συνάρτηση

3. Αν k>0, τότε η συνάρτηση μειώνεται στο διάστημα (0;+¥) και στο διάστημα (-¥;0). Αν κ<0, то функция возрастает на промежутке (-¥;0) и на промежутке (0;+¥).

Η γραφική παράσταση της συνάρτησης είναι υπερβολή .

5)Λειτουργία y=x2

Ιδιότητες συνάρτησης y=x2:

2. y=x2 - ομοιόμορφη λειτουργία

3. Η συνάρτηση μειώνεται στο διάστημα

Η γραφική παράσταση της συνάρτησης είναι παραβολή .

6)Λειτουργία y=x 3

Ιδιότητες συνάρτησης y=x3:

1. Το πεδίο ορισμού είναι ολόκληρη η αριθμητική γραμμή

2. y=x 3 - περιττή συνάρτηση

3. Η συνάρτηση αυξάνεται σε ολόκληρη την αριθμητική γραμμή

Η γραφική παράσταση της συνάρτησης είναι κυβική παραβολή

7)Συνάρτηση ισχύος με φυσικό εκθέτη-συνάρτηση που δίνεται από τον τύπο y=xn, όπου n- φυσικός αριθμός. Για n=1 παίρνουμε τη συνάρτηση y=x, οι ιδιότητές της εξετάζονται στην Ενότητα 2. Για n=2;3 παίρνουμε τις συναρτήσεις y=x 2 ; y=x 3 . Οι ιδιότητές τους συζητούνται παραπάνω.

Έστω n ένας αυθαίρετος ζυγός αριθμός μεγαλύτερος από δύο: 4,6,8... Σε αυτή την περίπτωση, η συνάρτηση y=xnέχει τις ίδιες ιδιότητες με τη συνάρτηση y=x 2 . Η γραφική παράσταση της συνάρτησης μοιάζει με παραβολή y=x 2 , μόνο οι κλάδοι της γραφικής παράστασης για |x|>1 ανεβαίνουν όσο πιο απότομα, τόσο μεγαλύτερο n, και για |x|<1 тем “теснее прижимаются” к оси Х, чем больше n.

Έστω n ένας αυθαίρετος περιττός αριθμός μεγαλύτερος από το τρία: 5,7,9... Σε αυτήν την περίπτωση, η συνάρτηση y=xnέχει τις ίδιες ιδιότητες με τη συνάρτηση y=x 3 . Το γράφημα της συνάρτησης μοιάζει με κυβική παραβολή.

8)Συνάρτηση ισχύος με ακέραιο αρνητικό εκθέτη -συνάρτηση που δίνεται από τον τύπο y=x-n , όπου n- φυσικός αριθμός. Για n=1 παίρνουμε y=1/x, οι ιδιότητες αυτής της συνάρτησης εξετάζονται στην Ενότητα 4.

Έστω n περιττός αριθμός μεγαλύτερος του ενός: 3,5,7... Στην περίπτωση αυτή η συνάρτηση y=x-nέχει βασικά τις ίδιες ιδιότητες με τη συνάρτηση y=1/x.

Έστω n ζυγός αριθμός, για παράδειγμα n=2.

Ιδιότητες συνάρτησης y=x -2 :

1. Η συνάρτηση ορίζεται για όλα τα x¹0

2. y=x -2 -ομοιόμορφη λειτουργία

3. Η συνάρτηση μειώνεται κατά (0;+¥) και αυξάνεται κατά (-¥;0).

Οποιαδήποτε συνάρτηση με άρτιο n μεγαλύτερο από δύο έχει τις ίδιες ιδιότητες.

9)Λειτουργία y= Ö Χ

Ιδιότητες συνάρτησης y= Ö Χ :

1. Το πεδίο ορισμού είναι μια ακτίνα και αυξάνεται στο διάστημα )