Näide

Segmendi jagamine pooleks

Bisektsiooni probleem. Kasutage selle segmendi jagamiseks kompassi ja joonlauda AB kaheks võrdseks osaks. Üks lahendustest on näidatud joonisel:

• Joonistame kompassi abil ringid, mille keskpunktid on punktides A Ja B raadius AB.
• Ristmispunktide leidmine P Ja K kaks konstrueeritud ringi (kaared).
• Joonistage joonlaua abil punkte läbiv lõik või joon P Ja K.
• Lõigu soovitud keskpunkti leidmine AB- ristumispunkt AB Ja PQ.

Ametlik määratlus

Ehitusülesannetes vaadeldakse tasandi kõigi punktide kogumit, tasandi kõigi sirgjoonte hulka ja tasandi kõigi ringide hulka, millel on lubatud järgmised toimingud:

1. Valige punkt kõigi punktide hulgast:
   1. suvaline punkt
   2. suvaline punkt antud sirgel
   3. suvaline punkt antud ringil
   4. kahe etteantud sirge lõikepunkt
   5. antud sirge ja antud ringi lõikepunkt/puutumine
   6. kahe etteantud ringi lõike-/puutepunktid
2. "Kasutades valitsejad» vali rida kõigi ridade hulgast:
   1. suvaline sirgjoon
   2. suvaline sirge, mis läbib antud punkti
   3. kahte etteantud punkti läbiv sirgjoon
3. "Kasutades kompass» vali suhtlusring kõigi suhtlusringide hulgast:
   1. suvaline ring
   2. suvaline ring, mille keskpunkt on antud punktis
   3. suvaline ring, mille raadius on võrdne kahe antud punkti vahelise kaugusega
   4. ringjoon, mille keskpunkt on antud punktis ja mille raadius on võrdne kahe antud punkti vahelise kaugusega

Ülesande tingimustes on määratud teatud punktide kogum. Eespool loetletud lubatavatest tehtetest piiratud arvu tehteid kasutades tuleb koostada veel üks punktide komplekt, mis on antud seoses algse hulgaga.

Ehitusprobleemi lahendus sisaldab kolme olulist osa:

1. Antud komplekti koostamise meetodi kirjeldus.
2. Tõestus, et kirjeldatud viisil konstrueeritud hulk on tõepoolest antud suhtes alghulgaga. Tavaliselt teostatakse konstruktsiooni tõestamine teoreemi tavatõestusena, tuginedes aksioomidele ja teistele tõestatud teoreemidele.
3. Kirjeldatud ehitusmeetodi analüüs selle rakendatavuse osas algtingimuste erinevatele versioonidele, samuti kirjeldatud meetodil saadud lahenduse unikaalsuse või mitteunikaalsuse osas.

teadaolevad probleemid

• Apolloniuse ülesanne kolme etteantud ringi puutuja ringi konstrueerimisest. Kui ükski antud ringidest ei asu teise sees, siis on sellel ülesandel 8 oluliselt erinevat lahendust.
• Brahmagupta probleem kirjutatud nelinurga konstrueerimisel, kasutades selle nelja külge.

Korrapäraste hulknurkade ehitamine

Muistsed geomeetrid teadsid, kuidas õigesti ehitada n-gons jaoks , , ja .

Võimalikud ja võimatud konstruktsioonid

Kõik konstruktsioonid pole midagi muud kui mõne võrrandi lahendid ja selle võrrandi koefitsiendid on seotud etteantud lõikude pikkustega. Seetõttu on mugav rääkida arvu konstrueerimisest - teatud tüüpi võrrandi graafilisest lahendusest. Ülaltoodud nõuete raames on võimalikud järgmised konstruktsioonid:

• Lineaarvõrrandite lahenduste konstrueerimine.
• Ruutvõrrandite lahenduste konstrueerimine.

Teisisõnu, aritmeetiliste avaldistega võrdseid arve on võimalik konstrueerida ainult algarvude ruutjuure (segmentide pikkuste) abil. Näiteks,

Variatsioonid ja üldistused

• Konstruktsioonid ühe kompassi abil. Mohr-Mascheroni teoreemi järgi saab ühe kompassi abil konstrueerida mis tahes kujundi, mida saab kompassi ja joonlauaga konstrueerida. Sel juhul loetakse sirgjoon konstrueerituks, kui sellele on määratud kaks punkti.
• Konstruktsioonid ühe joonlaua abil. On hästi näha, et ühe joonlaua abil saab teostada ainult projektiiv-invariantseid konstruktsioone. Eelkõige on võimatu isegi segmenti jagada kaheks võrdseks osaks või leida joonistatud ringi keskpunkti. Aga kui tasapinnal on eelnevalt joonistatud ring, millel on märgitud keskpunkt, saate joonlaua abil teha samu konstruktsioone nagu kompassi ja joonlauaga (Poncelet-Steineri teoreem ( Inglise)), 1833. Kui joonlaual on kaks sälku, siis on seda kasutavad konstruktsioonid samaväärsed kompassi ja joonlauda kasutavate konstruktsioonidega (selle tõestamisel astus Napoleon olulise sammu).
• Konstruktsioonid, mis kasutavad piiratud võimalustega tööriistu. Seda tüüpi ülesannete puhul ei peeta tööriistu (erinevalt ülesande klassikalisest sõnastusest) ideaalseks, vaid piiratuks: sirgjoont läbi kahe punkti saab joonlaua abil tõmmata ainult siis, kui nende punktide vaheline kaugus ei ületa teatud väärtus; kompassi abil joonistatud ringide raadiust saab piirata ülalt, alt või nii ülalt kui alt.
• Lameda origami konstruktsioonid. vaata Hujiti reegleid

Vaata ka

• Dünaamilise geomeetria programmid võimaldavad teostada konstruktsioone kompassi ja joonlaua abil arvutis.

Märkmed

Kirjandus

• A. Adler Geomeetriliste konstruktsioonide teooria / Saksa keelest tõlkinud G. M. Fikhtengolts. - Kolmas väljaanne. - L.: Uchpedgiz, 1940. - 232 lk.
• I. I. Aleksandrov Geomeetriliste ehitusülesannete kogu. - Kaheksateistkümnes väljaanne. - M.: Uchpedgiz, 1950. - 176 lk.
• B. I. Argunov, M. B. Balk. - Teine väljaanne. - M.: Uchpedgiz, 1957. - 268 lk.
• A. M. Voronets Kompassi geomeetria. - M.-L.: ONTI, 1934. - 40 lk. - (L. A. Lyusterniku üldtoimetuse all olev populaarne matemaatikaraamatukogu).
• V. A. Geiler Lahendamatud ehitusprobleemid // jahutusvedelik. - 1999. - nr 12. - Lk 115-118.
• V. A. Kiritšenko Konstruktsioonid kompassi ja joonlauaga ning Galois' teooria // Suvekool “Moodne matemaatika”. - Dubna, 2005.
• Yu. I. Manin IV raamat. Geomeetria // Elementaarmatemaatika entsüklopeedia. - M.: Fizmatgiz, 1963. - 568 lk.
• Y. Petersen Geomeetriliste ehitusülesannete lahendamise meetodid ja teooriad. - M.: E. Lissneri ja Y. Romani trükikoda, 1892. - 114 lk.
• V. V. Prasolov Kolm klassikalist ehitusprobleemi. Kuubi kahekordistamine, nurga kolmistamine, ringi nelinurksus. - M.: Nauka, 1992. - 80 lk. - (Matemaatika populaarsed loengud).
• J. Steiner Geomeetrilised konstruktsioonid, mis teostatakse sirgjoone ja fikseeritud ringi abil. - M.: Uchpedgiz, 1939. - 80 lk.
• Matemaatika valikkursus. 7-9 / Koost. I. L. Nikolskaja. - M.: Haridus, 1991. - Lk 80. - 383 lk. - ISBN 5-09-001287-3

Wikimedia sihtasutus. 2010. aasta.

Vaadake, mis on "Ehitamine kompassi ja joonlaua abil" teistes sõnaraamatutes:

Joonlauad – hankige Akademikast AllInstrumentsi allahindluseks töötav kupong või ostke tasuta kohaletoimetamisega joonlauad soodsalt AllInstrumentsis

Eukleidilise geomeetria haru, tuntud juba iidsetest aegadest. Ehitusülesannetes on võimalikud järgmised toimingud: Märgi tasapinnal suvaline punkt, punkt ühel konstrueeritud sirgel või kahe konstrueeritud sirge lõikepunkt. Abiga... ... Wikipedia

Kompassi ja joonlaudu kasutavad konstruktsioonid on iidsetest aegadest tuntud eukleidilise geomeetria haru. Ehitusülesannetes on võimalikud järgmised toimingud: Märgi tasapinnal suvaline punkt, punkt mõnel konstrueeritud sirgel või punkt... ... Wikipedia

Nimisõna, s., kasutatud. võrdlema sageli Morfoloogia: (ei) mida? ehitus, mis? ehitus, (ma näen) mida? ehitus, mis? ehitus, mille kohta? ehituse kohta; pl. Mida? ehitus, (ei) mis? konstruktsioonid, mis? konstruktsioonid, (ma näen) mida? ehitus, millega?... ... Dmitrijevi seletav sõnaraamat

KRIMI KOOLILASTE VÄIKE TEADUSTE AKADEEMIA

"OTSIJA"

Sektsioon "Matemaatika"

GEOMEETRILISED KONSTRUKTSIOONID KAHTEPOOLSE JOONULDI KASUTAMISEL

Olen töö ära teinud A

_____________

klassi õpilane

Teaduslik direktor

SISSEJUHATUS…………………………………………………………………………………..…..3

I. GEOMEETRILISED KONSTRUKTSIOONID TASANDIL……………………4

I.1. Konstruktiivse geomeetria üldaksioomid. Matemaatiliste instrumentide aksioomid…………………………………………………………………………………..4

I.2. ……………………….....5

I.3. Geomeetrilised konstruktsioonid ühe joonlauaga………………………………..7

I.4. Kahepoolse joonlauaga konstrueerimise põhiülesanded…………………..8

I.5. Erinevate ehitusprobleemide lahendamine ……………………………………12

I.6. Ühepoolse joonlauaga konstruktsioonid……………………………………………………………………………………………………………

I.7. Kahepoolse joonlaua vahetatavus sirkli ja joonlauaga....21

KOKKUVÕTE………………………………………………………………….24

Kasutatud kirjanduse loetelu………………………………………………….25

Sissejuhatus

Piiratud vahenditega ehitamisega seotud probleemid hõlmavad probleeme, mis on seotud ainult kompassi ja joonlauaga ehitamisega, mida käsitletakse kooli õppekavas. Kas ehitusprobleeme on võimalik lahendada ainult ühe joonlauaga? Tihti pole teil kompassi käepärast, kuid joonlaua leiate alati.

Geomeetria konstruktsioonide probleemid on põnev osa. Huvi selle vastu on tingitud geomeetrilise sisu ilust ja lihtsusest. Nende probleemide käsitlemise asjakohasus suureneb, kuna neid kasutatakse praktikas. Oskus kasutada ühte joonlauda selles töös käsitletavate probleemide lahendamisel on praktilises tegevuses suure tähtsusega, sest Pidevalt seisame silmitsi probleemidega, mis puudutavad segmendi pooleks jagamist, antud segmendi kahekordistamist jne.

Käesolevas artiklis vaadeldakse peamisi ehitusprobleeme, mis on aluseks keerukamate probleemide lahendamisel.

Nagu kogemus näitab, äratavad ehitusülesanded huvi ja aitavad kaasa vaimse tegevuse aktiveerimisele. Nende lahendamisel kasutatakse aktiivselt teadmisi figuuride omadustest, arendatakse arutlusvõimet, täiendatakse geomeetriliste konstruktsioonide oskusi. Selle tulemusena arenevad konstruktiivsed võimed, mis on geomeetria õppimise üks eesmärke.

Hüpotees: kõiki ehitusülesandeid, mida saab lahendada sirkli ja joonlaua abil, saab lahendada ainult kahepoolse joonlaua abil.

Õppeobjekt: ehitusülesanded ja kahepoolne joonlaud.

Uurimistöö eesmärgid: tõestada, et kõik ehitusprobleemid on lahendatavad ainult kahepoolse joonlaua abil.

Uurimiseesmärgid: uurida ehitusprobleemide lahendamise teoreetilisi aluseid; lahendada põhilisi ehitusülesandeid kasutades kahepoolset joonlauda; tuua näiteid keerulisematest ehitusprobleemidest; süstematiseerida teoreetilist ja praktilist materjali.

I. GEOMEETRILISED KONSTRUKTSIOONID LENKIL

I.1. Konstruktiivse geomeetria üldaksioomid. Matemaatiliste tööriistade aksioomid

Konstruktiivse geomeetria jaoks on vajalik konkreetse tööriista täpne ja matemaatilistel eesmärkidel täielik kirjeldus. See kirjeldus on antud aksioomide kujul. Need abstraktsel matemaatilisel kujul olevad aksioomid väljendavad reaalsete joonistusvahendite omadusi, mida kasutatakse geomeetriliste konstruktsioonide jaoks.

Kõige sagedamini kasutatavad geomeetrilised ehitustööriistad on:joonlaud (ühepoolne) , kompass, kahepoolne joonlaud (paralleelsete servadega) ja mõned teised.

A. Joonlaua aksioom.

Joonlaud võimaldab teil teostada järgmisi geomeetrilisi konstruktsioone:
a) konstrueerida kahte konstrueeritud punkti ühendav segment;

b) konstrueerida kahte konstrueeritud punkti läbiv sirge;

c) konstrueerida kiir, mis väljub konstrueeritud punktist ja läbib teist konstrueeritud punkti.

B. Kompassi aksioom.

Kompass võimaldab teil teostada järgmisi geomeetrilisi konstruktsioone:
a) konstrueerida ring, kui on konstrueeritud ringi keskpunkt ja ringi (või selle otste) raadiusega võrdne lõik;

B. Kahepoolse joonlaua aksioom.

Kahepoolne joonlaud võimaldab teil:

a) teostama mis tahes aksioomis A loetletud konstruktsioone;

b) konstrueerige igal konstrueeritud sirgega määratletud pooltasandil selle sirgega paralleelne ja sellest eemal kulgev sirgeA, Kus A - antud joonlaua jaoks fikseeritud segment (joonlaua laius);

c) kui on konstrueeritud kaks punkti A ja B, siis määrake, kas AB on suurem kui teatud fikseeritud segmentA (joonlaua laius) ja kui AB >A , seejärel konstrueerige kaks paari paralleelseid sirgeid, mis läbivad vastavalt punkte A ja B ja asuvad üksteisest teatud kauguselA .

Lisaks loetletud tööriistadele saate geomeetriliste konstruktsioonide jaoks kasutada muid tööriistu: suvaline nurk, ruut, märkidega joonlaud, täisnurkade paar, erinevad seadmed spetsiaalsete kõverate joonistamiseks jne.

I.2. Ehitusprobleemide lahendamise üldpõhimõtted

Ehitusülesanne seisneb selles, et kui on antud mõni muu kujund ja näidatakse teatud seosed soovitud kujundi elementide ja selle kujundi elementide vahel, on nõutav etteantud vahenditega mingi kujund.

Iga kujundit, mis vastab ülesande tingimustele, nimetatakseotsus see ülesanne.

Leia lahendus konstruktsiooniülesanne tähendab selle vähendamist lõplikule arvule põhikonstruktsioonidele, st põhikonstruktsioonide lõpliku jada näitamist, mille järel loetakse soovitud kujund juba konstrueerituks konstruktiivse geomeetria aktsepteeritud aksioomide alusel. Vastuvõetavate põhikonstruktsioonide loetelu ja sellest tulenevalt ka probleemi lahendamise käik sõltub oluliselt sellest, milliseid konkreetseid tööriistu konstruktsioonide jaoks kasutatakse.

Lahendage ehitusprobleem - Tähendab, leida kõik selle lahendused .

Viimane määratlus nõuab mõningast selgitust. Probleemi tingimustele vastavad figuurid võivad erineda nii kuju või suuruse kui ka asendi poolest tasapinnal. Asukoha erinevusi tasapinnal võetakse arvesse või ei võeta arvesse olenevalt konstruktsiooniprobleemi sõnastusest, sellest, kas ülesande seisukord näeb ette või ei näe ette soovitud kujundi kindlat asukohta mis tahes etteantud kujundite suhtes. .

Kui probleemile leitakse lahendus, siis on edaspidi lubatud seda lahendust kasutada “tervikuna”, st põhikonstruktsioonideks jagamata.

On mitmeid lihtsaid geomeetrilisi ehitusülesandeid, mis on eriti sageli kaasatud komponentidena keerukamate ülesannete lahendamisel. Nimetame neid elementaarseteks geomeetrilisteks ehitusülesanneteks. Elementaarsete ülesannete loetelu on loomulikult tingimuslik. Põhiülesanded hõlmavad tavaliselt järgmist:

Jagage see segment pooleks.

Etteantud nurga jagamine pooleks.

Antud sirgele lõigu konstrueerimine, mis on võrdne etteantud lõiguga.

Antud nurgaga võrdse nurga konstrueerimine.

Antud punkti läbiva sirge konstrueerimine paralleelselt antud sirgega.

Antud punkti läbiva sirge konstrueerimine, mis on antud sirgega risti.

Segmendi jagamine selles osas.

Kolmnurga konstrueerimine kolme etteantud külje abil.

Kolmnurga konstrueerimine külje ja kahe külgneva nurga abil.

Kolmnurga konstrueerimine kahe külje ja nendevahelise nurga abil.

Mis tahes mõnevõrra keeruka ehitusprobleemi lahendamisel tekib küsimus, kuidas arutleda, et leida lahendus probleemile, saada probleemile kõik lahendused, selgitada välja probleemi lahendamise võimalikkuse tingimused jne. , konstruktiivsete probleemide lahendamisel kasutavad nad lahendusskeemi, mis koosneb järgmisest neljast etapist:

1) analüüs;
2) ehitus;
3) tõend;
4) uuringud.

I.3. Geomeetrilised konstruktsioonid ühe joonlauaga

Vaatleme valitsejat kahest vaatenurgast: joonlauana ja kahepoolse joonlauana.

1. Kahepoolne joonlaud laius A nimetame joonlauda, ​​mille paralleelsed servad asuvad kaugusel A üksteisest, võimaldades otse ehitada:

a) suvaline sirge;

b) ülesande lahendamise käigus antud või saadud kahte punkti läbiv sirgjoon;

c) paralleelsed sirged, millest igaüks läbib ühte punkti, mille vaheline kaugus on suuremA (selles konstruktsioonis on joonlaud sellises asendis, et mõlemal tema kahel paralleelsel serval on üks kahest etteantud punktist; sel juhul räägime otsekonstruktsioonist).

Selle konstruktsiooni joonlaua laiust peetakse konstantseks ja seetõttu, kui konkreetse probleemi lahendamise käigus on vaja mõne saadud punkti suhtes otsest konstruktsiooni tehaA Ja IN , siis peame tõestama, et pikkusAB kauem A .

Punkti loetakse konstrueeritavaks, kui see on üks andmetest või kahe konstrueeritud sirge ristumiskoht; omakorda loeme sirge konstrueeritavaks, kui see läbib konstrueeritud või etteantud punkte.

Kahepoolse joonlaua abil saate konstrueerida järgmise.

a) Suvalise kahe punkti kaudu saate tõmmata sirge ja ainult ühe.

b) Olenemata sirgest, on tasapinnal täpselt kaks sirget, mis on sellega paralleelsed ja eraldatud sellest vahemaaga.a .

c) Läbi kahe punkti A ja B punktis AB A on võimalik tõmmata kaks paari paralleele sirge; koos AB = A saate joonistada paari paralleelseid sirgeid, mille vaheline kaugus on võrdneA .

Kui on antud üks, kaks, kolm punkti, siis uusi punkte konstrueerida ei saa

(Joonis 1);

kui on antud neli punkti, millest mingi kolm (või kõik neli) asuvad samal sirgel, siis teisi punkte konstrueerida ei saa (joonis 2);

Kui teile antakse neli punkti, mis asuvad rööpküliku tippudes, saate konstrueerida ainult ühe punkti - selle keskpunkti. (Joon.3).

Olles ülaltooduga nõustunud, vaatleme eraldi kahepoolse joonlauaga lahendatavaid probleeme.

I.4. Kahepoolse joonlauaga konstrueerimise põhiülesanded

1
. Nurga ABC poolitaja konstrueerimine.

Lahendus: (Joonis 4)

A  (IN C) Ja b  (AB) ja  b = D .

Saame B D- poolitaja  ABC.

Tõepoolest, saadud

rööpküliku konstrueerimine on

romb, kuna selle kõrgused on võrdsed. IND –

rombi diagonaal on poolitaja ABC. Joonis 4

2
. Kahekordistage antud nurk ABC

Lahendus : (Joonis 5) a) A  (AB),

A  (IN C)= D , läbi punktide B ja D

b otse;

b) läbi punktide B jaD m  b

otse,b Ç a = F .

Saame Ð AB F = 2 Ð ABC .

Joonis 5

3 . Antud sirgjoonele M N selles

tõmmake punktiga A risti

Lahendus : (Joon.6)

1) (AA 1) || (BB 1) || (SS 1) –

otse (B (M N),

KOOS Î (M N)); 2) läbi A ja B

m || n - otse,

m Ç (SS 1) = D .

Saame (A D )  (M N ).

Joonis 6.

4
. Läbi antud punkti mitte lamades

antud rida, joonistada risti

To see rida.

Lahendus: Selle punkti O kaudu me joonistame

kaks sirget, mis lõikuvad antud

sirgjoon AB ja kahekordistage saadud nurki

selle kõrval olevad kolmnurgad

otse.  OA N = 2  OAV ja

OB N = 2  OVA (joonis 7).

Joonis 7

5. Ehitage antud sirge suhtes sümmeetriline punkt antud sirge suhtes.

Lahendus: vaata ülesannet 4. (punkt O on punktiga sümmeetrilineN. Joon.7)

6. Viige läbi sirgjoon paralleelselt sellega

P
otse M N , läbi punkti A, mitte

kuuluvad liini M N .

Lahendus 1: (Joonis 8)

1) (AA 1) || (BB 1) || (SS 1) || (DD 1 ) || (КК 1) -

– otse, (SA)Ç (BB 1) = C2;

2) (2 K-ga) Ç (DD 1 ) = F .

(A F ) on soovitud sirgjoon.

Joonis 8

Lahendus 2 . Joonisel 8 on 1 nummerdatud

sirgjoonte jada,

millest 1, 2 ja 3 on paralleelsed

otseehitus;

(A F) || (M N).

Joon.8 1

7
. Jagage see segment AB pooleks.

Lahendus 1. (joonis 9) (ainult juhul, kui joonlaua laius on väiksem selle segmendi pikkusest). Tõmmake otse läbi kaks paari paralleelseid jooni

selle segmendi otsad ja seejärel diagonaal

tekkiv romb. O – keskmine AB.

Riis. 9.

Lahendus 2. (Joonis 9, a)

1) a || (AB) ja b || (AB) – otse;

2) (AR), (AR)Ç a = C, (AP) Ç b = D ;

3) (D IN) Ç a = M, (SV) Ç b = N ;

4) (M N ) Ç (AB) = K;

5) (D TO) Ç (A N ) = F ;

6) (B F ) Ç b = D 1, (B F ) Ç a = C1;

7) (D IN ) Ç (A D 1) = X,

(AC 1) Ç (SV) = Z.

8) (X Z) Ç (AB) =O. Saame AO = OB.

Joonis 9,a

Lahendus 3 .( Riis. 9,b)

Nagu teada , keskmises trapetsis

alused, ristumispunkt

diagonaalid ja lõikepunkt

külgede laiendused

lamada samal sirgel.

1) m || (AB) – otse;

2) C Î m , D Î m , (AS) Ç (IN D ) = TO; Joonis 9,b

3) (NE) Ç (A D ) = F ; 4) (K F ) Ç (AB) =O. Saame AO = OB.

I.5. Erinevate ehitusprobleemide lahendamine

Järgmiste konstruktsiooniülesannete lahendamisel ainult kahepoolse joonlaua abil kasutatakse paralleelsete joonte otsekonstruktsiooni ja ülaltoodud seitset põhiülesannet.

1. Tõmmake läbi selle punkti kaks vastastikku risti olevat joont.

R lahendus: lähme sellest punktist läbi

kaks suvalist rida,

ja siis - poolitajad

külgnevad nurgad. (Joonis 10)

Joonis 10

2. Antud segment A D antud pikkus a.

Ehitage segment, mille pikkus on võrdne .

R
otsus : Viime läbi m  A Ja h || m läbi

punkt A. f || (A D ) , k || (AD) otse.

Joonistame AB ja AC, kus B =f  m ,

a C = m  k . Tuntud viisil

jaga AB ja AC pooleks ning

joonestame kolmnurga mediaanid

ABC. Mediaanide omaduse järgi

kolmnurk, O D = – otsis

segment (joonis 11)

Riis. üksteist

3. Koostage lõik, mille pikkus on

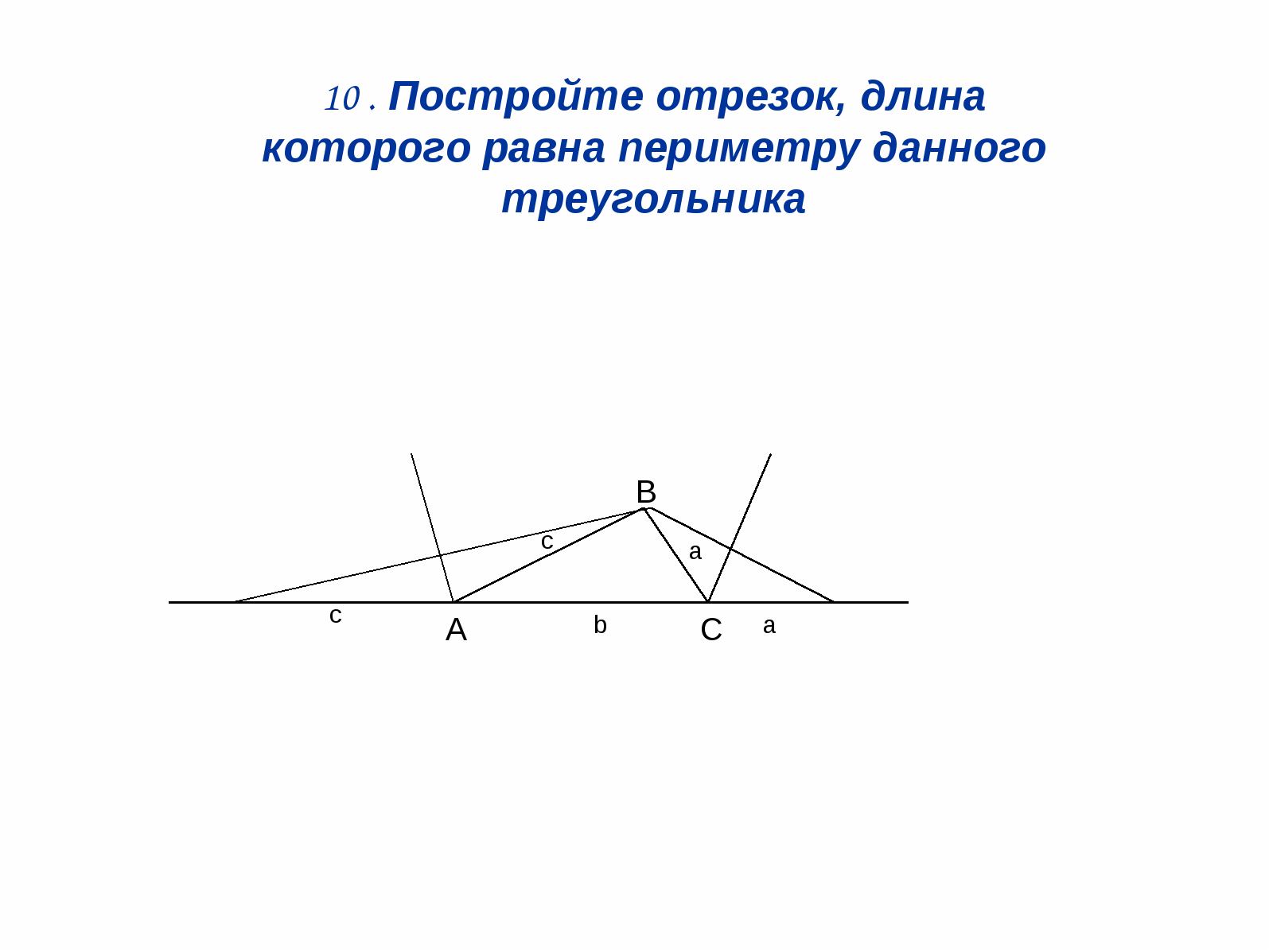võrdne antud kolmnurga ümbermõõduga.

Lahendus: (joonis 12). Ehitame poolitajad

kolmnurga kaks välimist nurka ja seejärel

3 tippu IN joonestame risti

nende poolitajate juurde.

DE = a + b + s

Joonis 12

4. Antud lõigu pikkusega a. Koostage pikkusega segmendid 2a, 3a.

R lahendus: (Joonis 13)

1 milj N) || (AB) ja (M 1 N 1 ) || (M N) || (M 2 N 2 ) –

otse;

2) (CA) ja (CB) läbi A ja B.

Segmendid A 1 B 1 ja A 2 B 2 on vajalikud.

Selle probleemi teine ​​lahendus võib olla

saadud ülesande 7 lahendusest.

Riis. 13

5. Sirgele on antud kaks lõiku, mille pikkused on a ja b . Koostage segmendid, mille pikkus on + b , b - A, ( a + b )/2 ja ( b - a )/2 .

Lahendus: ja eest a + b(Joonis 14, a)

Joon. 14, a

b) jaoks ( a + b)/2 (joonis 14, b)

1) (A 1 B 1) || (A 2 B 2) || (AB) – otse;

2) M Î (A 2 B 2), (MX) Ç (A 1 B 1 ) = N, (M H) Ç (A 1 B 1 ) = P;

3) (PY) Ç (A 2 B 2) = L, (LZ ) Ç (A 1 B 1 ) = O,

Saame: N O = N.P. + P.O. =
.

Riis. 14, sünd

c) jaoks b - A(Joonis 14, c)

Riis. 14,v

c) jaoks ( b - a )/2 (Joonis 14,d)

Riis. 14,g

6
. Ehitage selle ringi keskpunkt.

Lahendus : (Joonis 15) Joonistame sirge AB,

lõikuvad ringjoone punktides A ja B;

Päike  AB, kus C on lõikepunkt

ringiga.

Läbi punkti C tõmbame paralleelselt AB-ga

sirge C D; KOOSDlõikub ringiga

punktisD.

ÜhendamineDB-ga ja A-ga C saame

soovitud punkt on ringi keskpunkt. Riis. 15

Lahendus 2: (Joon. 16) Konstrueerige kahepoolse joonlaua abil kaks paralleelset kõõluAD JaB.C. . Saame võrdhaarse trapetsiABCD. LaseK JaP - joonte lõikepunktidA.C. JaBD , AB JaDC . Siis otseP K läbib nendega risti trapetsi aluste keskpunkte, mis tähendab, et läbib antud ringi keskpunkti. Sarnaselt teise sellise sirge konstrueerimisega leiame ringi keskpunkti.

Riis. 16

7. Ringjoone kaar on antud. Ehitage ringi keskpunkt

Lahendus . (Joonis 17) Märgi sellel kaarel kolm punkti A, B ja C. Aseta lõigu AB otstele joonlaud ja jälgi selle servad. Saame kaks paralleelset sirget. Muutes joonlaua asukohta, tõmbame veel kaks paralleelset joont. Saame rombi (võrdsete kõrgustega rööpküliku). Üks rombi diagonaale on lõiguga risti poolitajaAB , kuna rombi diagonaal asub teise diagonaaliga risti poolitajal. Samamoodi konstrueerime lõiguga risti poolitajaA.C. . Konstrueeritud poolitajate lõikepunkt on soovitud ringi keskpunkt.

Riis. 17

8. Antud on lõik AB, mitteparalleelne sirge l ja sellel olev punkt M. Ehitage ühe kahepoolse joonlaua abil sirge l lõikepunktid raadiusega AB ringiga, mille keskpunkt on M.

Lahendus: (Joon.18)

Täiendame kolmnurgaA.B.M. rööpkülikuleABNM . Konstrueerime poolitajad MT jaPRLvahelised nurgadMNja otsel . Joonistame punkti läbiN sirged, mis on paralleelsed nende poolitajatega:NQ || PRL, NR || M.T.. MT│ PRLkülgnevate nurkade poolitajatena. Tähendab,NQ │ MT, see tähendab kolmnurgasNMQpoolitaja on kõrgus, seega on kolmnurk võrdhaarne:MQ = MN. SamamoodiHÄRRA. = MN. PunktidKJaRotsitud.

Riis. 18

9. Antud sirge l ja l-ga paralleelne lõik OA. Ehitage ühe kahepoolse joonlaua abil sirge l lõikepunktid raadiusega OA ringiga, mille keskpunkt on O.

Lahendus: (Joonis 19,a)

Teeme otsel 1 , paralleelselt joonegaO.A. ja sellest kaugela . Võtame selle sirgjoonell suvaline punktB . LaseB 1 - joonte lõikepunktO.B. Jal 1 . Joonistame punkti läbiB 1 sirge, paralleelneAB ; see joon lõikub sirgegaO.A. punktisA 1 . Joonistame nüüd punktid läbiO JaA 1 paralleeljoonte paar, nende vaheline kaugus ona (sellist joonepaari võib olla kaks); laseX JaX 1 - punkti läbiva sirge lõikepunktidO , sirgete joontegal Jal 1 . SestO.A. 1 = HÄRG 1 ja ∆O.A. 1 X 1 ∆ OAX , siis OA = OX, punktX otsitud.

Samamoodi konstrueerime ringi ja sirge teise lõikepunkti - punktiY(joonis 18, b).

Riis. 18,a

Riis. 18, sünd

I.6.Ühepoolse joonlauaga konstruktsioonid

Z
Siin käsitleme erijuhtumit: olgu punktid P,K, R 1 JaK 1 . ja need asuvad trapetsi tippudes.

1. Jagage segment P K pooleks

Lahendus näidatud joonisel 19

Antud punktid P,K, R 1 JaK 1 ja paralleelsed jooned

RK, R 1 K 1 . Viime läbi RK 1  KR 1 = B , RR 1  QQ 1 = A

Ühendame punktid A ja B. AB RK = F- keskmine

segment PK.

Riis. 19

2. Kahekordne segment R 1 K 1.

R
otsus näidatud joonisel 20. Ehitame

punktF– segmendi P keskosaKja ühendage see

KoosK 1. R 1 K FQ 1 = M. Viime läbi RM. RM R 1 K 1 = R

võrdsusRQja P 1 K 1 tuleneb sarnasusest

kolmnurgad RMFJa RMK 1 ,

FMKJa R 1 MK 1 ja võrdsused PFJaFQ.

Riis. 20

3
. Koostage pikkusega segment n  R 1 K 1 .

m – 1 võrdsed segmendid PK 2 , K 2 K 3, … K m -1 K m

Siis ehitame (RR 1 ) JaK m K 1 ja ühendage

nende lõikepunkt A punktidega

K 2 , K 3, … K m Vastu võetudm -1 otsene

jagamaR 1 K 1 pealm võrdne osad.

Sestm = 4 lahendus on näidatud joonisel 22

Joonis 22

I.7. Kahepoolse joonlaua vahetatavus kompassi ja joonlauaga

Tõestame, et kahepoolne joonlaud on vahetatav kompassi ja joonlauaga. Selleks tõestame järgmisi väiteid:

Väide 1: kõiki konstruktsioone, mida saab teha sirkli ja joonlauaga, saab teha kahepoolse joonlauaga.

Kuna kompassi ja joonlauaga konstrueerimisel tõmbab joonlaud läbi kahe punkti joone ja kompass konstrueerib ringi (leiab antud punktist võrdsel kaugusel asuvaid punkte), siis kõik kompassi ja joonlauaga konstruktsioonid taandatakse kahe sirge, kahe ringi ja sirgjoonega ringi ristumiskoha konstrueerimine.

Kahe sirge ristumiskoha saab konstrueerida joonlaua abil.

Ringjoone ja sirge ristumiskoht (joonis 23):

Ehitus:Olgu antud lõik AB - ringi raadius, sirgel , ringi O keskpunkt, siis:

1) Teostame operatsioonisüsteemi ||l , OS = AB.

2) Teostame operatsioonisüsteemi ||kja puldiga a.

3) TeostameO.D., O.D. l = D; O.D. k) Thalese teoreemi järelduvalt

4) Võrdsuste transitiivsuse seaduse järgi

5) KaalugeOMQE. OMQEon rööpkülik, kuna OM ||EQja OE ||M.C.(joonlaua küljed on paralleelsed). Tõestame, et see on romb.

5.1) KäitumineQZ O.C.JaQG PEAL, SiisQG = QZ = a.

5.2)  OMQ =  RQM(lamades risti);  OS =PEAL, mida oli vaja tõestada.

Kahe ringi ristumiskoht: sarnane.

Väide 2: kõiki konstruktsioone, mida saab teha kahepoolse joonlauaga, saab teha sirkli ja sirgjoonega.

Selleks teostame kompassi ja joonlaua abil kahepoolse joonlaua konstruktsioonide standardi.

1) Kaht punkti kasutav sirgjoon on joonlaua abil hõlpsasti konstrueeritav.

2) Antud sirgega paralleelse ja sellest teatud kaugusel eemaldatud sirge ehitamine:

2.1) Olgu antud sirgekja pikkusega segmenta.

2.2) Ehitage suvaline sirgeb k, lasek b= B.

2.3) Seesbmõlemal pool punktiBsirgjoonelbkõrvale jätta tükk pikkusta, las punktidCJaD.

2.4) Punkti kauduCehitada sirgjoontc k.

2.5) Punkti kauduDehitada sirgjoontd k.

2.6) OtsenecJad- nõutav, sestB.C.JaBDvõrdneakonstruktsiooni järgi ja on võrdsed sirge vahelise kaugusegakja otse

3) Üksteisega paralleelsete ja kahte etteantud punkti läbivate sirgjoonte ehitamine ning nende vaheline kaugus on võrdne antud lõiguga:

3.1) Lastakse punkte andaAJaBja pikkusega segmenta.

3.2) Ringi konstrueerimine, mille keskpunkt on punktisAja raadiusa.

3.3) Ehitage antud ringi puutuja läbi punktiB; on kaks sellist puutujat kuiBasub väljaspool ringi (kuiAB> a), üks kuiBasub ringil (kuiAB= a), mitte kuiBasub ringi sees (AB< a). See puutuja on üks otsitavatest joontest; jääb üle punkti läbidaAsellega paralleelne sirgjoon.

3.4) Kuna üks sirgetest on puutujaga risti ringjoone raadiusega, siis teine ​​on ka sellega risti (kuna nad on paralleelsed), siis on nende vaheline kaugus võrdne raadiusega, mis ehituse järgi on võrdnea, mida oli vaja saada.

Seega oleme tõestanud kahepoolse joonlaua ning sirkli ja joonlaua vahetatavust.

Järeldus: Kahepoolne joonlaud on vahetatav kompassi ja joonlauaga.

Järeldus

Niisiis on kaalutud ja lahendatud küsimus, kas on võimalik kasutada ühte joonlauda klassikaliste ehitusülesannete lahendamiseks, kasutades kompassi ja joonlauda. Selgub, et ehitusprobleeme saab lahendada ainult paralleelsete servadega joonlaua abil. Keerulisemate probleemide lahendamisel tuleks edaspidi tugineda käesolevas töös käsitletud nn põhikonstruktsioonidele.

Esitatud materjali saab vahetult rakendada mitte ainult matemaatikatundides, matemaatikaringi tundides, vaid ka praktilises tegevuses.

Kasutatud kirjanduse loetelu

Aliev A.V. Geomeetrilised konstruktsioonid. Matemaatika koolis. 1978 nr 3

Glazer G.I. Matemaatika ajalugu koolis. M., Valgustus. 1981. aasta.

Depman I.Ya. Matemaatikaõpiku lehekülgede taga. M.. Valgustus. 1989.

Elensky Shch Pythagorase jälgedes. M., Detgiz. 1961. aasta.

Noore matemaatiku entsüklopeediline sõnastik. M., Pedagoogika. 1985. aastal

Ehitusülesannetes käsitleme geomeetrilise kujundi konstrueerimist, mida saab teha joonlaua ja kompassi abil.

Joonlaua abil saate:

suvaline sirgjoon;

antud punkti läbiv suvaline sirge;

kahte etteantud punkti läbiv sirgjoon.

Kompassi abil saate kirjeldada etteantud raadiusega ringi antud keskpunktist.

Kompassi abil saate joonistada lõigu antud punktist antud sirgele.

Vaatleme peamisi ehitusülesandeid.

Ülesanne 1. Koostage kolmnurk antud külgedega a, b, c (joonis 1).

Lahendus. Joonlaua abil tõmmake suvaline sirge ja võtke sellele suvaline punkt B. Kasutades kompassi ava, mis on võrdne a-ga, kirjeldame ringjoont, mille keskpunkt on B ja raadius a. Olgu C tema ja sirge lõikepunkt. Kui kompassi ava on võrdne c-ga, kirjeldame ringjoont keskpunktist B ja kompassi avaga b, kirjeldame ringi keskpunktist C. Olgu A nende ringide lõikepunkt. Kolmnurga ABC küljed on võrdsed a, b, c.

Kommenteeri. Selleks, et kolm sirget lõiku saaksid olla kolmnurga külgedena, on vajalik, et suurim neist oleks väiksem kui ülejäänud kahe summa (ja< b + с).

2. ülesanne.

Lahendus. See nurk tipuga A ja kiir OM on näidatud joonisel 2.

Joonistame suvalise ringi, mille keskpunkt on antud nurga tipus A. Olgu B ja C ringi lõikepunktid nurga külgedega (joon. 3, a). Raadiusega AB joonistame ringi, mille keskpunkt on punktis O - selle kiire alguspunkt (joonis 3, b). Tähistame selle ringi lõikepunkti selle kiirega kui C 1 . Kirjeldame ringjoont keskpunktiga C 1 ja raadiusega BC. Kahe ringi lõikepunkti punkt B 1 asub soovitud nurga küljel. See tuleneb võrdsusest Δ ABC = Δ OB 1 C 1 (kolmnurkade võrdsuse kolmas märk).

3. ülesanne. Koostage selle nurga poolitaja (joonis 4).

Lahendus. Antud nurga tipust A, nagu ka keskpunktist, joonistame suvalise raadiusega ringi. Olgu B ja C selle lõikepunktid nurga külgedega. Punktidest B ja C kirjeldame sama raadiusega ringe. Olgu D nende lõikepunkt, mis erineb punktist A. Kiir AD poolitab nurga A. See tuleneb võrdsusest Δ ABD = Δ ACD (kolmnurkade võrdsuse kolmas kriteerium).

4. ülesanne. Joonistage sellele lõigule risti poolitaja (joonis 5).

Lahendus. Kasutades suvalist, kuid identset kompassi ava (suurem kui 1/2 AB), kirjeldame kahte kaare keskpunktidega punktides A ja B, mis lõikuvad teineteisega mõnes punktis C ja D. Sirge CD on soovitud risti. Tõepoolest, nagu konstruktsioonist näha, on kõik punktid C ja D võrdselt kaugel A-st ja B-st; seetõttu peavad need punktid asuma lõigu AB poolitaja risti.

5. ülesanne. Jagage see segment pooleks. See lahendatakse samamoodi nagu ülesanne 4 (vt joonis 5).

6. ülesanne. Läbi etteantud punkti tõmmake antud sirgega risti olev joon.

Lahendus. Võimalikud on kaks juhtumit:

1) antud punkt O asub antud sirgel a (joonis 6).

Punktist O joonistame suvalise raadiusega ringi, mis lõikub punktides A ja B. Punktidest A ja B joonistame sama raadiusega ringid. Olgu O 1 nende lõikepunkt, mis erineb O-st. Saame OO 1 ⊥ AB. Tegelikult on punktid O ja O 1 lõigu AB otstest võrdsel kaugusel ja asuvad seetõttu selle lõiguga risti poolitajal.

Valla eelarveline õppeasutus

keskkool nr 34 üksikute ainete süvaõppega

MAN, füüsika ja matemaatika sektsioon

"Geomeetrilised konstruktsioonid kompassi ja joonlaua abil"

Lõpetanud: 7. klassi “A” õpilane

Batištševa Victoria

Juht: Koltovskaja V.V.

Voronež, 2013

3. Antud nurgaga võrdse nurga konstrueerimine.

P Joonistame suvalise ringi, mille keskpunkt on antud nurga tipus A (joonis 3). Olgu B ja C ringi lõikepunktid nurga külgedega. Raadiusega AB joonistame ringi, mille keskpunkt on punktis O, selle poolsirge alguspunktis. Tähistame selle ringjoone lõikepunkti selle pooljoonega tähega C 1 . Kirjeldame ringi keskpunktiga C 1 ja joonis 3

lennuki raadius. Punkt B 1 konstrueeritud ringide ristumiskoht näidatud pooltasandil asub soovitud nurga küljel.

6. Ristjoonte ehitamine.

Joonistame suvalise raadiusega r ringi, mille keskpunkt on joonisel 6. punktis O. Ringjoon lõikab sirget punktides A ja B.Punktidest A ja B joonistame ringid raadiusega AB. Olgu melanhoolia C nende ringide lõikepunktiks. Punktid A ja B saime esimeses etapis suvalise raadiusega ringi ehitamisel.

Soovitud sirge läbib punkte C ja O.

Joonis 6

teadaolevad probleemid

1.Brahmagupta probleem

Koostage sissekirjutatud nelinurk, kasutades selle nelja külge. Üks lahendus kasutab Apolloniuse ringi.Lahendame Apolloniuse ülesande kolmnurga ja kolmnurga analoogia abil. Kuidas leiame kolmnurka kantud ringi: konstrueerime poolitajate lõikepunkti, langetame sellest kolmnurga külgedele ristid, ristnurkade alused (risti lõikepunktid selle küljega langeb) ja andke meile kolm punkti, mis asuvad soovitud ringil. Joonista ring läbi nende kolme punkti – lahendus on valmis. Teeme sama ka Apolloniuse probleemiga.

2. Apolloniuse probleem

Koostage sirkli ja joonlaua abil ring, mis puutub kolme etteantud ringiga. Legendi järgi sõnastas probleemi Apollonius Pergast umbes 220 eKr. e. raamatus "Puudutus", mis läks kaduma, kuid mille taastas 1600. aastal François Viète, "galli Apollonius", nagu tema kaasaegsed teda kutsusid.

Kui ükski antud ringidest ei asu teise sees, siis on sellel ülesandel 8 oluliselt erinevat lahendust.

Korrapäraste hulknurkade ehitamine.

P

õige (või võrdkülgsed ) kolmnurk - See korrapärane hulknurkkolme küljega, esimene tavalistest hulknurkadest. Kõik korrapärase kolmnurga küljed on üksteisega võrdsed ja kõik nurgad on 60°. Võrdkülgse kolmnurga konstrueerimiseks tuleb ring jagada 3 võrdseks osaks. Selleks on vaja ainult läbimõõdu ühest otsast tõmmata selle ringi raadiusega R kaar, saame esimese ja teise jaotuse. Kolmas jaotus asub läbimõõdu vastasotsas. Neid punkte ühendades saame võrdkülgse kolmnurga.

Regulaarne kuusnurk Saabkonstrueerida kompassi ja joonlaua abil. allpoolehitusviis on antudjagades ringi 6 osaks. Kasutame korrapärase kuusnurga külgede võrdsust piiritletud ringi raadiusega. Ringjoone ühe läbimõõdu vastasotstest kirjeldame kaare raadiusega R. Nende kaare lõikepunktid antud ringiga jagavad selle 6 võrdseks osaks. Leitud punkte järjestikku ühendades saadakse korrapärane kuusnurk.

Korrapärase viisnurga ehitus.

P
tavaline viisnurk võib ollakonstrueeritud kasutades kompassi ja joonlauda või sobitades selle etteantud külgering või konstruktsioon, mis põhineb antud küljel. Seda protsessi kirjeldab Euclidtema elementides umbes 300 eKr. e.

Siin on üks meetod korrapärase viisnurga konstrueerimiseks antud ringis:

Koostage ring, millesse kantakse viisnurk, ja märkige selle keskpunktO . (See on roheline ring parempoolsel diagrammil).

Valige ringil punktA , millest saab üks viisnurga tippudest. Ehitage läbiv sirgjoonO JaA .

Ehitage sirgega risti olev sirgeO.A. , läbides punktiO . Määrake üks selle ristmik ringiga punktiksB .

Joonistage punktC keskel vahepealO JaB .

C punkti kauduA . Märkige selle ristumiskoht joonegaO.B. (algse ringi sees) punktinaD .

Joonistage ring, mille keskpunkt on punktisA läbi punkti D märgi punktidena selle ringi ristumiskoht originaaliga (roheline ring).E JaF .

Joonistage ring, mille keskpunkt on punktisE punkti kauduA G .

Joonistage ring, mille keskpunkt on punktisF punkti kauduA . Märgistage selle teine ​​ristmik algse ringiga punktiksH .

Ehitage tavaline viisnurkAEGHF .

Lahendamatud probleemid

Antiikajal püstitati järgmised kolm ehitusülesannet:

Nurga kolmiklõik - jagage suvaline nurk kolmeks võrdseks osaks.

Teisisõnu on vaja konstrueerida nurga kolmisektorid - kiired, mis jagavad nurga kolmeks võrdseks osaks. P. L. Wanzel tõestas 1837. aastal, et ülesanne on lahendatav ainult siis, kui näiteks nurkade α = 360°/n korral on võimalik kolmilõikamine eeldusel, et täisarv n ei jagu 3-ga. Ajakirjanduses aga aeg-ajalt (vale) ) avaldatakse meetodid nurga kolmiklõikamiseks sirkli ja joonlauaga.

Kuubi kahekordistamine - klassikaline antiikprobleem kompassi ja joonlauaga kuubi serva konstrueerimiseks, mille ruumala on kaks korda suurem etteantud kuubiku ruumalast.

Kaasaegses tähistuses taandub probleem võrrandi lahendamisele. See kõik taandub pikkuse segmendi konstrueerimise probleemile. P. Wantzel tõestas 1837. aastal, et seda probleemi ei saa lahendada kompassi ja sirge servaga.

Ringi ruudukujundamine - ülesanne, mis seisneb antud ringiga pindalalt võrdse ruudu konstruktsiooni leidmises kompassi ja joonlaua abil.

Nagu teate, saate kompassi ja joonlaua abil sooritada kõik 4 aritmeetilist toimingut ja eraldada ruutjuure; sellest järeldub, et ringjoone ruudustamiseks on võimalik siis ja ainult siis, kui selliste toimingute lõplikku arvu kasutades on võimalik konstrueerida segment pikkusega π. Seega tuleneb selle ülesande lahendamatus arvu π mittealgebralisest olemusest (transtsendentsusest), mille tõestas 1882. aastal Lindemann.

Teine tuntud probleem, mida ei saa kompassi ja joonlauaga lahendada, onkolmnurga konstrueerimine kolme etteantud poolitajapikkuse abil .

Pealegi jääb see probleem lahendamatuks isegi trisektori olemasolul.

Alles 19. sajandil tõestati, et kõiki kolme probleemi ei saa lahendada ainult kompassi ja sirgjoonega. Ehitamise võimalikkuse küsimus lahendatakse täielikult Galois' teoorial põhinevate algebraliste meetoditega.

KAS TEADSITE, ET...

(geomeetriliste konstruktsioonide ajaloost)

Kunagi oli korrapäraste hulknurkade ehitamisel müstiline tähendus.

Seega Pythagorase, Pythagorase rajatud religioosse ja filosoofilise õpetuse järgijad, kes elasid Vana-Kreekas (V I-I Vsajandite jooksul eKr eKr), võtsid nende liidu märgiks vastu tähekujulise hulknurga, mille moodustavad korrapärase viisnurga diagonaalid.

Mõne korrapärase hulknurga range geomeetrilise konstrueerimise reeglid on sätestatud Vana-Kreeka matemaatiku Eukleidese raamatus “Elements”, kes elas aastal.IIIV. eKr. Nende konstruktsioonide teostamiseks pakkus Euclid välja ainult joonlaua ja sirkli, millel tol ajal ei olnud liigendseadet jalgade ühendamiseks (selline instrumentide piirang oli iidse matemaatika muutumatu nõue).

Muistses astronoomias kasutati laialdaselt korrapäraseid hulknurki. Kui Eukleidest huvitas nende kujundite konstrueerimine matemaatika seisukohalt, siis Vana-Kreeka astronoomile Claudius Ptolemaiosele (umbes 90 - 160 pKr) osutus see vajalikuks abivahendina astronoomiliste ülesannete lahendamisel. Niisiis on Almagesti 1. raamatus terve kümnes peatükk pühendatud korrapäraste viisnurkade ja kümnenurkade ehitamisele.

Ehitajate, käsitööliste ja kunstnike raamatute lahutamatuks osaks oli aga puhtteaduslike tööde kõrval korrapäraste hulknurkade ehitamine. Arhitektuuris, ehtekunstis ja kaunites kunstides on juba pikka aega nõutud nende kujundite kujutamise oskust.

Rooma arhitekti Vitruviuse (kes elas umbes 63-14 eKr) "Kümme raamatut arhitektuurist" öeldakse, et linnamüürid peaksid olema plaanil korrapärase hulknurga kujulised ja kindluse tornid "tuleks teha ümmargused või hulknurksed. , piiramisrelvade poolt üsna hävitatud nelinurga jaoks.

Suurt huvi pakkus linnade paigutus Vitruviusele, kes arvas, et tänavad tuleb planeerida nii, et põhituuled mööda neid ei puhuks. Eeldati, et selliseid tuuli oli kaheksa ja need puhusid teatud suundades.

Renessansiajal ei olnud korrapäraste hulknurkade ja eriti viisnurga ehitamine lihtne matemaatiline mäng, vaid see oli linnuste ehitamise vajalik eeldus.

Suure saksa astronoom ja matemaatik Johannes Kepler (1571–1630) uuris korrapärast kuusnurka, millest ta räägib oma raamatus “Uusaastakingitus ehk kuusnurksed lumehelbed”. Arutledes põhjuste üle, miks lumehelvestel on kuusnurkne kuju, märgib ta eelkõige järgmist: „... tasapinda saab ilma tühikuteta katta ainult järgmiste kujunditega: võrdkülgsed kolmnurgad, ruudud ja korrapärased kuusnurgad. Nendest kujunditest katab kõige suurema ala tavaline kuusnurk."

Üks kuulsamaid geomeetriliste konstruktsioonidega tegelevaid teadlasi oli suur saksa kunstnik ja matemaatik Albrecht Durer (1471-1528), kes pühendas neile olulise osa oma raamatust “Manuals...”. Ta pakkus välja reeglid 3, 4, 5... 16 küljega korrapäraste hulknurkade ehitamiseks. Düreri pakutud ringi jagamise meetodid ei ole universaalsed, igal konkreetsel juhul kasutatakse individuaalset tehnikat.

Dürer kasutas kunstipraktikas korrapäraste hulknurkade konstrueerimise meetodeid, näiteks parketi mitmesuguste ornamentide ja mustrite loomisel. Sellised mustrid visandas ta reisil Hollandisse, kus paljudes kodudes leidus parkettpõrandaid.

Dürer koostas ornamendid korrapärastest hulknurkadest, mis on ühendatud rõngasteks (kuue võrdkülgse kolmnurga rõngad, neli nelinurka, kolm või kuus kuusnurka, neliteist seitsenurka, neli kaheksanurka).

Järeldus

Niisiis,geomeetrilised konstruktsioonid on ülesande lahendamise meetod, mille puhul vastus saadakse graafiliselt. Konstruktsioonid teostatakse joonestustööriistade abil maksimaalse täpsuse ja töötäpsusega, kuna sellest sõltub lahenduse õigsus.

Tänu sellele tööle tutvusin kompassi tekkelooga, tutvusin rohkem geomeetriliste konstruktsioonide teostamise reeglitega, sain uusi teadmisi ja rakendasin neid praktikas.
Kompassi ja joonlauaga ehitamisega seotud ülesannete lahendamine on kasulik ajaviide, mis võimaldab heita värske pilgu geomeetriliste kujundite ja nende elementide teadaolevatele omadustele.Selles artiklis käsitletakse kõige pakilisemaid probleeme, mis on seotud geomeetriliste konstruktsioonidega, kasutades kompassi ja joonlaudu. Vaadeldakse põhiprobleeme ja antakse neile lahendused. Antud ülesanded pakuvad olulist praktilist huvi, kinnistavad omandatud teadmisi geomeetrias ja on kasutatavad praktilises töös.
Seega on töö eesmärk saavutatud, määratud ülesanded täidetud.

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-1.jpg" alt=">Ehitamine joonlaua ja kompassi geomeetria abil">!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-2.jpg" alt="> Konstrueerige lõik, mis võrdub antud Ú Ülesanne A B"> Построить отрезок равный данному Ú Задача А В На данном луче от его начала С отложить отрезок, равный данному Ú Решение 1. Изобразим фигуры, данные в D условии задачи: луч ОС и отрезок АВ О 2. Затем циркулем построим окружность радиуса АВ и с центром О. 3. Эта окружность пересечёт луч ОС в некой точке D. Отрезок OD – искомый.!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-3.jpg" alt="> Antud nurgaga võrdse nurga konstrueerimine Vaatleme kolmnurki"> Построение угла равного данному Рассмотрим треугольники Ú АВС и ОDE. Задача В Отрезки АВ и АС являются равный Отложить от данного луча угол, данному Ú радиусами окружности с Решение 1. центром А, савершиной А и луч и ОЕ Построим угол отрезки OD ОМ А С 2. – радиусами окружности с Проведем окружность произвольного центром О. Таквершине А данного радиуса с центром в как по угла. 3. построениюпересекает стороны Эта окружность эти окружности имеют равные радиусы, то угла в точках В и С. 4. АВ=OD, AC=OE. Также же Затем проведём окружность того по Е радиуса с центром в начале данного построению ВС=DE. М луча ОМ. О D Следовательно, треугольники 5. Она пересекает луч в точке D. 6. равны по построим окружность с После этого 3 сторонам. Поэтому центром D, радиус которой равен ВС 7. угол DOEс= углу BAC. Т. е. Окружности центрами О и D построенный угол МОЕ равен пересекаются в двух точках. Одну из углу А. буквой Е них назовём 8. Докажем, что угол МОЕ - искомый!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-4.jpg" alt="> Nurga poolitaja konstrueerimine Ülesanne Ú"> Построение биссектрисы угла Задача Ú Рассмотрим треугольники Ú АСЕ и АВЕ. биссектрису угла Построить Они равны по Ú трём сторонам. АЕ – общая, Решение Е 1. АС и АВ равны как угол ВАС Изобразим данный радиусы 2. одной и тойокружность Проведём же окружности, В СЕ = ВЕ по построению. произвольного радиуса с С Ú Изцентром А. Она пересечёт равенства треугольников следует, что угол САЕ В и С стороны угла в точках = углу 3. ВАЕ, т. е. луч АЕдве Затем проведём – окружности одинакового биссектриса данного угла. А радиуса ВС с центрами в точках В и С 4. Докажем, что луч АЕ – биссектриса угла ВАС!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-5.jpg" alt="> Ristjoonte ehitamine Ú Ülesanne antud sirge"> Построение перпендикулярных прямых Ú Задача Даны прямая и точка на ней. Построить прямую, проходящую через данную точку Р и перпендикулярную данной прямой. Ú Решение 1. Построим прямую а и точку М, принадлежащую этой прямой. 2. На лучах прямой а, исходящих из точки М, отложим равные отрезки МА и МВ. М а Затем построим две окружности с центрами А и В радиуса АВ. Они пересекутся в двух точках: P и Q. А B 3. Проведём прямую через точку М и одну из этих точек, например прямую МР, и докажем, что эта прямая искомая, т. Е. что она перпендикулярна к данной прямой. 4. В самом деле, так как медиана РМ равнобедренного треугольника РАВ Q является также высотой, то РМ перпендикулярна а.!}

Src="https://present5.com/presentation/3/178794035_430371946.pdf-img/178794035_430371946.pdf-6.jpg" alt="> Lõigu keskpunkti konstrueerimine Ülesanne Ú Konstrueerige keskpunkt antud"> Построение середины отрезка Задача Ú Построить середину данного отрезка Ú Решение Р 1. Пусть АВ – данный отрезок. 2. Построим две окружности с 21 центрами А и В радиуса АВ. Они пересекаются в точках Р и Q. О 3. Проведём прямую РQ. Точка О пересечения этой прямой с А B отрезком АВ и есть искомая середина отрезка АВ 4. В самом деле, треугольники АРQ и ВРQ равны по трём сторонам, поэтому угол 1 = Q углу 2 5. Следовательно отрезок РО – биссектриса равнобедренного треугольника АРВ, а значит, и медиана, т. Е. точка О – середина отрезка АВ.!}