Екстремуми функції – простою мовою про складне. Як знайти точки екстремуму функції

Переходячи в цих нерівностях до межі при Δ x→ 0 та враховуючи, що похідна f "(x 0) існує, а отже межа, що стоїть зліва, не залежить від того, як Δ x→ 0, отримуємо: при Δ x → 0 – 0 f"(x 0) ≥ 0 а при Δ x → 0 + 0 f"(x 0) ≤ 0. Оскільки f "(x 0) визначає число, то ці дві нерівності спільні лише у тому випадку, коли f "(x 0) = 0.

Доведена теорема стверджує, що точки максимуму і мінімуму можуть бути лише серед тих значень аргументу, у яких похідна перетворюється на нуль.

Ми розглянули випадок, коли функція у всіх точках деякого відрізка має похідну. Яка ж справа в тих випадках, коли похідна не існує? Розглянемо приклади.

Приклади.

1. y=|x|.

   Функція не має похідної у точці x=0 (у цій точці графік функції немає певної дотичної), але у цій точці функція має мінімум, оскільки y(0)=0, а за всіх x≠ 0y > 0.



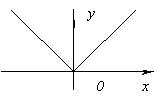
Функція не має похідної при x=0, так як звертається в нескінченність при x=0. Але у цій точці функція має максимум.



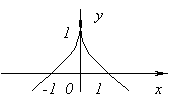
Функція не має похідної при x=0, оскільки при x→0. У цій точці функція немає ні максимуму, ні мінімуму. Справді, f(x)=0 і при x<0f(x)<0, а при x>0f(x)>0.



Таким чином, з наведених прикладів та сформульованої теореми видно, що функція може мати екстремум лише у двох випадках: 1) у точках, де похідна існує і дорівнює нулю; 2) у точці, де похідна немає.

Однак, якщо в деякій точці x 0 ми знаємо, що f "(x 0 ) =0, то звідси не можна робити висновок, що у точці x 0 функція має екстремум.

Наприклад. .



Але точка x=0 не є точкою екстремуму, оскільки зліва від цієї точки значення функції розташовані нижче за осі Ox, а праворуч вище.

Значення аргументу з області визначення функції, при яких похідна функції перетворюється на нуль або не існує, називаються критичними точками.




З усього вищесказаного випливає, що точки екстремуму функції знаходяться серед критичних точок, і, однак, не будь-яка критична точка є точкою екстремуму. Тому, щоб знайти екстремум функції, потрібно знайти всі критичні точки функції, а потім кожну з цих точок досліджувати окремо максимум і мінімум. І тому служить така теорема.

Теорема 2. (Достатня умова існування екстремуму.)Нехай функція безперервна на деякому інтервалі, що містить критичну точку x 0 , і диференційована у всіх точках цього інтервалу (крім, можливо, самої точки x 0). Якщо при переході зліва направо через цю точку похідна змінює знак із плюса на мінус, то в точці x = x 0 функція має максимум. Якщо ж при переході через x 0 зліва направо похідна змінює знак з мінусу на плюс, то функція має у цій точці мінімум.

Таким чином, якщо

Доведення. Припустимо спочатку, що при переході через x 0 похідна змінює знак із плюса на мінус, тобто. при всіх x, близьких до точки x 0 f"(x)> 0 для x< x 0 , f "(x)< 0 для x> x 0 . Застосуємо теорему Лагранжа до різниці f(x) - f(x 0 ) = f "(c)(x-x 0), де cлежить між xі x 0 .

1. Нехай x< x 0 . Тоді c< x 0 та f"(c)> 0. Тому f "(c)(x-x 0)< 0і, отже,

   f(x) - f(x 0 )< 0, тобто. f(x)< f(x 0 ).

2. Нехай x > x 0 . Тоді c> x 0 та f "(c)< 0. Значить f "(c)(x-x 0)< 0. Тому f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .

Таким чином, для всіх значень xдосить близьких до x 0 f(x)< f(x 0 ) . А це означає, що в точці x 0 функція має максимум.

Аналогічно доводиться друга частина теореми про мінімум.



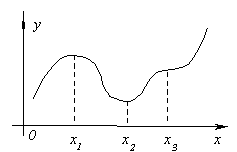
Проілюструємо сенс цієї теореми малюнку. Нехай f "(x 1 ) =0 і для будь-яких x,досить близьких до x 1 , виконуються нерівності

f "(x)< 0 при x< x 1 , f"(x)> 0 при x> x 1 .

Тоді зліва від точки x 1 функція зростає, а справа зменшується, отже, при x = x 1 функція переходить від зростання до спадання, тобто має максимум.

Аналогічно можна розглядати точки x 2 та x 3 .


Схематично все вищесказане можна зобразити на зображенні:

Правило дослідження функції y=f(x) на екстремум

1. Знайти область визначення функції f(x).
2. Знайти першу похідну функції f "(x).
3. Визначити критичні точки для цього:
   1. знайти дійсне коріння рівняння f "(x)=0;
   2. знайти всі значення xпри яких похідна f "(x)не існує.
4. Визначити знак похідної ліворуч і праворуч від критичної точки. Так як знак похідної залишається постійним між двома критичними точками, досить визначити знак похідної в якій-небудь одній точці зліва і в одній точці праворуч від критичної точки.
5. Обчислити значення функції у точках екстремуму.

Приклади. Дослідити функції на мінімум та максимум.




НАЙБІЛЬШЕ І НАЙМЕНШЕ ЗНАЧЕННЯ ФУНКЦІЇ НА ВІДРІЗКУ

Найбільшимзначенням функції на відрізку називається найбільше зі всіх її значень на цьому відрізку, а найменшим- Найменше з усіх її значень.

Розглянемо функцію y=f(x)безперервну на відрізку [ a, b]. Як відомо, така функція досягає свого найбільшого та найменшого значень, або на межі відрізка, або всередині нього. Якщо найбільше чи найменше значення функції досягається у внутрішній точці відрізка, це значення є максимумом чи мінімумом функції, тобто досягається в критичних точках.

Таким чином, отримуємо наступне правило знаходження найбільшого та найменшого значень функції на відрізку a, b] :

1. Знайти всі критичні точки функції в інтервалі ( a, b) і обчислити значення функції у цих точках.
2. Обчислити значення функції на кінцях відрізка при x = a, x = b.
3. З усіх отриманих значень вибрати найбільше та найменше.

Нехай функція $z=f(x,y)$ визначена в околиці точки $(x_0,y_0)$. Говорять, що $(x_0,y_0)$ - точка (локального) максимуму, якщо для всіх точок $(x,y)$ певної околиці точки $(x_0,y_0)$ виконана нерівність $f(x,y)< f(x_0,y_0)$. Если же для всех точек этой окрестности выполнено условие $f(x,y)>f(x_0,y_0)$, то точку $(x_0,y_0)$ називають точкою (локального) мінімуму.

Точки максимуму та мінімуму часто називають загальним терміном – точки екстремуму.

Якщо $(x_0,y_0)$ - точка максимуму, значення функції $f(x_0,y_0)$ у цій точці називають максимумом функції $z=f(x,y)$. Відповідно, значення функції у точці мінімуму називають мінімумом функції $ z = f (x, y) $. Мінімуми та максимуми функції поєднують загальним терміном - екстремуми функції.

Алгоритм дослідження функції $z = f (x, y) $ на екстремум

1. Знайти приватні похідні $\frac(\partial z)(\partial x)$ і $\frac(\partial z)(\partial y)$. Скласти і розв'язати систему рівнянь $ \left \( \begin(aligned) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0. \ end(aligned) \right.$ Точки, координати яких задовольняють зазначеній системі, називають стаціонарними.
2. Знайти $\frac(\partial^2z)(\partial x^2)$, $\frac(\partial^2z)(\partial x\partial y)$, $\frac(\partial^2z)(\partial y^2)$ і обчислити значення $\Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac (\partial^2z)(\partial x\partial y) \right)^2$ у кожній стаціонарній точці. Після цього використовувати наступну схему:
   1. Якщо $\Delta > 0$ і $\frac(\partial^2z)(\partial x^2) > 0$ (або $\frac(\partial^2z)(\partial y^2) > 0$), то досліджувана точка є точкою мінімуму.
   2. Якщо $\Delta > 0$ і $\frac(\partial^2z)(\partial x^2)< 0$ (или $\frac{\partial^2z}{\partial y^2} < 0$), то в исследуемая точка есть точкой максимума.
   3. Якщо $\Delta< 0$, то в расматриваемой стационарной точке экстремума нет.
   4. Якщо $ \ Delta = 0 $, то нічого певного про наявність екстремуму сказати не можна; потрібне додаткове дослідження.

Примітка (бажане для більш повного розуміння тексту): показати

Якщо $\Delta > 0$, то $\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\) partial^2z)(\partial x\partial y) \right)^2 > 0$. А звідси випливає, що $\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2) > \left(\frac(\partial^2z) (\partial x\partial y) \right)^2 ≥ 0$. Тобто. $\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2) > 0$. Якщо добуток деяких величин більше нуля, ці величини одного знака. Тобто, наприклад, якщо $\frac(\partial^2z)(\partial x^2) > 0$, то і $\frac(\partial^2z)(\partial y^2) > 0$. Коротше кажучи, якщо $\Delta > 0$ то знаки $\frac(\partial^2z)(\partial x^2)$ і $\frac(\partial^2z)(\partial y^2)$ збігаються.

Приклад №1

Дослідити на екстремум функцію $z=4x^2-6xy-34x+5y^2+42y+7$.

$$ \frac(\partial z)(\partial x)=8x-6y-34; \frac(\partial z)(\partial y)=-6x+10y+42. $$

$$ \left \( \begin(aligned) & 8x-6y-34=0;\\ & -6x+10y+42=0. \end(aligned) \right. $$

Скоротимо кожне рівняння цієї системи на $2$ і перенесемо числа у праві частини рівнянь:

$$ \left \( \begin(aligned) & 4x-3y=17;\\ & -3x+5y=-21. \end(aligned) \right. $$

Ми отримали систему лінійних рівнянь алгебри . Мені в цій ситуації здається найбільш зручним застосування методу Крамер для вирішення отриманої системи.

$$ \begin(aligned) & \Delta=\left| \begin(array) (cc) 4 & -3\\ -3 & 5 \end(array)\right|=4\cdot 5-(-3)\cdot (-3)=20-9=11;\ \ & \Delta_x=\left| \begin(array) (cc) 17 & -3\ -21 & 5 \end(array)\right|=17\cdot 5-(-3)\cdot (-21)=85-63=22;\ \ & \Delta_y=\left| \begin(array) (cc) 4 & 17\ -3 & -21 \end(array)\right|=4\cdot (-21)-17\cdot (-3)=-84+51=-33 .\end(aligned) \\ x=\frac(\Delta_(x))(\Delta)=\frac(22)(11)=2; \; y=\frac(\Delta_(y))(\Delta)=\frac(-33)(11)=-3. $$

Значення $x=2$, $y=-3$ - це координати стаціонарної точки $(2;-3)$.

$$ \frac(\partial^2 z)(\partial x^2)=8; \frac(\partial^2 z)(\partial y^2)=10; \frac(\partial^2 z)(\partial x \partial y)=-6. $$

Обчислимо значення $\Delta$:

$$ \Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\partial^2z)( \partial x\partial y) \right)^2= 8\cdot 10-(-6)^2=80-36=44. $$

Оскільки $\Delta > 0$ і $\frac(\partial^2 z)(\partial x^2) > 0$, то відповідно до точки $(2;-3)$ є точкою мінімуму функції $z$. Мінімум функції $z$ знайдемо, підставивши задану функцію координати точки $(2;-3)$:

$$ z_(min)=z(2;-3)=4\cdot 2^2-6\cdot 2 \cdot (-3)-34\cdot 2+5\cdot (-3)^2+42\ cdot (-3) +7 = -90. $$

Відповідь: $ (2; -3) $ - точка мінімуму; $ z_ (min) = -90 $.

Приклад №2

Дослідити на екстремум функцію $z=x^3+3xy^2-15x-12y+1$.

Наслідуватимемо вище . Для початку знайдемо приватні похідні першого порядку:

$$ \frac(\partial z)(\partial x)=3x^2+3y^2-15; \frac(\partial z)(\partial y) = 6xy-12. $$

Складемо систему рівнянь $ \left \( \begin(aligned) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0. \end( aligned) \right.$:

$$ \left \( \begin(aligned) & 3x^2+3y^2-15=0;\\ & 6xy-12=0. \end(aligned) \right. $$

Скоротимо перше рівняння на 3, а друге – на 6.

$$ \left \( \begin(aligned) & x^2+y^2-5=0;\\ & xy-2=0. \end(aligned) \right. $$

Якщо $x=0$, друге рівняння приведе нас до суперечності: $0\cdot y-2=0$, $-2=0$. Звідси висновок: $ x \ neq 0 $. Тоді з другого рівняння маємо $xy=2$, $y=\frac(2)(x)$. Підставляючи $y=\frac(2)(x)$ у перше рівняння, будемо мати:

$$ x^2+\left(\frac(2)(x) \right)^2-5=0;\\ x^2+\frac(4)(x^2)-5=0;\\ x^4-5x^2+4=0. $$

Здобули біквадратне рівняння. Робимо заміну $t=x^2$ (при цьому маємо на увазі, що $t > 0$):

$$ t^2-5t+4=0;\\ \begin(aligned) & D=(-5)^2-4\cdot 1 \cdot 4=9;\\ & t_1=\frac(-(- 5)-\sqrt(9))(2)=\frac(5-3)(2)=1;\\ & t_2=\frac(-(-5)+\sqrt(9))(2)= \frac(5+3)(2)=4.\end(aligned) $$

Якщо $t=1$, то $x^2=1$. Звідси маємо два значення $x$: $x_1=1$, $x_2=-1$. Якщо $t=4$, то $x^2=4$, тобто. $x_3=2$, $x_4=-2$. Згадуючи, що $y=\frac(2)(x)$, отримаємо:

\begin(aligned) & y_1=\frac(2)(x_1)=\frac(2)(1)=2;\\ & y_2=\frac(2)(x_2)=\frac(2)(-1 )=-2;\\&y_3=\frac(2)(x_3)=\frac(2)(2)=1;\\ & y_4=\frac(2)(x_4)=\frac(2)( -2) =-1. \end(aligned)

Отже, ми маємо чотири стаціонарні точки: $M_1(1;2)$, $M_2(-1;-2)$, $M_3(2;1)$, $M_4(-2;-1)$. У цьому перший крок алгоритму завершено.

Тепер приступимо до алгоритму. Знайдемо приватні похідні другого порядку:

$$ \frac(\partial^2 z)(\partial x^2)=6x; \frac(\partial^2 z)(\partial y^2)=6x; \frac(\partial^2 z)(\partial x \partial y)=6y. $$

Знайдемо $\Delta$:

$$ \Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\partial^2z)( \partial x\partial y) \right)^2= 6x\cdot 6x-(6y)^2=36x^2-36y^2=36(x^2-y^2). $$

Тепер обчислюватимемо значення $\Delta$ у кожній із знайдених раніше стаціонарних точок. Почнемо з точки $ M_1 (1; 2) $. У цій точці маємо: $ Delta (M_1) = 36 (1 ^ 2-2 ^ 2) = -108 $. Оскільки $\Delta(M_1)< 0$, то согласно в точке $M_1$ экстремума нет.

Досліджуємо точку $M_2(-1;-2)$. У цій точці маємо: $\Delta(M_2)=36((-1)^2-(-2)^2)=-108$. Оскільки $\Delta(M_2)< 0$, то согласно в точке $M_2$ экстремума нет.

Досліджуємо точку $M_3(2;1)$. У цій точці отримаємо:

$ $ \ Delta (M_3) = 36 (2 ^ 2-1 ^ 2) = 108; \; \; \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3)=6\cdot 2=12. $$

Оскільки $\Delta(M_3) > 0$ і $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3) > 0$, відповідно до $M_3(2; 1) $ є точкою мінімуму функції $ z $. Мінімум функції $z$ знайдемо, підставивши задану функцію координати точки $M_3$:

$$ z_(min)=z(2;1)=2^3+3cdot 2cdot 1^2-15cdot 2-12cdot 1+1=-27. $$

Залишилося дослідити точку $M_4(-2;-1)$. У цій точці отримаємо:

$$ \Delta(M_4)=36((-2)^2-(-1)^2)=108;\;\; \left.\frac(\partial^2 z)(\partial x^2)\right|_(M_4)=6\cdot (-2)=-12. $$

Оскільки $\Delta(M_4) > 0$ і $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_4)< 0$, то согласно $M_4(-2;-1)$ есть точкой максимума функции $z$. Максимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_4$:

$$ z_(max)=z(-2;-1)=(-2)^3+3\cdot (-2)\cdot (-1)^2-15\cdot (-2)-12\cdot (-1) +1 = 29. $$

Дослідження на екстремум завершено. Залишилося лише записати відповідь.

Відповідь:

• $ (2; 1) $ - точка мінімуму, $ z_ (min) = -27 $;
• $(-2;-1)$ - точка максимуму, $ z_(max) = 29 $.

Примітка

Обчислювати значення $\Delta$ у випадку немає необхідності, оскільки нас цікавить лише знак, а чи не конкретне значення даного параметра. Наприклад, для розглянутого вище прикладу №2 у точці $M_3(2;1)$ маємо $\Delta=36\cdot(2^2-1^2)$. Тут очевидно, що $\Delta > 0$ (оскільки обидва співмножники $36$ і $(2^2-1^2)$ позитивні) і можна не знаходити конкретне значення $\Delta$. Щоправда, для типових розрахунків це зауваження марна, - там вимагають довести обчислення до числа:)

Приклад №3

Дослідити на екстремум функцію $z=x^4+y^4-2x^2+4xy-2y^2+3$.

Наслідуватимемо . Для початку знайдемо приватні похідні першого порядку:

$$ \frac(\partial z)(\partial x)=4x^3-4x+4y; \frac(\partial z)(\partial y)=4y^3+4x-4y. $$

Складемо систему рівнянь $ \left \( \begin(aligned) & \frac(\partial z)(\partial x)=0;\\ & \frac(\partial z)(\partial y)=0. \end( aligned) \right.$:

$$ \left \( \begin(aligned) & 4x^3-4x+4y=0;\\ & 4y^3+4x-4y=0. \end(aligned) \right. $$

Скоротимо обидва рівняння на $4$:

$$ \left \( \begin(aligned) & x^3-x+y=0;\\ & y^3+x-y=0. \end(aligned) \right. $$

Додамо до другого рівняння перше і висловимо $y$ через $x$:

$$ y^3+x-y+(x^3-x+y)=0;\\y^3+x^3=0; y^3=-x^3; y=-x. $$

Підставляючи $y=-x$ у перше рівняння системи, матимемо:

$$ x^3-x-x=0; x^3-2x=0; x(x^2-2)=0. $$

З отриманого рівняння маємо $x=0$ або $x^2-2=0$. З рівняння $x^2-2=0$ слід, що $x=-\sqrt(2)$ або $x=\sqrt(2)$. Отже, знайдено три значення $x$, а саме: $x_1=0$, $x_2=-sqrt(2)$, $x_3=sqrt(2)$. Оскільки $y=-x$, то $y_1=-x_1=0$, $y_2=-x_2=\sqrt(2)$, $y_3=-x_3=-\sqrt(2)$.

Перший крок рішення закінчено. Ми отримали три стаціонарні точки: $M_1(0;0)$, $M_2(-\sqrt(2),\sqrt(2))$, $M_3(\sqrt(2),-\sqrt(2))$ .

Тепер приступимо до алгоритму. Знайдемо приватні похідні другого порядку:

$$ \frac(\partial^2 z)(\partial x^2)=12x^2-4; \frac(\partial^2 z)(\partial y^2)=12y^2-4; \frac(\partial^2 z)(\partial x \partial y)=4. $$

Знайдемо $\Delta$:

$$ \Delta=\frac(\partial^2z)(\partial x^2)\cdot \frac(\partial^2z)(\partial y^2)-\left(\frac(\partial^2z)( \partial x\partial y) \right)^2= (12x^2-4)(12y^2-4)-4^2=\\ =4(3x^2-1)\cdot 4(3y^2 -1)-16=16(3x^2-1)(3y^2-1)-16=16cdot((3x^2-1)(3y^2-1)-1). $$

Тепер обчислюватимемо значення $\Delta$ у кожній із знайдених раніше стаціонарних точок. Почнемо з точки $ M_1 (0; 0) $. У цій точці маємо: $ Delta (M_1) = 16 cdot ((3 cdot 0 ^ 2-1) (3 cdot 0 ^ 2-1) -1) = 16 cdot 0 = 0 $. Так як $ \ Delta (M_1) = 0 $, то згідно потрібно додаткове дослідження, бо нічого певного про наявність екстремуму в точці, що розглядається, сказати не можна. Дамо поки що цю точку в спокої і перейдемо в інші точки.

Досліджуємо точку $M_2(-\sqrt(2),\sqrt(2))$. У цій точці отримаємо:

\begin(aligned) & \Delta(M_2)=16\cdot((3\cdot (-\sqrt(2))^2-1)(3\cdot (\sqrt(2))^2-1)- 1) = 16 \ cdot 24 = 384; \ \ & \ left. \ frac ( \ partial ^ 2 z) ( \ partial x ^ 2) \ right | ) ^ 2-4 = 24-4 = 20. \end(aligned)

Оскільки $\Delta(M_2) > 0$ і $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_2) > 0$, то згідно $M_2(-\ sqrt(2),\sqrt(2))$ є точкою мінімуму функції $z$. Мінімум функції $z$ знайдемо, підставивши задану функцію координати точки $M_2$:

$$ z_(min)=z(-\sqrt(2),\sqrt(2))=(-\sqrt(2))^4+(\sqrt(2))^4-2(-\sqrt( 2))^2+4\cdot (-\sqrt(2))\sqrt(2)-2(\sqrt(2))^2+3=-5. $$

Аналогічно попередньому пункту досліджуємо точку $M_3(sqrt(2),-sqrt(2))$. У цій точці отримаємо:

\begin(aligned) & \Delta(M_3)=16\cdot((3\cdot (\sqrt(2))^2-1)(3\cdot (-\sqrt(2))^2-1)- 1) = 16 \ cdot 24 = 384; \ \ & \ left. \ frac ( \ partial ^ 2 z) ( \ partial x ^ 2) \ right | ^2-4=24-4=20. \end(aligned)

Оскільки $\Delta(M_3) > 0$ і $\left.\frac(\partial^2 z)(\partial x^2)\right|_(M_3) > 0$, то відповідно до $M_3(\sqrt (2),-\sqrt(2))$ є точкою мінімуму функції $z$. Мінімум функції $z$ знайдемо, підставивши задану функцію координати точки $M_3$:

$$ z_(min)=z(\sqrt(2),-\sqrt(2))=(\sqrt(2))^4+(-\sqrt(2))^4-2(\sqrt(2) ))^2+4\cdot \sqrt(2)(-\sqrt(2))-2(-\sqrt(2))^2+3=-5. $$

Настала черга повернутися до точки $M_1(0;0)$, у якій $\Delta(M_1) = 0$. Відповідно потрібне додаткове дослідження. Під цією ухильною фразою мається на увазі "робіть що хочете" :). Загального способу вирішення таких ситуацій немає, і це зрозуміло. Якби такий спосіб був, то він давно б увійшов до всіх підручників. А поки що доводиться шукати особливий підхід до кожної точки, в якій $ \ Delta = 0 $. Ну що ж, дослідимо поведінку функції на околиці точки $ M_1 (0; 0) $. Відразу зазначимо, що $z(M_1)=z(0;0)=3$. Припустимо, що $M_1(0;0)$ - точка мінімуму. Тоді для будь-якої точки $M$ з певної околиці точки $M_1(0;0)$ отримаємо $z(M) > z(M_1)$, тобто. $z(M) > 3$. А раптом будь-яка околиця містить точки, в яких $z(M)< 3$? Тогда в точке $M_1$ уж точно не будет минимума.

Розглянемо точки, які $y=0$, тобто. точки виду $ (x, 0) $. У цих точках функція $z$ прийматиме такі значення:

$$ z(x,0)=x^4+0^4-2x^2+4x\cdot 0-2\cdot 0^2+3=x^4-2x^2+3=x^2(x ^2-2) +3. $$

У всіх досить малих околицях $M_1(0;0)$ маємо $x^2-2< 0$, посему $x^2(x^2-2) < 0$, откуда следует $x^2(x^2-2)+3 < 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z < 3$, посему точка $M_1(0;0)$ не может быть точкой минимума.

Але, можливо, точка $ M_1 (0; 0) $ - точка максимуму? Якщо це так, то для будь-якої точки $M$ з деякої околиці точки $M_1(0;0)$ отримаємо $z(M)< z(M_1) $, т.е. $z(M) < 3$. А вдруг любая окрестность содержит точки, в которых $z(M) >3 $? Тоді в точці $M_1$ точно не буде максимуму.

Розглянемо точки, які $y=x$, тобто. точки виду $ (x, x) $. У цих точках функція $z$ прийматиме такі значення:

$$ z(x,x)=x^4+x^4-2x^2+4xcdot x-2cdot x^2+3=2x^4+3. $$

Оскільки в будь-якій околиці точки $M_1(0;0)$ маємо $2x^4 > 0$, то $2x^4+3 > 3$. Висновок: будь-яка околиця точки $M_1(0;0)$ містить точки, в яких $z > 3$, тому точка $M_1(0;0)$ не може бути точкою максимуму.

Точка $M_1(0;0)$ не є ні точкою максимуму, ні точкою мінімуму. Висновок: $ M_1 $ взагалі не є точкою екстремуму.

Відповідь: $(-\sqrt(2),\sqrt(2))$, $(\sqrt(2),-\sqrt(2))$ - точки мінімуму функції $z$. В обох точках $ z_ (min) = -5 $.

Що таке екстремум функції та яка необхідна умова екстремуму?

Екстремумом функції називається максимум і мінімум функції.

Необхідна умова максимуму і мінімуму (екстремуму) функції таке: якщо функція f(x) має екстремум у точці х = а, то цій точці похідна або дорівнює нулю, або нескінченна, або немає.

Ця умова необхідна, але не достатня. Похідна в точці х = а може звертатися в нуль, у нескінченність або не існувати без того, щоб функція мала екстремум у цій точці.

Яка достатня умова екстремуму функції (максимум або мінімум)?

Перша умова:

Якщо в достатній близькості від точки х = а похідна f? максимум

Якщо в достатній близькості від точки х = а похідна f? мінімумза умови, що функція f(x) тут безперервна.

Натомість можна скористатися другою достатньою умовою екстремуму функції:

Нехай у точці х = а перша похідна f?(x) перетворюється на нуль; якщо у своїй друга похідна f??(а) негативна, то функція f(x) має у точці x = a максимум, якщо позитивна - то мінімум.

Що таке критична точка функції та як її знайти?

Це значення аргументу функції, у якому функція має екстремум (тобто максимум чи мінімум). Щоб його знайти, потрібно знайти похіднуфункції f?(x) і, прирівнявши її до нуля, вирішити рівняння f?(x) = 0. Коріння цього рівняння, і навіть ті точки, у яких немає похідна цієї функції, є критичними точками, т. е. значеннями аргументу, у яких може бути екстремум. Їх можна легко визначити, глянувши на графік похідної: нас цікавлять ті значення аргументу, за яких графік функції перетинає вісь абсцис (вісь Ох) і ті, за яких графік зазнає розривів.

Наприклад знайдемо екстремум параболи.

Функція y(x) = 3x2 + 2x – 50.

Похідна функції: y? (x) = 6x + 2

Вирішуємо рівняння: y? (x) = 0

6х + 2 = 0, 6х = -2, х = -2/6 = -1/3

У разі критична точка - це х0=-1/3. Саме при цьому значенні аргументу функція має екстремум. Щоб його знайти, підставляємо для функції замість «х» знайдене число:

y0 = 3*(-1/3)2 + 2*(-1/3) - 50 = 3*1/9 - 2/3 - 50 = 1/3 - 2/3 - 50 = -1/3 - 50 = -50,333.

Як визначити максимум і мінімум функції, тобто. її найбільше та найменше значення?

Якщо знак похідної під час переходу через критичну точку х0 змінюється з «плюсу» на «мінус», то х0 є точка максимуму; якщо ж знак похідної змінюється з мінуса на плюс, то х0 є точка мінімуму; якщо знак не змінюється, то у точці х0 ні максимуму, ні мінімуму немає.

Для розглянутого прикладу:

Беремо довільне значення аргументу ліворуч від критичної точки: х = -1

При х = -1 значення похідної буде у? (-1) = 6 * (-1) + 2 = -6 + 2 = -4 (тобто знак - "мінус").

Тепер беремо довільне значення аргументу праворуч від критичної точки: х = 1

При х = 1 значення похідної буде у (1) = 6 * 1 + 2 = 6 + 2 = 8 (тобто знак - плюс).

Як бачимо, похідна під час переходу через критичну точку змінила знак із мінуса на плюс. Отже, за критичного значення х0 ми маємо точку мінімуму.

Найбільше та найменше значення функції на інтервалі(на відрізку) знаходять за такою ж процедурою тільки з урахуванням того, що, можливо, не всі критичні точки лежатимуть усередині зазначеного інтервалу. Ті критичні точки, які перебувають за межею інтервалу, слід виключити з розгляду. Якщо всередині інтервалу знаходиться лише одна критична точка – у ній буде або максимум, або мінімум. У цьому випадку для визначення найбільшого та найменшого значень функції враховуємо також значення функції на кінцях інтервалу.

Наприклад, знайдемо найбільше та найменше значення функції

y(x) = 3sin(x) - 0,5х

на інтервалах:

Отже, похідна функції -

y?(x) = 3cos(x) - 0,5

Вирішуємо рівняння 3cos(x) - 0,5 = 0

cos(x) = 0,5/3 = 0,16667

х = ± arccos (0,16667) + 2πk.

Знаходимо критичні точки на інтервалі [-9; 9]:

х = arccos (0,16667) - 2π * 2 = -11,163 (не входить в інтервал)

х = -arccos (0,16667) - 2π * 1 = -7,687

х = arccos (0,16667) - 2π * 1 = -4,88

x = -arccos(0,16667) + 2π*0 = -1,403

x = arccos(0,16667) + 2π*0 = 1,403

x = -arccos(0,16667) + 2π*1 = 4,88

x = arccos(0,16667) + 2π*1 = 7,687

х = -arccos(0,16667) + 2π*2 = 11,163 (не входить до інтервалу)

Знаходимо значення функції при критичних значеннях аргументу:

y(-7,687) = 3cos(-7,687) - 0,5 = 0,885

y(-4,88) = 3cos(-4,88) - 0,5 = 5,398

y(-1,403) = 3cos(-1,403) - 0,5 = -2,256

y(1,403) = 3cos(1,403) - 0,5 = 2,256

y(4,88) = 3cos(4,88) - 0,5 = -5,398

y(7,687) = 3cos(7,687) - 0,5 = -0,885

Видно, що на інтервалі [-9; 9] найбільше значення функція має за x = -4,88:

x = -4,88, у = 5,398,

а найменше – при х = 4,88:

x = 4,88, у = -5,398.

На інтервалі [-6; -3] маємо лише одну критичну точку: х = -4,88. Значення функції при х = -4,88 дорівнює у = 5,398.

Знаходимо значення функції на кінцях інтервалу:

y(-6) = 3cos(-6) - 0,5 = 3,838

y(-3) = 3cos(-3) - 0,5 = 1,077

На інтервалі [-6; -3] маємо найбільше значення функції

у = 5,398 при x = -4,88

найменше значення -

у = 1,077 при x = -3

Як знайти точки перегину графіка функції та визначити сторони опуклості та увігнутості?

Щоб знайти всі точки перегину лінії y = f(x), треба знайти другу похідну, прирівняти її до нуля (вирішити рівняння) і випробувати всі значення х, для яких друга похідна дорівнює нулю, нескінченна або не існує. Якщо при переході через одне з цих значень друга похідна змінює знак, графік функції має в цій точці перегин. Якщо ж не змінює, то перегину немає.

Коріння рівняння f? (x) = 0, а також можливі точки розриву функції та другої похідної розбивають область визначення функції на ряд інтервалів. Випуклість на кожному їх інтервалі визначається знаком другої похідної. Якщо друга похідна в точці на досліджуваному інтервалі позитивна, лінія y = f(x) звернена тут увігнутістю догори, і якщо негативна - то донизу.

Як знайти екстремуми функції двох змінних?

Щоб знайти екстремуми функції f(x,y), що диференціюється в області її завдання, потрібно:

1) знайти критичні точки, а для цього вирішити систему рівнянь

fх? (x, y) = 0, f? (x, y) = 0

2) для кожної критичної точки Р0(a;b) дослідити, чи залишається незмінним знак різниці

всім точок (х;у), досить близьких до Р0. Якщо різницю зберігає позитивний знак, то точці Р0 маємо мінімум, якщо негативний - то максимум. Якщо різницю не зберігає знака, то точці Р0 екстремуму немає.

Аналогічно визначають екстремуми функції за більшої кількості аргументів.

Який офіційний сайт співачки Мікі Ньютон та її групи
Нове українське диво – Міка Ньютон! Це група з 5 людей, що грає поп-рок, насолоджується життям, дарує драйв і позитивно дивиться на це життя. Зібралися хлопці у Києві, де зараз і мешкають. Діти ні в яку не погоджуються зі стандартними підвалинами в музиці та житті, відкриваючи своє нове звучання та ламаючи всілякі стандарти. Лідер колективу -

Як перевести мілілітри в кубічні метри
Основною одиницею довжини у системі СІ є метр. Виходячи з цього, основною одиницею об'єму слід вважати кубічний метр або, як його ще називають, кубометр або куб. Це обсяг куба з ребрами, рівними одному метру. Однак, на практиці виражати обсяг саме у кубометрах зручно не завжди. Наприклад, об'єм кімнати в кубічних метрах висловлювати зручно: помножили довжину

Яка калорійність манної крупи
Калорійність продуктів харчування, калорійності таблиці. Потреба людини у енергії вимірюється в кілокалоріях (ккал). Слово «калорія» надійшло з латинської мови і означає «тепло». У фізиці вимірюється калоріями енергія. Одна кілокалорія - це така кількість енергії,

Які є етапи розвитку реалізму у літературі
Реалізм (лат. речовий, дійсний) - напрям у літературі та мистецтві, що має на меті правдиве відтворення дійсності в її типових рисах. Загальні ознаки: Художнє зображення життя образах, відповідне суті явищ самого життя. Реальність є засобом пізнання людиною себе та навколишнього світу. Типізація

Який зв'язок між берклієм та 117-м елементом таблиці Менделєєва
Берклій, Berkelium, Bk - 97-й елемент таблиці Менделєєва. Відкритий у грудні 1949 р. Томпсоном, Гіорсо і Сіборгом в Каліфорнійському університеті в Берклі. При опроміненні 241Am альфа-частинками вони отримали ізотоп беркелію 243Вk. Оскільки Bk має структурну схожість з тербієм, що отримала свою назву від імені Ітербі в

Чим прославився Ярослав Мудрий
Ярослав Мудрий (980–1054), великий князь київський (1019). Син Володимира І Святославовича. Вигнав Святополка I Окаянного, боровся з братом Мстиславом, розділив з ним державу (1025), 1035 р. знову об'єднав його. Поруч перемог убезпечив південні та західні кордони Русі. Встановив династичні зв'язки з багатьма країнами Єв

Як з'явилася традиція кричати на весіллі "Гірко!"
Давним-давно з'явилася традиція кричати під час весільного застілля: «Гірко!», змушуючи молодят встати зі своїх місць і поцілуватися. Сьогодні багато хто навіть не здогадується, в чому ж полягає сенс цього обряду. За старих часів на весіллях кричали «Гірко!», даючи зрозуміти, що вино в чашах нібито несолодке. А

Які симптоми ларингіту
Ларингіт (від др.-грец. λ?ρυγξ - горло) - запалення гортані, пов'язане, як правило, з застудним захворюванням або з такими інфекційними захворюваннями, як кір, скарлатина, кашлюк. Розвитку захворювання сприяють переохолодження, дихання через рот, запилений

Чи визначається рід і відмінювання у іменників, які мають тільки форму множини
Число це граматична категорія, що виражає кількісну характеристику предмета. 1. Більшість іменників змінюється за числами, тобто. має дві форми - однини і множини. У формі однини іменник позначає один предмет, у формі множини — кілька предметів:

Чим корисна російська каша
Гречка каша Гречка - крупа особлива. З неї, виходить, мабуть, одна з найкорисніших каш. Недарма ми називаємо її першою. Гречка містить клітковину, цілий спектр вітамінів - Е, РР, В1, В2, фолієві та органічні кислоти, а також великий відсоток крохмалю, що сприяє потраплянню в організм потрібної кількості нео

Інтерактивну карту міста Архангельська можна переглянути на наступних сайтах: Карта1 - супутникова та стандартна карта; Карта2 - стандартна карта (1:350 000); Карта3 - є назви вулиць, номери будинків, можливий пошук по вулиці; Карта4 - карта з назвами вулиць Карта5 - інтерактивна карта міста; Карта6 - інтерактивна карта міста.

Крапка х 0 називається точкою максимуму(мінімуму) функції f(х), якщо в деякому околиці точки х 0 виконується нерівність f(х) ≤f(х 0) (f(х) ≥f(х 0)).

Значення функції у цій точці називається відповідно максимумомабо мінімумомфункції. Максимум і мінімум функції поєднуються загальною назвою екстремумуфункції.

Екстремум функції у цьому сенсі часто називають локальним екстремумом, Наголошуючи на тому факті, що це поняття пов'язане лише з досить малою околицею точки х 0 . На тому самому проміжку функція може мати кілька локальних максимумів і мінімумів, які обов'язково збігаються з глобальним максимумомабо мінімумом(Тобто найбільшим або найменшим значенням функції на всьому проміжку).

Необхідна умова екстремуму. Для того, щоб функція мала екстремум у точці, необхідно, щоб її похідна у цій точці дорівнювала нулю або не існувала.

Для функцій, що диференціюються, ця умова випливає з теореми Ферма. Крім того, воно передбачає і випадок, коли функція має екстремум у точці, в якій вона не диференційована.

Точки, в яких виконано необхідну умову екстремуму, називаються критичними(або стаціонарнимидля функції, що диференціюється). Ці точки повинні входити до області визначення функції.

Таким чином, якщо в будь-якій точці є екстремум, то ця точка критична (необхідність умови). Зауважимо, що зворотне твердження не так. Критична точка не обов'язково є точкою екстремуму, тобто. сформульована умова не є достатньою.

Перша достатня умова екстремуму. Якщо при переході через деяку точку похідна функції, що диференціюється змінює свій знак з плюсу на мінус, то це точка максимуму функції, а якщо з мінуса на плюс, - то точка мінімуму.

Доказ цієї умови випливає із достатньої умови монотонності (при зміні знака похідної відбувається перехід або від зростання функції до спадання, або від зменшення до зростання).

Друга достатня умова екстремуму. Якщо перша похідна двічі диференційованої функції у певній точці дорівнює нулю, а друга похідна у цій точці позитивна, це точка мінімуму функції; а якщо друга похідна негативна, це точка максимуму.

Доказ цієї умови також ґрунтується на достатній умові монотонності. Справді, якщо друга похідна є позитивною, то перша похідна є зростаючою функцією. Оскільки в точці, що розглядається, вона дорівнює нулю, отже, при переході через неї вона змінює знак з мінуса на плюс, що повертає нас до першої достатньої умови локального мінімуму. Аналогічно, якщо друга похідна негативна, то перша зменшується і змінює знак з плюсу на мінус, що є достатньою умовою локального максимуму.

Дослідження функції на екстремумвідповідно до сформульованих теорем включає наступні етапи:

1. Знайти першу похідну функції f`(x).

2. Перевірити виконання необхідної умови екстремуму, тобто. знайти критичні точки функції f(x), у яких похідна f`(x) = 0 або не існує.

3. Перевірити виконання достатньої умови екстремуму, тобто. або дослідити знак похідної ліворуч і праворуч від кожної критичної точки, або знайти другу похідну f``(x) та визначити її знак у кожній критичній точці. Зробити висновок про наявність екстремумів функції.

4. Знайти екстремуми (екстремальні значення) функції.

Знаходження глобального максимуму та мінімуму функціїна деякому проміжку також має велике прикладне значення. Розв'язання цієї задачі на відрізку засноване на теоремі Вейєрштраса, відповідно до якої безперервна функція приймає на відрізку свої найбільше та найменше значення. Вони можуть досягатись як у точках екстремуму, так і на кінцях відрізка. Тому рішення включає такі етапи:

1. Знайти похідну функції f`(x).

2. Знайти критичні точки функції f(x), у яких похідна f`(x) = 0 чи немає.

3. Знайти значення функції в критичних точках і кінцях відрізка і вибрати їх найбільше і найменше.