Окружність. Основні теореми
Згадаймо випадки взаємного розташування прямої та кола.
Задано коло з центром Про і радіусом r. Пряма Р, відстань від центру до прямої, тобто перпендикуляр ЗМ, дорівнює d.
Випадок 1- відстань від центру кола до прямої менше радіусу кола:
Ми довели, що у випадку, коли відстань d менша за радіус кола r, пряма і коло мають лише дві загальні точки (рис. 1).
Мал. 1. Ілюстрація на випадок 1
Випадок другий- відстань від центру кола до прямої дорівнює радіусу кола:
Ми довели, що у цьому випадку загальна точка єдина (рис. 2).

Мал. 2. Ілюстрація до випадку 2
Випадок 3- відстань від центру кола до прямої більше радіусу кола:
Ми довели, що в даному випадку коло і пряме не мають спільних точок (рис. 3).

Мал. 3. Ілюстрація на випадок 3
На даному уроці нас цікавить другий випадок, коли пряма та коло мають єдину спільну точку.
Визначення:
Пряма, що має з колом єдину загальну точку, називається дотичною до кола, загальна точка називається точкою торкання прямої та кола.
Пряма р – дотична, точка А – точка дотику (рис. 4).

Мал. 4. Стосовна
Теорема:
Дотична до кола перпендикулярна радіусу, проведеному в точку торкання (рис. 5).

Мал. 5. Ілюстрація до теореми
Доведення:
Від неприємного - нехай ОА не перпендикулярно прямий р. У такому разі опустимо з точки Про перпендикуляр на пряму р, який буде відстанню від центру кола до прямої:
З прямокутного трикутника можемо сказати, що гіпотенуза ВІН менше катета ОА, тобто пряма і коло мають дві загальні точки, пряма р є січною. Таким чином, ми набули протиріччя, а, отже, теорема доведена.

Мал. 6. Ілюстрація до теореми
Справедлива та зворотна теорема.
Теорема:
Якщо пряма проходить через кінець радіусу, що лежить на колі, і перпендикулярна до цього радіусу, то вона є дотичною.
Доведення:
Оскільки пряма перпендикулярна радіусу, то відстань ОА - це відстань від прямої до центру кола і вона дорівнює радіусу: . Тобто, а в цьому випадку, як ми раніше доводили, у прямої та кола єдина загальна точка - це точка А, таким чином, пряма р є дотичною до кола за визначенням (рис. 7).

Мал. 7. Ілюстрація до теореми
Пряму і зворотну теореми можна поєднати так (рис. 8):
Задано коло з центром О, пряма р, радіус ОА

Мал. 8. Ілюстрація до теореми
Теорема:
Пряма є дотичною до кола тоді і тільки тоді, коли радіус, проведений у точку торкання, перпендикулярний їй.
Дана теорема означає, що якщо пряма є дотичною, то радіус, проведений у точку торкання, перпендикулярний їй, і навпаки, з перпендикулярності ОА і р випливає, що р - дотична, тобто пряма та коло мають єдину загальну точку.
Розглянемо дві дотичні, проведені з однієї точки до кола.
Теорема:
Відрізки дотичних до кола, проведені з однієї точки, рівні і становлять рівні кути з прямої, проведеної через цю точку та центр кола.
Задано коло, центр О, точка А поза коло. З точки А проведено дві дотичні точки В і С - точки дотику. Потрібно довести, що і що дорівнюють кути 3 і 4.

Мал. 9. Ілюстрація до теореми
Доведення:
Доказ ґрунтується на рівності трикутників ![]() . Пояснимо рівність трикутників. Вони є прямокутними, оскільки радіус, проведений у точку торкання, перпендикулярний дотичній. Значить, кути і прямі і дорівнюють . Катети ОВ і ОС рівні, оскільки є радіусом кола. Гіпотенуза АТ – загальна.
. Пояснимо рівність трикутників. Вони є прямокутними, оскільки радіус, проведений у точку торкання, перпендикулярний дотичній. Значить, кути і прямі і дорівнюють . Катети ОВ і ОС рівні, оскільки є радіусом кола. Гіпотенуза АТ – загальна.
Таким чином, трикутники рівні за рівністю катета та гіпотенузи. Звідси очевидно, що катети АВ та АС також рівні. Також кути, що лежать навпроти рівних сторін, рівні, отже, рівні кути і , .
Теорему доведено.
Отже, ми познайомилися з поняттям щодо кола, на наступному уроці ми розглянемо градусну міру дуги кола.
Список літератури
- Александров А.Д. та ін. Геометрія 8 клас. - М: Просвітництво, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрія 8. – К.: Просвітництво, 2011.
- Мерзляк А.Г., Полонський В.Б., Якір С.М. Геометрія 8 клас. – К.: ВЕНТАНА-ГРАФ, 2009.
- Univer.omsk.su().
- Oldskola1.narod.ru ().
- School6.aviel.ru ().
Домашнє завдання
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. та ін, Геометрія 7-9, № 634-637, с. 168.
Стаття дає докладне роз'яснення визначень геометричного сенсу похідної з графічними позначеннями. Буде розглянуто рівняння дотичної прямої з наведенням прикладів, знайдено рівняння щодо кривих 2 порядку.
Визначення 1Кут нахилу прямої y = k x + b називається кут α, який відраховується від позитивного напрямку осі о х до прямої y = k x + b у позитивному напрямку.
На малюнку напрямок позначається за допомогою зеленої стрілки і у вигляді зеленої дуги, а кут нахилу за допомогою червоної дуги. Синя лінія відноситься до прямої.
Визначення 2
Кутовий коефіцієнт прямої y = k x + b називають числовим коефіцієнтом k.
Кутовий коефіцієнт дорівнює тангенсу нахилу прямої, інакше кажучи k = t g α.
- Кут нахилу прямої дорівнює 0 тільки при паралельності про х і кутовому коефіцієнті, що дорівнює нулю, тому як тангенс нуля дорівнює 0 . Отже, вид рівняння буде y = b.
- Якщо кут нахилу прямий y = k x + b гострий, виконуються умови 0< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0 , причому є зростання графіка.
- Якщо α = π 2 тоді розташування прямої перпендикулярно о х. Рівність задається за допомогою рівності x = c зі значенням с є дійсним числом.
- Якщо кут нахилу прямий y = k x + b тупий, то відповідає умовам π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.
Сікучою називають пряму, яка проходить через 2 точки функції f(x). Інакше висловлюючись, січна – це пряма, яка проводиться через будь-які дві точки графіка заданої функції.

На малюнку видно, що АВ є січною, а f (x) – чорна крива, α - червона дуга, що означає кут нахилу січної.
Коли кутовий коефіцієнт прямої дорівнює тангенсу кута нахилу, то видно, що тангенс з прямокутного трикутника АВС можна знайти по відношенню протилежного катета до прилеглого.
Визначення 4
Отримуємо формулу для знаходження січного виду:
k = t g α = B C A C = f (x B) - f x A x B - x A , де абсцисами точок А і є значення x A , x B , а f (x A) , f (x B) - це значення функції у цих точках.
Очевидно, що кутовий коефіцієнт січної визначено за допомогою рівності k = f (x B) - f (x A) x B - x A або k = f (x A) - f (x B) x A - x B , причому рівняння необхідно записати як y = f (x B) - f (x A) x B - x A · x - x A + f (x A) або
y = f (x A) - f (x B) x A - x B · x - x B + f (x B).
Секущая ділить графік візуально на 3 частини: зліва від точки А, від А до В, праворуч від В. На малюнку видно, що є три січні, які вважаються збігаються, тобто задаються за допомогою аналогічного рівняння.

За визначенням видно, що пряма та її січна у цьому випадку збігаються.
Січна може множино разів перетинати графік заданої функції. Якщо є рівняння виду у = 0 для січної, тоді кількість точок перетину з синусоїдою нескінченна.
Визначення 5
Дотична до графіка функції f (x) у точці x 0; f (x 0) називається пряма, що проходить через задану точку x 0; f (x 0) з наявністю відрізка, який має безліч значень х, близьких до x 0 .
Приклад 1
Розглянемо докладно на наведеному нижче прикладі. Тоді видно, що пряма, задана функцією y = x + 1 вважається дотичною до y = 2 x у точці з координатами (1 ; 2) . Для наочності необхідно розглянути графіки з наближеними до (1 ; 2) значеннями. Функція y = 2 x позначена чорним, синя лінія – дотична, червона точка – точка перетину.

Очевидно, що y = 2 x зливається із прямою у = х + 1 .
Для визначення дотичної слід розглянути поведінку дотичної АВ при нескінченному наближенні точки до точки А. Для наочності наведемо малюнок.

Сікуча АВ, позначена за допомогою синьої лінії, прагне положення самої дотичної, а кут нахилу секущої α почне прагнути до кута нахилу самої дотичної α x .
Визначення 6
Стосовною графіку функції y = f (x) у точці А вважається граничне положення січучої АВ при прагнучій до А, тобто B → A .
Тепер перейдемо до розгляду геометричного сенсу похідної функції у точці.
Перейдемо до розгляду сіючої АВ для функції f (x) , де А і В з координатами x 0 , f (x 0) і x 0 + ∆ x , f (x 0 + ∆ x) , а ∆ x позначаємо як збільшення аргументу . Тепер функція набуде вигляду ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . Для наочності наведемо приклад малюнок.

Розглянемо отриманий прямокутний трикутник АВС. Використовуємо визначення тангенсу для розв'язання, тобто отримаємо відношення ∆ y ∆ x = t g α . З визначення дотичної слідує, що lim ∆ x → 0 ∆ y ∆ x = t g α x . За правилом похідної в точці маємо, що похідну f (x) у точці x 0 називають межею відносин прирощення функції до прирощення аргументу, де ∆ x → 0 тоді позначимо як f (x 0) = lim ∆ x → 0 ∆ y ∆ x .
Звідси випливає, що f "(x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x , де k x позначають як кутовий коефіцієнт дотичної.
Тобто отримуємо, що f '(x) може існувати в точці x 0 причому як і дотична до заданого графіка функції в точці дотику дорівнює x 0 f 0 (x 0) де значення кутового коефіцієнта дотичної в точці дорівнює похідній в точці x 0 . Тоді отримуємо, що k x = f "(x0).
Геометричний зміст похідної функції у точці у цьому, що дається поняття існування щодо графіку у цій самій точці.
Щоб записати рівняння будь-якої прямої на площині, необхідно мати кутовий коефіцієнт з точкою, якою вона проходить. Його позначення приймається як x0 при перетині.
Рівняння дотичної до графіка функції y = f (x) у точці x 0 , f 0 (x 0) набуває вигляду y = f "(x 0) · x - x 0 + f (x 0).
Мається на увазі, що кінцевим значенням похідної f "(x 0) можна визначити положення дотичної, тобто вертикально за умови lim x → x 0 + 0 f "(x) = ∞ і lim x → x 0 - 0 f "(x ) = ∞ або відсутність зовсім за умови lim x → x 0 + 0 f "(x) ≠ lim x → x 0 - 0 f" (x).
Розташування дотичної залежить від значення її кутового коефіцієнта k x = f "(x 0). k x > 0 , меншає при k x< 0 .
Приклад 2
Зробити складання рівняння дотичної до графіка функції y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 у точці з координатами (1 ; 3) з визначенням кута нахилу.
Рішення
За умовою маємо, що функція визначається всім дійсних чисел. Отримуємо, що точка з координатами, заданими за умовою, (1 ; 3) є точкою дотику, тоді x 0 = - 1 f (x 0) = - 3 .
Необхідно знайти похідну у точці зі значенням -1. Отримуємо, що
y " = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = e x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = e x + 1 + x 2 - 6 - 3 3 y "(x 0) = y "(- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3
Значення f '(x) у точці дотику є кутовим коефіцієнтом дотичної, який дорівнює тангенсу нахилу.
Тоді k x = t g α x = y "(x 0) = 3 3
Звідси випливає, що x = r c t g 3 3 = π 6
Відповідь:рівняння дотичної набуває вигляду
y = f "(x 0) · x - x 0 + f (x 0) y = 3 3 (x + 1) - 3 y = 3 3 x - 9 - 3 3
Для наочності наведемо приклад у графічній ілюстрації.
Чорний колір використовується для графіка вихідної функції, синій колір - дотичне зображення, червона точка - точка дотику. Малюнок, розташований праворуч, показує у збільшеному вигляді.

Приклад 3
З'ясувати наявність існування щодо графіка заданої функції
y = 3 · x - 1 5 + 1 у точці з координатами (1 ; 1) . Скласти рівняння та визначити кут нахилу.
Рішення
За умовою маємо, що область визначення заданої функції вважається безліч усіх дійсних чисел.
Перейдемо до знаходження похідної
y " = 3 · x - 1 5 + 1 " = 3 · 1 5 · (x - 1) 1 5 - 1 = 3 5 · 1 (x - 1) 4 5
Якщо x 0 = 1 тоді f '(x) не визначена, але межі записуються як lim x → 1 + 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (+ 0) 4 5 = 3 5 · 1 + 0 = + ∞ і lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , що означає існування вертикальної дотичної в точці (1; 1) .
Відповідь:рівняння набуде вигляду х = 1 , де кут нахилу дорівнюватиме π 2 .
Для наочності зобразимо графічно.

Приклад 4
Знайти точки графіка функції y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2 де
- Стосовна не існує;
- Дотична розташовується паралельно о х;
- Дотична паралельна прямий y = 8 5 x + 4 .
Рішення
Необхідно звернути увагу до область визначення. За умовою маємо, що функція визначена на багатьох дійсних чисел. Розкриваємо модуль і розв'язуємо систему з проміжками x ∈ - ∞; 2 і [-2; + ∞). Отримуємо, що
y = -1 15 x 3 + 18 x 2 + 105 x + 176, x ∈ - ∞; - 2 1 15 x 3 - 6 x 2 + 9 x + 12, x ∈ [- 2; + ∞)
Потрібно продиференціювати функцію. Маємо, що
y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 ", x ∈ [- 2; + ∞) ⇔ y" = - 1 5 (x 2 + 12 x + 35), x ∈ - ∞; - 2 1 5 x 2 - 4 x + 3, x ∈ [-2; + ∞)
Коли х = - 2 тоді похідна не існує, тому що односторонні межі не рівні в цій точці:
lim x → - 2 - 0 y "(x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (-2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y "(x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3
Обчислюємо значення функції в точці х = - 2 де отримуємо, що
- y(-2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2 , тобто дотична в точці (- 2 ; - 2) не існуватиме.
- Дотична паралельна о х, коли кутовий коефіцієнт дорівнює нулю. Тоді k x = t g α x = f "(x 0). Тобто необхідно знайти значення таких х, коли похідна функції перетворює її в нуль. Тобто значення f '(x) і будуть точками дотику, де дотична є паралельною о х .
Коли x ∈ - ∞; - 2 , Тоді - 15 (x 2 + 12 x + 35) = 0, а при x ∈ (- 2 ; + ∞) отримуємо 1 5 (x 2 - 4 x + 3) = 0 .
1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 · 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2; + ∞
Обчислюємо відповідні значення функції
y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 · 1 2 - 16 5 · 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 · 3 2 - 16 5 · 3 - 26 5 + 3 3 + 2 = 4 3
Звідси - 5; 8 5 -4; 4 3, 1; 8 5, 3; 4 3 вважаються точками графіка функції, що шукаються.
Розглянемо графічне зображення рішення.

Чорна лінія – графік функції, червоні крапки – точки торкання.
- Коли прямі розташовуються паралельно, кутові коефіцієнти рівні. Тоді необхідно зайнятися пошуком точок графіка функції, де кутовий коефіцієнт дорівнюватиме значення 8 5 . Для цього потрібно розв'язати рівняння виду y" (x) = 8 5 . Тоді, якщо x ∈ - ∞ ; - 2; + ∞) , Тоді 15 (x 2 - 4 x + 3) = 8 5 .
Перше рівняння немає коренів, оскільки дискримінант менше нуля. Запишемо, що
1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 · 43 = - 28< 0
Інше рівняння має два дійсні корені, тоді
1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2; + ∞
Перейдемо до знаходження значень функції. Отримуємо, що
y 1 = y (-1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 · 5 2 - 16 5 · 5 - 26 5 + 3 5 + 2 = 8 3
Крапки зі значеннями - 1; 4 15, 5; 8 3 є точками, в яких дотичні паралельні до прямої y = 8 5 x + 4 .
Відповідь:чорна лінія - графік функції, червона лінія - графік y = 8 5 x + 4, синя лінія - дотичні в точках - 1; 4 15, 5; 8 3 .

Можливе існування нескінченної кількості дотичних до заданих функцій.
Приклад 5
Написати рівняння всіх дотичних функцій y = 3 cos 3 2 x - π 4 - 1 3 , які розташовуються перпендикулярно до прямої y = - 2 x + 1 2 .
Рішення
Для складання рівняння дотичної необхідно знайти коефіцієнт та координати точки дотику, виходячи з умови перпендикулярності прямих. Визначення звучить так: добуток кутових коефіцієнтів, які перпендикулярні до прямого, дорівнює - 1 , тобто записується як k x · k ⊥ = - 1 . З умови маємо, що кутовий коефіцієнт розташовується перпендикулярно до прямої і дорівнює k ⊥ = - 2 , тоді k x = - 1 k ⊥ = - 1 - 2 = 1 2 .
Тепер потрібно знайти координати точок торкання. Потрібно знайти х, після чого його значення для заданої функції. Зазначимо, що з геометричного сенсу похідної у точці
x 0 отримуємо, що k x = y "(x 0). З цієї рівності знайдемо значення х для точок дотику.
Отримуємо, що
y" (x 0) = 3 cos 3 2 x 0 - π 4 - 1 3 " = 3 · - sin 3 2 x 0 - π 4 · 3 2 x 0 - π 4 " = = - 3 · sin 3 2 x 0 - π 4 · 3 2 = - 9 2 · sin 3 2 x 0 - π 4 ⇒ k x = y "(x 0) ⇔ - 9 2 · sin 3 2 x 0 - π 4 = 1 2 ⇒ sin 3 2 x 0 - π 4 = - 1 9
Це тригонометричне рівняння буде використано для обчислення ординат точок торкання.
3 2 x 0 - ?
3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk або 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk
x 0 = 2 3 ?
Z – безліч цілих чисел.
Знайдено х точок торкання. Тепер необхідно перейти до пошуку значень у:
y 0 = 3 cos 3 2 x 0 - π 4 - 1 3
y 0 = 3 · 1 - sin 2 3 2 x 0 - π 4 - 1 3 або y 0 = 3 · - 1 - sin 2 3 2 x 0 - π 4 - 1 3
y 0 = 3 · 1 - - 1 9 2 - 1 3 або y 0 = 3 · - 1 - - 1 9 2 - 1 3
y 0 = 4 5 - 1 3 або y 0 = - 4 5 + 1 3
Звідси одержуємо, що 2 3 π 4 - a r c sin 1 9 + 2 πk; 4 5 - 1 3 , 2 3 5 π 4 + a rc sin 1 9 + 2 πk ; - 4 5 + 13 є точками торкання.
Відповідь:необхідні рівняння запишуться як
y = 1 2 x - 2 3 ? , k ∈ Z
Для наочного зображення розглянемо функцію та дотичну на координатній прямій.
Малюнок показує, що розташування функції йде на проміжку [- 10; 10 ] , де чорна пряма – графік функції, сині лінії – дотичні, які розташовуються перпендикулярно до заданої прямої виду y = - 2 x + 1 2 . Червоні крапки – це торкання.

Канонічні рівняння кривих 2 порядку є однозначними функціями. Рівняння дотичних їм складаються за відомими схемами.
Стосовно кола
Для завдання кола з центром у точці x c e n t e r ; y ce n t e r і радіусом R застосовується формула x - x ce n t e r 2 + y - y ce n t e r 2 = R 2 .
Ця рівність може бути записана як об'єднання двох функцій:
y = R 2 - x - x ce n t e r 2 + y ce n t e r y = - R 2 - x - x ce n t e r 2 + y ce n t e r
Перша функція розташовується вгорі, а друга внизу, як показано малюнку.

Для складання рівняння кола в точці x 0; y 0 , яка розташовується у верхньому або нижньому півкола, слід знайти рівняння графіка функції виду y = R 2 - x - x c e n t e r 2 + y c e n t e r або y = - R 2 - x - x c e n t e r t + t e n t .
Коли в точках x c e n t e r; y c e n t e r + R і x ce n t e r ; y c e n t e r - R дотичні можуть бути задані рівняннями y = y ce n t e r + R і y = y ce n t e r - R , а в точках x ce n t e r + R ; y c e n t e r і
x c e n t e r - R ; y c e n t e r будуть паралельними о у, тоді отримаємо рівняння виду x = x c e n t e r + R і x = x c e n t e r - R .

Стосовна до еліпса
Коли еліпс має центр у точці x c e n t e r; y c e n t e r з півосями a і b , тоді він може бути заданий за допомогою рівняння x - x ce n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1 .
Еліпс і коло може бути позначатися з допомогою об'єднання двох функцій, саме: верхнього і нижнього полуэллипса. Тоді отримуємо, що
y = b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a · a 2 - (x - x ce n t e r) 2 + y c en t e r

Якщо дотичні розташовуються на вершинах еліпса, тоді вони паралельні о х або у. Нижче для наочності розглянемо рисунок.

Приклад 6
Написати рівняння щодо до еліпсу x - 3 2 4 + y - 5 2 25 = 1 у точках зі значеннями x рівного х = 2 .
Рішення
Необхідно знайти точки дотику, які відповідають значенню х = 2. Виробляємо підстановку в наявне рівняння еліпса і отримуємо, що
x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 · 25 ⇒ y = ± 5 3 2 + 5
Тоді 2; 5 3 2 + 5 та 2 ; - 5 3 2 + 5 є точками торкання, які належать верхньому та нижньому напівеліпсу.
Перейдемо до знаходження та вирішення рівняння еліпса щодо y. Отримаємо, що
x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 · 1 - x - 3 2 4 y - 5 = ± 5 · 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2
Очевидно, що верхній напівеліпс задається за допомогою функції виду y = 5 + 5 2 4 - x - 3 2 а нижній y = 5 - 5 2 4 - x - 3 2 .
Застосуємо стандартний алгоритм у тому, щоб скласти рівняння дотичної до графіку функції у точці. Запишемо, що рівняння для першої дотичної у точці 2; 5 3 2 + 5 матиме вигляд
y " = 5 + 5 2 4 - x - 3 2 " = 5 2 · 1 2 4 - (x - 3) 2 · 4 - (x - 3) 2 " = = - 5 2 · x - 3 4 - ( x - 3) 2 ⇒ y "(x 0) = y "(2) = - 5 2 · 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y "(x 0) · x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5
Отримуємо, що рівняння другої дотичної зі значенням у точці
2; - 5 3 2 + 5 набуває вигляду
y " = 5 - 5 2 4 - (x - 3) 2 " = - 5 2 · 1 2 4 - (x - 3) 2 · 4 - (x - 3) 2 " = = 5 2 · x - 3 4 - (x - 3) 2 ⇒ y "(x 0) = y "(2) = 5 2 · 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y "(x 0) · x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5
Графічно дотичні позначаються так:

Щодо гіперболи
Коли гіпербола має центр у точці x c e n t e r; y c e n t e r і вершини x c e n t e r + α; y c e n t e r і x c e n t e r - α; y ce n t e r , має місце завдання нерівності x - x ce n t e r 2 α 2 - y - y ce n t e r 2 b 2 = 1 , якщо з вершинами x ce n t e r ; y c e n t e r + b і x c e n t e r ; y c e n t e r - b , тоді задається за допомогою нерівності x - x ce n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

Гіпербола може бути представлена у вигляді двох об'єднаних функцій виду
y = b a · (x - x ce n t e r) 2 - a 2 + y ce n t e r y = - ba · (x - x ce n t e r) 2 - a 2 + y ce n t e r або y = b a · (x - x ce e n e = - b a · (x - x ce n t e r) 2 + a 2 + y ce n t e r

У першому випадку маємо, що дотичні паралельні о у, а в другому паралельні о х.
Звідси випливає, що для того, щоб знайти рівняння до гіперболи, необхідно з'ясувати, якій функції належить точка дотику. Щоб визначити це, необхідно зробити підстановку рівняння і перевірити їх на тотожність.
Приклад 7
Скласти рівняння дотичної до гіперболи x - 3 2 4 - y + 3 2 9 = 1 у точці 7; - 3 3 - 3 .
Рішення
Необхідно перетворити запис рішення перебування гіперболи за допомогою двох функцій. Отримаємо, що
x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 · x - 3 2 4 - 1 ⇒ y + 3 = 3 2 · x - 3 2 - 4 і л і y + 3 = - 3 2 · x - 3 2 - 4 ⇒ y = 3 2 · x - 3 2 - 4 - 3 y = - 3 2 · x - 3 2 - 4 - 3
Необхідно виявити, якої функції належить задана точка з координатами 7 ; - 3 3 - 3 .
Очевидно, що для перевірки першої функції необхідно y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3 тоді точка графіку не належить, так як рівність не виконується.
Для другої функції маємо, що y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3 , отже, точка належить заданому графіку. Звідси слід знайти кутовий коефіцієнт.
Отримуємо, що
y " = - 3 2 · (x - 3) 2 - 4 - 3 " = - 3 2 · x - 3 (x - 3) 2 - 4 ⇒ k x = y "(x 0) = - 3 2 · x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 · 7 - 3 7 - 3 2 - 4 = - 3
Відповідь:рівняння дотичної можна уявити як
y = - 3 · x - 7 - 3 3 - 3 = - 3 · x + 4 3 - 3
Наочно зображується так:

Щодо параболи
Щоб скласти рівняння дотичної до параболи y = a x 2 + b x + c у точці x 0 , y (x 0) , необхідно використовувати стандартний алгоритм, тоді рівняння набуде вигляду y = y "(x 0) · x - x 0 + y ( x 0) . Така дотична у вершині паралельна про х.
Слід задати параболу x = a y 2 + b y + c як поєднання двох функцій. Тому потрібно розв'язати рівняння щодо у. Отримуємо, що
x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a
Графічно зобразимо як:

Для з'ясування належності точки x 0 , y (x 0) функції ніжно діяти за стандартним алгоритмом. Така дотична буде паралельна щодо відносно параболи.
Приклад 8
Написати рівняння дотичної до графіка x - 2 y 2 - 5 y + 3 коли маємо кут нахилу дотичної 150 ° .
Рішення
Починаємо рішення з представлення параболи як дві функції. Отримаємо, що
2 y 2 - 5 y + 3 - x = 0 D = (-5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4
Значення кутового коефіцієнта дорівнює значенню похідної у точці x 0 цієї функції та дорівнює тангенсу кута нахилу.
Отримуємо:
k x = y "(x 0) = t g α x = t g 150 ° = - 1 3
Звідси визначимо значення x точок торкання.
Перша функція запишеться як
y " = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3
Очевидно, що дійсних коренів немає, оскільки набули негативного значення. Робимо висновок, що дотичної з кутом 150° для такої функції не існує.
Друга функція запишеться як
y " = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 · 23 4 - 4 = - 5 + 3 4
Маємо, що точки дотику - 23 4; - 5 + 3 4 .
Відповідь:рівняння дотичної набуває вигляду
y = - 1 3 · x - 23 4 + - 5 + 3 4
Графічно зобразимо це так:

Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl+Enter
Визначення. Дотична до кола - це пряма на площині, що має рівно одну загальну точку з коло.
Ось кілька прикладів:
 Коло з центром Oстосується прямої lу точці A
Коло з центром Oстосується прямої lу точці A
 З будь-якої точки Mза межами кола можна провести рівно дві дотичні
З будь-якої точки Mза межами кола можна провести рівно дві дотичні  Відмінність між дотичною l, січеною BCі прямий m, що не має спільних точок з колом
Відмінність між дотичною l, січеною BCі прямий m, що не має спільних точок з колом На цьому можна було б закінчити, проте практика показує, що недостатньо просто зазубрити визначення — треба навчитися бачити дотичні на кресленнях, знати їхні властивості та до того ж добре попрактикуватися у застосуванні цих властивостей, вирішуючи реальні завдання. Усім цим усім ми сьогодні й займемося.
Основні властивості дотичних
Для того, щоб вирішувати будь-які завдання, потрібно знати чотири ключові властивості. Два з них описані в будь-якому довіднику/підручнику, а ось останні два – про них якось забувають, а дарма.
1. Відрізки дотичних, проведених із однієї точки, рівні
Трохи вище ми вже говорили про дві дотичні, проведені з однієї точки M. Так от:
Відрізки дотичних до кола, проведених з однієї точки, рівні.
 Відрізки AMі BMрівні
Відрізки AMі BMрівні 2. Дотична перпендикулярна радіусу, проведеному в точку торкання
Ще раз подивимося на картинку, наведену вище. Проведемо радіуси OAі OB, після чого виявимо, що кути OAMі OBM- Прямі.
Радіус, проведений у точку торкання, перпендикулярний дотичній.
Цей факт можна використовувати без доказів у будь-якій задачі:
 Радіуси, проведені в точку торкання, перпендикулярні дотичним.
Радіуси, проведені в точку торкання, перпендикулярні дотичним. До речі, зауважте: якщо провести відрізок OM, то ми отримаємо два рівні трикутники: OAMі OBM.
3. Співвідношення між дотичною та січною
А ось це вже факт серйозніший, і більшість школярів його не знають. Розглянемо дотичну та січну, які проходять через одну і ту ж загальну точку M. Звичайно, січна дасть нам два відрізки: всередині кола (відрізок BC- його ще називають хордою) і зовні (його так і називають - зовнішня частина MC).
Добуток всієї сіючої її зовнішню частину дорівнює квадрату відрізка дотичної
 Співвідношення між січною та дотичною
Співвідношення між січною та дотичною 4. Кут між дотичною та хордою
Ще більш просунутий факт, який часто використовується для вирішення складних завдань. Дуже рекомендую взяти на озброєння.
Кут між дотичною і хордою дорівнює вписаному кутку, що спирається на цю хорду.

Звідки береться крапка B? У реальних завданнях вона зазвичай «спливає» десь за умови. Тому важливо навчитися розпізнавати цю конфігурацію на кресленнях.
 Іноді таки стосується:)
Іноді таки стосується:) Доведення
Якщо хорда є діаметром, теорема очевидна.
На малюнку 287 зображено коло з центром O , M - точка перетину діаметра CD та хорди AB , CD ⊥ AB . Потрібно довести, що AM = MB .
Проведемо радіуси OA та OB. У рівнобедреному трикутнику AOB (OA = OB) відрізок OM - висота, а значить, і медіана, тобто AM = MB.
Теорема 20.2
Діаметр кола, що ділить хорду, відмінну від діаметра, навпіл, перпендикулярний цій хорді.
Доведіть цю теорему самостійно. Подумайте, чи буде вірним це твердження, якщо хорда є діаметром.
На малюнку 288 показані всі можливі випадки взаємного розташування прямої та кола. На малюнку 288, які мають спільних точок, малюнку 288, б - мають дві загальні точки, малюнку 288, в - одну.
|
Мал. 288 |
||
|
|
|
|
Визначення
Пряму, що має з колом лише одну загальну точку, називають дотичною до кола.
Дотична до кола має лише одну загальну точку з колом, обмеженим цим колом. На малюнку 288, пряма a - дотична до кола з центром у точці O , A - точка торкання.
Якщо відрізок (промінь) належить дотичному до кола і має із цим колом загальну точку, то кажуть, що відрізок (промінь) стосується кола. Наприклад, на малюнку 289 зображено відрізок AB , який стосується кола в точці С .
Теорема 20.3
(Властивість дотичної)
Дотична до кола перпендикулярна радіусу, проведеному в точку торкання.
Доведення
На малюнку 290 зображено коло з центром O , A - точка торкання прямої a та кола. Потрібно довести, що OA ⊥ a .
|
Мал. 289 |
Мал. 290 |
Мал. 291 |
|
|
|
|
Припустимо, що це не так, т. Е. Відрізок OA - похила до прямої a . Тоді з точки O опустимо перпендикуляр OM на пряму a (рис. 291). Оскільки точка A - єдина загальна точка прямої a і кола з центром O точка M не належить цьому колу. Звідси OM = MB + OB , де точка B - точка перетину кола та перпендикуляра OM . Відрізки OA та OB рівні як радіуси кола. Отже, OM > OA. Отримали протиріччя: перпендикуляр OM більший за похилу OA . Отже, OA ⊥ a .
Теорема 20.4
(Ознака дотичної до кола)
Якщо пряма, яка проходить через точку кола, перпендикулярна радіусу, проведеному в цю точку, то ця пряма є дотичною до цього кола.
Доведення
|
Мал. 292 |
|
|
На малюнку 290 зображено коло з центром у точці O , відрізок OA - її радіус, точка A належить прямій a , OA ⊥ a . Доведемо, що пряма a - дотична до кола.
Нехай пряма a не є дотичною, а має ще одну загальну точку B з колом (рис. 292). Тоді ∆ AOB – рівнобедрений (OA = OB як радіуси). Звідси ∠ OBA = ∠ OAB = 90 °. Отримуємо протиріччя: у трикутнику AOB є два прямі кути. Отже, пряма a є дотичною до кола.
Слідство
Якщо відстань від центру кола до деякої прямої дорівнює радіусу кола, то ця пряма є дотичною до цього кола.
|
Мал. 293 |
|
|
Доведіть це слідство самостійно.
Завдання. Доведіть, що якщо через цю точку до кола проведено дві дотичні, то відрізки дотичних, що з'єднують цю точку з точками дотику, дорівнюють.
Рішення. На малюнку 293 зображено коло з центром O. Прямі AB та AC - дотичні, точки B та C - точки дотику. Потрібно довести, що AB = AC .
Проведемо радіуси OB і OC у торканні точки. За якістю щодо OB ⊥ AB і OC ⊥ AC . У прямокутних трикутниках AOB та AOC катети OB та OC рівні як радіуси одного кола, AO – загальна гіпотенуза. Отже, трикутники AOB і AOC рівні з гіпотенузи та катету. Звідси AB = AC.

- Як ділить хорду діаметр перпендикулярний їй?
- Чому дорівнює кут між хордою, відмінною від діаметра, і діаметром, що ділить цю хорду навпіл?
- Опишіть усі можливі випадки взаємного розташування прямого та кола.
- Яку пряму називають дотичною до кола?
- Якою властивістю має радіус, проведений у точку торкання прямого та кола?
- Сформулюйте ознаку щодо кола.
- Яку властивість мають дотичні, проведені до кола через одну точку?

Практичні завдання

507. Накресліть коло з центром O, проведіть хорду AB. Користуючись косинцем, розділіть цю хорду навпіл.
508. Накресліть коло з центром O, проведіть хорду CD. Користуючись лінійкою зі шкалою, проведіть діаметр перпендикулярний хорді CD .
509. Накресліть коло, позначте на ньому точки A та B. Користуючись лінійкою та косинцем, проведіть прямі, які стосуються кола в точках A та B .
510. Проведіть пряму a і позначте на ній точку M. Користуючись косинцем, лінійкою та циркулем, проведіть коло радіуса 3 см, яке стосується прямої a у точці M. Скільки таких кіл можна провести?

Вправи
511. На малюнку 294 точка O - центр кола, діаметр CD перпендикулярний хорді AB . Доведіть, що ∠ AOD = ∠ BOD .
512. Доведіть, що рівні хорди кола рівновіддалені від її центру.
513. Доведіть, що й хорди кола рівновіддалені від її центру, всі вони рівні.
514. Чи вірно, що пряма, перпендикулярна радіусу кола, стосується цього кола?
515. Пряма CD стосується кола з центром O у точці A , відрізок AB - хорда кола, ∠ BAD = 35° (рис. 295). Знайдіть ∠ AOB.
516. Пряма CD стосується кола з центром O у точці A , відрізок AB - хорда кола, ∠ AOB = 80° (див. рис. 295). Знайдіть ∠BAC.
517. Дано коло, діаметр якого дорівнює 6 см. Пряма a віддалена від її центру на: 1) 2 см; 2) 3 см; 3) 6 см. У якому разі пряма a є дотичною до кола?
518. У трикутнику ABC відомо, що ∠C = 90°. Доведіть, що:
1) пряма BC є дотичною до кола з центром A, що проходить через точку C;
2) пряма AB не є дотичною до кола з центром C, що проходить через точку A.

519. Доведіть, що діаметр кола більший за будь-яку хорду, відмінну від діаметра.
520. В колі з центром O через середину радіусу провели хорду AB перпендикулярну йому. Доведіть, що AOB = 120°.
521. Знайдіть кут між радіусами OA та OB кола, якщо відстань від центру O кола до хорди AB у 2 рази менша: 1) довжини хорди AB ; 2) радіуса кола.
522. В колі провели діаметр AB та хорди AC і CD так, що AC = 12 см, ∠ BAC = 30°, AB ⊥ CD . Знайдіть довжину хорди CD.
523. Через точку M до кола з центром O провели дотичні MA та MB , A та B - точки дотику, ∠ OAB = 20°. Знайдіть ∠ AMB.
524. Через кінці хорди AB , що дорівнює радіусу кола, провели дві дотичні, що перетинаються в точці C .Знайдіть ∠ ACB .
525. Через точку З кола з центром O провели дотичну до цього кола, AB - діаметр кола. З точки A на дотику опущений перпендикуляр AD. Доведіть, що промінь AC - бісектриса кута BAD .
526. Пряма AC стосується кола з центром O у точці A (рис. 296). Доведіть, що кут BAC у 2 рази менший від кута AOB .
|
Мал. 294 |
Мал. 295 |
Мал. 296 |
|
|
|
|
527. Відрізки AB і BC - відповідно хорда та діаметр кола, ∠ ABC = 30°. Через точку A провели дотичну до кола, що перетинає пряму BC у точці D. Доведіть, що ∆ ABD - рівнобедрений.
528. Відомо, що діаметр AB ділить хорду CD навпіл, але не перпендикулярний їй. Доведіть, що CD – також діаметр.

529. Знайдіть геометричне місце центрів кіл, які стосуються даної прямої в даній точці.
530. Знайдіть геометричне місце центрів кіл, які стосуються обох сторін даного кута.
531. Знайдіть геометричне місце центрів кіл, які стосуються даної прямої.
532. Прямі, що стосуються кола з центром O в точках A і B перетинаються в точці K , ∠ AKB = 120°. Доведіть, що AK + BK = OK.
533. Окружність стосується сторони AB трикутника ABC у точці M і стосується продовження двох інших сторін. Доведіть, що сума довжин відрізків BC та BM дорівнює половині периметра трикутника ABC .
|
Мал. 297 |
|
|
534. Через точку C проведено дотичні AC та BC до кола, A та B - точки дотику (рис. 297). На колі взяли довільну точку M , що лежить в одній напівплощині з точкою C щодо прямої AB і через неї провели дотичну до кола, що перетинає прямі AC і BC в точках D і E відповідно. Доведіть, що периметр трикутника DEC залежить від вибору точки M .
Вправи для повторення
535. Доведіть, що середина M відрізка, кінці якого належать двом паралельним прямим, є серединою будь-якого відрізка, що проходить через точку M та кінці якого належать цим прямим.
536. Відрізки AB та CD лежать на одній прямій і мають загальну середину. Точку M вибрали так, що трикутник AMB - рівнобедрений з основою AB. Доведіть, що ∆ CMD також є рівнобедреним із основою CD .
537. На стороні MK трикутника MPK відзначили точки E і F так, що точка E лежить між точками M і F, ME = EP, PF = FK. Знайдіть кут M , якщо ∠ EPF = 92°, ∠ K = 26°.
538. У гострокутному трикутнику ABC проведено бісектрису BM, з точки M на бік BC опущено перпендикуляр MK, ∠ABM = ∠KMC. Доведіть, що трикутник ABC – рівнобедрений.
Спостерігайте, малюйте, конструюйте, фантазуйте
539. Встановіть закономірність форм фігур, зображених на малюнку 298. Яку фігуру треба поставити такою?
|
Мал. 298 |
Поняття щодо кола
Окружність має три можливі взаємні розташування відносно прямої:
Якщо відстань від центру кола до прямої менша за радіус, то пряма має дві точки перетину з колом.
Якщо відстань від центру кола до прямої дорівнює радіусу, то пряма має дві точки перетину з коло.
Якщо відстань від центру кола до прямої більша за радіус, то пряма має дві точки перетину з колом.
Введемо тепер поняття щодо прямої до кола.
Визначення 1
Дотичним до кола називається пряма, яка має з нею одну точку перетину.
Загальна точка кола та дотичної називається точкою дотику (рис 1).
Малюнок 1. Стосовно кола
Теореми, пов'язані з поняттям дотичного до кола
Теорема 1
Теорема про властивість дотичної: дотична до кола перпендикулярна до радіуса, проведеного в точку дотику.
Доведення.
Розглянемо коло із центром $O$. Проведемо в точці $A$ щодо $a$. $OA=r$ (Мал. 2).
Доведемо, що $a\bot r$
Будемо доводити теорему методом «від неприємного». Припустимо, що дотична $a$ не перпендикулярна радіусу кола.

Рисунок 2. Ілюстрація теореми 1
Тобто $OA$ - похильна до дотичної. Так як перпендикуляр до прямої $ a $ завжди менше похилої до цієї ж прямої, то відстань від центру кола до прямої менше радіусу. Як відомо, у разі пряма має дві точки перетину з окружностью. Що суперечить визначенню дотичної.
Отже, дотична перпендикулярна до радіусу кола.
Теорему доведено.
Теорема 2
Зворотна теорема про властивість дотичної: Якщо пряма, яка проходить через кінець радіусу будь-якого кола перпендикулярна радіусу, то дана пряма є дотичною до цього кола.
Доведення.
За умовою завдання маємо, що радіус - перпендикуляр, проведений із центру кола до цієї прямої. Отже, відстань від центру кола до прямої дорівнює довжині радіусу. Як ми знаємо, у цьому випадку коло має лише одну точку перетину з цієї прямої. За визначенням 1 і отримуємо, що ця пряма - дотична до кола.
Теорему доведено.
Теорема 3
Відрізки дотичних до кола, проведені з однієї точки, рівні і становлять рівні кути з прямої, що проходить через цю точку та центр кола.
Доведення.
Нехай дане коло з центром у точці $O$. З точки $A$ (що лежить усі кола) проведено дві різні дотичні. З точки дотику відповідно $B$ і $C$ (Рис. 3).
Доведемо, що $angle BAO=angle CAO$ і що $AB=AC$.

Рисунок 3. Ілюстрація теореми 3
По теоремі 1, маємо:
Отже, трикутники $ABO$ і $ACO$ - прямокутні. Оскільки $OB=OC=r$, а гіпотенуза $OA$ -- загальна, ці трикутники рівні по гіпотенузі і катету.
Звідси і отримуємо, що $ angle BAO = angle CAO $ і $ AB = AC $.
Теорему доведено.
Приклад завдання поняття дотичної до кола
Приклад 1
Дано коло з центром в точці $ O $ і радіусом $ r = 3 см $. Стосовна $AC$ має точку дотику $C$. $AO=4\ см$. Знайти $AC$.
Рішення.
Зобразимо спочатку все малюнку (Рис. 4).

Малюнок 4.
Оскільки $AC$ дотична, а $OC$ радіус, те теоремі 1, отримуємо, что$\angle ACO=(90)^(()^\circ )$. Отримали, що трикутник $ACO$ - прямокутний, отже, за теоремою Піфагора, маємо:
\[(AC)^2=(AO)^2+r^2\] \[(AC)^2=16+9\] \[(AC)^2=25\] \












 Історія стародавнього китаю Доповідь, повідомлення Де жили давні люди китаю
Історія стародавнього китаю Доповідь, повідомлення Де жили давні люди китаю Уроки хімії Йодом змочимо ми рясно, щоб було все стерильно
Уроки хімії Йодом змочимо ми рясно, щоб було все стерильно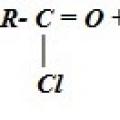 Хімічні властивості. Отримання. Одержання карбонових кислот Отримання карбонових кислот окисненням вуглеводнів
Хімічні властивості. Отримання. Одержання карбонових кислот Отримання карбонових кислот окисненням вуглеводнів